A Formally Reliable Cognitive Middleware for the Security of Industrial Control Systems

Abstract

In this paper, we present our results on the formal reliability analysis of the behavioral correctness of our cognitive middleware ARMET. The formally assured behavioral correctness of a software system is a fundamental prerequisite for the system’s security. Therefore, the goal of this study is to, first, formalize the behavioral semantics of the middleware and, second, to prove its behavioral correctness. In this study, we focus only on the core and critical component of the middleware: the execution monitor. The execution monitor identifies inconsistencies between runtime observations of an industrial control system (ICS) application and predictions of the specification of the application. As a starting point, we have defined the formal (denotational) semantics of the observations (produced by the application at run-time), and predictions (produced by the executable specification of the application). Then, based on the formal semantices, we have formalized the behavior of the execution monitor. Finally, based on the semantics, we have proved soundness (absence of false alarms) and completeness (detection of arbitrary attacks) to assure the behavioral correctness of the monitor.

1. Introduction

Defending industrial control systems (ICS) against cyber-attack requires us to be able to rapidly and accurately detect that an attack has occurred in order to, on one hand, assure the continuous operation of ICS and, on the other, to meet ICS real-time requirements. Today’s detection systems are woefully inadequate, suffering from both high false positive and false negative rates. There are two key reasons for this. First, the systems do not understand the complete behavior of the system they are protecting. The second is that they do not understand what an attacker is trying to achieve. Most systems that exhibit this behavior, in fact, are retrospective, that is they understand some surface signatures of previous attacks and attempt to recognize the same signature in current traffic. Furthermore, they are passive in character, they sit back and wait for something similar to what has already happened to reoccur. Attackers, of course, respond by varying their attacks, so as to avoid detection.

ARMET [1] is a representative of a new class of protection systems that employ a different, active form of perception, one that is informed both by knowledge of what the protected application is trying to do and by knowledge of how attackers think. It employs both bottom-up reasoning (going from sensors data to conclusions about what attacks might be in progress) and top-down reasoning (given a set of hypotheses about what attacks might be in progress, it focuses its attention to those events most likely to significantly help in discerning the ground truth).

Based on AWDRAT [2], ARMET is a general purpose middleware system that provides survivability to any kind of new and legacy software system and to ICS in particular. As shown in Figure 1, the run-time monitor (RSM) of ARMET checks consistency between the run-time behavior of the application implementation (AppImpl) and the specified behavior (AppSpec) of the system. If there is an attack, then the diagnostic engine identifies an attack (an illegal behavioral pattern) and the corresponding set of resources that were compromised during the attack. After identifying an attack, a larger system (e.g., AWDRAT) attempts to repair and then regenerate the compromised system into a safer state, to only allow fail-safe, if possible. The task of regeneration is based on the dependency-directed reasoning [3] engine of the system that contributes to self-organization and self-awareness. It does so by recording execution steps intrinsically, the states of the system and their corresponding justification (reason). The details on diagnosis and recovery are beyond the scope of this paper. Based on the execution monitor and the reasoning engine of ARMET, not only is the detection of known attacks possible but also the detection of unknown attacks and potential bugs in the application implementation is possible.

The RSM has been developed as prototype implementations in a general-purpose, computing environment (laptop) using a general-purpose functional programming environment (Lisp). In addition to the software’s ability to be easily ported to a wide range of systems, the software can be directly developed in any embedded OS and RTOS middleware environment, such as RTLinux, Windows CE, LynxOS, VxWorks, etc. The current trend toward sophisticated PLC and SCADA systems with advanced OS and middleware capabilities provides an appropriate environment for developing highly advanced software systems for control and management [4].

The rest of this paper is organized as follows: Section 2 presents the syntax and semantics of the specification language of ARMET, while Section 3 explains the syntax and semantics of the monitor. The proof of behavioral correctness (i.e., soundness and completeness) of the monitor is discussed in Section 4. Finally, we conclude in Section 5.

2. A Specification Language of ARMET

A specification language of ARMET allows the description of the behavior of ICS application implementation (AppImpl) based on a fairly high-level description written in a language of “Plan Calculus” [3], which is a decomposition of pre- and post-conditions and invariant for each computing component (module) of the system. The description can be considered as an executable specification of the system. The specification is a hierarchical nesting of a system’s components such that the input and output ports of each component are connected by data and control flow links of respective specifications. Furthermore, each component is specified with corresponding pre- and post-conditions. However, the specification also includes a variety of event specifications.

In detail, the behavioral specification (“AppSpec”—as shown in Figure 2) of an application implementation (“AppImpl”—as shown in Figure 3) is described at the following two logical levels:

• The control level describes the control structure of each of the component (e.g., sub-components, control flow and data flow links), which is:
  • Defined by the syntactic domain “StrModSeq”, while the control flow can further be elaborated with syntactic domain “SplModSeq”
• The behavior level describes the actual method’s behavioral specification of each of component, which is defined by the syntactic domain “BehModSeq”.

Furthermore, the registration of the observations is given by the syntactic domain “RegModSeq”, at the top of the above domains. All four of the aforementioned domains are the top-level syntactic domains of the specification. Our specification is hierarchical, i.e., it specifies the components of the implementations as hierarchical modules. In the following, we discuss the syntax of control and behavioral elements of the specification using the specification of a temperature control as an example, shown in Figure 2.

• The description of each component type consists of

  (a)

  Its interface, which is comprised of:

  • a list of inputs
  • a list of its outputs
  • a list of the resources it uses (e.g., files it reads, the code in memory that represents this component)
  • a list of sub-components required for the execution of the subject component
  • a list of events that represent entry into the component
  • a list of events that represent exit from the component
  • a list of events that are allowed to occur during any execution of this component
  • a set of conditional probabilities between the possible modes of the resources and the possible modes of the whole component
  • a list of known vulnerabilities occurred to the component

  (b)

  and a structural model that is a list of sub-components, some of which might be splits or joins of:

  • data-flows between linking ports of the sub-components (outputs of one to inputs of another)
  • control-flow links between cases of a branch and a component that will be enabled if that branch is taken.

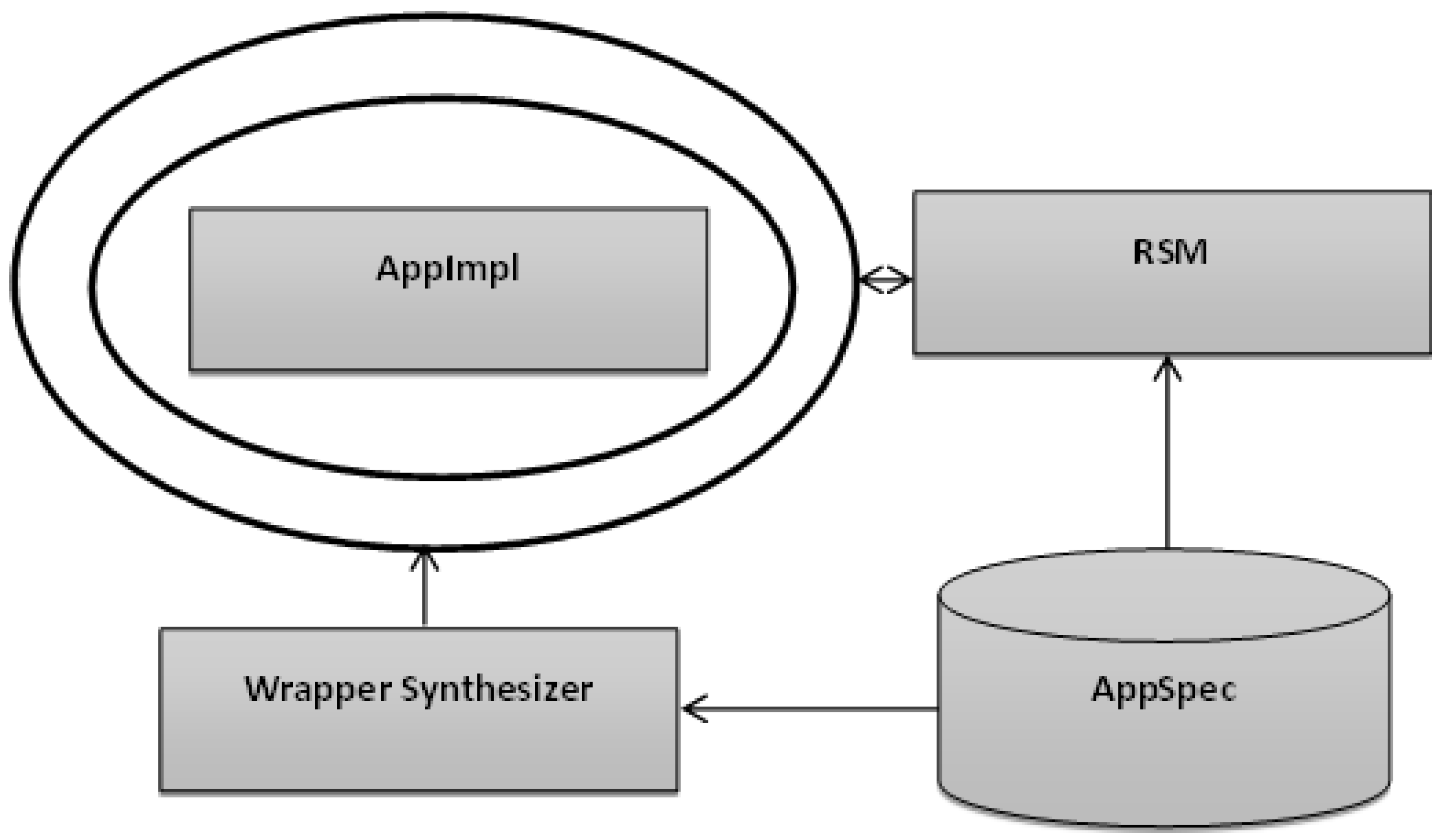
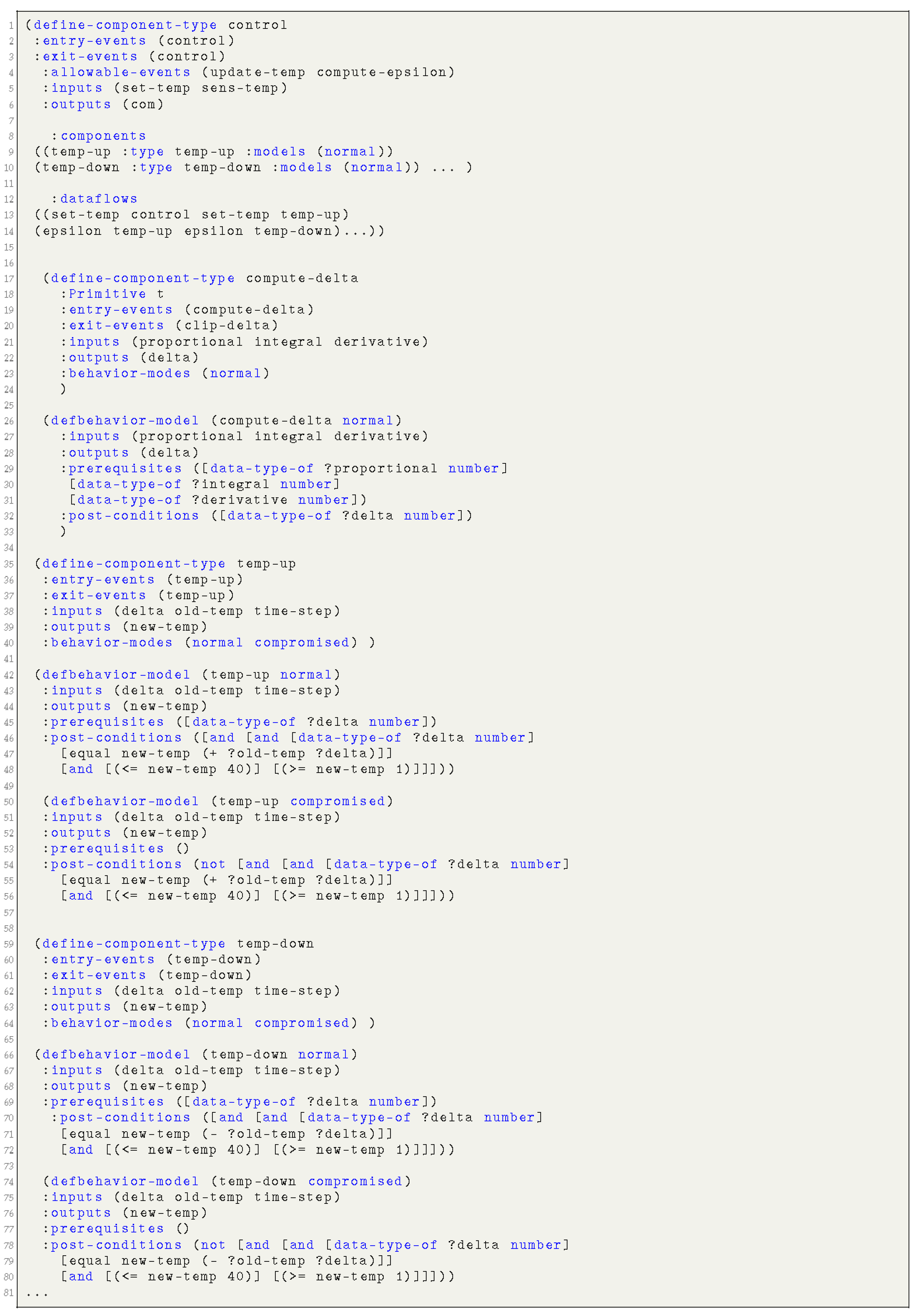
  The description of the component type is represented by the syntactical domain “StrMod”, which is defined as follows:

  StrMod ::= define-ensemble CompName

  :entry-events :auto| (EvntSeq)

  :exit-events (EvntSeq)

  :allowable-events (EvntSeq)

  :inputs (ObjNameSeq)

  :outputs (ObjNameSeq)

  :components (CompSeq)

  :controlflows (CtrlFlowSeq)

  :splits (SpltCFSeq)

  :joins (JoinCFSeq)

  :dataflows (DataFlowSeq)

  :resources (ResSeq)

  :resource-mapping (ResMapSeq)

  :model-mappings (ModMapSeq)

  :vulnerabilities (VulnrabltySeq)

  Example 1.

  For instance, a room temperature controller: control, periodically receives the current temperature value (sens-temp) from a sensor. The controller may also receive a user command (set-temp) to set (either increase or decrease) the current temperature of the room. Based on the received user command, the controller either raises the temperature through the sub-component temp-up or reduces the temperature through the sub-component temp-down, after computing the error compute-epsilon of the given command as shown in Figure 2. Furthermore, the controller issues a command as an output (com), which contains an updated temperature value. Figure 3 reflects the corresponding implementation parts of the controller.
• The behavioral specification of a component (a component type may have one normal behavioral specification and many abnormal behavioral specifications, each one representing some failure mode) consists of:
  • inputs and outputs
  • preconditions on the inputs (logical expressions involving one or more of the inputs)
  • postconditions (logical expressions involving one or more of the outputs and the inputs)
  • allowable events during the execution in this mode
  The behavioral specification of a component is represented by a corresponding syntactical domain “BehMod”, as follows:

  BehMod ::= defbehavior-model (CompName normal | compromised)

  :inputs (ObjNameSeq${}_1$)

  :outputs (ObjNameSeq${}_2$)

  :allowable-events (EvntSeq)

  :prerequisites (BehCondSeq${}_1$)

  :post-conditions (BehCondSeq${}_2$)

  Example 2.

  For instance, in our temperature control example, the normal and compromised behavior of a controller component temp-up is modeled in Figure 2. The normal behavior of a temperature raising component temp-up describes the: (i) input condition prerequisites, i.e., the component receives a valid input new-temp; and (ii) output conditions post-conditions, i.e., the new computed temperature new-temp is equal to the sum of the current temperature old-temp and the computed delta (error). The computed temperature respects the temperature range (1-40). Similarly, the compromised behavior of the component illustrates the corresponding input and output conditions. Figure 3 reflects the corresponding implementation parts of the temp-up component.

The complete syntactic details of the specification language are discussed in [5].

Based on the core idea of Lamport [6], we have defined the semantics of the specification as a state relationship to achieve the desired insight of the program’s behavior. This does so by relating pre- and post-states [7]. For simplicity, we chose to discuss semantics of the behavioral domain “BehMod”. The denotational semantics of the specification language is based on denotational algebras [8]. We define the result of semantic valuation function as a predicate. The behavioral relation (BehRel) is defined as a predicate over an environment, a pre-state, and a post-state. The corresponding relation is defined as:

BehRel := ℙ(Environment × State × State_⊥)

The valuation function for the abstract syntax domain “BehMod” values is defined as:

⟦BehMod⟧: Environment → BehRel

Semantically, normal and compromised behavioral models result in modifying the corresponding elements of the environment value “Component” as defined below:

⟦BehMod⟧(e)(e’, s, s’) ⇔

∀ e${}_1$∈ Environment, nseq ∈ EvntNameSeq, eseq ∈ ObsEvent*, inseq, outseq ∈ Value${}^{*}$:

⟦ObjNameSeq${}_1$⟧(e)(inState${}_{\perp }$(s), inseq) ∧ ⟦BehCondSeq${}_1$⟧(e) (inState${}_{\perp }$(s)) ∧

⟦EvntSeq⟧(e) (e${}_1$, s, s’, nseq, eseq)

⟦ObjNameSeq${}_2$⟧(e${}_1$)(s’, outseq) ∧ ⟦BehCondSeq${}_2$⟧(e${}_1$) (s’) ∧

∃ c ∈ Component: ⟦CompName⟧(e${}_1$)(inValue(c)) ∧

IF eqMode(inState${}_{\perp }$(s’), “normal”) THEN

LET sbeh = c[1], nbeh = <inseq, outseq, s, s’>, cbeh = c[3] IN

e’ = push(e${}_1$ store(inState(s’))(⟦CompName⟧(e${}_1$)), c(sbeh, nbeh, cbeh, s, s’))

END

ELSE

LET sbeh = c[1], nbeh = c[2], cbeh = <inseq, outseq, s, s’>  IN

e’ = push(e${}_1$ store(inState(s’))(⟦CompName⟧(e${}_1$)), c(sbeh, nbeh, cbeh, s, s’))

END

END

In detail, if the semantics of the syntactic domain “BehMod” holds in a given environment e, resulting in environment $e^{\prime }$ and transforming a pre-state s into a corresponding post-state $s^{\prime }$, then:

• The inputs “ObjNameSeq${}_1$” evaluate to a sequence of values $inseq$ in a given environment e and a given state s, which satisfies the corresponding pre-conditions “BehCondSeq${}_1$” in the same e and s.
• The allowable events happen and their evaluation results in new environment $e_1$ and a given post-state $s^{\prime }$ with some auxiliary sequences $nseq$ and $eseq$.
• The outputs “ObjNameSeq${}_2$” evaluates to a sequence of values $outseq$ in an environment $e_1$ and given post-state $s^{\prime }$, which satisfies the corresponding post-conditions “BehCondSeq${}_2$” in the same environment $e_1$. State $s^{\prime }$ and the given environment $e^{\prime }$ may be constructed such that:

  -

  If the post-state is “normal” then $e^{\prime }$ is an update to the normal behavior “nbeh” of the component “CompName” in environment $e_1$, otherwise

  -

  $e^{\prime }$ is an update to the compromised behavior “cbeh” of the component.

In the construction of the environment $e^{\prime }$, the rest of the semantics of the component do not change as represented in the corresponding LET-IN constructs.

The complete definitions of the auxiliary functions, predicates, and semantics are presented in [5].

3. An Execution Monitor of ARMET

In principle, an execution monitor interprets the event stream (traces of the execution of the target system, i.e., observations) against the system specification (the execution of the specification is also called predictions) by detecting inconsistencies between observations and the predictions, if there are any.

When the system implementation “AppImpl” (as shown in Figure 3) starts execution, an initial “startup” event is generated and dispatched to the top level component (module) of the system that transforms the execution state of the component into “running” mode. If there is a subnetwork of components, the component instantiates it and propagates the data along its data links by enabling the corresponding control links, if involved. When the data arrives on the input port of the component, the execution monitor checks if it is complete. If so, the execution monitor checks the preconditions of the component for the data and, if they succeed, it transforms the state of the component into “ready” mode. In the case that any of the preconditions fail, it enables the diagnosis engine.

After the startup of the implementation, described above, the execution monitor starts monitoring the arrival of every observation (runtime event) as follows:

• If the event is a “method entry”, the execution monitor checks if this is one of the “entry events” of the corresponding component in the “ready” state. If so, after receiving the data and when the respective preconditions are checked, if they succeed, the data is applied on the input port of the component and the mode of the execution state is changed to “running”.
• If the event is a “method exit”, the execution monitor checks if this one of the “exit events” of the component is in the “running” state. If so, it changes its state into “completed” mode, collects the data from the output port of the component, and checks for corresponding postconditions. Should the checks fail, the execution monitor enables the diagnosis engine.
• If the event is one of the “allowable events” of the component, it continues execution.
• If the event is an unexpected event (i.e., it is neither an “entry event”, an “exit event”, nor in the “allowable events”), the execution monitor starts its diagnosis.

Based on the above behavioral description of the execution monitor, we have formalized the corresponding semantics of the execution monitor as follows:

∀ app ∈ AppImpl, sam ∈ AppSpec, c ∈ Component,

s, s’ ∈ State, t, t’ ∈ States, d, d’ ∈ Environments, e, e’ ∈ Environment, rte ∈ RTEvent:

⟦sam⟧(d)(d’, t, t’) ∧ ⟦app⟧(e)(e’, s, s’) ∧ startup(s, app) ∧ isTop(c, ⟦app⟧(e)(e’, s, s’)) ∧

setMode(s, “running”) ∧ arrives(rte, s) ∧ equals(t, s) ∧ equals(d, e)

⇒

∀ p, p’ ∈ Environment*, m, n ∈ ${\mathrm{State}}_{\perp }^{*}$: equals(m(0), s) ∧ equals(p(0), e)

⇒

∃ k ∈ $\mathbb{N}$, p, p’ ∈ Environment*, m, n ∈ ${\mathrm{State}}_{\perp }^{*}$:

∀ i ∈ ${\mathbb{N}}_k$ : monitors(i, rte, c, p, p’, m, n) ∧

( ( eqMode(n(k), “completed”) ∧ eqFlag(n(k), “normal”) ∧ equals(s’, n(k) )

∨

eqFlag(n(k), “compromised”) )

⇒

enableDiagnosis(p’(k))(n(k), inBool(true)) ∧ equals(s’, n(k)) )

The semantics of recursive monitoring is determined by two sequences of states: pre and post, constructed from the pre-state of the monitor. Any $ith$ iteration of the monitor transforms the $pre\left(i\right)$ state into the $post(i+1)$ state, from which the $pre(i+1)$ state is constructed. No event can be accepted in an $Error$ state and the corresponding monitoring terminates when either the application has terminated with “normal” mode or when some misbehavior is detected, as indicated by the respective “compromised” state. This recursive idea of monitoring is formalized as a “monitors” predicate, as follows:

monitors ⊂ $\mathbb{N}$ × RTEvent × Component × Environment* × Environment* × State* × ${\mathbf{State}}_{\perp }^{*}$ monitors(i, ⟦rte⟧, ⟦c⟧, e, e’, s, s’) ⇔

( eqMode(s(i), “running”) ∨ eqMode(s(i), “ready”) ) ∧ ⟦c⟧(e(i))(e’(i), s(i), s’(i)) ∧

∃ oe ∈ ObEvent: equals(rte, store(⟦name(rte)⟧)(e(i))) ∧

IF entryEvent(oe, c) THEN

data(c, s(i), s’(i)) ∧

( preconditions(c, e(i), e’(i), s(i), s’(i), “compromised”) ⇒ equals(s(i+1), s(i)) ∧ equals(s’(i+1), s(i+1))

∧ setFlag(inState(s’(i+1)), “compromised”) ) ∨ ( preconditions(c, e(i), e’(i), s(i), s’(i), “normal”)

⇒ setMode(s(i), “running”) ∧

LET cseq = components(c) IN

equals(s(i+1), s’(i)) ∧ equals(e(i+1), e’(i)) ∧

∀ c1 ∈ cseq, rte1 ∈ RTEvent:

arrives(rte1, s(i+1)) ∧ monitor(i+1, rte1, c1, e(i+1), e’(i+1), s(i+1), s’(i+1))

END )

ELSE IF exitEvent(oe, c) THEN

data(c, s(i), s’(i)) ∧ eqMode(inState(s’(i)), “completed”) ∧

( postconditions(c, e(i), e’(i), s(i), s’(i), “compromised”) ⇒ equals(s(i+1), s(i)) ∧ equals(s’(i+1), s(i+1))

∧ setFlag(inState(s’(i+1)), “compromised”) ) ∨

( postconditions(c, e(i), e’(i), s(i), s’(i), “normal”) ⇒ equals(s(i+1), s’(i)) ∧ equals(e(i+1), e’(i)) ∧

setMode(inState(s’(i+1), “completed”) )

ELSE IF allowableEvent(oe, c) THEN equals(s(i+1), s’(i)) ∧ equals(e(i+1), e’(i))

ELSE equals(s(i+1), s(i)) ∧ equals(s’(i+1), s(i+1)) ∧ setFlag(inState(s’(i+1)), “compromised”)

END

The predicate “monitors” are defined as a relation on

• the number of observation i, with respect to the iteration of a component
• an observation (runtime event) $rte$
• the corresponding component c under observation
• a sequence of pre-environments e
• a sequence of post-environments $e^{\prime }$
• a sequence of pre-states s
• a sequence of post-states $s^{\prime }$

The predicate "monitors" are defined such that when an any arbitrary observation is made, if the current execution state $s\left(i\right)$ of component c is “ready” or “running”, the behavior of component c has been evaluated, and there is a prediction$oe$ that is semantically equal to an observation$rte$, any of the following can happen:

• The prediction or observation is an entry event of the component c and it waits until the complete data for the component c arrives. If this occurs then either:

  -

  Preconditions of “normal” behavior of the component hold.If so, the subnetwork of the component is initiated and the components in the subnetwork are monitored iteratively with the corresponding arrival of the observation, or

  -

  Preconditions of “compromised” behavior of the component hold. In this case, the state is marked as “compromised” and returns.

• The observation is an exit event and, after the completion of the data arrival, the postconditions hold and the resulting state is marked as “completed”.
• The observation is an allowable event and just continues the execution.
• The observation is an unexpected event (or any of the above does not hold) and the state is marked as “compromised”, and returns.

4. Proof of Behavioral Correctness

Based on the formalization of the denotational semantics of the specification language and the monitor, we have proved that the monitor is sound and complete, i.e., if the application implementation (AppImpl) is consistent with its specification (AppSpec), the security monitor will produce no false alarms (soundness) and the monitor will detect any deviation of the application execution from the behavior sanctioned by the specification language (completeness). In the following subsections, we articulate soundness and completeness statements and sketch their corresponding proofs.

4.1. Soundness

The intent of the soundness statement is to articulate whether the system’s behavior is consistent with behavioral specification. Essentially, the goal is to show the absence of a false negative alarm such that whenever the security monitor alarms, there is a semantic inconsistency between the post-state of the program execution and the post-state of the specification execution. The soundness theorem is stated as follows:

Theorem 1 (Soundness)

The result of the security monitor is sound for any execution of the target system and its specification, iff, the specification is consistent with the program and the program executes in a safe pre-state and in an environment that is consistent with the environment of the specification, then

• for the pre-state of the program, there is an equivalent safe pre-state for which the specification can be executed and the monitor can be observed and
• if we execute the specification in an equivalent safe pre-state and observe the monitor at any arbitrary (combined) post-state, then

  -

  either there is no alarm, and then the post-state is safe and the program execution (post-state) is semantically consistent with the specification execution (post-state)

  -

  or there is an alarm, and then the post-state is compromised and the program execution (post-state) and the specification execution (post-state) are semantically inconsistent.

Formally, the soundness theorem has the following signatures and definition.

Soundness ⊆$\mathbb{P}$(AppImpl × AppSpec × Bool)

Soundness($\kappa$, $\omega$, b) ⇔

∀ e${}_s$∈ Environment${}_s$, e${}_r$, e${}_r$’ ∈ Environment${}_r$, s, s’ ∈ State${}_r$: consistent(e${}_s$, e${}_r$) ∧ consistent($\kappa$, $\omega$) ∧

⟦$\kappa$⟧(e${}_r$)(e${}_r$’, s, s’) ∧ eqMode(s, "normal")

⇒

∃ t, t’ ∈ State${}_s$, e${}_s$’ ∈ Environment${}_s$: equals(s, t) ∧ ⟦$\omega$⟧(e${}_s$)(e${}_s$’, t, t’) ∧ monitor($\kappa$, $\omega$)(e${}_r$;e${}_s$)(s;t, s’;t’) ∧

∀ t, t’ ∈ State${}_s$, e${}_s$’ ∈ Environment${}_s$: equals(s, t) ∧ ⟦$\omega$⟧(e${}_s$)(e${}_s$’, t, t’) ∧ monitor($\kappa$, $\omega$)(e${}_r$;e${}_s$)(s;t, s’;t’)

⇒

LET b = eqMode(s’, "normal") IN

IF b = True THEN equals(s’, t’) ELSE ¬ equals(s’, t’)

In detail, the soundness statement says that, if the following are satisfied:

• a specification environment (e${}_s$) is consistent with a run-time environment (e${}_r$), and
• a target system ($\kappa$) is consistent with its specification ($\omega$), and
• in a given run-time environment (e${}_r$), execution of the system ($\kappa$) transforms the pre-state (s) into a post-state (s’), and
• the pre-state (s) is safe, i.e., the state is in “normal” mode,

Then the following occurs:

• there exist the pre- and post-states (t and t’, respectively) and the environment (e${}_s$’) of the specification execution such that in a given specification environment (e${}_s$), the execution of the specification ($\omega$) transforms the pre-state (t) into a post-state (t’)
• the pre-states s and t are equal and monitoring of the system ($\kappa$) transforms the combined pre-state (s; t) into a combined post-state (s’; t’)
• if both the following occur: in a given specification environment (e${}_s$), execution of the specification ($\omega$) transforms pre-state (t) into a post-state (t’); and the pre-states s and t are equal and monitoring of the system ($\kappa$) transforms the pre-state (s) into a post-state (s’), then either:

  -

  there is no alarm (b is True), the post-state s’ of a program execution is safe, and the resulting states s’ and t’ are semantically equal, or

  -

  the security monitor alarms (b is False), the post-state s’ of program execution is compromised, and the resulting states s’ and t’ are semantically not equal.

In the following section we present proof of the soundness statement.

Proof. 

The proof is essentially a structural induction on the elements of the specification ($\omega$) of the system ($\kappa$). We have proved only the interesting case $\beta$ of the specification to show that the proof works in principle. However, the proof of the remaining parts can easily be rehearsed following a similar approach.

The proof is based on certain lemmas, which are mainly about the relationships between different elements of the system and its specification (being at different levels of abstraction). These lemmas and relations can be proved based on the defined auxiliary functions and predicates that are based on the method suggested by Hoare [9]. The complete proof is presented in [10]. ☐

4.2. Completeness

The goal of the completeness statement is to show the absence of false positive alarms such that whenever there is a semantic inconsistency between the post-state of the program execution and the post-state of the specification execution, the security monitor alarms. The completeness theorem is stated as follows:

Theorem 2 (Completeness).

The result of the security monitor is complete for a given execution of the target system and its specification, iff, the specification is consistent with the program and the program executes in a safe pre-state and in an environment that is consistent with the environment of the specification, then

• for the pre-state of the program, there is an equivalent safe pre-state for which the specification can be executed and the monitor can be observed and
• if we execute the specification in an equivalent safe pre-state and observe the monitor at any arbitrary (combined) post-state, then

  -

  either the program execution (post-state) is semantically consistent with the specification execution (post-state), then there is no alarm and the program execution is safe

  -

  or the program execution (post-state) and the specification execution (post-state) are semantically inconsistent, then there is an alarm and the program execution has been compromised.

Formally, the completeness theorem has the following signatures and definition.

Completeness ⊆$\mathbb{P}$(AppImpl × AppSpec × Bool)

Completeness($\kappa$, $\omega$, b) ⇔

∀ e${}_s$∈ Environment${}_s$, e${}_r$, e${}_r$’ ∈ Environment${}_r$, s, s’ ∈ State${}_r$: consistent(e${}_s$, e${}_r$) ∧ consistent($\kappa$, $\omega$) ∧

⟦$\kappa$⟧(e${}_r$)(e${}_r$’, s, s’) ∧ eqMode(s, "normal")

⇒

∃ t, t’ ∈ State${}_s$, e${}_s$’ ∈ Environment${}_s$: equals(s, t) ∧ ⟦$\omega$⟧(e${}_s$)(e${}_s$’, t, t’) ∧ monitor($\kappa$, $\omega$)(e${}_r$;e${}_s$)(s;t, s’;t’) ∧

∀ t, t’ ∈ State${}_s$, e${}_s$’ ∈ Environment${}_s$: equals(s, t) ∧ ⟦$\omega$⟧(e${}_s$)(e${}_s$’, t, t’) ∧ monitor($\kappa$, $\omega$)(e${}_r$;e${}_s$)(s;t, s’;t’)

⇒

IF equals(s’, t’) THEN b = True∧ b = eqMode(s’, “normal”)

ELSE b = False ∧ b = eqMode(s’, "normal")

In detail, the completeness statement says that, if the following are satisfied:

• a specification environment (e${}_s$) is consistent with a run-time environment (e${}_r$), and
• a target system ($\kappa$) is consistent with its specification ($\omega$), and
• in a given run-time environment (e${}_r$), execution of the system ($\kappa$) transforms the pre-state (s) into a post-state (s’), and
• the pre-state (s) is safe, i.e., the state is in "normal" mode,

Then the following occurs:

• there exist the pre- and post-states (t and t’, respectively) and the environment (e${}_s$’) of specification execution such that, in a given specification environment (e${}_s$), execution of the specification ($\omega$) transforms the pre-state (t) into a post-state (t’)
• the pre-states s and t are equal and monitoring of the system ($\kappa$) transforms the combined pre-state (s; t) into a combined post-state (s’; t’)
• if both: in a given specification environment (e${}_s$), the execution of the specification ($\omega$) transforms the pre-state (t) into a post-state (t’); and the pre-states s and t are equal and monitoring of the system ($\kappa$) transforms the pre-state (s) into a post-state (s’), then either

  -

  the resulting two post-states s’ and t’ are semantically equal and there is no alarm, or

  -

  the resulting two post-states s’ and t’ are semantically not equal and the security monitor alarms.

Proof. 

The proof of completeness is very similar to the proof of soundness. The complete proof is presented in [10]. ☐

5. Conclusions

We have presented a formalization of the semantics of the specification language and monitor of the cognitive middleware ARMET. In order to assure the continuous operation of ICS applications and to meet the real-time requirements of ICS, we have proved that our run-time security monitor produces no false alarm and always detects behavioral deviation of the ICS application. We plan to integrate our run-time security monitor with a security-by-design component to ensure comprehensive security solution for ICS applications.