New Nonlinear Second-Order Phase-Locked Loop with Adaptive Bandwidth Regulation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Model of the Traditional Second-Order PLL
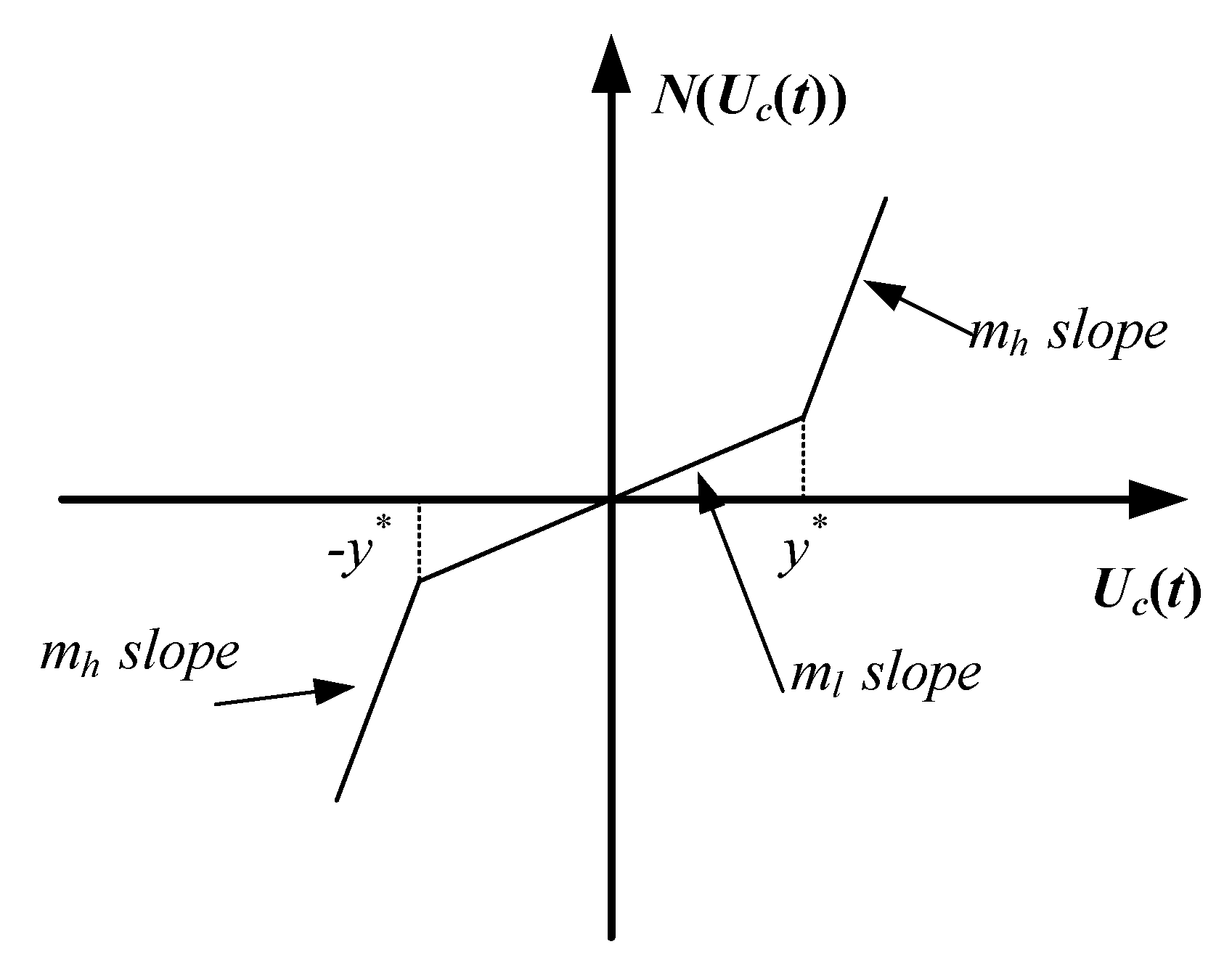
2.2. New PLL Coupled with a Nonlinear Element
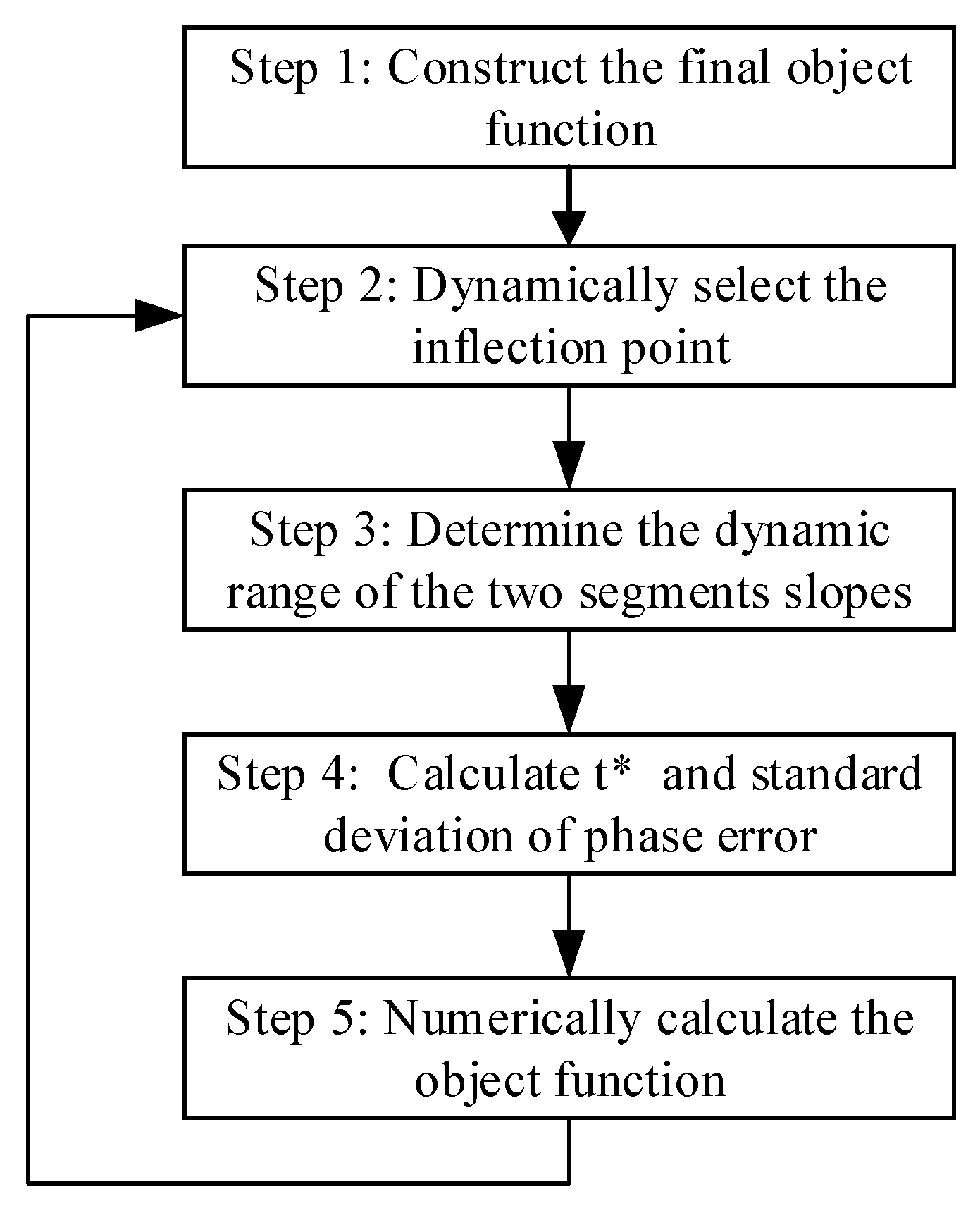
2.3. Design of the Nonlinear Element Parameters
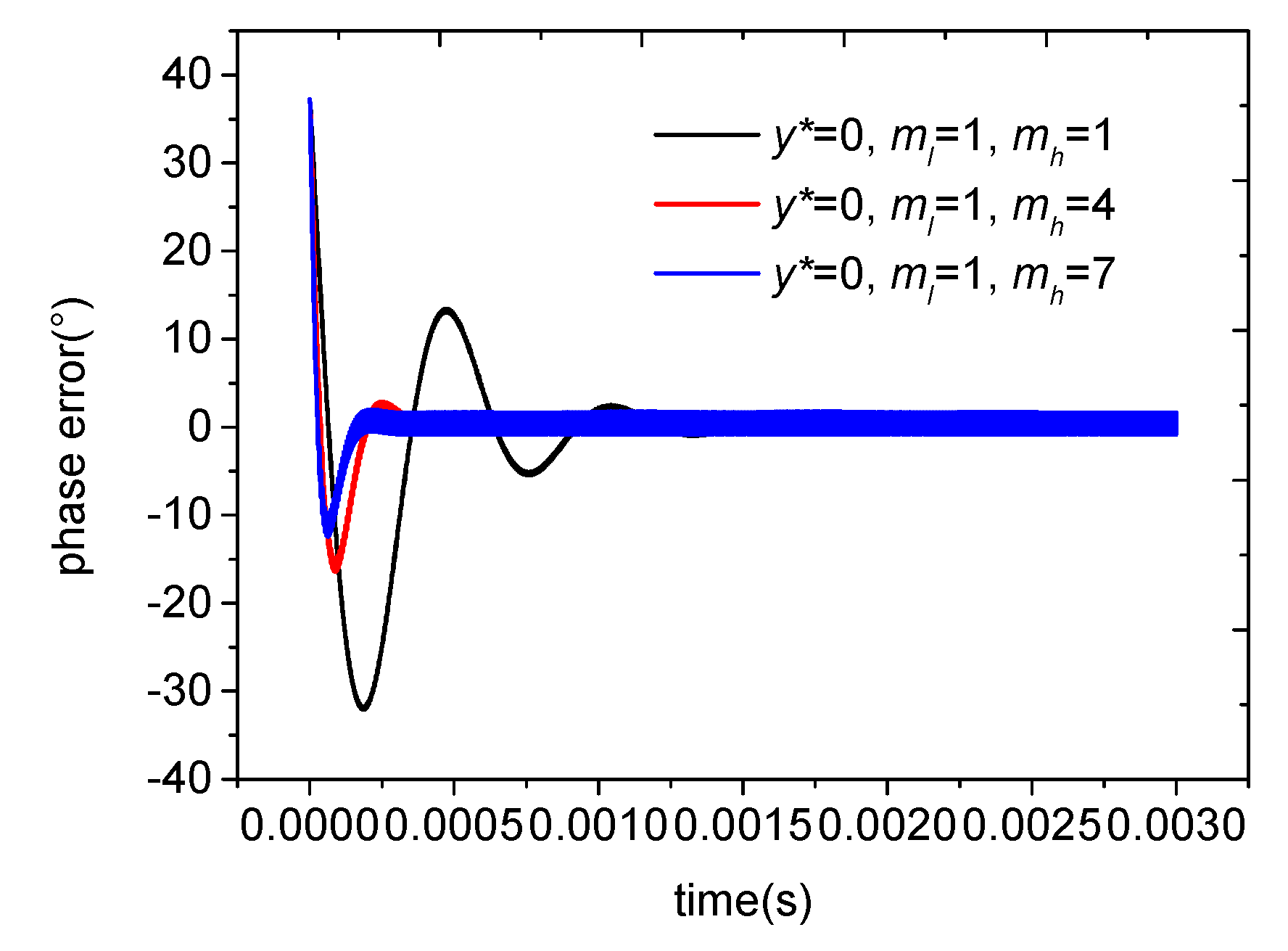
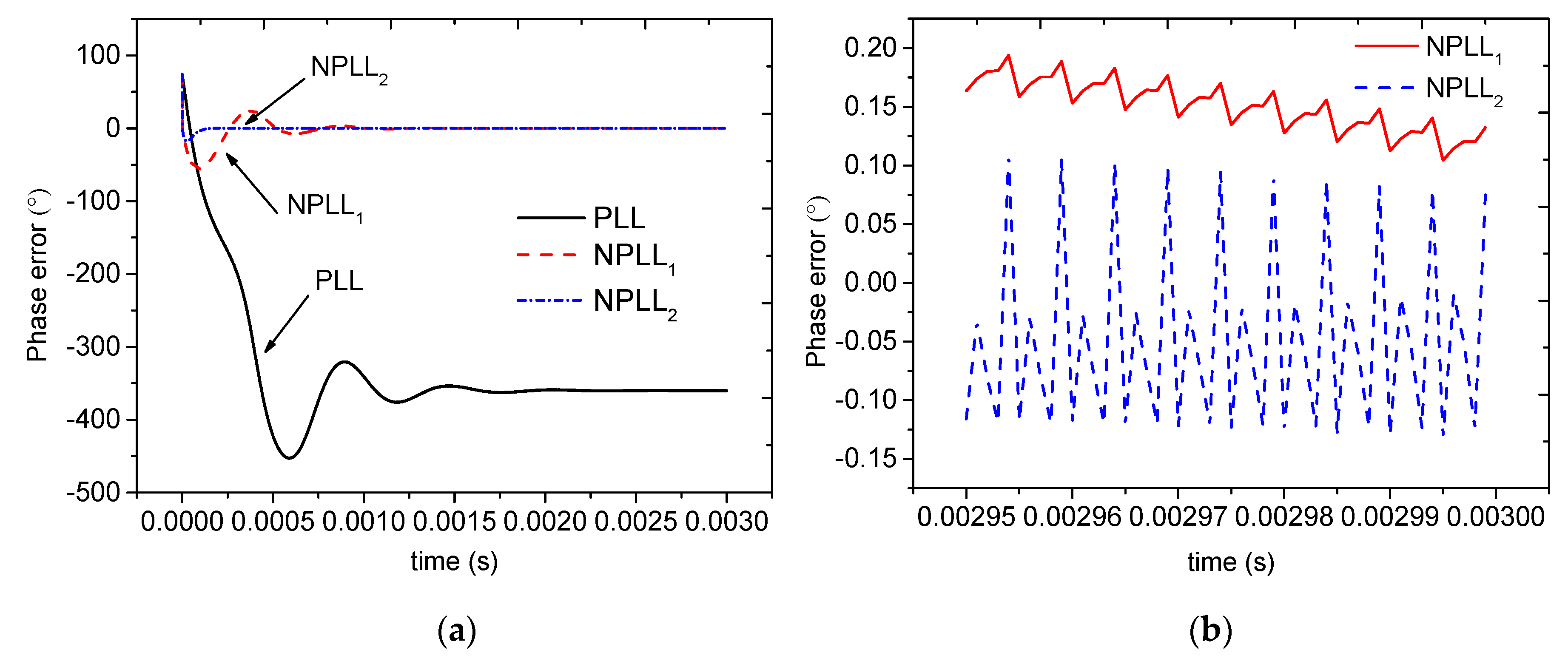
3. Simulation and Results
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Anantharamu, P.B.; Borio, D.; Lachapelle, G. Sub-carrier shaping for BOC modulated GNSS signals. EURASIP J. Adv. Signal Process. 2011, 2011, 133. [Google Scholar] [CrossRef]
- Xue, W.; Shang, W.; Makarov, S.B.; Xu, Y. A phase trajectories optimization method for CPM signal based on Pan-function model. EURASIP J. Adv. Signal Process. 2016, 2016, 55. [Google Scholar] [CrossRef]
- Xu, R.; Liu, Z.; Chen, W. Improved FLL-assisted PLL with in-phase pre-filtering to mitigate amplitude scintillation effects. GPS Solut. 2015, 19, 263–276. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. High-Order Frequency-Locked Loops: A Critical Analysis. IEEE Trans. Power Electron. 2017, 32, 3285–3291. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. An Open-Loop Grid Synchronization Approach for Single-Phase Applications. IEEE Trans. Power Electron. 2018, 33, 5548–5555. [Google Scholar] [CrossRef]
- Kanjiya, P.; Khadkikar, V.; Moursi, M.S.E. A Novel Type-1 Frequency-Locked Loop for Fast Detection of Frequency and Phase with Improved Stability Margins. IEEE Trans. Power Electron. 2016, 31, 2550–2561. [Google Scholar] [CrossRef]
- Byun, S. More Discussions on Intrinsic Frequency Detection Capability of Full-Rate Linear Phase Detector in Clock and Data Recovery. Electronics 2018, 7, 93. [Google Scholar] [CrossRef]
- Kamel, T.; Abdelkader, D.; Said, B.; Padmanaban, S.; Iqbal, A. Extended Kalman Filter Based Sliding Mode Control of Parallel-Connected Two Five-Phase PMSM Drive System. Electronics 2018, 7, 14. [Google Scholar] [CrossRef]
- Kuznetsov, N.V.; Kuznetsova, O.A.; Leonov, G.A.; Neittaanm¨aki, P.; Yuldashev, M.V.; Yuldashev, R.V. Limitations of the classical phase-locked loop analysis. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 533–536. [Google Scholar]
- Kuznetsov, N.V.; Leonov, G.A.; Yuldashev, M.V.; Yuldashev, R.V. Hidden attractors in dynamical models of phase-locked loop circuits: Limitations of simulation in MATLAB and SPICE. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 39–49. [Google Scholar] [CrossRef] [Green Version]
- Chandra, T.M.; Debasmita, M.; Karabi, B.; Siddhartha, S. Design and performance study of phase-locked loop using fractional-order loop filter. Int. J. Circuit Theory Appl. 2015, 43, 776–792. [Google Scholar] [CrossRef]
- Katsinis, G.; Tsiropoulou, E.E.; Papavassiliou, S. A game theoretic approach to the power control in D2D communications underlay cellular networks. In Proceedings of the IEEE International Workshop on Computer Aided Modeling and Design of Communication Links and Networks, Athens, Greece, 1–3 December 2014; pp. 208–212. [Google Scholar]
- Katsinis, G.; Tsiropoulou, E.E.; Papavassiliou, S. Joint Resource Block and Power Allocation for Interference Management in Device to Device Underlay Cellular Networks: A Game Theoretic Approach. Mob. Netw. Appl. 2017, 22, 539–551. [Google Scholar] [CrossRef]
- Bravo-Muñoz, I.; Lázaro-Galilea, J.L.; Gardel-Vicente, A. FPGA and SoC Devices Applied to New Trends in Image/Video and Signal Processing Fields. Electronics 2017, 6, 25. [Google Scholar] [CrossRef]
- Singh, S.; Shekhar, C.; Vohra, A. FPGA-Based Real-Time Motion Detection for Automated Video Surveillance Systems. Electronics 2016, 5, 10. [Google Scholar] [CrossRef]
- Choukri Benhabib, M.; Saadate, S. A New Robust Experimentally Validated Phase Locked Loop for Power Electronic Control. EPE J. 2005, 15, 36–48. [Google Scholar] [CrossRef]
- Humphreys, T.E.; Psiaki, M.L.; Kintner, P.M. GPS Carrier Tracking Loop Performance in the presence of Ionospheric Scintillations. In Proceedings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation, Long Beach, CA, USA, 13–16 September 2005. [Google Scholar]
- Ganguly, S.; Jovancevic, A.; Brown, A.; Kirchner, M.; Zigic, S.; Beach, T.; Groves, K.M. Ionospheric scintillation monitoring and mitigation using a software GPS receiver. Radio Sci. 2004, 39, 1–9. [Google Scholar] [CrossRef]
- Kiesel, S.; Ascher, C.; Gramm, D.; Trommer, G.F. GNSS receiver with vector based FLL-assisted PLL carrier tracking loop. In Proceedings of the ION GNSS, Savannah, GA, USA, 16–19 September 2008; pp. 197–203. [Google Scholar]
- Cupertino, F.; Lavopa, E.; Zanchetta, P.; Sumner, M.; Salvatore, L. Running DFT-Based PLL Algorithm for Frequency, Phase, and Amplitude Tracking in Aircraft Electrical Systems. IEEE Trans. Ind. Electron. 2011, 58, 1027–1035. [Google Scholar] [CrossRef]
- Legrand, F.; Macabiau, C.; Issler, J.-L.; Lestarquit, L.; Mehlen, C. Improvement of pseudorange measurements accuracy by using fast adaptive bandwidth lock loops. Proceedings of 13th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2000), Salt Lake City, UT, USA, 19–22 September 2000; pp. 2346–2356. [Google Scholar]
- Legrand, F.; Macabiau, C. Results of the implementation of the fast adaptive bandwidth lock loops on a real GPS receiver in a high dynamics context. In Proceedings of the International Conference on Global Navigation Satellite System (GNSS 2001), Seville, Spain, 8–11 May 2001. [Google Scholar]
- Vaucher, C.S. An adaptive PLL tuning system architecture combining high spectral purity and fast settling time. IEEE J. Solid-State Circuits 2000, 35, 490–502. [Google Scholar] [CrossRef] [Green Version]
- Ulvgård, L.; Kamf, T.; Leijon, M. Offshore Measurement System for Wave Power—Using Current Loop Feedback. Electronics 2016, 5, 86. [Google Scholar] [CrossRef]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Shi, L.; Zhu, C. New Nonlinear Second-Order Phase-Locked Loop with Adaptive Bandwidth Regulation. Electronics 2018, 7, 346. https://doi.org/10.3390/electronics7120346
Zhao L, Shi L, Zhu C. New Nonlinear Second-Order Phase-Locked Loop with Adaptive Bandwidth Regulation. Electronics. 2018; 7(12):346. https://doi.org/10.3390/electronics7120346
Chicago/Turabian StyleZhao, Lei, Lei Shi, and Congying Zhu. 2018. "New Nonlinear Second-Order Phase-Locked Loop with Adaptive Bandwidth Regulation" Electronics 7, no. 12: 346. https://doi.org/10.3390/electronics7120346




