Hybrid Current-Mode Control of PSFB Converter to Compensate Slew Interval and Prevent Magnetic Saturation of Transformers
Abstract
:1. Introduction
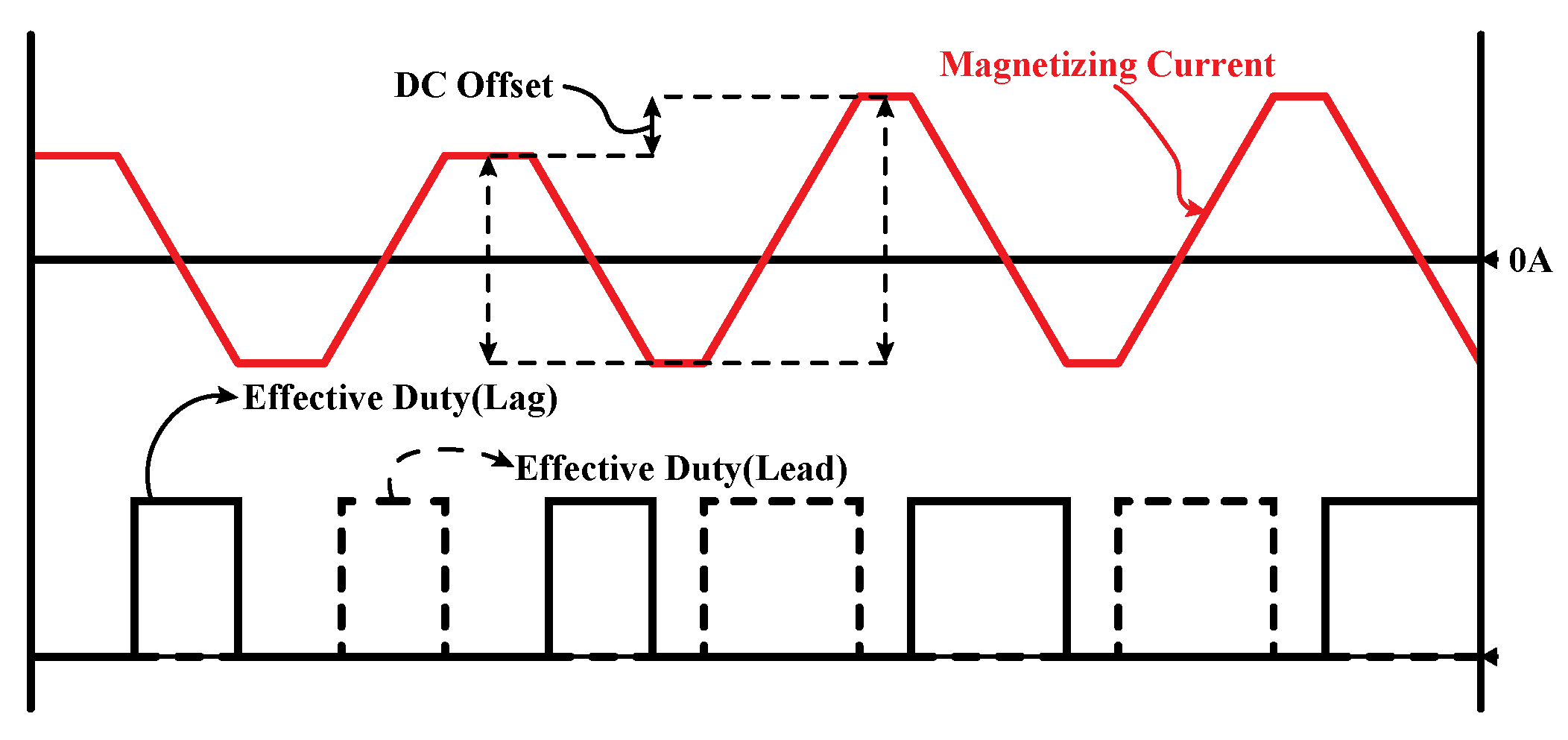
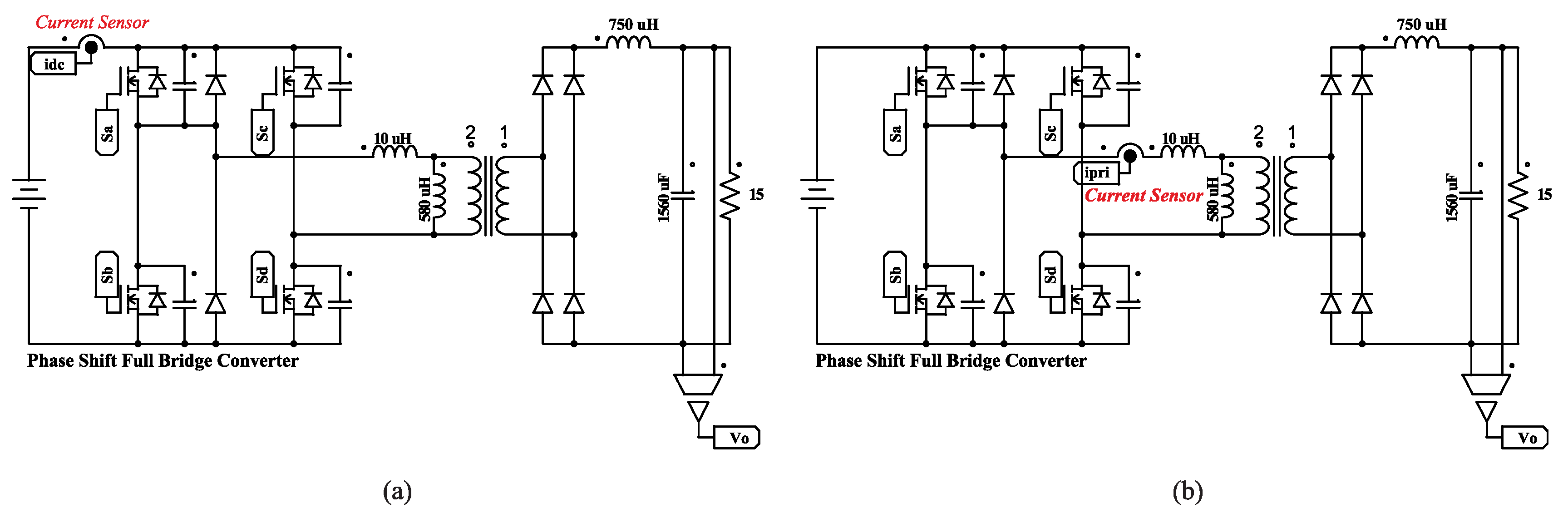
2. Primary-Side Current Imbalance of PSFB Converters
3. Conventional Method for Preventing Current Imbalance
3.1. Blocking Capacitor
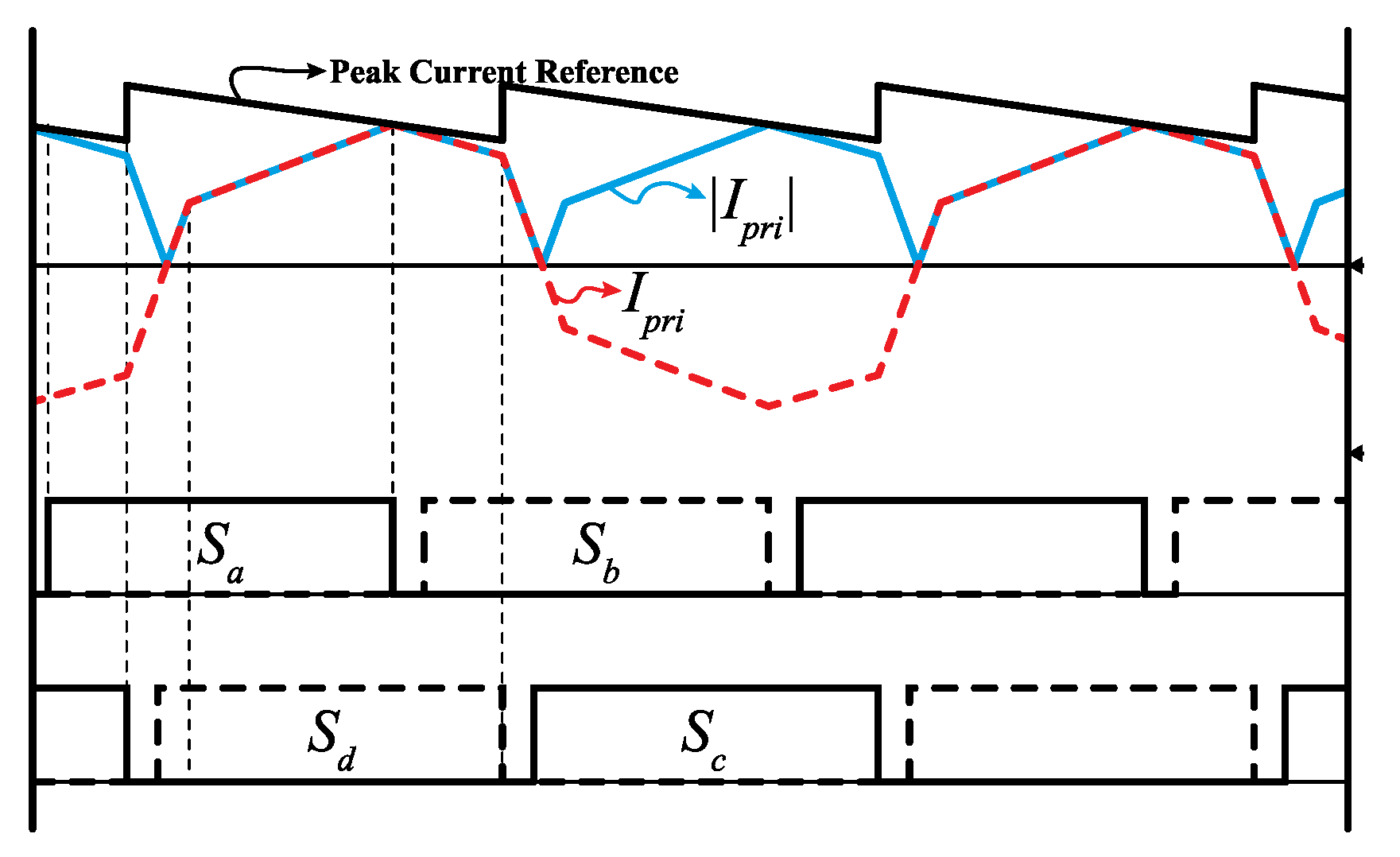
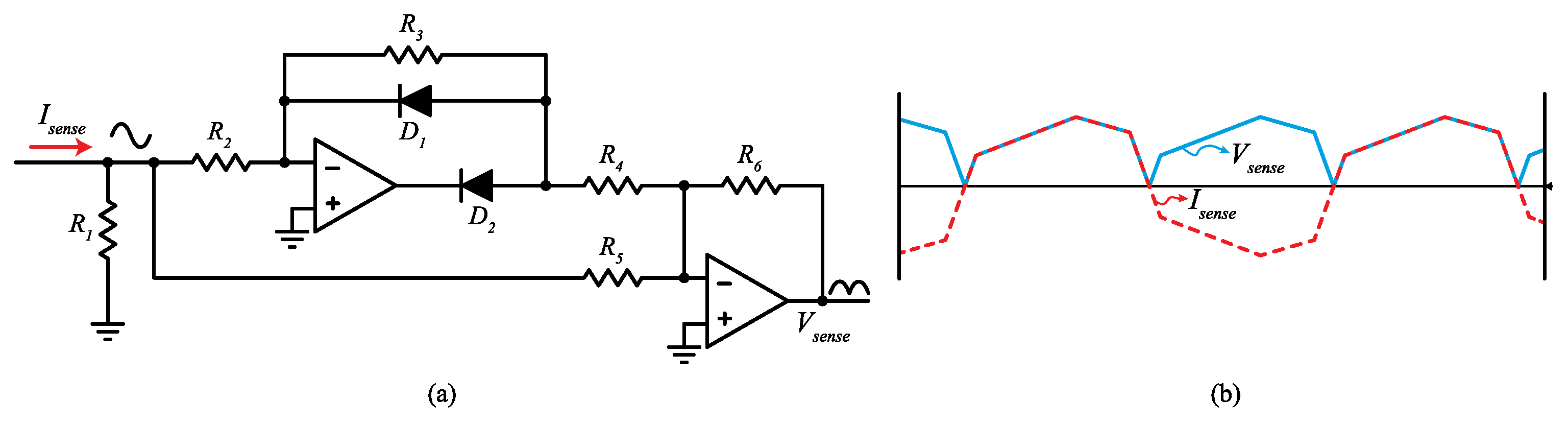
3.2. Peak Current-Mode Control with Slope Compensation
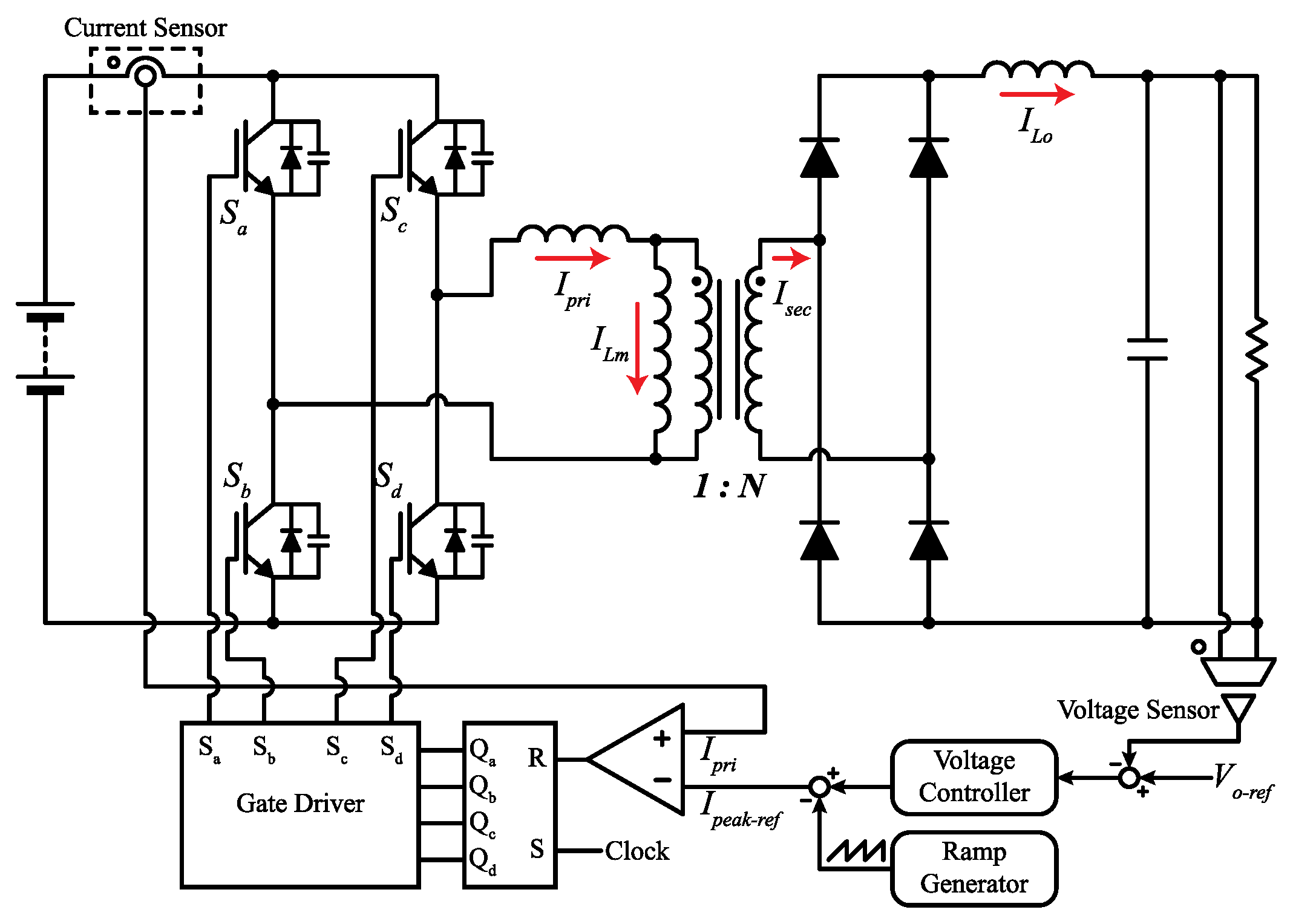
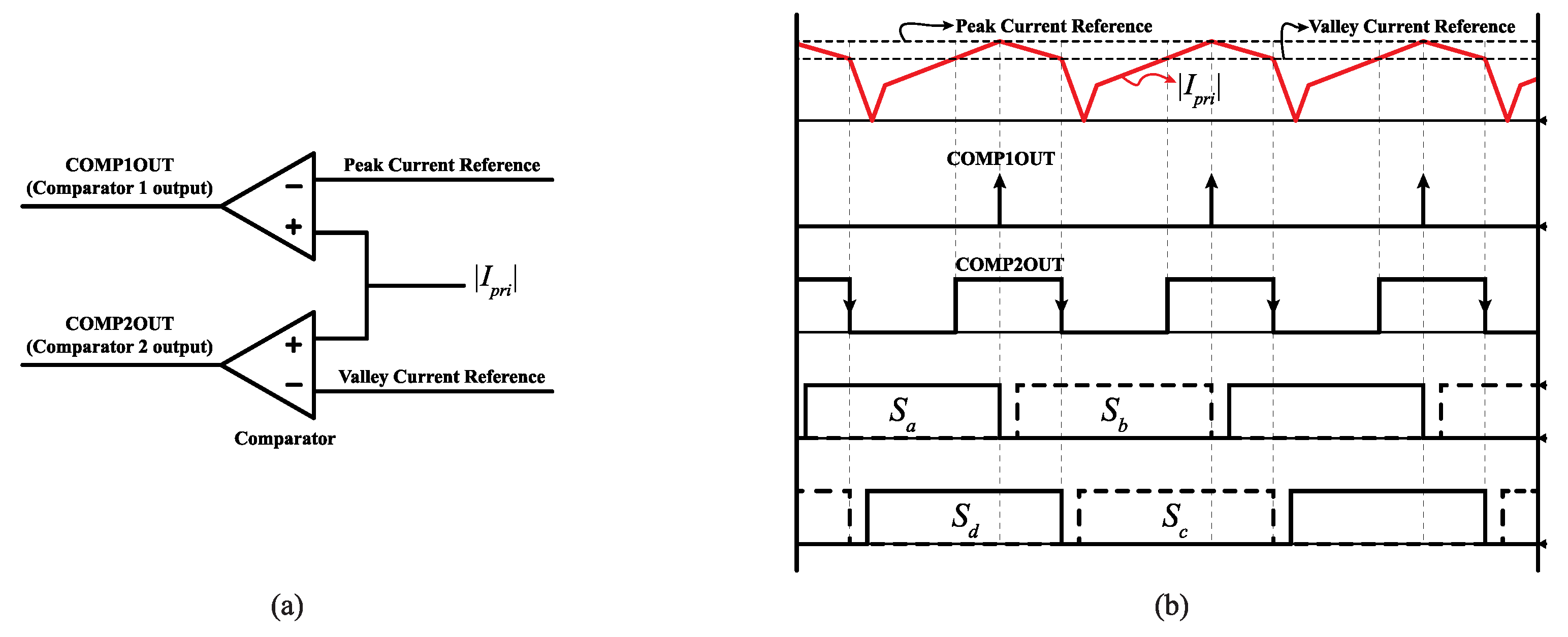
4. Proposed Hybrid Current-Mode Control of PSFB Converters
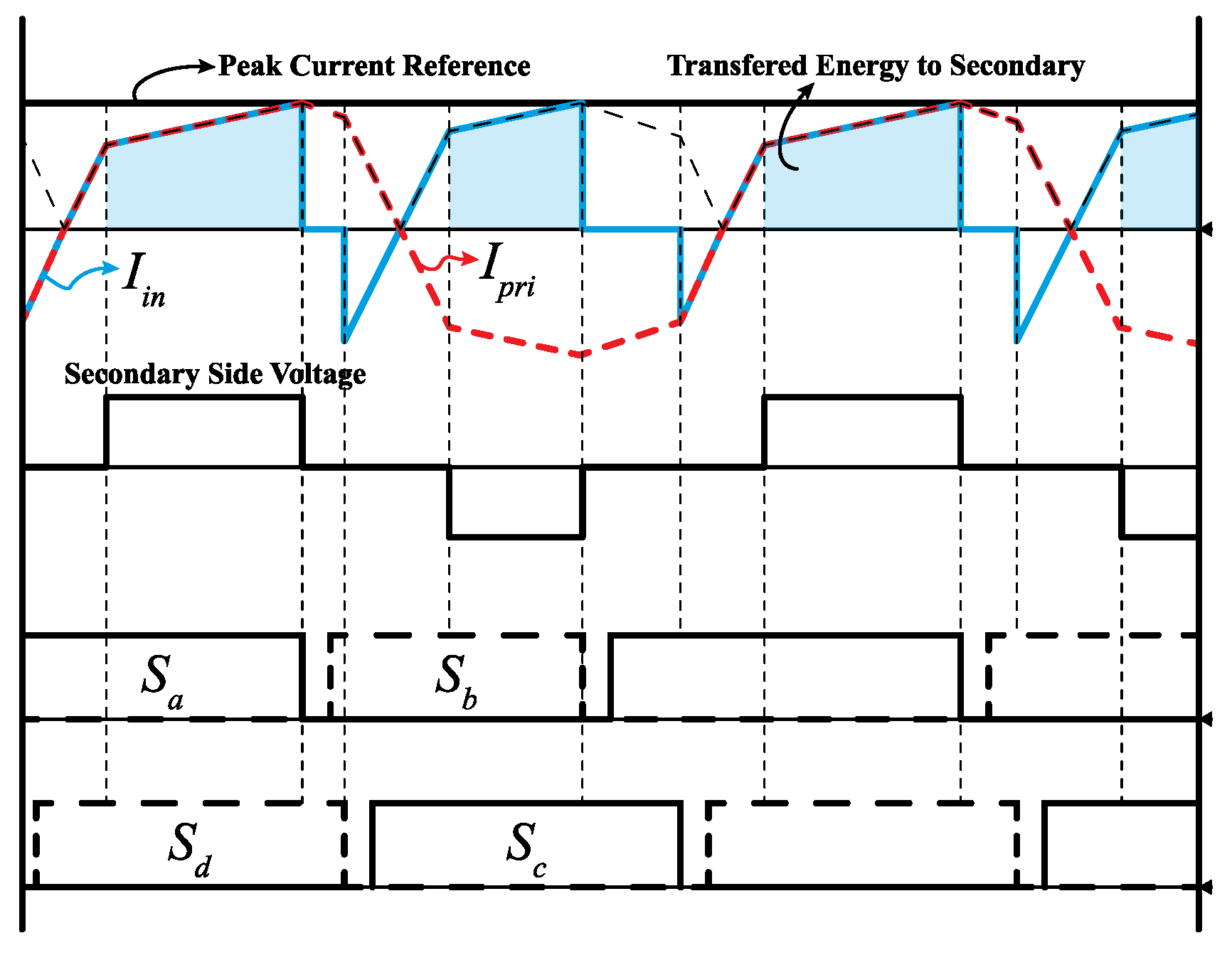
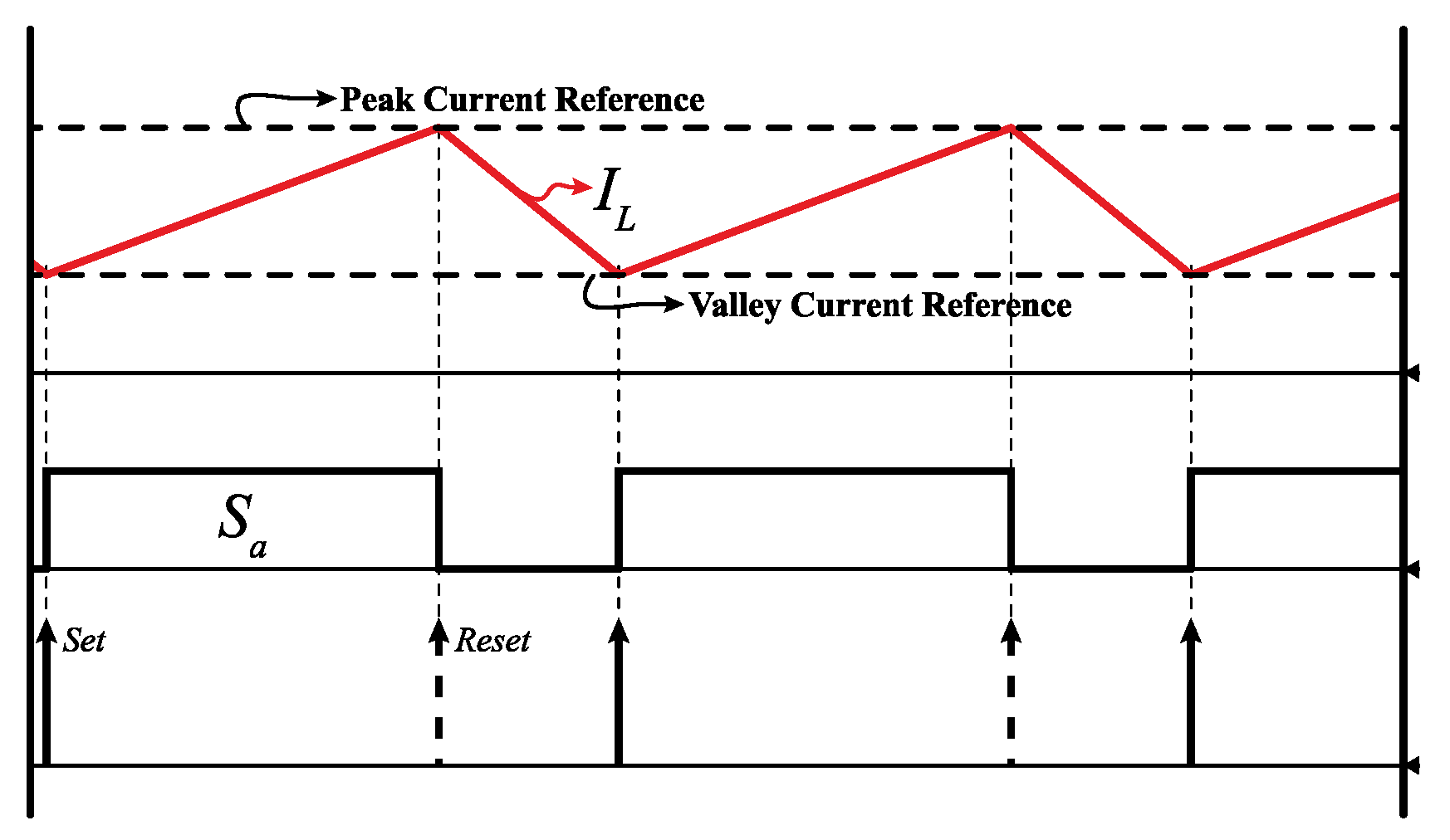
4.1. Hybrid Current-Mode Control of Boost Converter
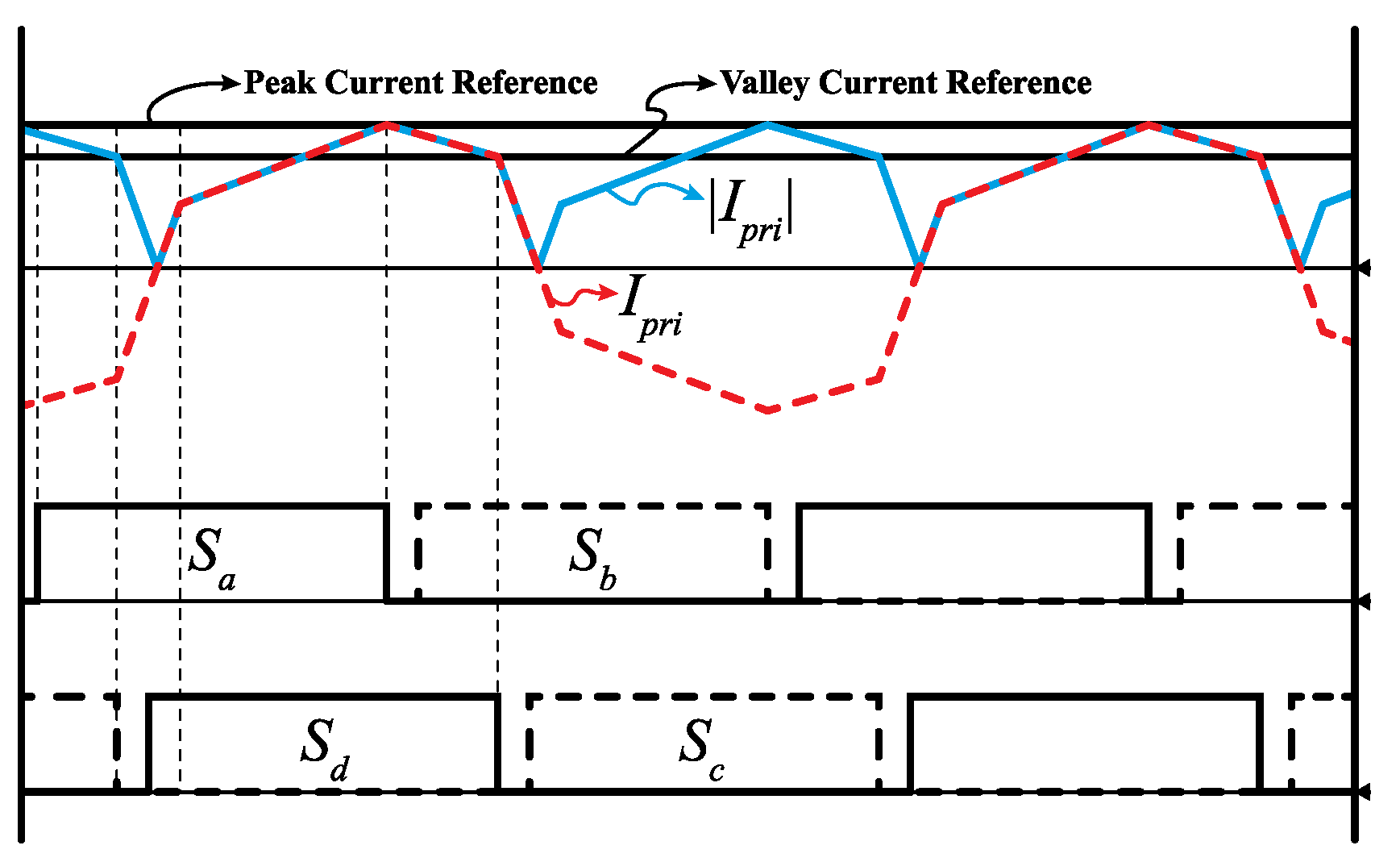
4.2. Hybrid Current-Mode Control for PSFB Converters
5. Simulation and Digital Code Initialization for Experiment
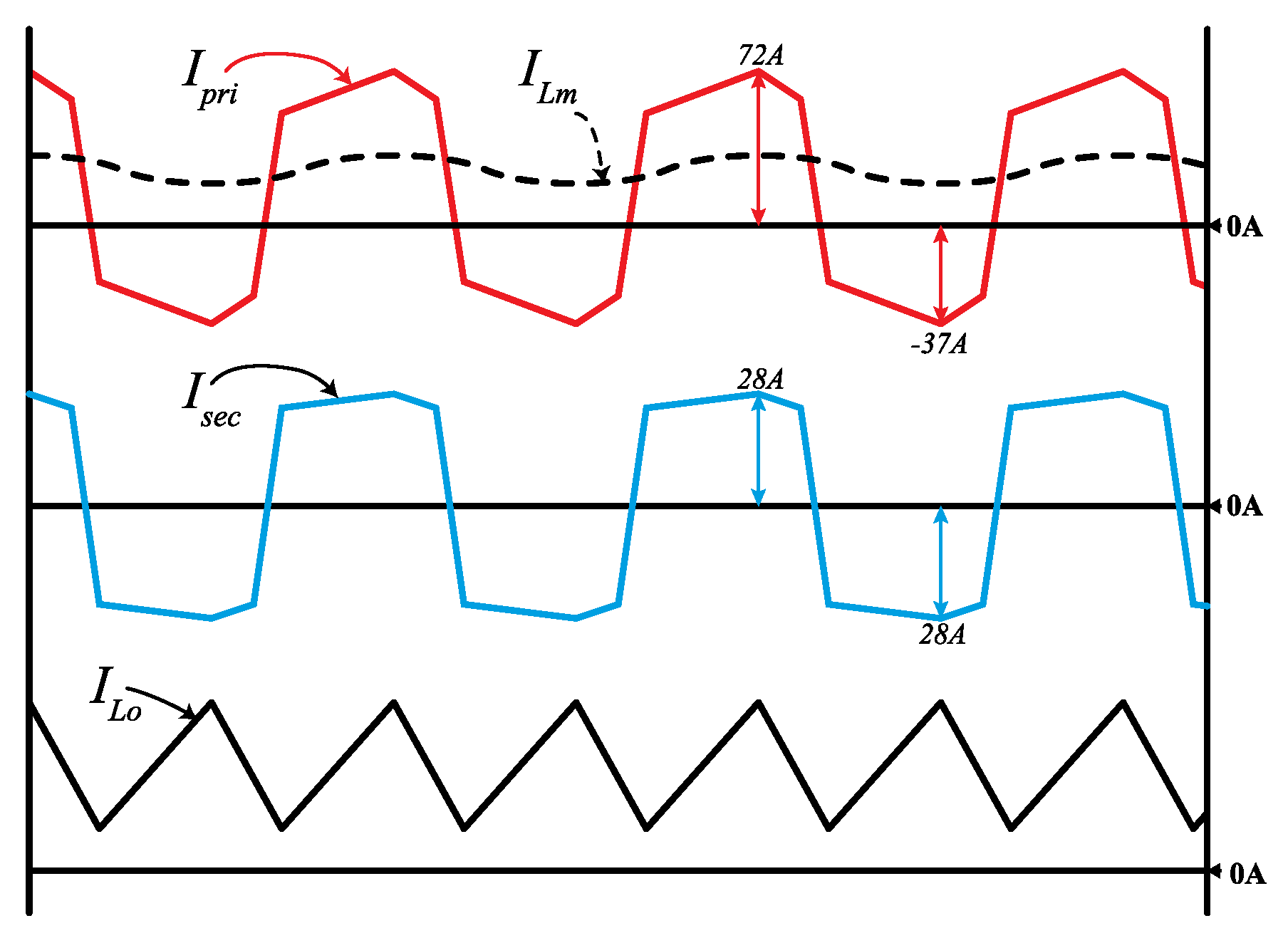
5.1. Simulation Result
5.2. Digital Code Initialization for Experiment
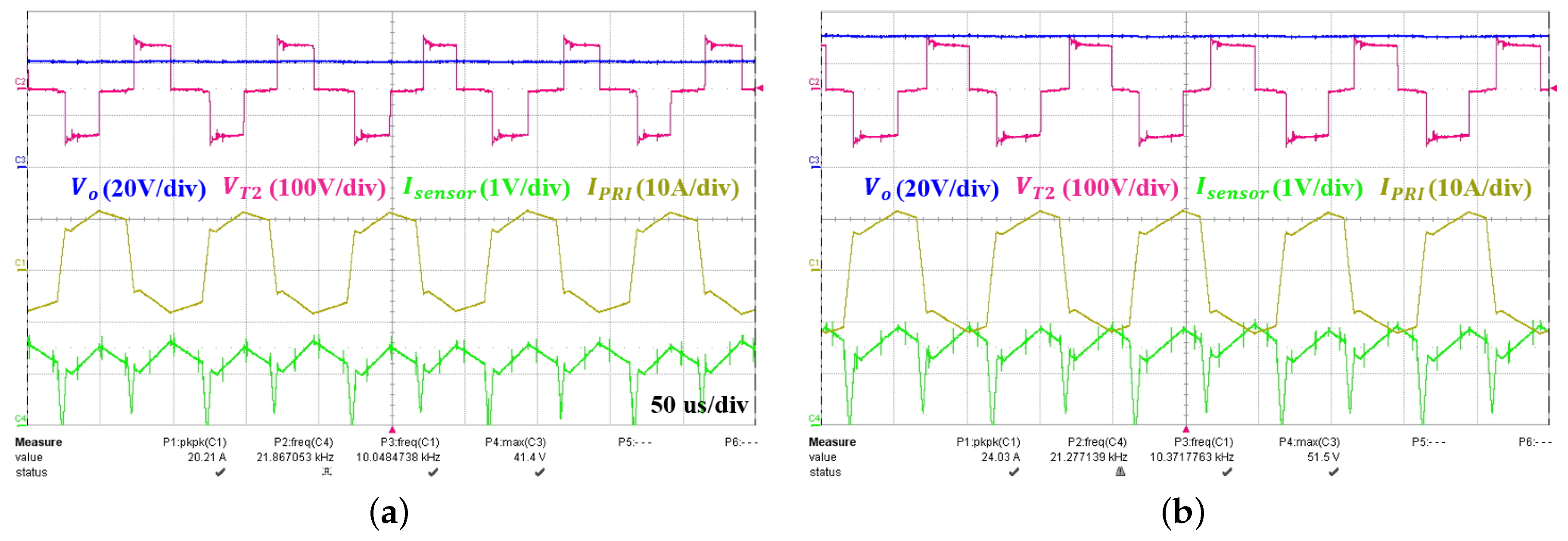
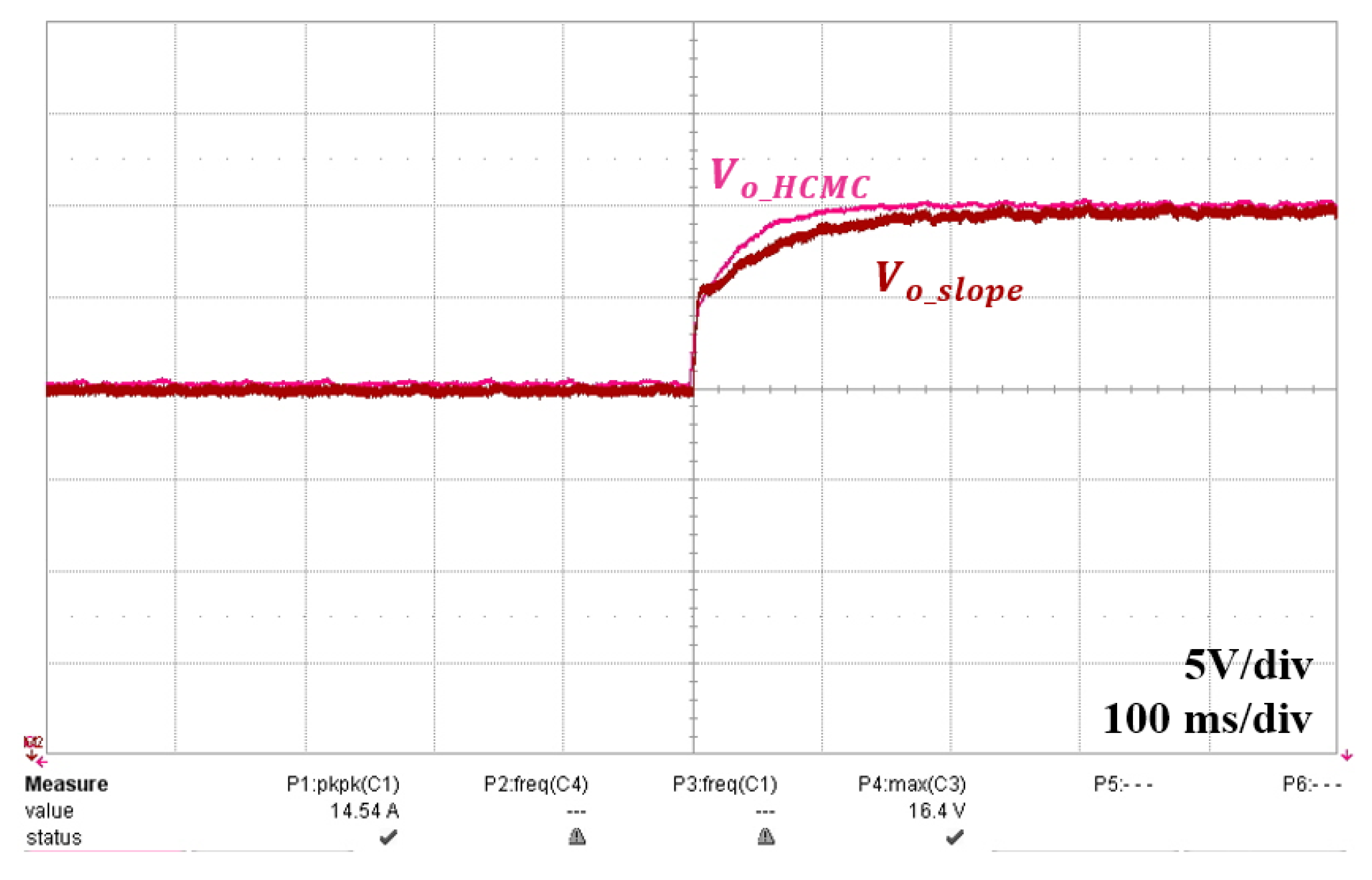
5.3. Experiment Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Khaligh, A.; Dusmez, S. Comprehensive topological analysis of conductive and inductive charging solutions for plug-in electric vehicles. IEEE Trans. Veh. Technol. 2012, 61, 3475–3489. [Google Scholar] [CrossRef]
- Yong, J.Y.; Ramachandaramurthy, V.K.; Tan, K.M.; Mithulananthan, N. A review on the state-of-the-art technologies of electric vehicle, its impacts and prospects. Renew. Sustain. Energy Rev. 2015, 49, 365–385. [Google Scholar] [CrossRef]
- Fahem, K.; Chariag, D.E.; Sbita, L. On-board bidirectional battery chargers topologies for plug-in hybrid electric vehicles. In Proceedings of the International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–6. [Google Scholar]
- Grenier, M.; Aghdam, M.G.H.; Thiringer, T. Design of on-board charger for plug-in hybrid electric vehicle. In Proceedings of the 5th IET International Conference on Power Electronics, Machines and Drives, Brighton, UK, 19–21 April 2010; pp. 1–6. [Google Scholar]
- Haghbin, S.; Khan, K.; Lundmark, S.; Alakula, M.; Carlson, O.; Leksell, M.; Wallmark, O. Integrated chargers for EV’s and PHEV’s: Examples and new solutions. In Proceedings of the XIX International Conference on Electrical Machines, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar]
- Haghbin, S.; Lundmark, S.; Alakula, M.; Carlson, O. Grid-connected integrated battery chargers in vehicle applications: Review and new solution. IEEE Trans. Ind. Electron. 2013, 40, 459–473. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of battery charger topologies, charging power levels, and infrastructure for plug-in electric and hybrid vehicles. IEEE Trans. Power Electron. 2013, 28, 2151–2169. [Google Scholar] [CrossRef]
- Lee, M.; Kim, C.L.K.; Park, M.; Moon, G. A phase-shift full-bridge converter with novel voltage oscillation clamping circuit for electric vehicle on-board charger. In Proceedings of the 10th International Conference on Power Electronics and ECCE Asia, Busan, Korea, 27–30 May 2019; pp. 2040–2045. [Google Scholar]
- Cha, H.; Chen, L.; Ding, R.; Tang, Q.; Peng, F.Z. An alternative energy recovery clamp circuit for full-bridge PWM converters with wide ranges of input voltage. IEEE Trans. Power Electron. 2008, 23, 2828–2837. [Google Scholar]
- Hsieh, Y.; Huang, C. Li-ion battery charger based on digitally controlled phase-shifted full-bridge converter. IET Power Electron. 2011, 4, 242–247. [Google Scholar] [CrossRef]
- Wang, H.; Shang, M.; Khaligh, A. A PSFB-based integrated PEV onboard charger with extended ZVS range and zero duty cycle loss. IEEE Trans. Ind. Appl. 2017, 53, 585–595. [Google Scholar] [CrossRef]
- Vlatkovic, V.; Sabate, J.A.; Ridley, R.B.; Lee, F.C.; Cho, B.H. Small-signal analysis of the phase-shifted PWM converter. IEEE Trans. Power Electron. 1992, 7, 128–135. [Google Scholar] [CrossRef]
- Claassens, J.A.; Hofsajer, I.W. A flux balancer for phase shift ZVS DC-DC converters under transient conditions. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 19–23 March 2006; pp. 523–527. [Google Scholar]
- Panov, Y.; Jovanovi, M.M.; Yueyong, L.G.M. Transformer-flux-balancing control in isolated bidirectional DC-DC converters. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC 2014), Fort Worth, TX, USA, 16–20 March 2014; pp. 49–56. [Google Scholar]
- Kutkut, N.H.; Luckjiff, G. Current mode control of a full bridge DC-to-DC converter with a two inductor rectifier. In Proceedings of the 28th Annual IEEE Power Electronics Specialists Conference, Saint Louis, MO, USA, 22–27 June 1997; pp. 203–209. [Google Scholar]
- Kim, T.; Lee, S.; Choi, W. Design and control of the phase shift full bridge converter for the on-board battery charger of the electric forklift. In Proceedings of the 8th International Conference on Power Electronics—ECCE Asia, Jeju, Korea, 30 May–3 June 2011; pp. 2709–2716. [Google Scholar]
- Jeong, C.-Y. Improved phase-shift pulse-width modulation full-bridge converter using a blocking capacitor. J. KIIEE 2011, 25, 20–29. [Google Scholar]
- Taeed, F.; Nymand, M. Adaptive slope compensation for high bandwidth digital current mode controller. In Proceedings of the 2015 IEEE 11th International Conference on Power Electronics and Drive Systems, Sydney, Australia, 9–12 June 2015; pp. 604–608. [Google Scholar]
- Sun, Y.; Jiao, B. Design of a soft-switched phase-shift full bridge converter. In Proceedings of the 2016 3rd International Conference on Systems and Informatics (ICSAI), Shanghai, China, 19–21 November 2016; pp. 230–234. [Google Scholar]
- Kondrath, N.; Kazimierczuk, M.K. Slope compensation and relative stability of peak current-mode controlled PWM dc-dc converters in CCM. In Proceedings of the 2013 IEEE 56th International Midwest Symposium on Circuits and Systems (MWSCAS), Columbus, OH, USA, 4–7 August 2013; pp. 477–480. [Google Scholar]
- Chen, J.; Hwang, Y.; Liou, J.; Ku, Y.; Yu, C. A new buck converter with optimum-damping and dynamic-slope compensation techniques. IEEE Trans. Ind. Electron. 2017, 64, 2373–2381. [Google Scholar] [CrossRef]
- Kim, M. High-performance current-mode-controller design of buck LED driver with slope compensation. IEEE Trans. Ind. Electron. 2018, 33, 641–649. [Google Scholar] [CrossRef]
- Oh, S.-M.; Ko, J.-H.; Kim, H.-W.; Cho, K.-Y. A Hybrid Current Mode Controller with Fast Response Characteristics for Super Capacitor Applications. Electronics 2019, 8, 112. [Google Scholar] [CrossRef] [Green Version]
- Cho, J.G.; Cho, G.H. Novel off-line zero-voltage switching PWM ac/dc converter for direct conversion from ac line to 48 VDC bus with power factor correction. In Proceedings of the IEEE Power Electronics Specialist Conference—PESC, Seattle, WA, USA, 20–24 June 1993; pp. 689–695. [Google Scholar]
- Cho, J.G.; Sabate, J.; Lee, F.C. Novel zero-voltage transition PWM dc/dc converter for high power applications. In Proceedings of the 1994 IEEE Applied Power Electronics Conference and Exposition—ASPEC, Orlando, FL, USA, 13–17 February 1994; pp. 143–149. [Google Scholar]
- Cho, J.G.; Sabate, J.A.; Hua, G.; Lee, F.C. Zero voltage and zero current switching full bridge PWM converter for high power applications. In Proceedings of the 1994 Power Electronics Specialist Conference—PESC, Taipei, Taiwan, 20–25 June 1994; pp. 102–108. [Google Scholar]










| Parameter | Value | Unit |
|---|---|---|
| Input Voltage | 45 | V |
| Output Voltage | 50 | V |
| Leakage inductance | 20 | uH |
| Magnetizing inductance | 580 | uH |
| Output inductor | 750 | uH |
| Load resister | 10 | Ω |
| Switching frequency | 20 | kHz |
| Max slope | 44,000 | A/s |
| Turns ratio | 2 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, J.-H.; Baek, S.-W.; Lee, K.-M.; Kim, H.-W.; Cho, K.-Y.; Kim, J.-M. Hybrid Current-Mode Control of PSFB Converter to Compensate Slew Interval and Prevent Magnetic Saturation of Transformers. Electronics 2020, 9, 1395. https://doi.org/10.3390/electronics9091395
Ko J-H, Baek S-W, Lee K-M, Kim H-W, Cho K-Y, Kim J-M. Hybrid Current-Mode Control of PSFB Converter to Compensate Slew Interval and Prevent Magnetic Saturation of Transformers. Electronics. 2020; 9(9):1395. https://doi.org/10.3390/electronics9091395
Chicago/Turabian StyleKo, Jae-Hak, Seung-Woo Baek, Kang-Mun Lee, Hag-Wone Kim, Kwan-Yul Cho, and Jae-Moon Kim. 2020. "Hybrid Current-Mode Control of PSFB Converter to Compensate Slew Interval and Prevent Magnetic Saturation of Transformers" Electronics 9, no. 9: 1395. https://doi.org/10.3390/electronics9091395





