On Minimal Entanglement Wedge Cross Section for Holographic Entanglement Negativity

Abstract

We demonstrate the equivalence of two different conjectures in the literature for the holographic entanglement negativity in AdS₃/CFT₂, modulo certain constants. These proposals involve certain algebraic sums of bulk geodesics homologous to specific combinations of subsystems, and the entanglement wedge cross section (EWCS) backreacted by a cosmic brane for the conical defect geometry in the bulk gravitational path integral. It is observed that the former conjectures reproduce the field theory replica technique results in the large central charge limit whereas the latter involves constants related to the Markov gap. In this context, we establish an alternative construction for the EWCS of a single interval in a CFT₂ at a finite temperature to resolve an issue for the latter proposal involving thermal entropy elimination for holographic entanglement negativity. Our construction for the EWCS correctly reproduces the corresponding field theory results modulo the Markov gap constant in the large central charge limit.

1. Introduction

Quantum entanglement has evolved as one of the dominant themes in diverse disciplines from many body condensed matter systems to black holes and quantum gravity. In this context, the entanglement entropy (EE), defined as the von Neumann entropy of the reduced density matrix, has been central to the characterization of pure state entanglement. For mixed states, however, the EE fails to correctly capture the entanglement as it involves irrelevant classical and quantum correlations (e.g., for finite temperature configurations, it includes the thermal correlations). Hence, the characterization of mixed state entanglement has been a significant issue in quantum information theory leading to proposals of various entanglement and correlation measures in the recent past. In this connection, Vidal and Werner [1] proposed a computable mixed state entanglement measure termed entanglement (logarithmic) negativity (EN), which characterized an upper bound on the distillable entanglement.1 It was defined as the logarithm of the trace norm for the partially transposed reduced density matrix. Subsequently, Plenio [2] established that despite being non convex, the entanglement negativity was an entanglement monotone under local operations and classical communication (LOCC), which justified its utility for the characterization of mixed state entanglement.

In a series of communications [3,4,5,6], the authors formulated a replica technique to compute the entanglement entropy in two-dimensional conformal field theories (CFT₂s). The procedure was later extended to configurations with multiple disjoint intervals in [7,8], where it was shown that the entanglement entropy receives non-universal contributions depending on the full operator content of the theory, which were sub-leading in the large central charge limit. A variant of the above replica technique was developed in [9,10,11] to compute the entanglement negativity of bipartite states in CFT₂s. It was also shown in [12] that for the mixed state of two disjoint intervals, the entanglement negativity was non-universal; however, it was possible to isolate a universal contribution in the large central charge limit. Interestingly, the entanglement negativity for this configuration was numerically shown to exhibit a phase transition depending upon the separation of the two intervals [12,13].

In a major development, Ryu and Takayanagi (RT) [14,15] proposed a holographic conjecture for the EE of a subsystem in a dual CFT_d involving the area of a homologous bulk codimension-two static minimal surface (RT surface), in the context of the AdS_d+1/CFT_d correspondence. This significant proposal led to the emergence of the field of holographic quantum entanglement (for a detailed review, see [15,16,17,18]). The RT conjecture was proved initially for the AdS₃/CFT₂ scenario, with later generalization to the AdS_d+1/CFT_d framework in [19,20,21,22]. Hubeny, Rangamani and Takayanagi (HRT) extended the RT conjecture to covariant scenarios in [23], a proof of which was established in [24].

Naturally, the above developments motivated the investigation of a corresponding holographic characterization for the entanglement negativity. One of the first steps in this direction was proposed in [25] for the pure vacuum state of a CFT_d dual to a bulk pure AdS_d+1 geometry although a general prescription for arbitrary bipartite states remained elusive. This significant issue was addressed in [26,27], where a holographic entanglement negativity conjecture and its covariant extension were advanced for bipartite mixed state configurations in the AdS₃/CFT₂ scenario, with the generalization to higher dimensions reported in [28]. These proposals involved certain algebraic sums of bulk geodesics homologous to appropriate combinations of subsystems. A large central charge analysis of the entanglement negativity through the monodromy technique for holographic CFT₂s was established in [29], which provided a strong substantiation for the proposals described above. Subsequently, in a series of works, the above holographic conjectures and their covariant extensions were utilized to obtain the entanglement negativity of various bipartite states in CFT₂s and their higher dimensional generalizations [30,31,32,33,34].

On a different note, motivated by the quantum error correcting codes, an alternate approach involving the backreacted entanglement wedge cross section (EWCS) to compute the holographic entanglement negativity for configurations with spherical entangling surfaces was advanced in [35]. Furthermore, a proof for this proposal, based on the reflected entropy [36], was established in another communication [37]. The entanglement wedge was earlier shown to be the bulk subregion dual to the reduced density matrix of the dual CFTs in [38,39,40,41,42]. Also, the EWCS has been proposed to be the bulk dual of the entanglement of purification (EoP) [43,44] (for recent progress, see [45,46,47,48,49,50,51,52,53,54,55]). The connection of the EWCS to the odd entanglement entropy (OEE) [56] and the reflected entropy [36,57,58,59] has also been explored.

As mentioned above, in [35,37], the authors proposed that for configurations involving spherical entangling surfaces, the holographic entanglement negativity may be expressed in terms of the EWCS backreacted by a cosmic brane for the conical defect of the replicated bulk geometry in a gravitational path integral. Utilizing this conjecture, the authors computed the holographic entanglement negativity for bipartite states in CFT₂s dual to bulk pure AdS₃ geometries and planar BTZ black hole, through the construction described in [43]. Their results for the holographic entanglement negativity following the above construction reproduced the corresponding field theory replica technique results in the large central charge limit, up to certain constants involving the Markov gap between the reflected entropy and the mutual information [60], except for the configuration of a single interval in a finite temperature CFT₂ described in [11]. Specifically, their result for this mixed state configuration missed the subtracted thermal entropy term in the expression for the entanglement negativity [11]. Given that their construction exactly reproduces the replica technique results for all the other mixed state configurations, the mismatch described above requires a resolution.

In this article, we demonstrate the equivalence of the two holographic proposals up to constants involving the Markov gap. In this connection, we also address the intriguing issue of the missing thermal entropy term for the single interval configuration at a finite temperature for the second proposal based on the EWCS through an alternative construction. Our construction is inspired by that of Calabrese et al. [11] and involves two symmetric auxiliary intervals on either side of the single interval under consideration. In this construction, we have utilized certain properties of the EWCS along with a specific relation valid for the dual bulk BTZ black hole geometry. Finally, we implement the bipartite limit, where the auxiliary intervals are allowed to be infinite and constitute the rest of the system, to arrive at the correct minimal EWCS for the configuration in question. The holographic entanglement negativity computed using the conjecture advanced in [35,37] through our alternative construction for the EWCS correctly reproduces the corresponding replica result in [11] mentioned earlier. In particular, we are able to obtain the missing thermal entropy term in the expression for the holographic entanglement negativity described in [11]. We further observe that the monodromy analysis employed by the authors in [37] and that in [29] lead to identical functional forms for the relevant four point correlation function for the twist fields, in the large central charge limit for the mixed state configuration of the single interval at a finite temperature.

This article is organized as follows. In Section 2, we briefly review the definition and holographic constructions involving the bulk geodesics for the entanglement negativity in the AdS₃/CFT₂ scenario. In Section 3, we review the entanglement wedge construction in [43]. In Section 4, we describe the computation of the holographic entanglement negativity based on the EWCS in [35,37] and demonstrate the equivalence of their results with those obtained from the former proposal. Following this, in Section 5, we describe an issue with the holographic entanglement negativity for a single interval at a finite temperature obtained from the EWCS, involving a subtracted thermal entropy term. We further propose an alternative construction of the EWCS for this configuration, which resolves this issue and restores the missing thermal entropy term. Finally, we summarize our results in Section 6 and present our conclusions. In Appendix A, we have included a short review of the derivation for the entanglement negativity of two disjoint intervals in a CFT₂. Additionally, in Appendix B and Appendix C, we briefly describe a sketch of a plausible proof of the holographic entanglement negativity proposal based on bulk geodesics from a gravitational path integral perspective and the issue of the holographic Markov gap.

2. Review of Earlier Literature

In this section, we review the holographic proposals for the entanglement negativity involving certain algebraic sums of the holographic Rényi entropies of order half described by the lengths of backreacting cosmic branes homologous to the subsystems, as described in [61].

2.1. Rényi Entanglement Entropy

Here, we briefly recapitulate the holographic construction for the Rényi entropy which was proposed in [62]. The author in [62] utilized the gravitational path integral technique developed in [22] to demonstrate that the holographic Rényi entropy of a subsystem in a CFT is related to the area of a codimension-two cosmic brane ${\mathcal{C}}_n$ with tension $T_n=\frac{n-1}{4n{G}_N}$ in the replicated bulk geometry, homologous to the subsystem under consideration as

$$\begin{array}{cc}\hfill n^2\frac{\partial }{\partial n}\left(\frac{n-1}{n}{S}^{\left(n\right)}\left(A\right)\right)& =\frac{\mathrm{Area}\left({\mathcal{C}}_n\right)}{4G_N},\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill n^2\frac{\partial }{\partial n}\left(\frac{n-1}{n}{\mathcal{A}}^{\left(n\right)}\right)& =\mathrm{Area}\left({\mathcal{C}}_n\right),\hfill \end{array}$$

(2)

where $S^{\left(n\right)}\left(A\right)$ is the Rényi entanglement entropy of order n for the subsystem A. Note that ${\mathcal{A}}^{\left(n\right)}$ is related to $S^{\left(n\right)}$ as follows:

$$S^{\left(n\right)}=\frac{{\mathcal{A}}^{\left(n\right)}}{4G_N}.$$

(3)

In the replica limit $n\to 1$, the tension vanishes and Equations (1)–(3) reduce to that of the usual RT proposal as

$$S_Y=\frac{{\mathcal{A}}_Y}{4G_N},$$

(4)

where ${\mathcal{A}}_Y$ denotes the area of the minimal surface homologous to the subsystem Y and $G_N$ is the $d+1$ dimensional gravitational constant. However, for $n\ne 1$, the backreaction from the brane is non-zero and it is difficult to determine the area of a cosmic brane homologous to a subsystem of an arbitrary geometry. Interestingly, for subsystems with spherical entangling surfaces, the backreaction was explicitly computed2 in [63], where the holographic Rényi entanglement entropy of a subsystem A in a CFT_d was expressed as

$$S^{\left(n\right)}\left(A\right)={\mathcal{X}}_d^{\left(n\right)}S\left(A\right).$$

(5)

In Equation (5), the proportionality constant has the following form:

$${\mathcal{X}}_d^{\left(n\right)}=\frac{n}{2(n-1)}\left(2-x_n^{d-2}\left(1+x_n^2\right)\right),$$

(6)

where

$$x_n=\frac{1}{nd}\left(1+\sqrt{1-2d{n}^2+d^2{n}^2}\right).$$

(7)

In the AdS₃/CFT₂ scenario, the holographic Rényi entropy of order half is given as

$$\begin{array}{cc}\hfill S^{(1/2)}\left(A\right)& ={\mathcal{X}}_d^{(1/2)}S\left(A\right)\hfill \\ \hfill & =\frac{3}{2}S\left(A\right)\hfill \\ \hfill & =\frac{3}{8G_N}{\mathcal{L}}_A,\hfill \end{array}$$

(8)

where in the second line, we have used Equations (6) and (7) to determine the constant ${\mathcal{X}}_2=3/2$ and ${\mathcal{L}}_A$ denotes the length of the geodesic homologous to the subsystem A.

2.2. Entanglement Negativity (EN) in a CFT₂

In this subsection, we provide a brief review of the definition of the entanglement negativity and its computation in a CFT₂. In this connection, we consider a tripartite system $ABC$ in a pure state, comprising the subsystems A, B, and C. The reduced density matrix ${\rho }_{AB}$ for the mixed state bipartite configuration $AB\equiv A\cup B$ may then be obtained by tracing over the subsystem C. The relevant Hilbert space is given by ${\mathcal{H}}_{AB}={\mathcal{H}}_A\otimes {\mathcal{H}}_B$, where ${\mathcal{H}}_{A,B}$ represents the Hilbert space for the subsystem $A,B$ respectively. The partial transpose of the reduced density matrix ${\rho }_{AB}$, denoted by ${\rho }_{AB}^{T_B}$, may then be defined as follows:

$$〈e_i^{\left(A\right)}{e}_j^{\left(B\right)}\left|{\rho }_{AB}^{T_B}\right|e_k^{\left(A\right)}{e}_l^{\left(B\right)}〉=〈e_i^{\left(A\right)}{e}_l^{\left(B\right)}\left|{\rho }_{AB}\right|e_k^{\left(A\right)}{e}_j^{\left(B\right)}〉,$$

(9)

where $|e_i^{(A,B)}\rangle$ describes the basis for ${\mathcal{H}}_{A,B}$, respectively. The entanglement negativity between the subsystems A and B is then defined in terms of the trace norm3 of the partially transposed reduced density matrix ${\rho }_{AB}^{T_B}$ as follows:

$$\mathcal{E}(A:B)=log∥{\rho }_{AB}^{T_B}∥.$$

(10)

In this context, we introduce below the definition of the Rényi entanglement negativity (REN) of order k following [9,10] as

$${\mathcal{N}}^{\left(k\right)}(A:B)=\mathrm{Tr}\left[{\left({\rho }_{AB}^{T_B}\right)}^k\right],$$

(11)

where k is a positive integer. The EN as defined in Equation (10) may then be expressed in terms of the REN as

$$\mathcal{E}(A:B)=\underset{n_e\to 1}{lim}log\left[{\mathcal{N}}^{\left(n_e\right)}(A:B)\right]=\underset{n_e\to 1}{lim}log\left[\mathrm{Tr}{\left({\rho }_{AB}^{T_B}\right)}^{n_e}\right].$$

(12)

Note that the right-hand side of Equation (12) indicates the analytic continuation of the REN of even orders, denoted by $n_e\in 2{\mathbb{Z}}^{+}$, to $n_e=1$.

For a CFT₂, the authors in [9,10,11] developed a replica technique involving $n_e\in 2{\mathbb{Z}}^{+}$ replicas of the original complex manifold $\mathcal{M}$ with branch cuts along A and B. The trace in Equation (12) may then be evaluated in terms of certain twist field correlators involving the end points of A and B. For example, in a zero-temperature CFT₂, when the subsystems (intervals in a CFT₂) $A=[a_1,a_2]$ and $B=[b_1,b_2]$ are disjoint, the entanglement negativity is given by the following four-point twist correlator:

$$\mathcal{E}(A:B)=\underset{n_e\to 1}{lim}log〈{\mathcal{T}}_{n_e}\left(a_1\right){\overline{\mathcal{T}}}_{n_e}\left(a_2\right){\overline{\mathcal{T}}}_{n_e}\left(b_1\right){\mathcal{T}}_{n_e}\left(b_2\right)〉,$$

(13)

where ${\mathcal{T}}_{n_e}$ and ${\overline{\mathcal{T}}}_{n_e}$ are twist and anti-twist operators, respectively.

2.3. Holographic Entanglement Negativity (HEN)

As discussed earlier, a replica technique proposed in [9,10] was utilized to compute the entanglement negativity for various pure and mixed state configurations of a CFT₂. Following this, several holographic proposals for the entanglement negativity of various configurations were advanced in [26,30,32] in terms of appropriate algebraic sums of the lengths of bulk geodesics in the AdS₃/CFT₂ framework. For example, the holographic entanglement negativity of two disjoint intervals A and B in proximity is given by [32]

$$\begin{array}{cc}\hfill \mathcal{E}& =\left.\frac{3}{16G_N}[{\mathcal{L}}_{A\cup C}+{\mathcal{L}}_{B\cup C}-{\mathcal{L}}_{A\cup B\cup C}-{\mathcal{L}}_C\right]\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & =\left.\frac{3}{4}[S(A\cup C)+S(B\cup C)-S(A\cup B\cup C)-S\left(C\right)\right],\hfill \end{array}$$

(15)

where C denotes the interval sandwiched between A and B. From the discussion in Section 2.1, it is clear that we may re-express the conjecture given in Equation (14) as follows:

$$\mathcal{E}=\left.\frac{{\mathcal{X}}_2}{8G_N}[{\mathcal{L}}_{A\cup C}+{\mathcal{L}}_{B\cup C}-{\mathcal{L}}_{A\cup B\cup C}-{\mathcal{L}}_C\right].$$

In the AdS₃/CFT₂ scenario, we now utilize the result given in Equation (8) to rewrite the above expression in the following way:

$$\begin{array}{cc}\hfill \mathcal{E}& =\frac{1}{8G_N}\left[{\mathcal{L}}_{A\cup C}^{(1/2)}+{\mathcal{L}}_{B\cup C}^{(1/2)}-{\mathcal{L}}_{A\cup B\cup C}^{(1/2)}-{\mathcal{L}}_C^{(1/2)}\right]\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & =\frac{1}{2}\left[S^{(1/2)}(A\cup C)+S^{(1/2)}(B\cup C)-S^{(1/2)}(A\cup B\cup C)-S^{(1/2)}\left(C\right)\right].\hfill \end{array}$$

(17)

Following the same procedure as above, we may re-express the holographic conjecture for the entanglement negativity of two adjacent intervals in [30] as

$$\mathcal{E}=\frac{1}{2}\left[S^{(1/2)}\left(A\right)+S^{(1/2)}\left(B\right)-S^{(1/2)}(A\cup B)\right].$$

(18)

Similarly, the holographic conjecture for the entanglement negativity of a single interval described in [26] may be expressed as follows:

$$\mathcal{E}=\underset{B_1\cup B_2\to A^c}{lim}\left.\frac{1}{2}[2S^{(1/2)}\left(A\right)+S^{(1/2)}\left(B_1\right)+S^{(1/2)}\left(B_2\right)-S^{(1/2)}(A\cup B_1)-S^{(1/2)}(A\cup B_2)\right].$$

(19)

A plausible derivation of these proposals as expressed in Equations (17)–(19), based on the replica symmetry breaking saddles for a gravitational path integral for spherical entangling surfaces, is described briefly in Appendix B.4

As mentioned earlier in Section 1, the above holographic proposals for the entanglement negativity were further generalized to covariant scenarios in [27,31,33]. Additionally, these holographic proposals were extended to the general AdS_d+1/CFT_d framework in terms of similar algebraic sums of the areas of bulk RT surfaces for certain combinations of the subsystems [28,34].

3. Entanglement Wedge Cross Section (EWCS)

We begin this section by reviewing the construction for the bulk entanglement wedge cross section (EWCS) in AdS/CFT described in [43,44]. To this end, spatial subsystems A and B need to be considered in a CFT_d dual to static bulk AdS_d+1 geometry. Let $\Xi$ be a constant time slice in the bulk and ${\Gamma }_{AB}$ be an RT surface for the subsystem $A\cup B$. Then, the codimension-one spatial region in $\Xi$ bounded by $A\cup B\cup {\Gamma }_{AB}$ is described as the entanglement wedge for subsystems A and B. Finally, we consider the minimal area surface ${\Sigma }_{AB}^{\min }$ which terminates on the boundary of the entanglement wedge, dividing the total entanglement wedge into two parts, as illustrated in Figure 1.

The entanglement wedge cross section (EWCS), denoted by $E_W$, may then be defined as5

$$E_W(A:B)=\frac{\mathrm{Area}\left({\Sigma }_{AB}^{\min }\right)}{4G_N},$$

(20)

where $G_N$ is the Newton constant. The reduced density matrix ${\rho }_{AB}$ is dual to the corresponding entanglement wedge [38,39,40]. Note that the entanglement wedge includes the bulk region, which is defined as the domain of dependence for the space-like homology surface $R_A$ bounded by subsystem A and its RT surface ${\Gamma }_A$. Some of the properties of the EWCS are listed below [43,44].

• For a pure state ${\rho }_{AB}$, $E_W$ is equal to the entanglement entropy:

  $$E_W(A:B)=S\left(A\right)=S\left(B\right).$$

  (21)
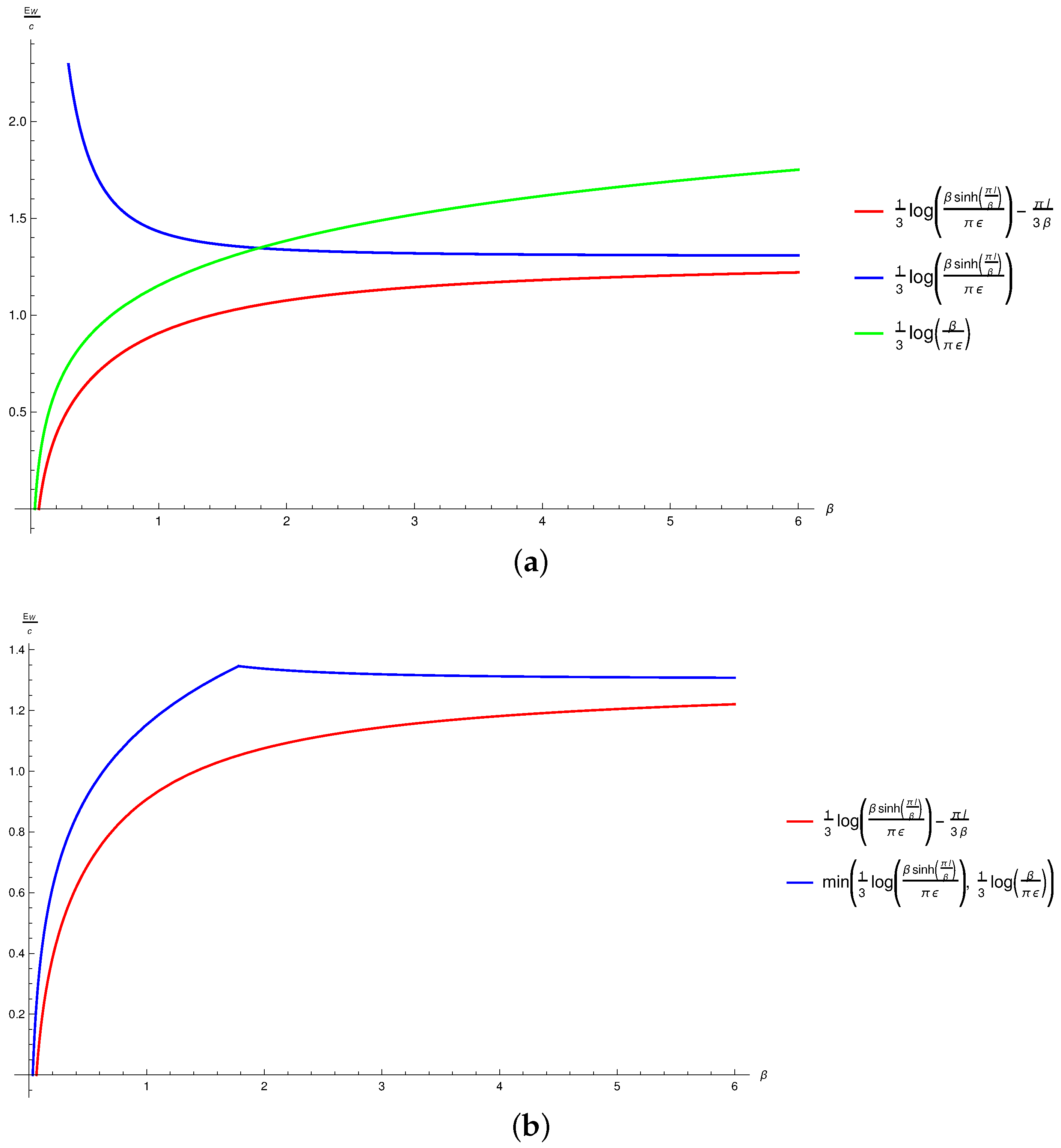
• For a mixed state ${\rho }_{AB}$, $E_W$ is bounded above by the entanglement entropy:

  $$E_W(A:B)\le min[S\left(A\right),S\left(B\right)].$$

  (22)
• For a mixed state ${\rho }_{AB}$, $E_W$ is bounded below by half the mutual information:

  $$E_W(A:B)\ge \frac{I(A:B)}{2}.$$

  (23)
• $E_W$ is monotonic, i.e., it never increases upon discarding a subsystem:

  $$E_W(A:BC)\ge E_W(A:B).$$

  (24)
• For a tripartite system, $E_W$ has the following bound:

  $$E_W(A:BC)\ge \frac{I(A:B)}{2}+\frac{I(A:C)}{2}.$$

  (25)
• In a bipartite state that saturates the Araki–Lieb inequality, $S\left(AB\right)=\left|S\right(A)-S(B\left)\right|$, we have $E_W(A:B)=min[S\left(A\right),S\left(B\right)]$.
• For a tripartite pure state, the $E_W$ is polygamous:

  $$E_W(A:BC)\le E_W(A:B)+E_W(A:C).$$

  (26)

Note that these properties conform to the properties of the entanglement of purification (EoP) described in quantum information theory [64].

3.1. Computation of the EWCS

We now proceed to review the computation of the EWCS in the AdS₃/CFT₂ scenario. For this purpose, a configuration of two subsystems A and B at zero temperature needs to be considered in the dual CFT₂ vacuum. These subsystems are described by spatial intervals $A=[a_1,a_2]$ and $B=[b_1,b_2]$ with lengths $l_1$ and $l_2$, respectively, and are separated by distance d. The bulk dual for this case is a pure AdS₃ geometry in Poincaré coordinates whose metric on a constant time slice is given by

$$d{s}^2=\frac{d{x}^2+d{z}^2}{z^2},$$

(27)

where we have set the AdS₃ radius $R=1$. When the mutual information $I(A:B)>0$, the entanglement wedge remains connected; otherwise, it is disconnected. The EWCS for this configuration may be expressed as [43]

$$E_W(A:B)=\left\{\begin{array}{cc}{\displaystyle \frac{c}{6}ln\left(1+2z+2\sqrt{z(z+1)}\right),}\hfill & z>1,\hfill \\ \\ 0,\hfill & 0<z<1,\hfill \end{array}\right.$$

(28)

where the conformal cross ratio z is given by

$$z=\frac{(a_2-a_1)(b_2-b_1)}{(b_1-a_2)(b_2-a_1)}=\frac{l_1{l}_2}{d(l_1+l_2+d)}.$$

(29)

Note that Equation (28) may be rewritten in the following form [35,65]:

$$E_W=\left\{\begin{array}{cc}{\displaystyle \frac{c}{6}ln\frac{1+\sqrt{x}}{1-\sqrt{x}},}\hfill & 1/2<x<1,\hfill \\ \\ 0,\hfill & 0<x<1/2,\hfill \end{array}\right.$$

(30)

where the cross ratio

$$x=\frac{(a_2-a_1)(b_2-b_1)}{(b_1-a_1)(b_2-a_2)}=\frac{l_1{l}_2}{(l_1+d)(l_2+d)}$$

(31)

is related to z through $z=x/(1-x)$.

For a finite temperature state in a CFT₂ defined on an infinite line, the bulk dual is a planar BTZ black hole (black string) whose metric is given as

$$d{s}^2=\frac{1}{z^2}\left(-f\left(z\right)d{t}^2+\frac{d{z}^2}{f\left(z\right)}+d{x}^2\right),f\left(z\right)\equiv 1-z^2/z_H^2,$$

(32)

where the event horizon is located at $z=z_H$ and $z_H$ is related to the inverse temperature $\beta$ as $\beta =2\pi z_H$. The EWCS corresponding to the intervals $A=[a_1,a_2]$ and $B=[b_1,b_2]$ in a dual CFT₂ is given as follows [43]:

$$E_W(A:B)=\frac{c}{6}ln\left(1+2\zeta +2\sqrt{\zeta (\zeta +1)}\right),$$

(33)

with $\zeta$ given as

$$\zeta \equiv \frac{sinh\left(\frac{\pi (a_2-a_1)}{\beta }\right)sinh\left(\frac{\pi (b_2-b_1)}{\beta }\right)}{sinh\left(\frac{\pi (b_1-a_2)}{\beta }\right)sinh\left(\frac{\pi (b_2-a_1)}{\beta }\right)}=\frac{sinh\left(\frac{\pi l_1}{\beta }\right)sinh\left(\frac{\pi l_2}{\beta }\right)}{sinh\left(\frac{\pi d}{\beta }\right)sinh\left(\frac{\pi (l_1+l_2+d)}{\beta }\right)}.$$

(34)

3.1.1. EWCS for Two Disjoint Intervals

For this configuration, we will only describe the scenario where the two disjoint intervals are in proximity, which corresponds to the regime $x\approx 1$ following [10,12]. It was shown there that the entanglement negativity obtained through a replica technique in a CFT₂ was non-universal, and a dominant universal form could be obtained only for the above proximity regime in the large central charge limit. Note that, as explained in [10,12], the regime $x\approx 1$ involves $l_1,l_2>>d$.6 In this regime, the EWCS for the two disjoint intervals in proximity is then obtained from Equation (30) as follows:

$$E_W(A:B)=\frac{c}{6}ln\left(\frac{1}{1-x}\right)+\frac{c}{6}ln4.$$

(35)

The EWCS for two disjoint intervals in proximity at zero temperature in a dual CFT₂ may be derived by substituting Equation (31) into Equation (35) as follows:

$$E_W(A:B)=\frac{c}{6}ln\left[\frac{(l_1+d)(l_2+d)}{d(l_1+l_2+d)}\right]+\frac{c}{6}ln4.$$

(36)

For the intervals A and B in a finite size system of length L at zero temperature, the EWCS may be obtained via the conformal map from the plane to cylinder $z\to w=(iL/2\pi )lnz$ from Equation (35) as

$$E_W(A:B)=\frac{c}{6}ln\left[\frac{sin\left(\frac{\pi (l_1+d)}{L}\right)sin\left(\frac{\pi (l_2+d)}{L}\right)}{sin\left(\frac{\pi d}{L}\right)sin\left(\frac{\pi (l_1+l_2+d)}{L}\right)}\right]+\frac{c}{6}ln4.$$

(37)

The EWCS for two disjoint intervals in proximity at a finite temperature may be obtained from Equation (35) by employing the conformal transformation $z\to w=(\beta /2\pi )lnz$ from the plane to the cylinder. It is then given by

$$E_W(A:B)=\frac{c}{6}ln\left[\frac{sinh\left(\frac{\pi (l_1+d)}{\beta }\right)sinh\left(\frac{\pi (l_2+d)}{\beta }\right)}{sinh\left(\frac{\pi d}{\beta }\right)sinh\left(\frac{\pi (l_1+l_2+d)}{\beta }\right)}\right]+\frac{c}{6}ln4.$$

(38)

3.1.2. EWCS for Two Adjacent Intervals

The mixed state configuration of two adjacent intervals may be constructed from the corresponding disjoint setup by taking the adjacent limit $d\to ϵ$, where $ϵ$ is the UV cutoff of the CFT₂ in the boundary. The EWCS for this configuration may now be obtained from Equation (36) as follows:

$$E_W(A:B)=\frac{c}{6}ln\left(\frac{l_1{l}_2}{ϵ(l_1+l_2)}\right)+\frac{c}{6}ln4.$$

(39)

By taking the adjacent limit $d\to ϵ$ in Equation (37), the EWCS for two adjacent intervals in a finite size system of length L may expressed as

$$E_W(A:B)=\frac{c}{6}ln\left[\left(\frac{L}{\pi ϵ}\right)\frac{sin\left(\frac{\pi l_1}{L}\right)sin\left(\frac{\pi l_2}{L}\right)}{sin\left(\frac{\pi (l_1+l_2)}{L}\right)}\right]+\frac{c}{6}ln4.$$

(40)

The EWCS for two adjacent intervals at a finite temperature may be computed from Equation (38) by taking the adjacent limit $d\to ϵ$ as follows:

$$E_W(A:B)=\frac{c}{6}ln\left[\left(\frac{\beta }{\pi ϵ}\right)\frac{sinh\left(\frac{\pi l_1}{\beta }\right)sinh\left(\frac{\pi l_2}{\beta }\right)}{sinh\left(\frac{\pi (l_1+l_2)}{\beta }\right)}\right]+\frac{c}{6}ln4.$$

(41)

3.1.3. EWCS for a Single Interval

The EWCS for a pure state configuration of a single interval A of length l at zero temperature may be obtained from the property of the EWCS for a pure state, as described in Equation (21). It is given as

$$E_W(A:B)=S\left(A\right)=\frac{c}{3}ln\left(\frac{l}{ϵ}\right).$$

(42)

Similarly, the EWCS for a pure state configuration of a single interval A in a finite size system of length L may be computed using Equation (21) and given by

$$E_W(A:B)=\frac{c}{3}ln\left(\frac{L}{\pi ϵ}sin\frac{\pi l}{L}\right).$$

(43)

Subsequently, the authors in [43] proposed the EWCS for a mixed state configuration of a single interval A of length l at finite temperature as the minimum of two possible candidates, as expressed below:

$$E_W(A:B)=\frac{c}{3}min\left[ln\left(\frac{\beta }{\pi ϵ}\right),ln\left(\frac{\beta }{\pi ϵ}sinh\frac{\pi l}{\beta }\right)\right].$$

(44)

The EWCS construction for this configuration will be described in detail in Section 4.3.3.

4. HEN from EWCS in AdS₃/CFT₂

In this section, we describe the construction in [35,37], which proposed the entanglement wedge cross section as the holographic dual of entanglement negativity. The authors in [43,44] had demonstrated that the EWCS was dual to the entanglement of purification (EoP) and followed all the properties of the EoP in quantum in formation theory [64]. Motivated by these developments and results from quantum error correcting codes, the authors in [35,37] conjectured that the EWCS backreacted by a bulk cosmic brane for the conical defect geometry is also dual to the entanglement negativity for configurations involving spherical entangling surfaces. The holographic entanglement negativity for the corresponding dual CFTs was then expressed in terms of the bulk EWCS as follows [35,37]:

$$\mathcal{E}={\mathcal{X}}_d{E}_W,$$

(45)

where ${\mathcal{X}}_d$ is the same dimension-dependent constant described in Section 2.1. The above conjecture was substantiated more concisely for holographic CFTs as [37]

$$\mathcal{E}=\frac{S_R^{(1/2)}}{2},$$

(46)

where $S_R$ is a correlation measure termed as the reflected entropy and $S_R^{(1/2)}$ is the Rényi reflected entropy of order half. In the next few subsections, we briefly review the computation of the holographic entanglement negativity from the EWCS for various bipartite states described by two disjoint intervals, two adjacent intervals, and a single interval in the context of the AdS₃/CFT₂ scenario.

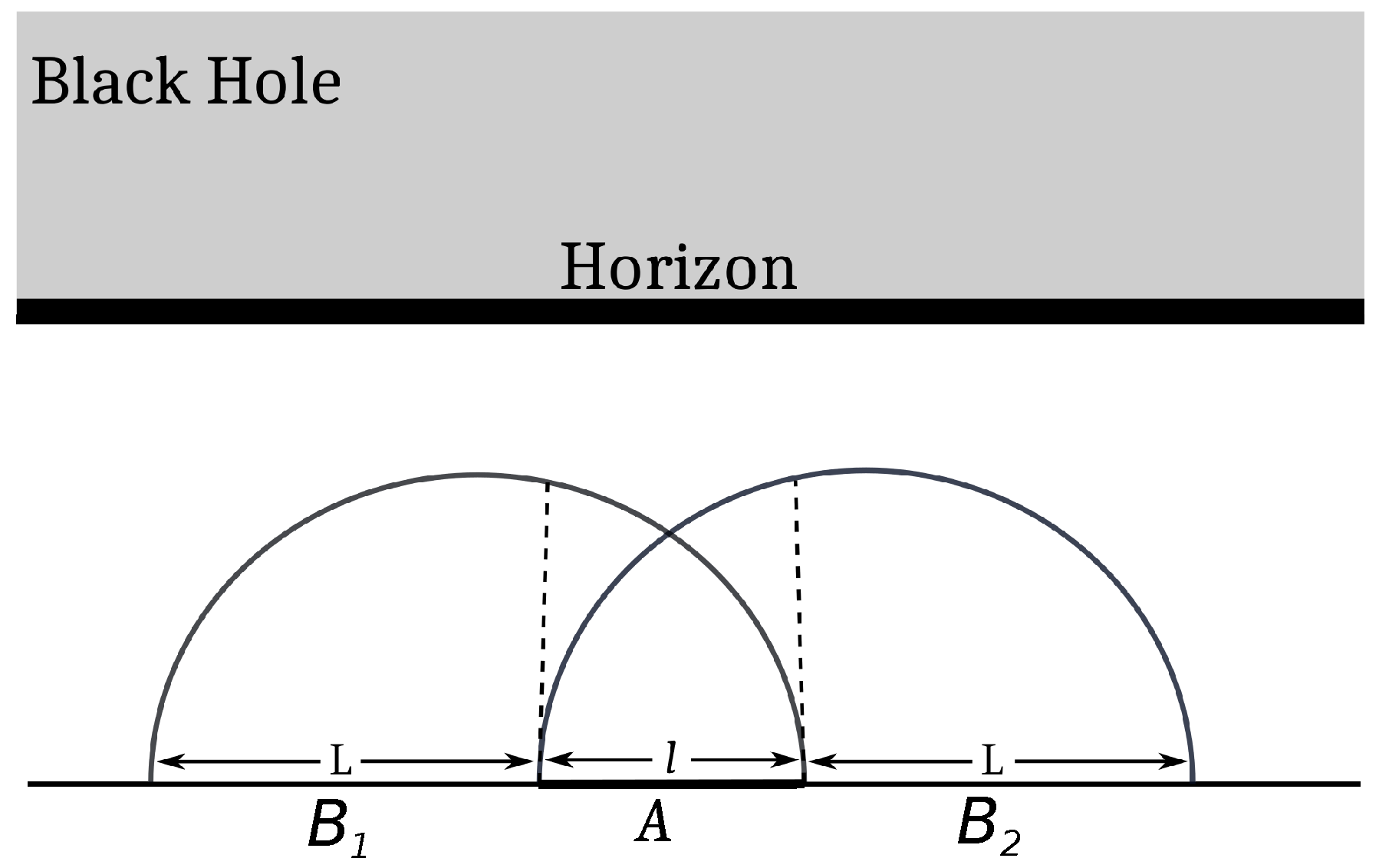
4.1. Negativity for Two Disjoint Intervals

4.1.1. Zero Temperature

The computation of the entanglement negativity for two disjoint intervals involves the four-point twist correlator whose explicit form contains an arbitrary non-universal function of the cross ratio and depends on the full operator content of the corresponding CFT₂. Using Zamolodchikov recursion relations, the authors in [37] have numerically shown that the entanglement negativity for disjoint intervals is proportional to the EWCS. However, a recent development indicates the presence of an extra additive constant in the EWCS for two disjoint intervals in a CFT₂, which may be determined through careful bulk computation [60]. As described earlier in Section 3.1.1, the entanglement negativity for two disjoint intervals in a CFT₂ is non-universal for general values of the cross ratio x and a universal divergent behavior in the large central charge limit may be obtained for the regime $x\approx 1$, where the intervals are in proximity ($l_1,l_2>>d$).7 For this regime on using Equations (35) and (45), the holographic entanglement negativity for the mixed state of two disjoint intervals in proximity at zero temperature may be expressed as

$$\mathcal{E}=\frac{c}{4}ln\left[\frac{(l_1+d)(l_2+d)}{d(l_1+l_2+d)}\right]+\frac{c}{4}ln4,$$

(47)

where $l_1$, $l_2$ are lengths of the intervals, and d is the length of the separation between intervals A and B. Note that the above result is cutoff-independent. The above result matches with the corresponding CFT₂ replica result [9,10,12] obtained with the monodromy technique for the t channel in the regime $x\approx 1$ modulo the second constant term. As discussed in Section 1, the constant second term in Equation (47) arises from the Markov gap.8 However, the result of holographic entanglement negativity for the two disjoint intervals obtained in [32] matches exactly with the corresponding field theory replica technique results. This illustrates the equivalence of the two holographic proposals for the entanglement negativity expressed in Equations (17) and (45) up to an additive constant.

4.1.2. Finite Size

The holographic entanglement negativity for the configuration of two disjoint intervals in a finite size CFT₂ may be obtained using Equations (37) and (45) as

$$\mathcal{E}=\frac{c}{4}ln\left[\frac{sin\left(\frac{\pi (l_1+d)}{L}\right)sin\left(\frac{\pi (l_2+d)}{L}\right)}{sin\left(\frac{\pi d}{L}\right)sin\left(\frac{\pi (l_1+l_2+d)}{L}\right)}\right]+\frac{c}{4}ln4.$$

(48)

Note again that the result in Equation (48) is cutoff-independent. We observe again that apart from the constant term, the holographic entanglement negativity for two disjoint intervals in Equation (48) matches with the corresponding result from an earlier alternative proposal described in Equation (17) [32], demonstrating their equivalence.

4.1.3. Finite Temperature

For the mixed state configuration of two disjoint intervals at a finite temperature, the holographic entanglement negativity may be computed using Equations (38) and (45) as

$$\mathcal{E}=\frac{c}{4}ln\left[\frac{sinh\left(\frac{\pi (l_1+d)}{\beta }\right)sinh\left(\frac{\pi (l_2+d)}{\beta }\right)}{sinh\left(\frac{\pi d}{\beta }\right)sinh\left(\frac{\pi (l_1+l_2+d)}{\beta }\right)}\right]+\frac{c}{4}ln4.$$

(49)

Note that the expression in Equation (49) is once again cutoff-independent. The above equation matches with the entanglement negativity obtained by the field theory replica technique in CFT₂s [10], modulo the additive constant in the large central charge limit. Once again, we observe that the holographic entanglement negativity in Equation (49) matches with that obtained from the alternative proposal described in Equation (17) [32] modulo the constant term, establishing their equivalence.

4.2. Negativity for Two Adjacent Intervals

4.2.1. Zero Temperature

The holographic entanglement negativity for the bipartite mixed state configuration described by two adjacent intervals at zero temperature in a CFT₂ may be obtained from the backreacted EWCS using Equations (39) and (45) as follows:

$$\mathcal{E}=\frac{c}{4}ln\left(\frac{l_1{l}_2}{ϵ(l_1+l_2)}\right)+\frac{c}{4}ln4,$$

(50)

where $ϵ$ is the UV cutoff. We observe that the above result matches with the entanglement negativity obtained by the field theory replica technique in the large central charge limit [10] modulo the constant term related to the holographic Markov gap (see Appendix C). Note, however, that the holographic entanglement negativity for this mixed state configuration obtained through the alternate conjecture involving an algebraic sum of lengths of bulk geodesics in [30] matches exactly with the field theory results in the large c limit. This demonstrates the equivalence of the two holographic proposals for the entanglement negativity modulo the constant from the Markov gap.

4.2.2. Finite Size

The holographic entanglement negativity for the configuration of two adjacent intervals for a finite size CFT₂ may be obtained using Equations (40) and (45) as

$$\mathcal{E}=\frac{c}{4}ln\left[\left(\frac{L}{\pi ϵ}\right)\frac{sin\left(\frac{\pi l_1}{L}\right)sin\left(\frac{\pi l_2}{L}\right)}{sin\left(\frac{\pi (l_1+l_2)}{L}\right)}\right]+\frac{c}{4}ln4,$$

(51)

where $ϵ$ is the UV cutoff. The above result also matches with the corresponding replica technique results [10] in the large central charge limit up to the Markov gap constant. Note that the above result in Equation (51) modulo the constant may also be obtained using the alternative proposal described in Equation (18) [30] which involves an algebraic sum of lengths of the bulk geodesics homologous to appropriate combinations of the intervals and illustrates their equivalence.

4.2.3. Finite Temperature

The EWCS for two adjacent intervals at a finite temperature may be computed from Equation (33) by taking the adjacent limit $d\to ϵ$. Now, using Equation (45), the holographic entanglement negativity for the finite temperature mixed state configuration of two adjacent intervals in a CFT₂ may be expressed as

$$\mathcal{E}=\frac{c}{4}ln\left[\left(\frac{\beta }{\pi ϵ}\right)\frac{sinh\left(\frac{\pi l_1}{\beta }\right)sinh\left(\frac{\pi l_2}{\beta }\right)}{sinh\left(\frac{\pi (l_1+l_2)}{\beta }\right)}\right]+\frac{c}{4}ln4,$$

(52)

where $ϵ$ is the UV cutoff. As discussed earlier, the constant second term in the above equation may be related to the holographic Markov gap. The first term in Equation (52) matches with the corresponding result for holographic entanglement negativity in [30] using the alternate construction given in Equation (18) and the CFT₂ replica technique result [10] in the large central charge limit. This once again demonstrates the equivalence of the two holographic entanglement negativity proposals modulo the Markov gap constant.

4.3. Negativity for a Single Interval

In this section, we consider the bipartite configuration of a single interval in a dual CFT₂. To this end, the system $A\cup B$, which includes the interval A of length l, with the rest of the system denoted as B, needs to be considered.

4.3.1. Zero Temperature

The holographic entanglement negativity for the pure state of a single interval A in a CFT₂ at zero temperature may be obtained by considering the property of the EWCS described in Equation (21). Utilizing the holographic prescription from Equation (45) and the expression for the corresponding EWCS in Equation (42), the entanglement negativity for this pure state is given as

$$\mathcal{E}=\frac{c}{2}ln\left(\frac{l}{ϵ}\right).$$

(53)

The above result matches exactly with the corresponding CFT₂ replica technique result, as described in [9,10], in the large central charge limit. Interestingly, here, we observe the absence of any contribution related to the holographic Markov gap as the configuration of a single interval in zero temperature CFT₂ is in a pure state. Thus, the holographic entanglement negativity in Equation (53) matches with that obtained from the alternative proposal in Equation (19) [26], once again illustrating their equivalence.

4.3.2. Finite Size

The holographic entanglement negativity for the pure state configuration of a single interval in a finite size system may be computed using Equations (43) and (45) as follows:

$$\mathcal{E}=\frac{c}{3}ln\left(\frac{L}{\pi ϵ}sin\frac{\pi l}{L}\right).$$

(54)

Note that the above result may also be obtained using the alternative holographic proposal, as described in Equation (19).

4.3.3. Finite Temperature

We begin with a brief review of the entanglement wedge construction in the context of a single interval in a CFT₂ at a finite temperature, dual to a bulk planar BTZ black hole, as described in [43]. The authors in [43] considered the bipartition (Figure 2) comprising a single interval (of length l), denoted by A, with the rest of the system denoted by B. Note that in [43], ${\Sigma }_{AB}^{\min }$, the minimal cross section of the entanglement wedge for the intervals A and B, has two possible candidates. The first one, denoted by ${\Sigma }_{AB}^{\left(1\right)}$, is the union of the two dotted lines depicted in Figure 2, while the other one, ${\Sigma }_{AB}^{\left(2\right)}$, is given by the RT surface ${\Gamma }_A$. Then, the EWCS is given as [43]

$$\begin{array}{cc}\hfill E_W(A:B)& =\frac{c}{3}min\left[\mathrm{Area}\left({\Sigma }_{AB}^{\left(1\right)}\right),\mathrm{Area}\left({\Sigma }_{AB}^{\left(2\right)}\right)\right]\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill & =\frac{c}{3}min\left[ln\left(\frac{\beta }{\pi ϵ}\right),ln\left(\frac{\beta }{\pi ϵ}sinh\frac{\pi l}{\beta }\right)\right],\hfill \end{array}$$

(56)

where $ϵ$ is the UV cutoff and $\beta$ is the inverse temperature.

Using the result of Equation (56), the authors in [35,37] described the holographic entanglement negativity of the single interval in a CFT₂ at a finite temperature as

$$\mathcal{E}=\frac{c}{2}min\left[ln\left(\frac{\beta }{\pi ϵ}sinh\frac{\pi l}{\beta }\right),ln\left(\frac{\beta }{\pi ϵ}\right)\right].$$

(57)

The authors substantiated their results utilizing the monodromy technique to extract the dominant contribution in the s and t channels for the relevant four-point twist correlator. However, the above results do not exactly reproduce the corresponding replica technique results for the mixed state configuration in question described in [11] except in the low- and high-temperature limits. Specifically, the subtracted thermal entropy term is missing from the holographic entanglement negativity and this issue requires further analysis. In Section 5, we will carefully investigate the above issue for the computation of the holographic entanglement negativity from the EWCS in [35,37] for the configuration in question.

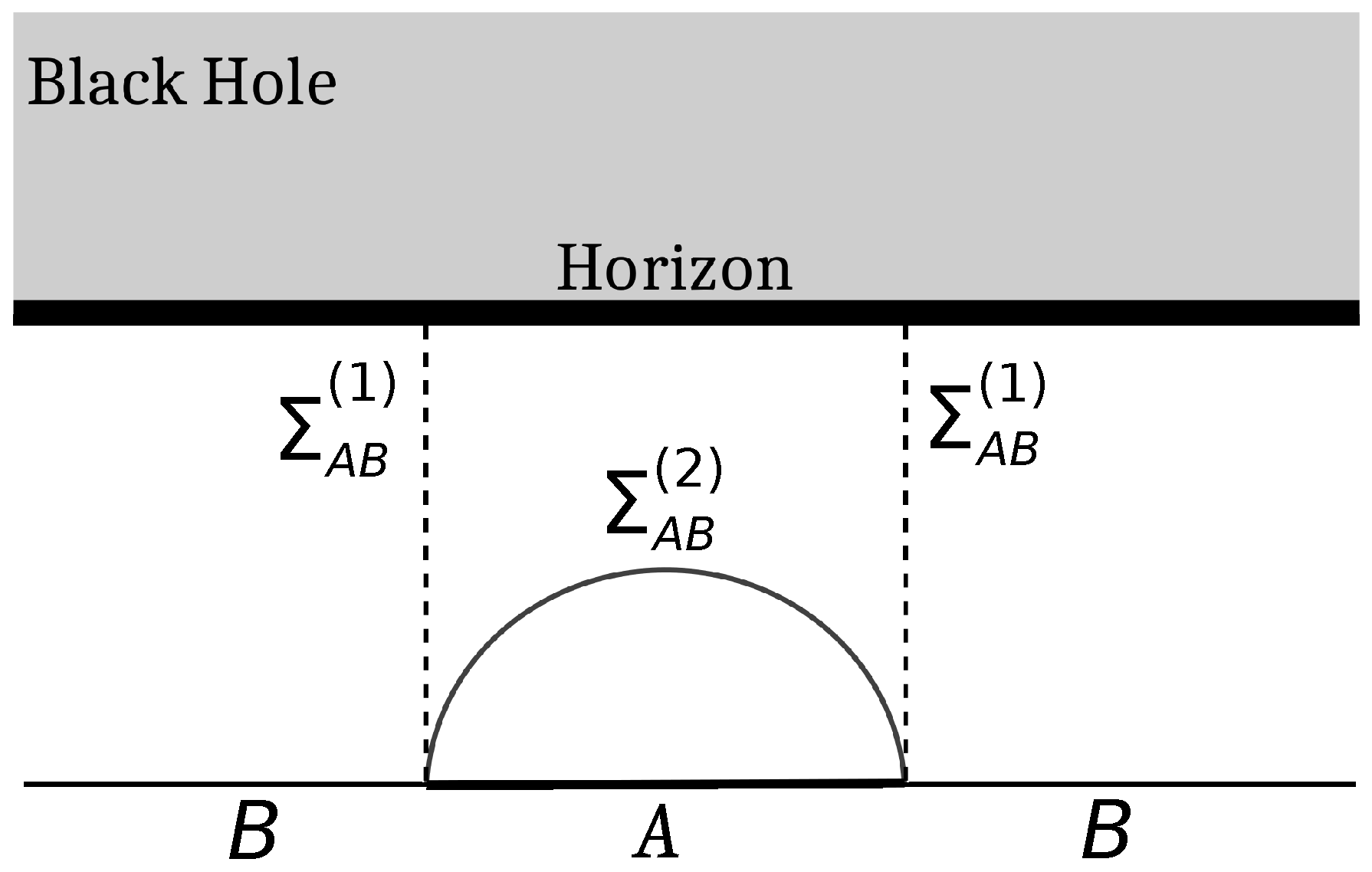
5. Issue with the Thermal Entropy Term

Calabrese, Cardy, and Tonni in a significant communication [11] computed the entanglement negativity of a single interval (of length l) for a CFT₂ at a finite temperature, which is given by

$$\mathcal{E}=\frac{c}{2}ln\left(\frac{\beta }{\pi ϵ}sinh\frac{\pi l}{\beta }\right)-\frac{\pi cl}{2\beta }+f\left(e^{-2\pi l/\beta }\right)+2ln{c}_{1/2},$$

(58)

where $ϵ$ is the UV cutoff. Here, f is an arbitrary function and $c_{1/2}$ is a constant, which are non-universal and depend on the full operator content of the theory.

Comparing Equation (57) with Equation (58), we note that the holographic entanglement negativity, as computed from Equation (45), does not match exactly9 with the corresponding replica technique result reported in [11], in the large central charge limit. Specifically, the subtracted thermal entropy term in the large c replica technique result is missing in the expression for the holographic entanglement negativity of a single interval at a finite temperature described in [35,37]. One may further observe that the entanglement negativity in Equation (58) reduces to that in Equation (57) only in the specific limits of low temperature ($\beta \to \infty$) and high temperature ($\beta \to 0$). In the next subsection, we briefly describe the monodromy analysis of the four-point twist correlator relevant for this configuration towards a resolution of the above issue with the subtracted thermal entropy term for the entanglement negativity.

5.1. Large Central Charge Limit

We begin by reviewing the results obtained through the monodromy technique employed in [37] to compute the entanglement negativity of a single interval, as given in Equation (57). To this end, two auxiliary intervals $B_1=[-L,0]$ and $B_2=[l,L]$ on either side of the single interval $A=[0,l]$ (see [11] for details) need to be considered. The rest of the system is denoted by $B\equiv B_1\cup B_2$. Finally, we implement the bipartite limit $B\to A^c$ through $L\to \infty$ to arrive at the required configuration for the single interval A and the rest of the system $B=A^c$. The entanglement negativity of a single interval at zero temperature in a CFT₂ may then be described by the following four-point twist correlator on the complex plane [11]

$$\mathcal{E}=\underset{L\to \infty }{lim}\underset{n_e\to 1}{lim}ln{〈{\mathcal{T}}_{n_e}(-L){\overline{\mathcal{T}}}_{n_e}^2\left(0\right){\overline{\mathcal{T}}}_{n_e}^2\left(l\right){\mathcal{T}}_{n_e}\left(L\right)〉}_{\mathbb{C}}.$$

(59)

Through a suitable conformal transformation (see [32] for a detailed review), Equation (59) may be recast as [37]

$$\mathcal{E}=\underset{L\to \infty }{lim}\underset{n_e\to 1}{lim}ln{〈{\mathcal{T}}_{n_e}\left(0\right){\overline{\mathcal{T}}}_{n_e}^2\left(x\right){\overline{\mathcal{T}}}_{n_e}^2\left(1\right){\mathcal{T}}_{n_e}(\infty )〉}_{\mathbb{C}}.$$

(60)

For a CFT₂ at a finite temperature $1/\beta$, the entanglement negativity for a single interval may be computed from Equation (59) or Equation (60) through the conformal transformation $z\to w=(\beta /2\pi )lnz$ from the complex plane to the cylinder. The entanglement negativity for a single interval in a thermal CFT₂ may then be obtained as follows [11,37]:

$$\begin{array}{cc}\hfill \mathcal{E}& =\underset{L\to \infty }{lim}\underset{n_e\to 1}{lim}ln{〈{\mathcal{T}}_{n_e}(-L){\overline{\mathcal{T}}}_{n_e}^2\left(0\right){\overline{\mathcal{T}}}_{n_e}^2\left(l\right){\mathcal{T}}_{n_e}\left(L\right)〉}_{\mathrm{cyl}\left(\beta \right)}\hfill \\ \hfill & =\underset{L\to \infty }{lim}\underset{n_e\to 1}{lim}ln{〈{\mathcal{T}}_{n_e}\left(0\right){\overline{\mathcal{T}}}_{n_e}^2\left(x\right){\overline{\mathcal{T}}}_{n_e}^2\left(1\right){\mathcal{T}}_{n_e}(\infty )〉}_{\mathbb{C}}+\frac{c}{2}ln\left(\frac{\beta }{2\pi ϵ}{e}^{\frac{\pi l}{\beta }}\right),\hfill \end{array}$$

(61)

where the cross ratio x is specified by $\underset{L\to \infty }{lim}x=e^{-2\pi l/\beta }$.

In the large central charge limit, the four-point twist correlator in Equation (61) may be expressed in terms of a dominant single conformal block in the s and t channels depending on the cross ratio x, as described in [29].

For the s channel (described by $x\approx 0$), the authors in [37] have computed the four point function on the complex plane as

$$\underset{L\to \infty }{lim}\underset{n_e\to 1}{lim}ln{〈{\mathcal{T}}_{n_e}\left(0\right){\overline{\mathcal{T}}}_{n_e}^2\left(x\right){\overline{\mathcal{T}}}_{n_e}^2\left(1\right){\mathcal{T}}_{n_e}(\infty )〉}_{\mathbb{C}}=\frac{c}{4}lnx.$$

(62)

Utilizing the above four-point twist correlator, the entanglement negativity may be computed from Equation (61) as10

$$\mathcal{E}=\frac{c}{2}ln\left(\frac{\beta }{\pi ϵ}\right).$$

(63)

For the t channel (given by $x\approx 1$), the authors in [37] have obtained the following four-point function:

$$\underset{L\to \infty }{lim}\underset{n_e\to 1}{lim}ln{〈{\mathcal{T}}_{n_e}\left(0\right){\overline{\mathcal{T}}}_{n_e}^2\left(x\right){\overline{\mathcal{T}}}_{n_e}^2\left(1\right){\mathcal{T}}_{n_e}(\infty )〉}_{\mathbb{C}}=\frac{c}{2}ln\left(1-x\right),$$

(64)

from which the entanglement negativity may be obtained Equation (61):

$$\mathcal{E}=\frac{c}{2}ln\left(\frac{\beta }{\pi ϵ}sinh\frac{\pi l}{\beta }\right).$$

(65)

We note that the four-point functions on the complex plane given in Equations (62) and (64), utilized to compute the entanglement negativity for both the channels, match those obtained in [29]. We further observe that the monodromy technique employed in [26,29] and the monodromy method utilized by the authors in [37] all produce identical large central charge limits for the four-point function.

However, we would like to emphasize here that the authors in [37], motivated by the large c computations for the entanglement entropy in [7,8], assumed that the s and t channel results are valid beyond their usual regimes $x\approx 0$ and $x\approx 1$, that is, for $0<x<1/2$ and $1/2<x<1$, respectively. In other words, their computation involves an assumption that there is a phase transition for the large central charge limit for the entanglement negativity of a single interval at $x=1/2$. Although this is true for the entanglement entropy [7,8], for this specific case of the entanglement negativity for a single interval, this assumption is not valid, as the required four-point twist correlator is obtained from a specific channel for the corresponding six-point correlator, as described in [29]. The above conclusion is also supported by an alternate EWCS construction for this configuration proposed in Section 5.2 to resolve the issue with the missing thermal term for the holographic entanglement negativity in [35,37].

5.2. Alternate EWCS Construction

In this subsection, we propose an alternative construction to that described in [43] for the mixed state configuration of a single interval at a finite temperature in AdS₃/CFT₂. To this end, we consider the following properties [refer to Equation (26)] of the EWCS for tripartite pure state configurations comprising subsystems A, B, and C (see [43,44] for a review):

$$E_W(A:BC)\le E_W(A:B)+E_W(A:C),$$

(66)

$$\frac{1}{2}I(A:B)+\frac{1}{2}I(A:C)\le E_W(A:BC),$$

(67)

where $I(A:B)$ is the mutual information between A and B. For two adjacent intervals A and B at a finite temperature in a CFT₂ dual to a bulk planar BTZ black hole, the EWCS may be explicitly computed through the adjacent limit in the corresponding disjoint interval result derived in [43]. The holographic mutual information for these adjacent intervals may also be explicitly calculated from the corresponding entanglement entropies. Comparing these results, we obtain the following relation for this specific configuration:

$$E_W(A:B)=\frac{1}{2}I(A:B).$$

(68)

Substituting the result described in Equation (68) into Equation (67) and comparing them with Equation (66), we arrive at the following equality for the bulk BTZ black hole configuration:

$$E_W(A:BC)=E_W(A:B)+E_W(A:C),$$

(69)

where B and C are adjacent to A.

Following the construction in [11], we now consider a tripartition (see Figure 3) consisting of interval A of length l, with two auxiliary intervals $B_1$ and $B_2$, each of length L, on either side of A where $B\equiv B_1\cup B_2$. Next, we implement the bipartite limit $L\to \infty$ to recover the original configuration with a single interval A and the rest of the system given by $B=A^c$. Note that in the bipartite limit, $A\cup B$ describes the full system, which is in a pure state and obeys Equation (69). Thus, for this configuration (in the bipartite limit),

$$\underset{L\to \infty }{lim}{E}_W(A:B_1{B}_2)=\left.\underset{L\to \infty }{lim}[E_W(A:B_1)+E_W(A:B_2)\right].$$

(70)

Computing the right-hand side of Equation (70), we obtain the EWCS for the bipartition involving the interval A and the rest of the system $B=A^c$ as follows:

$$E_W(A:B)=\frac{c}{3}ln\left(\frac{\beta }{\pi ϵ}sinh\frac{\pi l}{\beta }\right)-\frac{\pi cl}{3\beta }+\frac{c}{3}ln4.$$

(71)

The holographic entanglement negativity for the mixed state configuration of a single interval A in a CFT₂ at a finite temperature dual to the bulk planar BTZ black hole may now be obtained by utilizing Equations (45) and (71) as follows:

$$\mathcal{E}=\frac{c}{2}ln\left(\frac{\beta }{\pi ϵ}sinh\frac{\pi l}{\beta }\right)-\frac{\pi cl}{2\beta }+\frac{c}{2}ln4.$$

(72)

The above expression matches exactly with the corresponding field theory replica technique result for the entanglement negativity described in Equation (58) in the large central charge limit up to a constant related to the Markov gap. Interestingly, the result for the holographic entanglement negativity for this mixed state configuration utilizing the alternate holographic construction involving the algebraic sum of bulk geodesics as reported in [26] matches exactly with the corresponding field theory replica technique results in the large c limit without the constant. This once again indicates the equivalence of the two proposals up to a constant.

In Figure 4, we have plotted the possible candidates for the EWCS as a function of the inverse temperature $\beta$ to compare our construction with that described in [43] for this configuration. In Figure 4a, the two possible candidates (green and blue curves) for the EWCS described in Equation (56) have been compared with our expression given in Equation (71) without the third term (red curve). In Figure 4b, the proposed EWCS (blue curve), as prescribed in [43], given in Equation (56), has been plotted along with the EWCS modulo the constant (red curve) obtained by utilizing our alternative proposal, as described in Equation (71). It is interesting to note that our proposed EWCS always remains strictly less than that advanced in [43] for the range of $\beta$ used in the plot. This conclusively singles out our construction for the EWCS over the other proposal as the correct minimal EWCS, which also reproduces the replica technique result described in [11], in the large c limit. We also observe that Equations (56) and (71) asymptotically approaches each other in the limits of high ($\beta \to 0$) and low ($\beta \to \infty$) temperatures. Naturally, this resolves the issue with the holographic entanglement negativity for this configuration and restores the missing thermal entropy term.

6. Discussions and Conclusions

To summarize, we have established the equivalence modulo the Markov gap constant of two different proposals in the literature for the holographic entanglement negativity of bipartite states in the context of the AdS₃/CFT₂ correspondence. The first proposal described in [26,30,32] involved an algebraic sum of the lengths of bulk geodesics homologous to certain combinations of subsystems, and the second one reported in [35,37] was based on the EWCS backreacted by a cosmic brane for the conical defect of the replicated bulk geometry in a gravitational path integral.

In this connection, we have analyzed and compared the results for the holographic entanglement negativity following from the above two proposals for various bipartite state configurations described by two disjoint intervals, two adjacent intervals, and a single interval in dual CFT₂s. We observe that the results obtained from these two proposals match each other up to certain constants which arise from the Markov gap for the EWCS, establishing their equivalence.

In this context, we have investigated a critical issue with the proposal involving the backreacted EWCS for the holographic entanglement negativity of a single interval in a finite temperature CFT₂ dual to a bulk planar BTZ black hole. Specifically, the holographic entanglement negativity obtained for the above configuration from the backreacted EWCS excluded a subtracted thermal entropy term in the corresponding field theory replica technique result at large c. In this article, we have resolved this significant issue by proposing an alternative construction for the EWCS of this configuration, which is actually the minimal one. Our construction involved the introduction of two large auxiliary intervals adjacent to the single interval in question. Subsequently, a bipartite limit for this configuration was implemented through the consideration of the auxiliary intervals to be infinite and constitute the rest of the system. To this end, we utilized certain polygamy properties to obtain the correct bulk EWCS for the single interval in a holographic CFT₂. Interestingly, our results following from the above construction reproduced the excluded thermal term and matched the field theory replica technique result exactly in the large central charge limit in the literature. Naturally, the holographic entanglement negativity proposal involving the backreacted EWCS requires substantiation from explicit higher-dimensional examples for generic AdS_d+1/CFT_d scenarios. However, the difficulties for the computation of the EWCS for higher dimensions are well known. We hope to address some of these issues in the near future.