Impact of Newly Measured Nuclear Reaction Rates on 26Al Ejected Yields from Massive Stars
Abstract
:1. Introduction
2. Computational Methods
2.1. Simulation Setup
2.2. Description of the Stellar Models
- Complete Si burning (): GK;
- Incomplete Si burning (): ;
- Explosive O burning (O): ;
- Explosive Ne burning (Ne): ;
- Explosive C burning (C): .
3. Results
3.1. Impact of New Nuclear Reaction Rates on the Ejected Yields
3.2. Comparison to Ess Ratios
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diehl, R.; Lugaro, M.; Heger, A.; Sieverding, A.; Tang, X.; Li, K.A.; Li, E.T.; Doherty, C.L.; Krause, M.G.H.; Wallner, A.; et al. The radioactive nuclei 26Al and 60Fe in the Cosmos and in the solar system. Publ. Astron. Soc. Aust. 2021, 38, e062. [Google Scholar] [CrossRef]
- Laird, A.M.; Lugaro, M.; Kankainen, A.; Adsley, P.; Bardayan, D.W.; Brinkman, H.E.; Côté, B.; Deibel, C.M.; Diehl, R.; Hammache, F.; et al. Progress on nuclear reaction rates affecting the stellar production of 26Al. J. Phys. Nucl. Phys. 2023, 50, 033002. [Google Scholar] [CrossRef]
- Diehl, R.; Halloin, H.; Kretschmer, K.; Lichti, G.G.; Schönfelder, V.; Strong, A.W.; von Kienlin, A.; Wang, W.; Jean, P.; Knödlseder, J.; et al. COMPTEL observations of galactic 26Al emission. Nature 2006, 439, 45. [Google Scholar] [CrossRef] [PubMed]
- Lugaro, M.; Ott, U.; Kereszturi, Á. Radioactive nuclei from cosmochronology to habitability. Prog. Part. Nucl. Phys. 2018, 102, 1–47. [Google Scholar] [CrossRef]
- Diehl, R.; Steinle, H.; Strong, A.; Schoenfelder, V.; Varendorff, M.; Bennett, K.; Lichti, G.G.; Blömen, H.; Dupraz, C.; Hermsen, W.; et al. COMPTEL observations of Galactic 26Al emission. Astron. Astrophys. 1995, 298, 445. [Google Scholar]
- Georgy, C.; Ekström, S.; Meynet, G.; Lichti, G.G.; Schönfelder, V.; Strong, A.W.; von Kienlin, A.; Wang, W.; Jean, P.; Knödlseder, J.; et al. Radioactive 26Al from massive stars in the Galaxy. Nature 2012, 542, A29. [Google Scholar] [CrossRef]
- Brinkman, H.E.; Doherty, C.L.; Pols, O.R.; Li, E.T.; Côté, B.; Lugaro, M. Aluminium-26 from Massive Binary Stars. I. Nonrotating Models. Astrophys. J. 2019, 884, 38. [Google Scholar] [CrossRef]
- Prantzos, N.; Doom, C.; de Loore, C.; Arnould, M. Nucleosynthesis and evolution of massive stars with mass loss and overshooting. Astrophys. J. 1986, 304, 695. [Google Scholar] [CrossRef]
- Palacios, A.; Meynet, G.; Vuissoz, C.; Knödlseder, J.; Schaerer, D.; Cerviño, M.; Mowlavi, N. New estimates of the contribution of Wolf-Rayet stellar winds to the Galactic 26Al. Anesth. Analg. 2005, 429, 613. [Google Scholar] [CrossRef]
- Vasini, A.; Matteucci, F.; Spitoni, E. Chemical evolution of 26Al and 60Fe in the Milky Way. Mon. Not. R. Astron. Soc. 2022, 517, 4256–4264. [Google Scholar] [CrossRef]
- Limongi, M.; Chieffi, A. The Nucleosynthesis of 26Al and60Fe in Solar Metallicity Stars Extending in Mass from 11 to 120M⊙: The Hydrostatic and Explosive Contributions. Astrophys. J. 2006, 647, 483. [Google Scholar] [CrossRef]
- Lawson, T.V.; Pignatari, M.; Stancliffe, R.J.; Hartogh, J.D.; Jones, S.; Fryer, C.L.; Gibson, B.K.; Lugaro, M. Radioactive nuclei in the early Solar system: Analysis of the 15 isotopes produced by core-collapse supernovae. Mon. Not. R. Astron. Soc. 2022, 511, 886. [Google Scholar] [CrossRef]
- José, J.; Hernanz, M.; Coc, A. New Results on 26Al Production in Classical Novae. Astrophys. J. 1997, 479, L55. [Google Scholar] [CrossRef]
- Guélin, M.; Forestini, M.; Valiron, P.; Ziurys, L.M.; Anderson, M.A.; Cernicharo, J.; Kahane, C. Nucleosynthesis in AGB stars: Observation of 25Mg and 26Mg in IRC+10216 and possible detection of 26Al. AStronomy Astrophys. 1995, 297, 183–196. [Google Scholar]
- Bennett, M.B.; Wrede, C.; Chipps, K.A.; José, J.; Liddick, S.N.; Santia, M.; Bowe, A.; Chen, A.A.; Cooper, N.; Irvine, D.; et al. Classical-Nova Contribution to the Milky Way’s 26Al Abundance: Exit Channel of the Key 25Al(p,γ)26Si Resonance. Phys. Rev. Lett. 2013, 111, 232503. [Google Scholar] [CrossRef]
- Forestini, M.; Arnould, M.; Paulus, G. On the production of Al-26 in AGB stars. Astron. Astrophys. 1991, 252, 597–604. [Google Scholar]
- Meisel, Z.; Merz, G.; Medvid, S. Influence of Nuclear Reaction Rate Uncertainties on Neutron Star Properties Extracted from X-ray Burst Model-Observation Comparisons. Astrophys. J. 2019, 872, 84. [Google Scholar] [CrossRef]
- Iliadis, C.; Champagne, A.; Chieffi, A.; Limongi, M. The effects of thermonuclear reaction rate variations on 26Al production in massive stars: A sensitivity study. Astrophys. J. 2011, 193, 16. [Google Scholar] [CrossRef]
- Straniero, O.; Imbriani, G.; Strieder, F.; Bemmerer, D.; Broggini, C.; Caciolli, A.; Corvisiero, P.; Costantini, H.; Cristallo, S.; DiLeva, A.; et al. Impact of a revised 25Mg(p,γ)26Al reaction rate on the operation of the Mg-Al cycle. Astrophys. J. 2013, 763, 100. [Google Scholar] [CrossRef]
- Zhang, H.; Su, J.; Li, Z.H.; Li, Y.J.; Li, E.T.; Chen, C.; He, J.J.; Shen, Y.P.; Lian, G.; Guo, B.; et al. Updated reaction rate of 25Mg(p,γ)26Al and its astrophysical implication. Phys. Rev. C 2023, 107, 065801. [Google Scholar] [CrossRef]
- Battino, U.; Lederer-Woods, C.; Pignatari, M.; Soós, B.; Lugaro, M.; Vescovi, D.; Cristallo, S.; Woods, P.J.; Karakas, A. Impact of newly measured 26Al(n, p)26Mg and 26Al(n, α)23Na reaction rates on the nucleosynthesis of 26Al in stars. Mon. Not. R. Astron. Soc. 2023, 520, 2436. [Google Scholar] [CrossRef]
- Borcea, C.; Cennini, P.; Dahlfors, M.; Ferrari, A.; Garcia-Muñoz, G.; Haefner, P.; Herrera-Martınez, A.; Kadi, Y.; Lacoste, V.; Radermacher, E.; et al. Results from the commissioning of the n_TOF spallation neutron source at CERN. Nucl. Instruments Methods Phys. Res. A 2003, 513, 524–537. [Google Scholar] [CrossRef]
- Lederer-Woods, C.; Battino, U.; Ferreira, P.; Gawlik, A.; Guerrero, C.; Gunsing, F.; Heinitz, S.; Lerendegui-Marco, J.; Mengoni, A.; Reifarth, R.; et al. Measurement of 73Ge(n,γ) cross sections and implications for stellar nucleosynthesis. Phys. Lett. B 2019, 790, 458–465. [Google Scholar] [CrossRef]
- Domingo-Pardo, C.; Babiano-Suarez, V.; Balibrea-Correa, J.; Caballero, L.; Ladarescu, I.; Lerendegui-Marco, J.; Tain, J.L.; Tarifeño-Saldivia, A.; Aberle, O.; Alcayne, V.; et al. Advances and new ideas for neutron-capture astrophysics experiments at CERN n_TOF. Eur. Phys. J. A 2023, 59, 8. [Google Scholar] [CrossRef]
- Trautvetter, H.P.; Becker, H.W.; Heinemann, U.; Buchmann, L.; Rolfs, C.; Baumann, M.; Freiesleben, H.; Geltenbort, P.; Käppeler, F.; Lütke-Stetzkamp, H.J.; et al. Destruction of 26Al in explosive nucleosynthesis. Z. Fur Phys. Hadron. Nucl. 1986, 323, 1–11. [Google Scholar] [CrossRef]
- Chieffi, A.; Limongi, M. Pre-supernova evolution of rotating solar metallicity stars in the mass range 13–120 M⊙ and their explosive yields. Astrophys. J. 2013, 764, 21. [Google Scholar] [CrossRef]
- Limongi, M.; Chieffi, A. Presupernova Evolution and Explosive Nucleosynthesis of Rotating Massive Stars in the Metallicity Range −3 ≤ [Fe/H] ≤ 0. Astrophys. J. Suppl. Ser. 2018, 237, 13. [Google Scholar] [CrossRef]
- Asplund, M.; Grevesse, N.; Sauval, A.J.; Scott, P. The Chemical Composition of the Sun. Annu. Rev. Astron. Astrophys. 2009, 47, 481–522. [Google Scholar] [CrossRef]
- Roberti, L.; Limongi, M.; Chieffi, A. Zero and Extremely Low-metallicity Rotating Massive Stars: Evolution, Explosion, and Nucleosynthesis Up to the Heaviest Nuclei. Astrophys. J. Suppl. Ser. 2024, 270, 28. [Google Scholar] [CrossRef]
- Limongi, M.; Chieffi, A. Hydrodynamical Modeling of the Light Curves of Core-collapse Supernovae with HYPERION. I. The Mass Range 13–25 M⊙, the Metallicities −3 ≤ [Fe/H] ≤ 0, and the Case of SN 1999em. Astrophys. J. 2020, 902, 95. [Google Scholar] [CrossRef]
- Colella, P.; Woodward, P.R. The Piecewise Parabolic Method (PPM) for gas-dynamical simulations. J. Comput. Phys. 1984, 54, 174. [Google Scholar] [CrossRef]
- Iliadis, C.; Longland, R.; Champagne, A.E.; Coc, A.; Fitzgerald, R. Charged-particle thermonuclear reaction rates: II. Tables and graphs of reaction rates and probability density functions. Nucl. Phys. A 2010, 841, 31. [Google Scholar] [CrossRef]
- Caughlan, G.R.; Fowler, W.A. Thermonuclear reaction rates V. At. Data Nucl. Data Tables 1988, 40, 283. [Google Scholar] [CrossRef]
- Angulo, C.; Arnould, M.; Rayet, M.; Descouvemont, P.; Baye, D.; Leclercq-Willain, C.; Coc, A.; Barhoumi, S.; Aguer, P.; Rolfs, C.; et al. A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. A 1999, 656, 3. [Google Scholar] [CrossRef]
- Langer, N. Evolution of massive stars in the Large Magellanic Cloud: Models with semiconvection. Astron. Astrophys. 1991, 252, 669–688. [Google Scholar]
- Vink, J.S.; de Koter, A.; Lamers, H.J.G.L.M. New theoretical Mass-loss rates of O and B Stars. Anesth. Analg. 2000, 362, 295. [Google Scholar] [CrossRef]
- Vink, J.S.; de Koter, A.; Lamers, H.J.G.L.M. Mass-loss predictions for O and B stars as a function of metallicity. Anesth. Analg. 2001, 369, 574–588. [Google Scholar] [CrossRef]
- de Jager, C.; Nieuwenhuijzen, H.; van der Hucht, K.A. Mass loss rates in the Hertzsprung-Russell diagram. Astron. Astrophys. Suppl. Ser. 1988, 72, 259–289. [Google Scholar]
- van Loon, J.T.; Oliveira, J.M.; Wood, P.R.; Zijlstra, A.A.; Sloan, G.C.; Matsuura, M.; Whitelock, P.A.; Groenewegen, M.A.T.; Blommaert, J.A.D.L.; Cioni, M.R.L.; et al. ESO-VLT and Spitzer spectroscopy of IRAS 05328-6827: A massive young stellar object in the Large Magellanic Cloud. Mon. Not. R. Astron. Soc. 2005, 364, L71. [Google Scholar] [CrossRef]
- Nugis, T.; Lamers, H.J.G.L.M. Mass-loss rates of Wolf-Rayet stars as a function of stellar parameters. Astron. Astrophys. 2000, 360, 227–244. [Google Scholar]
- Woosley, S.E. SN 1987A—After the peak. Astrophys. J. 1988, 330, 218–253. [Google Scholar] [CrossRef]
- Rauscher, T.; Heger, A.; Hoffman, R.D.; Woosley, S.E. Nucleosynthesis in Massive Stars with Improved Nuclear and Stellar Physics. Astrophys. J. 2002, 576, 323. [Google Scholar] [CrossRef]
- Limongi, M.; Chieffi, A. Evolution, Explosion, and Nucleosynthesis of Core-Collapse Supernovae. Astrophys. J. 2003, 592, 404–433. [Google Scholar] [CrossRef]
- Sieverding, A.; Martínez-Pinedo, G.; Huther, L.; Langanke, K.; Heger, A. The v-Process in the Light of an Improved Understanding of Supernova Neutrino Spectra. Astrophys. J. 2018, 865, 143. [Google Scholar] [CrossRef]
- Ritter, C.; Andrassy, R.; Côté, B.; Herwig, F.; Woodward, P.R.; Pignatari, M.; Jones, S. Convective-reactive nucleosynthesis of K, Sc, Cl and p-process isotopes in O-C shell mergers. Mon. Not. R. Astron. Soc. 2018, 474, L1–L6. [Google Scholar] [CrossRef]
- Fryer, C.L.; Belczynski, K.; Wiktorowicz, G.; Dominik, M.; Kalogera, V.; Holz, D.E. Compact remnant mass function: Dependence on the explosion mechanism and metallicity. Astrophys. J. 2012, 749, 91. [Google Scholar] [CrossRef]
- Umeda, H.; Nomoto, K. Nucleosynthesis of Zinc and Iron Peak Elements in Population III Type II Supernovae: Comparison with Abundances of Very Metal Poor Halo Stars. Astrophys. J. 2002, 565, 385. [Google Scholar] [CrossRef]
- Umeda, H.; Nomoto, K. Variations in the Abundance Pattern of Extremely Metal-Poor Stars and Nucleosynthesis in Population III Supernovae. Astrophys. J. 2005, 619, 427–445. [Google Scholar] [CrossRef]
- Woosley, S.E.; Heger, A.; Weaver, T.A. The evolution and explosion of massive stars. Rev. Mod. Phys. 2002, 74, 1015–1071. [Google Scholar] [CrossRef]
- Limongi, M.; Chieffi, A. Final stages of massive stars. SN explosion and explosive nucleosynthesis. Eas Publ. Ser. 2008, 32, 233–281. [Google Scholar] [CrossRef]
- Nomoto, K.; Kobayashi, C.; Tominaga, N. Nucleosynthesis in Stars and the Chemical Enrichment of Galaxies. Annu. Rev. Astron. Astrophys. 2013, 51, 457–509. [Google Scholar] [CrossRef]
- Pignatari, M.; Hoppe, P.; Trappitsch, R.; Fryer, C.; Timmes, F.; Herwig, F.; Hirschi, R. The neutron capture process in the He shell in core-collapse supernovae: Presolar silicon carbide grains as a diagnostic tool for nuclear astrophysics. Geochim. Cosmochim. Acta 2018, 221, 37. [Google Scholar] [CrossRef]
- Trueman, T.C.L.; Côté, B.; Yagüe López, A.; Hartogh, J.D.; Pignatari, M.; Soós, B.; Karakas, A.I.; Lugaro, M. Galactic Chemical Evolution of Radioactive Isotopes with an s-process Contribution. Astrophys. J. 2022, 924, 10. [Google Scholar] [CrossRef]
- Murray, N. Star formation efficiencies and lifetimes of giant molecular clouds in the milky way. Astrophys. J. 2011, 729, 133. [Google Scholar] [CrossRef]
- Lee, T.; Papanastassiou, D.A.; Wasserburg, G.J. Aluminum-26 in the early solar system—Fossil or fuel. Astrophys. J. 1977, 211, L107. [Google Scholar] [CrossRef]
- Yin, Q.Z.; Jacobsen, B.; Moynier, F.; Amelin, Y.; Krot, A.N.; Nagashima, K.; Hutcheon, I.D.; Palme, H. 26Al-26Mg and 207Pb-206Pb Systematics of Allende CAIs: Reinstated Canonical Solar Initial 26Al/27Al Ratio, Variable kappa-Values (232Th/238U) and the Age of the Galaxy. In Proceedings of the 39th Annual Lunar and Planetary Science Conference, Houston, TX, USA, 10–14 March 2008. [Google Scholar]
- Luu, T.-H.; Hin, R.C.; Coath, C.D.; Elliott, T. Bulk chondrite variability in mass independent magnesium isotope compositions—Implications for initial solar system 26Al/27Al and the timing of terrestrial accretion. Earth Planet. Sci. Lett. 2019, 522, 166. [Google Scholar] [CrossRef]
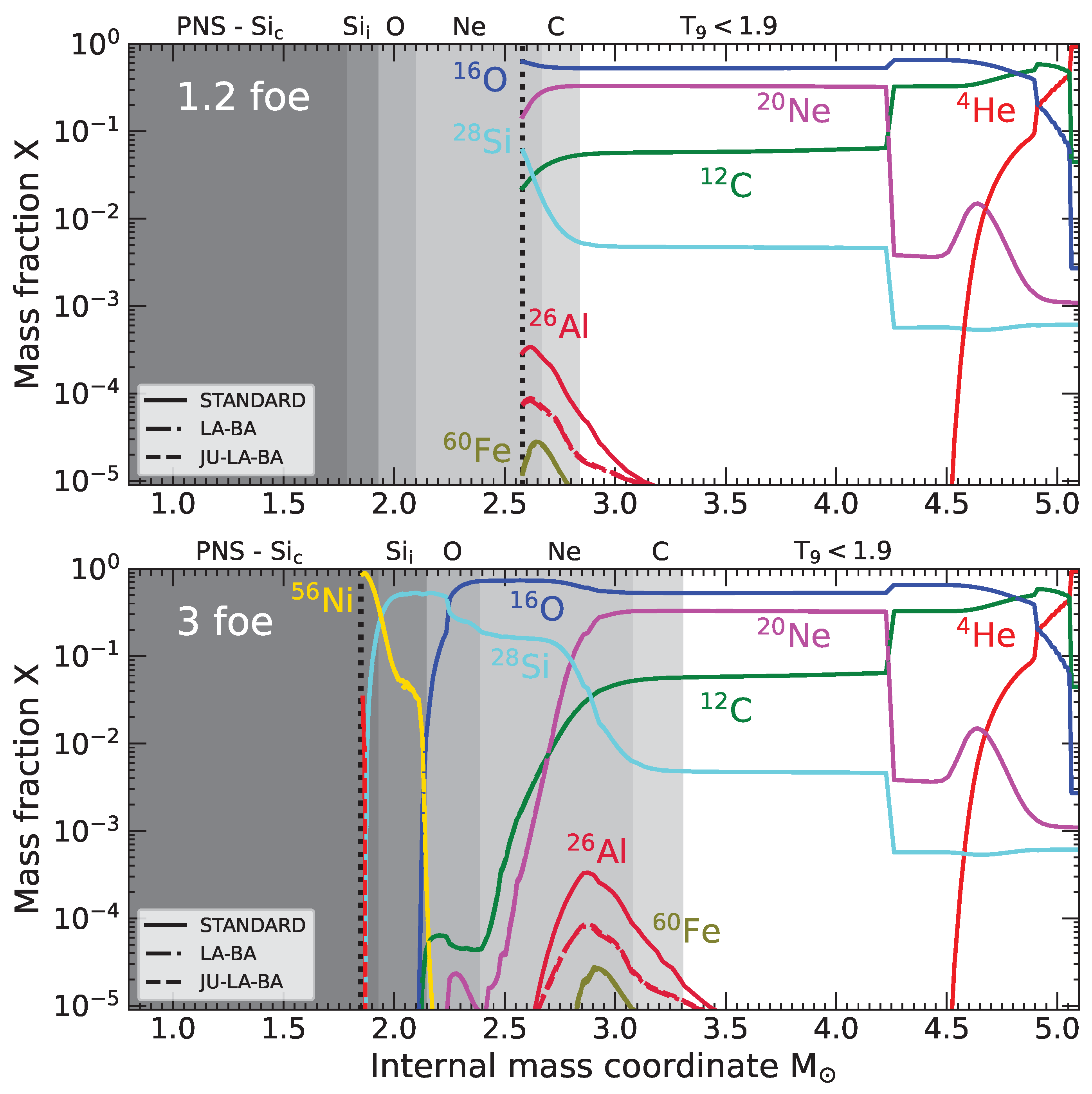
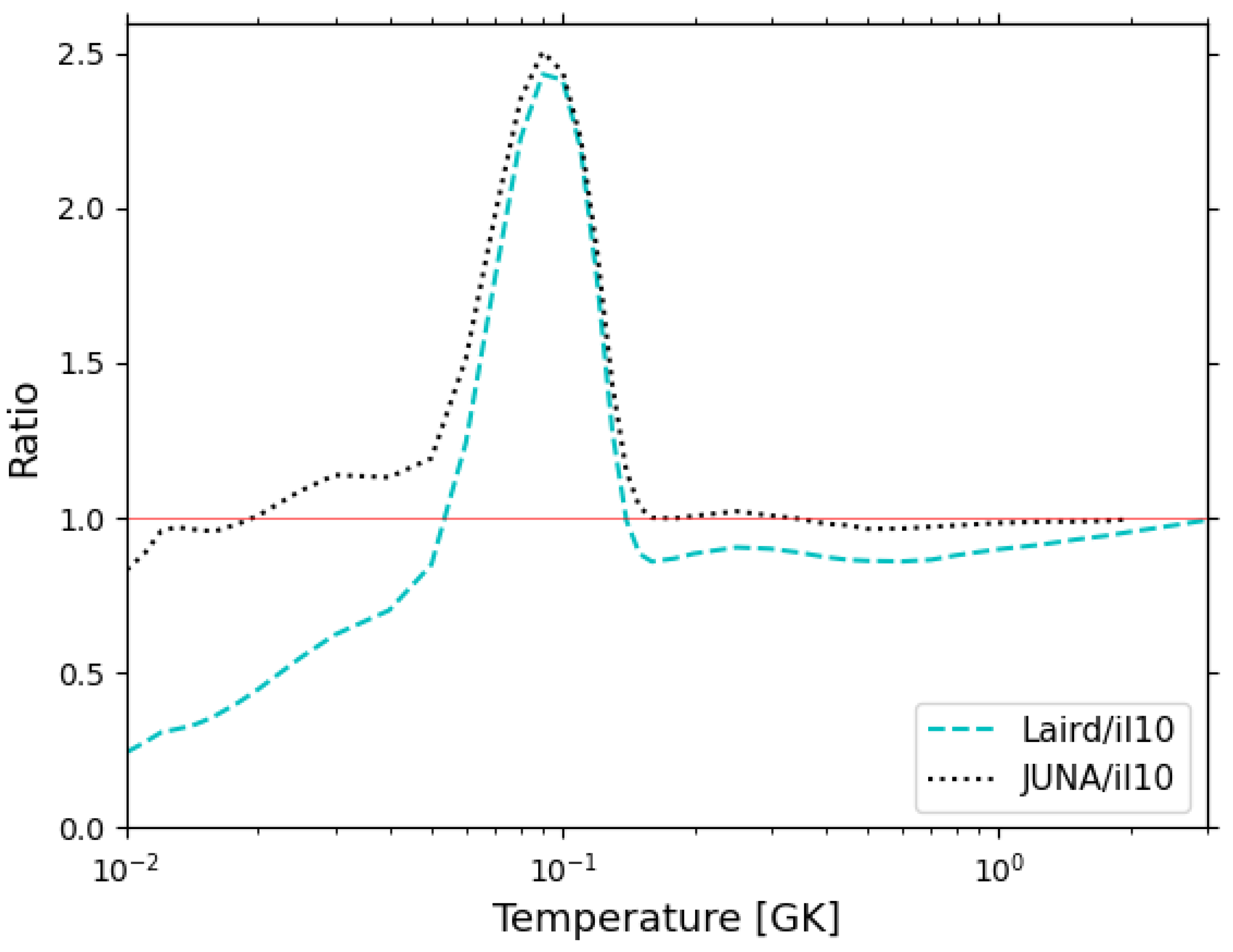
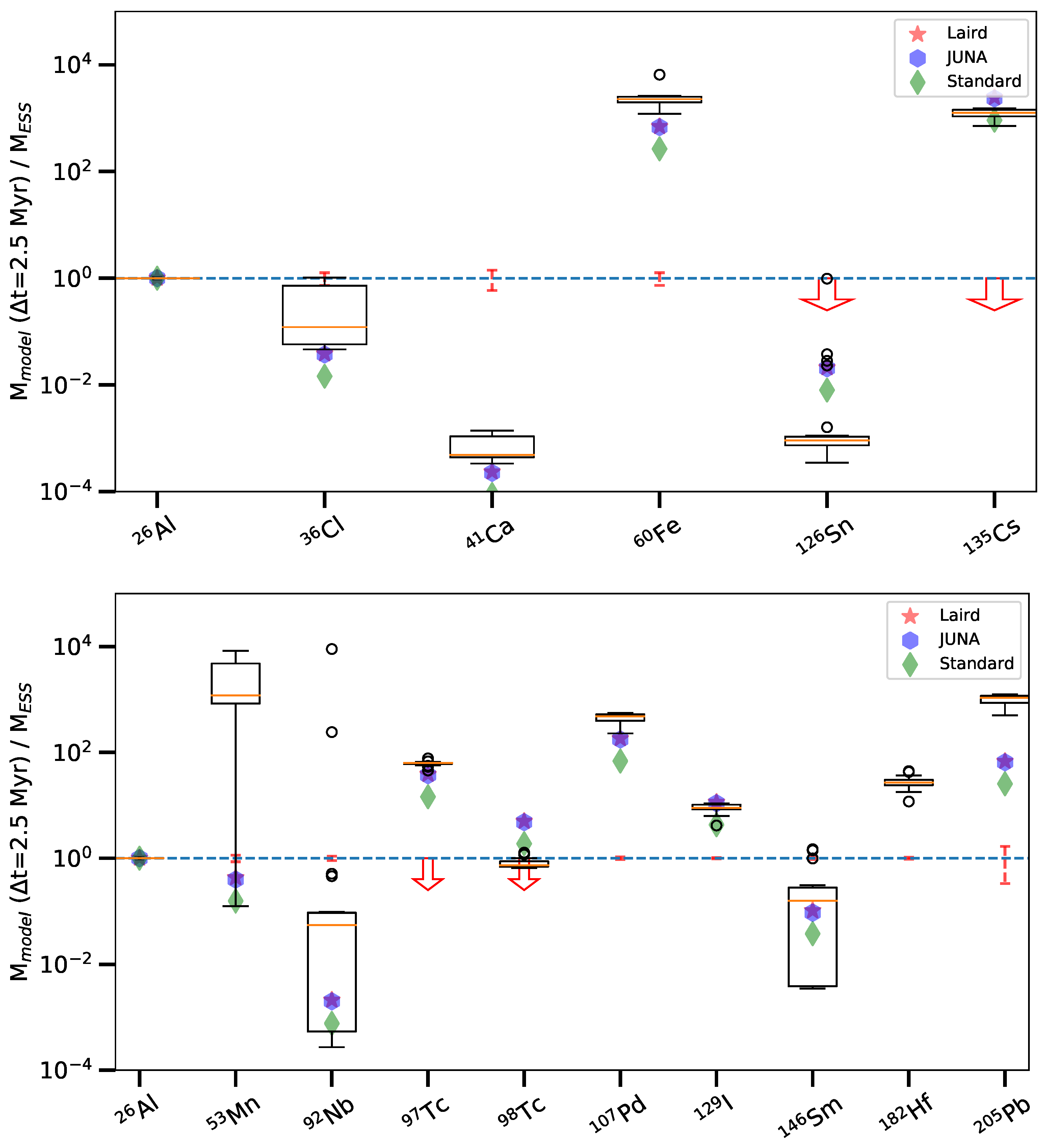
| Nuclear Reaction | STANDARD | JU-LA-BA | LA-BA |
|---|---|---|---|
| 25Mg()26Al | Iliadis et al., 2010 [32] | Zhang et al., 2023 [20] | Laird et al., 2023 [2] |
| 26Al()27Si | Iliadis et al., 2010 [32] | Laird et al., 2023 [2] | Laird et al., 2023 [2] |
| 26Al()26Mg | Caughlan & Fowler 1988 [33] | Battino et al., 2023 [21] | Battino et al., 2023 [21] |
| 26Al()23Na | Angulo et al., 1999 [34] | Battino et al., 2023 [21] | Battino et al., 2023 [21] |
| T[GK] | Lower Limit | Median Rate | Upper Limit |
|---|---|---|---|
| 0.700 | 1.027 × 102 | 1.078 × 102 | 1.136 × 102 |
| 0.800 | 1.933 × 102 | 2.022 × 102 | 2.121 × 102 |
| 0.900 | 3.195 × 102 | 3.333 × 102 | 3.488 × 102 |
| 1.000 | 4.810 × 102 | 5.011 × 102 | 5.240 × 102 |
| 1.250 | 1.026 × 103 | 1.068 × 103 | 1.118 × 103 |
| 1.500 | 1.740 × 103 | 1.811 × 103 | 1.897 × 103 |
| 1.750 | 2.586 × 103 | 2.689 × 103 | 2.815 × 103 |
| 2.000 | 3.532 × 103 | 3.667 × 103 | 3.831 × 103 |
| 2.500 | 5.615 × 103 | 5.809 × 103 | 6.039 × 103 |
| 3.000 | 7.804 × 103 | 8.047 × 103 | 8.329 × 103 |
| 3.500 | 9.946 × 103 | 1.023 × 104 | 1.055 × 104 |
| 4.000 | 1.193 × 104 | 1.225 × 104 | 1.261 × 104 |
| 5.000 | 1.520 × 104 | 1.559 × 104 | 1.600 × 104 |
| 6.000 | 1.748 × 104 | 1.792 × 104 | 1.839 × 104 |
| 7.000 | 1.890 × 104 | 1.938 × 104 | 1.989 × 104 |
| 8.000 | 1.966 × 104 | 2.017 × 104 | 2.071 × 104 |
| 9.000 | 1.994 × 104 | 2.047 × 104 | 2.103 × 104 |
| 10.000 | 1.989 × 104 | 2.043 × 104 | 2.100 × 104 |
| T[GK] | Lower Limit | Median Rate | Upper Limit |
|---|---|---|---|
| 0.700 | 2.887 × 101 | 3.054 × 101 | 3.237 × 101 |
| 0.800 | 5.899 × 101 | 6.232 × 101 | 6.610 × 101 |
| 0.900 | 1.043 × 102 | 1.102 × 102 | 1.171 × 102 |
| 1.000 | 1.661 × 102 | 1.756 × 102 | 1.870 × 102 |
| 1.250 | 3.944 × 102 | 4.169 × 102 | 4.451 × 102 |
| 1.500 | 7.198 × 102 | 7.593 × 102 | 8.101 × 102 |
| 1.750 | 1.125 × 103 | 1.183 × 103 | 1.259 × 103 |
| 2.000 | 1.592 × 103 | 1.668 × 103 | 1.767 × 103 |
| 2.500 | 2.631 × 103 | 2.741 × 103 | 2.881 × 103 |
| 3.000 | 3.705 × 103 | 3.843 × 103 | 4.016 × 103 |
| 3.500 | 4.720 × 103 | 4.883 × 103 | 5.079 × 103 |
| 4.000 | 5.626 × 103 | 5.807 × 103 | 6.020 × 103 |
| 5.000 | 7.033 × 103 | 7.240 × 103 | 7.474 × 103 |
| 6.000 | 7.930 × 103 | 8.154 × 103 | 8.400 × 103 |
| 7.000 | 8.428 × 103 | 8.660 × 103 | 8.910 × 103 |
| 8.000 | 8.641 × 103 | 8.873 × 103 | 9.124 × 103 |
| 9.000 | 8.660 × 103 | 8.890 × 103 | 9.135 × 103 |
| 10.000 | 8.550 × 103 | 8.776 × 103 | 9.015 × 103 |
| T[GK] | Lower Limit | Median Rate | Upper Limit |
|---|---|---|---|
| 0.700 | 4.640 × 101 | 5.050 × 101 | 5.500 × 101 |
| 0.800 | 8.020 × 101 | 8.730 × 101 | 9.520 × 101 |
| 0.900 | 1.220 × 102 | 1.330 × 102 | 1.450 × 102 |
| 1.000 | 1.710 × 102 | 1.860 × 102 | 2.020 × 102 |
| 1.250 | 3.170 × 102 | 3.420 × 102 | 3.700 × 102 |
| 1.500 | 4.880 × 102 | 5.230 × 102 | 5.610 × 102 |
| 1.750 | 6.730 × 102 | 7.160 × 102 | 7.640 × 102 |
| 2.000 | 8.600 × 102 | 9.120 × 102 | 9.680 × 102 |
| 2.500 | 1.210 × 103 | 1.280 × 103 | 1.350 × 103 |
| 3.000 | 1.500 × 103 | 1.580 × 103 | 1.670 × 103 |
| 3.500 | 1.720 × 103 | 1.820 × 103 | 1.920 × 103 |
| 4.000 | 1.880 × 103 | 1.990 × 103 | 2.100 × 103 |
| 5.000 | 2.040 × 103 | 2.160 × 103 | 2.300 × 103 |
| 6.000 | 2.050 × 103 | 2.170 × 103 | 2.320 × 103 |
| 7.000 | 1.960 × 103 | 2.080 × 103 | 2.210 × 103 |
| 8.000 | 1.830 × 103 | 1.930 × 103 | 2.050 × 103 |
| 9.000 | 1.680 × 103 | 1.780 × 103 | 1.880 × 103 |
| 10.000 | 1.550 × 103 | 1.630 × 103 | 1.730 × 103 |
| Mass-loss scheme | Vink [36,37], de Jaeger [38], Nugis [40], van Loon [39] |
| Convection criteria | Ledoux in H burning zones, Schwarzschild elsewhere |
| 2.1 | |
| 0.02 | |
| CBM | 0.2 of overshooting (H burning) |
| Initial mass | 20 |
| Initial metallicity | (Asplund 2009 [28]) |
| Initial H mass fraction | 0.721 |
| Initial 4He mass fraction | 0.265 |
| 12C mass fraction (He exhaustion) | 0.286 |
| CO core (He exhaustion) | 4.91 |
| Lifetime (PSN) | 9.87 Myr |
| Total Mass (PSN) | 7.46 |
| (PSN) | 4.30 |
| (PSN) | 5.31 |
| Explosion scheme | Thermal bomb [30] |
| Thermal energy injected | erg, erg |
| Explosion energy (at infinity) | erg, erg |
| Remnant mass | 2.58 , 1.86 |
| Species | STANDARD | JU-LA-BA | LA-BA |
|---|---|---|---|
| 1.2 × erg | |||
| 20Ne | 5.60 × 10−1 | 5.60 × 10−1 | 5.60 × 10−1 |
| 23Na | 1.07 × 10−2 | 1.07 × 10−2 | 1.07 × 10−2 |
| 24Mg | 9.32 × 10−2 | 9.32 × 10−2 | 9.33 × 10−2 |
| 25Mg | 1.66 × 10−2 | 1.66 × 10−2 | 1.66 × 10−2 |
| 26Mg | 1.65 × 10−2 | 1.65 × 10−2 | 1.65 × 10−2 |
| 26Al | 7.02 × 10−5 | 2.75 × 10−5 | 2.65 × 10−5 |
| 27Al | 1.14 × 10−2 | 1.13 × 10−2 | 1.14 × 10−2 |
| 28Si | 2.13 × 10−2 | 2.14 × 10−2 | 2.13 × 10−2 |
| 29Si | 3.17 × 10−3 | 3.17 × 10−3 | 3.18 × 10−3 |
| 30Si | 1.96 × 10−3 | 1.94 × 10−3 | 1.95 × 10−3 |
| 60Fe | 1.19 × 10−5 | 1.19 × 10−5 | 1.17 × 10−5 |
| 3 × erg | |||
| 20Ne | 4.79 × 10−1 | 4.79 × 10−1 | 4.79 × 10−1 |
| 23Na | 8.80 × 10−3 | 8.79 × 10−3 | 8.79 × 10−3 |
| 24Mg | 9.81 × 10−2 | 9.78 × 10−2 | 9.82 × 10−2 |
| 25Mg | 1.44 × 10−2 | 1.44 × 10−2 | 1.44 × 10−2 |
| 26Mg | 1.44 × 10−2 | 1.44 × 10−2 | 1.44 × 10−2 |
| 26Al | 9.68 × 10−5 | 3.36 × 10−5 | 3.26 × 10−5 |
| 27Al | 1.20 × 10−2 | 1.19 × 10−2 | 1.20 × 10−2 |
| 28Si | 2.82 × 10−1 | 2.82 × 10−1 | 2.82 × 10−1 |
| 29Si | 4.99 × 10−3 | 5.03 × 10−3 | 5.03 × 10−3 |
| 30Si | 6.94 × 10−3 | 6.88 × 10−3 | 6.89 × 10−3 |
| 60Fe | 1.14 × 10−5 | 1.14 × 10−5 | 1.12 × 10−5 |
| SLR | Daughter | Reference | T1/2 (yr) | (yr) | ESS Ratio |
|---|---|---|---|---|---|
| 26Al | 26Mg | 27Al | 7.170 × 105 | 1.034 × 106 | (5.23 ± 0.13) × 10−5 |
| 36Cl | 36S | 35Cl | 3.010 × 105 | 4.343 × 105 | (2.44 ± 0.65) × 10−5 |
| 41Ca | 41K | 40Ca | 9.940 × 104 | 1.434 × 105 | (4.6 ± 1.9) × 10−9 |
| 53Mn | 53Cr | 55Mn | 3.740 × 106 | 5.396 × 106 | (7 ± 1) × 10−6 |
| 60Fe | 60Ni | 56Fe | 2.620 × 106 | 3.780 × 106 | (1.01 ± 0.27) × 10−8 |
| 92Nb | 92Zr | 92Mo | 3.470 × 107 | 5.006 × 107 | (3.2 ± 0.3) × 10−5 |
| 97Tc | 97Mo | 98Ru | 4.210 × 106 | 6.074 × 106 | <1.1 × 10−5 |
| 98Tc | 98Ru | 98Ru | 4.200 × 106 | 6.059 × 106 | <6 × 10−5 |
| 107Pd | 107Ag | 108Pd | 6.500 × 106 | 9.378 × 106 | (6.6 ± 0.4) × 10−5 |
| 126Sn | 126Te | 124Sn | 2.300 × 105 | 3.318 × 105 | <3 × 10−6 |
| 129I | 129Xe | 127I | 1.570 × 107 | 2.265 × 107 | (1.28 ± 0.03) × 10−4 |
| 135Cs | 135Ba | 133Cs | 2.300 × 106 | 3.318 × 106 | <2.8 × 10−6 |
| 146Sm | 142Nd | 144Sm | 6.800 × 107 | 9.810 × 107 | (8.28 ± 0.44) × 10−3 |
| 182Hf | 182W | 180Hf | 8.900 × 106 | 1.284 × 107 | (1.018 ± 0.043) × 10−4 |
| 205Pb | 205Tl | 204Pb | 1.730 × 107 | 2.496 × 107 | (1.8 ± 1.2) × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Battino, U.; Roberti, L.; Lawson, T.V.; Laird, A.M.; Todd, L. Impact of Newly Measured Nuclear Reaction Rates on 26Al Ejected Yields from Massive Stars. Universe 2024, 10, 204. https://doi.org/10.3390/universe10050204
Battino U, Roberti L, Lawson TV, Laird AM, Todd L. Impact of Newly Measured Nuclear Reaction Rates on 26Al Ejected Yields from Massive Stars. Universe. 2024; 10(5):204. https://doi.org/10.3390/universe10050204
Chicago/Turabian StyleBattino, Umberto, Lorenzo Roberti, Thomas V. Lawson, Alison M. Laird, and Lewis Todd. 2024. "Impact of Newly Measured Nuclear Reaction Rates on 26Al Ejected Yields from Massive Stars" Universe 10, no. 5: 204. https://doi.org/10.3390/universe10050204
APA StyleBattino, U., Roberti, L., Lawson, T. V., Laird, A. M., & Todd, L. (2024). Impact of Newly Measured Nuclear Reaction Rates on 26Al Ejected Yields from Massive Stars. Universe, 10(5), 204. https://doi.org/10.3390/universe10050204






