Cosmological Inference from within the Peculiar Local Universe
Abstract
1. Introduction
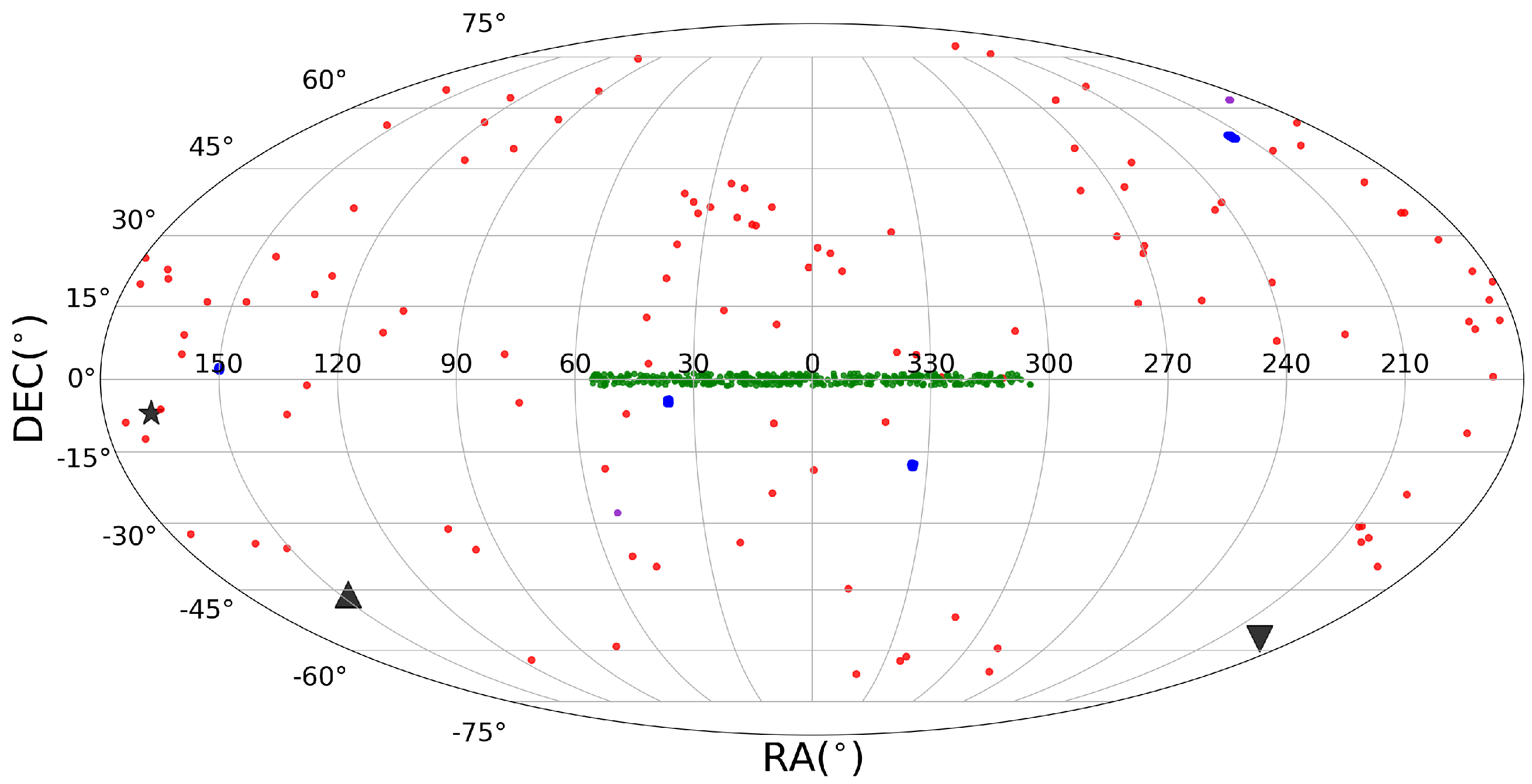
2. Selecting Local Universe Like Environments
- (i)
- The observer halo has a Milky Way (MW)-like mass, in the range [40] for the halo mass contained within 200 kpc.
- (ii)
- The bulk velocity in a sphere of radius Mpc centred on the observer is km s−1
- (iii)
- A Virgo-cluster like halo of mass is present at a distance Mpc from the observer.
- (iv)
- The angle between the bulk flow of (ii) and the direction to the Virgo-like halo of (iii) is
- (v)
- The bulk velocity in a sphere of Mpc centered on the observer is km s−1 [19].
- (vi)
- The angle between the bulk flow of (v) and the direction to the Virgo-like halo of (iii) is .
- (vii)
- The angle between the bulk flows of (ii) and (v) is .
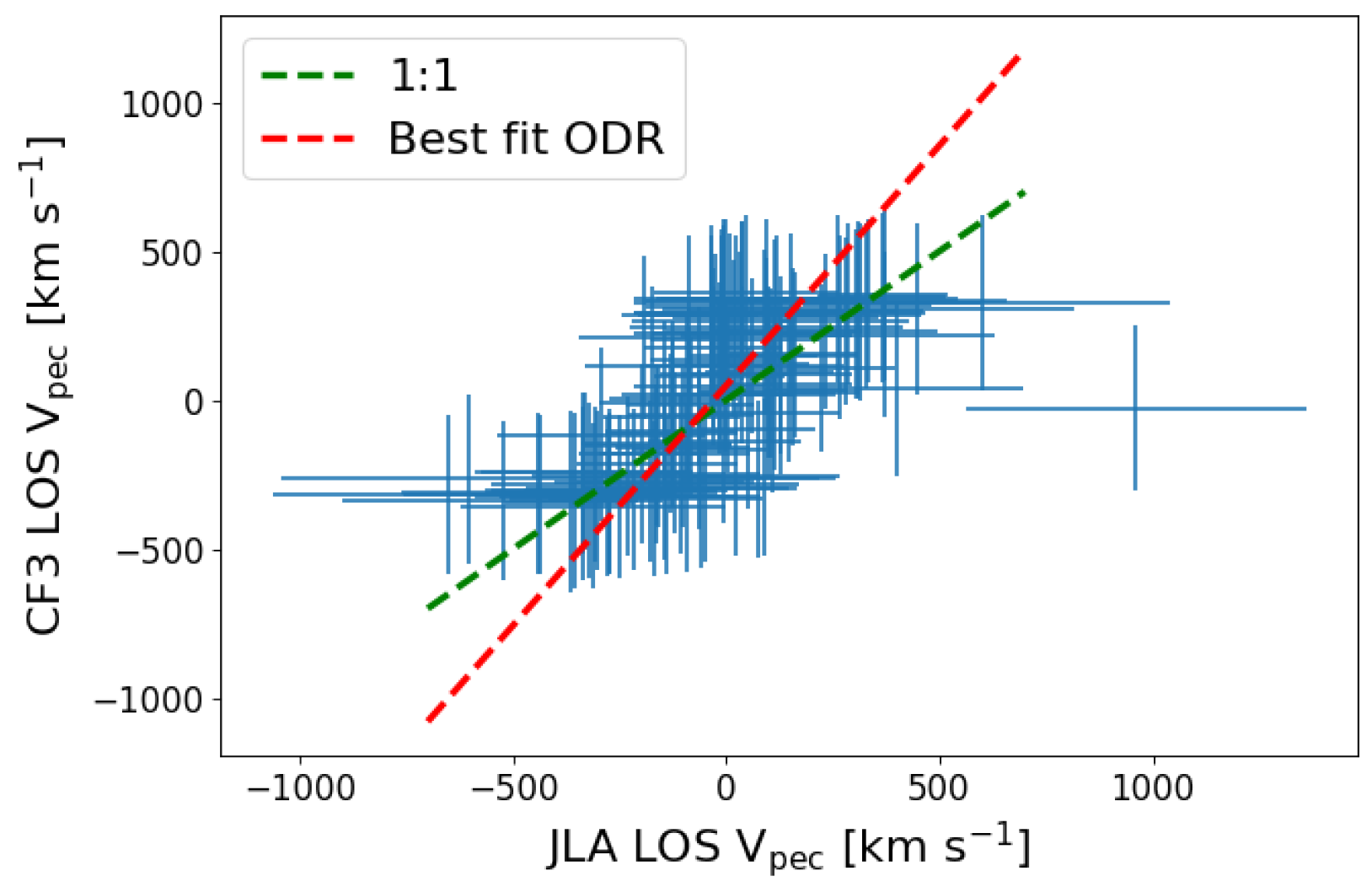
2.1. Peculiar Velocity Corrections in JLA
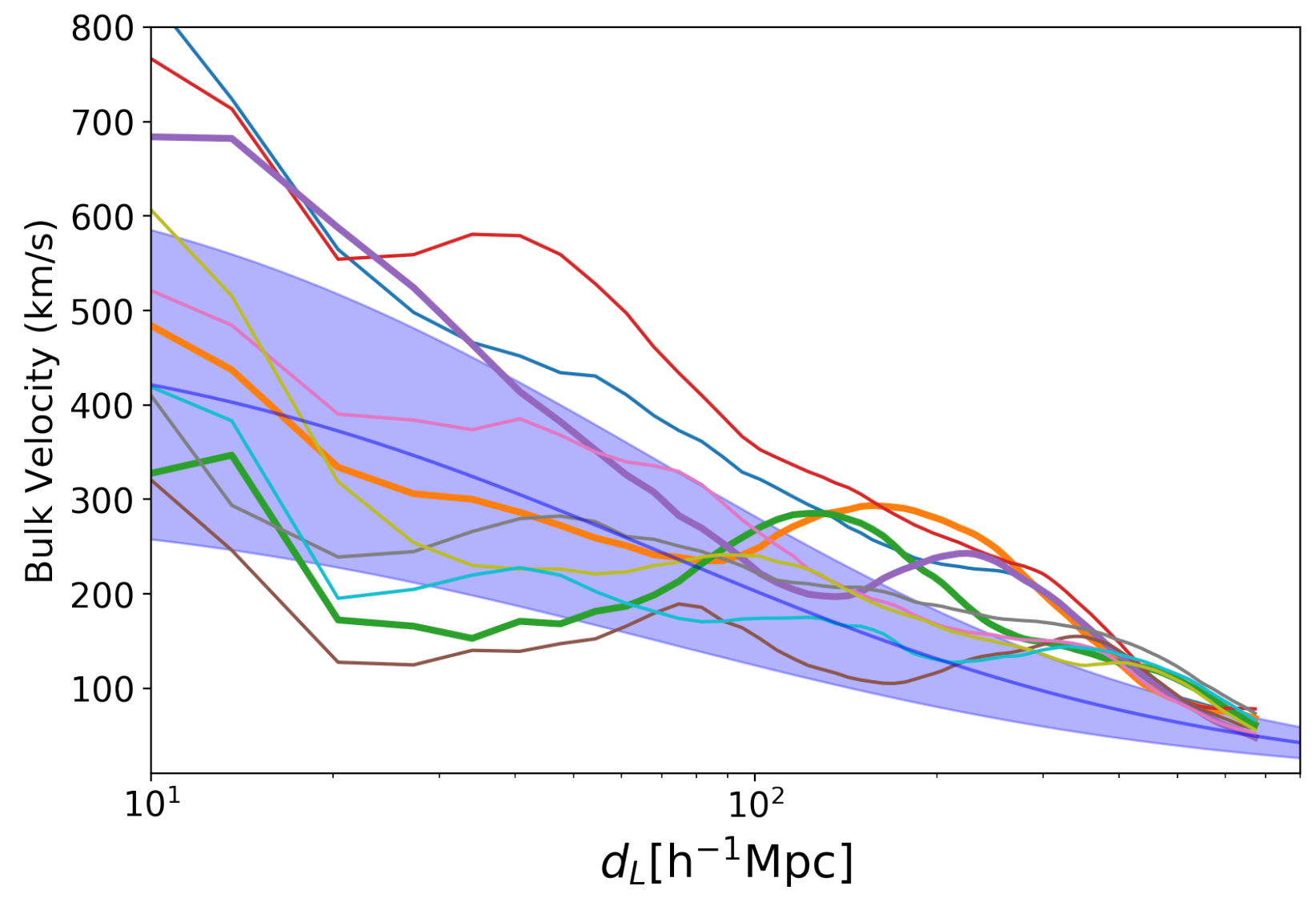
2.2. Fitting for a Bulk Flow
2.3. The Likelihood Analysis
- The same 10-parameter fit as in Ref. [37], using only the values provided by JLA.
- The 10-parameter fit using —as used in Ref. [28]—and the JLA provided and values.
- The 10-parameter fit as in 1, using only values (JLA provided) as was done in all SNe Ia analyses until 2011.
- The 10-parameter fit as in 1, using JLA provided values, after subtracting out bias corrections to .
- Exponentially falling bulk flow: 12-parameter fit (including the P and Q parameters of Equation (6), using only JLA provided values. No peculiar velocity corrections are applied.
- Linearly falling bulk flow: 12-parameter fit (including the P and Q parameters of Equation (5) using only JLA provided values. No peculiar velocity corrections are applied.
- JLA-corrected redshifts + Exponential bulk flow: 12-parameter fit: SNe Ia with peculiar velocity corrections applied by JLA, are treated as in (ii) above, while an exponentially falling bulk flow is fitted to the remaining SNe.
- JLA-corrected redshifts + Linear bulk flow: As in 7, but with the linear parametrisation of the bulk flow.
- CF-3 data and the exponential bulk flow fit: 12-parameter fit using Equation (2) with the -derived values of and (see Section 2.1) used for the low z SNe Ia to which the velocity correction can be applied. For the remaining objects, we use the JLA values, and an Exponential bulk flow is fitted using Equation (6) as described above.
- CF-3 data and the linear bulk flow fit: 12-parameter fit using Equation (5) with the -derived values of and (see Section 2.1) used for the low z SNe Ia to which the velocity correction can be applied. For the remaining objects, we use the JLA values, and a linear bulk flow is fitted using Equation (5).
| Fit | −2 log | V (km s−1) @Mpc | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | As in Ref. [37] | −214.97 | 0.341 | 0.569 | 0.134 | 0.0385 | 0.931 | 3.059 | −0.016 | 0.071 | −19.052 | 0.108 | - |
| No acceleration | −203.93 | 0.068 | 0.034 | 0.132 | 0.0327 | 0.932 | 3.045 | −0.013 | 0.071 | −19.006 | 0.110 | - | |
| 2. | [37] + JLA z | −221.93 | 0.340 | 0.565 | 0.133 | 0.0385 | 0.932 | 3.056 | −0.016 | 0.071 | −19.051 | 0.107 | - |
| No acceleration | −210.99 | 0.070 | 0.035 | 0.131 | 0.0328 | 0.932 | 3.042 | −0.013 | 0.071 | −19.006 | 0.109 | - | |
| 3. | No pec. vel. corr. to z | −215.40 | 0.285 | 0.483 | 0.134 | 0.0398 | 0.932 | 3.038 | −0.016 | 0.071 | −19.051 | 0.108 | - |
| No acceleration | −207.67 | 0.051 | 0.025 | 0.132 | 0.0348 | 0.932 | 3.023 | −0.014 | 0.071 | −19.012 | 0.110 | - | |
| 4. | No pec. vel. corr. to z or | −216.89 | 0.235 | 0.396 | 0.135 | 0.0397 | 0.932 | 3.029 | −0.016 | 0.071 | −19.040 | 0.109 | - |
| No acceleration | −211.84 | 0.0413 | 0.021 | 0.133 | 0.0357 | 0.932 | 3.016 | −0.014 | 0.071 | −19.008 | 0.110 | - | |
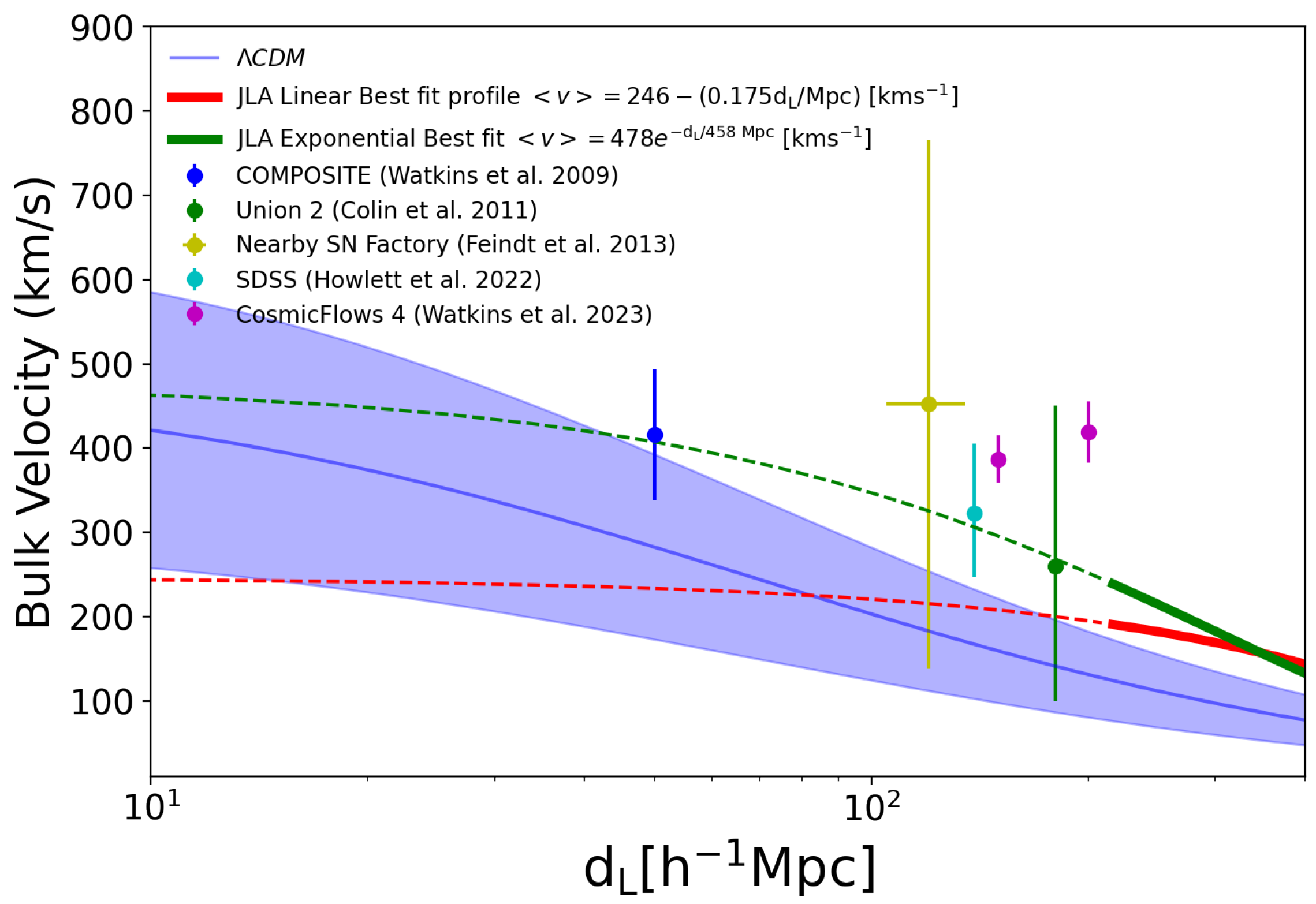
| 5. | Exponential bulk flow | −217.51 | 0.289 | 0.452 | 0.134 | 0.0390 | 0.932 | 3.036 | −0.016 | 0.071 | −19.037 | 0.107 | 253 |
| No acceleration | −211.3 | 0.077 | 0.039 | 0.132 | 0.0347 | 0.932 | 3.024 | −0.014 | 0.071 | −19.002 | 0.108 | 292 | |
| 6. | Linear bulk flow | −217.47 | 0.290 | 0.455 | 0.134 | 0.0390 | 0.932 | 3.036 | −0.016 | 0.071 | −19.038 | 0.107 | 265 |
| No acceleration | −211.99 | 0.082 | 0.041 | 0.132 | 0.0347 | 0.932 | 3.025 | −0.014 | 0.071 | −19.002 | 0.108 | 282 | |
| 7. | JLA + Exp. bulk flow | −224.87 | 0.340 | 0.570 | 0.133 | 0.0387 | 0.932 | 3.051 | −0.016 | 0.072 | −19.052 | 0.107 | 271 |
| No acceleration | −216.3 | 0.077 | 0.039 | 0.132 | 0.0347 | 0.932 | 3.024 | −0.014 | 0.071 | −19.002 | 0.108 | 295 | |
| 8. | JLA + Lin. bulk flow | −225.08 | 0.341 | 0.577 | 0.133 | 0.0387 | 0.932 | 3.050 | −0.016 | 0.071 | −19.054 | 0.107 | 238 |
| No acceleration | −214.14 | 0.072 | 0.036 | 0.131 | 0.0328 | 0.932 | 3.041 | −0.013 | 0.071 | −19.005 | 0.109 | 251 | |
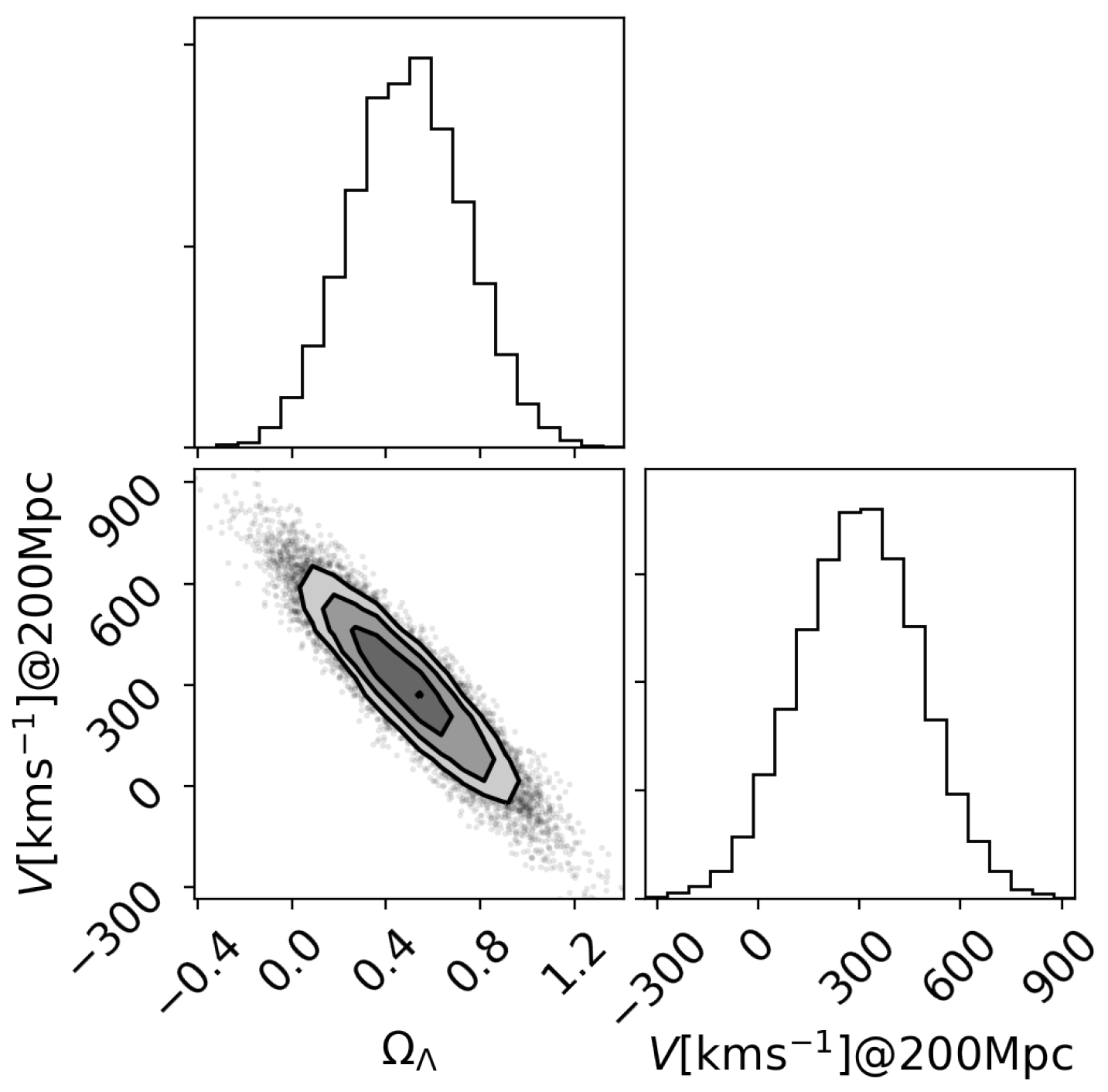
| 9. | + Exp. Bulk Flow | −225.61 | 0.279 | 0.427 | 0.133 | 0.0386 | 0.932 | 3.001 | −0.016 | 0.071 | −19.034 | 0.109 | 309 |
| No acceleration | −220.72 | 0.086 | 0.043 | 0.132 | 0.0346 | 0.932 | 2.990 | −0.015 | 0.071 | −19.001 | 0.110 | 398 | |
| Flat | −223.96 | 0.393 | 0.607 | 0.133 | 0.0357 | 0.933 | 2.998 | −0.016 | 0.071 | −19.045 | 0.110 | 338 | |
| 10. | + Lin. bulk flow | −225.73 | 0.277 | 0.431 | 0.133 | 0.0386 | 0.932 | 3.002 | −0.016 | 0.071 | −19.037 | 0.109 | 211 |
| No acceleration | −220.16 | 0.085 | 0.042 | 0.132 | 0.0346 | 0.932 | 2.991 | −0.015 | 0.071 | −19.001 | 0.110 | 249 | |
| Flat | −224.18 | 0.390 | 0.610 | 0.134 | 0.0399 | 0.932 | 3.006 | −0.016 | 0.071 | −19.047 | 0.109 | 215 |
- Of all the fits, the only ones favouring are just those that include the incorrect and incomplete peculiar velocity ‘corrections’ of JLA [25].
- While previous work has suggested that bulk flows should not bias , it in fact drops by ∼ if we undo the peculiar velocity ‘corrections’ of JLA and instead use the kinematic data from. This illustrates the huge impact of considering a realistic LU-like observer such as ourselves, rather than the randomly located observer assumed in all previous analyses [16,28,29,30]. In particular this contradicts what is stated in Table 11 of Ref. [25].
3. Extracting S8
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
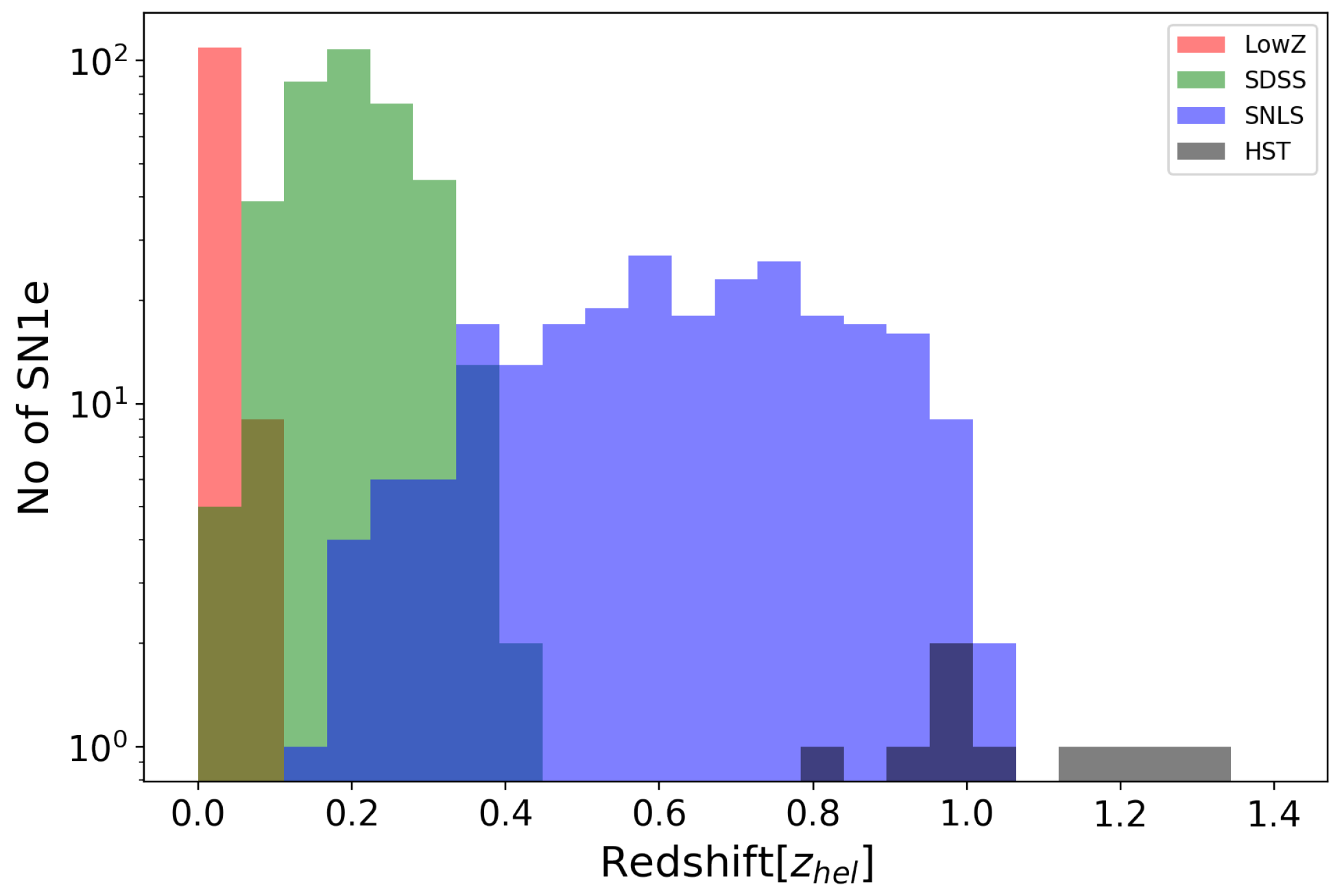
Appendix A. Supernova Cosmology
Appendix B. The Joint Lightcurve Analysis Catalogue
| 1 | There are other corrections too such as for gravitational lensing, which become more important than the effect of peculiar velocities at redshift —see Figure B.1 of Ref. [6]. |
References
- Peebles, P.J.E. Anomalies in physical cosmology. Ann. Phys. 2022, 447, 169159. [Google Scholar] [CrossRef]
- Freedman, W.L. Measurements of the Hubble constant: Tensions in perspective. Astrophys. J. 2021, 919, 16. [Google Scholar] [CrossRef]
- Abdalla, E.; Franco Abellán, G.; Aboubrahim, A.; Agnello, A.; Akarsu, O.; Akrami, Y.; Alestas, G.; Aloni, D.; Amendola, L.; Anchordoqui, L.A.; et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. J. High Energy Astropys. 2022, 34, 49. [Google Scholar] [CrossRef]
- Secrest, N.J.; von Hausegger, S.; Rameez, M.; Mohayaee, R.; Sarkar, S.; Colin, J. A Test of the Cosmological Principle with Quasars. Astrophys. J. Lett. 2021, 908, L51. [Google Scholar] [CrossRef]
- Secrest, N.J.; von Hausegger, S.; Rameez, M.; Mohayaee, R.; Sarkar, S. A Challenge to the Standard Cosmological Model. Astrophys. J. Lett. 2022, 937, L31. [Google Scholar] [CrossRef]
- Colin, J.; Mohayaee, R.; Rameez, M.; Sarkar, S. Evidence for anisotropy of cosmic acceleration. Astron. Astrophys. 2019, 631, L13. [Google Scholar] [CrossRef]
- Tsagas, C.G.; Kadiltzoglou, M.I.; Asvesta, K. The deceleration parameter in “tilted” Friedmann universes: Newtonian vs relativistic treatment. Astrophys. Space Sci. 2021, 366, 90. [Google Scholar] [CrossRef]
- Watkins, R.; Allen, T.; Bradford, C.J.; Walker, A.; Feldman, H.A.; Cionitti, R.; Al-Shorman, Y.; Kourkchi, E.; Tully, R.B. Analysing the large-scale bulk flow using Cosmicflows4: Increasing tension with the standard cosmological model. Mon. Not. Roy. Astron. Soc. 2023, 524, 1885. [Google Scholar] [CrossRef]
- McClure, M.L.; Dyer, C.C. Anisotropy in the Hubble constant as observed in the HST Extragalactic Distance Scale Key Project results. New Astron. 2007, 12, 533. [Google Scholar] [CrossRef]
- Leibundgut, B. Type Ia supernovae. Astron. Astrophys. Rev. 2000, 10, 179. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Zuntz, J.; Kessler, R.; Carr, A.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Hudson, M.J.; Smith, R.J.; Lucey, J.R.; Branchini, E. Streaming motions of galaxy clusters within 12000 km/s. 5. The peculiar velocity field. Mon. Not. Roy. Astron. Soc. 2004, 352, 61. [Google Scholar] [CrossRef]
- Conley, A.; Guy, J.; Sullivan, M.; Regnault, N.; Astier, P.; Ball, C.; Basa, S.; Carlberg, R.G.; Fouchez, D.; Hardin, D.; et al. Supernova Constraints and Systematic Uncertainties from the First 3 Years of the Supernova Legacy Survey. Astrophys. J. Suppl. 2011, 192, 1. [Google Scholar] [CrossRef]
- Neill, J.D.; Hudson, M.J.; Conley, A. The peculiar velocities of local Type Ia supernovae and their impact on cosmology. Astrophys. J. Lett. 2007, 661, L123. [Google Scholar] [CrossRef]
- Saunders, W.; Sutherl, W.J.; Maddox, S.J.; Keeble, O.; Oliver, S.J.; Rowan-Robinson, M.; McMahon, R.G.; Efstathiou, G.P.; Tadros, H.; White, S.D.; et al. The PSCz catalogue. Mon. Not. Roy. Astron. Soc. 2000, 317, 55. [Google Scholar] [CrossRef]
- Carrick, J.; Turnbull, S.J.; Lavaux, G.; Hudson, M.J. Cosmological parameters from the comparison of peculiar velocities with predictions from the 2M++ density field. Mon. Not. Roy. Astron. Soc. 2015, 450, 317. [Google Scholar] [CrossRef]
- Colin, J.; Mohayaee, R.; Sarkar, S.; Shafieloo, A. Probing the anisotropic local universe and beyond with SNe Ia data. Mon. Not. Roy. Astron. Soc. 2011, 414, 264. [Google Scholar] [CrossRef]
- Feindt, U.; Kerschhaggl, M.; Kowalski, M.; Aldering, G.; Antilogus, P.; Aragon, C.; Bailey, S.; Baltay, C.; Bongard, S.; Buton, C.; et al. Measuring cosmic bulk flows with Type Ia supernovae from the Nearby Supernova Factory. Astron. Astrophys. 2013, 560, A90. [Google Scholar] [CrossRef]
- Howlett, C.; Said, K.; Lucey, J.R.; Colless, M.; Qin, F.; Lai, Y.; Tully, R.B.; Davis, T.M. The sloan digital sky survey peculiar velocity catalogue. Mon. Not. Roy. Astron. Soc. 2022, 515, 953. [Google Scholar] [CrossRef]
- Lavaux, G.; Tully, R.B.; Mohayaee, R.; Colombi, S. Cosmic flow from 2MASS redshift survey: The origin of CMB dipole and implications for LCDM cosmology. Astrophys. J. 2010, 709, 48. [Google Scholar] [CrossRef]
- Magoulas, C.; Springob, C.; Colless, M.; Mould, J.; Lucey, J.; Erdoğdu, P.; Jones, D.H. Measuring the cosmic bulk flow with 6dFGSv. Proc. IAU Symp. 2016, 308, 336. [Google Scholar] [CrossRef]
- Watkins, R.; Feldman, H.A.; Hudson, M.J. Large-scale bulk flows from the Cosmicflows-2 catalogue. Mon. Not. Roy. Astron. Soc. 2009, 392, 743. [Google Scholar] [CrossRef]
- Betoule, M.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Rameez, M.; Sarkar, S. Is there really a Hubble tension? Class. Quant. Grav. 2021, 38, 154005. [Google Scholar] [CrossRef]
- Davis, T.M.; Hui, L.; Frieman, J.A.; Haugbølle, T.; Kessler, R.; Sinclair, B.; Sollerman, J.; Bassett, B.; Marriner, J.; Mørtsell, E.; et al. The effect of peculiar velocities on supernova cosmology. Astrophys. J. 2011, 741, 67. [Google Scholar] [CrossRef]
- Hui, L.; Greene, P.B. Correlated fluctuations in luminosity distance and the (surprising) importance of peculiar motion in supernova surveys. Phys. Rev. D 2006, 73, 123526. [Google Scholar] [CrossRef]
- Huterer, D.; Shafer, D.L.; Schmidt, F. No evidence for bulk velocity from Type Ia supernovae. J. Cosmo. Astropart. Phys. 2015, 12, 033. [Google Scholar] [CrossRef]
- Hunt, P.; Sarkar, S. Constraints on large scale inhomogeneities from WMAP-5 and SDSS: Confrontation with recent observations. Mon. Not. Roy. Astron. Soc. 2010, 401, 547. [Google Scholar] [CrossRef]
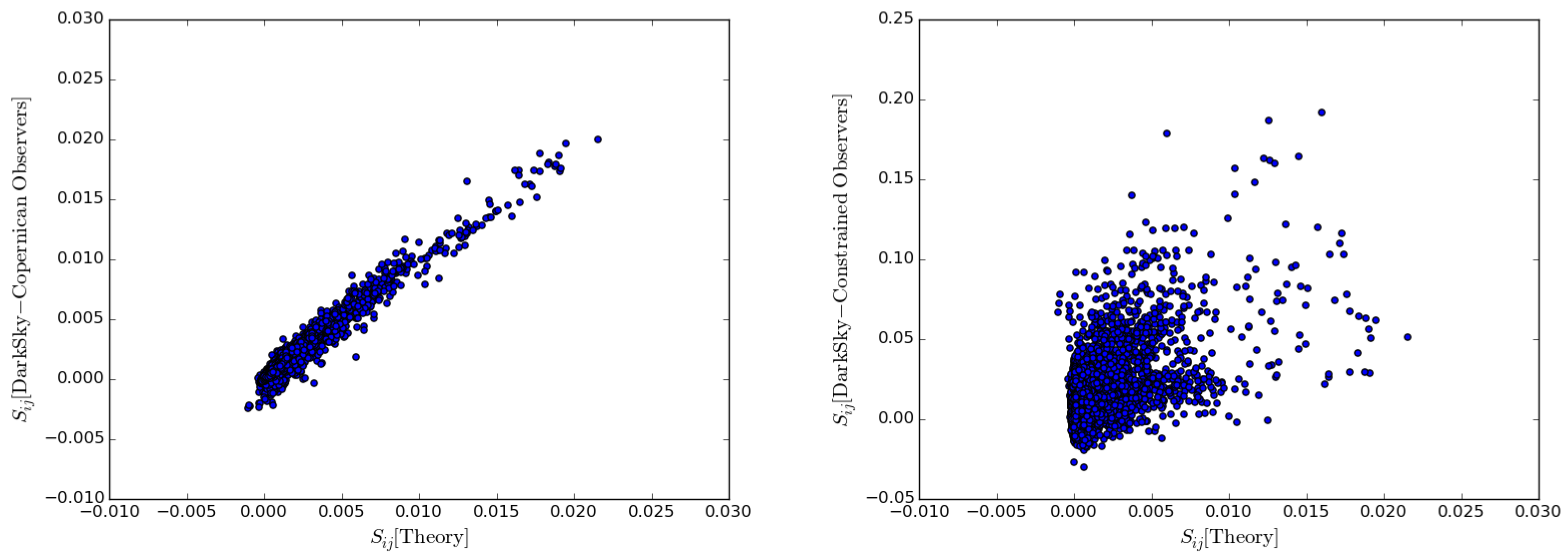
- Hellwing, W.A.; Nusser, A.; Feix, M.; Bilicki, M. Not a Copernican observer: Biased peculiar velocity statistics in the local universe. Mon. Not. Roy. Astron. Soc. 2017, 467, 2787. [Google Scholar] [CrossRef]
- Hellwing, W.A.; Bilicki, M.; Libeskind, N.I. Uneven flows: On cosmic bulk flows, local observers, and gravity. Phys. Rev. D 2018, 97, 103519. [Google Scholar] [CrossRef]
- Rameez, M.; Mohayaee, R.; Sarkar, S.; Colin, J. The dipole anisotropy of AllWISE galaxies. Mon. Not. Roy. Astron. Soc. 2018, 477, 1772. [Google Scholar] [CrossRef]
- Skillman, S.W.; Warren, M.S.; Turk, M.J.; Wechsler, R.H.; Holz, D.E.; Sutter, P.M. Dark Sky simulations: Early data release. arXiv 2014, arXiv:1407.2600. [Google Scholar]
- Tully, R.B.; Courtois, H.M.; Sorce, J.G. Cosmicflows-3. Astron J. 2016, 152, 50. [Google Scholar] [CrossRef]
- Nielsen, J.T.; Guffanti, A.; Sarkar, S. Marginal evidence for cosmic acceleration from Type Ia supernovae. Sci. Rep. 2016, 6, 35596. [Google Scholar] [CrossRef] [PubMed]
- Rubin, D.; Hayden, B. Is the expansion of the universe accelerating? All signs point to yes. Astrophys. J. Lett. 2016, 833, L30. [Google Scholar] [CrossRef]
- Boruah, S.S.; Hudson, M.J.; Lavaux, G. Cosmic flows in the nearby universe: New peculiar velocities from SNe and cosmological constraints. Mon. Not. Roy. Astron. Soc. 2020, 498, 2703. [Google Scholar] [CrossRef]
- Cautun, M.; Frenk, C.S.; van de Weygaert, R.; Hellwing, W.A.; Jones, B.J.T. Milky Way mass constraints from the Galactic satellite gap. Mon. Not. Roy. Astron. Soc. 2014, 445, 2049. [Google Scholar] [CrossRef]
- Hong, T.; Springob, C.M.; Staveley-Smith, L.; Scrimgeour, M.I.; Masters, K.L.; Macri, L.M.; Koribalski, B.S.; Jones, D.H.; Jarrett, T.H. 2MTF – IV. A bulk flow measurement of the local universe. Mon. Not. Roy. Astron. Soc. 2014, 445, 402. [Google Scholar] [CrossRef]
- Boggs, P.T.; Rogers, J.E. Orthogonal distance regression. Contemp. Math. 1990, 112, 183. [Google Scholar] [CrossRef]
- Colin, J.; Mohayaee, R.; Rameez, M.; Sarkar, S. High redshift radio galaxies and divergence from the CMB dipole. Mon. Not. Roy. Astron. Soc. 2017, 471, 1045. [Google Scholar] [CrossRef]
- Nielsen, J.T. Supernovae as cosmological probes. arXiv 2015, arXiv:1508.07850. [Google Scholar]
- Hollinger, A.M.; Hudson, M.J. Assessing the accuracy of cosmological parameters estimated from velocity – density comparisons via simulations. Mon. Not. Roy. Astron. Soc. 2021, 502, 3723. [Google Scholar] [CrossRef]
- Said, K.; Colless, M.; Magoulas, C.; Lucey, J.R.; Hudson, M.J. Joint analysis of 6dFGS and SDSS peculiar velocities for the growth rate of cosmic structure and tests of gravity. Mon. Not. Roy. Astron. Soc. 2020, 497, 1275. [Google Scholar] [CrossRef]
- Huterer, D. Specific effect of peculiar velocities on dark-energy constraints from Type Ia supernovae. Astrophys. J. Lett. 2020, 904, L28. [Google Scholar] [CrossRef]
- Bertschinger, E. Cosmological dynamics: Course 1. arXiv 1993, arXiv:astro-ph/9503125. [Google Scholar]
- Mukhanov, V.F.; Feldman, H.A.; Brandenberger, R.K. Theory of cosmological perturbations. Part 1. Classical perturbations. Part 2. Quantum theory of perturbations. Part 3. Extensions. Phys. Rep. 1992, 215, 203. [Google Scholar] [CrossRef]
- D’Eath, P.D. On the existence of perturbed Robertson-Walker universes. Ann. Phys. 1976, 98, 237. [Google Scholar] [CrossRef]
- Giblin, J.T.; Mertens, J.B.; Starkman, G.D. Departures from the Friedmann-Lemaitre-Robertston-Walker cosmological model in an inhomogeneous universe: A numerical examination. Phys. Rev. Lett. 2015, 116, 251301. [Google Scholar] [CrossRef]
- Buchert, T.; Carfora, M.; Ellis, G.F.R.; Kolb, E.W.; MacCallum, M.A.H.; Ostrowski, J.J.; Räsänen, S.; Roukema, B.F.; Andersson, L.; Coley, A.A.; et al. Is there proof that backreaction of inhomogeneities is irrelevant in cosmology? Class. Quant. Grav. 2015, 32, 215021. [Google Scholar] [CrossRef]
- Guy, J.; Astier, P.; Baumont, S.; Hardin, D.; Pain, R.; Regnault, N.; Basa, S.; Carlberg, R.G.; Conley, A.; Fabbro, S.; et al. SALT2: Using distant supernovae to improve the use of Type Ia supernovae as distance indicators. Astron. Astrophys. 2007, 466, 11. [Google Scholar] [CrossRef]
- March, M.; Trotta, R.; Berkes, P.; Starkman, G.; Vaudrevange, P. Improved constraints on cosmological parameters from Type Ia supernova data. Mon. Not. Roy. Astron. Soc. 2011, 418, 2308–2329. [Google Scholar] [CrossRef]
- Shariff, H.; Xiao, J.; Trotta, R.; van Dyk, D.A. BAHAMAS: New analysis of Type Ia supernovae reveals inconsistencies with standard cosmology. Astrophys. J. 2016, 827, 1. [Google Scholar] [CrossRef]
- Dam, L.H.; Heinesen, A.; Wiltshire, D.L. Apparent cosmic acceleration from Type Ia supernovae. Mon. Not. Roy. Astron. Soc. 2017, 472, 835. [Google Scholar] [CrossRef]
- Desgrange, C.; Heinesen, A.; Buchert, T. Dynamical spatial curvature as a fit to Type Ia supernovae. Intern. J. Mod. Phys. D 2019, 28, 1950143. [Google Scholar] [CrossRef]
- Colin, J.; Mohayaee, R.; Rameez, M.; Sarkar, S. A response to Rubin & Heitlauf: “Is the expansion of the universe accelerating? All signs still point to yes”. arXiv 2019, arXiv:1912.04257. [Google Scholar]
- Karpenka, N.V. The supernova cosmology cookbook: Bayesian numerical recipes. arXiv 2015, arXiv:1503.03844. [Google Scholar]
- Mohayaee, R.; Rameez, M.; Sarkar, S. Do supernovae indicate an accelerating universe? Eur. Phys. J. ST 2021, 230, 2067. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohayaee, R.; Rameez, M.; Sarkar, S. Cosmological Inference from within the Peculiar Local Universe. Universe 2024, 10, 209. https://doi.org/10.3390/universe10050209
Mohayaee R, Rameez M, Sarkar S. Cosmological Inference from within the Peculiar Local Universe. Universe. 2024; 10(5):209. https://doi.org/10.3390/universe10050209
Chicago/Turabian StyleMohayaee, Roya, Mohamed Rameez, and Subir Sarkar. 2024. "Cosmological Inference from within the Peculiar Local Universe" Universe 10, no. 5: 209. https://doi.org/10.3390/universe10050209
APA StyleMohayaee, R., Rameez, M., & Sarkar, S. (2024). Cosmological Inference from within the Peculiar Local Universe. Universe, 10(5), 209. https://doi.org/10.3390/universe10050209







