Hard-Core Radius of Nucleons within the Induced Surface Tension Approach ^†

Abstract

We review the recent approach to model the hadronic and nuclear matter equations of state using the induced surface tension concept, which allows one to go far beyond the usual Van der Waals approximation. Since the obtained equations of state, classical and quantum, are among the most successful ones in describing the properties of low density phases of strongly interacting matter, they set strong restrictions on the possible value of the hard-core radius of nucleons, which is widely used in phenomenological equations of state. We summarize the latest results obtained within this novel approach and perform a new detailed analysis of the hard-core radius of nucleons, which follows from hadronic and nuclear matter properties. Such an analysis allows us to find the most trustworthy range of its values: the hard-core radius of nucleons is 0.3–0.36 fm. A comparison with the phenomenology of neutron stars implies that the hard-core radius of nucleons has to be temperature and density dependent. Such a finding is supported when the eigenvolume of composite particles like hadrons originates from their fermionic substructure due to the Pauli blocking effect.

1. Introduction

A reliable and precise determination of major characteristics of symmetric nuclear matter is of fundamental importance [1,2,3,4,5] not only for the nuclear spectroscopy and for nuclear physics of intermediate energies, but also for nuclear astrophysics in view of possible phase transformations which may occur in compact astrophysical objects such as neutron stars, and hypothetical hybrid and quark stars. Such characteristics of infinite nuclear matter as the normal density $n_0\simeq 0.16$ fm⁻³ at zero pressure and zero temperature, its binding energy per nucleon $W_0=-16$ MeV, and its incompressibility factor $K_0$ are of great importance for various phenomenological approaches, since these characteristics are widely used for determination of the model parameters. However, there exists a significant uncertainty in the $K_0$ value, since earlier estimates provide $K_0\simeq 220-260$ MeV [6], while the more recent ones give us $K_0\simeq 250-315$ MeV [7]. Furthermore, such a parameter of the nuclear matter as the hard-core radius (HCR) of nucleons $R_N$ plays an important role not only in nuclear physics [1,3], but also in nuclear astrophysics [2,4] and in the physics of heavy ion collisions (HIC) [8,9,10,11,12,13,14,15,16,17,18]. However, in the literature one can find any value of $R_N$ in the range 0.3–0.7 fm. The problem is partly related to the fact that almost all equations of state (EoS) with the hard-core repulsion employ the Van der Waals (VdW) approximation, which is applicable only at low particle number densities.

Therefore, the results obtained within a novel and convenient approach which allows one to safely go beyond the VdW approximation for any number of HCR (multicomponent case) [19,20,21,22] are of great importance for all field of physics mentioned above. Having a single additional parameter compared to the multicomponent VdW EoS this approach based on the induced surface tension (IST) concept [23] enables us to describe on the same footing the data measured in HIC, to reproduce the nuclear matter properties up to five normal nuclear densities, and to describe the mass-radius relation of neutron stars. Since different applications of the developed equation of state provide us with a few ranges of $R_N$ values, it is important to find the most trustworthy one. For this purpose, here we review the main features of the IST equation of state, both classical and quantum, and consider the constraints on $R_N$ values which follow from the proton flow. The new and significant element of this study is a comparison of quantum virial coefficients with the S-matrix approach, which allows us to determine the most trustworthy range of $R_N$ values. Besides, we draw some conclusions for developing the EoS of neutron star matter.

It is appropriate to stress here that the IST approach allows one to account for the effect of interaction of particle of finite size with a thermal medium. This is another principal difference from the VdW equation of state, which makes the IST approach a very promising one. The point is that composite physical objects with large spatial size (large nuclei, large clusters of molecules, heavy quark gluon bags, etc.) should have eigensurface tension which accounts for the degeneracy of their internal degrees of freedom [24,25]. The other parts of the surface tension coefficient are related to the induced one by the interaction with the medium and, perhaps, the one appearing due to interference of the eigen and induced parts. At present state of art it is unclear how to account for such an interference effect, but, probably, the density, temperature, or pressure dependence of the radius of such composite objects can be a good approximation for it (see a discussion below).

As it was shown in Ref. [23], the presence of the IST coefficient allows one to correctly reproduce the low density behavior of partition function of a mixture of nuclear fragments consisting of any number of nucleons, which is traditionally studied within the eigenvolume (or high density) approximation in a framework of the statistical multifragmentation model [26,27]. Apparently, the same should be true for the statistical models considering the phase transition between hadrons and quark gluon bags [25,28,29]. Therefore, the IST concept is of great importance for a correct modeling the quark-gluon-hadron phase transition in heavy ion collisions [16,17,18,19,30], inside the hybrid neutron stars [31,32,33,34], and for the cosmological phase transition in the early Universe [35] (see also [36,37,38] and references therein), since in all these transitions the surface tension of quark gluon bags play a decisive role.

The review is organized as follows. In Section 2 we recall the main equations of the hadron resonance gas model (HRGM) [20,21,22] based on the concept of induced surface tension [23]. The new results on the quantum formulation of the induced surface tension equation of state for nuclear matter are discussed in Section 3, whereas our conclusions are summarized in Section 4.

2. Multicomponent Formulation of HRGM with Hard-Core Repulsion

For many years the HRGM [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] is successfully used to find out the parameters of chemical freeze-out (CFO) from the hadronic yields measured experimentally in high energy nuclear collisions. Presently, the HRGM based on the EoS with the multicomponent hard-core repulsion between hadrons [9,10,11,12,13,16,17,18,19,20,21,22] gives the most successful description of all independent hadronic multiplicity ratios, which have been measured in the high energy heavy ion collision experiments performed starting from the early 70-ies (Bevalac) until present over BNL-AGS, GSI-SIS, CERN-SPS, BNL-RHIC, to CERN-LHC in the broad range of center of mass energies ${\sqrt{s}}_{NN}$ from 2.7 to 5020 GeV. There exist three major grounds to consider the HRGM with multicomponent hard-core repulsion as the realistic EoS of hadronic matter at high temperatures and moderate particle number densities. Firstly, for a long time it was well known that for temperatures below 170 MeV and moderate baryonic charge densities (below about twice nuclear saturation density), the mixture of stable hadrons and their resonances whose interaction is described by the quantum second virial coefficients behaves almost like a mixture of ideal gases of stable particles which, however, includes both the hadrons and their resonances, but with their averaged vacuum values of masses [39]. As it was demonstrated in Ref. [39], the main physical reason for this kind of behavior is rooted in an almost complete cancellation between the attractive and repulsive terms in the quantum second virial coefficients. Hence, the residual deviation from the ideal gas (a weak repulsion) can be modeled by the classical second virial coefficients.

Secondly, by considering the HRGM as the hadronic matter EoS one can be sure that its pressure will never exceed the one of the quark-gluon plasma. The latter may occur if the hadrons are treated as the mixture of ideal gases [20,40]. It is well-known that the number of spin-isospin degeneracies of all hadrons and their resonances with the masses up to 2.6 GeV is so large that, if one does not take into account the hard-core repulsion between them, then at temperatures above 180 MeV their pressure will be larger than the pressure of the quark-gluon plasma (for a comparison with the lattice QCD results, see, for instance, Figure 8 in [20]).

Thirdly, an additional reason to regard the HRGM as hadronic matter EoS in the vicinity of CFO is the practical one: since the hard-core repulsion is a contact interaction, the energy per particle of such an EoS equals to the one of the ideal gas, even for the case of quantum statistics [22]. Therefore, during the evolution of the system after CFO to the kinetic freeze-out one will not face a hard mathematical problem [41,42] to somehow “convert” the potential energy of interacting particles into their kinetic energy and into the masses of particles which appear due to resonance decays.

Apparently, these reasons allow one to consider the HRGM as an extension of the statistical bootstrap model [43] for a truncated hadronic mass-volume spectrum which is augmented with the hard-core repulsion. Because of these reasons the HRGM enables us to achieve a very good description of the hadronic multiplicities measured in heavy ion collision experiments.

Although many valuable findings were obtained with the HRGM during last few years, at the moment the HCR are well established for the most abundant hadrons only, i.e., for pions ($R_{\pi }\simeq 0.15\pm 0.02$ fm), for the lightest K^±-mesons ($R_K\simeq 0.395\pm 0.03$ fm), for nucleons ($R_p\simeq 0.365\pm 0.03$ fm), and for the lightest (anti)$\Lambda$-hyperons ($R_{\Lambda }\simeq 0.085\pm 0.015$ fm) [20,21]. Nevertheless, there is a confidence that in few years from now the new data of high quality which will be measured at RHIC BNL (Brookhaven) [44], NICA JINR (Dubna) [45], and FAIR GSI (Darmstadt) [46], will help us to find out the HCR of other measured hadrons with unprecedentedly high accuracy. However, one should remember that the traditional multicomponent HRGM based on the VdW approximation is not suited for such a purpose, since for $N\sim 100$ different HCR, where N corresponds to the various hadronic species produced in a collision, one has to find a solution of N transcendental equations. Therefore, an increase of the number of HCR to $N\sim 100$ will lead to hard computational problems for the traditional HRGM with multicomponent hard-core repulsion. To resolve this principal problem, the new HRGM based on the IST concept [23] was recently developed in Refs. [20,21,22].

The IST EoS is a system of two coupled equations for the pressure p and the IST coefficient $\Sigma$

$$\begin{array}{}(1)& \hfill p& =& \sum _{k=1}^N{p}_k=T\sum _{k=1}^N{\varphi }_{k}exp\left[\frac{{\mu }_k}{T}-\frac{4}{3}\pi R_k^3\frac{p}{T}-4\pi R_k^2\frac{\Sigma }{T}\right],\hfill (2)& \hfill \Sigma & =& \sum _{k=1}^N{\Sigma }_k=T\sum _{k=1}^N{R}_k{\varphi }_{k}exp\left[\frac{{\mu }_k}{T}-\frac{4}{3}\pi R_k^3\frac{p}{T}-4\pi R_k^2\alpha \frac{\Sigma }{T}\right],\hfill (3)& \hfill {\mu }_k& =& {\mu }_B{B}_k+{\mu }_{I3}{I}_{3k}+{\mu }_S{S}_k,\hfill \end{array}$$

where $\alpha =1.245$, and ${\mu }_B$, ${\mu }_S$, ${\mu }_{I3}$ are the chemical potentials of baryon number, the strangeness, and the third projection of the isospin, respectively. Here $B_k$, $S_k$, $I_{3k}$, $m_k$, and $R_k$ denote, respectively, the corresponding charges, mass, and HCR of the k-th hadronic species. The sums in Equations (1) and (2) run over all hadronic species including their antiparticles which are considered as independent species. Therefore, $p_k$ and ${\Sigma }_k$ are, respectively, the partial pressure and the partial induced surface tension coefficient of the k-th hadronic species.

In Equations (1) and (2) the thermal density ${\varphi }_k$ of the k-th hadronic sort contains the Breit-Wigner mass attenuation. Hence, in the Boltzmann approximation (the quantum gases are discussed in Ref. [22]) it can be cast

$$\begin{array}{c}\hfill {\varphi }_k=g_k{\gamma }_S^{|s_k|}\underset{M_k^{Th}}{\overset{\infty }{\int }}\frac{dm}{N_k(M_k^{Th})}\frac{{\Gamma }_k}{{(m-m_k)}^2+{\Gamma }_k^2/4}\int \frac{d^{3}p}{{(2\pi )}^3}exp\left[-\frac{\sqrt{p^2+m^2}}{T}\right].\end{array}$$

(4)

Here $g_k$ is the degeneracy factor of the k-th hadronic species, ${\gamma }_S$ is the strangeness suppression factor [47], $|s_k|$ is the number of valence strange quarks and antiquarks in this hadron species, and the quantity ${\displaystyle N_k(M_k^{Th})\equiv \underset{M_k^{Th}}{\overset{\infty }{\int }}\frac{dm{\Gamma }_k}{{(m-m_k)}^2+{\Gamma }_k^2/4}}$ denotes a normalization factor with $M_k^{Th}$ being the decay threshold mass of the k-th hadronic sort, while ${\Gamma }_k$ denotes its width. It is necessary to remind that the Breit-Wigner ansatz for the mass distribution is an approximation which holds for relatively narrow resonances only. The formulation of the thermodynamics for unstable particles (4) in the spirit of a Beth-Uhlenbeck EoS [48], however, holds for more general mass distributions which may replace this ansatz. Nevertheless, such an ansatz can be rigorously derived for a mixture of hadron resonances [49,50] from the Phi-functional approach [51], if the Phi-functional is chosen from the class of two-loop diagrams only [52,53].

To employ the system of Equations (1)–(3) to an investigation of heavy ion collisions one has to supplement it by the strange charge conservation condition

$$\begin{array}{c}\hfill n_S\equiv \frac{\partial p}{\partial {\mu }_S}=\sum _k{S}_k{n}_k=0,\end{array}$$

(5)

which provides a vanishing net strange charge. Here $n_k$ is the particle number density of hadrons of sort k defined by the following system of equations

$$\begin{array}{}(6)& n_k\equiv \frac{\partial p}{\partial {\mu }_k}=\frac{1}{T}·\frac{p_k{a}_{22}-{\Sigma }_k{a}_{12}}{a_{11}{a}_{22}-a_{12}{a}_{21}},a_{11}=1+\frac{4}{3}\pi \sum _k{R}_k^3\frac{p_k}{T},a_{12}=4\pi \sum _k{R}_k^2\frac{p_k}{T},(7)& a_{22}=1+4\pi \alpha \sum _k{R}_k^2\frac{{\Sigma }_k}{T},a_{21}=\frac{4}{3}\pi \sum _k{R}_k^3\frac{{\Sigma }_k}{T}.\end{array}$$

In contrast to the traditional multicomponent HRGM formulations to determine the particle number densities $\left\{n_k\right\}$ one needs to solve only a system of three equations, i.e., Equations (1), (2), and (5), irrespective of the number of different HCR in the EoS. Hence, we believe that the IST EoS given by the system (1)–(5) is well suited for the analysis of all hadronic multiplicities which will be measured soon at RHIC, NICA, and FAIR.

Compared to the VdW EoS, the IST EoS has another great advantage over the IST EoS, since it is valid up to the packing fractions $\eta \equiv {\sum }_k\frac{4}{3}\pi R_k^3{n}_k\simeq 0.2$ [20,21,22], at which the VdW approximation employed in the traditional HRGM [8,9,10,11,12,13] becomes completely incorrect (see a discussion below).

From the particle number density (6) of the k-th species of hadrons, one can find out their thermal $N_k^{\mathrm{th}}=V{n}_k$ (V is the effective volume of CFO hyper-surface) and total multiplicity $N_k^{tot}$. The total multiplicity $N_k^{\mathrm{tot}}$ accounts for the hadronic decays after the CFO and, hence, the ratio of total hadronic multiplicities at CFO can be written

$$\frac{N_k^{\mathrm{tot}}}{N_j^{\mathrm{tot}}}=\frac{n_k+{\sum }_{l\ne k}{n}_{l}B{r}_{l\to k}}{n_j+{\sum }_{l\ne j}{n}_{l}B{r}_{l\to j}}.$$

(8)

Here $B{r}_{l\to k}$ denotes the branching ratio, i.e., a probability of particle l to decay strongly into a particle k. Further details on the actual fitting procedure of experimental hadronic multiplicities by the HRGM can be found in [12,20].

The parameter $\alpha =1.25$ was fixed in Refs. [20,21], since this value allows us to simultaneously reproduce the third and forth virial coefficients of the gas of classical hard spheres. Such a formulation of the IST EoS is used to simultaneously fit 111 independent hadron yield ratios measured at AGS, SPS, and RHIC energies. In this fit the factor ${\gamma }_s$ and the chemical potentials ${\mu }_B$ and ${\mu }_{I3}$ are regarded as the free parameters and we found that the best description of these data is reached for the following HCR of baryons $R_b=0.365\pm 0.03$ fm, mesons $R_m=0.42\pm 0.04$ fm, pions $R_{\pi }=0.15\pm 0.02$ fm, kaons $R_K=0.395\pm 0.03$ fm, and $\Lambda$-hyperons $R_{\Lambda }=0.085\pm 0.015$ fm (new radii hereafter). These values of the HCR generate ${\chi }_1^2/\mathrm{dof}=57.099/50\simeq 1.14$ [21]. Some selected results of this fit are shown in Figure 1 and Figure 2.

The found HCR were fixed and then used to fit 11 independent hadron yield ratios measured by the ALICE Collaboration (for details see [20,21]) with a single fitting parameter, namely the CFO temperature, since all the chemical potentials were set to zero, while the factor ${\gamma }_s$ was set to 1. The fit quality ${\chi }_2^2/\mathrm{dof}\simeq 8.92/10\simeq 0.89$ of the ALICE data is similar to the one found for the combined fit of the AGS, SPS, and RHIC data (see Figure 3). Therefore, the combined quality of the AGS, SPS, RHIC, and ALICE data description achieved by the IST EoS [21] is ${\chi }_{tot}^2/\mathrm{dof}\simeq 66.02/60\simeq 1.1$, which corresponds to the probability $p\simeq 0.723$ of ${\chi }^2$ distribution with 60 degrees of freedom.

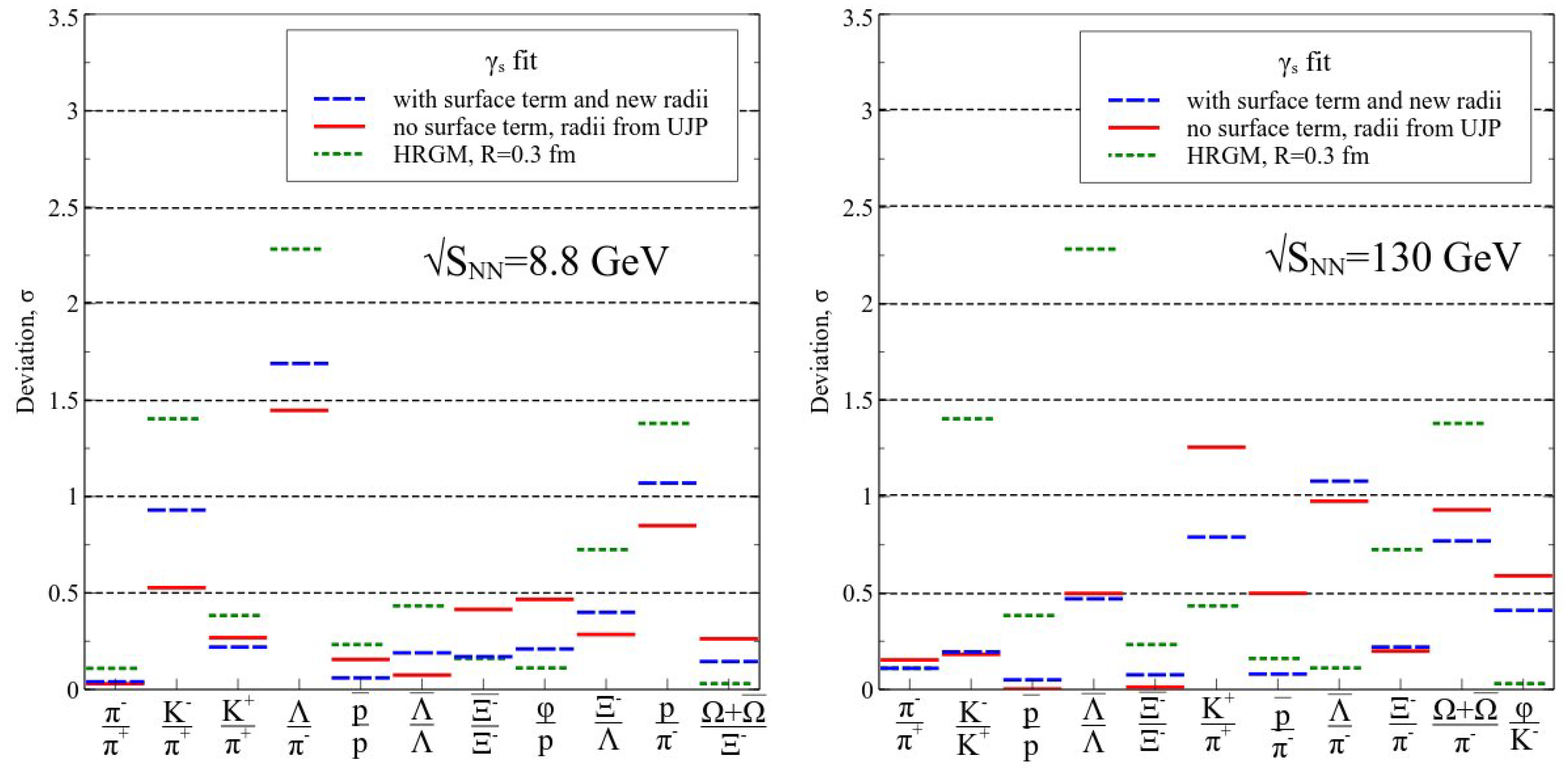
In order to show the importance of the multicomponent hard-core repulsion in Figure 1 the obtained results are compared to the HRGM with a single HCR of hadrons $R_{\mathrm{all}}=0.3$ fm (HRGM1 hereafter). The HRGM1 employs the quantum statistics for all hadrons and, hence, it is similar to the model of Ref. [8]. The main differences with Refs. [8,14] are: the HRGM1 includes the widths of all hadronic resonances for all temperatures and it is used not to fit all hadronic ratios, but only the independent ones. Such a comparison with the multicomponent versions of HRGM is necessary in order to illustrate the disadvantages of the one component case compared to the multicomponent formulation. The fit quality obtained by the HRGM1 for AGS, SPS, and RHIC energies is ${\chi }_1^2/\mathrm{dof}=75.134/54\simeq 1.39$ [21], which is essentially worse compared to the IST results. For this case the value of common HCR was not fitted and, hence, the number of degrees of freedom for HRGM1 is 54. Using the HRGM1 to fit the ALICE data we obtained the fit quality ${\chi }_2^2/dof\simeq 12.4/10\simeq 1.24$ [21]. Hence, the quality of the combined fit for all energies with the HRGM1 is ${\chi }_{tot}^2/\mathrm{dof}\simeq 87.53/64\simeq 1.37$, i.e., it is worse than the one found for the multicomponent IST EoS. The latter value corresponds to the probability $p\simeq 0.974$ of ${\chi }^2$ distribution with 64 degrees of freedom.

These results clearly demonstrate that additional 3 or 4 HCR can, indeed, essentially improve the quality of the fit of more than hundred independent hadron multiplicity ratios and, hence, such an improvement provides a high confidence in the extracted parameters of CFO. Apparently, this is also a strong argument in favor of $R_N=0.365\pm 0.03$ fm found by the IST EoS. Moreover, from the left panel of Figure 1 one can see that the proton to negative pion ratio (short dashed line with the deviation value about 1.4) cannot be described within the HRGM1, while it is well described within either of the HRGM multicomponent formulations. From both panels of this figure one can see that the ratios involving negative kaons and (anti)$\Lambda$ are also not well described by the HRGM1.

3. Nuclear Matter IST EoS and Proton Flow Constraint

Now we turn to a discussion the quantum version of the IST EoS used to model the nuclear liquid-gas phase transition. The model pressure p is a solution of the system ($R_N$ is the HCR on nucleons)

$$\begin{array}{ccc}\hfill p& =& p_{\mathrm{id}}(T,{\nu }_p)-p_{\mathrm{int}}(n_{\mathrm{id}}(T,{\nu }_p)),\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill \Sigma & =& R_N{p}_{\mathrm{id}}(T,{\nu }_{\Sigma }),\hfill \end{array}$$

(10)

where the grand canonical pressure $p_{\mathrm{id}}(T,\nu )$ and particle number density $n_{\mathrm{id}}(T,\nu )=\frac{\partial p_{\mathrm{id}}}{\partial \nu }$ of noninteracting point-like fermions are given by the expressions [54]

$$\begin{array}{c}\hfill p_{\mathrm{id}}=T{g}_N\int \frac{d^{3}p}{{(2\pi )}^3}ln\left[1+exp\left(\frac{\nu -\sqrt{p^2+m^2}}{T}\right)\right],n_{\mathrm{id}}=g_N\int \frac{d^{3}p}{{(2\pi )}^3}{\left[exp\left(\frac{\sqrt{p^2+m^2}-\nu }{T}\right)+1\right]}^{-1}.\end{array}$$

(11)

Here the system temperature is T, $m_N=940$ MeV is the nucleon mass and the nucleon degeneracy factor is $g_N=4$.

The term $-p_{\mathrm{int}}$ in Equation (9) represents the mean-field contribution to the pressure generated by an attraction between the nucleons. Clearly, the repulsive scattering channels are also present in nuclear matter. However, at densities below $n_{\max }\simeq$ 0.8 fm⁻³, which is the maximal density of the flow constraint [55], the repulsion is suppressed, since at these particle number densities the mean nucleon separation is larger than $r_{\min }={\left(\frac{3}{4\pi n_{\max }}\right)}^{1/3}\simeq 0.7$ fm. But at such distances the microscopic nucleon-nucleon potential is attractive [56], whereas the remaining repulsive interaction can be safely accounted by the particle hard-core repulsion.

The quantity $\Sigma$ in Equation (10) is a one-component analog of the IST coefficient of Equation (2) first introduced in Ref. [23] in order to distinguish it from the eigensurface tension of ordinary nuclei. Here it is appropriate to explain that the IST appears because the virial expansion of the pressure includes the terms which are proportional not only to the eigenvolume $V_0=\frac{4\pi }{3}{R}_N^3$, but also to the eigensurface $S_0=4\pi R_N^2$ of a particle with the HCR $R_N$ [23]. This surface term contribution is just accounted by the IST coefficient $\Sigma$. The meaning of $\Sigma$ as the surface tension coefficient can be easily seen from the effective chemical potentials which are related to the baryonic chemical potential $\mu$ as

$$\begin{array}{}(12)& \hfill {\nu }_p& =& \mu -p{V}_0-\Sigma S_0+U(n_{\mathrm{id}}(T,{\nu }_p)),\hfill (13)& \hfill {\nu }_{\Sigma }& =& \mu -p{V}_0-\alpha \Sigma S_0+U_0.\hfill \end{array}$$

Here $\Sigma$ is conjugated to $S_0$, while the attractive mean-field potentials are denoted as $U(n_{\mathrm{id}}(T,{\nu }_p))$ and $U_0=$ const. From these expressions one can conclude that the effects of hard-core repulsion are only partly accounted by the eigenvolume of particles, while the rest is determined by their eigensurface and the IST coefficient $\Sigma$ (for more details see [23]). Note that the presence of the pressure of point-like particles $p_{\mathrm{id}}$ in Equations (9) and (10) is a typical feature of EoSs formulated in the Grand Canonical Ensemble.

The system (9)–(13) is a concrete realization of the quantum model suggested in [22]. The self-consistency condition

$$p_{\mathrm{int}}(n)=nU(n)-{\int }_0^{n}d{n}^{\prime }U(n^{\prime })$$

(14)

relates the interaction pressure $p_{\mathrm{int}}(n_{\mathrm{id}}(T,{\nu }_p))$ and the corresponding mean-field potential $U(n_{\mathrm{id}}(T,{\nu }_p))$, and it guarantees the fulfillment of all thermodynamic identities [22] for the quantum IST (QIST) EoS.

It is necessary to stress that substituting the constant potential $U_0\left(n_{\mathrm{id}}(T,{\nu }_{\Sigma })\right)=$ const into the consistency condition (14), one automatically finds that the corresponding mean-field pressure should vanish, i.e., ${\tilde{p}}_{\mathrm{int}}(n_{\mathrm{id}}(T,{\nu }_{\Sigma }))=0$. Note also that different density dependences of the attractive mean-field potentials $U(n_{\mathrm{id}})$ and $U_0$ simply reflect the different origins of their forces. Thus, $U(n_{\mathrm{id}})$ is generated by the bulk part of interaction, while $U_0$ is related to the surface part. The meaning of $U_0$ potential can be better understood after the non-relativistic expansion of the nucleon energy $\sqrt{m^2+p^2}\simeq m+\frac{p^2}{2m}$ staying in the momentum distribution function of Equation (11): $U_0$ lowers the nucleon mass to the value $m-U_0$, which is similar to the relativistic mean-field approach. The particle number density can be found from the usual thermodynamic identity

$$n_N=\frac{\partial p}{\partial \mu }=\frac{n_{\mathrm{id}}(T,{\nu }_p)}{1+V_0{n}_{\mathrm{id}}(T,{\nu }_p)+\frac{3V_0{n}_{\mathrm{id}}(T,{\nu }_{\Sigma })}{1+3(\alpha -1)V_0{n}_{\mathrm{id}}(T,{\nu }_{\Sigma })}}.$$

(15)

To be specific the power form of the mean-field potential [54] motivated by Ref. [57]

$$\begin{array}{c}\hfill U(n_N)=C_d^2{n}_N^{\kappa }\Rightarrow p_{\mathrm{int}}(n_N)=\frac{\kappa }{\kappa +1}{C}_d^2{n}_N^{\kappa +1},\end{array}$$

(16)

is used. Here the mean-field contribution to the pressure $p_{\mathrm{int}}(n_N)$ is found from the consistency condition (14). This is one of the simplest choices of the mean-field potential which includes two parameters $C_d^2$ and $\kappa$ only. It corresponds to the well-known polytropic form of the EoS, where $\kappa$ is related to the adiabatic index and $C_d^2$ is a constant of proportionality. Since the parameter $\alpha$ is fixed already (see preceding section), the other two parameters of the QIST model are the hard-core radius $R_N$ and the constant potential $U_0$.

The QIST EoS with four adjustable parameters is able to simultaneously reproduce the main properties of symmetric nuclear matter, i.e., a vanishing pressure $p_N=0$ at zero temperature $T=0$ and the normal nuclear particle number density $n_0=0.16$ fm⁻³ and the value of its binding energy per nucleon $W_0=\frac{{ϵ}_N}{n_N}-m=-16$ MeV (where ${ϵ}_N$ is the energy density). Hence, the baryonic chemical potential of nucleons is $\mu =923$ MeV. The QIST EoS with the attraction term (16) was normalized to these properties of nuclear matter ground state and, simultaneously, it was fitted [54] to obey the proton flow constraint [55]. The region in the pressure-density plane deduced from flow observables has become an easy-to-use standard to constrain the behavior of phenomenological $T=0$ EoS at supersaturation densities. See, e.g., Ref. [58] for its usage in the context of compact star astrophysics. Although at a given value of particle number density the allowed range of pressure values of symmetric nuclear matter is rather wide, it is not easy to obey it and to simultaneously achieve the available range range of the incompressibility constant $K_0$, since they anti-correlate with each other.

In the present analysis we consider a few values of parameter $\kappa =0.1,0.15,0.2,0.25$. For each value of parameter $\kappa$ the two curves in the $n_N-p$ plane were found in such a way that the upper curve is located not above the upper branch of the flow constraint, while the lower curve is located not below the lower branch of this constraint. The details are clear from two panels of Figure 4. Notice that this is a highly nontrivial result for an EoS with only four adjustable parameters, since to parametrize the proton flow constraint alone one needs at least 8 independent points. For a comparison we mention that in Ref. [5] it is shown that only 104 of relativistic mean-field EoS out of 263 analyzed in there are able to obey the proton flow constraint [55], despite the fact that they have 10 or even more adjustable parameters.

However, as was demonstrated in Ref. [58], the lower bound of the proton flow constraint would correspond to a sequence of neutron stars with a maximum mass of only ∼1 M_⊙ and thus would not fulfill the constraint from the observed mass of $2.01\pm 0.04$ M_⊙ for pulsar PSR J0348+432 [59]. In Ref. [58] it was also shown that an equation of state which should fulfill the maximum mass constraint should follow the upper bound of the flow constraint. As a guideline may serve the ab-initio EoS DBHF from Ref. [58], which is soft enough to explain kaon production data in heavy-ion collisions at SIS energies but at the same time even exceeds the upper limit of the flow constraint at higher densities $n>0.5$ fm⁻³ and yields a maximum mass larger than 2.3 M_⊙, thus being even stiffer than required by the observed mass of pulsar PSR J0348+432 [59]. It has been shown recently in Ref. [60] that the IST EoS in the parametrization optimized for explaining particle yields from heavy-ion collisions is in accordance with the phenomenology of neutron stars, i.e., at $T=0$.

Since for $\kappa \ge 0.33$ a good description of the proton flow constraint cannot be achieved [54], those values for the parameter $\kappa$ were not considered. The reason for such a behavior is that for $\kappa \ge 0.33$ the attractive pressure $p_{\mathrm{int}}(n_N)$ is growing with density so fast that the pressure of point-like nucleons $p_{\mathrm{id}}$ has to grow even faster to obey the proton flow constraint. However, both functions nonlinearly depend on the particle number density and, hence, if the resulting pressure obeys the flow constraint at low densities, it cannot obey it at the high ones, and vice versa. On the other hand, the values of parameter $\kappa$ below 0.1 were not considered either since they correspond to unrealistically large values of the incompressibility constant $K_0\equiv 9\frac{\partial p}{\partial n_N}{|}_{T=0,n_N=n_0}$. As one can find from

Table 1. Several sets of parameters which simultaneously reproduce the properties of normal nuclear matter ($p=0$ and $n=n_0$ = 0.16 fm⁻³ at $\mu =923$ MeV, see text for details) and obey the proton flow constraint on the nuclear matter equations of state (EoS) along with incompressibility factor $K_0$ and parameters of critical endpoint (CEP). $R_N,C_d^2,U_0$, and $\kappa$ are the adjustable parameters of quantum induced surface tension (QIST) EoS.

	$\mathit{\kappa }$ = 0.1		$\mathit{\kappa }$ = 0.15		$\mathit{\kappa }$ = 0.2		$\mathit{\kappa }$ = 0.25
$R_N$ [fm]	0.28	0.42	0.35	0.48	0.41	0.50	0.47	0.52
$C_d^2$ [MeV· fm3κ]	284.98	325.06	206.05	229.57	168.15	179.67	146.97	152.00
$U_0$ [MeV]	567.32	501.65	343.93	312.83	231.42	217.76	162.03	157.41
$K_0$ [MeV]	306.09	465.13	272.55	405.97	242.56	322.80	217.16	256.44

for $\kappa =0.1$, the minimal value of the incompressibility constant $K_0$ is about 306 MeV, while for $\kappa <0.1$ it is even larger.

From Table 1 one can see that the range of $R_N$ is still wide, i.e., $R_N\in [0.28;0.52]$ fm. The QIST EoS, however, allows one to obtain an essentially narrower range of the nucleon HCR $R_N$. Indeed, if one requires that this EoS should be applicable at the maximal value of particle number density $n_{max}\simeq 0.8$ fm⁻³ of the proton flow constraint, then such a condition can be written as

$$\begin{array}{c}\hfill \frac{4}{3}\pi R_N^3{n}_{\max }\le {\eta }_{\max }.\end{array}$$

(17)

Here the range of the QIST EoS applicability is given by the maximal packing fraction ${\eta }_{\max }$ of the model. Assuming that the maximal packing fraction of the QIST EoS is ${\eta }_{\max }=0.2$, i.e., it is similar to the Boltzmann version of the IST EoS [20,21], one gets the following inequality on the nucleon hard-core radius $R_N\le 0.4$ fm and, hence, one finally obtains $0.28\mathrm{fm}\le R_N\le 0.4$ fm.

The quantum virial expansion developed in [22] both for the quantum VdW and QIST EoS allows us to obtain even a narrower range of values which is consistent with the S-matrix approach [61] to the EoS of the gas of nucleons at temperatures above 100 MeV [62,63]. For an extended discussion see also Ref. [64]. In particular, the quantum second virial coefficient $a_2^S(T)$ of a nucleon gas as obtained from realistic S-matrix approach provides approximately the following inequalities [63,64]

$$\begin{array}{c}\hfill 0.5{\mathrm{fm}}^3\le a_2^S(T)\le 1.25{\mathrm{fm}}^3\mathrm{for}100\mathrm{MeV}\le T\le 170\mathrm{MeV}.\end{array}$$

(18)

These inequalities correspond to the conditions 0.31 fm ≤ $R_N$ ≤ 0.42 fm, if one uses the classical definition of the HCR. It is interesting that these inequalities are similar to the ones found above for the QIST EoS. Using the results of Ref. [22] the second $a_2^{IST}$ and third $a_3^{IST}$ virial coefficients for the repulsive part of the QIST EoS for nucleons can be cast as

$$\begin{array}{c}\hfill a_2^{\mathrm{IST}}=4V_0+a_2^{(0)},a_3^{\mathrm{IST}}\simeq [16-18(\alpha -1)]V_0^2+5V_0{a}_2^{(0)}+a_3^{(0)},\end{array}$$

(19)

where the second $a_2^{(0)}$ and the third $a_3^{(0)}$ virial coefficients of a point-like hadron which in the non-relativistic approximation for fermions can be written as

$$\begin{array}{c}\hfill a_2^{(0)}\simeq \pm 2^{-\frac{5}{2}}{\omega }_h\simeq \pm 0.177{\omega }_h,a_3^{(0)}\simeq 2\left[2^{-4}-3^{-\frac{5}{2}}\right]{\omega }_h^2\simeq -3.4·{10}^{-3}{\omega }_h^2,{\omega }_h=\frac{1}{g_h}{\left[\frac{2\pi {\hslash }^2}{T{m}_h}\right]}^{\frac{3}{2}},\end{array}$$

(20)

where $m_h$ is the hadron mass, $g_h$ is its degeneracy, and the upper (lower) sign corresponds to baryons (mesons). Introducing an effective second virial coefficient of nucleons $a_{2N}^{\mathrm{eff}}(n_N)\equiv a_2^{\mathrm{IST}}+n_N{a}_3^{\mathrm{IST}}$ which depends on particle number density of nucleons $n_N$ and assuming that the nucleonic contribution to the HRGM is given by the repulsive part of the QIST EoS (9), one can use the effective second virial coefficient $a_{2N}^{\mathrm{eff}}(n_N)$ to constrain the values of HCR further. Our analysis shows that for the nucleon densities below $n_N\simeq 3n_0=0.48$ fm⁻³ the fourth and higher virial coefficients are not important and, hence, we can require that up to this nucleon density the coefficient $a_{2N}^{\mathrm{eff}}(n_N)$ obeys the constraint (18). This leads to the follows range of $R_N$ values: $R_N\in [0.275;0.36]$ fm. In other words, for such a range of values of the nucleonic HCR not only the second, but also the third virial coefficient of nucleons will provide the fulfillment of the constraint (18).

At first glance this result may look surprising, since one does not see any important role of the quantum third virial coefficient. A close inspection shows that due to the small value of the coefficient which enters the expression for $a_3^{(0)}$, the quantum effects are important at temperatures below 20 MeV, while at $T\ge 100$ MeV the coefficients $a_3^{(0)}$ and $a_2^{(0)}$ are rather small, since ${\omega }_N(T=100\mathrm{MeV})\simeq 1$ fm³ and it is a decreasing function of T. A simple analysis shows that for nucleons $a_2^{(0)}(T=32\mathrm{MeV})\simeq 1$ fm³, while for $T=50$ MeV one finds $a_2^{(0)}(T=50\mathrm{MeV})\simeq 0.5$ fm³ and this coefficient decreases fast with temperature.

As a result at $T\ge 100$ MeV the values of the coefficients $a_2^{\mathrm{IST}}$ and $a_3^{\mathrm{IST}}$ are defined by the HCR of nucleons and the parameter $\alpha$. Moreover, this is a generic result for all hadrons and hadronic resonances heavier than kaons. For baryons this is evident, since the nucleons are the lightest among them. For kaons and heavier mesons ($\omega$, $\rho$ etc) the coefficient $a_3^{(0)}$ remains very small at $T\ge 50$ MeV, while the value of the coefficient $|a_2^{(0)}|$ for such mesons can be a bit larger than for nucleons. However, the coefficient $a_2^{(0)}$ for mesons is negative and, hence, it simply compensates the larger value of the classical excluded volume (with hard-core radius $R_m=0.42\pm 0.04$ fm) of such mesons found within the HRGM [20,21,22]. These findings on the second and third virial coefficient of hadrons heavier than kaons are in line with the results of Ref. [39]. Moreover, they explain the reason of why the classical second virial coefficient is sufficient for the HRGM at all collision energies. Indeed, for CFO temperatures in the range between 50 and 100 MeV the particle number density of all mesons is almost negligible, while for all baryons it does not exceeds 0.075 fm⁻³ (see Figure 3 in [19]). Hence, in this range of CFO temperatures the hard-core corrections are negligible. On the other hand, for CFO temperatures above 100 MeV and below 170 MeV the quantum effects are small not only for kaons and heavier mesons as we discussed above, but for all mesons [9,10]. Thus, at CFO the classical formulation of HRGM is rather accurate.

However, when the QIST EoS is required to simultaneously fulfill the gravitational mass-radius relation of neutron stars and the proton flow constraint, one finds somewhat larger values of the HCR of nucleons, namely $R_N\in [0.42;0.47]$ fm [60]. Note that within the recent excluded nucleon volume generalization of the relativistic meanfield model “DD2” by Typel [65] even larger values of the HCR of nucleons were used in the description of neutron star phenomenology such as mass-radius relations [66], moment of inertia [67], tidal deformabilities [67,68], and cooling [69]. The “DD2 p40” EoS used in these works would correspond to a nucleon HCR of $R_N=0.62$ fm which is at the very limit of what is compatible with the recent constraint on the compactness of neutron stars stemming from the gravitational wave signal measured for the inspiral phase of the neutron star merger GW170817 [70]. These results indicate that the repulsive core of the nucleon-nucleon interaction depends on the properties of the medium since the description of static neutron star properties at zero temperature require a stiffer EoS than the one which is successfully reproducing the hadronic multiplicities measured in HIC. What is the physical reason for such a difference?

We suggest as an answer to this question that inasmuch as the excluded volume is due to Pauli blocking, the nucleonic excluded volume (and thus the nucleon radii) shall be as temperature dependent as the quark Pauli blocking effect is. The relationship between Pauli blocking and excluded volume is known from the fact that the hard-sphere model of molecular interactions is based on the electron exchange interaction among atoms (see, e.g., Ebeling et al. [71]) which is captured, e.g., in the Carnahan-Starling EoS [72]. Note that the IST approach is reproducing the Carnahan-Starling EoS for not too large packing fractions [21]. It is found that the Pauli blocking effect decreases with increasing temperature, see for instance Equation (6) of [71]. A recent application to the equation of state for warm dense plasmas can be found in [73] where the effect of ionization potential depression accessible in high-pressure experiments is discussed.

Detailed parametrizations of the Pauli shift for nuclear clusters are found in [74] with the similar trend. The temperature-, density-, and momentum-dependence of the Pauli blocking depends on the generic form of bound state wave functions and results could thus be taken over from atomic to hadronic systems. Therefore it is plausible that the phenomenological radii for hadrons at high temperatures are smaller than those required for compact star properties at zero temperature. The repulsive Pauli blocking effect between composite particles is especially pronounced at low temperatures, in the regime of quantum degeneracy.

In Ref. [75] it has been demonstrated that the repulsive part of effective density-dependent nucleon-nucleon interactions of the Skyrme type (e.g., the one by Vautherin and Brink [76]) can be reproduced by the quark exchange interaction between nucleons. Recently the relation between quark Pauli blocking excluded volume effects in the nuclear EoS have been revisited and the effects of chiral symmetry restoration in the quark sector have been studied [77]. A comparison to the relativistic mean field approach DD2 with excluded volume [65] allowed to extract a density-dependent excluded volume and thus a radius parameter at $T=0$ in the range of 0.45–0.70 fm.

Note that the QIST model offers a simple way to make a stiffer EoS at higher pressures or densities. Actually, as it was mentioned in the first paper on IST EoS [23], the parameter $\alpha$ may, in principle, be a function which depends on the system pressure. Therefore, it would be interesting to generalize the QIST EoS and to include into it the pressure or density dependence of the parameter $\alpha$ and/or of the HCR of nucleons. Then having more adjustable parameters and adding more astrophysical constraints as, e.g., for an upper limit on the maximum mass as well as lower and upper bounds on the neutron star radius from the binary neutron star merger, one could aim at a best possible description including the proton flow constraint and to find a realistic functional dependence of $\alpha$ and $R_N$ on density and temperature. In this respect we would like to mention the possibility to model the excluded nucleon volume in a density and temperature dependent way, even changing the sign so that also attractive interactions are accessible. In this form, Typels excluded volume model [65] has been used to obtain an equation of state and phase diagram with a second critical endpoint (CEP) beyond the gas-liquid one [30]. This could be used to mimic effects of the nuclear-to-quark matter phase transition in the QCD phase diagram. Within the IST approach the IST coefficient $\Sigma$ stands for attraction effects and therefore the interplay of attraction and repulsion as captured in the (medium dependent) parameters $\alpha$ and $R_N$, respectively, could eventually lead to similar behaviour and a second CEP in the phase diagram.

4. Conclusions

In this review we thoroughly discussed the IST approach to model the EoS of hadronic and nuclear matter and analyzed different constraints on the HCR of nucleons. The most successful formulation of the HRGM gives $R_N\simeq 0.365\pm 0.03$ fm, while the QIST EoS of nuclear matter leads to $R_N\simeq 0.34\pm 0.06$ fm. At the same time, a comparison of quantum virial coefficients with the S-matrix approach gives $R_N\simeq 0.32\pm 0.04$ fm. Therefore, the most probable range of HCR of nucleons which is consistent with different constraints following from the hadronic and nuclear matter properties is $R_N\in [0.3;0.36]$ fm. Since applications of the QIST EoS to the description of neutron star properties require somewhat larger HCR of nucleons [60], we conclude that the QIST EoS for neutron stars should be improved further, especially by improving the model for the interaction between nucleons at high particle number densities typical for the neutron stars core. The generalized QIST EoS which considers the density and temperature dependence of the parameters $\alpha$ and $R_N$ may provide a very effective way to solve this problem.