Rotational Energy Extraction from the Kerr Black Hole’s Mimickers
Abstract
:1. Introduction
2. The Penrose Process for Energy Extraction from a Rotating Black Hole
3. Rotating Simpson–Visser Spacetime
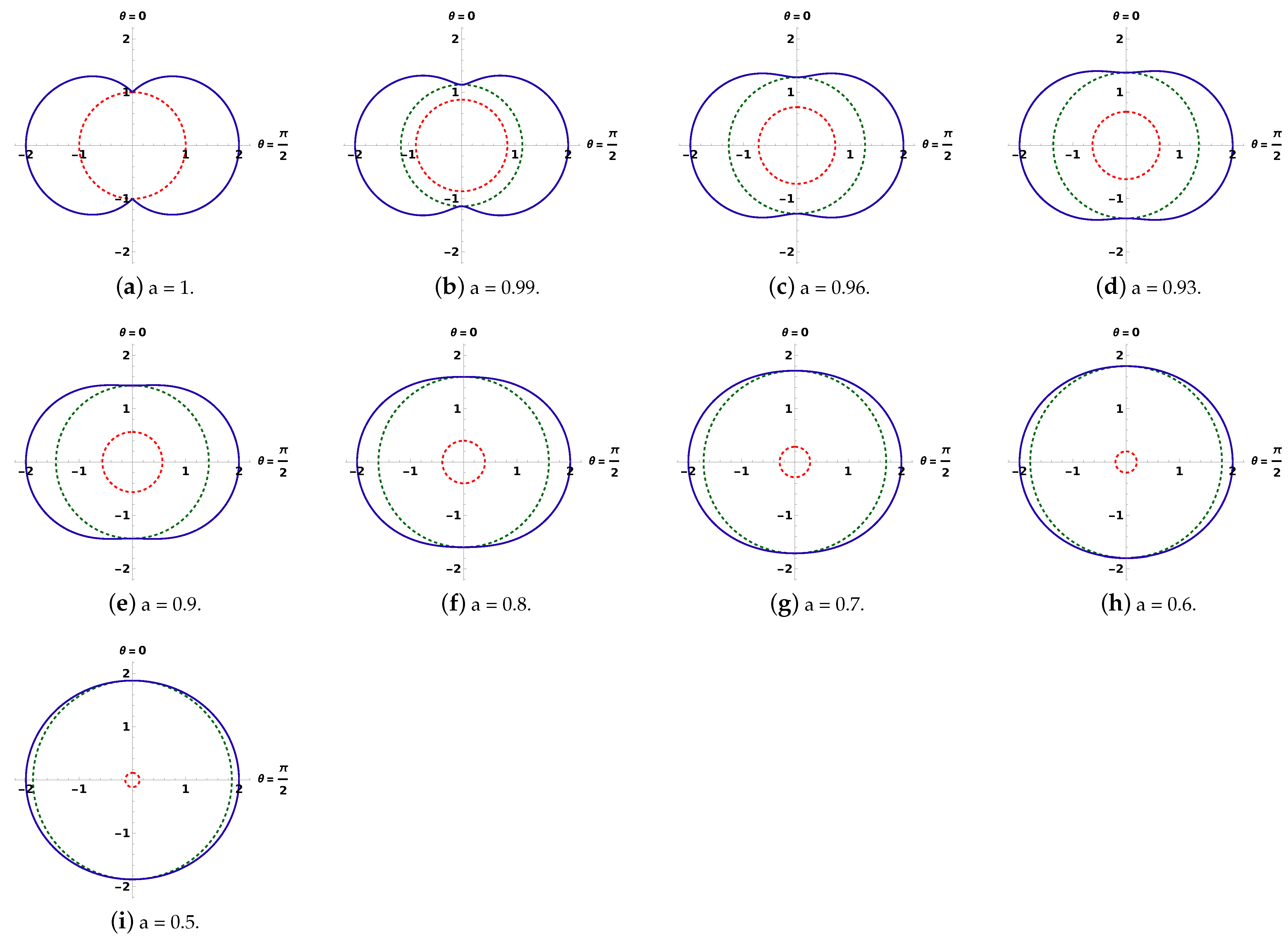
Energy Extraction by Penrose Process from Rotating Simpson–Visser Spacetime
4. Regular and Singular Black Hole Spacetimes
4.1. A Regular Black Hole
4.2. A Singular Black Hole
5. Discussion and Conclusions
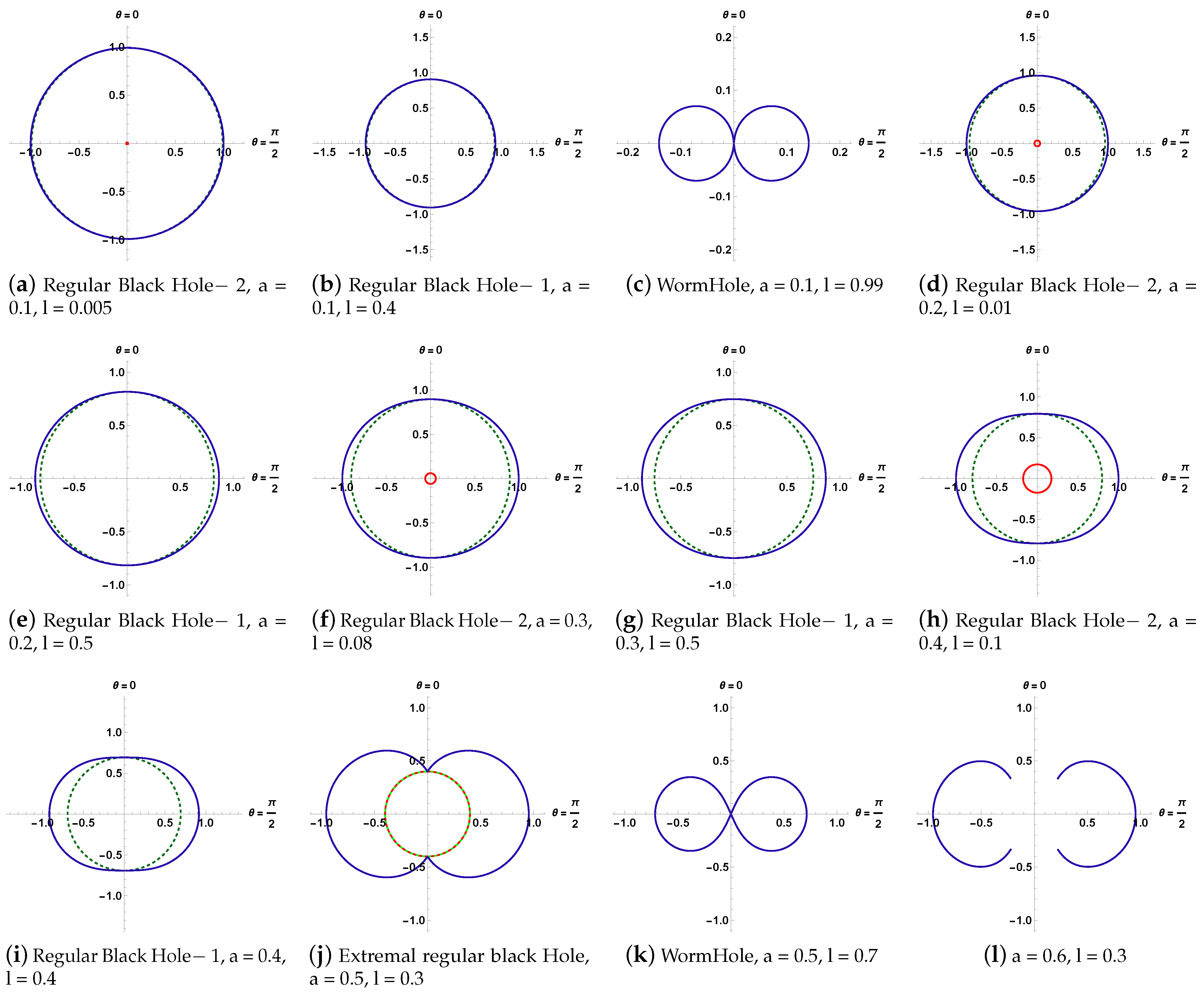
- In Simpson–Visser spacetime, the ergoregion is dependent on the regularisation parameter (l). It is evident that the ergoregion and outer/inner horizons show significant changes as the spin parameter and regularisation parameter change. The Penrose process to extract rotational energy from rotating objects is exclusively dependent on the ergoregion, and the purpose of this study was to see how the Penrose process might be used to extract the maximum energy from a non-singular compact object such as a wormhole or a regular black hole. As the ergoregion and horizons differ from that of a Kerr black hole, the efficiency of energy extraction should be different from that of a Kerr black hole. Unexpectedly, we found that the energy extraction in rotating Simpson–Visser spacetime is the same as in a Kerr black hole. This is because the efficiency of energy extraction () is independent of the regularisation parameter l. The study in [102] gives a similar type of conclusion that the size of the ergoregion seems to play no role in energy extraction using the Penrose process.
- The possible reason behind this is that in the rotating Simpson–Visser case, the energy extraction efficiency remains unchanged as we change the regularisation parameter, and thus the corresponding event horizon radius, Cauchy horizon radius, and ergo-radius change. Now, we have considered the Penrose process taking place just at the event horizon. Hence, changing the regularisation parameter does not change the scenario of the process, as the phenomena still occur at the event horizons of two corresponding different regular black hole structures. In that case, since we have considered similar values of spin parameter a, the frame-dragging rates of spacetime geometries with corresponding values of the regularisation parameter will be the same. Now, as the Penrose process mainly depends on the frame-dragging effect of the spacetime, at the event horizon, the efficiency will always be maximum. In that case, for any given rotating Simpson–Visser black hole, for different regularisation parameters, and thus for corresponding different event horizon radii, the energy extraction efficiency remains the same.
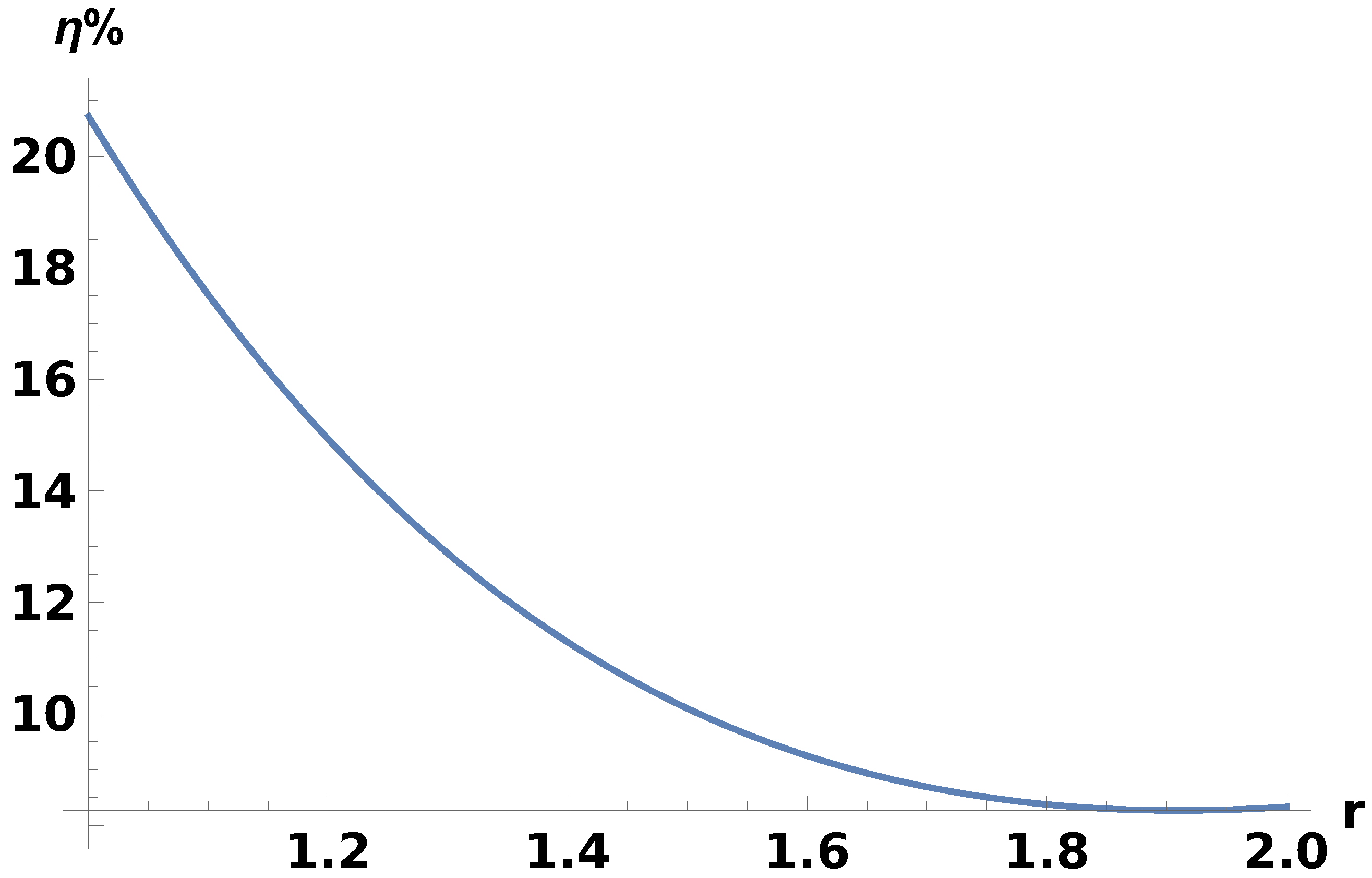
- However, one can consider the case in which for specific values of event horizon radius, Cauchy horizon radius, and ergo-radius, the Penrose process takes place at a different radial distance r. In such a case, as the radial distance increases from event horizon radius to outer ergoradius , the efficiency gradually decreases. This is because as we move away from the horizon, the frame-dragging effect of spacetime structure and thus the angular velocity decreases.
- Using the conformal transformation classically, one can resolve the spacetime singularity problem that arises in Einstein’s general theory of relativity. The singular and regular black holes considered here are the solutions of CEFE derived in [97]. Depending on the parameter , one gets the spacetime solution with or without singularity. The expressions of ergoregions in singular and regular black hole spacetimes are independent of the regularisation parameter (l). Thus, the ergoregions for regular and singular black holes are similar to that of the Kerr black hole. As explained earlier, the ergoregions and horizons show significantly evident changes for the cases and . However, we consider only the case in which for which the horizons exist.
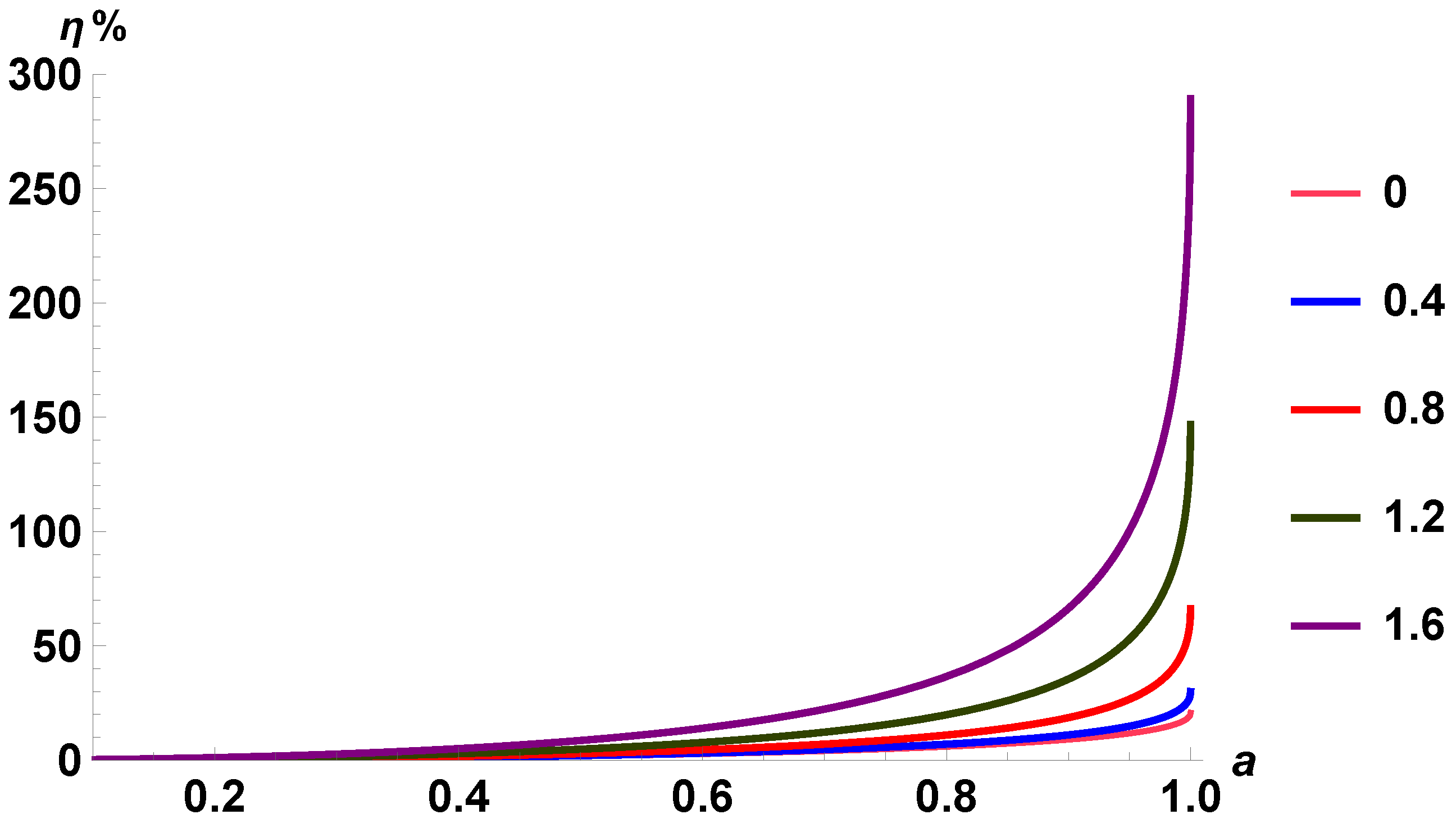
- It is evident from this investigation that the efficiency of energy extraction varies as the size of the ergoregion changes. Interestingly, even though the ergoregions in regular and singular black holes are similar to those in the Kerr black hole, the efficiency for energy extraction is significantly larger in regular and singular black holes. In a CEFE solution, the efficiency of energy extraction is large enough in a regular black hole rather than in a singular black hole case. However, one may notice from Figure 3 and Figure 4 that in all compact objects, the energy extraction is nearly the same for spin parameters up to 0.5. The maximum difference in energy extraction efficiency occurs at the extreme spin parameter (a = M).
- Here, the energy extraction efficiency with the conformal transformation is more than , which means that after the Penrose process when a particle escapes the ergoregion, it has energy higher than its initial energy when the particle entered in the negative energy orbit region. The energy extraction efficiency of was first shown in 1985 [103,104]. Additionally, based on the conformal geometry in [105], it has been shown that the energy extraction efficiency from a Kerr naked singularity can reach using the magnetic Penrose process.
- In this work, the phenomenology of energy extraction for a neutral test particle is explained for singular and regular black holes. One may study the efficiency of energy extraction in the presence of a magnetic field or for charged test particles.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akiyama, K. et al. [Event Horizon Telescope] First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, L12. [Google Scholar] [CrossRef]
- Broderick, A.E. et al. [Event Horizon Telescope] Characterizing and Mitigating Intraday Variability: Reconstructing Source Structure in Accreting Black Holes with mm-VLBI. Astrophys. J. Lett. 2022, 930, L21. [Google Scholar] [CrossRef]
- Wielgus, M. et al. [Event Horizon Telescope] Millimeter Light Curves of Sagittarius A* Observed during the 2017 Event Horizon Telescope Campaign. Astrophys. J. Lett. 2022, 930, L19. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope] First Sagittarius A* Event Horizon Telescope Results. II. EHT and Multiwavelength Observations, Data Processing, and Calibration. Astrophys. J. Lett. 2022, 930, L13. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope] First Sagittarius A* Event Horizon Telescope Results. III. Imaging of the Galactic Center Supermassive Black Hole. Astrophys. J. Lett. 2022, 930, L14. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope] First Sagittarius A* Event Horizon Telescope Results. V. Testing Astrophysical Models of the Galactic Center Black Hole. Astrophys. J. Lett. 2022, 930, L16. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope] First Sagittarius A* Event Horizon Telescope Results. VI. Testing the Black Hole Metric. Astrophys. J. Lett. 2022, 930, L17. [Google Scholar] [CrossRef]
- Farah, J. et al. [Event Horizon Telescope] Selective Dynamical Imaging of Interferometric Data. Astrophys. J. Lett. 2022, 930, L18. [Google Scholar] [CrossRef]
- Gralla, S.E.; Holz, D.E.; Wald, R.M. Black hole shadows, photon rings, and lensing rings. Phys. Rev. D 2019, 100, 024018. [Google Scholar] [CrossRef] [Green Version]
- Abdikamalov, A.B.; Abdujabbarov, A.A.; Ayzenberg, D.; Malafarina, D.; Bambi, C.; Ahmedov, B. Black hole mimicker hiding in the shadow: Optical properties of the γ metric. Phys. Rev. D 2019, 100, 024014. [Google Scholar] [CrossRef]
- Dey, D.; Bhattacharya, K.; Sarkar, T. Astrophysics of Bertrand space-times. Phys. Rev. D 2013, 88, 083532. [Google Scholar] [CrossRef] [Green Version]
- Dey, D.; Shaikh, R.; Joshi, P.S. Perihelion precession and shadows near black holes and naked singularities. Phys. Rev. D 2020, 102, 044042. [Google Scholar] [CrossRef]
- Ohgami, T.; Sakai, N. Wormhole shadows. Phys. Rev. D 2015, 91, 124020. [Google Scholar] [CrossRef] [Green Version]
- Sakai, N.; Saida, H.; Tamaki, T. Gravastar shadows. Phys. Rev. D 2014, 90, 104013. [Google Scholar] [CrossRef] [Green Version]
- Bambhaniya, P.; Joshi, P.S. Probing the Shadow Image of the Sagittarius A* with Event Horizon Telescope. arXiv 2022, arXiv:2202.00588. [Google Scholar]
- Solanki, D.N.; Bambhaniya, P.; Dey, D.; Joshi, P.S.; Pathak, K.N. Shadows and precession of orbits in rotating Janis–Newman–Winicour spacetime. Eur. Phys. J. C 2022, 82, 1–13. [Google Scholar] [CrossRef]
- Bambhaniya, P.; Dey, D.; Joshi, A.B.; Joshi, P.S.; Solanki, D.N.; Mehta, A. Shadows and negative precession in non-Kerr spacetime. Phys. Rev. D 2021, 103, 084005. [Google Scholar] [CrossRef]
- Bambi, C. Testing black hole candidates with electromagnetic radiation. Rev. Mod. Phys. 2017, 89, 025001. [Google Scholar] [CrossRef] [Green Version]
- Shaikh, R. Shadows of rotating wormholes. Phys. Rev. D 2018, 98, 024044. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Saurabh, S. Black hole shadows in Verlinde’s emergent gravity. Mon. Not. R. Astron. Soc. 2021, 503, 1310–1318. [Google Scholar] [CrossRef]
- Lee, B.-H.; Lee, W.; Myung, Y.S. Shadow cast by a rotating black hole with anisotropic matter. Phys. Rev. D 2021, 103, 064026. [Google Scholar] [CrossRef]
- Shaikh, R.; Banerjee, P.; Paul, S.; Sarkar, T. Strong gravitational lensing by wormholes. J. Cosmol. Astropart. Phys. 2019, 2019, 28. [Google Scholar] [CrossRef] [Green Version]
- Shaikh, R.; Banerjee, P.; Paul, S.; Sarkar, T. A novel gravitational lensing feature by wormholes. Phys. Lett. B 2018, 789, 270–275. [Google Scholar] [CrossRef]
- Paul, S. Strong gravitational lensing by a strongly naked null singularity. Phys. Rev. D 2020, 102, 064045. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Keeton, C.R. Time delay and magnification centroid due to gravitational lensing by black holes and naked singularities. Phys. Rev. D 2008, 77, 124014. [Google Scholar] [CrossRef] [Green Version]
- Gyulchev, G.N.; Yazadjiev, S.S. Gravitational lensing by rotating naked singularities. Phys. Rev. D 2008, 78, 083004. [Google Scholar] [CrossRef] [Green Version]
- Kala, S.; Saurabh; Nandan, H.; Sharma, P. Deflection of light and shadow cast by a dual-charged stringy black hole. Int. J. Mod. Phys. A 2020, 35, 2050177. [Google Scholar] [CrossRef]
- Sahu, S.; Patil, M.; Narasimha, D.; Joshi, P.S. Can strong gravitational lensing distinguish naked singularities from black holes? Phys. Rev. D 2012, 86, 063010. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Zhu, T.; Wu, Q. Thin accretion disk around a four-dimensional Einstein-Gauss-Bonnet black hole *. Chin. Phys. C 2021, 45, 015105. [Google Scholar] [CrossRef]
- Joshi, P.S.; Malafarina, D.; Narayan, R. Distinguishing black holes from naked singularities through their accretion disc properties. Class. Quantum Gravity 2013, 31, 015002. [Google Scholar] [CrossRef]
- Bambhaniya, P.; Saurabh; Jusufi, K.; Joshi, P.S. Thin accretion disk in the Simpson-Visser black-bounce and wormhole spacetimes. Phys. Rev. D 2022, 105, 023021. [Google Scholar] [CrossRef]
- Rahaman, F.; Manna, T.; Shaikh, R.; Aktar, S.; Mondal, M.; Samanta, B. Thin accretion disks around traversable wormholes. Nucl. Phys. B 2021, 972. [Google Scholar] [CrossRef]
- Harko, T.; Kovacs, Z.; Lobo, F.S.N. Can accretion disk properties distinguish gravastars from black holes? Class. Quantum Gravity 2009, 26, 215006. [Google Scholar] [CrossRef]
- Tahelyani, D.; Joshi, A.B.; Dey, D.; Joshi, P.S. Comparing thin accretion disk properties of naked singularities and black holes. arXiv 2022, arXiv:2205.04055. [Google Scholar] [CrossRef]
- Guo, J.-Q.; Joshi, P.S.; Narayan, R.; Zhang, L. Accretion disks around naked singularities. Class. Quantum Gravity 2020, 38, 035012. [Google Scholar] [CrossRef]
- Chowdhury, A.N.; Patil, M.; Malafarina, D.; Joshi, P.S. Circular geodesics and accretion disks in the Janis-Newman-Winicour and gamma metric spacetimes. Phys. Rev. D 2012, 85, 104031. [Google Scholar] [CrossRef] [Green Version]
- Martínez, C.; Parra, N.; Valdés, N.; Zanelli, J. Geodesic structure of naked singularities in AdS3 spacetime. Phys. Rev. D 2019, 100, 024026. [Google Scholar] [CrossRef] [Green Version]
- Madan, S.; Bambhaniya, P. Tidal force effects and periodic orbits in null naked singularity spacetime. arXiv 2022, arXiv:2201.13163. [Google Scholar]
- Hackmann, E.; Kagramanova, V.; Kunz, J.; Lämmerzahl, C. Analytic solutions of the geodesic equation in axially symmetric space-times. Eur. Lett. 2009, 88, 30008. [Google Scholar] [CrossRef] [Green Version]
- Hackmann, E.; Lämmerzahl, C.; Obukhov, Y.N.; Puetzfeld, D.; Schaffer, I. Motion of spinning test bodies in Kerr spacetime. Phys. Rev. D 2014, 90, 064035. [Google Scholar] [CrossRef] [Green Version]
- Potashov, I.M.; Tchemarina, J.; Tsirulev, A.N. Bound orbits near scalar field naked singularities. Eur. Phys. J. C 2019, 79, 709. [Google Scholar] [CrossRef] [Green Version]
- Joshi, A.B.; Bambhaniya, P.; Dey, D.; Joshi, P.S. Timelike geodesics in naked singularity and black hole spacetimes II. arXiv 2019, arXiv:1909.08873. [Google Scholar]
- Bambhaniya, P.; Joshi, A.B.; Dey, D.; Joshi, P.S. Timelike geodesics in naked singularity and black hole spacetimes. Phys. Rev. D 2019, 100, 124020. [Google Scholar] [CrossRef]
- Dey, D.; Joshi, P.S.; Joshi, A.; Bambhaniya, P. Towards an observational test of black hole versus naked singularity at the galactic center. Int. J. Mod. Phys. D 2019, 28, 1930024. [Google Scholar] [CrossRef] [Green Version]
- Bambhaniya, P.; Solanki, D.N.; Dey, D.; Joshi, A.B.; Joshi, P.S.; Patel, V. Precession of timelike bound orbits in Kerr spacetime. Eur. Phys. J. 2021, 81, 1–11. [Google Scholar] [CrossRef]
- Guo, S.; Li, G.R.; Li, G.P. Shadow thermodynamics of AdS black hole in regular spacetime. arXiv 2022, arXiv:2205.04957. [Google Scholar] [CrossRef]
- Kala, S.; Nandan, H.; Sharma, P. Shadow and weak gravitational lensing of a rotating regular black hole in a non-minimally coupled Einstein-Yang-Mills theory in the presence of plasma. Eur. Phys. J. Plus 2022, 137, 1–18. [Google Scholar] [CrossRef]
- Ahmed, F.; Singh, D.V.; Ghosh, S.G. Five dimensional rotating regular black holes and shadow. Gen. Relativ. Gravit. 2022, 54, 1–22. [Google Scholar] [CrossRef]
- Jafarzade, K.; Zangeneh, M.K.; Lobo, F.S. Observational optical constraints of regular black holes. arXiv 2022, arXiv:2106.13893. [Google Scholar]
- Qin, X.; Chen, S.; Jing, J. Image of a regular phantom compact object and its luminosity under spherical accretions. Class. Quantum Gravity 2021, 38, 115008. [Google Scholar] [CrossRef]
- Mondal, M.; Yadav, A.K.; Pradhan, P.; Islam, S.; Rahaman, F. Null geodesics and QNMs in the field of regular black holes. Int. J. Mod. Phys. D 2021, 30, 2150095. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Amir, M.; Maharaj, S.D. Ergosphere and shadow of a rotating regular black hole. Nucl. Phys. B 2020, 957, 115088. [Google Scholar] [CrossRef]
- Kumar, R.; Ghosh, S.G. Photon ring structure of rotating regular black holes and no-horizon spacetimes. Class. Quantum Gravity 2021, 38, 085010. [Google Scholar] [CrossRef]
- Li, Z.; Bambi, C. Measuring the Kerr spin parameter of regular black holes from their shadow. J. Cosmol. Astropart. Phys. 2014, 2014, 041. [Google Scholar] [CrossRef]
- Narzilloev, B.; Rayimbaev, J.; Shaymatov, S.; Abdujabbarov, A.; Ahmedov, B.; Bambi, C. Dynamics of test particles around a Bardeen black hole surrounded by perfect fluid dark matter. Phys. Rev. D 2020, 102, 104062. [Google Scholar] [CrossRef]
- Benavides-Gallego, C.A.; Abdujabbarov, A.; Malafarina, D.; Ahmedov, B.; Bambi, C. Charged particle motion and electromagnetic field in γ spacetime. Phys. Rev. D 2019, 99, 044012. [Google Scholar] [CrossRef] [Green Version]
- Fathi, M.; Olivares, M.; Villanueva, J. Ergosphere, Photon Region Structure, and the Shadow of a Rotating Charged Weyl Black Hole. Galaxies 2021, 9, 43. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Calvani, M.; Nobili, L. Runaway instability in accretion disks orbiting black holes. Nature 1983, 302, 597–599. [Google Scholar] [CrossRef]
- Rees, M.J.; Begelman, M.C.; Blandford, R.D.; Phinney, S. Ion-supported tori and the origin of radio jets. Nature 1982, 295, 17–21. [Google Scholar] [CrossRef]
- Penrose, R.; Floyd, R.M. Extraction of Rotational Energy from a Black Hole. Nat. Phys. Sci. 1971, 229, 177–179. [Google Scholar] [CrossRef]
- Wheeler, J. Study Week on Nuclei of Galaxies, ed DJK O’Connell. North Holl. Pontif. Acad. Scr. Varia 1971, 35, 539. [Google Scholar]
- Ghosh, S.G.; Sheoran, P. Higher dimensional non-Kerr black hole and energy extraction. Phys. Rev. D 2014, 89, 024023. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Chen, S.; Jing, J. ROTATING NON-KERR BLACK HOLE AND ENERGY EXTRACTION. Astrophys. J. Lett. 2012, 751, 148. [Google Scholar] [CrossRef]
- Nozawa, M.; Maeda, K.-I. Energy extraction from higher dimensional black holes and black rings. Phys. Rev. D 2005, 71, 084028. [Google Scholar] [CrossRef] [Green Version]
- Wagh, S.M.; Dadhich, N. The energetics of black holes in electromagnetic fields by the penrose process. Phys. Rep. 1989, 183, 137–192. [Google Scholar] [CrossRef]
- Zaslavskii, O.B. High-energy collision of particles in the magnetic field far from black holes. Mod. Phys. Lett. A 2014, 29, 1450151. [Google Scholar] [CrossRef] [Green Version]
- Zaslavskii, O.B. Energy extraction from extremal charged black holes due to the Banados-Silk-West effect. Phys. Rev. D 2012, 86, 124039. [Google Scholar] [CrossRef] [Green Version]
- Tsukamoto, N.; Bambi, C. Collisional Penrose process in a rotating wormhole spacetime. Phys. Rev. D 2015, 91, 104040. [Google Scholar] [CrossRef] [Green Version]
- Zaslavskii, O.B. Super-Penrose process with charged particles near naked singularity. arXiv 2022, arXiv:2204.03314. [Google Scholar]
- Zaslavskii, O.B. Super-Penrose process for extremal charged white holes. Mod. Phys. Lett. A 2020, 36, 2150020. [Google Scholar] [CrossRef]
- Gupta, K.; Law, Y.T.A.; Levin, J. Penrose process for a charged black hole in a uniform magnetic field. Phys. Rev. D 2021, 104, 084059. [Google Scholar] [CrossRef]
- Zaslavskii, O.B. Super-Penrose process for extremal rotating neutral white holes. Gen. Relativ. Gravit. 2020, 52, 1–11. [Google Scholar] [CrossRef]
- Zaslavskii, O.B. Center of mass energy of colliding electrically neutral particles and super-Penrose process. Phys. Rev. D 2019, 100, 024050. [Google Scholar] [CrossRef] [Green Version]
- Hejda, F.; Lemos, J.P.S.; Zaslavskii, O.B. Extraction of energy from an extremal rotating electrovacuum black hole: Particle collisions in the equatorial plane. Phys. Rev. D 2022, 105, 024014. [Google Scholar] [CrossRef]
- Hejda, F.; Bičák, J.; Zaslavskii, O.B. Extraction of energy from an extremal rotating electrovacuum black hole: Particle collisions along the axis of symmetry. Phys. Rev. D 2019, 100, 064041. [Google Scholar] [CrossRef] [Green Version]
- Zaslavskii, O.B. New Scenarios of High-Energy Particle Collisions Near Wormholes. Universe 2020, 6, 227. [Google Scholar] [CrossRef]
- Pavlov, Y.V.; Zaslavskii, O.B. Kinematic Censorship as a Constraint on Allowed Scenarios of High-Energy Particle Collisions. Gravit. Cosmol. 2019, 25, 390–396. [Google Scholar] [CrossRef] [Green Version]
- Zaslavskii, O.B. Maximum efficiency of the collisional Penrose process. Phys. Rev. D 2016, 94, 064048. [Google Scholar] [CrossRef] [Green Version]
- Zaslavskii, O.B. Rotation as an origin of high energy particle collisions. Mod. Phys. Lett. A 2016, 31, 1650029. [Google Scholar] [CrossRef] [Green Version]
- Shaymatov, S.; Sheoran, P.; Becerril, R.; Nucamendi, U.; Ahmedov, B. Efficiency of Penrose process in spacetime of axially symmetric magnetized Reissner-Nordströ m black hole. arXiv 2022, arXiv:2204.02026. [Google Scholar]
- Gibbons, G.W.; Horowitz, G.T.; Townsend, P.K. Higher-dimensional resolution of dilatonic black-hole singularities. Class. Quantum Gravity 1995, 12, 297–317. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, A.; Martinec, E. String field theory in curved spacetime and the resolution of spacelike singularities. Class. Quantum Gravity 1996, 13, 63–95. [Google Scholar] [CrossRef]
- Easson, D.A. Towards a stringy resolution of the cosmological singularity. Phys. Rev. D 2003, 68, 043514. [Google Scholar] [CrossRef] [Green Version]
- Husain, V.; Winkler, O. Quantum resolution of black hole singularities. Class. Quantum Gravity 2005, 22, L127–L133. [Google Scholar] [CrossRef] [Green Version]
- De Roo, F. Geometrical Resolution of Spacetime Singularities. Ph.D. Thesis, Vrije Universiteit Brussel, Brussel, Belgium, 2010. [Google Scholar]
- Cheng-Zhou, L.; Guo-Xiang, Y.; Zhi-Kun, X. The spacetime singularity resolution of Schwarichild-de Sitter black hole in loop quantum gravity. Acta Phys. Sin. 2010, 59, 1487–1493. [Google Scholar] [CrossRef]
- Philipp, H.v.L. Resolution of Curvature Singularities in Black Holes and the Early Universe. 2010. Available online: https://edoc.ub.uni-muenchen.de/11865/ (accessed on 8 September 2022).
- Singh, P. Bianchi-I spacetimes in loop quantum cosmology: Physics of singularity resolution. J. Phys. Conf. Ser. 2012, 360, 012008. [Google Scholar] [CrossRef]
- Corichi, A.; Karami, A.; Montoya, E. Loop Quantum Cosmology: Anisotropy and Singularity Resolution. In Relativity and Gravitation; Springer: Cham, Switzerland, 2014; pp. 469–477. [Google Scholar] [CrossRef]
- Lee, S.; Roychowdhury, R.; Yang, H.S. Topology change of spacetime and resolution of spacetime singularity in emergent gravity. Phys. Rev. D 2013, 87, 126002. [Google Scholar] [CrossRef] [Green Version]
- Kreienbuehl, A.; Pawłowski, T. Singularity resolution from polymer quantum matter. Phys. Rev. D 2013, 88, 043504. [Google Scholar] [CrossRef] [Green Version]
- Blanchette, K.; Das, S.; Hergott, S.; Rastgoo, S. Black hole singularity resolution via the modified Raychaudhuri equation in loop quantum gravity. Phys. Rev. D 2021, 103, 084038. [Google Scholar] [CrossRef]
- Mosani, K.; Dey, D.; Bhattacharya, K.; Joshi, P.S. Singularity resolution in gravitational collapse. Phys. Rev. D 2022, 105, 064048. [Google Scholar] [CrossRef]
- Shaikh, R.; Pal, K.; Sarkar, T. Constraining alternatives to the Kerr black hole. Mon. Not. R. Astron. Soc. 2021, 506, 1229–1236. [Google Scholar] [CrossRef]
- Mazza, J.; Franzin, E.; Liberati, S. A novel family of rotating black hole mimickers. J. Cosmol. Astropart. Phys. 2021, 2021, 082. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Walia, R.K. Field sources for Simpson-Visser spacetimes. Phys. Rev. D 2022, 105, 044039. [Google Scholar] [CrossRef]
- Bambi, C.; Modesto, L.; Rachwal, L. Spacetime completeness of non-singular black holes in conformal gravity. J. Cosmol. Astropart. Phys. 2017, 2017, 003. [Google Scholar] [CrossRef]
- Zhang, Q.; Modesto, L.; Bambi, C. A general study of regular and singular black hole solutions in Einstein’s conformal gravity. Eur. Phys. J. C 2018, 78, 506. [Google Scholar] [CrossRef]
- Glass, E.N.; Krisch, J.P. Spinning up asymptotically flat spacetimes. Class. Quantum Gravity 2004, 21, 5543–5553. [Google Scholar] [CrossRef]
- Simpson, A.; Visser, M. Black-bounce to traversable wormhole. J. Cosmol. Astropart. Phys. 2019, 2019, 042. [Google Scholar] [CrossRef] [Green Version]
- Islam, S.U.; Kumar, J.; Ghosh, S.G. Strong gravitational lensing by rotating Simpson-Visser black holes. J. Cosmol. Astropart. Phys. 2021, 2021, 13. [Google Scholar] [CrossRef]
- Franzin, E.; Liberati, S.; Mazza, J.; Dey, R.; Chakraborty, S. Scalar perturbations around rotating regular black holes and wormholes: Quasinormal modes, ergoregion instability, and superradiance. Phys. Rev. D 2022, 105, 124051. [Google Scholar] [CrossRef]
- Wagh, S.M.; Dhurandhar, S.V.; Dadhich, N. Revival of the Penrose process for astrophysical applications. Astrophys. J. Lett. 1985, 290, 12–14. [Google Scholar] [CrossRef]
- Tursunov, A.; Dadhich, N. Fifty Years of Energy Extraction from Rotating Black Hole: Revisiting Magnetic Penrose Process. Universe 2019, 5, 125. [Google Scholar] [CrossRef]
- Stuchlik, Z. Bulletin of the Astronomical Institute of Czechoslovakia. 1980, Volume 31, p. 129. Available online: https://ui.adsabs.harvard.edu/abs/1980BAICz..31..129S/abstract (accessed on 8 September 2022).

| No. | Spin Parameter (a) | l = 0 | l = 0.4 | l = 0.8 | l = 1.2 | l = 1.6 |
|---|---|---|---|---|---|---|
| 1 | 0.1 | 0.0627 | 0.0706 | 0.0981 | 0.1583 | 0.4558 |
| 2 | 0.2 | 0.2544 | 0.2868 | 0.4000 | 0.6480 | 1.8704 |
| 3 | 0.3 | 0.5859 | 0.6621 | 0.9295 | 1.5163 | 4.3963 |
| 4 | 0.4 | 1.0774 | 1.2226 | 1.7331 | 2.8560 | 8.3360 |
| 5 | 0.5 | 1.7638 | 2.0133 | 2.8939 | 4.8358 | 14.2433 |
| 6 | 0.6 | 2.7046 | 3.1130 | 4.5622 | 7.7680 | 23.161 |
| 7 | 0.7 | 4.0084 | 4.6698 | 7.0349 | 12.2844 | 37.2457 |
| 8 | 0.8 | 5.9017 | 7.0058 | 10.9976 | 19.887 | 61.8034 |
| 9 | 0.9 | 9.0098 | 11.0657 | 18.6299 | 35.51 | 115.227 |
| 10 | 0.93 | 10.466 | 13.0792 | 22.7707 | 44.3966 | 147.24 |
| 11 | 0.96 | 12.5 | 16.0286 | 29.2575 | 58.7556 | 201.265 |
| 12 | 0.99 | 16.1956 | 21.8635 | 43.5115 | 91.6925 | 334.925 |
| 13 | 1 | 20.7107 | 30.014 | 66.3072 | 147.02 | 585.65 |
| No. | Spin Parameter (a) | l = 0 | l = 0.4 | l = 0.8 | l = 1.2 | l = 1.6 |
|---|---|---|---|---|---|---|
| 1 | 0.1 | 0.0627 | 0.0734 | 0.1139 | 0.2155 | 0.2779 |
| 2 | 0.2 | 0.2544 | 0.2985 | 0.4650 | 0.8840 | 1.1396 |
| 3 | 0.3 | 0.5859 | 0.6897 | 1.0836 | 2.0767 | 2.6758 |
| 4 | 0.4 | 1.0774 | 1.2752 | 2.0292 | 3.9345 | 5.0652 |
| 5 | 0.5 | 1.7638 | 2.104 | 3.4087 | 6.7152 | 8.6324 |
| 6 | 0.6 | 2.7046 | 3.2620 | 5.4190 | 10.9033 | 13.9803 |
| 7 | 0.7 | 4.0084 | 4.9127 | 8.4550 | 17.4932 | 22.3309 |
| 8 | 0.8 | 5.9017 | 7.4153 | 13.4498 | 28.9005 | 36.6025 |
| 9 | 0.9 | 9.0098 | 11.8417 | 23.4581 | 53.3091 | 66.4615 |
| 10 | 0.93 | 10.466 | 14.0743 | 29.0711 | 67.6721 | 83.6705 |
| 11 | 0.96 | 12.5 | 17.3899 | 38.0852 | 91.5133 | 111.747 |
| 12 | 0.99 | 16.1956 | 24.1065 | 58.6912 | 148.786 | 177.178 |
| 13 | 1 | 20.7107 | 33.8248 | 93.4743 | 251.85 | 289.551 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patel, V.; Acharya, K.; Bambhaniya, P.; Joshi, P.S. Rotational Energy Extraction from the Kerr Black Hole’s Mimickers. Universe 2022, 8, 571. https://doi.org/10.3390/universe8110571
Patel V, Acharya K, Bambhaniya P, Joshi PS. Rotational Energy Extraction from the Kerr Black Hole’s Mimickers. Universe. 2022; 8(11):571. https://doi.org/10.3390/universe8110571
Chicago/Turabian StylePatel, Vishva, Kauntey Acharya, Parth Bambhaniya, and Pankaj S. Joshi. 2022. "Rotational Energy Extraction from the Kerr Black Hole’s Mimickers" Universe 8, no. 11: 571. https://doi.org/10.3390/universe8110571







