Quasiperiodic Oscillations and Dynamics of Test Particles around Quasi- and Non-Schwarzschild Black Holes

Abstract

One of the open problems in black hole physics is testing spacetime around black holes through astrophysical observations in the strong field regime. In fact, black holes cannot produce radiation themselves in the electromagnetic spectrum. However, a black hole’s gravity plays an important role in the production of the radiation of the accretion disc around it. One may obtain valuable information from the electromagnetic radiation of accretion discs about the gravitational properties of the spacetime around black holes. In this work, we study particle dynamics in the spacetime of quasi- and non-Schwarzschild black holes. We compare the gravitational effects of the spacetime deformation parameters of both black hole solutions on the innermost stable circular orbit (ISCO) radius, position, energy, and angular momentum of test particles at the ISCO, together with the energy efficiency of the accretion disc in the thin Novikov–Thorn model. Furthermore, we study the frequencies of particle oscillations in the radial and angular directions along circular stable orbits around both deformed black holes. Furthermore, we investigate quasiperiodic oscillations around the black holes in the relativistic precession model. We show the dependence of the deviation parameters on the orbits of twin peak QPOs with the frequency ratio 3:2. In the obtained results, we compare the gravitational effects of deviation parameters with the spin of a rotating Kerr black hole. Finally, we obtain constraints on the values of the deviation parameter of the spacetime around the black hole at the center of the microquasars GRO J1655-40 and GRS 1915-105 and their mass, using the ${\chi }^2$ method.

1. Introduction

From the mathematical point of view, black holes (BHs) are exact solutions to the gravitational field equations. For the first time, Karl Schwarzschild found a spherically symmetric BH solution that has only one parameter, total mass, as an exact vacuum solution to Einstein’s field equations in 1916. From an astrophysical point of view, these compact objects are relativistic gravitational astrophysical objects formed at the end stage of stellar evolution. There are three types of black holes according to their mass: super-massive black holes (${10}^6$–${10}^{10}$ solar masses), which are located in galactic centers [1]; intermediate-mass black holes, whose mass is ${10}^2$–${10}^5$ solar masses), and their distribution in galaxies is still uncertain [2]; and finally, black holes with masses from 3 to 100 solar masses are called stellar mass astrophysical black holes, and they are primarily found in binary systems [3]. Recent observations with the Event Horizon Telescope and GRAVITY collaborations have demonstrated the first detected shadows of two supermassive black holes (SMBHs), M87* and Sgr A*, and the precise motion of the S2 star in the Milky Way galaxy center, which allowed us an independent way to estimate their masses and spin parameters [4,5]. However, due to their small angular size, astrophysical black holes of medium and stellar mass cannot be observed. Fortunately, astrophysical black holes can be mainly observed by the radiation luminosity of the accretion disk, in particular by quasi-periodic oscillation (QPO) frequencies with the ratio 3:2 [6,7]. Using QPOs it is possible to obtain information about spacetime around the black holes and constraints on their total mass, charge, and spin parameters estimated, e.g., in [8,9,10,11,12].

In fact, the BH charge or parameters of alternative and modified gravity (MOG) theories may provide gravitational effects around non-rotating black holes similar to the spin of rotating Kerr black holes, which can reduce the decrease of the inner radii of the photospheres and accretion disks of black holes [13,14,15,16]. In this sense, their effects on the spacetime geometry around the black holes are similar, and these parameters can mimic each other. Another fact, Einstein’s general theory of relativity has been well tested in both weak and strong gravitational regimes and has been confirmed by many astrophysical observations so far [17]. However, alternative and modified theories of gravity have also successfully passed through astrophysical tests where GR could not play a role [18,19]. All of the above-mentioned facts imply that testing the theories of gravity and parameters of black holes using observational data from astrophysical black holes is one of the most actual and important issues in theoretical and observational astrophysics [20,21,22,23,24,25,26,27,28,29].

From these points, the quasi-Schwarzschild black hole solution is one of the key concepts in general relativity, describing the geometry of spacetime around a non-rotating black hole, which differs from around a Schwarzschild black hole by a small deviation parameter. Oscillations in the spacetime around black holes, known as quasinormal modes have been investigated and estimations of black hole mass and spin have also been obtained in Ref. [30]. The quasi-Schwarzschild black hole solution may also be considered as a black hole solution in modified theories of gravity, such as Horndeski’s theory, in testing the gravity theories [31].

The thermodynamics of quasi-Schwarzschild black holes is studied in Ref. [32] and as a minimal extension of general relativity for astrophysics [33]. Additionally, they have been investigated in the context of modified theories of gravity, such as gravity’s rainbow [34]. In our previous work [35] we have studied electromagnetic fields and charged particles’ dynamics in spacetime around the black hole.

For the first time, the non-Schwarzschild black hole solution has been obtained by Jonassen and Psaltis [36,37]. The quasinormal modes of the black holes have been studied and different from those of Schwarzschild ones are shown in Refs. [38,39]. Later, several authors have carried out various studies on this spacetime [40,41,42,43,44,45,46,47,48,49,50].

Studies on non-Schwarzschild black holes have become an important factor in relativistic astrophysics that may allow an understanding of the gravitational properties of the spacetime around black holes. There are lots of observations of black holes, including images of the supermassive black holes M87 and Sgr A*, to provide opportunities to test gravitational theories and obtain constraints on black hole parameters [51]. One such interesting phenomenon found in the noisy X-ray emission data from accretion disks around black holes are QPOs [52]. The detection and study of QPOs has provided important insights into the physical properties of black holes and their surrounding accretion disks.

In recent years, there has been a growing interest in studying QPOs in the environment of non-Schwarzschild and quasi-Schwarzschild black holes. Non-Schwarzschild black holes are those that are rotating or have other deviations from the spherically symmetric geometry, while quasi-Schwarzschild black holes are those that are nearly spherically symmetric but have small deviations from the Schwarzschild geometry [53]. Studying QPOs in these black holes can provide insights into their properties and help test our understanding of black hole physics.

Several theoretical models have been proposed to explain the presence of QPOs in non-Schwarzschild and quasi-Schwarzschild black holes. One such model is the trapped oscillation model, which suggests that QPOs arise from trapped oscillations of the accretion disk in the black hole potential [54]. Another model is the relativistic precession model, which proposes that QPOs arise from the relativistic precession of the accretion disk around the black hole [55].

Observations of QPOs in non-Schwarzschild and quasi-Schwarzschild black holes have been made by several X-ray observatories, including the Rossi X-ray Timing Explorer (RXTE) [56], the Chandra X-ray Observatory [57], and the X-ray Multi-Mirror Mission (XMM-Newton) [58]. These observations have provided important insights into the physical properties of black holes and their surrounding accretion disks.

In the present work, we aimed to study particle dynamics and oscillations of the particles along stable circular orbits around both non-Schwarzschild and quasi-Schwarzschild black holes.

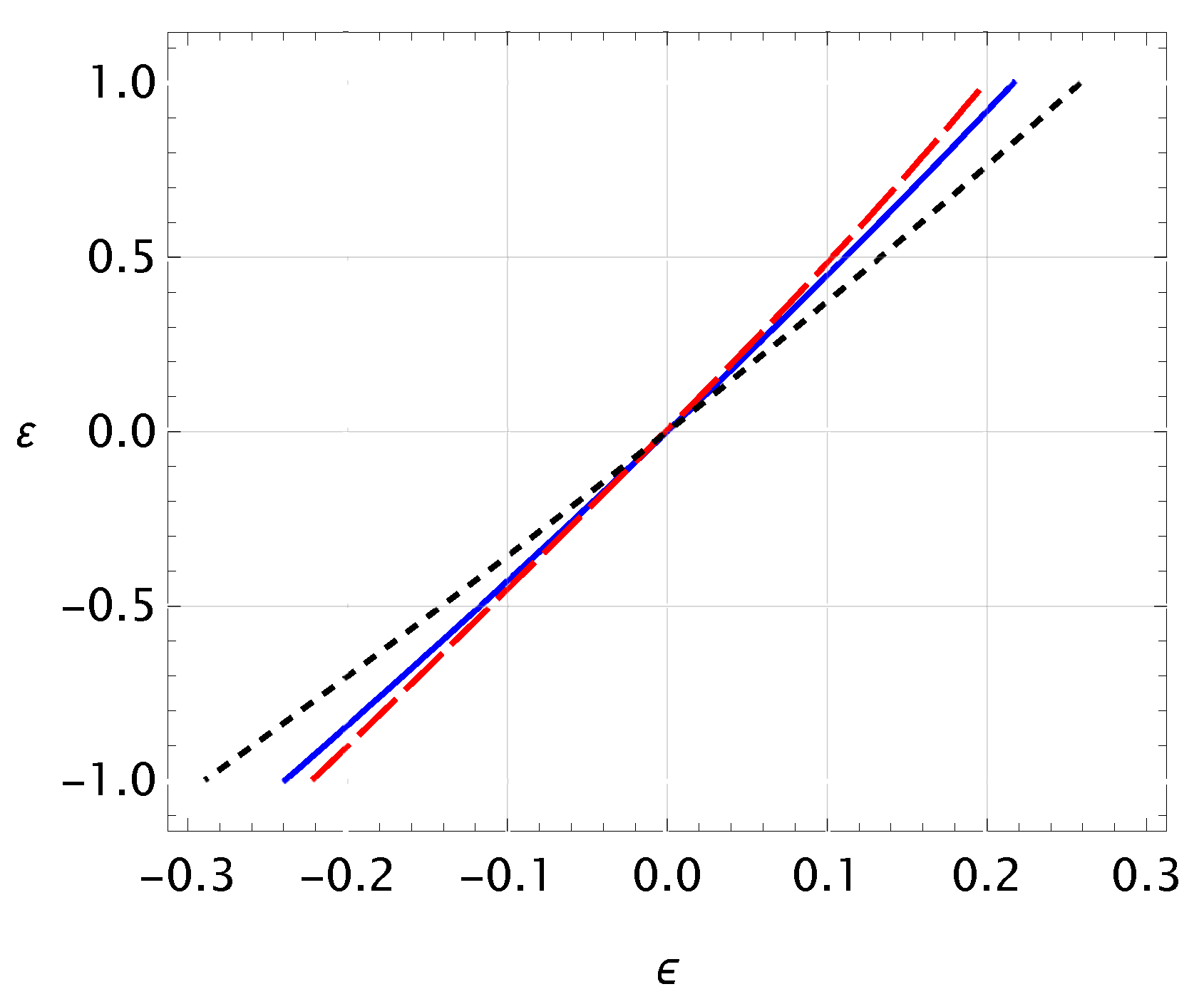
2. “Deformed” Black Hole Solutions

2.1. Quasi-Schwarzschild Black Holes

The spacetime metric of quasi-Schwarzschild black holes is obtained in Ref. [59] using a small variation of the Schwarzschild spacetime metric in the following form,

$$g_{\mu \nu }=g_{\mu \nu }^{\mathrm{Schw}}+ϵh_{\mu \nu },$$

(1)

where $g_{\mu \nu }^{\mathrm{Schw}}$ is the standard Schwarzschild metric, $ϵh_{\mu \nu }$ is a small deviation of the spacetime from the Schwarzschild one, and $ϵ$ is a deviation parameter that defines how spherically symmetric spacetime deforms due to an additional mass quadrupole moment Q of the black hole $Q=-ϵM^3$, and can be negative or positive [59]. The contravariant components of the additional term in the metric $h^{\mu \nu }$ are found in Ref. [59] in the following form,

$$\begin{array}{ccc}\hfill h^{tt}& =& \frac{r}{r-2M}(1-3{cos}^2\theta )F_1\left(r\right),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill h^{rr}& =& \left(1-\frac{2M}{r}\right)(1-3{cos}^2\theta )F_1\left(r\right),\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill h^{\theta \theta }& =& -\frac{1}{r^2}(1-3{cos}^2\theta )F_2\left(r\right),\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill h^{\varphi \varphi }& =& -\frac{1}{r^2{sin}^2\theta }(1-3{cos}^2\theta )F_2\left(r\right),\hfill \end{array}$$

(5)

where the radial functions $F_1\left(r\right)$ and $F_2\left(r\right)$ read

$$\begin{array}{ccc}\hfill F_1\left(r\right)& =& -\frac{5(r-M)}{8Mr(r-2M)}\left(2M^2+6Mr-3r^2\right)-\frac{15r(r-2M)}{16M^2}ln\frac{r}{r-2M},\hfill \\ \hfill F_2\left(r\right)& =& \frac{5\left(2M^2-3Mr-3r^2\right)}{8Mr}+\frac{15\left(r^2-2M^2\right)}{16M^2}ln\frac{r}{r-2M}.\hfill \end{array}$$

After lowering the indices of $h^{\mu \nu }$ with the use of $g_{\mu \nu }^{\mathrm{Schw}}$ the quasi-Schwarzschild spacetime metric takes the following form

$$\begin{array}{c}\hfill d{s}^2=g_{tt}d{t}^2+g_{rr}d{r}^2+k(r,\theta )r^{2}d{\Omega }^2,\end{array}$$

(6)

where

$$\begin{array}{ccc}\hfill g_{tt}& =& -\left(1-\frac{2M}{r}\right)[1-ϵF_1(1-3{cos}^2\theta )],\hfill \\ \hfill g_{rr}& =& \frac{r}{r-2M}[1+ϵF_1(1-3{cos}^2\theta )],\hfill \\ \hfill k(r,\theta )& =& 1-ϵF_2(1-3{cos}^2\theta ).\hfill \end{array}$$

2.2. Non-Schwarzschild Black Holes

The spacetime around a black hole that is a so-called non-Schwarzschild black hole, obtained by Johansen and Psaltis, in spherical coordinates has the form [37]:

$$\begin{array}{ccc}\hfill d{s}^2& =& -f\left(r\right)\left(1+h\left(r\right)\right)d{t}^2+\frac{1+h\left(r\right)}{f\left(r\right)}d{r}^2+r^{2}d{\theta }^2+r^2{sin}^2\theta d{\varphi }^2,\hfill \end{array}$$

(7)

with the radial functions

$$f\left(r\right)=1-\frac{2M}{r},h\left(r\right)=\sum _{k=1}^{\infty }{\epsilon }_k{\left(\frac{M}{r}\right)}^k.$$

(8)

where $h\left(r\right)$ stands for the deviation of the spacetime from Schwarzschild spacetime and $\epsilon$ is the deformation parameter, and it takes either positive or negative values, namely, $\epsilon >0$ or $\epsilon <0$, describing oblate and prolate deformations, respectively. If there is no deformation in the spacetime $\epsilon =0$, the metric (8) becomes Schwarzschild. The zero term is extremely small ${\epsilon }_0\ll 1$ or ${\epsilon }_0=0$, and similarly ${\epsilon }_1\ll M/r$ and the authors of Ref. [60] have shown that ${\epsilon }_2\simeq 4.6\times {10}^{-6}$ using observational data from Laser Lunar Ranging experiments, so one may neglect it. The lowest-order at $k=3$ non-vanishing parameter ${\epsilon }_3=\epsilon$ is mentioned above as the deformation parameter [37].

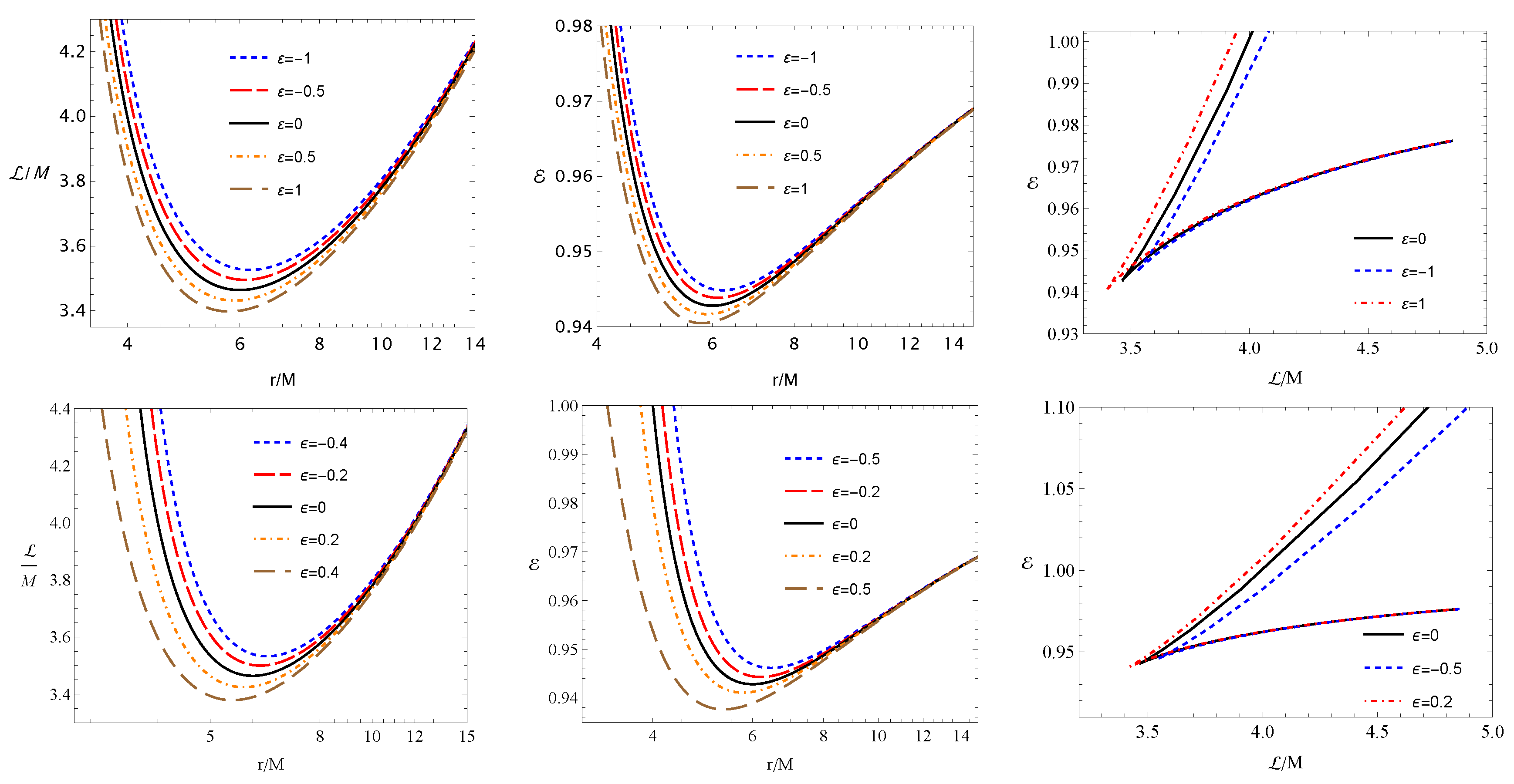
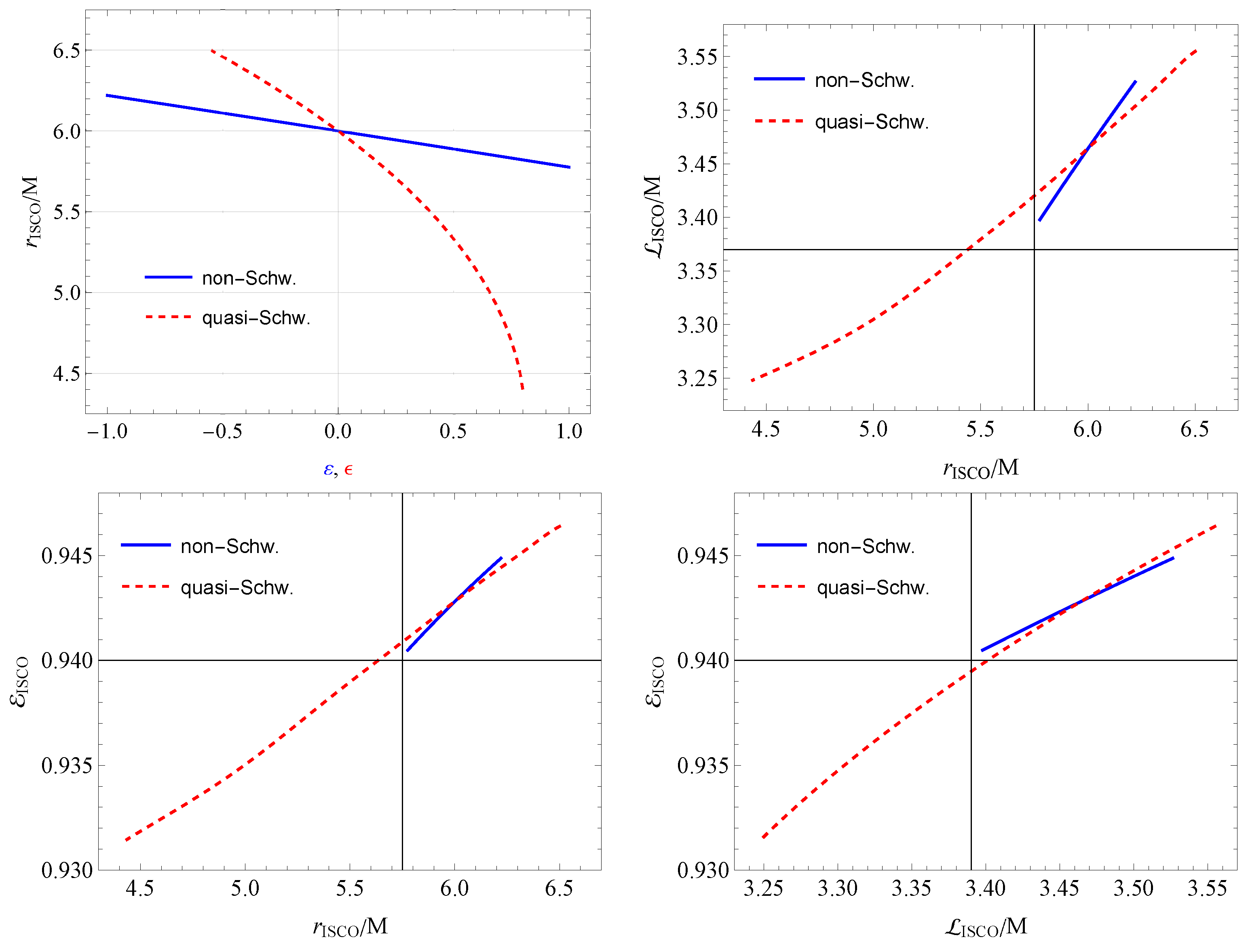
3. Motion of Test Particles

The present section is devoted to exploring the circular orbit of test particles with mass m around both non-Schwarzschild and quasi-Schwarzshild black holes employing the Hamilton–Jacobi equation.

$$g^{\mu \nu }\frac{\partial S}{\partial x^{\mu }}\frac{\partial S}{\partial x^{\nu }}=-m^2,$$

(9)

One can derive the equations of motion for the test files using the following standard separable form of the action S as,

$$S=-Et+L\phi +S_r+S_{\theta },$$

(10)

where E and L are the energy and angular momentum of the test particle, i.e., integrals of the motion. One may easily find the effective potential of the test particles for circular motion ($\dot{r}=0$) in a fixed plane ($\dot{\theta }=0)$ in the following form

$$V_{eff}=-g_{tt}\left(1+\frac{{\mathcal{L}}^2}{g_{\varphi \varphi }}\right).$$

(11)

The values of specific angular momentum of the test particles corresponding to circular orbits can be obtained by solving the equation ${\partial }_r{V}_{eff}\left(r\right)=0$, given as

$${\mathcal{L}}_c^2=\frac{g_{ff}^2{\partial }_r{g}_{tt}}{g_{tt}{\partial }_r{g}_{ff}-g_{ff}{\partial }_r{g}_{tt}}$$

(12)

and the corresponding energy

$$\mathcal{E}=-g_{tt}\left(1+\frac{{\mathcal{L}}_c^2}{g_{\varphi \varphi }}\right).$$

(13)

Below, we analyze the effects of deviation parameters of both non- and quasi-Schwarzschild black holes on the values of specific angular momentum and energy of particles in circular orbits.

Figure 1 shows radial profiles of the angular momentum of test particles in circular orbits as well as their energy. It is observed that the minimum in the values of the angular momentum and energy is increased (decreased) when the parameters are negative (positive) and the position where both quantities take a minimum is shifted towards the central object. The effect of the deviation parameter in quasi-Schwarzschild spacetime on the energy and angular momentum is stronger than in non-Schwarzschild spacetime.

Now, we study the effect of spacetime deformation on the innermost stable circular orbits (ISCOs) of the test particles. ($dr/d\tau =0$ & $p^r=0$) $V_{eff}=\mathcal{E}$ and $d^{2}r/d{\tau }^2=0$ or $d{V}_{eff}/dr=0$, together with $d^2{V}_{eff}/d{r}^2=0$.

The radius of the ISCO satisfies the conditions $V_{eff}=\mathcal{E}$, $d{V}_{eff}/dr=0$, and $d^2{V}_{eff}/d{r}^2=0$ and to obtain the ISCO region we solve the non-linear system of equations. Due to the complicated form of the equations, we analyze the ISCO profiles graphically.

In Figure 2, we demonstrate the dependence of the ISCO radius on the deviation parameter in the top left panel. In addition, in the rest of the panels, we analyze possible values of the particle energy and angular momentum at the ISCOs corresponding to the range $ϵ,\epsilon \in (-1,1)$. Our analyses have shown that there is an upper limit for the deviation parameter of quasi-Schwarzschild spacetime near ${ϵ}_{upp}\simeq 0.8$, in which the ISCO radius takes a minimum value, while $\epsilon$ causes a linear decrease in ISCO in the given range. It is observed from the figure that the range of the ISCO radius, energy, and angular moment of particles in the ISCO in the quasi-Schwarzschild case is much larger than in the non-Schwarzschild case.

The Keplerian accretion disc around astrophysical black holes in the Novikov–Thorn model is a model for the geometrically thin disc governed by circular geodesic properties in spacetime [61].

Accreting matter orbiting black holes results in the extraction of high-energy gravitational and electromagnetic radiation. The energy efficiency of the accretion disc is the maximum value of the released energy from the accretion disc. Falling matter consisting of test particles becomes ionized as they obtain a relativistic high speed and viscosity in the denser matter. The energy efficiency of an isolated particle is proportional to the total luminosity of the accretion disk in the optical band of the electromagnetic waves.

The efficiency of energy release processes in the accretion disc is the difference between the rest energy of the test particles and their energy at ISCO $\eta =1-{\mathcal{E}}_{\mathrm{ISCO}}$, where ${\mathcal{E}}_{\mathrm{ISCO}}=\mathcal{E}(r=r_{\mathrm{ISCO}})$ describes the ratio of the binding energy of the particles with respect to the black hole particle system.

We investigate the energy efficiency around non-Schwarzschild and quasi- Schwarzschild black holes. The obtained results have shown that the efficiency increases as the deformation parameters increase. The rate increases in the quasi-Schwarzschild black hole case with respect to the non-Schwarzschild one.

In Figure 3 we show the effects of the deviation parameters of non & quasi-Schwarzschild black hole spacteimes in the range $ϵ,\epsilon \in (-1,1)$, on the energy efficiency of their accretion disks. It is observed that the efficiency is growth faster with the increase of $ϵ$ than the increase of $\epsilon$, and reaches about 7%.

4. Fundamental Frequencies of Oscillating Particles in the Deformed Spacetimes

4.1. Keplerian Frequency

The angular velocity of the test particle around both deformed black holes, as measured by a distant observer, is commonly referred to as the Keplerian frequency ${\Omega }_K=\frac{d\varphi }{dt}$. In our further analyses, we define the fundamental frequencies in units of Hz, multiplying the frequencies by the term $c^3/\left(2\pi GM\right)$. The speed of light in a vacuum is $c=3\times {10}^8$$\mathrm{m}/\sec$, and the gravitational constant $G=6.67\times {10}^{-11}$${\mathrm{m}}^3/({\mathrm{kg}}^2·\sec )$.

4.2. Harmonic Oscillations

When a test particle is in a stable circular orbit at the equatorial plane around the black hole, small perturbations in its radial ($r\to r_0+\delta r$) and vertical ($\theta \to {\theta }_0+\delta \theta$) coordinates cause oscillations along these axes.

In order to derive the equations that govern these oscillations, we expand the effective potential in terms of the coordinates r and $\theta$ and use the conditions for the extreme of the effective potential, namely, $V_{\mathrm{eff}}(r_0,{\theta }_0)=0$ and ${\partial }_{r\left(\theta \right)}{V}_{\mathrm{eff}}=0$. This leads to the following expressions [62]

$$\begin{array}{c}\hfill \frac{d^2\delta r}{d{t}^2}+{\Omega }_r^2\delta r=0,\frac{d^2\delta \theta }{d{t}^2}+{\Omega }_{\theta }^2\delta \theta =0.\end{array}$$

(14)

Here, ${\Omega }_r^2$ and ${\Omega }_{\theta }^2$ represent the square of the radial and vertical angular frequencies of the particles around the black hole, respectively, as measured by a distant observer, and they are given as

$$\begin{array}{c}\hfill {\Omega }_r^2=-\frac{1}{2g_{rr}{\left(u^t\right)}^2}{\partial }_r^2{V}_{\mathrm{eff}}(r,\theta ){|}_{\theta =\pi /2},\end{array}$$

(15)

$$\begin{array}{c}\hfill {\Omega }_{\theta }^2=-\frac{1}{2g_{\theta \theta }{\left(u^t\right)}^2}{\partial }_{\theta }^2{V}_{\mathrm{eff}}(r,\theta ){|}_{\theta =\pi /2},\end{array}$$

(16)

After performing some algebraic calculations, we obtain the expressions for the radial and vertical frequencies and apply them to a QPOs analysis.

5. Quasiperiodic Oscillations in Relativistic Precession Model

The source mechanism of electromagnetic emission in the accretion disk around the central black hole may be connected with particle oscillations. In fact, charged particles radiate with a frequency the same as their oscillation frequency around the central black hole. The dynamics of the charged test particles around black holes explain the existence of QPOs based on (quasi-)harmonic oscillations of the charged particles in the radial and angular directions.

Many QPOs are observed in such systems with high-accuracy measurements of the frequencies having been made. However, the exact and unique physical mechanisms of QPOs formation have not been found. The problem is still under active discussion in testing gravity theories and measurements of the inner edge of the accretion disc, which helps to obtain information about ISCO radii [8,10]. In this sense, the QPOs studies are a powerful tool to estimate the radii of the innermost regions of accretion disks as well as the central black hole mass, and to learn more about gravity’s properties.

We investigate the relationships between the upper and lower frequencies of twin peak QPOs around quasi- and non-Schwarzschild black holes and compare the obtained results on the frequency relationship with neutral particles orbiting both Schwarzschild and Kerr black holes [63].

First, we obtain equations for the upper and lower frequencies in the relativistic precession (RP) model where the upper and lower frequencies of twin peak QPOs are defined by the radial and orbital frequencies as ${\nu }_U={\nu }_{\varphi }$ and ${\nu }_L={\nu }_{\varphi }-{\nu }_r$, respectively [64]. We provide graphical analyses of the upper–lower frequency diagram.

In Figure 4, we show diagrams for the upper and lower frequencies of twin peak QPOs in the quasi- and non-Schwarzschild spacetimes in the left and right panels, respectively. In this figure, the inclined light blue line corresponds to the death line for twin peak QPOs that under the line QPOs cannot be observed, and the orange one for the QPOs with the ratio 3:2. In both cases a negative (positive) deviation parameter decreases (increases) the frequencies. Our performed comparisons have shown that the deviation parameter of quasi-Schwarzschild spacetime can mimic the spin of Kerr black holes $a=0.1M$ at $ϵ\simeq 0.3$ in terms of the same values of upper and lower frequencies. However, the deviation in non-Schwarzschild spacetime cannot mimic the spin $a=0.1M$ when $\epsilon <1$.

QPO Orbits

Now, we study the effects of the spacetime deviation parameters on the radii of orbits where QPOs with the ratio 3:2 can be generated in the RP model using the equations

$$\begin{array}{c}\hfill 3{\nu }_L(M,r,ϵ)=2{\nu }_U(M,r,ϵ),3{\nu }_L(M,r,\epsilon )=2{\nu }_U(M,r,\epsilon ).\end{array}$$

(17)

It is seen that Equation (17) is also too complicated to solve analytically. Therefore, we solve it numerically and provide graphical analyses.

In Figure 5, we present the radii of orbits of QPOs with the upper and lower frequency ratio around rotating Kerr (in both co-rotating and counter-rotating cases), non-, and quasi-Schwarzschild black holes (left panel) together with the distance between QPO orbits and the ISCO around the bumpy black holes as a function of the deviation parameters $\epsilon$ and $ϵ$. It is observed from the figure that QPO orbits come close to the central black hole for all spin and deviation parameters. Moreover, there are upper and lower limits in the values of the spin of a Kerr black hole and the deviation parameter of quasi-Schwarzchild black holes in which QPOs with a 3:2 frequency ratio can exist. It is also observed that the QPO orbit shifts out from the ISCO as $ϵ$ increases, while $\epsilon$ causes the orbits to be close to the ISCO.

6. Astrophysical Applications

The analysis of observational data from astrophysical gravitating compact objects such as black holes and neutron stars allow gravitational theories to be tested in both the strong and weak gravitational field regimes. The importance of this content is connected with free parameters in different modified gravity theories, which may demonstrate similar or the same gravitational effects on the spacetime around black holes. In fact, astrophysical black holes can be rotating and electrically charged. In many cases, astrophysical black holes are modeled using Kerr black holes or Kerr-like black holes in modified gravity theories. However, for simplicity, static and spherically/axially symmetric black holes with different parameters in alternative gravity theories can be considered as a suitable model for astrophysical black holes. The gravitational effects of the black hole’s spin on the dynamics test (charged) particle motion may also mimic the effects.

6.1. Deformed Black Hole Mimickers

Here, we discuss and compare the gravitational effects of the spin of a rotating Kerr black hole and deviation parameters of non- and quasi-Schwarzchild black holes on the ISCO radius, energy release efficiency, and twin peak QPO frequencies.

Figure 6 demonstrates the degeneracy values of the deviation parameters of non- and quasi-Schwarzschild black hole spacetimes providing the same values of the ISCO in the red large-dashed line, the energy efficiency and QPO frequencies are in black dashed and blue solid lines. It is observed from the figure that the deviation parameter in the quasi-Schwarzschild spacetime in the range $ϵ\in (-0.3,0.3)$ can mimic the range of the non-Schwarzschild spacetime deviation parameter $\epsilon \in (-1,1)$.

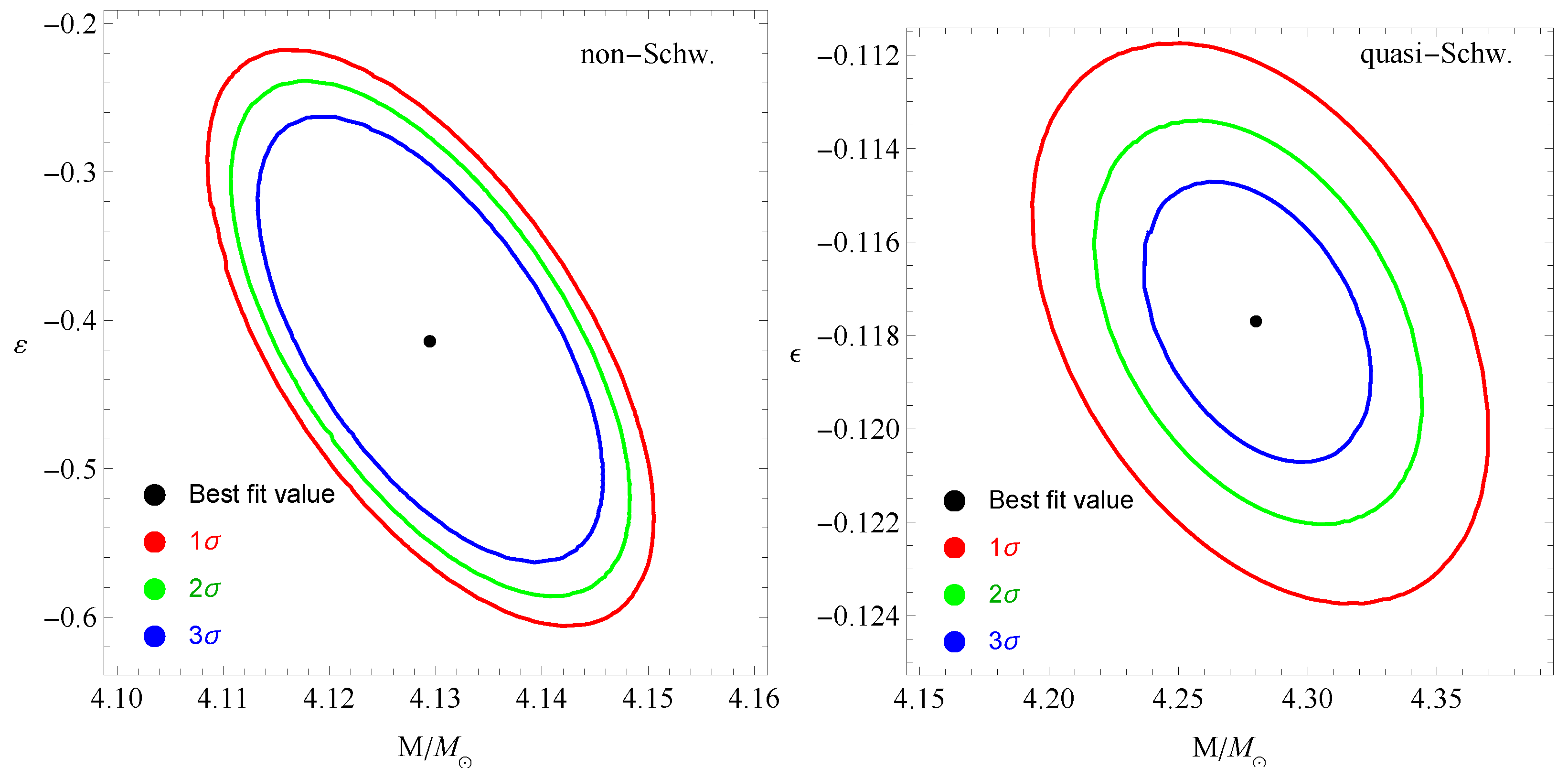
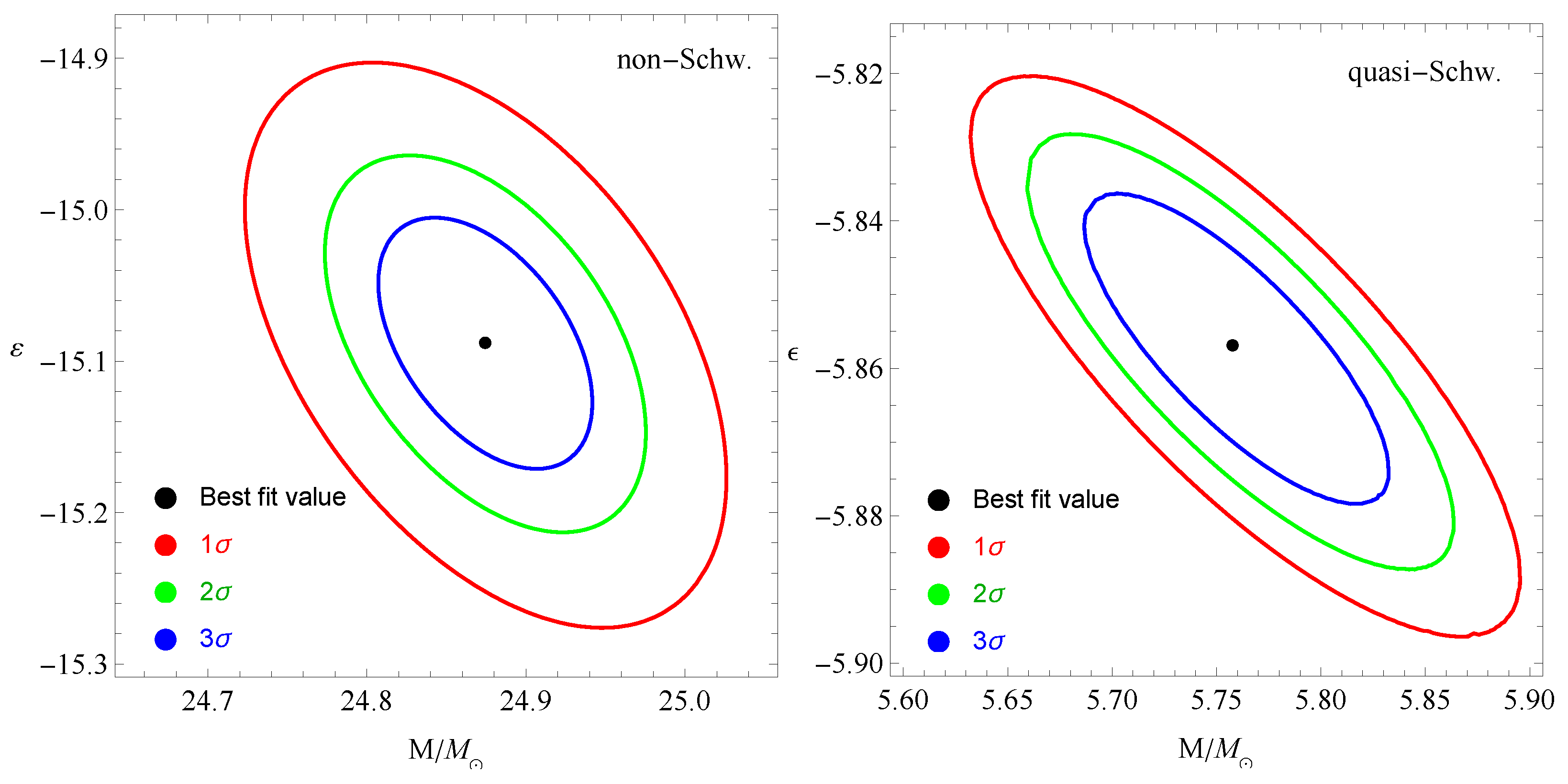
6.2. Constraints on the BH Mass and Deviation Parameters

In this section, we focus on obtaining constraints on the values of the deviation parameters of both non- and quasi-Schwarzschild black holes together with their mass using frequencies of the QPOs from the microquasars GRO J1655-40 and GRS 1915+105. In the relativistic precession model, the frequencies of the periastron precession ${\nu }_{\mathrm{per}}$ and the nodal precession ${\nu }_{\mathrm{nod}}$ are defined by the following relations: ${\nu }_{\mathrm{per}}={\nu }_{\varphi }-{\nu }_r$ and ${\nu }_{\mathrm{nod}}={\nu }_{\varphi }-{\nu }_{\theta }$, respectively [64].

In order to obtain the estimation for the five parameters as the peak frequencies of QPOs observed in the microquasars, we perform the ${\chi }^2$ analysis with [65]

$$\begin{array}{ccc}\hfill {\chi }^2(M,B,r_1,r_2)& =& \frac{{({\nu }_{1\varphi }-{\nu }_{1\mathrm{U}})}^2}{{\sigma }_{1\mathrm{U}}^2}+\frac{{({\nu }_{1\mathrm{per}}-{\nu }_{1\mathrm{L}})}^2}{{\sigma }_{1\mathrm{L}}^2}\hfill \\ & +& \frac{{({\nu }_{1\mathrm{nod}}-{\nu }_{1\mathrm{C}})}^2}{{\sigma }_{1\mathrm{C}}^2}+\frac{{({\nu }_{2\varphi }-{\nu }_{2\mathrm{U}})}^2}{{\sigma }_{2\mathrm{U}}^2}+\frac{{({\nu }_{2\mathrm{nod}}-{\nu }_{2\mathrm{C}})}^2}{{\sigma }_{2\mathrm{C}}^2}.\hfill \end{array}$$

(18)

In fact, the best estimates for the values of the parameters M, $\gamma$, $\alpha$, $r_1$, and $r_2$ should be at the minimum of ${\chi }_{\min }^2$ and the range of the parameters at the confidence level (C.L.) can be determined in the interval ${\chi }_{\min }^2+\Delta {\chi }^2$.

6.3. GRO J1655-40

Here, we obtain constraints on the mass of the black hole and surrounding magnetic fields in the microquasar GRO J1655-40 using the two sets of QPO frequencies in the astrophysical observations [66],

$$\begin{array}{cc}\hfill {\nu }_{1\mathrm{U}}=441\mathrm{Hz},& {\sigma }_{1\mathrm{U}}=2\mathrm{Hz},\\ \hfill {\nu }_{1\mathrm{L}}=298\mathrm{Hz},& {\sigma }_{1\mathrm{L}}=4\mathrm{Hz},\\ \hfill {\nu }_{1\mathrm{C}}=17.3\mathrm{Hz},& {\sigma }_{1\mathrm{C}}=0.1\mathrm{Hz},\end{array}$$

(19)

and

$$\begin{array}{cc}\hfill {\nu }_{2\mathrm{U}}=451\mathrm{Hz},& {\sigma }_{2\mathrm{U}}=5\mathrm{Hz},\\ \hfill {\nu }_{2\mathrm{C}}=18.3\mathrm{Hz},& {\sigma }_{2\mathrm{C}}=0.1\mathrm{Hz}.\end{array}$$

(20)

It is obtained that ${\chi }^2$ takes a minimum at $M=4.12944M_{\odot }$, $\epsilon =-0.414178$, $r_1=6.80526M$, and $r_2=6.70466M$ in the case of non-Schwarzschild spacetime, and $M=4.27999M_{\odot }$, $\epsilon =-0.1177$, $r_1=5.99437M$, and $r_2=3.18481M$, in the case of quasi-Schwarzschild spacetime.

While estimations of the black hole mass using QPOs around rotating Kerr black holes generated by charged test particles without external magnetic fields in the RP model have shown that it is about $M/M_{\odot }=5.3\pm 0.1$ [67], in our case, the constraint value of the central black hole mass is $M=4.12944M_{\odot }$ in the non-Scharzschild black hole model, while it is $M=4.27999M_{\odot }$ in the quasi-Scharzschild model, which are very close to the results obtained in Ref. [67].

6.4. GRS 1915+105

Furthermore, we perform a similar analysis on the GRS 1915+105 microquasar with QPO frequencies [68],

$$\begin{array}{cc}\hfill {\nu }_{1\mathrm{U}}=184.10\mathrm{Hz},& {\sigma }_{1\mathrm{U}}=1.84\mathrm{Hz},\\ \hfill {\nu }_{2\mathrm{U}}=142.98\mathrm{Hz},& {\sigma }_{2\mathrm{U}}=3.48\mathrm{Hz},\end{array}$$

(21)

and

$$\begin{array}{cc}\hfill {\nu }_{1\mathrm{L}}=67.40\mathrm{Hz},& {\sigma }_{1\mathrm{L}}=0.60\mathrm{Hz},\\ \hfill {\nu }_{2\mathrm{L}}=65.89\mathrm{Hz},& {\sigma }_{2\mathrm{L}}=0.52\mathrm{Hz},\\ \hfill {\nu }_{3\mathrm{L}}=69.58\mathrm{Hz},& {\sigma }_{3\mathrm{L}}=0.49\mathrm{Hz}.\end{array}$$

(22)

Our analyses show that ${\chi }^2$ is a minimum at $M=24.8744M_{\odot }$, $\epsilon =-15.0879$, $r_1=7.19483M$, $r_2=8.55071M$, and $r_3=8.34285M$ in the case of non-Schwarzschild spacetime, and $M=5.7577M_{\odot }$, $\epsilon =-5.85688$, $r_1=1.8459M$, $r_2=5.44028M$, and $r_3=1.90958M$ in the case of quasi-Schwarzschild spacetime.

The authors in Ref. [69] have studied QPOs around rotating Kerr black holes in the absence of magnetic fields in the RP model and have estimated that the mass of the central black hole is about $M/M_{\odot }=13.1\pm 0.2$.

Our studies have shown that (see Figure 7 and Figure 8) the mass of the black hole located in GRS 1915+105 is about $M=24.8744M_{\odot }$ in the non-Schwarzschild case, while calculations in quasi-Schwarzschild spacetime have given that the value for the black hole mass is $M=5.7577M_{\odot }$.

7. Conclusions

In this paper, we have focused on comparing the gravitational effects of the deviation parameters of the spacetime of quasi- and non-Schwarzschild black holes. To achieve this, we first study the dynamics of test particles in spacetime around both quasi- and non-Schwarzschild black holes. We also compare the effects of the spacetime deformation parameters on the black hole and the black hole on the ISCO position, energy, and angular momentum of test particles corresponding to circular orbits and their values at the ISCO, together with the energy efficiency of the accretion disc around the black holes in the Novikov–Thorn model. In our tests, we use the deviation parameters from −1 to 1. Our studies have shown that there is an upper limit for the deviation parameter of a quasi-Schwarzschild black hole of about $ϵ\simeq 0.8$ where the ISCO can exist. If the deviation parameter exceeds this upper value, the ISCO does not exist. The variation of the ISCO around a non-Schwarzschild black hole corresponding to the deviation range $\epsilon \in (-1,1)$ is about $(5.8-6.3)M$ and this is much less than the quasi-Schwarzschild case (which is about $(4.3-6.5)M$). Similar results have also been obtained for the energy and angular momentum of the particles at the ISCO. The possible range for the value of the ISCO’s energy is between 0.94 and 0.945 in the non-Schwarzschild case. While for the quasi-Schwarzschild case it is between 0.93 and 0.947. Our investigations on the efficiency of energy release processes from the accretion disc around the black holes have also shown that the efficiency is much higher in the quasi-Schwarzschild case compared to the non-Schwarzschild case.

Moreover, we have also studied frequencies of test particles’ oscillations in the radial and angular directions along circular stable orbits around both deformed black holes. Then, we have investigated quasiperiodic oscillations around these black holes in the frame of a relativistic precession model. The dependencies of the deviation parameters on the orbits of twin peak QPOs with the frequency ratio 3:2 are also obtained. It is also shown from the obtained results that the gravitational effects of the deviation parameters and the spin of rotating Kerr black holes are similar to each other.

Finally, we have obtained constraints on the values of the deviation parameter of the spacetime around quasi- and non-Schwarzschild black holes at the center of the microquasars GRO J1655-40 and GRS 1915-105 and their mass, using the ${\chi }^2$ method.