Relativistic Ionization of Hydrogen Atoms by Positron Impact
Abstract
:1. Introduction
2. Theoretical Model
3. Results and Discussion
3.1. Testing of the Model in Non-Relativistic Limit
3.2. Relativistic Regime
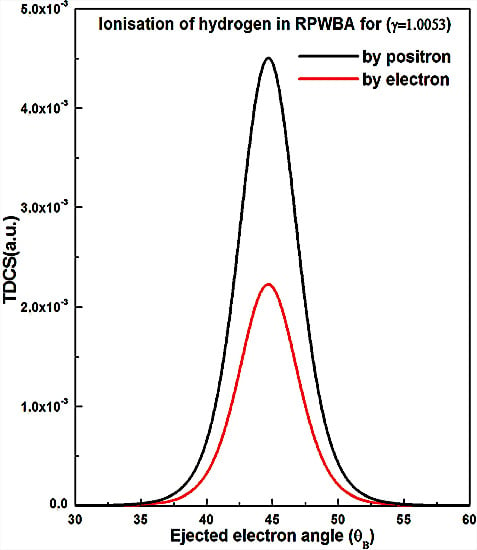
4. Comparison of Positron and Electron Results
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Charlton, M.; Humberston, J.W. Positron physics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Brauner, M.; Briggs, J.S.; Klar, H. Triply-differential cross sections for ionisation of hydrogen atoms by electrons and positrons. J. Phys. B At. Mol. Opt. Phys. 1989, 22, 2265. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Roy, K.; Sil, N.C. Triple differential ionisation cross-section of hydrogen atom bye ±-impact including exchange. Z. Phys. D 1994, 30, 35–38. [Google Scholar] [CrossRef]
- Chakrabarti, K. Schwinger variational calculation of ionization of hydrogen atoms for large momentum transfers. Pramana 2002, 58, 529–536. [Google Scholar] [CrossRef]
- An, Z.; Luo, Z.M.; Tang, C. Study of cross-sections for the K-shell ionization of atoms by electron and positron impact. Nucl. Instrum. Meth. Phys. Res. B 2001, 179, 334–342. [Google Scholar] [CrossRef]
- Chakrabarti, K. Positron impact ionization of atomic hydrogen at low energies. Pramana 2001, 56, 545–550. [Google Scholar] [CrossRef]
- Tőkési, K.; Barna, I.F.; Burgdörfer, J. Ionization of helium in positron impact. Nucl. Instrum. Meth. Phys. Res. B 2005, 233, 307–311. [Google Scholar] [CrossRef]
- Campeanu, R.I.; Chis, V.; Nagy, L.; Stauffer, A.D. Positron impact ionization of CH 4. Nucl. Instrum. Meth. Phys. Res. B 2006, 247, 58–60. [Google Scholar] [CrossRef]
- Campeanu, R.I. Positron-impact ionization of atoms and molecules. Nucl. Instrum. Meth. Phys. Res. B 2009, 267, 239–243. [Google Scholar] [CrossRef]
- Purohit, G.; Patidar, V.; Sud, K.K. Differential cross section calculations of positron and electron impact ionization of Ar (3p). Nucl. Instrum. Meth. Phys. Res. B 2011, 269, 745–751. [Google Scholar] [CrossRef]
- Kuo, T.-Y.; Chen, C.J.; Hsu, S.-W.; Huang, K.-N. Relativistic cross sections of positron-impact ionization of hydrogenic ions. Relativistic cross sections of positron-impact ionization of hydrogenic ions. Phys. Rev. A 1993. [Google Scholar] [CrossRef]
- De Lucio, O.G.; Otranto, S.; Olson, R.E.; DuBois, R.D. Triply differential single ionization of argon: charge effects for positron and electron impact. Phys. Rev. Lett. 2010, 104, 163201. [Google Scholar] [CrossRef] [PubMed]
- Tóth, I.; Campeanu, R.I.; Nagy, L. Triple differential cross sections for the ionization of water by electron and positron impact. Eur. Phys. J. D 2012, 66, 21. [Google Scholar] [CrossRef]
- Campeanu, R.I.; Alam, M. DWBA double differential ionization cross sections for positron impact on argon. Eur. Phys. J. D 2012, 66, 19. [Google Scholar] [CrossRef]
- Dey, R.; Roy, A.C.; Dal Cappello, C. Fivefold differential cross sections for the ionization of aligned hydrogen molecule by electron and positron impact. Nucl. Instrum. Meth. Phys. Res. B 2012, 271, 82–91. [Google Scholar] [CrossRef]
- Brauner, M.; Briggs, J.S. Structures in differential cross sections for positron impact ionization of hydrogen. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 2227–2236. [Google Scholar] [CrossRef]
- Berakdar, J.; Klar, H. Structures in triply and doubly differential ionization cross sections of atomic hydrogen. J. Phys. B At. Mol. Opt. Phys. 1993, 26, 3891. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Roy, K.; Mandal, P.; Sil, N.C. Ionization of atomic hydrogen by positron impact. J. Phys. B At. Mol. Opt. Phys. 1994, 27, 4337. [Google Scholar] [CrossRef]
- Das, J.N.; Dhar Pramana, S. Symmetric scattering in electron and positron impact ionization of metastable 2s-state hydrogen atoms. J. Phys. 1996, 47, 263. [Google Scholar] [CrossRef]
- Attaourti, Y.; Taj, S. Relativistic electronic dressing in laser-assisted ionization of atomic hydrogen by electron impact. Phys. Rev. A 2004, 69, 063411. [Google Scholar] [CrossRef]
- Taj, S.; Manaut, B.; Attaourti, Y.; Elhandi, S. Instantaneous Versus Non-Instantaneous Approach to Relativistic Ionization of Atomic Hydrogen by Electron Impact. Chin. J. Phys. 2010, 48, 197–211. [Google Scholar]
- Taj, S.; Manaut, B.; El Idrissi, M.; Attaourti, Y.; Oufni, L. The Electron’s Anomalous Magnetic Moment Effects on the Laser Assisted Ionization of Atomic Hydrogen by Electronic Impact. Chin. J. Phys. 2013, 51, 945–953. [Google Scholar]
- Huang, K.N. Theoretical triply differential cross section of electron-impact ionization of atoms. Phys. Rev. A 1983, 28, 1869–1872. [Google Scholar] [CrossRef]
- Boudet, R. Violation de T et masse positive du positron. Ann. Fond. Louis de Broglie 2013, 38, 1. [Google Scholar]
- Truebenbacher, E. Dirac equation: The positron wave function and the relativistic energy-momentum operators. Am. J. Mod. Phys. 2013, 2, 38. [Google Scholar]
- Boudet, R. Quantum Mechanics in the Geometry of Space-Time: Elementary Theory; Springer-Verlag: Berlin, Germany, 2011. [Google Scholar]
- Feynman, R.P. Space-time approach to non-relativistic quantum mechanics. Rev. Mod. Phys. 1948, 20, 367–387. [Google Scholar] [CrossRef]
- Feynman, R.P. The theory of positrons. Phys. Rev. 1949, 76, 749–759. [Google Scholar] [CrossRef]
- Feynman, R.P. Space-time approach to quantum electrodynamics. Phys. Rev. 1949, 76, 769–789. [Google Scholar] [CrossRef]
- Feynman, R.P. The development of the space-time view of quantum electrodynamics. Science 1966, 153, 699–708. [Google Scholar] [CrossRef] [PubMed]
- DuBois, R.D.; de Lucio, O.G.; Santos, A.C.F. Radiation Physics Research Progress; Camilleri, A.N., Ed.; Nova Science Publishers, Inc.: Nova, NY, USA, 2008. [Google Scholar]
- Joachain, C.J.; Piraux, B. Recent progress in the theory of (e,2e) reactions. Comments in At. and Mol. Phys. 1986, 17, 261–283. [Google Scholar]






| γ | Positron triple differential cross-sections (TDCS) (a.u) | (degree) |
|---|---|---|
| 1.0053 | 4.63 × 10 | 45 |
| 2 | 1.29 × 10 | 40 |
| 3 | 4.10 × 10 | 37 |
| 4 | 5.03 × 10 | 36 |
| 5 | 2.59 × 10 | 35 |
| γ | Positron TDCS (a.u) | Electron TDCS (a.u) | Q |
|---|---|---|---|
| 1.0053 | 4.63 × 10 | 2.29 × | 2.02 |
| 2 | 1.29 × | 5.38 × | 2.39 |
| 3 | 4.10 × | 1.54 × | 2.66 |
| 4 | 5.03 × | 1.76 × | 2.85 |
| 5 | 2.59 × | 8.36 × | 3.09 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chahboune, A.; Manaut, B.; Hrour, E.; Taj, S. Relativistic Ionization of Hydrogen Atoms by Positron Impact. Atoms 2016, 4, 10. https://doi.org/10.3390/atoms4010010
Chahboune A, Manaut B, Hrour E, Taj S. Relativistic Ionization of Hydrogen Atoms by Positron Impact. Atoms. 2016; 4(1):10. https://doi.org/10.3390/atoms4010010
Chicago/Turabian StyleChahboune, Amal, Bouzid Manaut, Elmostafa Hrour, and Souad Taj. 2016. "Relativistic Ionization of Hydrogen Atoms by Positron Impact" Atoms 4, no. 1: 10. https://doi.org/10.3390/atoms4010010
APA StyleChahboune, A., Manaut, B., Hrour, E., & Taj, S. (2016). Relativistic Ionization of Hydrogen Atoms by Positron Impact. Atoms, 4(1), 10. https://doi.org/10.3390/atoms4010010