Using the Pairs of Lines Broadened by Collisions with Neutral and Charged Particles for Gas Temperature Determination of Argon Non-Thermal Plasmas at Atmospheric Pressure
Abstract
:1. Introduction
2. Method
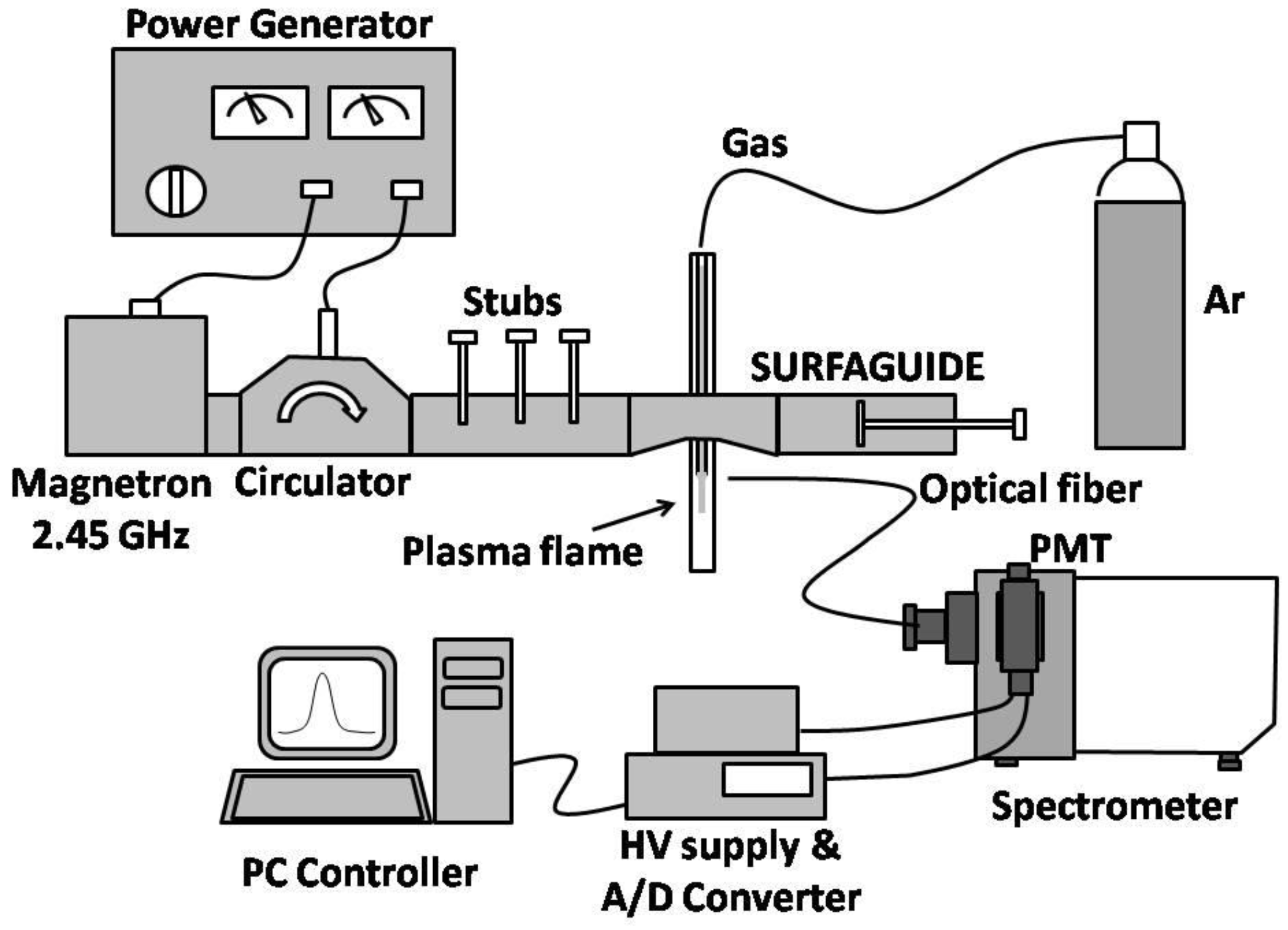
3. Experimental Set-Up
4. Results
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nassar, H.; Pellerin, S.; Mussiol, K.; Martinie, O.; Pellerin, M.N.; Cormier, J.M. N2(+)/N2 ratio and temperature 2 measurements based on the first negative N-2(+) and second positive N-2 overlapped molecular emission spectra. J. Phys. D Appl. Phys. 2004, 37, 1904. [Google Scholar] [CrossRef]
- Britun, N.; Gaillard, M.; Ricard, A.; Kim, Y.M.; Kim, K.S.; Han, H.G. Determination of the vibrational, rotational and electron temperatures in N2 and Ar-N2 rf discharge. J. Phys. D Appl. Phys. 2007, 40, 1022. [Google Scholar] [CrossRef]
- Zhu, X.M.; Chen, W.C.; Pu, Y.K. Gas temperature, electron density and electron temperature measurement in a microwave excited microplasma. J. Phys. D Appl. Phys. 2008, 41, 105212. [Google Scholar] [CrossRef]
- Wang, Q.; Koleva, I.; Donnelly, V.M.; Economou, D.J. Spatially resolved diagnostics of an atmospheric pressure direct current helium microplasma. J. Phys. D Appl. Phys. 2005, 38, 1690. [Google Scholar] [CrossRef]
- Abdallah, M.H.; Mermet, J.M. The Behavior of Nitrogen Excited in an Inductively Coupled Argon Plasma. J. Quant. Spectrosc. Radiat. Transf. 1978, 19, 83–91. [Google Scholar] [CrossRef]
- Laux, C.O.; Spence, T.G.; Kruger, C.H.; Zare, R.N. Optical diagnostics of atmospheric pressure air plasmas. Plasma Sources Sci. Technol. 2003, 12, 125. [Google Scholar] [CrossRef]
- Fantz, U. Emission spectroscopy of molecular low pressure plasmas. Contrib. Plasma Phys. 2004, 44, 508–515. [Google Scholar] [CrossRef]
- Mora, M.; García, M.C.; Jiménez-Sanchidrián, C.; Romero-Salguero, F.J. Transformation of light paraffins in a microwave-induced plasma-based reactor at reduced pressure. Int. J. Hydrog. Energy 2010, 35, 4111–4122. [Google Scholar] [CrossRef]
- Iza, F.; Hopwood, J.A. Rotational, vibrational, and excitation temperatures of a microwave-frequency microplasma. IEEE Trans. Plasma Sci. 2004, 32, 498–504. [Google Scholar] [CrossRef]
- Lombardi, G.; Benedic, F.; Mohasseb, F.; Hassouni, K.; Gicquel, A. Determination of gas temperature and C-2 absolute density in Ar/H-2/CH4 microwave discharges used for nanocrystalline diamond deposition from the C-2 Mulliken system. Plasma Sources Sci. Technol. 2004, 13, 375. [Google Scholar] [CrossRef]
- Christova, M.; Castaños-Martínez, E.; Calzada, M.D.; Kabouzi, Y.; Luque, J.M.; Moisan, M. Electron density and gas temperature from line broadening in an argon surface-wave-sustained discharge at atmospheric pressure. Appl. Spectrosc. 2004, 58, 1032–1037. [Google Scholar] [CrossRef] [PubMed]
- Christova, M.; Gagov, V.; Koleva, I. Analysis of the profiles of the argon 696.5 nm spectral line excited in non-stationary wave-guided discharges. Spectrochim. Acta B 2000, 55, 815–822. [Google Scholar] [CrossRef]
- Yubero, C.; Dimitrijevic, M.S.; García, M.C.; Calzada, M.D. Using the van der Waals broadening of the spectral atomic lines to measure the gas temperature of an argon microwave plasma at atmospheric pressure. Spectrochim. Acta B 2007, 62, 169–176. [Google Scholar] [CrossRef]
- Muñoz, J.; Dimitrijevic, M.S.; Yubero, C.; Calzada, M.D. Using the van der Waals broadening of spectral atomic lines to measure the gas temperature of an argon-helium microwave plasma at atmospheric pressure. Spectrochim. Acta B 2009, 64, 167–172. [Google Scholar] [CrossRef]
- Gigosos, M.A.; Cardeñoso, V. New plasma diagnosis tables of hydrogen Stark broadening including ion dynamics. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 4795. [Google Scholar] [CrossRef]
- Yubero, C.; Rodero, A.; Dimitrijevic, M.; Gamero, A.; García, M.C. Gas temperature determination in an argon non-thermal plasma at atmospheric pressure from broadenings of atomic emission lines. Spectrochim. Acta Part B 2017, 129, 14–20. [Google Scholar] [CrossRef]
- Zaghloul, M.R. On the calculation of the Voigt line profile: A single proper integral with a damped sine integrand MNRAS. Mon. Not. R. Astron. Soc. 2007, 375, 1043–1048. [Google Scholar] [CrossRef]
- Griem, H.R. Spectral Line Broadening by Plasmas; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Allard, N.; Kielkopf, J. The effect of neutral non resonant collisions on atomic spectral lines. Rev. Mod. Phys. 1982, 54, 1103. [Google Scholar] [CrossRef]
- Griem, H.R. Stark broadening of isolated spectral lines from heavy elements in a plasma. Phys. Rev. 1962, 128, 515–531. [Google Scholar] [CrossRef]
- Konjevic, N. Plasma broadening and shifting of non-hydrogenic spectral lines: Present status and applications. Phys. Rep. 1999, 316, 339–401. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Konjević, N. Stark broadenings of isolated spectral-lines of heavy-elements in plasmas. J. Quant. Spectrosc. Radiat. Transf. 1983, 30, 45–54. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Christova, M.; Sahal-Bréchot, S. Stark broadening of visible Ar I spectral lines. Phys. Scr. 2007, 75, 809–819. [Google Scholar] [CrossRef]
- Christova, M.; Dimitrijević, M.S.; Sahal-Bréchot, S. Stark broadening of Ar I spectral lines emitted in surface wave sustained discharges. Mem. Della Soc. Astron. Ital. Suppl. 2005, 7, 238. [Google Scholar]
- Dimitrijević, M.S. A programme to provide Stark broadening data for stellar and laboratory plasma investigations. Zh. Prikl. Spektrosk. 1996, 63, 810. [Google Scholar]
- Sahal-Bréchot, S. Théorie de l’élargissement et du déplacement des raies spectrales sous l’effect des chocs avec les électrons et les ions dans l’approximation des impacts. Astron. Astrophys. 1959, 1, 91–123. [Google Scholar]
- Moisan, M.; Etermandi, E.; Rostaing, J.C. Excitation System for a Gas Plasma Surface Wave, and Associated Gas Processing System—Has Electromagnetic Material Sleeve Surrounding Gas Circulating Tube (European Patent EP 0874 537 A1). French Patent N. 2,762,748, 1998. [Google Scholar]
- García, M.C.; Rodero, A.; Sola, A.; Gamero, A. Spectroscopic study of a stationary surface-wave sustained argon plasma column at atmospheric pressure. Spectrochim. Acta Part B 2000, 55, 1733–1745. [Google Scholar] [CrossRef]
- Santiago, I.; Christova, M.; García, M.C.; Calzada, M.D. Self-absorbing method to determine the population of the metastable levels in an argon microwave plasma at atmospheric pressure. Eur. Phys. J. Appl. Phys. 2004, 28, 325–330. [Google Scholar] [CrossRef]
- Temme, N.M. Voigt function. In NIST Handbook of Mathematical Functions; Olver Frank, W.J., Lozier, D.M., Boisvert, R.F., Eds.; Cambridge University Press: New York, NY, USA, 2010; ISBN 978-0521192255. [Google Scholar]
- Olivero, J.J.; Longbothum, R.L. Empirical fits to the Voigt line width: A brief review. J. Quant. Spectrosc. Radiat. Transf. 1977, 17, 233–236. [Google Scholar] [CrossRef]
- Ali, A.W.; Giem, H.R. Theory of Resonance Broadening of Spectral Lines by Atom-Atom Impacts. Phys. Rev. 1965, 140, 1044. [Google Scholar] [CrossRef]
- Ali, A.W.; Giem, H.R. Theory of Resonance Broadening of Spectral Lines by Atom-Atom Impacts (ERRATA). Phys. Rev. 1966, 144, 366. [Google Scholar] [CrossRef]

| Ar I Line (nm) | C | (nm) |
|---|---|---|
| 603.2 | 4.2 | 0.149 |
| 549.6 | 4.9 | 0.305 |
| 522.1 | 5.9 | 0.588 |
| 560.7 | 3.6 | 0.145 |
| 518.8 | 4.1 | 0.104 |
| z (cm) | z = 4 cm | z = 8 cm | z = 12 cm |
|---|---|---|---|
| W L603 (nm) | 0.0411 ± 0.0014 | 0.0437 ± 0.0016 | 0.0459 ± 0.0014 |
| W L549 (nm) | 0.0594 ± 0.0019 | 0.0626 ± 0.0016 | 0.0731 ± 0.0012 |
| W L522 (nm) | 0.0958 ± 0.0024 | 0.1020 ± 0.0019 | 0.122 ± 0.002 |
| W L560 (nm) | 0.0342 ± 0.0024 | 0.0377 ± 0.0024 | 0.0429 ± 0.0012 |
| W L518 (nm) | 0.0372 ± 0.0021 | 0.0418 ± 0.0016 | 0.0472 ± 0.0018 |
| z = 4 cm TBPg (K) = 1390 ± 70 | Ar I 549 nm | Ar I 522 nm | Ar I 560 nm | Ar I 518 nm |
| Ar I 603 nm | 1300 ± 300 | 1420 ± 180 | 570 ± 240 | 1100 ± 500 |
| Ar I 549 nm | - | 1800 ± 900 | 2200 ± 1300 | 1200 ± 230 |
| Ar I 522 nm | - | 2000 ± 700 | 1300 ± 200 | |
| Ar I 560 nm | - | 900 ± 300 | ||
| z = 8 cm TBPg (K) = 1330 ± 70 | Ar I 549 nm | Ar I 522 nm | Ar I 560 nm | Ar I 518 nm |
| Ar I 603 nm | 1100 ± 220 | 1300 ± 200 | 700 ± 600 | 760 ± 220 |
| Ar I 549 nm | - | 1700 ± 500 | 1400 ± 500 | 920 ± 120 |
| Ar I 522 nm | - | 1600 ± 500 | 1030 ± 110 | |
| Ar I 560 nm | - | 800 ± 300 | ||
| z = 12 cm TBPg (K) = 1520 ± 70 | Ar I 549 nm | Ar I 522 nm | Ar I 560 nm | Ar I 518 nm |
| Ar I 603 nm | 1600 ± 400 | 1680 ± 220 | 3000 ± 3000 | 500 ± 130 |
| Ar I 549 nm | - | 1800 ± 500 | 1400 ± 400 | 810 ± 110 |
| Ar I 522 nm | - | 1500 ± 300 | 930 ± 110 | |
| Ar I 560 nm | - | 640 ± 130 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yubero, C.; Rodero, A.; Dimitrijevic, M.S.; Gamero, A.; García, M.D.C. Using the Pairs of Lines Broadened by Collisions with Neutral and Charged Particles for Gas Temperature Determination of Argon Non-Thermal Plasmas at Atmospheric Pressure. Atoms 2017, 5, 41. https://doi.org/10.3390/atoms5040041
Yubero C, Rodero A, Dimitrijevic MS, Gamero A, García MDC. Using the Pairs of Lines Broadened by Collisions with Neutral and Charged Particles for Gas Temperature Determination of Argon Non-Thermal Plasmas at Atmospheric Pressure. Atoms. 2017; 5(4):41. https://doi.org/10.3390/atoms5040041
Chicago/Turabian StyleYubero, Cristina, Antonio Rodero, Milan S. Dimitrijevic, Antonio Gamero, and Maria Del Carmen García. 2017. "Using the Pairs of Lines Broadened by Collisions with Neutral and Charged Particles for Gas Temperature Determination of Argon Non-Thermal Plasmas at Atmospheric Pressure" Atoms 5, no. 4: 41. https://doi.org/10.3390/atoms5040041
APA StyleYubero, C., Rodero, A., Dimitrijevic, M. S., Gamero, A., & García, M. D. C. (2017). Using the Pairs of Lines Broadened by Collisions with Neutral and Charged Particles for Gas Temperature Determination of Argon Non-Thermal Plasmas at Atmospheric Pressure. Atoms, 5(4), 41. https://doi.org/10.3390/atoms5040041








