Review of Recent Advances in the Analytical Theory of Stark Broadening of Hydrogenic Spectral Lines in Plasmas: Applications to Laboratory Discharges and Astrophysical Objects
Abstract
:- Introduction
- Advanced Analytical Treatment of the Stark Broadening of Hydrogenic Spectral Lines by Plasma Electrons
- Center-of-Mass Effects for Hydrogen Atoms in a Nonuniform Electric Field: Applications to Magnetic Fusion, Radiofrequency Discharges, and Flare Stars.
- New Source of Shift of Hydrogenic Spectral Lines in Plasmas: Analytical Treatment of the Effect of Penetrating Ions
- Revision of the Method for Measuring the Electron Density Based on the Asymmetry of Hydrogenic Spectral Lines in Dense Plasmas
- Lorentz–Doppler Broadening of Hydrogen/Deuterium Spectral Lines: Analytical Solution for Any Angle of Observation and any Magnetic Field Strength, and Its Applications to Magnetic Fusion and Solar Physics
- Revision of the Inglis-Teller Diagnostic Method
- Stark Broadening of Hydrogen/Deuterium Spectral Lines by a Relativistic Electron Beam: Analytical Results and Applications to Magnetic Fusion
- Influence of Magnetic-Field-Caused Modifications of Trajectories of Plasma Electrons on Shifts and Relative Intensities of Zeeman Components of Hydrogen/Deuterium Spectral Lines: Applications to Magnetic Fusion and White Dwarfs
- Influence of Magnetic-Field-Caused Modifications of trajectoRies of Plasma Electrons on the Width of Hydrogen/Deuterium Spectral Lines: Applications to White Dwarfs
- Stark Broadening of Hydrogen Lines in Plasmas of Electron Densities up to or More Than Ne~1020 cm−3
- The Shape of Spectral Lines of Two-Electron Rydberg Atoms/Ions: A Peculiar Stark Broadening
- Conclusions
1. Introduction
2. Advanced Analytical Treatment of the Stark Broadening of Hydrogenic Spectral Lines by Plasma Electrons
3. Center-of-Mass Effects for Hydrogen Atoms in a Nonuniform Electric Field: Applications to Magnetic Fusion, Radiofrequency Discharges, and Flare Stars
4. New Source of Shift of Hydrogenic Spectral Lines in Plasmas: Analytical Treatment of the Effect of Penetrating Ions
4.1. Preamble
4.2. “Standard” Shifts of Hydrogenic Spectral Lines
4.3. New Source of the Red Shift and the Comparison with Experiments/Observations
- For the SL H13, there is an excellent agreement between the total theoretical shift Stot and the experimental shift Sexp. No data for the shift of this SL from Sirius.
- For the SL H14, there is a good agreement of the total theoretical shift with the shift of this SL observed from Sirius and a satisfactory agreement (within the error margins) with the experimental shift of this SL.
- For the SL H15, there is a good agreement of the total theoretical shift with the shift of this SL observed from Sirius and a satisfactory agreement (almost within the error margins) with the experimental shift of this SL.
- For the SL H16, there is a satisfactory agreement (within the error margins) of the total theoretical shift with both the shift of this SL as observed from Sirius and the experimental shift of this SL.
- For the SL H17, there is a satisfactory agreement (within the error margins) of the total theoretical shift with the shift of this SL observed from Sirius, but a disagreement with the experimental shift of this SL; however, the latter disagreement is not anymore by two orders of magnitude, as it was the case before the allowance for the shift by penetrating ions, but rather just by a factor of two (after allowing for the error margins).
5. Revision of the Method for Measuring the Electron Density Based on the Asymmetry of Hydrogenic Spectral Lines in Dense Plasmas
- -
- the theoretical degree of asymmetry ρact calculated with the allowance for penetrating ions,
- -
- the theoretical degree of asymmetry ρquad calculated without the allowance for penetrating ions,
- -
- the electron density Ne,quad that would be deduced from the experimental asymmetry degree while disregarding the contribution of the penetrating ions, and
- -
- the relative error |Ne,quad–Ne,act|/Ne,act in determining the electron density from the experimental asymmetry degree while disregarding the contribution of the penetrating ions.
6. Lorentz–Doppler Broadening of Hydrogen/Deuterium Spectral Lines: Analytical Solution for Any Angle of Observation and Any Magnetic Field Strength, and Its Applications to Magnetic Fusion and Solar Physics
6.1. Preamble
6.2. Analytical Results
6.3. Validity and Applications
7. Revision of the Inglis-Teller Diagnostic Method
8. Stark Broadening of Hydrogen/Deuterium Spectral Lines by a Relativistic Electron Beam: Analytical Results and Applications to Magnetic Fusion
8.1. Preamble
8.2. Analytical Results and Applications to Magnetic Fusion
9. Influence of Magnetic-Field-Caused Modifications of Trajectories of Plasma Electrons on Shifts and Relative Intensities of Spectral Line Components: Applications to Magnetic Fusion and White Dwarfs
10. Influence of Magnetic-Field-Caused Modifications of Trajectories of Plasma Electrons on Shifts and Relative Intensities of Zeeman Components of Hydrogen/Deuterium Spectral Lines: Applications to Magnetic Fusion and White Dwarfs
10.1. Preamble
10.2. Analytical Results
K1[(vp2/vz2)1/2]2}
10.3. Comparison with the Existing Simulation
10.4. Closing Remarks
- -
- the overestimation of the Stark width by up to one order of magnitude for the alpha- and beta-lines of the Lyman and Balmer series;
- -
- the underestimation of the Stark width by several times for the delta- and higher-lines of the Balmer series.
11. Stark Broadening of Hydrogen Lines in Plasmas of Electron Densities up to or More than Ne~1020 cm−3
11.1. Preamble
11.2. Theory and the Comparison with the Experiment
11.3. Closing Remarks
12. The Shape of Spectral Lines of Two-Electron Rydberg Atoms/Ions: A Peculiar Stark Broadening
12.1. Preamble
12.2. Instantaneous Eigenvalues (“Energies”) and Instantaneous Eigenfunctions of the Inner Electron
12.3. Spectral Lineshape
12.4. Closing Remarks
13. Conclusions
13.1. Fundamental Results for Atomic Physics
13.2. Fundamental Results for Plasma Spectroscopy
13.3. Practical Applications
Conflicts of Interest
References
- Oks, E. Plasma Spectroscopy: The Influence of Microwave and Laser Fields; Series on Atoms and Plasmas; Springer: New York, NY, USA, 1995; Volume 9. [Google Scholar]
- Griem, H.R. Principles of Plasma Spectroscopy; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Salzman, D. Atomic Physics in Hot Plasmas; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Fujimoto, T. Plasma Spectroscopy; Clarendon Press: Oxford, UK, 2004. [Google Scholar]
- Oks, E. Stark Broadening of Hydrogen and Hydrogenlike Spectral Lines in Plasmas: The Physical Insight; Alpha Science International: Oxford, UK, 2006. [Google Scholar]
- Kunze, H.-J. Introduction to Plasma Spectroscopy; Springer: Berlin, Germany, 2009. [Google Scholar]
- Oks, E. Diagnostics of Laboratory and Astrophysical Plasmas Using Spectral Lines of One-, Two-, and Three-Electron Systems; World Scientific: Hackensack, NJ, USA, 2017. [Google Scholar]
- Lisitsa, V.S. Stark broadening of hydrogen lines in plasmas. Sov. Phys. Uspekhi 1977, 122, 603. [Google Scholar] [CrossRef]
- Post, D.E.; Votta, L.G. Computational science demand a new paradigm. Phys. Today 2005, 58, 35–41. [Google Scholar] [CrossRef]
- Oks, E. Theories, experiments, and simulations of spectral line shapes: Pitfalls in the network. AIP Conf. Proc. 2010, 1290, 6–13. [Google Scholar]
- Griem, H.R.; Shen, K.Y. Stark broadening of hydrogenic ion lines in a plasma. Phys. Rev. 1961, 122, 1490–1496. [Google Scholar] [CrossRef]
- Griem, H.R. Plasma Spectroscopy; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Griem, H.R. Spectral Line Broadening by Plasmas; Academic Press: Cambridge, MA, USA, 1974; Chapter II.3b. [Google Scholar]
- Sanders, P.; Oks, E. Allowance for more realistic trajectories of plasma electrons in the Stark broadening of hydrogenlike spectral lines. J. Phys. Commun. 2018, 2, 035033. [Google Scholar] [CrossRef] [Green Version]
- Galitski, V.; Karnakov, B.; Kogan, V.; Galitski, V., Jr. Exploring Quantum Mechanics; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Kotkin, G.L.; Serbo, V.G. Collection of Problems in Classical Mechanics; 1971; Pergamon: Oxford, UK, problem 2.3. [Google Scholar]
- Oks, E. Center-of-mass effects for hydrogen atoms in a nonuniform electric field: Applications to magnetic fusion, radiofrequency discharges, and flare stars. J. Phys. Commun. 2018, 2, 045005. [Google Scholar] [CrossRef]
- Kotkin, G.L.; Serbo, V.G. Collection of Problems in Classical Mechanics; Pergamon: Oxford, UK, 1971; problem 2.22. [Google Scholar]
- Fox, K. Classical motion of an electron in an electric-dipole field II. Point dipole case. J. Phys. A 1968, 1, 124–127. [Google Scholar] [CrossRef]
- Abramov, V.A.; Lisitsa, V.S. Sov. J. Plasma Phys. 1977, 3, 451.
- Seidel, J. Hydrogen stark broadening by ion impacts on moving emitters. Z. Naturforsch. 1979, 34, 1385–1397. [Google Scholar] [CrossRef]
- Stehle, C.; Feautrier, N. Stark broadening of the Hα line of hydrogen at low densities: Quantal and semiclassical results. J. Phys. B 1984, 17, 1477–1490. [Google Scholar] [CrossRef]
- Derevianko, A.; Oks, E. Generalized theory of ion impact broadening in magnetized plasmas and its applications for tokamaks. Phys. Rev. Lett. 1994, 73, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- Derevianko, A.; Oks, E. Ion impacts on moving emitters: A convergent theory of anisotropic broadening in high-temperature plasmas. J. Quant. Spectr. Radiat. Transf. 1995, 54, 137–142. [Google Scholar] [CrossRef]
- Derevianko, A.; Oks, E. Dual purpose diagnostics of edge plasmas of tokamaks based on a novel spectroscopic effect. Rev. Sci. Instrum. 1997, 68, 998–1001. [Google Scholar] [CrossRef]
- Kolb, A.C.; Griem, H.R. Theory of line broadening in multiplet spectra. Phys. Rev. 1958, 111, 514–521. [Google Scholar] [CrossRef]
- Baranger, M. Problem of overlapping lines in the theory of pressure broadening. Phys. Rev. 1958, 111, 494–504. [Google Scholar] [CrossRef]
- Kepple, P.; Griem, H.R. Improved stark profile calculations for the hydrogen lines Hα, Hβ, Hγ, and Hδ. Phys. Rev. 1968, 173, 317–325. [Google Scholar] [CrossRef]
- Griem, H.R. Spectral Line Broadening by Plasmas; Academic Press: Cambridge, MA, USA, 1974; Chapter II.3a. [Google Scholar]
- Pospieszczyk, A. Spectroscopic diagnostics of tokamak edge plasmas. Phys. Scr. 2005, 2005, 71–82. [Google Scholar] [CrossRef]
- Gershberg, R.E. Solar-Type Activity in Main-Sequence Stars; Springer: Berlin, Germany, 2005. [Google Scholar]
- Oks, E.; Gershberg, R.E. Flare stars—A favorable object for studying mechanisms of nonthermal astrophysical phenomena. Astrophys. J. 2016, 819, 16. [Google Scholar] [CrossRef]
- Bengston, R.D.; Tannich, J.D.; Kepple, P. Comparison between measured and theoretical stark-broadened profiles of H6–H12 emitted from a low-density plasma. Phys. Rev. A 1970, 1, 532–533. [Google Scholar]
- Bengtson, R.D.; Chester, G.R. Observation of shifts of hydrogen lines. Astrophys. J. 1972, 178, 565–569. [Google Scholar] [CrossRef]
- Himmel, G. Plasma effects in the spectrum of high Balmer lines. J. Quant. Spectrosc. RadIAT. Transf. 1976, 16, 529–536. [Google Scholar] [CrossRef]
- Nussbaumer, H.; Bieri, L. Discovering the Expanding Universe; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Parigger, C.G.; Plemmons, D.H.; Oks, E. Balmer series H-beta measurements in a laser-induced hydrogen plasma. Appl. Opt. 2003, 42, 5992–6000. [Google Scholar] [CrossRef] [PubMed]
- Oks, E. New source of the red shift of highly-excited hydrogenic spectral lines in astrophysical and laboratory plasmas. J. Astrophys. Aerosp. Technol. 2017, 5. [Google Scholar] [CrossRef]
- Sanders, P.; Oks, E. Estimate of the Stark shift by penetrating ions within the nearest perturber approximation for hydrogenlike spectral lines in plasmas. J. Phys. B 2017, 50, 245002. [Google Scholar] [CrossRef] [Green Version]
- Pittman, T.L.; Fleurier, C. Plasma shifts of the He II Hα and Pα lines. Phys. Rev. A 1986, 33, 1291–1296. [Google Scholar] [CrossRef]
- Griem, H.R. Shift of hydrogen lines from electron collisions in dense plasmas. Phys. Rev. A 1983, 28, 1596–1601. [Google Scholar] [CrossRef]
- Boercker, D.B.; Iglesias, C.A. Static and dynamic shifts of spectral lines. Phys. Rev. A 1984, 30, 2771–2774. [Google Scholar] [CrossRef]
- Griem, H.R. Shift of hydrogen and ionized-helium lines from Δn = 0 interactions with electrons in dense plasmas. Phys. Rev. A 1988, 38, 2943–2952. [Google Scholar] [CrossRef]
- Renner, O.; Salzmann, D.; Sondhauss, P.; Djaoui, A.; Krousky, E.; Förster, E. Experimental evidence for plasma shifts in Lyman series of aluminum. J. Phys. B 1998, 31, 1379–1390. [Google Scholar] [CrossRef]
- Berg, H.F.; Ali, A.W.; Lincke, R.; Griem, H.R. Measurements of Stark profiles of neutral and ionized helium and hydrogen lines from shock-heated plasmas in electromagnetic T tubes. Phys. Rev. 1962, 125, 199–206. [Google Scholar] [CrossRef]
- Oks, E. New type of shift of hydrogen- and hydrogenlike spectral lines. J. Quant. Spectrosc. Radiat. Transf. 1997, 58, 821–826. [Google Scholar] [CrossRef]
- Könies, A.; Günter, S. Asymmetry and shifts of the Lα- and Lβ-lines of hydrogen. J. Quant. Spectrosc. Radiat. Transf. 1994, 52, 825–830. [Google Scholar] [CrossRef]
- Günter, S.; Könies, A. Shifts and asymmetry parameters of hydrogen Balmer lines on dense plasmas. Phys. Rev. E 1977, 55, 907–911. [Google Scholar] [CrossRef]
- Demura, A.V.; Helbig, V.; Nikolic, D. Spectral Line Shapes, 16th ICSLS; Back, C.A., Ed.; AIP Conference Proceedings; American Institute of Physics: New York, NY, USA, 2002; Volume 645. [Google Scholar]
- Sholin, G.V. On the nature of the asymmetry of the spectral line profiles of hydrogen in dense plasmas. Opt. Spectosc. 1969, 26, 275–282. [Google Scholar]
- Komarov, I.V.; Ponomarev, L.I.; Yu, S. Slavyanov, Spheroidal and Coulomb Spheroidal Functions; Nauka: Moscow, Russia, 1976. [Google Scholar]
- Held, B. Electric microfield distribution in multicomponent plasmas. J. Phys. 1984, 45, 1731–1750. [Google Scholar] [CrossRef]
- Held, B.; Deutsch, C.; Gombert, M.-M. Low-frequency electric microfield in dense and hot multicomponent plasmas. Phys. Rev. A 1984, 29, 880–895. [Google Scholar] [CrossRef]
- Podder, N.K.; Clothiaux, E.J.; Oks, E. A method for density measurements employing an asymmetry of lineshapes in dense plasmas and its implementation in a vacuum spark discharge. J. Quant. Spectrosc. Radiat. Transf. 2000, 65, 441–453. [Google Scholar] [CrossRef]
- Parigger, C.G.; Swafford, L.D.; Woods, A.C.; Surmick, D.M.; Witte, M.J. Asymmetric hydrogen beta electron density diagnostics of laser-induced plasma. Spectrochim. Acta Part B 2014, 99, 28–33. [Google Scholar] [CrossRef]
- Sanders, P.; Oks, E. Improving the method of measuring the electron density via the asymmetry of hydrogenic spectral lines in plasmas by allowing for penetrating ions. Atoms 2018, 6, 21. [Google Scholar] [CrossRef]
- Oks, E.; Uzer, T. A robust perturbation theory for degenerate states based on exact constants of the motion. Europhys. Lett. 2000, 49, 554–557. [Google Scholar] [CrossRef]
- Kryukov, N.; Oks, E. Super-generalized Runge-Lenz vector in the problem of two Coulomb or Newton centers. Phys. Rev. A 2012, 85. [Google Scholar] [CrossRef]
- Oks, E. Role of Lorentz-Stark broadening of hydrogen spectral lines in magnetized plasmas: Applications to magnetic fusion and solar physics. J. Quant. Spectr. Radiat. Transf. 2015, 156, 24–35. [Google Scholar] [CrossRef]
- Welch, B.L.; Griem, H.R.; Terry, J.; Kurz, C.; LaBombard, B.; Lipschultz, B.; Marmar, E.; McCracken, J. Density measurements in the edge, divertor, and X-point regions of Alcator C-Mod from Balmer series emission. Phys. Plasmas 1995, 2, 4246–4251. [Google Scholar] [CrossRef]
- Brooks, N.H.; Lisgo, S.; Oks, E.; Volodko, D.; Groth, M.; Leonard, A.W.; DIII-D Team. Benchmarking of alternate theories for Stark broadening against experimental data from DIII-D diagnostics. Plasma Phys. Rep. 2009, 35, 112–117. [Google Scholar] [CrossRef]
- Oks, E. Atomic Processes in Basic and Applied Physics; Shevelko, V., Tawara, H., Eds.; Springer: Heidelberg, Germany, 2012; Chapter 15. [Google Scholar]
- Oks, E.; Bengtson, R.D.; Touma, J. Application of the generalized theory of Stark broadening to experimental highly-excited Balmer lines from a radio-frequency discharge. Contrib. Plasma Phys. 2000, 40, 158–161. [Google Scholar] [CrossRef]
- Feldman, U.; Doschek, G.A. The emission spectrum of the hydrogen Balmer series observed above the solar limb from SKYLAB. II. Active regions. Astrophys. J. 1977, 212, 913–922. [Google Scholar] [CrossRef]
- Galushkin, Y.I. Electrodynamic broadening of the spectral lines with the linear Stark effect. Sov. Astron. 1970, 14, 301–309. [Google Scholar]
- Sanders, P.; Oks, E. Lorentz–Doppler profiles of hydrogen/deuterium lines for magnetic fusion: Analytical solution for any angle of observation and any magnetic field strength. J. Phys. Commun. 2017, 1, 055011. [Google Scholar] [CrossRef]
- Neu, R.; Summers, H.P.; Ralchenko, Y. Spectroscopic diagnostics of magnetic fusion plasmas. J. Phys. B 2010, 43, 140201. [Google Scholar] [CrossRef] [Green Version]
- Rosenberg, F.D.; Feldman, U.; Doschek, G.A. The emission spectrum of the hydrogen Balmer series observed above the solar limb from SKYLAB. I. A quiet Sun and a polar coronal hole. Astrophys. J. 1977, 212, 905–912. [Google Scholar] [CrossRef]
- Inglis, D.R.; Teller, E. Ionic depression of series limits in one-electron spectra. Astrophys. J. 1939, 90, 439–448. [Google Scholar] [CrossRef]
- Hey, J. Does atomic polarizability play a role in hydrogen radiorecombination spectra from Galactic H II regions? J. Phys. B 2013, 46, 175702. [Google Scholar] [CrossRef]
- Oks, E. Aspects of Lorentz-Stark broadening of hydrogen spectral lines in magnetized, turbulent and non-turbulent plasmas important for magnetic fusion and solar physics Intern. Rev. Atom. Mol. Phys. 2013, 4, 105–119. [Google Scholar]
- Rosato, J.; Marandet, Y.; Stamm, R. Stark broadening by Lorentz fields in magnetically confined plasmas. J. Phys. B 2014, 47, 105702. [Google Scholar] [CrossRef]
- Guenot, D.; Gustas, D.; Vernier, A.; Beaurepaire, B.; Böhle, F.; Bocoum, M.; Losano, M.; Jullien, A.; Lopez-Martins, A.; Lifschitz, A.; et al. Relativistic electron beams driven by kHzsingle cycle light pulses. Nat. Photonics 2017, 11, 293–296. [Google Scholar] [CrossRef]
- Kurkin, S.A.; Hramov, A.E.; Koronovskii, A.A. Microwave radiation power of relativistic electron beam with virtual cathode in the external magnetic field. Appl. Phys. Lett. 2013, 103, 043507. [Google Scholar] [CrossRef]
- De Jagher, P.C.; Sluijter, F.W.; Hopman, H.J. Relativistic electron beams and beam-plasma interactions. Phys. Rep. 1988, 167, 177–239. [Google Scholar] [CrossRef]
- Boozer, A.H. Runaway electrons and ITER. Nucl. Fusion 2017, 57, 056018. [Google Scholar] [CrossRef] [Green Version]
- Decker, J.; Hirvijoki, E.; Embreus, O.; Peysson, Y.; Stahl, A.; Pusztai, I.; Fülöp, T. Numerical characterization of bump formation in the runaway electron tail. Plasma Phys. Control. Fusion 2016, 58, 025016. [Google Scholar] [CrossRef]
- Smith, H.; Helander, P.; Eriksson, L.-G.; Anderson, D.; Lisak, M.; Andersson, F. Runaway electrons and the evolution of the plasma current in tokamak disruptions. Phys. Plasmas 2006, 13, 102502. [Google Scholar] [CrossRef]
- Minashin, P.V.; Kukushkin, A.B.; Poznyak, V.I. Reconstruction of superthermal electron velocity distribution function from electron cyclotron spectra at down-shifted frequencies in tokamak T-10. Eur. Phys. J. Conf. 2012, 32, 01015. [Google Scholar] [CrossRef] [Green Version]
- Kurzan, B.; Steuer, K.-H.; Suttrop, W. Runaway electrons in a tokamak: A free-electron maser. Rev. Sci. Instrum. 1997, 68, 423–426. [Google Scholar] [CrossRef]
- Ide, S.; Ogura, K.; Tanaka, H.; Iida, M.; Hanada, K.; Itoh, T.; Iwamasa, M.; Sakakibara, H.; Minami, T.; Yoshida, M.; et al. Investigation of high energy electrons in lower hybrid current drive plasma with electron cyclotron emission measurement in the WT-3 tokamak. Nucl. Fusion 1989, 29, 1325–1338. [Google Scholar] [CrossRef]
- Oks, E.; Sanders, P. Stark broadening of hydrogen/deuterium spectral lines by a relativistic electron beam: Analytical results and possible applications to magnetic fusion edge plasmas. J. Phys. Commun. 2018, 2, 015030. [Google Scholar] [CrossRef]
- Rosato, J.; Pandya, S.P.; Logeais, C.; Meireni, M.; Hannachi, I.; Reichle, R.; Barnsley, R.; Marandet, Y.; Stamm, R. A study for Stark broadening for the diagnostic of runaway electrons in ITER. AIP Conf. Proc. 2017, 1811, 110001. [Google Scholar] [CrossRef]
- Ispolatov, Y.; Oks, E. A convergent theory of Stark broadening of hydrogen lines in dense plasmas. J. Quant. Spectrosc. Radiat. Transf. 1994, 51, 129–138. [Google Scholar] [CrossRef]
- Krasovitskiy, V.B. Instabilities of Relativistic Electron Beam in Plasma; Nova Publishers: New York, NY, USA, 2008. [Google Scholar]
- Gavrilenko, V.P.; Oks, E. A new effect in the Stark spectroscopy of atomic Hydrogen: Dynamic resonance. Sov. Phys. JETP 1981, 53, 1122–1127. [Google Scholar]
- Dalimier, E.; Oks, E.; Renner, O. Review of Langmuir-wave-caused dips and charge-exchange-caused dips in spectral lines from plasmas and their applications. Atoms 2014, 2, 178–194. [Google Scholar] [CrossRef]
- Dalimier, E.; Faenov, A.Y.; Oks, E.; Angelo, P.; Pikuz, T.A.; Fukuda, Y.; Andreev, A.; Koga, J.; Sakaki, H.; Kotaki, H.; et al. X-ray spectroscopy of super-intense laser-produced plasmas for the study of nonlinear processes. Comparison with PIC simulations. J. Phys. Conf. Ser. 2017, 810, 012004. [Google Scholar] [CrossRef] [Green Version]
- Dalimier, E.; Oks, E.; Renner, O. Dips in spectral line profiles and their applications in plasma physics and atomic physics. AIP Conf. Proc. 2017, 1811. [Google Scholar] [CrossRef]
- Oks, E.; Böddeker, S.; Kunze, H.-J. Spectroscopy of atomic hydrogen in dense plasmas in the presence of dynamic fields: Intra-Stark spectroscopy. Phys. Rev. A 1991, 44, 8338–8347. [Google Scholar] [CrossRef] [PubMed]
- Renner, O.; Dalimier, E.; Oks, E.; Krasniqi, F.; Dufour, E.; Schott, R.; Foerster, E. Experimental evidence of Langmuir-wave-caused features in spectral lines of laser-produced plasmas. J. Quant. Spectr. Radiat. Transf. 2006, 99, 439–450. [Google Scholar] [CrossRef]
- Oks, E.; Dalimier, E.; Faenov, A.Y.; Pikuz, T.; Fukuda, Y.; Jinno, S.; Sakaki, H.; Kotaki, H.; Pirozhkov, A.; Hayashi, Y.; et al. Two-plasmon decay instability’s signature in spectral lines and spectroscopic measurements of charge exchange rate in a femtosecond laser-driven cluster-based plasma. Fast Track Communications. J. Phys. B 2014, 47, 221001. [Google Scholar] [CrossRef]
- Oks, E.; Dalimier, E.; Faenov, A.Y.; Angelo, P.; Pikuz, S.A.; Tubman, E.; Butler, N.M.H.; Dance, R.J.; Pikuz, T.A.; Skobelev, I.Y.; et al. Using X-ray spectroscopy of relativistic laser plasma interaction to reveal parametric decay instabilities: A modeling tool for astrophysics. Opt. Express 2017, 25, 1958–1972. [Google Scholar] [CrossRef] [PubMed]
- Wagner, U.; Tatarakis, M.; Gopal, A.; Beg, F.N.; Clark, E.L.; Dangor, A.E.; Evans, R.G.; Haines, M.G.; Mangles, S.P.D.; Norreys, P.A.; et al. Laboratory measurements of 0.7 GG magnetic fields generated during high intensity laser interactions with dense plasmas. Phys. Rev. E 2004, 70. [Google Scholar] [CrossRef] [PubMed]
- Fujioka, S.; Zhang, Z.; Ishihara, K.; Shigemori, K.; Hironaka, Y.; Johzaki, T.; Sunahara, A.; Yamamoto, N.; Nakashima, H.; Watanabe, T.; et al. Kilotesla magnetic field due to a capacitor-coil target driven byhigh power laser. Sci. Rep. 2013, 3, 1170. [Google Scholar] [CrossRef] [PubMed]
- Silvers, L.J. Magnetic fields in astrophysical objects. Phil. Trans. R. Soc. A 2008, 366, 4453–4464. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schekochihin, A.A.; Cowley, S.C.; Yousef, T.A. MHD turbulence: Nonlocal, anisotropic, nonuniversal? In Magnetohydrodynamics—Historical Evolution and Trends; Molokov, S., Moreau, R., Moffett, H.K., Eds.; Springer: Berlin, Germany, 2007. [Google Scholar]
- Oks, E. Influence of magnetic-field-caused modifications of trajectories of plasma electrons on spectral line shapes: Applications to magnetic fusion and white dwarfs. J. Quant. Spectrosc. Radiat. Transf. 2016, 171, 15–27. [Google Scholar] [CrossRef]
- Tremblay, P.-E.; Bergeron, P. Spectroscopic analysis of DA white dwarfs: Stark broadening of hydrogen lines including non-ideal effects. Astrophys. J. 2009, 696, 1755–1770. [Google Scholar] [CrossRef]
- Oks, E.; Rantsev-Kartinov, V.A. Spectroscopic observation and analysis of plasma turbulence in a Z-pinch. Sov. Phys. JETP 1980, 52, 50–58. [Google Scholar]
- Oks, E. Effect of helical trajectories of electrons in strongly magnetized plasmas on the width of hydrogen/deuterium spectral lines: Analytical results and applications to white dwarfs. Int. Rev. At. Mol. Phys. 2017, 8, 61–72. [Google Scholar]
- Oks, E. Latest advances in the semiclassical theory of the Stark broadening of spectral lines in plasmas. J. Phys. Conf. Ser. 2017, 810, 012006. [Google Scholar] [CrossRef] [Green Version]
- Oks, E. Refinement of the semiclassical theory of the Stark broadening of hydrogen spectral lines in plasmas. J. Quant. Spectrosc. Radiat. Transf. 2015, 152, 74–83. [Google Scholar] [CrossRef]
- Franzon, B.; Schramm, S. Effect of the magnetic field in white dwards. J. Phys. Conf. Ser. 2017, 861, 012015. [Google Scholar] [CrossRef]
- Reimers, D.; Jordan, S.; Koester, D.; Bade, N.; Köhler, T.; Wisotzki, L. Discoveryof four white dwarfs with strong magnetic fields by the Hamburg/ESO survey. Astron. Astrophys. 1996, 311, 572–578. [Google Scholar]
- Rosato, J.; Ferri, S.; Stamm, R. Influence of helical trajectories of perturbers on Stark line shapes in magnetized plasmas. Atoms 2018, 6, 12. [Google Scholar] [CrossRef]
- Rosato, J.; Capes, H.; Godbert-Mouret, L.; Koubiti, M.; Marandet, Y.; Stamm, R. Accuracy of impact broadening models in low-density magnetized hydrogen plasmas. J. Phys. B 2012, 45, 165701. [Google Scholar] [CrossRef] [Green Version]
- Sholin, G.V.; Demura, A.V.; Lisitsa, V.S. Theory of Stark broadening of hydrogen lines in plasmas. Sov. Phys. JETP 1973, 37, 1057–1065. [Google Scholar]
- Kielkopf, J.F.; Allard, N.F. Shift and width of the Balmer series Hα line at high electron density in a laser-produced plasma. J. Phys. B 2014, 47, 155701. [Google Scholar] [CrossRef]
- Büscher, S.; Wrubel, T.; Ferri, S.; Kunze, H.-J. The Stark width and shift of the hydrogen Hα line. J. Phys. B 2002, 35, 2889–2897. [Google Scholar] [CrossRef]
- Böddeker, S.; Günter, S.; Könies, A.; Hitzschke, L.; Kunze, H.-J. Shift and width of the Hα line of hydrogen in dense plasmas. Phys. Rev. E 1993, 47, 2785–2791. [Google Scholar] [CrossRef]
- Flih, S.A.; Oks, E.; Vitel, Y. Comparison of the Stark widths and shifts of the H-alpha line measured in a flash tube plasma with theoretical results. J. Phys. B 2003, 36, 283–296. [Google Scholar] [CrossRef]
- Gigosos, M.A.; Cardenoso, V. New plasma diagnosis tables of hydrogen Stark broadening including ion dynamics. J. Phys. B 1996, 29, 4795–4838. [Google Scholar] [CrossRef]
- Gigosos, M.A. Stark broadening models for plasma diagnostics. J. Phys. D 2014, 47, 343001. [Google Scholar] [CrossRef]
- Oks, E. Effect of thermal collective modes on the Stark broadening of hydrogen spectral lines in strongly coupled plasmas. J. Phys. B 2016, 49, 065701. [Google Scholar] [CrossRef]
- Antonov, A.S.; Zinov’ev, O.A.; Rusanov, V.D.; Titov, A.V. Broadening of hydrogen spectral lines during turbulent heating of a plasma. Sov. Phys. JETP 1970, 31, 838–839. [Google Scholar]
- Zagorodnikov, S.P.; Smolkin, G.E.; Striganova, E.A.; Sholin, G.V. Determination of the turbulence level in a collisionless magnetosonic shock wave by measuring the Stark broadening of the Balmer Hβ line. JETP Lett. 1970, 11, 323–326. [Google Scholar]
- Zagorodnikov, S.P.; Smolkin, G.E.; Striganova, E.A.; Sholin, G.V. A method of measurement of nonequilibrium electric fields in turbulent plasma based on Stark broadening of hydrogen spectral lines. Sov. Phys. Dokl. 1970, 195, 1065–1068. [Google Scholar]
- Zavojskij, E.K.; Kalinin, Y.G.; Skorjupin, V.A.; Shapkin, V.V.; Sholin, G.V. Measurement of electric fields in turbulent plasma based on Stark broadening of hydrogen spectral lines. Sov. Phys. Dokl. 1970, 194, 55–58. [Google Scholar]
- Zavojskij, E.K.; Kalinin, Y.G.; Skorjupin, V.A.; Shapkin, V.V.; Sholin, G.V. Observation of asymmetry of the distribution of turbulent electric fields in a direct discharge pIasma by means of the polarization in the Stark profile of the Hα line. JETP Lett. 1970, 13, 12–14. [Google Scholar]
- Levine, M.A.; Gallagher, C.C. Stark broadening for turbulence studies in a confined plasma. Phys. Lett. 1970, A32, 14–15. [Google Scholar] [CrossRef]
- Ben-Yosef, N.; Rubin, A.G. Optical investigations of electrostatic turbulence in plasmas. Phys. Lett. 1970, A33, 222–223. [Google Scholar] [CrossRef]
- Zakatov, I.P.; Plakhov, A.G.; Shapkin, V.V.; Sholin, G.V. Measurement of noise level of Langmuir oscillations in the plasma—Beam system according to Stark broadening of hydrogen spectral lines. Sov. Phys. Dokl. 1971, 198, 1306–1309. [Google Scholar]
- Berezin, A.B.; Dubovoj, A.V.; Ljublin, B.V. Sov. Phys. Tech. Phys. 1971, 41, 2323.
- Babykin, M.V.; Zhuzhunashvili, A.I.; Oks, E.; Shapkin, V.V.; Sholin, G.V. Polarization spectroscopic analysis of noise produced in a turbulent plasma upon annihilation of oppositely moving magnetic fields. Sov. Phys. JETP 1974, 38, 86–92. [Google Scholar]
- Volkov, Y.F.; Djatlov, V.G.; Mitina, A.I. Sov. Phys. Tech. Phys. 1974, 44, 1448.
- Zhuzhunashvili, A.I.; Oks, E. Technique of optical polarization measurements of the plasma Langmuir turbulence spectrum. Sov. Phys. JETP 1977, 46, 1122–1132. [Google Scholar]
- Berezin, A.B.; Ljublin, B.V.; Jakovlev, D.G. Sov. Phys. Tech. Phys. 1983, 53, 642.
- Koval, A.N.; Oks, E. Some results of searching for low-frequency plasma turbulence in large chromospheric flares. Bull. Crimean Astrophys. Obs. 1983, 67, 78–89. [Google Scholar]
- Bohm, D.; Pines, D. A collective description of electron interactions: III. Coulomb interactions in a degenerate electron gas. Phys. Rev. 1953, 92, 609–625. [Google Scholar] [CrossRef]
- Oks, E.; Sholin, G.V. On Stark profiles of hydrogen lines in a plasma with low-frequency turbulence. Sov. Phys. Tech. Phys. 1977, 21, 144–151. [Google Scholar]
- Iglesias, C.A.; DeWitt, H.E.; Lebowitz, J.L.; MacGowan, D.; Hubbard, W.B. Low-frequency electric microfield distributions in plasmas. Phys. Rev. A 1985, 31, 1698–1702. [Google Scholar] [CrossRef]
- Oks, E.; Sholin, G.V. On Stark profiles of hydrogen spectral lines in a plasma with Langmuir Turbulence. Sov. Phys. JETP 1975, 41, 482–490. [Google Scholar]
- Huba, J.D. NRL Plasma Formulary; Naval Research Laboratory: Washington, DC, USA, 2013. [Google Scholar]
- Bellan, P.M. Fundamentals of Plasma Physics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Kadomtsev, B.B. Collective Phenomena in Plasma; Nauka: Moscow, Russia, 1988. [Google Scholar]
- Spitzer, L. Stark-effect broadening of hydrogen lines. Phys. Rev. 1939, 55, 699–708. [Google Scholar] [CrossRef]
- Spitzer, L. Stark-effect broadening of hydrogen lines. II. Observable profiles. Phys. Rev. 1939, 56, 39–47. [Google Scholar] [CrossRef]
- Spitzer, L. Impact broadening of spectral lines. Phys. Rev. 1940, 58, 348–357. [Google Scholar] [CrossRef]
- Ishimura, T. Stark effect of the Lymann alpha line by a rotating electric field. J. Phys. Soc. Jpn. 1967, 23, 422–429. [Google Scholar] [CrossRef]
- Lisitsa, V.S. Hydrogen atom in a rotating electric field. Opt. Spectrosc. 1971, 31, 468–469. [Google Scholar]
- Fock, V. Zur Theorie des Wasserstoffatoms. Z. Phys. 1935, 98, 145–154. [Google Scholar] [CrossRef]
- Hughes, J.W.B. Stark states and O(4) symmetry of hydrogenic atoms. Proc. Phys. Soc. 1967, 91, 810–818. [Google Scholar] [CrossRef]
- Goldstein, H. More on the prehistory of the Laplace or Runge-Lenz vector. Am. J. Phys. 1976, 44, 1123–1124. [Google Scholar] [CrossRef]
- Demkov, Y.N.; Monozon, B.S.; Ostrovsky, V.N. Energy levels of a hydrogen atom in crossed electric and magnetic fields. Sov. Phys. JETP 1970, 30, 775–776. [Google Scholar]
- Lisita, V.S.; Sholin, G.V. Exact solution of the problem of the broadening of the hydrogen spectral lines in the one-electron theory. Sov. Phys. JETP 1972, 34, 484–489. [Google Scholar]
- Greene, R.L.; Cooper, J.; Smith, E.W. A unified theory of Stark broadening for hydrogenic ions—I: A general theory (including time ordering). J. Quant. Spectrosc. Radiat. Transf. 1975, 15, 1025–1036. [Google Scholar] [CrossRef]
- Derevianko, A.; Oks, E. Exact solution for the impact broadening of hydrogen spectral lines. In Physics of Strongly Coupled Plasmas; Kraeft, W.D., Schlanges, M., Eds.; World Scientific: Singapore, 1996. [Google Scholar]
- Derevianko, A.; Oks, E. Exact solution for the impact broadening of the hydrogen lines Lyman-beta and Lyman-gamma. AIP Conf. Proc. 1999, 467, 148–149. [Google Scholar]
- Oks, E. The shape of spectral lines of two-electron Rydberg atoms/ions: Analytical solution. J. Phys. B 2017, 50, 115001. [Google Scholar] [CrossRef]
- Nikitin, S.I.; Ostrovsky, V.N. The symmetry of the electron-electron interaction operator in the dipole approximation. J. Phys. B 1978, 11, 1681–1694. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Mechanics; Pergamon: Oxford, UK, 1960. [Google Scholar]
- Born, M. Vorlesungen Über Atommechanik; Springer: Berlin, Germany, 1925. [Google Scholar]
- Kotkin, G.L.; Serbo, V.G. Sbornik Zadach po Klassicheskoj Mechanike (Collection of Problems in Classical Mechanics), 2nd ed.; Nauka: Moscow, Russia, 1977. [Google Scholar]
- Kotkin, G.L.; Serbo, V.G. Collection of Problems in Classical Mechanics, 1st ed.; Pergamon: Oxford, UK, 1971. [Google Scholar]
- Sobel’man, I.I. An Introduction to the Theory of Atomic Spectra; Pergamon: Oxford, UK, 1972. [Google Scholar]
- Wigner, E.P. Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra; Academic Press: New York, NY, USA, 1959. [Google Scholar]
| 1 | We note in passing that in paper [59] there were minor typographic errors in Equations (31) and (32). In Equation (31), the factor in front of the integral should be π−1|2w|−½. In Equation (32), the factor in front of the last brackets should be [Γ(1/4)Γ(−1/4)]−1|w|−1/2. |
| 2 | A shorter version of the present paper was published in 2013 in the fast track journal IRAMP [71], a publication in which does not prevent publishing a more extended version elsewhere. We note that later, in 2014, Rosato et al. published a paper [72], where they reinvented some results from our paper [71] concerning the principal quantum number nmax of the last observable hydrogen spectral line without referring to paper [71]. Namely, they reinvented our preliminary approximate formula for the product nmax10B2 T (where B is the magnetic field and T is the atomic temperature), but did not come up with our more accurate results for nmax10B2 T based on our calculations of Lorentz-broadened profiles of high-n Balmer lines. Just as in our paper [71], Rosato et al. applied their results to magnetic fusion, but they did not apply their results to solar physics—in distinction to our paper [71]. |
| 3 | We note that Rosato et al. [83] attempted studying the Stark broadening of hydrogen line by a REB in magnetic fusion edge plasmas. However, they used the quasistatic approximation, which is totally inappropriate for the broadening by fast electrons of a REB (it is inappropriate even for the broadening by thermal electrons in such plasmas). |
| 4 | So far, we used, as an example the Ly-alpha line just to get the message across (since we obtained relatively simple analytical expressions for the shape of this line). We note that at Ne~1015 cm−3, the Stark width of the Lyman-alpha line calculated by Equations (8.11)–(8.14) would be by about two and a half orders of magnitude below the natural width. However, the dynamical Stark width scales ~ n4, while the natural width scales ~ 1/n5 (n being the principal quantum number). Therefore, for the lines that are originating from the level of n = 4 (such as Ly-gamma, Balmer-beta, Paschen-alpha) and higher levels, the corresponding dynamical Stark width would exceed the natural width. |
| 5 | For example, simulations by Rosato et al. [107] yielded a non-zero impact shift of the σ-components of the Lyα line (for rectilinear trajectories of the perturbers)—contrary to the well-known rigorous analytical result [108]. Also, Rosato et al. [107] overestimated the primary, adiabatic contribution to the dynamical Stark broadening by ions in magnetic fusion plasmas by up to an order of magnitude [98,102]. In addition, for the Lyα line, simulations by Rosato et al. [108] yielded an infinite result for the broadening function A–(ρ) at ρ = 0—contrary to the rigorous analytical result A–(ρ) = const ρ = 0 at ρ = 0 [98,102]. |
| 6 | In the earlier experiment at the gas-liner pinch (Böddeker et al. [111]), the densities up to Ne~1019 cm−3 had been reached. However, the experiment by Böddeker et al. [111] had deficiencies, which were addressed and eliminated in the experiment by Büscher et al. [110]. In distinction to the former experiment, in the latter one: (a) the spectroscopic measurements were performed simultaneously with the diagnostics; (b) highly reproducible discharge condition was used where the Hα line was measured spatially resolved along the discharge axis indicating that no inhomogeneities along the axis existed; and, (c) high care has been taken to prevent the optical thickness. |
| 7 | In paper [150], the intent was to keep the quantum-classical correspondence for the problem of a hydrogenic atom/ion in crossed electric and magnetic fields. There were used some notations from the classical solution presented in the book by Kotkin and Serbo, the 2nd Russian edition, problem 2.37 [154], based partially on the solution of problem 2.36 dealing with the dynamics of the angular momentum M and the Runge-Lenz vector A in a time-independent electric field [154]. We note that only the 1st Russian edition of this book was published in English [155]; problem 2.37 from [154] was not in the 1st Russian edition and in its English version [155], but problem 2.36 from [154] and its solution is available in [155] numbered as problem 2.32. |


















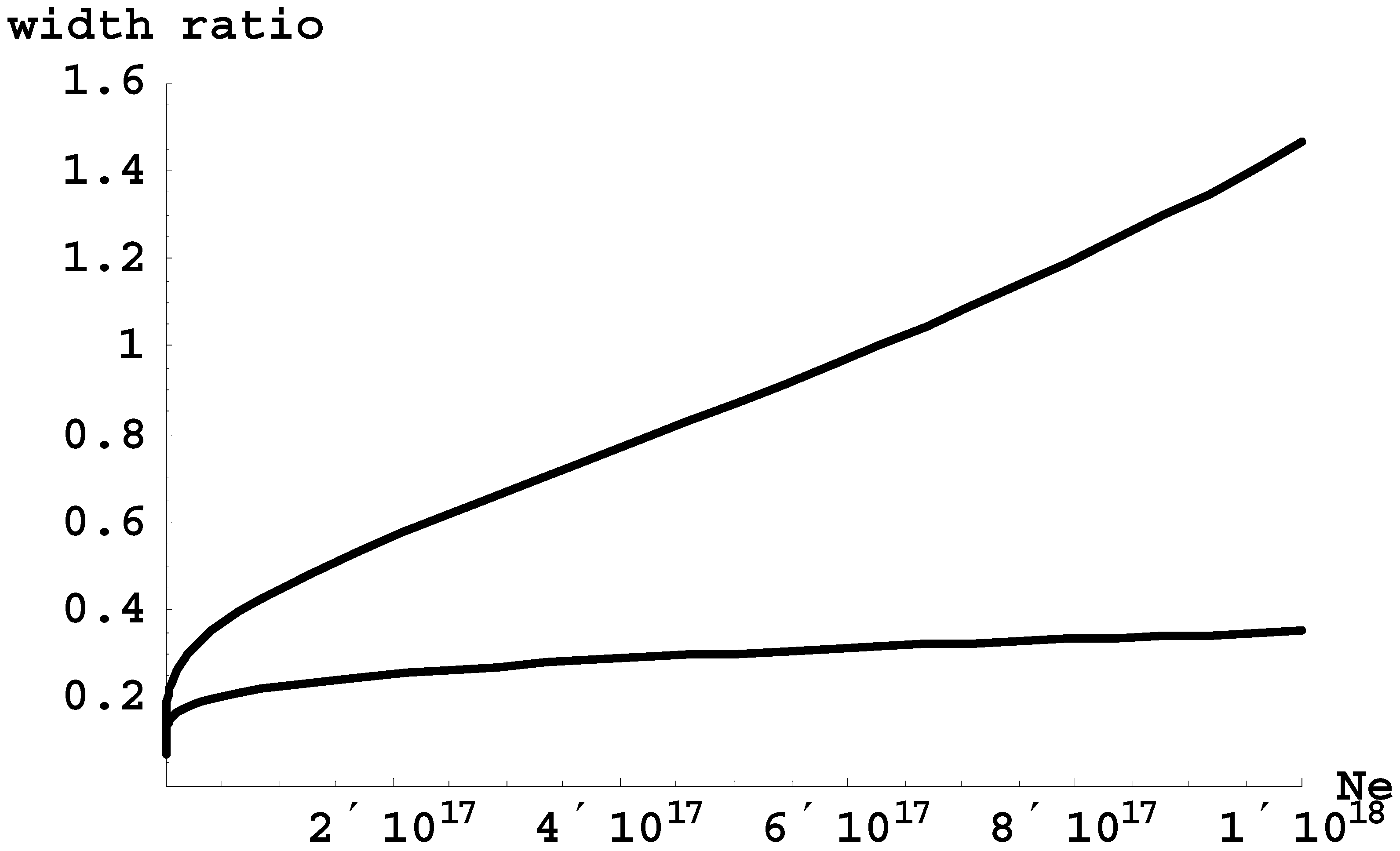



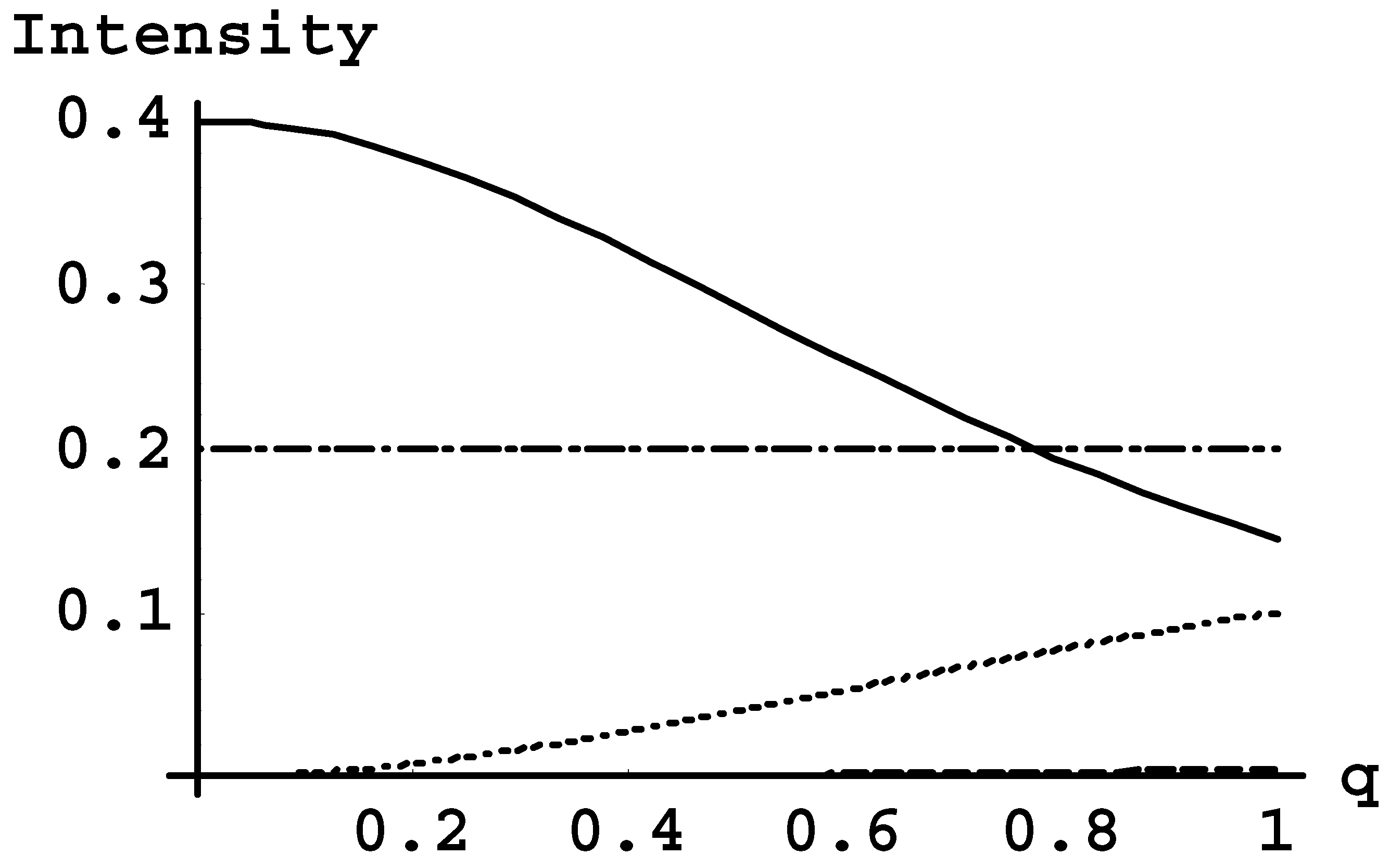



| n | |q| | Ratio |
|---|---|---|
| 2 | 1 | 0.3261 |
| 3 | 1 | 0.3748 |
| 3 | 2 | 0.7496 |
| 4 | 1 | 0.5156 |
| 4 | 2 | 1.0311 |
| 4 | 3 | 1.5467 |
| n | λn(A) | Se(A) | SSirius(A) | Sexp(A) |
|---|---|---|---|---|
| 13 | 3734 | 0.0017 | 0.03 ± 0.03 | |
| 14 | 3722 | 0.0021 | 0.03 ± 0.05 | 0.00 ± 0.04 |
| 15 | 3712 | 0.0026 | 0.09 ± 0.07 | 0.15 ± 0.05 |
| 16 | 3704 | 0.0032 | −0.007 ± 0.05 | 0.00 ± 0.05 |
| 17 | 3697 | 0.0038 | 0.21 ± 0.08 | 0.30 ± 0.08 |
| n | λn(A) | Se(A) | Si,penetr(A) | Stot(A) | SSirius(A) | Sexp(A) |
|---|---|---|---|---|---|---|
| 13 | 3734 | 0.0017 | 0.032 | 0.034 ± 0.010 | 0.03 ± 0.03 | |
| 14 | 3722 | 0.0021 | 0.043 | 0.045 ± 0.014 | 0.03 ± 0.05 | 0.00 ± 0.04 |
| 15 | 3712 | 0.0026 | 0.057 | 0.060 ± 0.018 | 0.09 ± 0.07 | 0.15 ± 0.05 |
| 16 | 3704 | 0.0032 | 0.073 | 0.076 ± 0.023 | −0.007 ± 0.05 | 0.00 ± 0.05 |
| 17 | 3697 | 0.0038 | 0.093 | 0.10 ± 0.03 | 0.21 ± 0.08 | 0.30 ± 0.08 |
| Ne,act/(1018cm−3) | ρact | ρquad | Ne,quad/(1018cm−3) | |Ne,quad − Ne,act|/Ne,act |
|---|---|---|---|---|
| 2 | 0.0925 | 0.0955 | 1.82 | 9.03% |
| 4 | 0.114 | 0.120 | 3.42 | 14.5% |
| 6 | 0.128 | 0.138 | 4.86 | 19.1% |
| 8 | 0.139 | 0.152 | 6.16 | 23.1% |
| 10 | 0.147 | 0.163 | 7.33 | 26.7% |
| Central frequency λj + k | ±[(1 + q2)1/2 − 1] | ±[(1 + q2)1/2 + 1] | ±1 | 0 |
| Relative intensity | [(1+q2)1/2 + 1]/[10(1 + q2)] | [(1 + q2)1/2 − 1]/[10(1 + q2)] | q2/[5(1 + q2)] | 1/5 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oks, E. Review of Recent Advances in the Analytical Theory of Stark Broadening of Hydrogenic Spectral Lines in Plasmas: Applications to Laboratory Discharges and Astrophysical Objects. Atoms 2018, 6, 50. https://doi.org/10.3390/atoms6030050
Oks E. Review of Recent Advances in the Analytical Theory of Stark Broadening of Hydrogenic Spectral Lines in Plasmas: Applications to Laboratory Discharges and Astrophysical Objects. Atoms. 2018; 6(3):50. https://doi.org/10.3390/atoms6030050
Chicago/Turabian StyleOks, Eugene. 2018. "Review of Recent Advances in the Analytical Theory of Stark Broadening of Hydrogenic Spectral Lines in Plasmas: Applications to Laboratory Discharges and Astrophysical Objects" Atoms 6, no. 3: 50. https://doi.org/10.3390/atoms6030050





