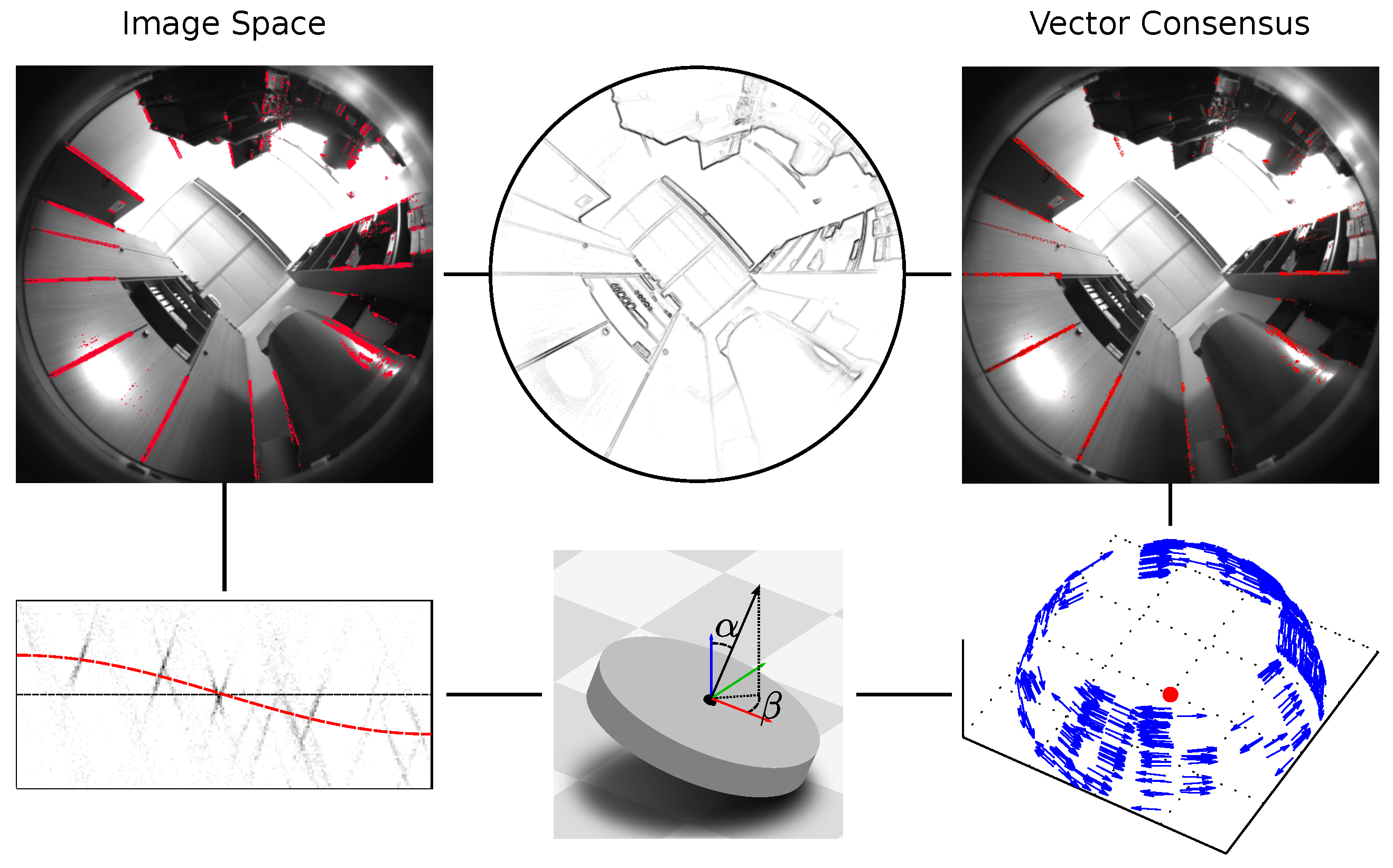
1. Introduction
Visual methods operating on images from a robot’s onboard camera have many applications in mobile robotics. These include relative-pose estimation [
1], visual odometry [
2,
3], place recognition [
4], and simultaneous localization and mapping (SLAM) [
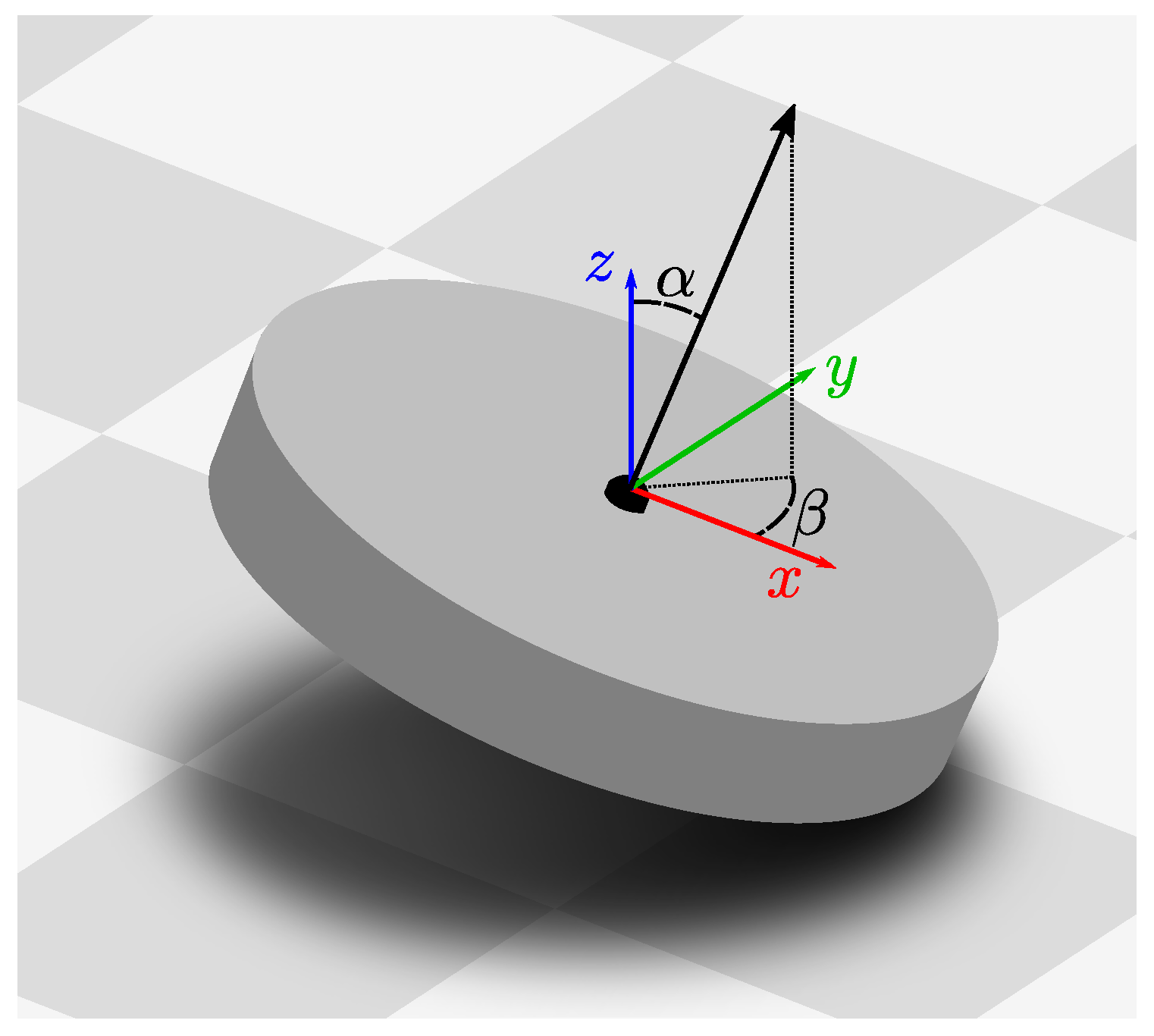
5]. Some of these visual methods are based on a planar-motion assumption: under this assumption, the robot travels in a flat plane without pitching or rolling. As a result, the robot moves with only three instead of six degrees of freedom (DOF), as illustrated in
Figure 1. This simplification is used, for example, in visual relative-pose estimation [
6,
7,
8,
9,
10,
11] or place recognition [
12]. We previously compared visual relative-pose estimation methods in the context of a domestic cleaning robot [
1]. We found that planar-motion methods [
9,
10] can be more accurate and faster than their nonplanar counterparts [
13,
14].
However, even in a benign indoor environment, uneven ground may cause the robot to pitch or roll. Tilting the robot in such a manner violates the planar-motion assumption. For our pose-estimation experiments, this introduced large errors in the results [
1]. Here, even a small tilt of ≈2° eliminated the quality advantage of the planar-motion methods. Larger tilts then increased these errors beyond those of the nonplanar motions. Such a small angle can be caused even by a slight roughness of the movement surface (see
Section 2.3). Booij et al. [
11] encountered a similar effect while testing planar-motion pose-estimation methods. The authors suspected tilts from an accelerating robot as the cause.
To tackle this problem, we estimate the tilt angle
and tilt direction
(
Figure 1) with which an image was captured. A planar-motion method can then use this information to correct for tilts in the input image. The tilt could be measured using an additional sensor, such as an inertial measurement unit (IMU). However, this increases the cost and complexity of the robot, more so because the sensor needs to be calibrated [
15] and synchronized relative to the camera. Instead, we estimate the tilt parameters
from a single panoramic camera image by following the algorithm outlined in
Figure 3. This estimate is based on vertical elements, which are commonly found in indoor environments. These elements are orthogonal to the floor, and thus orthogonal to the robot’s movement plane. Some of the elements will appear as edges in the camera image. Locating the vanishing point of these edges lets us determine the robot’s tilt. We evaluate our results in the context of the visual pose-estimation methods compared in [
1]: the tilt-estimation accuracy should allow the planar-motion methods to remain competitive with their nonplanar counterparts. Furthermore, tilt estimation should add only a small overhead to the time required for planar-motion pose estimation.
1.1. Related Works
Visually estimating a camera’s orientation relative to the world is a prominent research problem. As in our work, vanishing points are widely used, and offer several advantages [
16]: because they lie at infinity, their position is not affected by camera translation. Furthermore, the vanishing points are determined from an image’s edge pixels. Thus, many non-edge pixels can be disregarded, which speeds up processing time.
A popular class of methods assumes a
Manhattan world, as described by Coughlan and Yuille [
17]: here, image edges are assumed to belong to world elements that are either parallel or orthogonal to each other. These three orthogonal sets of parallel elements serve as the axes of a world coordinate system. One example for such a world is an environment consisting only of parallel cuboids.
Košecká and Zhang [
18] present one early work based on the Manhattan world. The authors group edge pixels from nonpanoramic images into distinct straight lines. They then determine the Manhattan-world vanishing points from these lines using expectation maximization [
19]. Denis et al. [
20] compare several early Manhattan-world orientation-estimation methods. This work also introduces additional methods based on straight lines in nonpanoramic images. Tardif [
21] uses the J-Linkage algorithm [
22] to identify distinct vanishing points from straight image edges. This method then selects those three vanishing points that best correspond to the Manhattan directions. All of these works require straight image edges. For this reason, they are not directly applicable to our fisheye images, which contain strong radial distortions.
Bazin et al. [
16] search panoramic images for edges belonging to straight elements in the world [
23]. They then perform a coarse-fine search over the space of possible camera orientations. For a Manhattan world, each hypothetical orientation predicts a distinct set of vanishing points. This method selects the orientation under which the highest number of images edges are consistent with these predicted vanishing points. Another work by Bazin et al. [
16] follows the same Manhattan-world approach. As before, orientations are scored by comparing their predicted vanishing points to the image edges. To find the best orientation, a branch-and-bound algorithm [
24] divides the orientation space into intervals. Those intervals that contain only inferior solutions are discarded using interval analysis. The orientation estimate is then narrowed down by subdividing the remaining intervals.
In the Manhattan world, there are six (three orthogonal, plus their antipodals) vanishing points: one vertical pair, and two additional orthogonal pairs that lie on the horizon. Schindler and Dellaert [
25] generalize this to an
Atlanta world. In contrast to the Manhattan case, this world may contain additional vanishing point pairs located on the horizon. The authors estimate these vanishing points for nonpanoramic images using expectation maximization [
19]. Tretyak et al. [
26] also use an Atlanta-like world. They propose a scene model that encompasses lines, their vanishing points, and the resulting horizon and zenith location. The model parameters are then jointly optimized based on the edge pixels in a nonpanoramic image. Thus, the detection of lines, vanishing points, and the horizon and zenith are performed in a single step. However, these two methods assume images without radial distortion; thus, they cannot directly be used for our panoramic fisheye images.
Antone and Teller [
27] also estimate camera orientations using vanishing points, but do not assume a specific world. Vanishing-point candidates are found by a Hough transform (survey: [
28]), and then refined through expectation maximization [
19]. The authors then identify a set of global vanishing points that appear across an entire collection of images. Camera orientations relative to these global vanishing points are then jointly estimated for all images. Lee and Yoon [
29] also do not require a Manhattan or Atlanta world. Using an extended Kalman filter, they jointly estimate the vanishing points and camera orientations over a sequence. These two methods place no prior restrictions on the locations of vanishing points. Consequently, the alignment between the vanishing points and the robot’s movement plane is not known. To use them for tilt correction, this alignment must first be determined. Thus, these methods are not directly suitable to estimate the tilt from a single image.
The works discussed above estimate camera orientations relative to global vanishing points. Many other works determine the relative camera poses between two images [
2,
3]: one popular approach works by matching local visual features, such as those from the Scale-Invariant Feature Transform (SIFT) [
30], between two images. The relative pose can then estimated from epipolar geometry [
14]. However, these relative poses provide no information about the ground plane. Subsequently, they cannot be used to estimate tilts for planar-motion methods.
Some of the methods discussed here may also solve the tilt-estimation problem. For example, Bazin et al. [
16] determine the camera orientation relative to a Manhattan world from a single panoramic image. However, we seek a solution that is optimized specifically towards tilt-estimation for planar-motion methods: within this problem, we need only the tilt angle and direction, and can ignore the robot’s yaw. These angles can be estimated from vertical elements alone, without requiring a full Manhattan or Atlanta world. Additionally, the tilt angle
is bound to be small, which allows further simplifications. By exploiting these properties, we can can achieve good and fast tilt estimates using considerably simpler methods.
1.2. Contributions of This Study
In this work, we use two different visual methods to determine a robot’s tilt relative to a ground plane. We evaluate and discuss these methods within the context of a domestic floor-cleaning robot. These robots are a popular application of mobile robotics, being extensively sold on the commercial market. Our research group also has a long-standing interest in this application [
31,
32,
33]. Specifically, we have previously developed a prototype for an autonomous floor-cleaning robot, shown in
Figure 2.
Our prototype uses a planar-motion visual pose-estimation method [
10] for localization and mapping. This method accurately estimates the relative camera pose between two images using very few computational resources [
1]. However, the robot may tilt when driving over uneven ground, such as carpets or door thresholds. This violates the planar-motion assumption, which degrades the pose-estimation quality [
1]. In this work, we use these results as a guide for designing experiments (
Section 2.3 and
Section 2.4) or evaluating results (
Section 4). We also use our robot prototype to record a plausible image database, as described in
Section 2.3. However, the methods presented here are not limited to this specific scenario; they may be used with other robots or planar-motion methods.
Both methods in this work operate on panoramic fisheye images, as captured by the robot’s on-board camera (
Figure 3). These images show the hemisphere above the robot, but exclude everything below the horizon. Thus, the camera cannot see the ground plane, relative to which the tilt should be measured. Instead, we use vertical elements in the environment, which are orthogonal to the movement plane. Examples include room corners, door- and window frames, as well as the edges of furniture such as shelves. Some of these parallel elements appear as visually distinct edges in the robot’s camera images.
We now estimate the tilt parameters from the vanishing point of these edges: first, we apply an edge filter to the camera image and extract pixels with a strong edge response. Second, we identify the set of edge pixels belonging to vertical elements in the world, while rejecting those from non-vertical elements. Here, we assume that the tilt angle is small and that vertical elements far outnumber the near-vertical ones. Third, we determine the tilt angle
and direction
from the remaining edge pixels. Step one is identical for both methods, but steps two and three differ. The
image-space method uses several approximations to simplify vanishing-point detection in the fisheye images. We then apply a correction factor to reduce the tilt-estimation errors introduced by these approximations. Operating directly on the panoramic fisheye image, this method is fast and simple to implement. In contrast, the
vector-consensus method solves the tilt-estimation problem in 3D world coordinates. This method makes fewer approximations, but requires a calibrated camera model. It is also more similar to the existing vanishing-point methods discussed in
Section 1.1.
We test the two methods on images recorded by the on-board camera of our cleaning-robot prototype. The robot was positioned at 43 locations spread across six different environments. At each location, we recorded images for the untilted and six different tilted configurations. The tilts estimated from these images were then compared to the ground truth, giving a tilt estimation error. We also measure the execution time required for tilt correction on a desktop and embedded system.
The rest of this work is structured as follows:
Section 2.1 and
Section 2.2 describe the two methods used in this work. We introduce the image database in
Section 2.3, and the experiments in
Section 2.4.
Section 3 contains the results of these experiments, which we discuss in
Section 4. Finally, we summarize our results and give an outlook to possible future developments in
Section 5.
2. Materials and Methods
Our specific goal is to estimate the robot’s tilt angle
and tilt direction
, as shown in
Figure 1.
is given relative to the robot’s heading, with
= 0° and
= 90° describing a forward and leftward tilt, respectively.
is measured relative to the robot’s untilted pose on a planar surface, thus, for an untilted robot, we have
= 0°. We choose our world coordinate system so that
is the surface normal of the movement plane. If
is the normal vector in the coordinate system of a tilted robot, we then find that
Here,
is the rotation matrix for the tilt
, and atan2 is the quadrant-aware arctangent function. We can therefore determine
by first determining
. Both methods perform this step using visually distinct environment elements that are parallel to
.
2.1. Image-Space Method
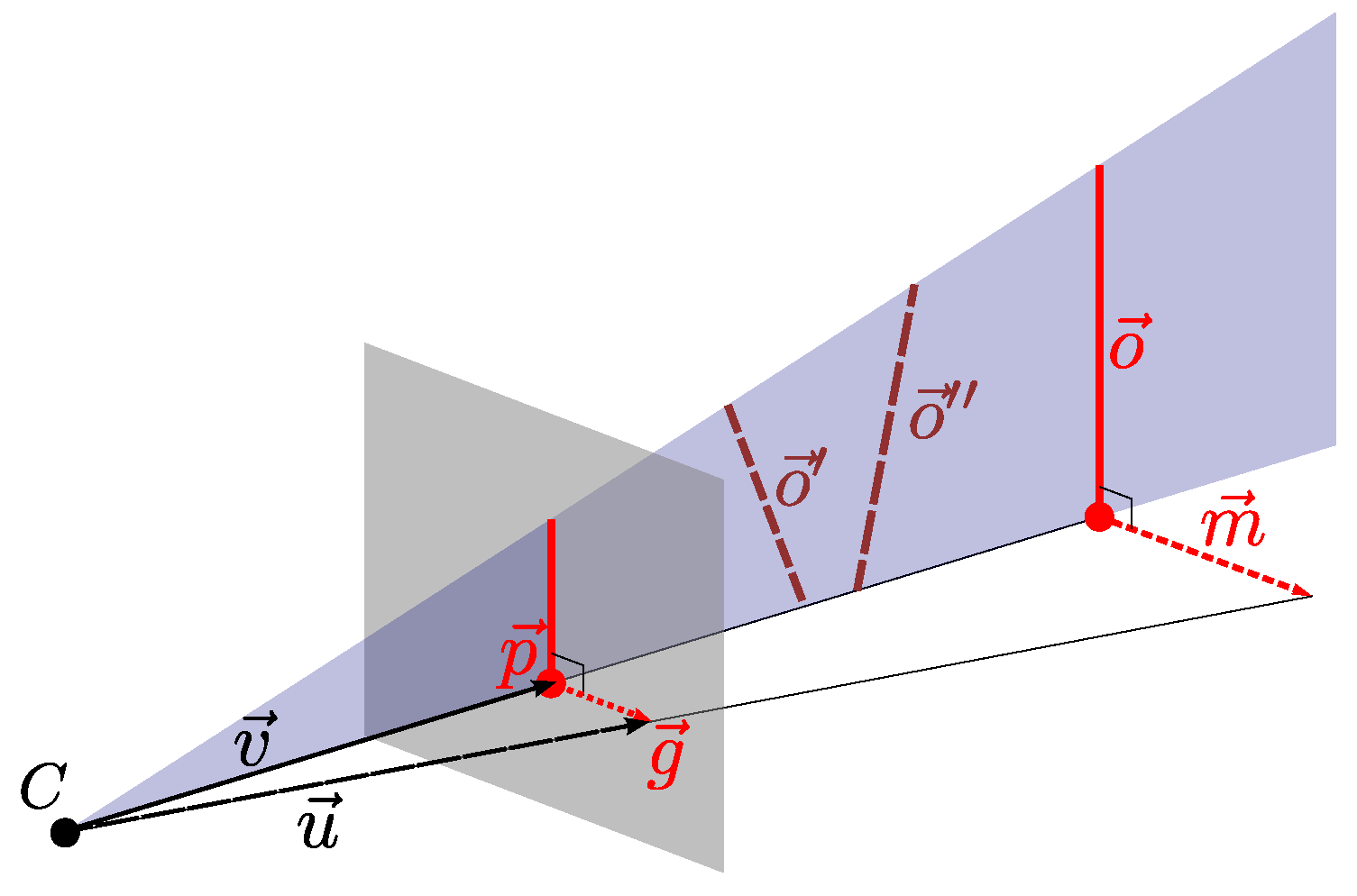
This method is based on the apparent location of the vertical elements’ vanishing point. is the point in the camera image where the vertical elements would appear to meet, if they were extended to infinity. We estimate using several problem-specific approximations, which simplify and speed up the method. We then determine the tilt parameters using the location of .
2.1.1. Preliminary Calculations
We first determine the vanishing point for an untilted robot, which we call
. For convenience, we find
using an existing camera calibration based on [
34]. However, this point could also be determined separately, without requiring a fully calibrated camera. The calibrated camera model provides a projection function
P.
P maps the camera-relative bearing vector
to the image point
. Multiplying with the extrinsic rotation matrix
R gives the bearing vector
in robot coordinates. By definition, the surface normal is
for an untilted robot.
is parallel to the environment’s vertical elements, and consequently shares their vanishing point. Transforming
into camera coordinates and projecting it gives us
If the robot is tilted, the apparent vanishing point
will be shifted from
. We will determine the tilt parameters
from this shift.
Figure 4 illustrates
and
for an untilted example image.
Note that it is irrelevant whether or not the camera image actually shows the environment at or around . Thus, this method would still work for robots where this part of the field of view is obscured. For a robot with an upward-facing fisheye camera, lies close to the geometric center of the image. However, this may not apply for an upward-facing camera that captures panoramic images using a mirror. Here, the image center corresponds to a direction below instead of above the robot. In this case, we can simply use the antipodal vanishing point of the vertical elements. This vanishing point lies below the robot, and thus we calculate from instead. Subsequent steps in the method then use this antipodal vanishing point.
2.1.2. Edge Pixel Extraction
As a first step towards tilt estimation, we detect edges in the camera image. We apply the Scharr operator to compute the horizontal and vertical edge gradients
and
for each pixel. This edge detector is somewhat similar to the popular Sobel operator, but was optimized to be invariant to edge orientation [
35,
36]. Since vertical elements can appear at any orientation within the image, this is a highly desirable property. In this work, we use the implementation provided by the OpenCV library [
37].
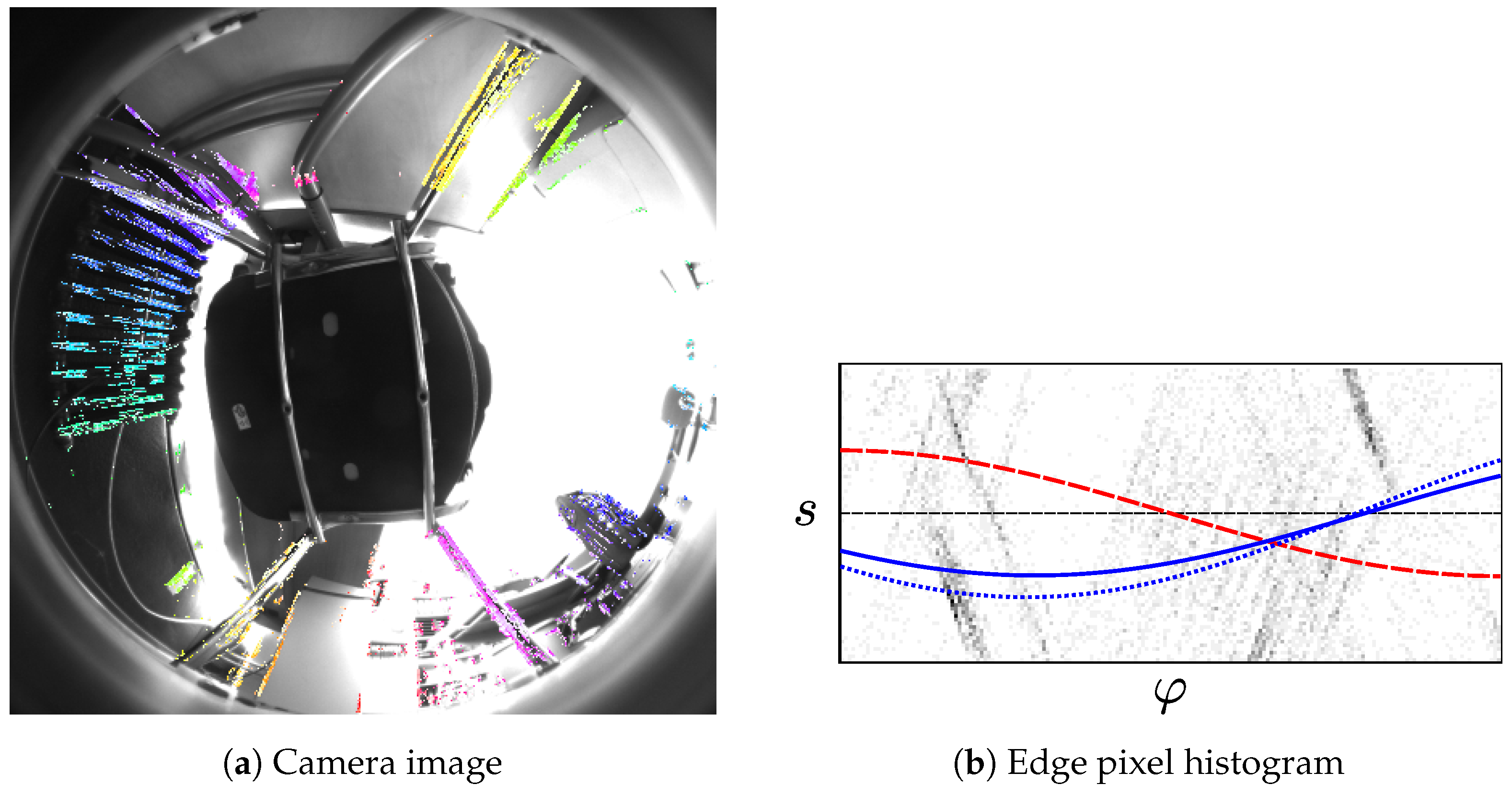
Figure 5 contains an example of the resulting edge gradients.
We ignore pixels below the camera’s horizon, since they mostly show the robot’s chassis. We also reject pixels with a bearing of more than 45° above the camera horizon. Such pixels mainly show the ceiling, which contains horizontal elements that may be mistaken for vertical ones. To speed up computations, we only apply the Scharr operator to a bounding box around the remaining pixels. Finally, we discard pixels with a low gradient intensity . Such pixels are of limited use to us, since camera noise may strongly disturb their edge gradients. Eliminating these pixels also speeds up subsequent processing steps.
We do not try to identify straight lines of edge pixels, instead considering each pixel individually. This simplifies and speeds up our method, and lets us extract information even from very short edges. In contrast, combining connected pixels into long edges (as in [
23]) may reduce the number of incorrect edge pixels, and may make the edge-gradient estimate more accurate [
20]. However, within the scope of this work, we do not evaluate the trade-off between using individual edge pixels or long edges.
2.1.3. Edge Pixel Processing
Next, we estimate the tilt from the edge pixels identified in
Section 2.1.2. For a camera with linear projection, a linear element in the environment would appear as a straight edge in the image. We can derive the edge direction for each pixel from the gradient
. Extending each edge pixel along its edge direction result in a vanishing point, similar to
Figure 4.
However, here we assume that the robot’s camera fits the model proposed by Scaramuzza et al. [
34]; this panoramic camera model is not linear. Due to radial distortion, straight environment elements commonly appear as curves in the camera image. One example is given by the horizontal elements in
Figure 4. However, for this tilt-estimation problem, we can use two simplifying approximations: first, we assume that vertical elements appear as straight edges in the panoramic image. This is approximately true for small tilt angles, as for example in
Figure 6. Second, since
is small, we assume that a tilt appears as a shift in the image. The edges and their vanishing point thus appear to move by a uniform amount (
Figure 7c). In reality, tilting changes the orientation of these edges in the image. Due to the radial distortions of our fisheye lens, the vertical elements may also appear as curves (
Figure 7b). Under our approximations, we ignore these effects and determine only an approximated vanishing point
(
Figure 6) instead of the actual vanishing point
. This greatly simplifies our method, but also introduces tilt-estimation errors. We therefore apply a correction factor after estimating the tilt from the shift between
and
.
Panoramic Projections of Vertical Elements
We use the camera model to justify our previous assumption that vertical elements are projected linearly. According to the projection
P [
34], a bearing vector
and corresponding image point
are related by
Here,
and
are camera parameters, while
. While
refers to the actual pixel coordinates in the image,
is the corresponding point in an idealized sensor plane. This idealized sensor plane is orthogonal to the optical axis, which corresponds to the camera’s
z-axis.
Figure 8 illustrates this camera model.
The
coefficients
of the polynomial function
are also camera parameters determined during calibration; in our experiments, we use
. We now consider a straight line in space that is parallel to the camera’s optical axis. In camera coordinates, such a line consists of all points
, which satisfy
where
is a point on the line and
. The bearing vector from the projection center to
is simply
; here,
is the unknown distance factor. From Equation (
3), we see that the sensor-plane projection of this line must fulfill
We now express this projection in polar coordinates
and, from Equation (
7), find that
is constant. Since the orientation
for the projection of
is constant, the vertical element
appears as a straight line in the sensor plane. Because Equation (4) is linear, this also corresponds to a line in the final image.
From Equation (
8), we note that the sensor-plane projections of all lines
intersect at the origin point
for
. At this origin point, we have
, and thus the distance factor from Equation (
7) must be
(except for lines with
). We now wish to find the specific point along a line
that is projected to the sensor-plane origin. At this origin
, and we thus evaluate
We can assume that
, since Equation (
3) would otherwise give a malformed bearing of
for the origin
.
We have now shown that lines parallel to the optical axis are projected linearly. Furthermore, these projections all meet at the vanishing point as Z approaches infinity. As per Equation (4), this point corresponds to in image coordinates. However, even for an untilted robot, the optical axis is usually not perfectly parallel to the vertical elements. Here, we assume that this misalignment is small for an upward-facing panoramic camera (≈0.16° in our cleaning-robot prototype, as calculated from the extrinsic calibration matrix R). We therefore choose to ignore this effect.
Approximating Tilts through Image Shifts
Next, we determine how tilting the robot affects the vanishing point of the vertical elements. A tilt is a rotation around an axis
parallel to the movement plane, with
. We derive the rotation matrix
for such a tilt from by Rodrigues’ formula [
38], with
For a small tilt angle
, we approximate
using
and
, which gives us
As discussed above, we assume that the optical axis is parallel to the vertical elements for an untilted robot. Thus, these elements are parallel to
in camera coordinates. After rotating the camera around
by a small angle
, this is
. According to Equation (
3), the sensor-plane projection
of
obeys
Here, is sensor-plane location of the vanishing point for the tilted camera.
Since
is small, this vanishing point shifts only a small distance from its untilted location of
. In that case,
, and we can approximate Equation (
5) as
. This approximation is favorable because
for cameras with fisheye lenses, or parabolic or hyperbolic mirrors [
34]. A tilt around the axis
therefore shifts the vanishing point in proportion to the tilt angle
:
Here, is the vanishing-point location in the actual image. The direction of this shift depends , and thus on the tilt direction .
Next, we estimate the shift of
from the edge pixels extracted in
Section 2.1.2. For each edge pixel
k, we know the position
, as well as the horizontal and vertical edge gradients
and
. From this, we calculate the gradient direction angle
This two-part definition ensures that
is the same for both light-dark and dark-light edges. We also calculate the edge offset
is the distance between
and a line orthogonal to
that passes through
.
Figure 9 illustrates this geometry for a single edge pixel. If we treat
k as part of an infinite, straight edge,
would be the distance between that edge and
. A similar parameterization for edge pixels was previously suggested by Davies [
39]. For edge pixels
k from vertical elements, we expect
for an untilted robot. If the robot is tilted,
will change based on the tilt parameters
.
Tilt Parameters from Vanishing Point Shifts
In
Figure 9, a tilt has shifted the vanishing point’s location from the expected point
. The new vanishing point at
is specified by the angle
and the distance
l from
. Here,
is the image-space tilt direction, from which we will later calculate the tilt direction
of the robot. Due to this shift, the blue line extended from
no longer passes through
. According to
Figure 9, the edge offset
between the blue line and
is
Using the trigonometric theorem of addition, we can rewrite this as
Each edge pixel
k from a vertical element provides us with one instance of Equation (
19). For
N such edge pixels, we then have a system with two unknowns
and
N linear equations. We can solve this overdetermined system for
using a linear least squares approach. This lets us determine
Knowing and l gives us the position of the approximate vanishing point.
Using
as a substitute for the true location
in Equation (15), we get
Recall that, for an untilted robot, we assume the optical axis to be orthogonal to the movement plane. In this case, Equation (
2) simplifies to
, and from this we can show that
using Equations (3), (4) and (7). With this result, we can write Equation (
22) as
with the magnitude
. We note that the two vectors in square brackets both have a length of 1, and can therefore write
For a conventional camera with square pixels, we can approximate
and
, resulting in
Note that the tilt axis
is given in the camera reference frame. Since we assume that the camera is mounted facing upwards, the
z-axis of the robot and the camera should be parallel. However, the
-axes of the robot and the camera may be rotated relative to each other. This rotation is described by the extrinsic calibration matrix
R (
Section 2.1.1). To estimate the tilt direction
in the robot reference frame, we first determine the robot tilt axis
From
, we can finally calculate the tilt direction
Note that Equation (
29) includes the term
because the tilt direction is at a right angle to the tilt axis.
We have made a number of approximations during this derivation. Most noticeably, we assume that a tilt causes a shift in the camera image, disregarding the effects shown in
Figure 7. During preliminary experiments, we found that this method exhibits systematic errors in the estimated tilt angle
. As per Equation (
26),
should be proportional to the shift distance
l with a coefficient of
. Since this gives poor results in practice, we replace the camera parameter
with a correction factor
a, so that
a is the proportionality constant relating
l and
, which we estimate from a set of training images using
Here,
is the shift distance
l measured for the image with index
i.
0° is the ground truth for
in the
ith image, determined according to
Section 2.3. Thus,
a equals the mean ratio between the shift
and true tilt angle
over a training set of
m tilted images. Using this heuristic, we can improve the accuracy of our estimates while still benefiting from the numerous simplifications made above.
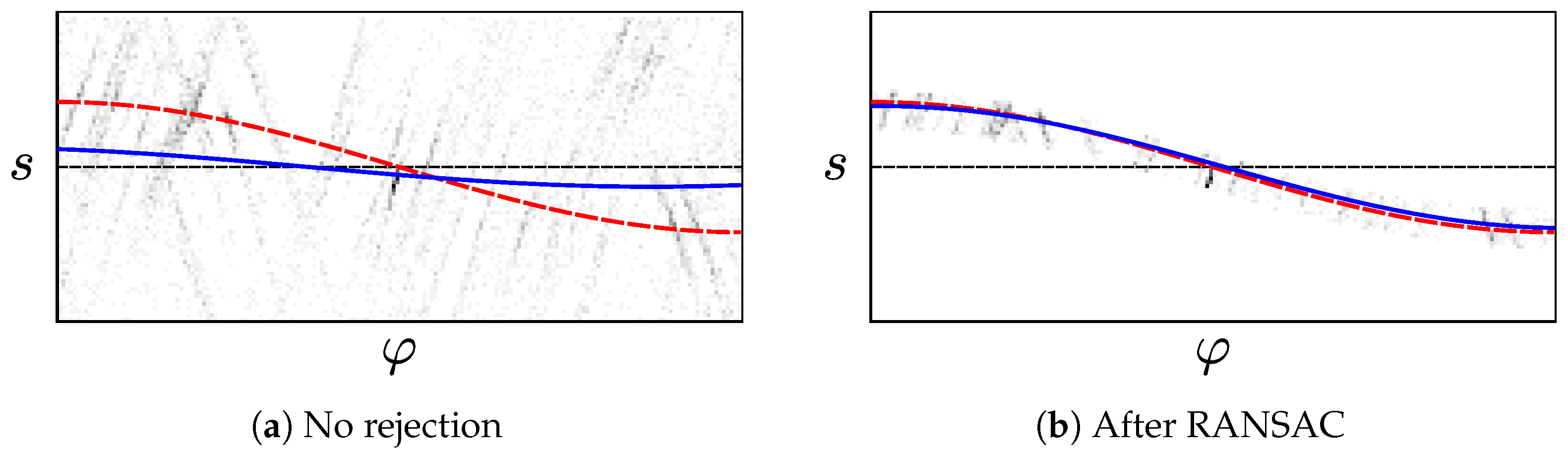
2.1.4. Rejecting Incorrect Pixels
So far, we have assumed that all edge pixels correspond to vertical elements. This is not the case in a real environment, as shown by the many non-vertical elements in
Figure 5. We therefore have to reject incorrect edge pixels caused by these non-vertical elements. Edge pixels disturbed by image artifacts and camera noise should also be filtered out.
As a first step, we apply a prefilter that discards all pixels with a large edge offset
: as before, we assume a small tilt angle
. According to Equation (
30), an upper bound for
also limits
l. From Equation (
18), we see that
, and thus a limit on
l implies a limit
. We therefore discard edge pixels
k with large
, as they are not consistent with
. After this prefiltering, the remaining edge pixels form the set
F. In this work, we chose
, which corresponds to
10°; the precise value of
depends on the choice of
a in Equation (
30).
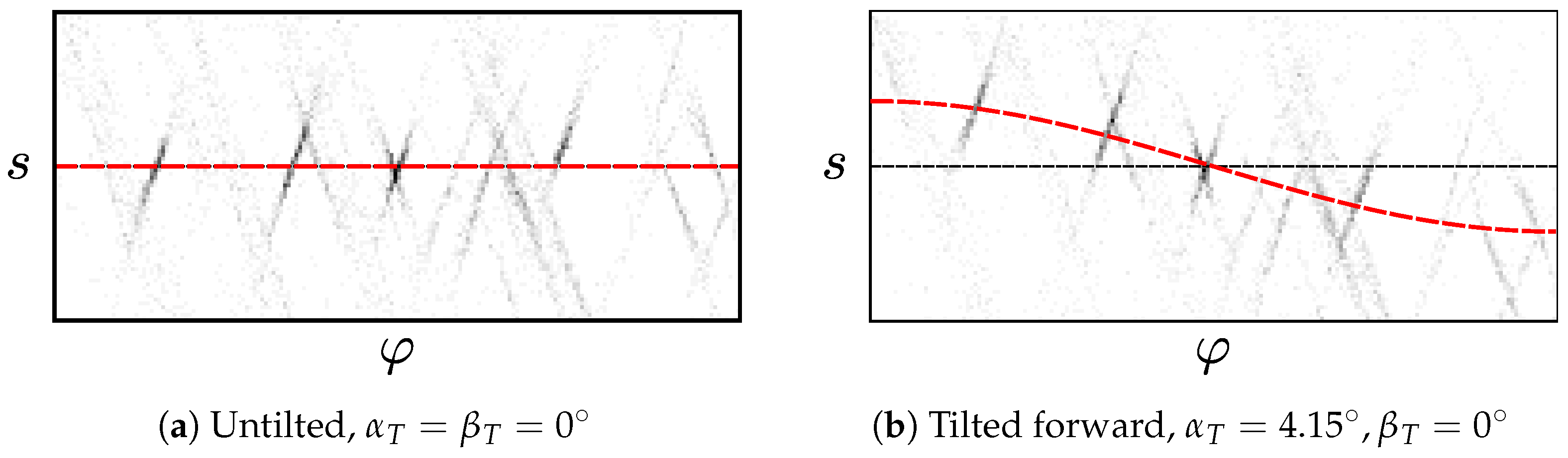
Figure 10 shows the result of this prefiltering step.
We now estimate the tilt parameters
by fitting a cosine to the
of the edge pixels in the prefiltered set
F. This step is described in
Section 2.1.3 and illustrated in
Figure 11. Here, incorrect edge pixels may cause large errors, as demonstrated by
Figure 12a. Such pixels can arise from non-vertical elements or noise, as seen in
Figure 13. One solution uses the popular Random Sample Consensus (RANSAC) hypothesize-and-test scheme [
40]. RANSAC has previously been used to identify vanishing points from straight lines, for example by Aguilera et al. [
41,
42]. Under RANSAC, we generate tilt hypotheses from randomly-chosen edge pixels in the prefiltered set
F. We then select the hypothesis
in consensus with the highest number of pixels. Alternatively, we try a reject-refit scheme based on repeated least-squares estimation. Here, we reject edge pixels that disagree with our most recent
estimate.
are then re-estimated from the remaining pixels. This repeats until the estimate converges, or an iteration limit is reached.
RANSAC Variant
For the RANSAC approach, we randomly select two pixels
i and
from the prefiltered set
F. Solving a system of Equation (
19) for the pixels
gives us the hypothesis
. We use Equation (
19) to identify the set of edge pixels in consensus with this hypothesis as
We repeat this up to
times, and select the edge pixels
which maximize
. In our experiments, we use a systematic search to select the threshold
(
Section 2.4). If RANSAC is successful,
contains no incorrect edge pixels. We now construct a linear system of Equation (
19) using the
of the edge pixels
. Solving this system through linear least-squares gives us
; here, we use the QR decomposition implemented by the Eigen library [
43]. From these
, we can finally estimate
according to
Section 2.1.3.
To speed up this process, RANSAC may terminate before reaching the iteration limit
[
40]: let
p be the fraction of correct edge pixels in the prefiltered set
F, with
. The probability of drawing at least one pair of correct edge pixels in
n attempts is
. Since we do not know
p, we estimate its lower bound as
;
is the largest set
encountered after
n iterations [
44]. The probability of encountering at least one correct pixel pair after
n iterations is thus estimated as
. We then terminate once
, here using a value of
.
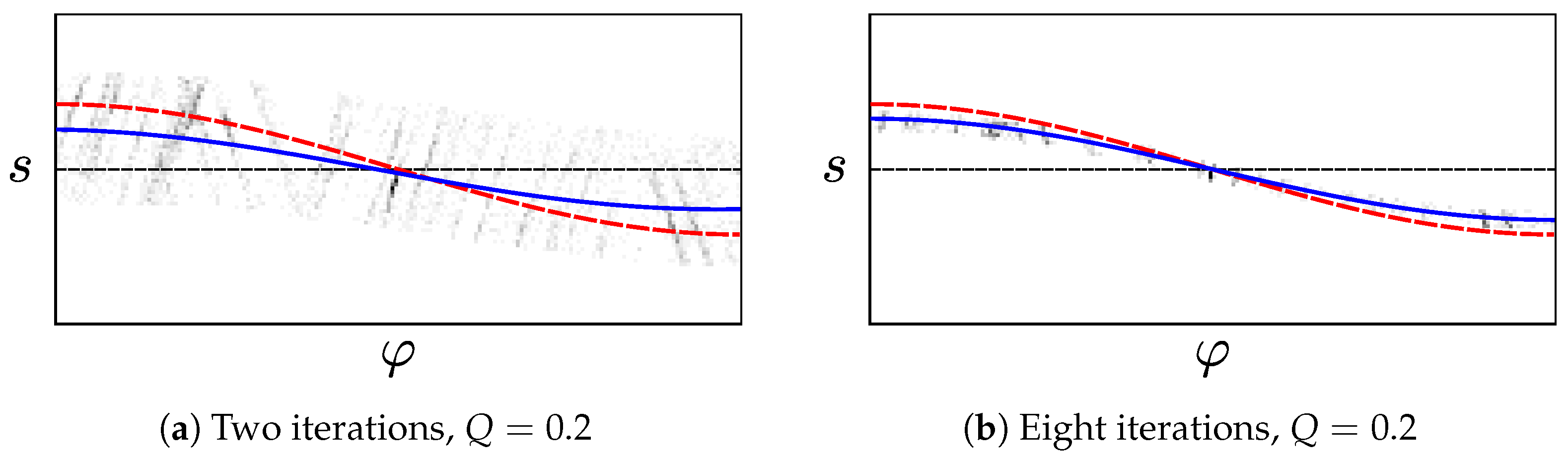
Reject-Refit-Variant
In our reject-refit scheme, we alternate between estimating
from Equation (
19) and rejecting incorrect pixels. We use least squares to estimate
from the edge pixels in
, beginning with
. This estimate is affected by incorrect pixels in
F, as shown in
Figure 12a. To reject these pixels, we calculate the residual error
for each pixel in
. Next, we form
by rejecting a fraction
Q of pixels in
that have the largest absolute error
. Identifying the actual set of pixels with the largest
requires sorting
. This is computationally expensive, and thus we use another heuristic: we assume that the
of the pixels in
are normally distributed, with mean
and standard deviation
. In an idealized case, only a fraction
of the edge pixels
k in
satisfies
[
45]; here,
is the cumulative distribution function of the standard normal distribution. For the remaining fraction
Q with
outside of this interval, we therefore expect
We can thus simply construct the next, smaller set
without sorting
.
While the
in
are not actually normally distributed, we found that this fast heuristic nonetheless gives good results. After these two fitting and rejection steps, we increment
n and repeat the procedure. This continues until the tilt estimate converges, or until
n reaches the limit
. We assume that the estimate has converged once
, as calculated from Equation (
20).
Figure 14 demonstrates the effect of this reject-refit heuristic.
2.2. Vector-Consensus Method
The vector-consensus method is the second tilt-estimation scheme used in this work. It operates on the same edge pixels as the image-space method described in
Section 2.1.2. As before, we assume that many of these pixels correspond to vertical elements
k in the environment. Since they are vertical, their orientations
are parallel to the movement-plane normal
. We illustrate this relationship in
Figure 15a. Knowing their orientation
in robot coordinates lets us calculate
using Equation (
1). However, as seen in
Figure 15b, our camera image shows only projections of the elements. We therefore cannot determine
from any single edge pixel
k, and instead use several pixels from different vertical elements. We identify a set of such edge pixels by combining a problem-specific prefilter with RANSAC. This approach is highly similar to RANSAC-based vanishing-point detection, as for example in [
41].
2.2.1. Orientation Estimation
We first estimate
of two separate parallel elements from the edge pixels
; here,
is
in the camera reference frame. From
Section 2.1.2, we know the image position
and gradient vector
for both
i and
j. The camera’s inverse projection function
provides the bearing
from the projection center towards the edge pixel
i. As illustrated in
Figure 16,
and
define a plane in space. This plane has the normal vector
. We repeat this step for a second edge pixel
j, giving us the normal
for a plane containing
and
. Since the orientations
are orthogonal to both
and
, we have
This plane-based formalism [
46] is commonly used in vanishing-point estimation, for example in [
27,
29,
47].
While we do not know
, we can estimate it using the edge gradient
. Shifting the pixel position
by a small distance
along the gradient
, we calculate
; in this work we use
. As illustrated in
Figure 16,
is a projection of
, and
,
, and
lie in the same plane.
is a normal vector of this plane, and therefore orthogonal to
. By definition,
is also orthogonal to
, leading us to
Note that we have assumed a continuous
when calculating
. Therefore, shifting
by a small distance
leads to only a small change in
. In addition, the camera should use central projection. The camera model used in this work [
34] generally fulfills these requirements. From Equation (
36) and Equation (
37), we estimate the orientation
from the pixel positions
and gradients
.
In practice, estimating
from just two pixels will give poor results due to noise. We therefore use a set
E of two or more edge pixels with
. Using Equation (
37), we determine
for each pixel
. Each
is orthogonal to
, with
. Since all
in
E are parallel, we replace them with a general orientation
, giving us the constraint
We now construct a system of equations that contains one instance of Equation (
38) for each pixel
. To avoid the trivial solution of
, we add the additional equation of
to the system. Solving this overdetermined system using linear least squares gives us an estimate for
. In practice, we use Singular Value Decomposition (SVD) implemented in the Eigen library [
43].
2.2.2. Vertical Edge Selection
Next, we identify a set of edge pixels that corresponds to vertical elements in the environment. Using a prefilter, we discard any edge pixels that indicate an implausibly large tilt angle
. Note that
is given in the camera reference frame, which may be rotated relative to the robot reference frame. We therefore transform
to the robot frame by multiplying with the extrinsic calibration matrix
R. If
is vertical, then
is parallel to the robot’s movement plane, and
If , we therefore reject the edge pixel k. The remaining edge pixels form the set E. Note that is always 0 if the tilt axis is parallel to .
Similar to
Section 2.1.3, we apply RANSAC to identify edge pixels with vertical
[
40]. We randomly select two edge pixels
from
E, and use Equation (
36) to generate a hypothesis
. The set
of edge pixels in consensus with this hypothesis is
As in
Section 2.1.3, we repeat this step until termination (
and
). If RANSAC is successful, the largest consensus set
contains only vertical edge pixels with
.
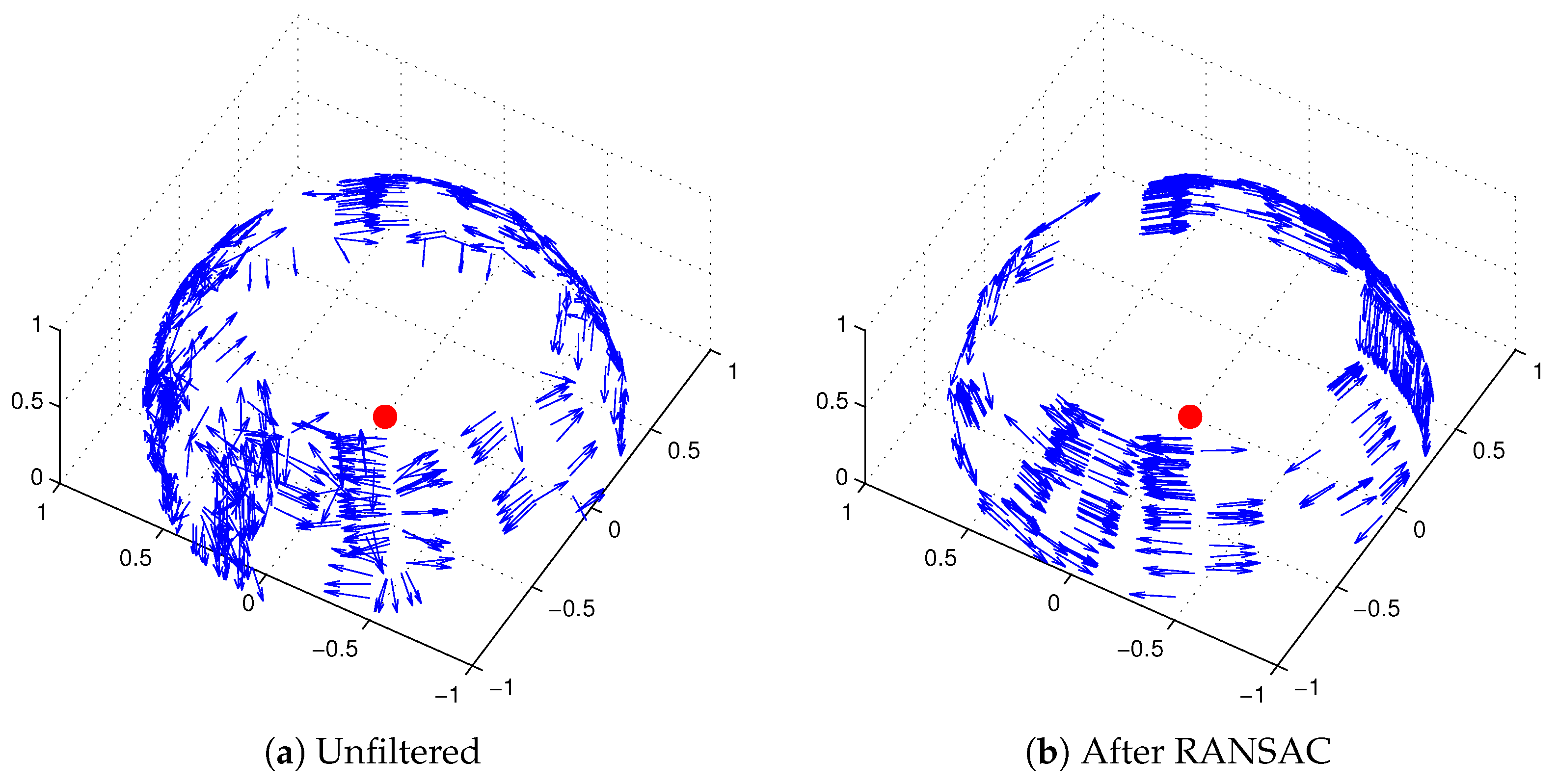
Figure 17 shows an example for the pixels in
.
Figure 18 shows examples of the edge pixels in
.
We now use the least-squares approach from
Section 2.2.1 to determine the common orientation
from the pixels in
. Since
should be vertical, we estimate the movement plane normal
as
Finally, we calculate the tilt parameters
from
using Equation (
1). For some
R, the constraint
in
Section 2.2.1 may result in a
that is antiparallel to
. Since we know that
90°, we simply flip
for results of
°.
2.3. Image Database
To evaluate the methods from
Section 2.1 and
Section 2.2, we recorded an image database using our cleaning-robot prototype. Our robot carries a center-mounted, upward-facing monochrome camera with a panoramic fisheye lens, as shown in
Figure 2. While resolutions up to
are supported, a lower resolution can offer advantages for visual pose estimation [
1]. We therefore capture
pixel images, which show a 185° field of view in azimuthal equidistant projection. This reduced resolution also speeds up processing time. As per
Section 2.1.2, we mask out pixels showing areas below the horizon. The remaining pixels form a disc-shaped area with a diameter of 439 pixels, as seen in
Figure 4. While capturing images, the exposure time is automatically adjusted to maintain a set average image brightness. For further details on image acquisition, we point the reader to [
1]; we also use the intrinsic and extrinsic camera parameters from this work.
We captured images in 43 different locations spread across six different environments. The six environments consist of four different offices, as well as two lab environments. In some cases, we positioned the robot in narrow spaces or under furniture, as in
Figure 19. The restricted field of view may pose a special challenge for tilt estimation. Our image database contains between four and eleven locations per environment. Due to this limited number, the locations do not provide a representative sample of their environment. However, completely covering each environment would require a large number of images. We also expect that many of these locations would be visually similar. Instead, we focused on picking a smaller, but highly varied set of locations.
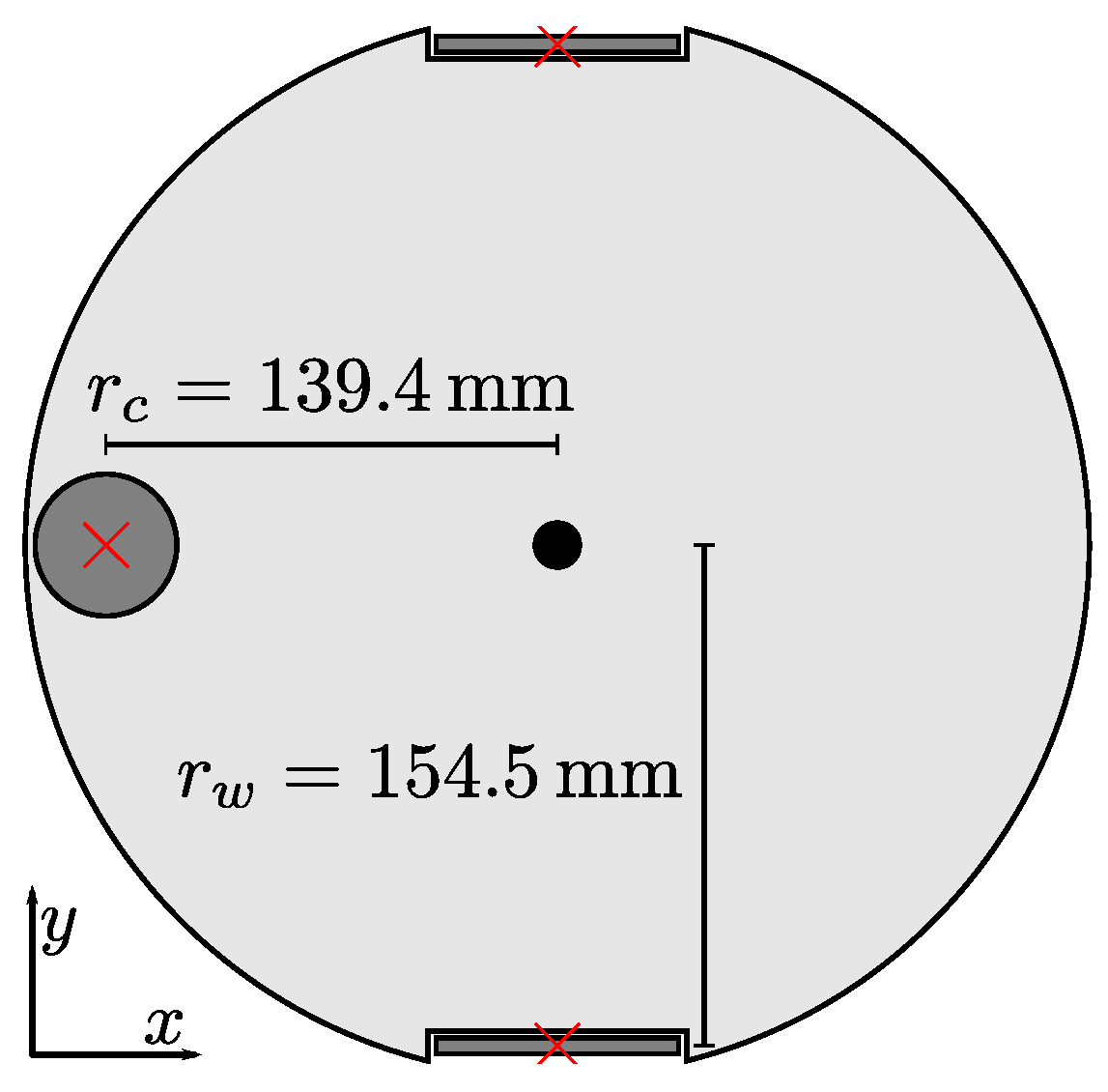
At each location, we captured one untilted plus six tilted image, for a total of
. We produced six distinct tilts by placing a 5 mm or 10.1 mm metal spacer under one of the robot’s three wheels. The thickness of these spacers is similar to common sources of uneven ground: in preliminary experiments, various types of carpet raised the robot’s wheels by 4.4 mm to 7.4 mm. Similarly, a typical door threshold raised it by 5.3 mm.
Table 1 lists the tilts experienced by the robot for these wheel heights. Note that placing the spacers may cause slight changes in robot position or heading between images.
We use a simple static model to calculate the true tilt angle
and direction
from the measured wheel heights
and
c. Assuming that the left wheel as our reference point, we calculate the relative heights
and
. From the robot geometry shown in
Figure 20, we find that
for the tilt angle
. If the robot is tilted with
, the tilt direction is
2.4. Experiment Design
We test the methods from
Section 2.1 and
Section 2.2 on the images gathered in
Section 2.3. The estimation-error angle
serves as our measure of tilt-estimation accuracy.
is the residual, uncorrected tilt angle that remains after a tilt correction based on the estimate
.
and
are calculated from
and
respectively, by inverting Equation (
1).
We evaluate numerous parameter values for our methods, seeking to minimize the mean error
. For both methods, we try several gradient-intensity thresholds
. With the image-space method, we also vary the rejection fraction
Q or the RANSAC threshold
from
Section 2.1.4. Similarly, we investigated multiple values for the RANSAC threshold
in
Section 2.2.2.
Table 2 lists the specific values tested during our experiments.
For the image-space method, we determine the factor
a from Equation (
30) using cross-validation: Given a location
L, the set
contains all tilted images not captured at
L. Next, we compute the factor
by applying Equation (
31) to the
images in
. For images taken at location
L, we then calculate the tilt angle
by using Equation (
30) with
. Using the parameters from
Table 3, we find
pixels per radian when using RANSAC. Likewise,
pixels per radian for the reject-refit variant. By comparison, the coefficient determined through camera calibration is
pixels per radians (Equation (
26)).
The vector-consensus method estimates the tilt angle
without major approximations, and should not require a correction factor. However, for the sake of fairness, we also tested this method with an optional correction factor
. The corrected tilt-angle estimate is then
for this corrected vector-consensus variant is then calculated from
instead of
. We determine the specific
for the location
L using the same cross-validation scheme as for
. For the parameters in
Table 3, we find a unitless factor
.
When running on a robot’s onboard CPU, real-time constraints may subject the tilt-estimation methods to strict time limits. As part of our experiments, we therefore measure execution times on two different systems. The first system uses the 1.6 GHz dual-core Intel (Santa Clara, CA, USA) Atom N2600 CPU, and represents a typical embedded platform. This CPU is used for autonomous control of our cleaning-robot prototype. For comparison, we also include a modern desktop system with a quad-core Intel Core i7-4790K.
We measure the wall-clock execution time using each system’s monotonic, high-resolution clock. This includes all major steps required to estimate
from a camera image. Non-essential operations, such as loading and converting input data, were excluded from this measurement. All experiments involving RANSAC use the same random seed on both platforms. This ensures that the number of RANSAC iterations is identical. So far, our implementations do not consistently support multi-core execution. We therefore use Linux’s Non-Uniform Memory Access (NUMA) policies to restrict each experiment to a single, fixed CPU core. These systems and procedures correspond to those used in [
1]. Thus, we can directly compare the tilt-estimation execution times to our previous pose-estimation measurements.
4. Discussion
As shown by
Table 3, all variants achieve at least fair results, with
°. The image-space method with the reject-refit scheme achieves the lowest mean and median error. Combining the image-space method with a basic RANSAC scheme gives only mediocre results. In contrast, the vector-consensus approach led to the highest
. However, its accuracy improves noticeably when the tilt-angle estimate is corrected by the factor
.
The practical impact of the tilt-estimation error
depends on the application. For example, our cleaning-robot prototype uses Min-Warping [
10] for planar-motion pose estimation. Here, the pose-estimation error increases rapidly for
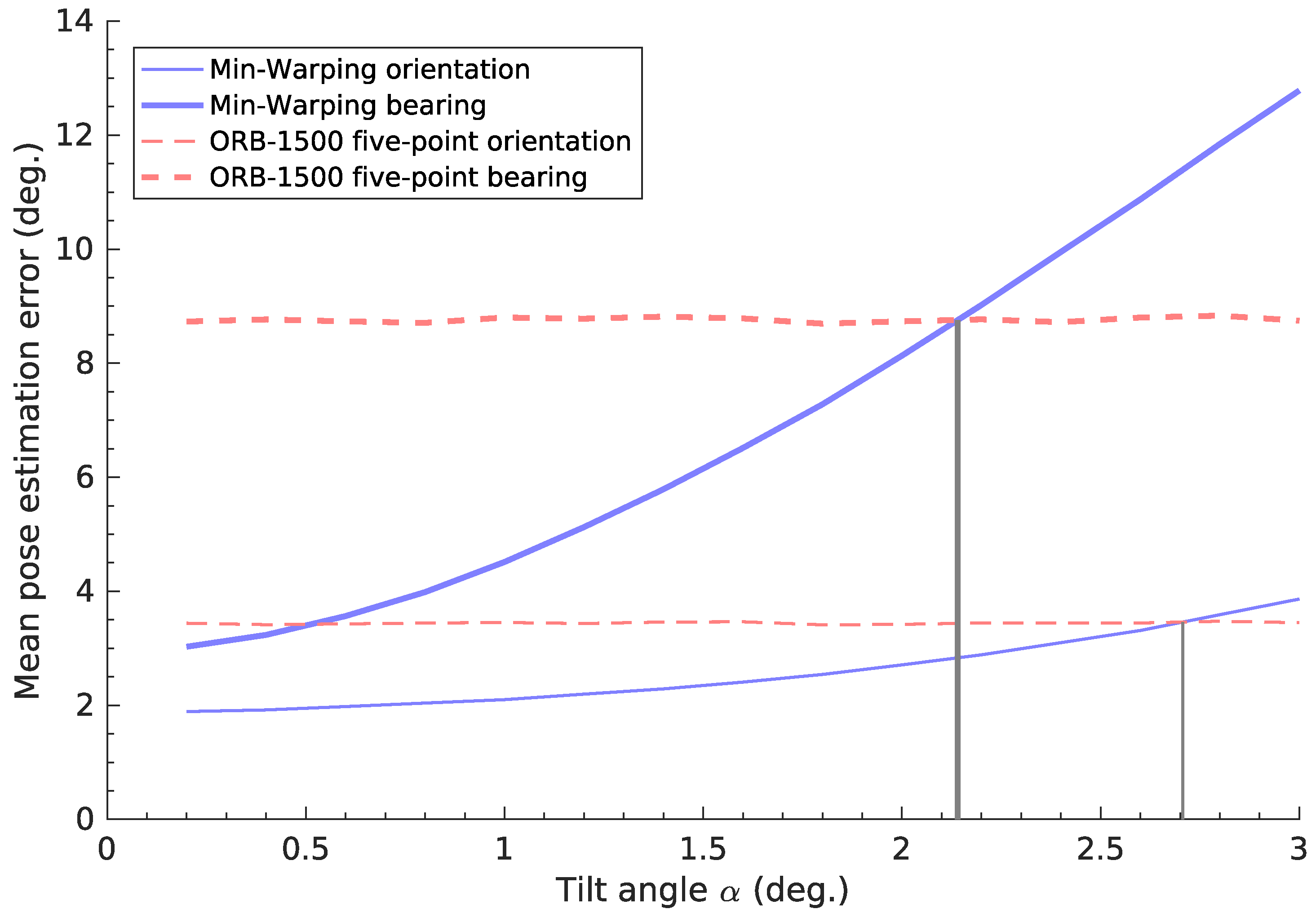
over ≈1°, as seen in
Figure 26 [
1]. Beyond ≈2°, the pose-estimation error exceeds that of a nonplanar method [
1,
14]. In
Figure 21, we see that the best candidate (image space, reject-refit) achieves
° for
of all images. All but the worst candidate (vector consensus, no correction) also attain
° for at least
of images. For tilt correction,
is the angle
of the remaining uncorrected tilt. We thus expect that a correction based on these estimates should make planar-motion pose estimation more resilient to tilts. However, we believe that comprehensive tests of this specific application lie beyond the scope of this initial work; we therefore do not include them here.
Besides the comparatively low average errors, all methods do exhibit occasional high
. These errors can even exceed the highest tilt angle
° in the database. A correction with such an erroneous estimate would likely give worse results than any uncorrected tilt. The fraction of images for which this occurs varies by method, as shown in
Figure 21. In our experiments, such failures generally result from a violation of our world assumption: both methods rely on visually-distinct vertical elements in the environment. In some locations, such elements are rare, or are drowned out by many near-vertical elements. As an example,
Figure 19c shows the robot surrounded by a chair and table with angled legs. For the image-space method, this produces the worst tilt-estimation error out of all locations: using the parameters from
Table 3,
° for the reject-refit scheme, and
° for RANSAC. The reason for this poor estimate is illustrated in
Figure 27: most of the edge pixels extracted from the camera image do not correspond to vertical elements. The
curve fitted to these incorrect edge pixels thus gives a poor tilt estimate. Conversely, the curve for the correct tilt parameters matches few of the edge pixels.
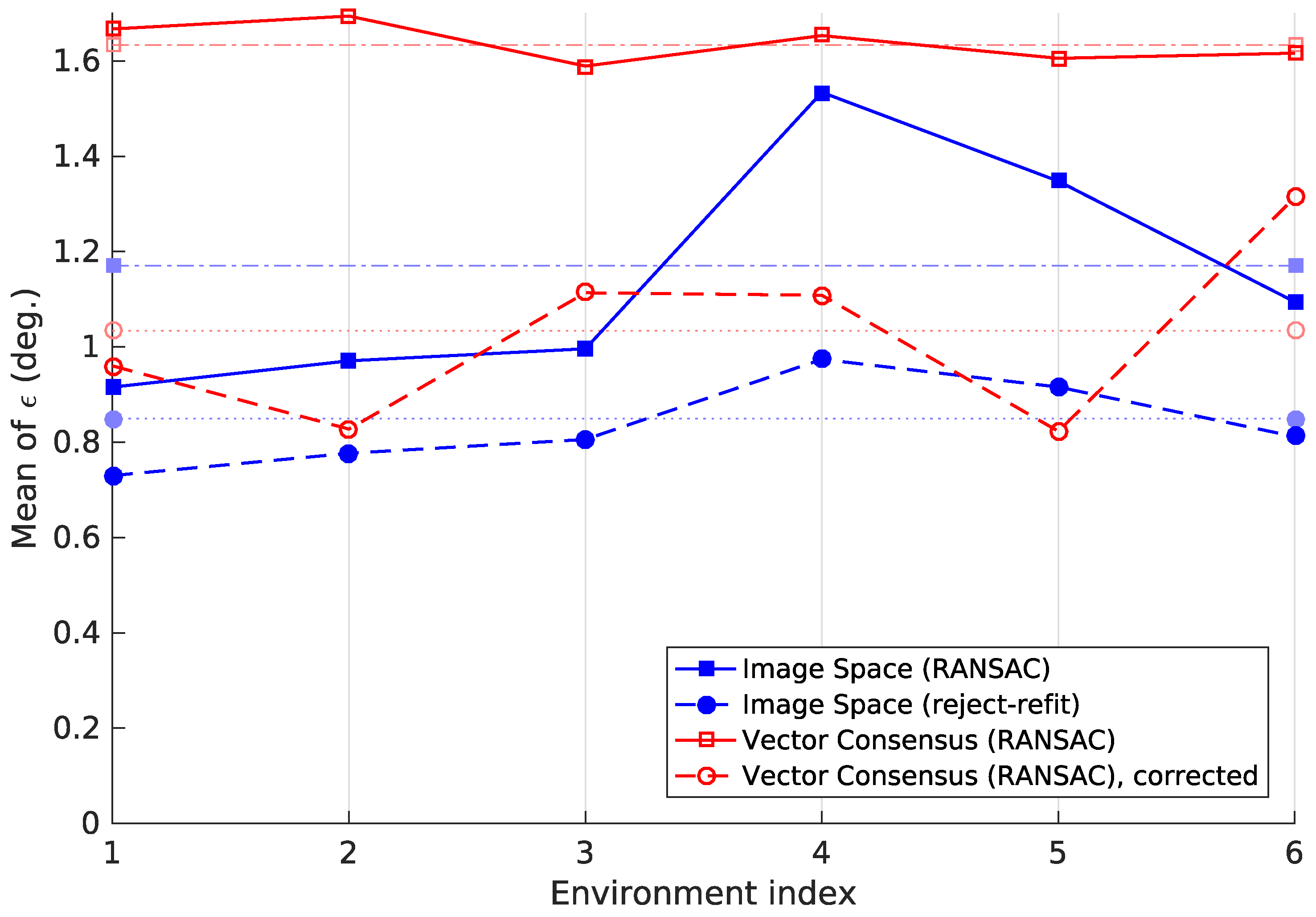
While individual locations may produce high tilt-estimation errors, no environment causes a general failure for any method.
Figure 23 illustrates this by showing
for each method and environment. Although there is some variation in
, it remains below 2° in all cases.
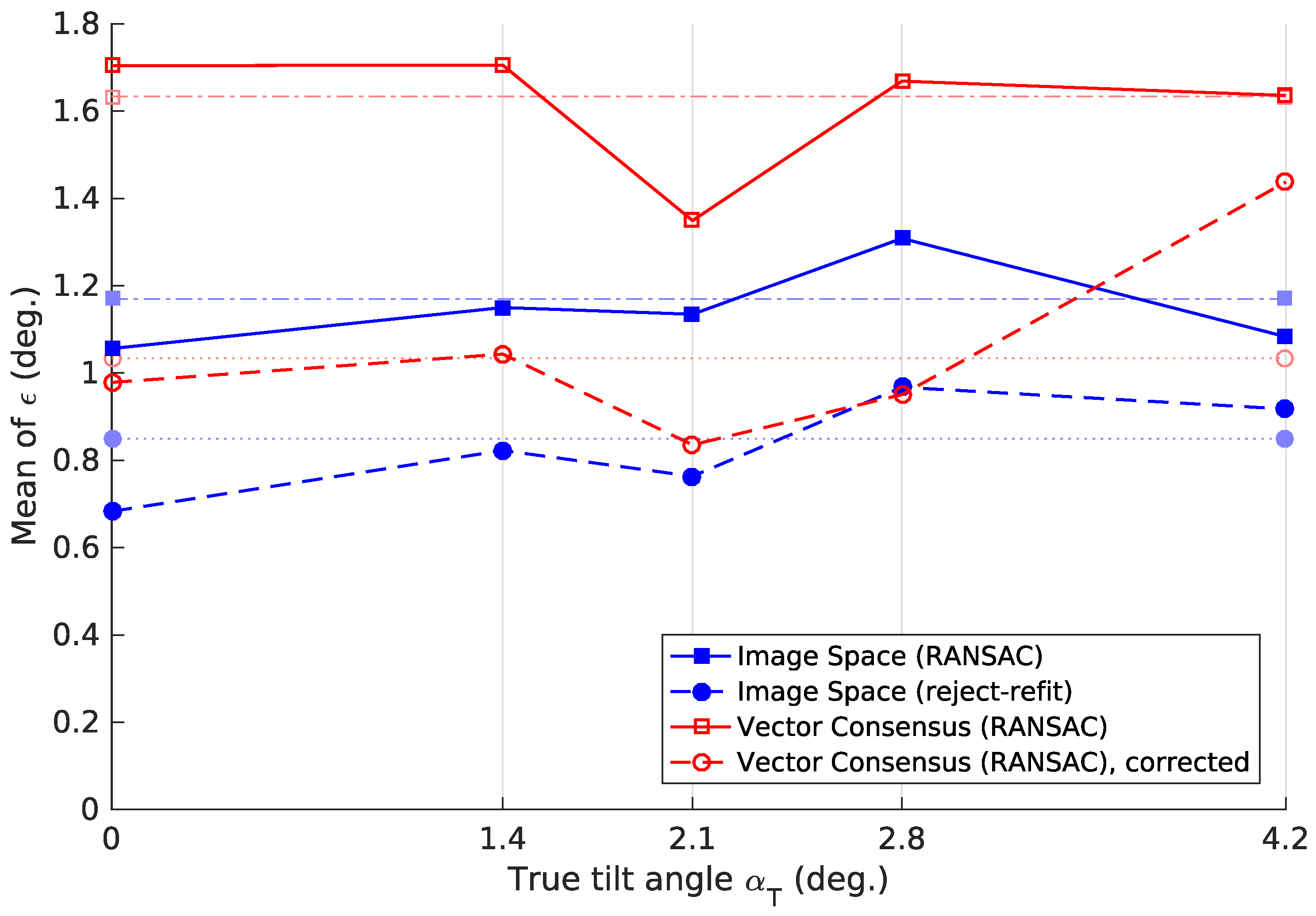
In this discussion, we have frequently used the mean tilt-estimation error
. This measure depends on the composition of the image set on which it was calculated. For example, a method may give especially high
for images with a high
. In this case, a set with many such images gives a higher mean
, compared to a set with few such images. We therefore calculated
for each true tilt angle
. In
Figure 22,
shows only a moderate dependence on the tilt angle
. We note that tilt-estimation errors also occur for an untilted robot (
°).
In
Section 2.4, we included a corrected vector-consensus variant that uses the factor
(Equation (
45)). We first introduced a similar factor
a (Equation (
30)) to compensate for the approximations made in the image-space method.
Figure 28 plots the true and estimated tilt angle with and without these corrections. We note that, on average, the uncorrected methods overestimate
for all true tilt angles
. However, the corrected methods merely divide
by a finite constant. Thus, they cannot correct the difference between
and
for
. In future experiments, it might be worthwhile to include an additive correction with
and
.
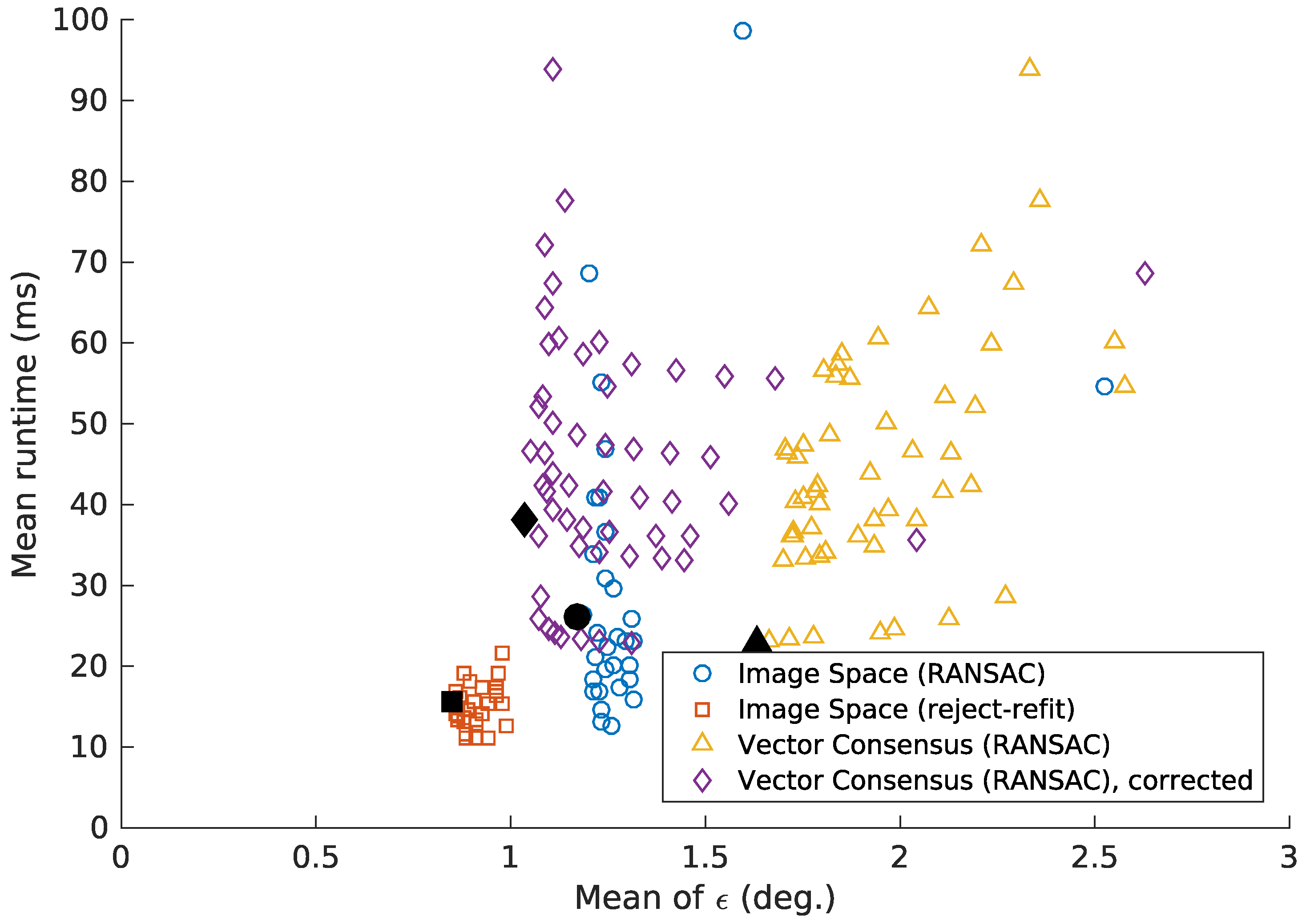
As shown in
Figure 24 and
Figure 25, the tilt estimation time noticeably depends on the parameters used. Choosing parameters with a somewhat higher mean error
can reduce the mean execution time by more than half. Under such a trade-off, all methods achieve a mean execution time below 30 ms on the embedded CPU (
Figure 25). On the desktop system, this time is less than 5 ms. However the time required for some images can be considerably higher, as seen in the 95th percentile values from
Table 4. This must be taken into account for systems with strict real-time constraints.
For our cleaning-robot example, one onboard pose-estimation process requires
ms Table 11 [
1]. In comparison, the reject-refit image-space method requires only
ms to estimate the tilt (
Table 4). Adding tilt estimation to the pose-estimation process thus increases the total time by only
. Overall, we deem all methods suitable for onboard use on a typical mobile robot.
The utility of tilt corrections for planar-motion methods depends on the prevalence and magnitude of tilts encountered in an environment. Corrections can be beneficial if the robot is frequently tilted, or if uncorrected tilts have a large effect. In other cases, the tilt-estimation errors may cause greater problems than the actual tilts. Such errors occur even if robot motion was perfectly planar. The use of tilt correction thus needs to be evaluated for each application. We once more use the pose-estimation example from cleaning robot prototype: in a previous experiment, a nonplanar method gave more accurate results for tilts over ≈2°, as shown in
Figure 26 [
1]. However for the image-space method, the residual error
will usually remain below this value (
Figure 21). The combined execution time for tilt estimation and planar pose estimation is
. This is much faster than the fastest nonplanar pose-estimation method (
) ([
1] Table 11). Thus, tilt estimation should help preserve the advantages of the planar-motion method if the robot is tilted. However, this is limited to small tilt angles and requires visually distinct vertical elements—limitations not shared by the nonplanar method.
5. Conclusions
In this work, we wanted to measure a robot’s tilt relative to a movement plane in an indoor environment. All methods tested here solve this problem based on panoramic images (
Table 3). They do so across different environments (
Figure 23) and tilt angles (
Figure 22). Their fast execution time makes them suitable for real-time use, even on a modest embedded CPU (
Table 4 and
Figure 25). Although average errors are low, tilt-estimation failures can occasionally occur (
Figure 21). Such failures are likely if the environment lacks visually-distinct vertical elements (
Figure 27). Furthermore, even an untilted robot will experience some tilt-estimation errors (
Figure 22).
Overall, the image-space reject-refit variant had the lowest estimation error (
Table 3) and execution time (
Table 4 and
Figure 25). A variant that uses RANSAC to reject incorrect edge pixels offered no advantage in quality or speed. The vector-consensus method was also slower, and resulted in higher errors. However, using a correction factor (Equation (
45)) reduced these errors. The vector-consensus method makes fewer approximations than the image-space method. It may thus still be useful in applications where these approximations are invalid.
5.1. Outlook
In light of these results, we note several possibilities for future improvements.
This work uses the visually-distinct vertical elements that appear in a typical indoor environment. If these elements are rare or drowned out by near-vertical ones, large errors
may ensure (
Figure 27). A confidence measure would be useful to detect these incorrect results. Such a measure might be based on the fraction of incorrect edge pixels rejected during tilt estimation.
The methods in this initial study used only a basic RANSAC scheme. However, the literature contains numerous advanced RANSAC variants, which may achieve better results [
44,
49,
50,
51,
52]. We currently use a very simple heuristic to correct the tilt-angle estimate
(Equations (30) and (45)). However, as seen in
Figure 28, this is not sufficient to fully correct the error in
. A more sophisticated approach may calculate
. This is the probability that the robot is tilted by
given the vanishing-point shift
l. We could use Bayesian techniques to evaluate
. This also lets us incorporate the tilt-angle distribution
for a specific environment. However, finding the parameters for such a probabilistic model may require a large amount of training data. We therefore leave such attempts for future works.
The implementations used in this work are not fully optimized. For example, a greater use of Single Instruction Multiple Data (SIMD) instructions would likely improve the execution speed. Such instructions are supported on both the desktop and embedded processors. However, we feel the speed of our implementations is adequate, and did not attempt such improvements here.
In this work, we focused on simple methods that leverage the specific properties of the tilt-estimation problem. As discussed in
Section 1.1, other works present more general solutions to estimate camera orientations. We believe that a comprehensive comparison between these two approaches would be highly useful.