Large Scale Landform Mapping Using Lidar DEM
Abstract
:1. Introduction
2. Methodology
2.1. Data Source
2.2. Classification Method

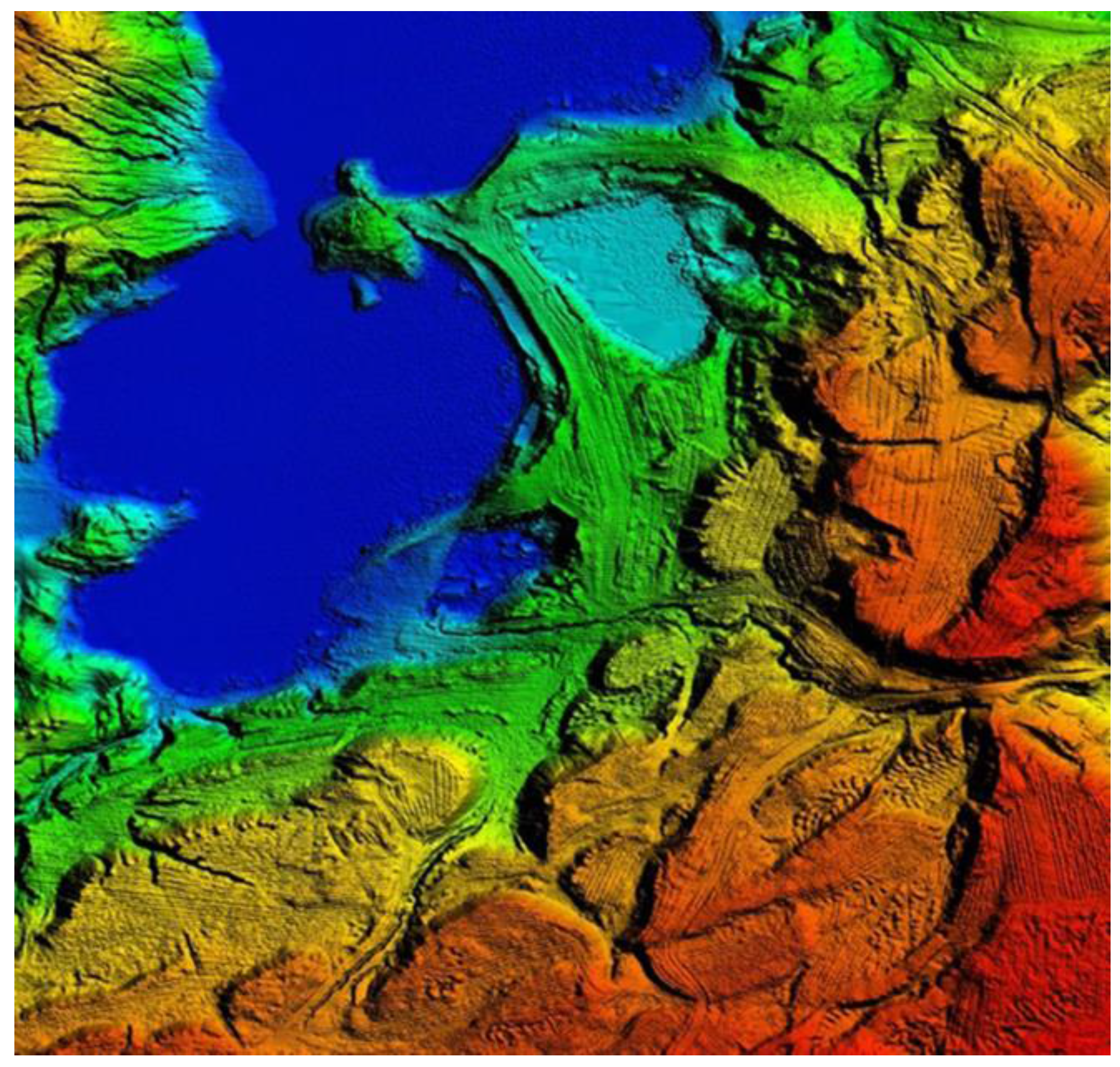
2.3. Cartographic Generalization Condition: Minimum Area
- -
- Important objects should be immediately obvious, not just perceptible;
- -
- The difference in form should be clearly distinguishable;
- -
- Faint illumination and light printing colors reduce the contrast;
- -
- The best reproduction and printing techniques and equipment are not always available or may not be economical.
| Scale | Minimum Area (m2) | Number of Pixels |
|---|---|---|
| 1:1000 | 0.09 | 2 |
| 1:5000 | 2.25 | 36 |
| 1:10,000 | 9.00 | 144 |
| 1:25,000 | 56.25 | 900 |
| 1:50,000 | 225.00 | 3600 |
| 1:100,000 | 900.00 | 14,400 |
| 1:250,000 | 5625.00 | 90,000 |
3. Results and Discussion
| Result Maps | Minimum Area (m2) |
|---|---|
| Primary Landform Map | 0.0625 |
| Generalized Landform Map at 1:1000 | 1.1875 (>0.0900) |
| Generalized Landform Map at 1:5000 | 3.1250 (>2.2500) |
| Landform Type | Primary Landform Map | Generalized Landform Map | ||||
|---|---|---|---|---|---|---|
| 1:1000 | 1:5000 | |||||
| m2 | % | m2 | % | m2 | % | |
| Open Very Low Hills | 200,746.500 | 46.46 | 200,806.688 | 46.47 | 201,082.750 | 46.54 |
| Very Low Hills | 138,289.625 | 32.00 | 138,264.875 | 32.00 | 138,146.250 | 31.97 |
| Flat or Nearly Flat Plains | 62,359.938 | 14.43 | 62,365.188 | 14.43 | 62,375.188 | 14.44 |
| Irregular Plains with Low Relief | 30,700.250 | 7.11 | 30,660.250 | 7.10 | 30,493.500 | 7.05 |



4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Hammond, E.H. Small scale continental landform maps. Ann. Assoc. Am. Geogr. 1954, 44, 32–42. [Google Scholar] [CrossRef]
- Hammond, E.H. Analysis of properties in landform geography: An application to broad scale landform mapping. Ann. Assoc. Am. Geogr. 1964, 54, 11–19. [Google Scholar] [CrossRef]
- Dikau, R.; Brabb, E.E.; Mark, R.M. Landform Classification of New Mexico by Computer. U.S. Geological Survey; US Geological Survey: Menlo Park, CA, USA, 1991.
- Dikau, R.; Brabb, E.E.; Mark, R.M.; Pike, R.J. Morphometric landform analysis of New Mexico. Adv. Geomorphom. Z Geomorphol. 1995, 101, 109–126. [Google Scholar]
- Brabyn, L. Classification of Macro and forms using GIS. ITC J. 1997, 1, 26–40. [Google Scholar]
- Morgan, J.M.; Lesh, A. Developing landform maps using ESRI’s model builder. In Proceedings of the 2005 ESRI International User Conference, San Diego, CA, USA, 25–29 July 2005.
- Gallant, A.L.; Brown, D.D.; Hoffer, R.M. Automated mapping of Hammond’s landforms. IEEE Geosci. Remote. Sens. Lett. 2005, 2, 384–388. [Google Scholar] [CrossRef]
- Hrvatin, M.; Perko, D. Suitability of Hammond’s method for determining landform units in Slovenia. Acta Geogr. Slov. 2009, 49, 343–366. [Google Scholar] [CrossRef]
- Merina, A.P.; Perucho, M.A.; Ruiz, M.A.; Guerrero, I.C. Landform of Alicante province by using GIS. In Proceedings of the 2011 International Conference on Innovative Methods in Product Design (IMProVe 2011), San Servolo, Venice, Italy, 15–17 June 2011.
- Williams, M.; Kuhn, W.; Painho, M. The influence of landscape variation on landform categorization. J. Spat. Inf. Sci. 2012, 5, 51–73. [Google Scholar] [CrossRef]
- Rytz, A.; Bantel, E.; Hoinkes, C.; Merkle, G.; Schelling, G. Kartographische Generalisierung: Topographische Karten. In Kartographische Schriftenreihe Herausgegeben Von Der Schweizerischen; Schweizerische Gesellschaft für Kartographie: Bern, Switzerland, 1975; pp. 12–17. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gökgöz, T.; Baker, M.K.M. Large Scale Landform Mapping Using Lidar DEM. ISPRS Int. J. Geo-Inf. 2015, 4, 1336-1345. https://doi.org/10.3390/ijgi4031336
Gökgöz T, Baker MKM. Large Scale Landform Mapping Using Lidar DEM. ISPRS International Journal of Geo-Information. 2015; 4(3):1336-1345. https://doi.org/10.3390/ijgi4031336
Chicago/Turabian StyleGökgöz, Türkay, and Moustafa Khalil M. Baker. 2015. "Large Scale Landform Mapping Using Lidar DEM" ISPRS International Journal of Geo-Information 4, no. 3: 1336-1345. https://doi.org/10.3390/ijgi4031336
APA StyleGökgöz, T., & Baker, M. K. M. (2015). Large Scale Landform Mapping Using Lidar DEM. ISPRS International Journal of Geo-Information, 4(3), 1336-1345. https://doi.org/10.3390/ijgi4031336





