1. Introduction
In recent years, the industry of oversized cargo transportation has developed because of the rapid development and increasing construction efforts of industries such as electric power, energy, chemicals, and building materials in China [
1]. Compared with the traditional mode of transport, oversized cargo transportations refer to those that transport overlong, oversized, or overweight equipment [
2]. Generally, the route of oversized cargo transportation is longer, and the prices of the materials and equipment to be transported are relatively expensive; thus, designing a reasonable transportation scheme can greatly improve its efficiency [
3]. On the one hand, as the main mode of oversized cargo transportation, highway transportation is flexible such that the devices can be directly transported to their destination by avoiding secondary transportation, and hence, it saves transportation costs [
4]. On the other hand, even if waterways or railways are used for transporting important objects, the journey from or to the pier or train station will finally be covered by highway transportation [
4]. Therefore, designing an optimal path for oversized cargo transportation schemes on the highway is not only an urgent need for many transportation carriage units, but it can also provide an important guarantee for the security and reliability of transporting equipment in large-scale projects. The optimization of route selection of oversized cargo transportation scheme on highways has currently become a topic with practical significance [
2].
Conducting a plan of traveling routes in a road network can always be achieved through the shortest path analysis. An associated weight value, such as the time spent by vehicles to pass through a road segment [
5], is set to the edge of each path that corresponds to a road, and the shortest path with respective weight values can be obtained by using the traditional Dijkstra algorithm. However, as to the route selection of oversized cargo transportation scheme, due to its characteristics of being extremely high, long, and heavy, oversized trucks will encounter restrictions while traveling on roads with obstacles, such as the ground bearing capacity of the road, bend radius requirements of the road, the maximum longitudinal pavement, the width of the curve on the road, and the requirements of cross slope [
1]. Only considering the influence of the length of the road upon the total running time is insufficient. In fact, there are quite a few significant differences in the amount of time spent on steering and in restrictions with different transportation trucks at different road intersections in the traffic system in the urban areas [
6]. For oversized trucks on highways, large flat trailers or trailers that have longer bodies are commonly used; some even use bridge trailers to connect groups of flatbed trailers [
7]. Steering becomes very inconvenient for large trucks at intersections within the road network in urban areas, which is particularly true for articulated lorries; large trucks, therefore, need to spend much more time at intersections compared with common cars. Caldwell [
8] proposed that the delay caused by steering restrictions at road intersections by transportation trucks can reach 17%–35% of the total traveling time. If steering restrictions were ignored during route planning and route selection, the basic characteristics of the road network will be lost; thus, the optimal route obtained is not practical or does not consider traffic rules. Nielsen [
9] proposed that the road intersection is an important part of a road network, and the delay at road intersections caused by steering indicates the continuity on the node within the transportation network, which will influence the total traveling time. Therefore, in designing route of highway transportation scheme for oversized cargos, the cost of steering at road intersections in the city is a factor that cannot be ignored. In particular, for oversized trucks, the delay effect brought by steering restrictions at road intersections should be emphasized. Gutiérrez and Medaglia [
10] tried to find the shortest path with steering limitation by means of improving the Dijkstra algorithm. Schmid and Zeiler [
11] proposed to split each node in the road network into four subnodes and the path where each road is located was replaced by three arcs that show connectivity to represent the cost of steering by trucks at road intersections. However, the increase in number of nodes and links will lead to great reduction in efficiency of computing the optimal path. In addition, de la Barra [
12] proposed a data structure called dual graph to describe the transportation network model with steering limitations. Dual graph uses arcs that express the relationship of the turning to represent turning relationship (or restrictions) at nodes within the model of the road network, which can not only fully express the connectional relationship and steering restrictions but also greatly reduce data redundancy [
13].
The traditional plan for an oversized cargo transportation scheme simply considers some fundamental factors of transportation cost and the driving possibility, such as the length and width of the road and the conditions of the road, without making a comprehensive consideration about the required time consumed by oversized trucks when they make turns at intersections in the road network. As for highway transportation scheme for oversized cargos, many planners choose nighttime for transportation to avoid peak traffic. Thus, the volume of the road traffic has relatively low influence on the scheme. In addition, many traffic lights at intersections in urban areas will be automatically set in yellow after midnight. Therefore, the delay effect of waiting for traffic lights at the crossroads can be also ignored. Based on the model of road network and the traditional Dijkstra algorithm, this present study comprehensively considers both the running time to go through the road and the traveling cost of making turns at road intersections, and established a data model of network based on the weight values of road corners. Then, an algorithm of the shortest path analysis based on the size of the turn angle was proposed to optimize the shortest path algorithm existed. By analyzing and comparing with the traditional shortest path algorithm, which treats the actual length of the road as the value of running weight, we concluded that the turning model based on the road corners at intersections has a better design of operational routes for oversized trucks and that it can provide a reliable theoretical basis and technical support to highway transportation scheme for oversized cargo. The algorithm of the shortest path analysis based on the model of weight values of the road corners presented in this paper has promising future application and will effectively help to design and plan the operating routes for oversized cargo transportation in industries such as electric power, energy, chemicals, and building materials. Such algorithm will greatly reduce the cost and the price of transportation on highways, and provide a strong theoretical foundation and feasibility analysis in the route design for oversized cargo transportation schemes.
The rest of this paper is organized as follows:
Section 2 introduces the model of network based on weight values of steering.
Section 3 describes the process of the algorithm with examples.
Section 4 presents the comparative experiments and the analysis of the results. Finally,
Section 5 contains the conclusions and the prospective application of the proposed algorithm.
3. Examples and Verification of the Algorithm
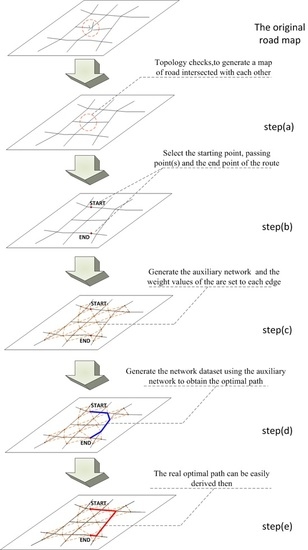
Based on the aforementioned cost model, we design an algorithm to calculate the shortest path, which is shown in
Figure 7.
(a) For the existing layer data of urban roads, the process of editing is first conducted (preprocessing), making the road in the model consistent with the actual roads. Topology checks is necessary to generate a map of roads whose sections are intersected with each other [
26]. The contents of preprocessing include checking the accuracy, completeness, and consistency of the roads. Accuracy checking mainly refers to the error message that exists at the endpoint of the road that should be deleted. Integrity checks include roads that should intersect at a road intersection do not intersect at one point, which should be intersected by manual handling. Consistency checks are for the presence of some multiple overlapping lines, in which case unwanted sections should be deleted. Finally, all roads have to be interrupted at road intersections to facilitate the construction of the model of road network, which is made up of connected sections, as shown in
Figure 8a.
Figure 7.
Basic flow of algorithm
Figure 7.
Basic flow of algorithm
(b) Via human interaction, the starting point, passing point(s), and the end point of the route are assigned in the road network.
Figure 8.
Comparison of the results of the traditional algorithm and the one based on the weighted model of corners: (a) road map of a city in Qingdao; (b) network based on the weight values of the corners at road intersections; (c) superimposed renderings; (d) result of the shortest path analysis with the weighted model of corners; and (e) result of the existing traditional algorithm.
Figure 8.
Comparison of the results of the traditional algorithm and the one based on the weighted model of corners: (a) road map of a city in Qingdao; (b) network based on the weight values of the corners at road intersections; (c) superimposed renderings; (d) result of the shortest path analysis with the weighted model of corners; and (e) result of the existing traditional algorithm.
(c) The existing layer data of roads, the starting point, the end point, and the passing point(s) of the route to be selected were used to generate the auxiliary network based on corners and the weight values of the corners are set to each auxiliary edge of the network. For all roads, except the one where the starting point, end point, or the passing point(s) is located, the midpoint is taken as the secondary node in the auxiliary network of the road. For roads where the starting point, ending point, or passing point(s) is located, the assigned node, instead of the midpoint, is taken as the secondary node to facilitate the construction of the auxiliary network based on the weight values of the corner. Connecting the corresponding secondary nodes located on roads that are linked together in the actual road network will generate a new network, namely the auxiliary network based on the weight values of the corners, as shown in
Figure 8b.
Figure 8c shows the renderings of the stacking effect of the auxiliary network based on the weight values of the corner and the original road map.
(d) Finally, the network dataset is generated using the auxiliary network based on the weight values of the corner, and both the cost value of steering and the actual length of the road are set as passing costs. The shortest path analysis would be performed on the network dataset generated, and then, the optimal path will be obtained, as shown by the blue dotted routes in
Figure 8d.
(e) Depending on the direction of the turn angle and the optimal path generated, the real optimal path can be easily derived from the real road network, as shown by the red solid route in
Figure 8d. This result is compared with the one using the algorithm of the shortest path analysis based on the length of the road as its traveling cost, as shown by the blue route in
Figure 8e.
As shown in
Figure 8, the shortest path obtained by using the traditional shortest path algorithm may have the shortest length in geometry (4001.9 m). However, multiple situations occurred where trucks turn left or turn right, which increases the total time spent by oversized trucks on the road. Using the algorithm proposed in this article, although a longer geometric distance is covered (4009 m), more instances of going straight or turning right at the road intersections were recorded. Even though cases of left turns exist, the steering angle is relatively small. Thus, transportation trucks can effectively save time that spent on the road.
4. Comparative Experiments and Analysis
To verify the effectiveness and superiority of the algorithm of the shortest path analysis based on the network with weight values of road corner in the route selection of oversized cargo transportation scheme, this paper randomly selected another 10 blocks of areas of roads as the experimental samples, where the traditional algorithm and improved algorithms were compared from the derived shortest path.
Table 3 shows the results from our experiment.
Compared with the traditional algorithm, the improved algorithm offers obvious advantages for oversized trucks when making turns, even though it does not provide the shortest geometric distance. As shown in the table, when the network of roads has a regular grid distribution, the path computed by the optimal path algorithm proposed in this article is basically consistent with the one made by the traditional algorithm. However, when the roads are in the form of an irregular grid, the optimal path algorithm effectively reduces the number of left turns made by oversized trucks in the process of running, under the premise of not significantly increasing the total length of the route, and the number of straight-going has also been improved to some extent. Considering all factors, the optimal path algorithm proposed in this article has better adaptability.
The comparison of the time consumed to pass through all routes in the experiments mentioned above is shown in
Figure 9, with the traditional algorithm and the steering-consumed model based on the corners at road intersections proposed in this paper (assuming that the oversized trucks will travel at an average speed of 15 km/h).
As shown in
Figure 9, the total time spent to pass through the route using the shortest path algorithm based on the size of the corner is less than that with the traditional shortest path algorithm. The advantage of using the algorithm is also quite obvious then.
Table 3.
Statistics results of the analysis of test areas that were randomly sampled.
Figure 9.
Total time spent by oversized trucks to pass through different routes with the traditional shortest path algorithm and the one based on the size of the corners.
Figure 9.
Total time spent by oversized trucks to pass through different routes with the traditional shortest path algorithm and the one based on the size of the corners.
To further verify that the shortest path algorithm based on the corners has better characteristics for oversized trucks to pass through road intersections than that of the traditional shortest path analysis, statistical analysis was performed. A comparison of the possibility of turning left, going straight, and turning right is also shown in the result of the routes selected based on both the algorithms mentioned above, considering a condition with the same number of intersections passed through by the oversized trucks (
Figure 10 and
Figure 11).
Figure 10.
Statistics of the number of turns made at road intersections using the shortest path algorithm based on the size of the corner.
Figure 10.
Statistics of the number of turns made at road intersections using the shortest path algorithm based on the size of the corner.
Figure 11.
Statistics of the number of turns made at road intersections based on the traditional shortest path algorithm.
Figure 11.
Statistics of the number of turns made at road intersections based on the traditional shortest path algorithm.
As shown in
Figure 10 and
Figure 11, for the route obtained by the shortest path algorithm based on the size of the corners on the road, the likelihood of going straight is greatly improved, and the number of left turns has been effectively reduced compared with the traditional shortest path algorithm, which can significantly shorten the time spent by transportation trucks to make turns at road intersections. The more intersections passed through by trucks, the more obvious this characteristic becomes.
In summary, the shortest path algorithm based on the weight values of corners at road intersections proposed in this article can calculate an optimal path that offers the shortest time for transportation trucks to make turns, according to the corner size at road intersections along the path. It not only effectively reduces the traffic pressure of transportation trucks at road intersections, which shortens the total running time spent by transportation trucks on the road, but also meets the need of complex peculiarities within the road network and assists in solving the problems related to route selection with the industry of oversized cargo transportation in China.
5. Conclusions
By processing and modeling the data of urban road network, this research, combined with the operational need of oversized cargo transportation system, has designed a weighted model that is based on the size of the corner at road intersections. Through the analysis of the traditional shortest path algorithm, the model is introduced to the classical Dijkstra algorithm, and an algorithm of the optimal path analysis is presented with detailed discussion on the theory and the realization. The model abandons the drawbacks of the traditional algorithm that only considers the length or the width of the road. Experimental results have shown that the algorithm can reduce the time for trucks to make turns at road intersections in complex transportation networks, which is feasible in the actual planning of driving routes for oversized trucks.
The operational route for transportation trucks computed by the optimal path algorithm proposed in this article can not only serve as a new strategy to ease congestion, but can also improve the dysfunctional transportation systems in urban areas today and guide in route planning in cities. Traffic flows concentrated in a few roads will also increase the pressure on road traffic. Accordingly, using the optimal path algorithm presented in this paper to develop running route for vehicles could reform the urban transportation system, which will play a role in traffic diversion in certain ways. The shortest path algorithm based on the size of the corner at road intersections proposed in this article achieves good results in practice and represents potential applications.