Morphological Principal Component Analysis for Hyperspectral Image Analysis ^†

Abstract

This article deals with the issue of reducing the spectral dimension of a hyperspectral image using principal component analysis (PCA). To perform this dimensionality reduction, we propose the addition of spatial information in order to improve the features that are extracted. Several approaches proposed to add spatial information are discussed in this article. They are based on mathematical morphology operators. These morphological operators are the area opening/closing, granulometries and grey-scale distance function. We name the proposed family of techniques the Morphological Principal Component Analysis (MorphPCA). Present approaches provide new feature spaces able to jointly handle the spatial and spectral information of hyperspectral images. They are computationally simple since the key element is the computation of an empirical covariance matrix which integrates simultaneously both spatial and spectral information. The performance of the different feature spaces is assessed for different tasks in order to prove their practical interest.

1. Introduction

Hyperspectral images allow us to reconstruct the spectral profiles of objects imaged by the acquisition of several tens or hundreds of narrow spectral bands. Conventionally, in many applications hyperspectral images are reduced in the spectral dimension before any processing. Most hyperspectral image reduction methods are linear and are not concerned with the multiple sources of nonlinearity present in this kind of image [1]. Nonlinear reduction techniques are nowadays widely used on data reduction, and some of them have been used for hyperspectral images [2]. Nevertheless, most of these techniques present some disadvantages [3] in comparison to the canonical linear principal component analysis (PCA). That is the rationale behind our choice of PCA as starting point. In particular, one major drawback of those nonlinear techniques is that they are computationally too complex in comparison to PCA. Hence most of the time, they cannot be applied on real full resolution images. Another common disadvantage of both classical linear and nonlinear dimensionality reduction techniques is that they consider a hyperspectral image as a set of vectors. They are appropriate when the data do not present useful spatial information, and therefore they are not totally adapted to images.

As mentioned above, dimensionality reduction in hyperspectral images is usually considered as a preprocessing step for supervised pixel classification as well as for other hyperspectral image tasks such as unmixing, target detection, etc. Hence, our goal is to incorporate spatial information into the dimensionality reduction (DR).

The contribution of our approach can be summarized as follows. We propose to add spatial information on the estimation of the covariance matrix used for PCA computation. This is done by means of morphological image representations, which involve a nonlinear embedding of the original hyperspectral image into a morphological feature space.

Many previous works have considered how to introduce spatial information into hyperspectral dimensionality image reduction. We can divide these techniques into different fields. The first family of techniques is close to our paradigm since they are based on mathematical morphology [4,5,6,7,8]. Other approaches are founded on Markov random field image representation such as [9,10]. Another family of techniques uses kernel methods, where kernels for spatial information and kernels for spectral information are combined together [11,12,13,14]. Techniques based on tensor representation of hyperspectral images [15,16] have been successfully considered. Finally, wavelet representation and image extracted features have also been used to add spatial information [17].

The rest of the paper is organized as follows. Section 2 provides a remind on the mathematical morphology multi-scale representation tools used in our approach. Section 3 introduces in detail our approach named morphological principal component analysis (MorphPCA). In order to justify our framework, a summary of the classical theory underlying the standard PCA is provided as well as the notion of Pearson image correlation. Then, the four variants of MorphPCA are discussed, including an analysis of their corresponding covariance matrix meaning. The application of MorphPCA to hyperspectral dimensionality image reduction is considered in Section 4. That involves an assessment of the different variants according to different criteria. For some of the criteria, new techniques to evaluate the quality of dimensionality reduction techniques on image processing are introduced. Techniques arising from manifold learning are also considered in the comparaison. Finally, Section 5 closes the paper with the conclusions.

We note that this paper is an extended and improved version of the conference contribution [18]. Besides a more detailed discussion on the techniques, a larger set of hyperspectral images is used in the assessment of the different approaches. The first one which was acquired over the city of Pavia (Italy), is a hyperspectral image of spatial size : 610 × 340 pixels, with 103 spectral bands. The second image, which represents the University of Houston, is a hyperspectral image of spatial size 349 × 1905 pixels and with 144 spectral bands [19]. The last one called Indian Pines is a hyperspectral image of spatial size 145 × 145 pixels, and with 224 spectral bands. Moreover, on this extended version new measures of comparison have been introduced.

2. Basics on Morphological Image Representation

The goal of this section is to introduce a short background on morphological operators and transforms used in the sequel. Notation considered in the rest of this paper is also stated.

2.1. Notation

Let E be a subset of the discrete space ${\mathbb{Z}}^2$, which represents the support space of a 2D image and $F\subseteq {\mathbb{R}}^D$ be a set of pixel values in dimension D. Hence, it is assumed in our case that the value of a pixel $x\in E$ is represented by a vector $v\in F$ of dimension D, where discrete space E has a size of $n_1\times n_2$ pixels. This vector v represents the spectrum at position x. Additionally, we will write higher order tensors by calligraphic upper-case letters $(\mathcal{I},\mathcal{S},\dots )$. The order of tensor $\mathcal{I}\in {\mathbb{R}}^{n_1\times n_2\times \dots \times n_J}$ is J. Moreover, if $\mathcal{I}\in {\mathbb{R}}^{n_1\times n_2\times n_3}$, for all $i\in [1,n_3]$ ${\mathcal{I}}_{:,:,i}$ represents a matrix of size $n_1\times n_2$ where the third component is equal to i. In our case we can also associate a tensor to the hyperspectral image $\mathcal{F}\in {\mathbb{R}}^{n_1\times n_2\times D}$.

2.2. Nonlinear Scale-Spaces and Morphological Decomposition

Mathematical morphology is a well known nonlinear image processing methodology based on the application of complete lattice theory to spatial structures. Let $f:E\to \mathbb{Z}$ be a grey-scale image. Area openings ${\gamma }_{s_l}^a\left(f\right)$ (resp. area closings ${\phi }_{s_l}^a\left(f\right)$) are morphological filters that remove from the image f the bright (resp. dark) connected components having a surface area smaller than the parameter $s_l\in \mathbb{N}$ [20]:

$$\begin{array}{c}{\gamma }_{s_l}^a\left(f\right)=\underset{i}{\bigvee }\left\{{\gamma }_{B_i}\left(f\right)\right|B_i\text{is}\text{connected}\text{and}\text{card}(B_i)=s_l\}\end{array}$$

(1)

$$\begin{array}{c}{\phi }_{s_l}^a\left(f\right)=\underset{i}{\bigwedge }\left\{{\phi }_{B_i}\left(f\right)\right|B_i\text{is}\text{connected}\text{and}\text{card}(B_i)=s_l\}\end{array}$$

(2)

where ${\gamma }_B\left(f\right)$ and ${\phi }_B\left(f\right)$ represent respectively the morphological flat opening and closing according to structuring element B [21]. We note that these connected filters can be implemented as binary filters on the stack decomposition of f into upper level sets. Figure 1 illustrates how area opening and area closing modify a simple image f. The image f in this toy example is composed of one black triangle of area equal to 30, 2 diamonds, one black and one white of area equal to 15. Finally the last connected components are 4 white circles and 5 black ones of area equal to 5. When an area opening is used (respectively closing) of threshold $s_l=7$, just the white (respectively black) circles are removed.

Area opening and area closing are very relevant to simplify images, without deforming the contours of the objects remaining. In addition, area opening and closing can be used to produce a multi-scale decomposition of an image. The notion of morphological decomposition is related to the granulometry axiomatic [21]. Let us consider $\left\{{\gamma }_{s_l}^a\right\}$, $1\le l\le S$ and $\left\{{\phi }_{s_l}^a\right\}$, $1\le l\le S$, two indexed families of area openings and closings respectively. Typically, the index l is associated to scale, or more precisely to the surface area. Namely, we have on the one hand:

$$\begin{array}{ccc}\hfill f& =& {\displaystyle \sum _{l=1}^S}({\gamma }_{s_{l-1}}^a\left(f\right)-{\gamma }_{s_l}^a\left(f\right))+{\gamma }_{s_S}^a\left(f\right)\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill f& =& {\phi }_{s_S}^a\left(f\right)-{\displaystyle \sum _{l=1}^S}({\phi }_{s_l}^a\left(f\right)-{\phi }_{s_{l-1}}^a\left(f\right))\hfill \end{array}$$

(4)

On the other hand, we can rewrite the decomposition [15]:

$$\begin{array}{c}\hfill f=1/2\left(({\gamma }_{s_S}\left(f\right)+{\phi }_{s_S}\left(f\right))+{\displaystyle \sum _{l=1}^S}({\gamma }_{s_{l-1}}^a\left(f\right)-{\gamma }_{s_l}^a\left(f\right))-{\displaystyle \sum _{l=1}^S}({\phi }_{s_l}^a\left(f\right)-{\phi }_{s_{l-1}}^a\left(f\right))\right)\end{array}$$

Therefore we have an additive decomposition of the initial image f into S scales, together with the average largest area opening and closing. We remark that the residue $({\gamma }_{s_{l-1}}^a\left(f\right)-{\gamma }_{s_l}^a\left(f\right))$ represents bright details between levels $s_l$ and $s_{l-1}$. Similarly, $({\phi }_{s_l}^a\left(f\right)-{\phi }_{s_{l-1}}^a\left(f\right))$ stands for dark details between levels $s_l$ and $s_{l-1}$. At this point, some issues must be taken into account. First, after decomposing an image into S scales, we have now to deal with an image representation of higher dimensionality. Second, the decomposition may not be optimal since it depends on the discretization of S scales, i.e., size of each scale. In order to illustrate that issue, we have represented in Figure 2a a channel of Pavia hyperspectral image and in Figure 2b its morphological decomposition by area openings that we have over-estimated. As it may be noticed from Figure 2b, the choice of the scales is fundamental in order to avoid a redundant decomposition.

In order to deal with the problem of scale discretization, we propose to use the pattern spectrum that provides information about the image component size distribution. We can also notice another technique to find the optimal discretization [22].

2.3. Pattern Spectrum

The notion of pattern spectrum (PS) [23] corresponds to the probability density function (pdf) underlying a granulometric decomposition by morphological openings and closings [21,24]. The area-based PS of f at size $s_l$ is given by

$$\begin{array}{c}\hfill P{S}^a(f,l)=\left[\text{Mes}({\gamma }_{s_l}^a\left(f\right)-{\gamma }_{s_{l+1}}^a\left(f\right))\right]/\text{Mes}\left(f\right)\end{array}$$

(5)

$$\begin{array}{c}\hfill P{S}^a(f,-l)=\left[\text{Mes}({\phi }_{s_{l+1}}^a\left(f\right)-{\phi }_{s_l}^a\left(f\right))\right]/\text{Mes}\left(f\right)\end{array}$$

(6)

where Mes represents here the integral of the grey-scale image. Two images having the same pattern spectrum have the same morphological distribution according to the choice of the family of openings/closings. Since our goal is to have a non-redundant multi-scale representation with the same morphological representation than the original image, then by sampling the PS and choosing the scales of the distribution which keep it as similar as possible to the image PS, we can expect to find the appropriate discretization of scales. However, one can see in Figure 3, the PS is not a smooth function, and consequently, sampling it with a limited number of scales would not lead to a good result.

Based on the analogy between the PS and probability density function, we can compute its corresponding cumulative pattern spectrum (CPS) for both sides $l\ge 0$ and $l\le 0$. Naturally, this function is smoother than the PS. In order to select the appropriate scales, the CPS for openings and closings are sampled, where the number of samples is fixed and is equal to S, under the constraint that the sampled function must be as similar as possible to the original function.

An example of such sampling is given in Figure 3, where the approximation of the CPS is depicted in red and the CPS of the original image in blue. It is well known in probability that two distributions that have the same cumulative distribution function have the same probability distribution function. Based on this property, we can expect that the discretization from the CPS approximates the original PS of the image and consequently, the selected scales properly represent the size distribution of the image.

2.4. Grey-Scale Distance Function

Let X be the closed set associated to a binary image. The distance function corresponding to set X gives at each point $x\in X$ a positive number that depends on the position of x with respect to X and is given by [25]:

$$\begin{array}{ccc}\hfill dist\left(X\right)\left(x\right)& =& min\{d(x,y):y\in X^c\}\hfill \end{array}$$

(7)

where $d(x,y)$ is the Euclidean distance between points x and y, and where $X^c$ is the complement of set X. This well known transform is very useful in image processing [25].

Distance function of binary images can be extended to grey-scale images f by considering its representation into upper level sets ${\left\{X_h\left(f\right)\right\}}_{a\le h\le b}$, where

$$X_h\left(f\right)=\left\{x\in E:f\left(x\right)\ge h\right\}$$

such that $a=min\left\{f\right(x),x\in E\}$, and $b=max\left\{f\right(x),x\in E\}$. Then, the so-called the grey-scale distance transform of f is defined as [26]:

$$\begin{array}{ccc}\hfill dist\left(f\right)\left(x\right)& =& {(b-a)}^{-1}{\displaystyle \sum _{h=a}^b}dist\left(X_h\left(f\right)\right)\left(x\right)\hfill \end{array}$$

(8)

That is, the grey-scale distance transform of f is equal to the sum of the distance functions from its upper level sets.

3. Morphological Principal Component Analysis

We introduce in this section the notion of Morphological Principal Component Analysis (MorphPCA) and its variants. Before that, a mathematical background on PCA and covariance/correlation matrix is provided in order to state the rationale behind MorphPCA.

3.1. Remind on Classical PCA

Principal Component Analysis (PCA), also known as Karhunen-Loève transform, Hotelling transform, SVD transform, etc., is without any doubt the most useful technique for data dimensionality reduction.

Let us start with a set of vectors $\left\{v_i\right\}\in {\mathbb{R}}^D$, $1\le i\le n$, where n represents the number of vectors; in our case it corresponds to the number of image pixels, i.e., $n=n_1{n}_2$ since $n_1$ and $n_2$ are the two spatial dimensions. The goal of the PCA is to reduce the dimension of this vector space thanks to a projection on the principal component space, namely

$$\begin{array}{c}\hfill F={\left\{v_i\right\}}_{i=1}^n⟶F^{\prime }={\left\{v_i^{\prime }\right\}}_{i=1}^n\end{array}$$

(9)

with $v_i^{\prime }\in {\mathbb{R}}^d$, where $d\ll D$. In our case, dataset $F\in M_{n,D}\left(\mathbb{R}\right)$ represents the hyperspectral image $\mathcal{F}$, where each column $F_k\in {\mathbb{R}}^n$, $1\le k\le D$ corresponds to a vectorized spectral band. PCA should find a projective space such that the mean squared distance between the original vectors and their projections is as small as possible. As we just show, this is equivalent to find the projection that maximizes the variance.

Let us call $w_j\in {\mathbb{R}}^D$, where j are the principal components. The aim of PCA is to find the set of vectors $\{w_j,1\le j\le D\}$ such as

$$\begin{array}{c}\hfill \underset{w_j}{arg\; min}\left[n^{-1}{\displaystyle \sum _{i=1}^n}{\parallel v_i-<v_i,w_j>w_j\parallel }^2\right],\forall 1\le j\le D\end{array}$$

(10)

Developing now the distance we have:

$$\parallel v_i-<v_i,w_j>w_j\parallel ={\parallel v_i\parallel }^2-2{<v_i,w_j>}^2+{<v_i,w_j>}^2·{\parallel w_j\parallel }^2$$

then, by adding the additional constraint that ${\parallel w_j\parallel }^2=1$, replacing in Equation (10), and keeping only terms that depend on $w_j$, we obtain the following new objective function:

$$\begin{array}{c}\hfill \underset{w_j,{\parallel w_j\parallel }^2=1}{arg\; max}{n}^{-1}{\displaystyle \sum _{i=1}^n}{<v_i,w_j>}^2,\forall 1\le j\le D\end{array}$$

(11)

Since

$$var(<v_i,w_j>)=n^{-1}{\displaystyle \sum _{i=1}^n}{(<v_i,w_j>)}^2-{(n^{-1}{\displaystyle \sum _i^n}(<v_i,w_j>))}^2$$

if we consider that the dataset F has been column-centered, which means that ${\sum }_{i=1}^n{v}_i=0$, then $var(<v_i,w_j>)=n^{-1}$ ${\sum }_{i=1}^n{(<v_i,w_j>)}^2$. Thus we can see that the PCA aims at finding principal components that maximize the variance. The problem can be rewritten in a matrix way using the development:

$$\begin{array}{ccc}\hfill n^{-1}{\displaystyle \sum _{i=1}^n}{<v_i,w_j>}^2& =& n^{-1}{\left(F{w}_j\right)}^T\left(F{w}_j\right)\hfill \\ & =& w_j^T\left(n^{-1}\left(F^{T}F\right)\right)w_j=w_j^{T}V{w}_j\hfill \end{array}$$

where $V=n^{-1}\left(F^{T}F\right)$, $V\in M_{D,D}\left(\mathbb{R}\right)$, is the covariance matrix of F. Hence the problem to be optimized is written as

$$\begin{array}{c}\hfill \underset{w_j,{\parallel w_j\parallel }^2=1}{arg\; max}{w}_j^{T}V{w}_j,\forall 1\le j\le D\end{array}$$

(12)

Thanks to Lagrange multiplier theorem, we can rewrite the objective function Equation (12) as:

$$\begin{array}{c}\hfill \mathbf{L}(w_j,\lambda )=w_j^{T}V{w}_j-\lambda (w_j^T{w}_j-1)\end{array}$$

(13)

where $\lambda \in \mathbb{R}$. Since one should maximize this function, we had to derive it and to make it equal to zero, i.e.,

$$\begin{array}{c}\hfill \frac{\partial \mathbf{L}}{\partial w_j}(w_j,\lambda )=2V{w}_j-2\lambda w_j=0\end{array}$$

Finally, we obtain the solution:

$$\begin{array}{c}\hfill V{w}_j=\lambda w_j\end{array}$$

(14)

Thus, the principal component $w_j$ that satisfies the objective function is an eigenvector of the covariance matrix V, and the one maximizing $\mathbf{L}(w_j,\lambda )$ is the one with the largest eigenvalue. Then we can have all the $w_j$ by simply computing the SVD of V.

There are different approaches to choose the reduced dimension d, that is the number of the principal component to be kept. The underlying assumption is the following: if the intrinsic dimension of the data is d, then the remaining $d-D$ eigenvalues, corresponding to the eigenvectors that are discarded, should be significantly small. This principle is expressed using $Prop=$${\sum }_{j=1}^d{\lambda }_j/{\sum }_{j=1}^D{\lambda }_j$, which is equal to the proportion of the original variance kept. Typically, in all our examples we fix Prop = 0.9.

3.2. Covariance Matrix and Pearson Correlation Matrix

The covariance between two channels (or spectral bands) of an hyperspectral image $\mathcal{F}$ is computed as

$$\begin{array}{c}\hfill Covar\left({\mathcal{F}}_{:,:,k},{\mathcal{F}}_{:,:,k^{\prime }}\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^{n_1}}{\displaystyle \sum _{j=1}^{n_2}}\left[{\mathcal{F}}_{i,j,k}-\mathbb{E}\left(\mathcal{F}\right)\right]\left[{\mathcal{F}}_{i,j,k^{\prime }}-\mathbb{E}\left(\mathcal{F}\right)\right]\end{array}$$

(15)

where $\mathbb{E}\left(\mathcal{F}\right)$ is the mean of the hyperspectral image. The covariance is very meaningful; however, this is not a similarity measure [27], in the sense of a metric, since it is not range limited. In order to fulfill this requirement, a solution consists in normalizing the covariance, which leads to the notion of Pearson correlation:

$$\begin{array}{c}\hfill Corr\left({\mathcal{F}}_{:,:,k},{\mathcal{F}}_{:,:,k^{\prime }}\right)={\displaystyle \sum _{i=1}^{n_1}}{\displaystyle \sum _{j=1}^{n_2}}\left[\frac{{\mathcal{F}}_{i,j,k}-\mathbb{E}\left(\mathcal{F}\right)}{{\sigma }_k}\right]\left[\frac{{\mathcal{F}}_{i,j,k^{\prime }}-\mathbb{E}\left(\mathcal{F}\right)}{{\sigma }_k^{\prime }}\right]\end{array}$$

(16)

where ${\sigma }_k={\left[\frac{1}{n}{\sum }_{i=1}^{n_1}{\sum }_{j=1}^{n_2}{\left({\mathcal{F}}_{i,j,k}-\mathbb{E}\left(\mathcal{F}\right)\right)}^2\right]}^{1/2}$ The correlation coefficient varies between $+1$ and $-1$, such that $Corr\left({\mathcal{F}}_{:,:,k},{\mathcal{F}}_{:,:,k^{\prime }}\right)=1$ involves that ${\mathcal{F}}_{:,:,k}$ and ${\mathcal{F}}_{:,:,k^{\prime }}$ perfectly coincide. It has been proved that the best fitting case corresponds to [28]:

$$\begin{array}{c}\hfill {\mathcal{F}}_{i,j,k}=Corr\left({\mathcal{F}}_{:,:,k},{\mathcal{F}}_{:,:,k^{\prime }}\right)\frac{{\sigma }_k}{{\sigma }_k^{\prime }}({\mathcal{F}}_{i,j,k^{\prime }}-\mathbb{E}\left(\mathcal{F}\right))+\mathbb{E}\left(\mathcal{F}\right)\end{array}$$

(17)

Therefore, from Equation (17), we can see that the correlation is a linear coefficient between ${\mathcal{F}}_{i,j,k}$ and ${\mathcal{F}}_{i,j,k^{\prime }}$. This means that Pearson correlation is a similarity criterion which depends on the intensities of the images and their linear relations.

3.3. MorphPCA and Its Variants

The fundamental idea of MorphPCA consists in replacing the covariance matrix V of PCA, which represents the statistical interaction of spectral bands, by a covariance matrix $V_{\text{Morpho}}$ computed from a morphological representation of the bands. Therefore, mathematical morphology is fully integrated in the dimensionality reduction problem by standard SVD computation to solve

$$V_{\text{Morpho}}{w}_j={\lambda }_j{w}_j$$

The corresponding principal components $w_j$ provide the projection space for the hyperspectral image $\mathcal{F}$. This principle is illustrated in the diagram of Figure 4.

We propose three variants of MorphPCA which are summarized in the flowchart of Figure 5, Figure 6 and Figure 7. An example of three different bands embedded in the space produced by these MorphPCA techniques is depicted in Figure 8.

3.3.1. Scale-Space Decomposition MorphPCA

In the first variant, we just use the area-based nonlinear scale-space discussed in the previous section. So the grey-scale image of each spectral band ${\mathcal{F}}_{:,:,k}$ is decomposed into residues of area openings and area closings according to the discretization into S scales for each operator, i.e., $r_l\left({\mathcal{F}}_{:,:,k}\right)={\gamma }_{s_{l-1}}^a\left({\mathcal{F}}_{:,:,k}\right)-{\gamma }_{s_l}^a\left({\mathcal{F}}_{:,:,k}\right)$ and $r_{-l}\left({\mathcal{F}}_{:,:,k}\right)={\phi }_{s_l}^a\left({\mathcal{F}}_{:,:,k}\right)-{\phi }_{s_{l-1}}^a\left({\mathcal{F}}_{:,:,k}\right)$, $1\le l\le S$. Thus we have increased the dimensionality of the initial dataset from a tensor $(n_1,n_2,D)$ to a tensor $(n_1,n_2,D,2S+1)$. As discussed in [15], this tensor can be reduced using high order-SVD techniques. We propose here to simply compute a covariance matrix as the sum of the covariance matrices from the various scales. More precisely, we introduce $V_{\text{Morpho-1}}\in M_{D,D}\left(\mathbb{R}\right)$ with:

$$\begin{array}{ccc}\hfill V_{\text{Morpho-1}}& =& {\displaystyle \sum _{l=1}^S}\left(V\left(l\right)\right)+{\displaystyle \sum _{l=1}^S}\left(V(-l)\right)\hfill \end{array}$$

(18)

where the covariance matrices at each scale l is obtained as

$$V{\left(l\right)}_{k,k^{\prime }}=Covar\left(r_l\left({\mathcal{F}}_{:,:,k}\right),r_l\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right),1\le k,k^{\prime }\le D$$

We note that it involves an assumption of independence of the various scales. We remark also that this technique is different from the classical approaches of differential profiles as [5] where the morphological decomposition is applied after computing the spectral PCA (i.e., morphology plays a role in spatial/spectral classification but not for spatial/spectral dimensionality reduction as in our case).

3.3.2. Pattern Spectrum MorphPCA

In the second variant, we can consider a very compact representation of the morphological information associated to the area-based nonlinear scale-space of each spectral band. It simply involves considering the area-based PS of each spectral band as the variable to be used to find statistical redundancy on the data. In other words, the corresponding covariance matrix $V_{\text{Morpho-2}}\in M_{D,D}\left(\mathbb{R}\right)$ is defined as:

$$\begin{array}{ccc}\hfill V_{\text{Morpho-2}k,k^{\prime }}& =& Covar\left(P{S}^a({\mathcal{F}}_{:,:,k},l),P{S}^a({\mathcal{F}}_{:,:,k^{\prime }},l)\right)\hfill \end{array}$$

(19)

with $1\le k,k^{\prime }\le D$ and where $P{S}^a({\mathcal{F}}_{:,:,k},l)$, $-S\le l\le S$, is the area-based pattern spectrum obtained by area-openings and area-closings. We note that the pattern spectrum can be seen as a kind of pdf of image structures. Consequently the MorphPCA associated to it explores the intrinsic dimensionality of sets of distributions instead of sets of vectors. For illustrating the information carried out by the PS, we have provided in Figure 8 the pattern spectra computed from three different bands of a hyperspectral image.

In order to better understand the interest of $V_{\text{Morpho-2}}$, we propose an analysis based on its Pearson correlation counterpart. Once the correlation of PS distribution is calculated, we have a linear coefficient between $P{S}^a({\mathcal{F}}_{:,:,k},l)$ and $P{S}^a({\mathcal{F}}_{:,:,k^{\prime }},l)$. However, since the PS is the result of nonlinear operations, the underlying extracted features are naturally nonlinear.

Let us consider the two binary images of Figure 9a, which represent two objects having exactly the same size. If the correlations are calculated, we have:

$$\begin{array}{ccc}\hfill Corr\left(\text{image}1,\text{image}2\right)& =& 0\hfill \\ \hfill Corr\left(P{S}^a\left(\text{image}1\right),P{S}^a\left(\text{image}2\right)\right)& =& 1\hfill \end{array}$$

Hence, we can see that the morphological distribution being the same, the PS correlation is maximal. In a certain way, we observe that this transform builds size-invariants from the images and consequently it is robust to some groups of transforms and deformations. For instance, it is invariant to rotation and to translation.

Classical PCA on the spectral bands and the MorphPCA based on the PS can be compared by the corresponding correlation matrices from a hyperspectral image, such as the example plotted in Figure 10a,b. From this visualization, we already observe that the bands are better discriminated between them.

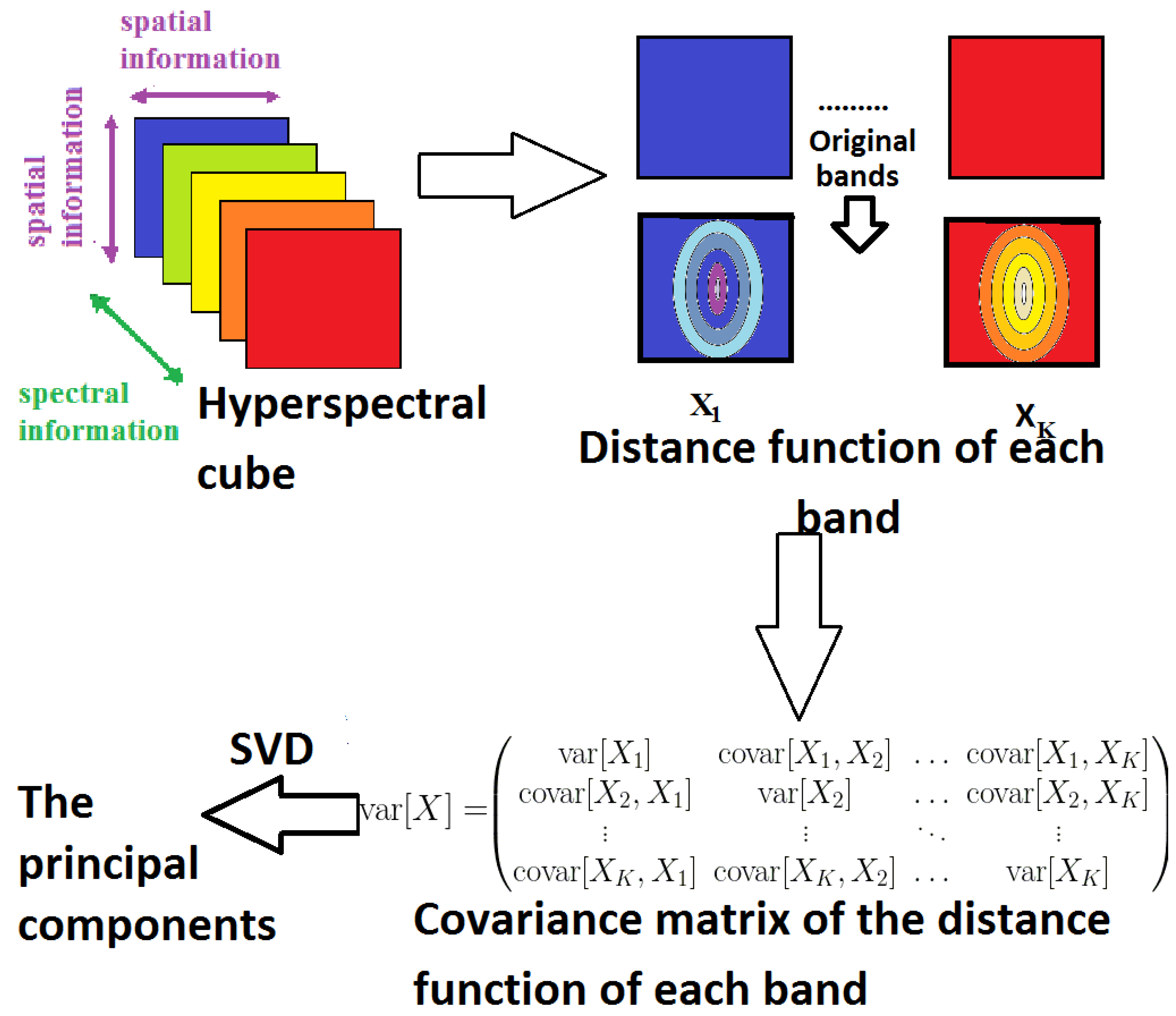
3.3.3. Distance Function MorphPCA

Classical PCA for hyperspectral images is based on exploring covariances between spectral intensities. The previous MorphPCA involves changing the covariance into a morphological scale-space representation of the images. An alternative is founded when transforming each spectral band from an intensity based map to a metric based map where at each pixel the value is associated to both the initial intensity and the spatial relationships between the image structures. This objective can be achieved using the Molchanov grey-scale distance function [26] for each spectral band $dist\left({\mathcal{F}}_{:,:,k}\right)$. The new covariance matrix $V_{\text{Morpho-3}}\in M_{D,D}\left(\mathbb{R}\right)$ is now defined as:

$$\begin{array}{ccc}\hfill V_{\text{Morpho-3}k,k^{\prime }}& =& Covar\left(dist\left({\mathcal{F}}_{:,:,k}\right),dist\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right)\hfill \end{array}$$

(20)

with $1\le k,k^{\prime }\le D$. Figure 8 depicts the corresponding grey-scale distance function from three spectral band of a hyperspectral image. We note that this function carries out simultaneously both intensity and shape information from the image.

Let consider in detail the expression of the covariance of distance functions:

$$\begin{array}{c}\hfill Covar\left(dist\left({\mathcal{F}}_{:,:,k}\right),dist\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right)=\\ \hfill Covar\left({\displaystyle \sum _{h=min\left({\mathcal{F}}_{:,:,k}\right)}^{max\left({\mathcal{F}}_{:,:,k}\right)}}d\left(X_s\left({\mathcal{F}}_{:,:,k}\right)\right),{\displaystyle \sum _{h^{\prime }=min\left({\mathcal{F}}_{:,:,k}\right)}^{max\left({\mathcal{F}}_{:,:,k}\right)}}d\left(X_{h^{\prime }}\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right)\right)=\\ \hfill {\displaystyle \sum _{h=min\left({\mathcal{F}}_{:,:,k}\right)}^{max\left({\mathcal{F}}_{:,:,k}\right)}}{\displaystyle \sum _{h^{\prime }=min\left({\mathcal{F}}_{:,:,k}\right)}^{max\left({\mathcal{F}}_{:,:,k}\right)}}Covar\left(d\left(X_h\left({\mathcal{F}}_{:,:,k}\right)\right),d\left(X_{h^{\prime }}\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right)\right)\end{array}$$

where $X_h\left({\mathcal{F}}_{:,:,k}\right)$ denotes an upper level set at threshold h. The central term is the covariance between two binary distance functions and can be developed as follows:

$$\begin{array}{c}\hfill Covar\left(d\left(X_h\left({\mathcal{F}}_{:,:,k}\right)\right),d\left(X_{h^{\prime }}\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right)\right)=\\ \hfill \mathbb{E}\left(d\left(X_h\left({\mathcal{F}}_{:,:,k}\right)\right),d\left(X_{h^{\prime }}\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right)\right)-\mathbb{E}\left(d\left(X_h\left({\mathcal{F}}_{:,:,k}\right)\right)\right)\mathbb{E}\left(d\left(X_{h^{\prime }}\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right)\right)=\\ \hfill n^{-1}<d\left(X_h\left({\mathcal{F}}_{:,:,k}\right)\right),d\left(X_{h^{\prime }}\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right){>}_{L^2}-\mathbb{E}\left(d\left(X_h\left({\mathcal{F}}_{:,:,k}\right)\right)\right)\mathbb{E}\left(d\left(X_{h^{\prime }}\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right)\right)\end{array}$$

where $<·,·{>}_{L^2}$ denotes the $L^2$ inner product. Using the classical relationship:

$$\begin{array}{c}\hfill {\parallel A-B\parallel }_{L^2}^2={\parallel A\parallel }_{L^2}^2+{\parallel B\parallel }_{L^2}^2-2<A,B{>}_{L^2},\forall A,B\in {\mathbb{R}}^n\end{array}$$

we finally obtain that:

$$\begin{array}{c}\hfill Covar\left(d\left(X_h\left({\mathcal{F}}_{:,:,k}\right)\right),d\left(X_{h^{\prime }}\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right)\right)={\left(2n\right)}^{-1}({\parallel d\left(X_h\left({\mathcal{F}}_{:,:,k}\right)\right)\parallel }_{L^2}^2+{\parallel d\left(X_{h^{\prime }}\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right)\parallel }_{L^2}^2)\\ \hfill -{\left(2n\right)}^{-1}{\parallel d\left(X_h\left({\mathcal{F}}_{:,:,k}\right)\right)-d\left(X_{h^{\prime }}\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right)\parallel }_{L^2}^2-n^{-1}{\parallel d\left(X_h\left({\mathcal{F}}_{:,:,k}\right)\right)\parallel }_{L^2}^2{\parallel d\left(X_{h^{\prime }}\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right)\parallel }_{L^2}^2\end{array}$$

From this latter expression, the term

$$\parallel d\left(X_h\left({\mathcal{F}}_{:,:,k}\right)\right)-d\left(X_{h^{\prime }}\left({\mathcal{F}}_{:,:,k^{\prime }}\right)\right){\parallel }_{L^2}^2$$

can be identified as the Baddeley distance [29] used in shape analysis. This distance is somehow equivalent to the most classical Hausdorff distance between the upper level sets h of spectral band k and $h^{\prime }$ of spectral band $k^{\prime }$. Thus, the underlying similarity from this covariance compares the shape of the spectral channels, and extracts a richer description than Pearson correlation from the spectral channels themselves. We note that the use of Hausdorff distance between upper level sets of hyperspectral bands was previously used in [30].

Finally, to illustrate qualitatively the behavior of the distance function correlation, let us consider this time the three binary images depicted in Figure 9b, where image 2 and image 3 represent the same object placed at a different location on the image. One has:

$$\begin{array}{ccc}\hfill Corr\left(\text{image}1,\text{image}2\right)& =& Corr\left(\text{image}1,\text{image}3\right)\hfill \\ \hfill Corr\left(dist\left(\text{image}1\right),dist\left(\text{image}2\right)\right)& \ne & Corr\left(dist\left(\text{image}1\right),dist\left(\text{image}3\right)\right)\hfill \end{array}$$

That is, this similarity criterion related to the use of distance function is more discriminative to the relative position of the objects on the image than the classical Pearson Correlation.

From Figure 10c, one can compare now the correlation matrix using the grey-scale distance function with the usual correlation matrix Figure 10a. We note that this matrix provided also a better discrimination of bands cluster than the Pearson correlation matrix used in standard PCA.

3.3.4. Spatial/Spectral MorphPCA

As we have discussed, $V_{\text{Morpho-2}}$ represents a compact morphological representation of the image; however, the spectral intensity information is also important for dimensionality reduction. To come with a last variant of MorphPCA, we build another covariance matrix $V_{\text{Morpho-4}}$ that represents the spectral and spatial information without increasing the dimensionality by the sum of two covariance matrices:

$$\begin{array}{c}\hfill V_{\text{Morpho-4}}{}_{\beta }=(1-\beta )V+\beta V_{\text{Morpho-2}}\end{array}$$

(21)

with $\beta \in [0,1]$, and where obviously $V_{k,k^{\prime }}=$ $Covar\left({\mathcal{F}}_{:,:,k},{\mathcal{F}}_{:,:,k^{\prime }}\right)$ and β stands for a regularization term that balances the spatial over the spectral information. This kind of linear combination of covariance matrices is similar to the one used in the combination of kernels, where kernels providing different information sources are combined to have a new kernel which integrates the various contributions [12].

4. MorphPCA Applied to Hyperspectral Images

4.1. Criteria to Evaluate PCA vs. MorphPCA

We can now use PCA and the four variants of MorphPCA to achieve dimensionality reduction (DR) of hyperspectral images. In order to evaluate the interest for such a purpose, it is necessary to establish quantitative criteria that should be assessed. These criteria will evaluate both locally and globally the effectiveness of the dimension reduction techniques.

• Local criteria.

  Criterion 1 (C1) 

  The reconstructed hyperspectral image $\tilde{\mathcal{F}}$ using the first d principal components should be a regularized version of $\mathcal{F}$ in order to be more spatially sparse.

  Criterion 2 (C2) 

  The reconstructed hyperspectral image $\tilde{\mathcal{F}}$ using the first d principal components should preserve local homogeneity and be coherent with the original hyperspectral image $\mathcal{F}$.

  Criterion 3 (C3) 

  The manifold of variables (i.e., intrinsic geometry) from the reconstructed hyperspectral image $\tilde{\mathcal{F}}$ should be as similar as possible to the manifold from original hyperspectral image $\mathcal{F}$.

• Global criteria.

  Criterion 4 (C4) 

  The number of bands d of the reduced hyperspectral image should be reduced as much as possible. It means that a spectrally sparse image is obtained.

  Criterion 5 (C5) 

  The reconstructed hyperspectral image $\tilde{\mathcal{F}}$ using the first d principal components should preserve the global similarity with the original hyperspectral image $\mathcal{F}$. Or in other words, it should be a good noise-free approximation.

  Criterion 6 (C6) 

  Separability of spectral classes should be improved in the dimensionality reduced space. That involves in particular a better pixel classification.

These criteria are used to analyze the effectiveness of the DR methods studying locally and globally their ability to remove redundancy and to preserve the fully richness of the spectral and spatial information.

In order to assess C1, we compute the watershed transform [25] on each channel ${\mathcal{F}}_k$ of the hyperspectral image. Watershed transform is a morphological image segmentation approach which in a certain way can be seen as an unsupervised classification technique. The advantage of using the watershed is that it allows us to cluster the image according to the local homogeneity; thus, an image with less details will have less spatial classes than an image with many insignificant details. Then, the number of clusters $\parallel N_k\parallel$ of ${\mathcal{F}}_k$ is considered as an estimation of the image complexity. To evaluate the complexity of the reconstructed hyperspectral image, the number of spatial classes is counted after having done a watershed on each band. Finally, the mean of the number of spatial classes is taken, i.e.,

$${Error}_{\text{sparse}\text{spatially}}=\left(D^{-1}\right){\displaystyle \sum _{k=1}^D}\parallel N_k\parallel$$

Assessment of C2, which involves image homogeneity, is based on a partition of the image into homogenous regions. Let us first remind the definition of a α-flat zones [31], used for such a purpose. Given a distance $d:{\mathbb{R}}^D\times {\mathbb{R}}^D⟶\mathbb{R}$, two pixels $(f\left(x\right),f\left(y\right))\in {\left({\mathbb{R}}^D\right)}^2$, from a vector-valued image f, belong to the same α-flat zone of f if and only if there is a path $(p_0,\dots ,p_n)\in E^n$ such as $p_0=x$ and $p_n=y$ and $\forall i\in [1,n-1]$, $d\left(f\left(p_i\right),f\left(p_{i+1}\right)\right)\le \alpha$, with $\alpha \in {\mathbb{R}}^{+}$. Computing the α-flat zones for a given value of α produces therefore a spatial partition of the image into classes such that in each connected class the image values are linked by paths of local bounded variation. Working on the d eigenvectors, the image partition ${\pi }_{\alpha }$ associated to the α-flat zones quantize spatially and spectrally an hyperspectral image, see example given in Figure 11. The goal of simultaneous spatial and spectral quantization of a hyperspectral image has been studied in [32], where we have studied in detail the dependency on the distance. Moreover, we have shown that in high dimensional spaces quantization results are generally not good. For the case considered here, we propose to use the Euclidean distance on the reduced space by PCA or MorphPCA. The choice of α is done in order to guarantee a number C of α-flat zones similar for all the compared approaches. We can expect that, by fixing the number of zones in the partition, the difference between a partition and another one depends exclusively on the homogeneity of the image. Now, using the partition ${\pi }_{\alpha }$, the spectral mean value of pixels from the original image $\mathcal{F}$ in each spatial zone is computed. This quantization produces a simplified hyperspectral image, denoted ${\overline{\mathcal{F}}}^{{\pi }_{\alpha }}$. Finally, we assess how far pixels of the original image from each α-flat zone are from their mean; which involves computing the following error

$${Error}_{\text{Homg}}={\displaystyle \sum _{k=1}^D}{\displaystyle \sum _{i,j=1}^{n_1,n_2}}{|{\mathcal{F}}_{i,j,k}-{\overline{\mathcal{F}}}_{i,j,k}^{{\pi }_{\alpha }}|}^2$$

This criterion can consequently be seen as a way to see the trustworthiness of the DR technique, since it measures if the homogeneous partition of the reduced hyperspectral image corresponds to the homogeneous zone of the original image.

C3 has been evaluated by means of two manifold learning criteria called the K-intrusion and K-extrusion [33]. They are based on other criteria called continuity and trustworthiness [34]. These criteria reveal DR behavior in terms of its ability to preserve the data manifold structure. We have first sampled randomly 10 thousands spectra from our hyperspectral images, where each spectrum is a vector of dimension D. Then we have modelled the manifold by a graph where each node is a vector and each edge is the pairwise distance. We used the Euclidean distance as the pairwise distance. For the rest of the paragraph we note by $x_i$ a point from the original manifold, ${\nu }_i^K$ its neighborhood of size K, ${\tilde{x}}_i$ the same point from the manifold after a DR and ${\tilde{\nu }}_i^K$ its corresponding neighborhood of size K. A neighborhood of size K at point $x_i$ is composed of the K closest points to $x_i$ according to used metric. More precisely, the goal of K-extrusion is to measure how the points that were in the K-neighborhood of $x_i$ are not preserved in the K-neighborhood of ${\tilde{x}}_i$ after DR. The K-intrusion evaluates if points on the K-neighborhood of ${\tilde{x}}_i$ on the DR manifold were in the K-neighborhood of $x_i$, i.e.,

$$\begin{array}{ccc}\hfill M_{\text{intrusion}}\left(K\right)& =& 1-\frac{2}{G\left(K\right)}\times {\displaystyle \sum _{i=1}^n}\sum _{j\in {\tilde{\nu }}_i^K\backslash {\nu }_i^K}r(i,j)-K\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill M_{\text{extrusion}}\left(K\right)& =& 1-\frac{2}{G\left(K\right)}\times {\displaystyle \sum _{i=1}^n}\sum _{j\in {\nu }_i^K\backslash {\tilde{\nu }}_i^K}r(\tilde{i},j)-K\hfill \end{array}$$

(23)

where $r(i,j)$ is the rank of the data $x_j$ in the ordering according to the distance from $x_i$, and respectively $r(\tilde{i},j)$ the rank of ${\tilde{x}}_j$ in the ordering according to the distance from ${\tilde{x}}_i$, and the term $G_K$ scales the measure to be between zero and one, i.e.,

$$\begin{array}{c}\hfill G\left(K\right)=\left\{\begin{array}{c}NK(2N-3K-1) if K<N\backslash 2\\ N(N-K)(N-K-1) if K\ge N\backslash 2\end{array}\right.\end{array}$$

(24)

For a better understanding of these formulae, see [35]. An important point is the dependence of these parameters on the size of the neighborhood. From Equations (22) and (23), the following parameters are computed [35]:

$$\begin{array}{ccc}\hfill Q\left(K\right)& =& \frac{M_{\text{extrusion}}\left(K\right)+M_{\text{intrusion}}\left(K\right)}{2}\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill B\left(K\right)& =& M_{\text{intrusion}}\left(K\right)-M_{\text{extrusion}}\left(K\right)\hfill \end{array}$$

(26)

The interest of $Q\left(K\right)$ is that it estimates in average the quality of a DR technique, whereas $B\left(K\right)$ reveals its behavior as being more intrusive or extrusive.

In order to assess C4, as classically done, the fraction of explained covariance is fixed. Then, the number of principal components needed is counted. The rationale is based on the fact that a good DR technique should reduce the number of dimensions and extract a limited number of features that would explain most of the image. However, since this criterion is linked to a sparsity criterion, we would like to add a distortion criterion, C5.

The evaluation of C5 is founded on computing a pattern spectrum of both the original hyperspectral image and the DR image. An important point is that the pattern spectrum will be computed by openings on the hyperspectral image viewed as a 3D image. By doing such assumption, the 3D openings are decomposing in a simultaneous way the spatial/spectral object of the image and the corresponding curves of the PS will represent the distribution of both the spatial and the spectral objects. Two hyperspectral images are similar if they have the same spectral/spatial size distribution. As discussed in Section 2, we prefer to use the cumulative PS in order to obtain a smoother curve. Normally we cannot deal with both spatial/spectral distortions with the reconstruction error of the two images. However we will also assess the SNR of the reconstruction error as an additional parameter.

Finally, C6 is related to supervised pixel classification of the hyperspectral image. We have considered the least square SVM algorithm [11] as a learning technique, with a linear kernel or RBF kernel, where the RBF kernel is initialized for each DR technique using cross validation. For each supervised classification run, we used for the AVIRIS Indian Pine Image 5% of the available data as a training set and the remaining 95% to validate. For the ROSIS Pavia University image we use a subset of 50 spectra (about 1% of the available data) per class as a training set and the remaining spectra to validate.

4.2. Evaluation of Algorithms

The studied DR techniques presented are listed and compared upon three mathematical and computing properties in

Table 1. Comparison of the properties of dimensionality reduction algorithms for hyperspectral images.

Technique	Parameter (1)	Computational (2)	Memory (3)
PCA	Prop	$O\left(D^3\right)$	$O\left(D^2\right)$
MorphPCA Morpho-1	Prop, S	$O\left(Dn{S}_S(2S+1)\right)$	$O\left(D^2(2S+1)\right)$
MorphPCA Morpho-2	Prop	$O\left(Dn{S}_S(2S+1)\right)$	$O\left(D^2\right)$
MorphPCA Morpho- 3	Prop	$O\left(Dn\right(b-a\left)\right)$	$O\left(D^2\right)$
MorphPCA Morpho-4 β	Prop, β	$O\left(Dn{S}_S(2S+1)\right)$	$O\left(2D^2\right)$
KPCA	Prop, K	$O\left(n^3\right)$	$O\left(n^2\right)$

. These properties were also considered in the excellent comparative review [3]. For comparison, we have also included in the table the Kernel-PCA (KPCA), which is a powerful generalization of PCA allowing integrating morphological and spatial features into DR.

The first one is the number of free parameters to be chosen. The interest of having these free parameters is that it provides more flexibility to the techniques, whereas the related inconvenient is the difficulty for properly tuning the right parameter. We notice that KPCA provides good flexibility thanks to the choice of any possible kernel which fits the data geometry. The most simple algorithms are the PCA, and the distance function MorphPCA. Then, we have the scale-space decomposition MorphPCA, and finally the pattern spectrum MorphPCA. The second issue analyzed is the computational complexity, and the third one is the memory requirements. From a computational viewpoint, the most demanding step in the PCA is the SVD, which can be done in $O\left(D^3\right)$. PCA is the technique with the smallest computational need. On the contrary, the computational requirement of KPCA is $O\left(n^3\right)$; since $n\gg D$, this kind of algorithm seems infeasible in standard hyperspectral images. That is the reason why most of hyperspectral KPCA techniques use tricks to be able to deal with the high number of spectra [13,36,37]. All these techniques lead to a spatial distortion, which is not avoidable by the need of a sampling procedure aiming at reducing the number of spectra. Between the complexity of PCA and KPCA, we have our proposed MorphPCA algorithms. Regarding MorphPCA, the computationally demanding step is the computation of the morphological representation used in the corresponding covariance matrix. The complexity estimation has been carried out each time in the worse case; however, efficient morphological algorithms can improve this part. Distance function MorphPCA is last demanding, then the scale-space decomposition MorphPCA and finally the pattern spectrum MorphPCA. Regarding memory needs, for the PCA, the pattern spectrum MorphPCA, and the distance function MorphPCA, the steps requiring more memory is the storage of the covariance matrix, just of $O\left(D^2\right)$. The Spatial/Spectral MorphPCA needs to store 2 covariance matrices then its memory need is $O\left(2D^2\right)$; similarly the scale-space MorphPCA needs to store $2S+1$ covariance matrices, then its required memory is $O\left((2S+1)D^2\right)$. Note that KPCA uses a Gram matrix of size $(n\times n)$.

4.3. Evaluation on Hyperspectral Images

The assessment of the performance of PCA and MorphPCA has been carried out on three hyperspectral images. The first image was acquired over the city of Pavia (Italy) and it represents the university campus. The dimensions of the image are $610\times 340$ pixels, with $D=103$ spectral bands and its geometrical resolution is of 1.3 m. We also used a second hyperspectral image which represents the University of Houston campus and the neighboring urban area at the spatial resolution of 2.5 m and which dimensions are $349\times 1905$ pixels and $D=144$ spectral bands [19]. The third image, acquired over the region of the Indian Pines test site in North-western Indiana, is composed for two-thirds of agriculture, and one-third of forest. The dimensions of this image are $145\times 145$ pixels, $D=224$ spectral bands and its geometrical resolution is of 3.7 m.

We have applied classical PCA and the different variants of MorphPCA to Pavia hyperspectral image. Figure 12 shows the first three eigenimages, visualized as a RGB false color. We note that the pattern spectrum MorphPCA requires $d=5$ to represent 92% of the variance whereas the other approaches only impose $d=3$. An interesting aspect observed on the projection of the 103 spectral channels of Pavia hyperspectral image into the first two eigenvectors is how PCA and the scale-space decomposition MorphPCA cluster the bands linearly, see Figure 13a,b. Bands close in the projection are also near in the spectral domain, whereas the pattern spectrum MorphPCA, Figure 13c, and distance function MorphPCA, Figure 13d, tend to cluster spectral bands which are not necessary spectrally contiguous. This can be explained thanks to Figure 10, where the MorphPCA correlation matrices are different from the classical PCA one.

It can be noticed that in classical manifold learning techniques, the goal is to decrease the dimension of the data while keeping some properties on the data manifold. We work here on the manifold of the channels. This manifold is easier to use, but finding the good β in $V_{\text{Morpho-4}}{}_{\beta }$ that would maintain some properties of the manifold is not always easy, since we had to deal with a double optimization problem, i.e., β and d.

From a quantitative viewpoint, one can see in

Table 2. Comparison of PCA and MorphPCA analysis using criteria C1 and C2: (a) for Pavia hyperspectral image; (b) for Houston hyperspectral image; (c) for Indian Pines hyperspectral image. The values have been normalized to the worst case, which gives 100.

(a)
	V	VMorpho-1	VMorpho-2	VMorpho-3
ErrorHomg	100	100	95.9	79.3
Errorsparse spatially	99.8	99.7	100	88.3
		VMorpho-4 β β = 0.8	VMorpho-4 β β = 0.2	VMorpho-4 β β = 0.5
ErrorHomg		93.2	83.9	88.3
Errorsparse spatially		93.3	96.7	98.6
(b)
	V	VMorpho-1	VMorpho-2	VMorpho-3
ErrorHomg	100	90.4	35.3	38.3
Errorsparse spatially	97.7	97.6	100	89
(c)
	V	VMorpho-1	VMorpho-2	VMorpho-3
ErrorHomg	98.1	100	96.5	97.8
Errorsparse spatially	91	100	91.2	82.7

that globally MorphPCA produces a more homogenous regularization of the image than classical PCA, especially the distance function MorphPCA and Spatial/Spectral MorphPCA with an appropriate $\beta =0.2$, which gives the lowest values of ${Error}_{\text{Homg}}$. We noted that ${Error}_{\text{sparse}\text{spatially}}$ follows a different ranking. A good method is the one with a good trade-off between both criteria, since one wants a DR to be trustworthy, which is evaluated thanks to ${Error}_{\text{Homg}}$. However, if the signal is too noisy, one may prefer a sparser representation. According to these criteria, the distance function MorphPCA and the pattern spectrum MorphPCA seem to have the best result. We can also note that if we use manifold learning parameters for criterion C3, see Figure 14, the pattern spectrum MorphPCA has the best results.

With respect to criterion C5, we have computed the 3D pattern spectrum distribution of Pavia hyperspectral image and of the different reduced images into d components, see Figure 15. From this result, we can see that both PCA and scale-space decomposition MorphPCA follow very well the hyperspectral image, since their spatial and spectral cumulative distributions are similar. However, if one would like to denoise the hyperspectral image thanks to a DR technique, these results are not always positive. If we compare the spatial and spectral cumulative distribution of the distance function MorphPCA and the one of the hyperspectral image, we notice that for small 3D size (i.e., small spatial/spectral variations) that can be considered as noise, there are differences between these two distributions. However, when the size increases, the distribution of the the distance function MorphPCA tends to the hyperspectral image one. So it seems that the distance function MorphPCA simplifies the spectral/spatial noise, considered as the small 3D objects, but keeps the objects of interest.

Finally,

Table 3. Comparison of hyperspectral supervised classification on PCA and MorphPCA spaces using least square SVM algorithm and different kernels: (a) Pavia hyperspectral image; (b) Indian Pines hyperspectral image.

(a) Pavia Image
	Overall Accuracy with Linear Kernel	Overall Accuracy with RBF Kernel	Kappa Statistic with RBF Kernel
V	51.51 ± 0.9	84.9 ± 3.1	0.84 ± 1 × 10−4
VMorpho-1	59.6 ± 2.2	85.8 ± 2.6	0.84 ± 1 × 10−4
VMorpho-2	56.99 ± 1.1	85.2 ± 2.1	0.84 ± 1 × 10−4
VMorpho-3	59.9 ± 2.5	86.0 ± 1.9	0.84 ± 1 × 10−4
VMorpho-4 β, β = 0.2	61.0 ± 1.73	85.2 ± 1.1	0.83 ± 1 × 10−4
VMorpho-4 β, β = 0.5	59.9 ± 1.5	84.6 ± 1.0	0.83 ± 1 × 10−4
VMorpho-4 β, β = 0.8	57.87 ± 3	84.7 ± 2.5	0.83 ± 2 × 10−4
(b) Indian Pine image
	Overall Accuracy with Linear Kernel	Overall Accuracy with RBF Kernel	Kappa Statistic with RBF Kernel
V	43.9 ± 3.6	75.2 ± 3.7	0.73 ± 4.3 × 10−4
VMorpho-1	50.5 ± 3.8	79.6 ± 3.7	0.78 ± 4 × 10−4
VMorpho-2	41.5 ± 3.8	66.6 ± 4.6	0.63 ± 4.5 × 10−4
VMorpho-3	51.3 ± 3.2	79.1 ± 3.2	0.77 ± 3.7 × 10−4
VMorpho-4 β, β = 0.2	43.5 ± 3.3	75.1 ± 2.3	0.72 ± 2.6 × 10−4
VMorpho-4 β, β = 0.5	43.1 ± 2.9	71.2 ± 2.6	0.68 ± 3 × 10−4
VMorpho-4 β, β = 0.8	43.0 ± 2.2	69.7 ± 3.3	0.67 ± 3.9 × 10−4

summarizes the results of supervised classification of respectively Pavia and Indian Pine hyperspectral images. We note that results for Pavia image are quite similar in all the cases even if MorphPCA seems to be better than PCA. Therefore, we have chosen to focus on the Indian Pine image, which is more challenging for supervised classification benchmark, see also Figure 16 and Figure 17. We note that MorphPCA improves the results, especially the scale-space decomposition MorphPCA. To evaluate the classification results, first we fixed the dimension d of the reduce image. We have chosen $d=5$. Then, we used the least square SVM, which is a multi-class classification technique, contrary to classical two-class SVM. We also used two simple kernels: the linear one, which is the simplest one, and the RBF one, which is appropriate for hyperspectral images since we can assume that these data follow Gaussian distribution. Finally, we study the influence of dimension d and of the size of the training set on the different DR techniques over the classification results. For this purpose we have depicted in Figure 18 and Figure 19 the evolution of the kappa statistics. From the latter plot we can see that the PCA and the pattern spectrum PCA have the worst results. By combining the spectral and the spatial information, a better classification can be achieved. This is the case of the distance function MorphPCA, the scale-space decomposition MorphPCA, and the Spatial-Spectral MorphPCA for $\beta =0.2$.

5. Conclusions

We have shown in this paper how to introduce spatial information in the process of dimensionality reduction thanks to mathematical morphology operators. The representation techniques that we introduced in the paper are based on the notion the MorphPCA. As we said in the introduction, it might be possible to consider for such purpose a Kernel Principal Component Analysis (KPCA), where the kernel handles jointly spatial and spectral information. However, as discussed in Section 4.2, KPCA needs a Gram matrix of size $n\times n$, where n is the number of pixels. It is impossible to manipulate such a matrix with our test images on a standard computer. That is why there are some works trying to approximate the gram matrix in order to perform the KPCA. Some of them consider a small subset of the data which can be chosen randomly or according to some spatial information. This kind of approach has been used with hyperspectral images for spectral-spatial processing. However, these kind of works approximate the kernel, to perform dimensionality reduction on the considered Hilbert space. Here dimensionality reduction is done on the space of the data without any approximation on the morphological covariance $V_{\text{Morpho}}$.

That is why we proposed techniques that are simple in computation and in memory storage and that can reduce the dimension while considering the spatial information. To assess these techniques we used typical criteria of dimensionality reduction which evaluate the fact that some properties are kept on the manifold of data after the dimensionality reduction. Moreover, we also proposed some criteria to evaluate the quality of the image after the dimensionality reduction. Some of them are based on mathematical morphology, namely the 3D pattern spectrum and the α-flat zone to check that the reconstructed image preserves global and local similarity to the original hyperspectral image. Finally, we also perform a classification of the reduced data with different techniques. According to the entire set of criteria, adding spatial information improves the dimensionality reduction. However, as we can see a good dimensionality reduction is obtained when we combine spatial and spectral feature space. A technique that seems to fulfil this optimum is the MorphPCA based on the distance function.

Finally, PCA has multiple applications on image processing; typically one can use the PCA to perform denoising. For example in the case of multiple images representing the same scene but corrupted by a Gaussian noise (like on multi-temporal images), it is possible to use the PCA to reduce the dimension of the temporal data and then to project the data back on the high dimensional space, so that we reduce the influence of the noise. This process can be done with MorphPCA. Moreover, another case would be to use MorphPCA on fusion of information techniques like pansharpening, which consists of increasing the spatial resolution of a multispectral or hyperspectral image thanks to a grey scale image at high resolution. Some techniques for pansharpening are based on PCA. In summary, MorphPCA can be an appropiate alternative to PCA in different image processing applications.