Interpreting the Fuzzy Semantics of Natural-Language Spatial Relation Terms with the Fuzzy Random Forest Algorithm

Abstract

Naïve Geography, intelligent geographical information systems (GIS), and spatial data mining especially from social media all rely on natural-language spatial relations (NLSR) terms to incorporate commonsense spatial knowledge into conventional GIS and to enhance the semantic interoperability of spatial information in social media data. Yet, the inherent fuzziness of NLSR terms makes them challenging to interpret. This study proposes to interpret the fuzzy semantics of NLSR terms using the fuzzy random forest (FRF) algorithm. Based on a large number of fuzzy samples acquired by transforming a set of crisp samples with the random forest algorithm, two FRF models with different membership assembling strategies are trained to obtain the fuzzy interpretation of three line-region geometric representations using 69 NLSR terms. Experimental results demonstrate that the two FRF models achieve good accuracy in interpreting line-region geometric representations using fuzzy NLSR terms. In addition, fuzzy classification of FRF can interpret the fuzzy semantics of NLSR terms more fully than their crisp counterparts.

1. Introduction

Adequate specifications of qualitative commonsense information are indispensable to Naïve Geography, which formalizes common people’s knowledge about the geographic world [1], and serves as a mechanism of intelligent geographic information retrieval. Its importance is especially evident in mining human-as-sensor data and social media for spatial information and in enhancing the semantic interoperability of spatial information in social media [2]. One key step to achieving adequate specifications of qualitative commonsense information has been to bridge natural-language spatial relation (NLSR) terms and geometric information [3,4,5,6,7]. However, the inherent fuzziness in the semantics of NLSR terms due to the generality, hierarchy, and indefinite semantic intension or extension of natural languages [8] poses a great challenge to the accomplishment of this task. 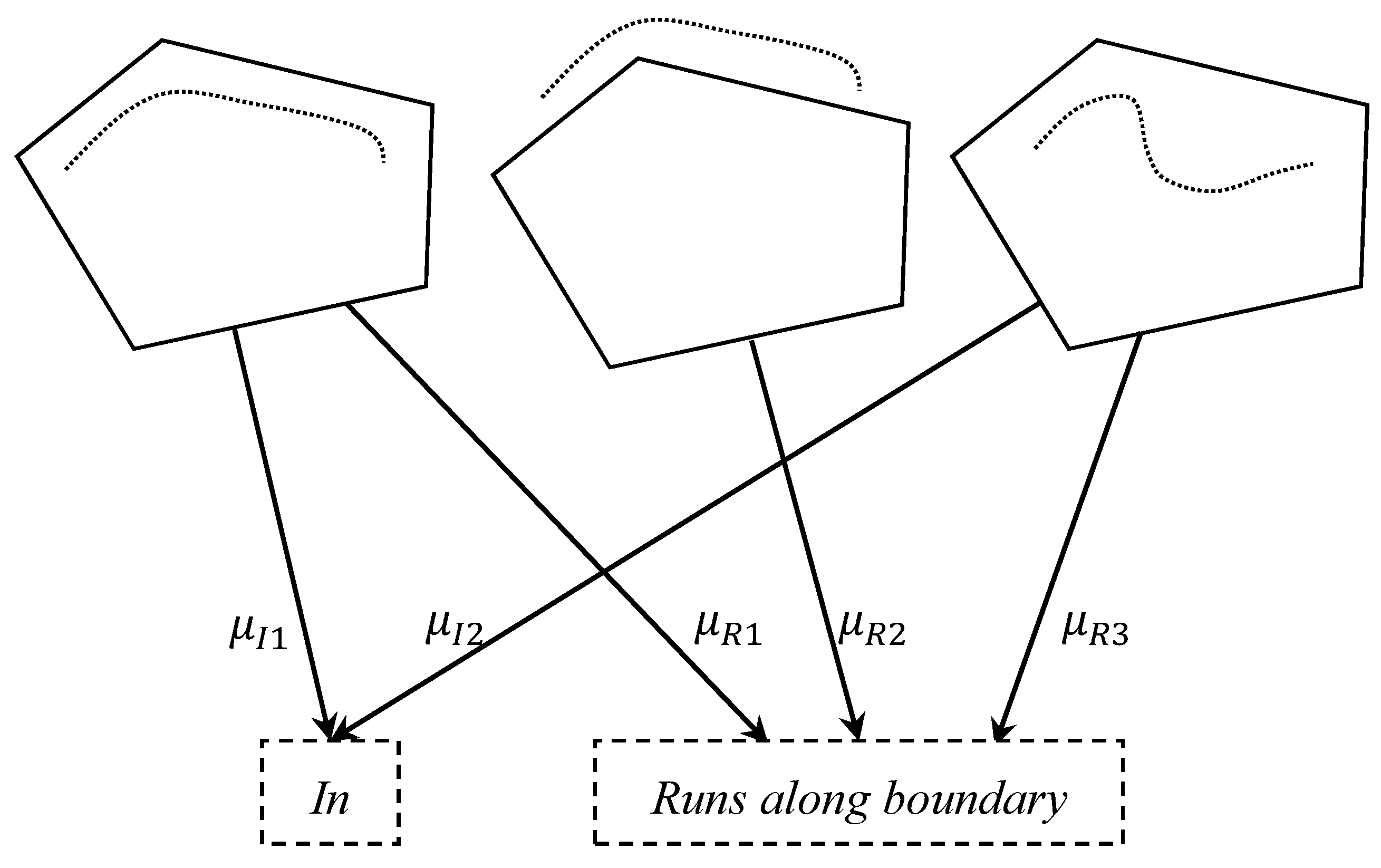For example, in Figure 1, the mappings from the three line-region sketches to both NLSR terms in and runs along boundary are many-to-many. In addition, the sketches may have different levels of belongingness with regard to the mapped NLSR terms; the first sketch may belong to the term runs along boundary more than the third sketch. Capturing such intuition requires the development of effective methods to translate geometric representations into NLSR terms.

This study proposes to use a fuzzy random forest (FRF) algorithm to implement the fuzzy transformation from line-region geometric representations to NLSR terms. Based on the robust FRF algorithm, the learned model can predict the NLSR terms and the corresponding fuzzy membership degrees for each geometric configuration. A total of 69 NLSR terms are involved in the study. Fuzzy functions in the model are learned exclusively during the automatic learning process of FRF. Line-region terms are then interpreted by the established FRF model. The experimental results indicate that our model is robust and accurate. To the best of our knowledge, this is the first work in the GIScience field on automatically learning the fuzzy model to interpret the fuzzy semantics of NLSR terms.

The paper is organized as follows. Section 2 provides a review of related work. Section 3 introduces quantitative fuzzy semantics to lay the foundation for the methodology in Section 4, which introduces the explanatory variables used, the fuzzy semantics of NLSR terms, the FRF algorithm, and the acquisition of fuzzy samples. Section 5 describes the data and the three experimental designs for producing fuzzy samples, training the FRF models, and obtaining subjective judgements that are subsequently used for validating the proposed approach. Section 6 presents the results of three experiments. Section 7 provides some a discussion about this research. Finally, conclusions of the research are given in Section 8.

2. Related Work

Existing literature mainly focuses on formal modeling of geometric relations and crisp mapping of geometric representations to NLSR terms. In current GIS, formal models, such as 9-intersection model [9], region connection calculus [10], combination of F-histogram and Allen’s relationships [11], and projective relations [12], are used to represent various spatial relations between geometric objects. These models, while effective in characterizing relations between geometric objects, are inadequate for bridging the geometric representations and NLSR, as they are based on crisp mapping models to reduce the gap between geometric representations and NLSR terms. For example, Shariff et al. [4] analyzed the value ranges of metric variables corresponding to 59 English NLSR terms. Xu [6] built a decision tree to map metric properties of line-line configurations to topological NLSR terms. Du et al. [7] used the random forest (RF) algorithm to build a mapping model between NLSR terms and topological and metric variables. As these crisp models translate one geometric representation to one and only one term, they cannot handle the mapping of multiple terms, let alone different levels of belongingness as shown in Figure 1.

Existing studies have suggested the potential usefulness of fuzzy set theory in handling the above two issues [13,14]. Indeed, it has been proven to be useful at handling non-spatial information, spatial objects, formalized relations and remote sensing images [15,16]. Wang et al. [17] and Wang [18] developed fuzzy models to improve the representation, analysis, and query of non-spatial information in natural languages, such as low humidity and high elevation. Modeling fuzzy spatiotemporal objects [19,20,21] was studied to facilitate fuzzy spatial queries. Models for fuzzifying the 9-intersection model [22,23] and RCC [24,25] have been also proposed. However, for handling NLSR terms only a handful of fuzzy models were developed, and these models can handle only a limited number of NLSR terms, such as proximity [26,27], along, surround, overlap and disjoint [28], and north and south [29]. As such, they are not robust in differentiating large number of NLSR terms.

3. Quantitative Fuzzy Semantics

Existing literature in quantitative fuzzy semantics provides insights into quantifying the fuzziness of meaning in a language. Zadeh [14] defines the meaning of a term using a fuzzy subset of objects characterized by a membership function. Below a brief introduction of fuzzy set theory is given using distance terms as examples. Let $T$ be a set of terms describing the distance between two objects, i.e., close, middle, and far, $U$ be the universe of distances between object pairs, and $y$ be a member in $U$. For a term $c$ in $T$, the meaning of an element belonging to term $c$ is denoted as $M\left(c\right)$, which is a subset of $U$ and is characterized by ${\mu }_c\left(y\right)$, the membership function describing the membership degree for $y$ in $M\left(c\right)$. 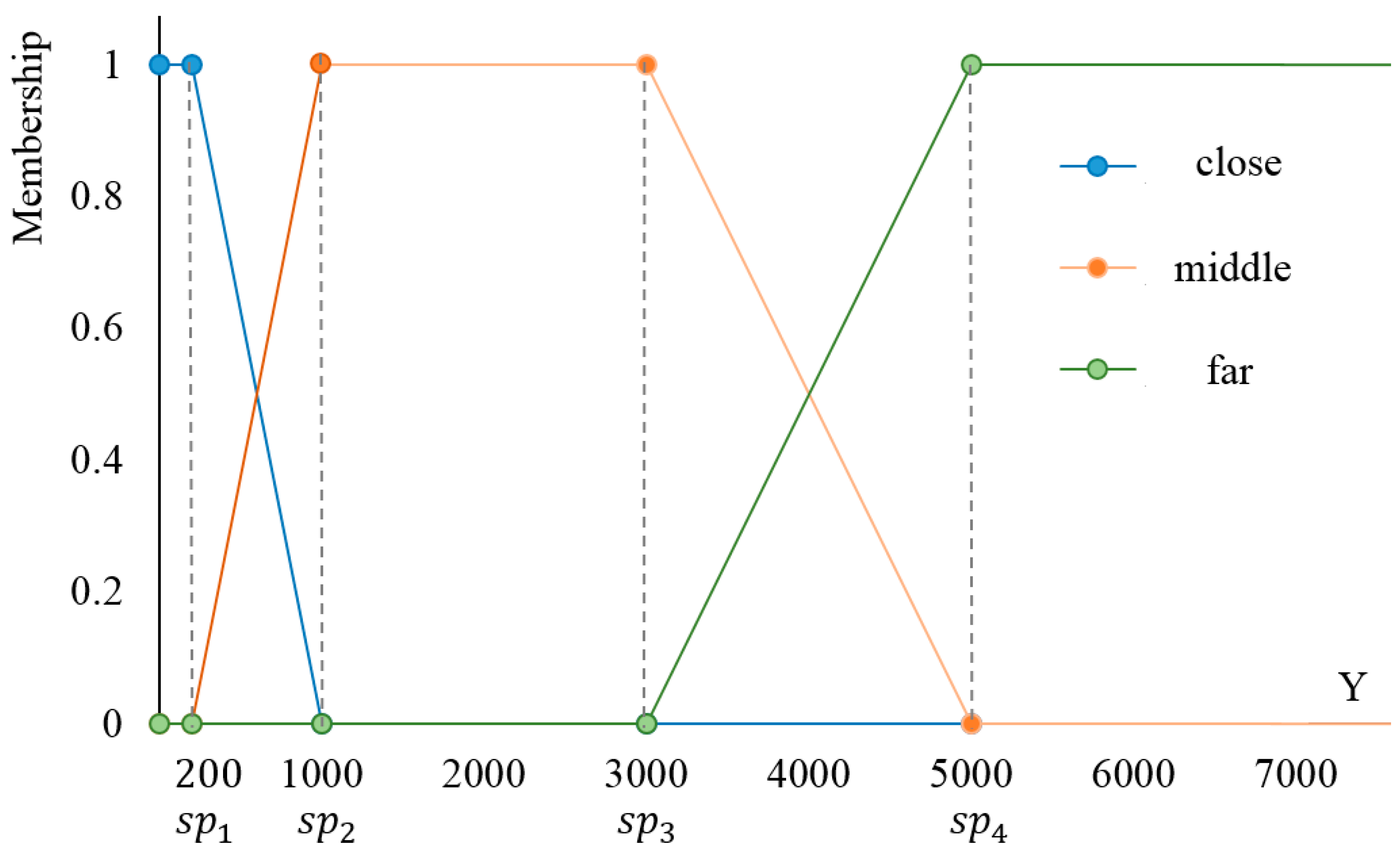The degree is between [0,1], with 0 representing non-membership and 1 representing full-membership. The membership functions in Equations (1)–(3) are used as examples to show how fuzzy theory works.

$${\mu }_{close}\left(y\right)=\{\begin{array}{cc}1,& 0\le y\le 200\\ \left(1000-y\right)/800,& 200<y\le 1000\\ 0& 1000<y\end{array},$$

(1)

$${\mu }_{middle}\left(y\right)=\{\begin{array}{cc}0,& y\le 200\\ \begin{array}{c}\left(y-200\right)/800,\\ 1\\ \left(5000-y\right)/2000\end{array}& \begin{array}{c}200<y\le 1000\\ 1000<y\le 3000\\ 3000<y\le 5000\end{array}\\ 0& 5000<y\end{array},$$

(2)

$${\mu }_{far}\left(y\right)=\{\begin{array}{cc}0,& y\le 3000\\ \left(y-3000\right)/2000,& 3000<y\le 5000\\ 1& 5000<y\end{array},$$

(3)

In Equations (1)–(3), $y$ is a distance value, ${\mu }_{close}\left(y\right)$, ${\mu }_{middle}\left(y\right),$ and ${\mu }_{far}\left(y\right)$ are the three membership functions, which define the degrees of fulfillment of distance values $y$ belonging to the three terms close, middle, and far, respectively. Using the membership functions, the fuzzy membership degrees of terms can be obtained. For an object pair with a distance of 350 units, its fuzzy membership degrees of the terms close, middle, and far are 0.81, 0.19, and 0.0, respectively. A fuzzy member function actually implies a fuzzy partition on the domain of distance between object pairs, which is specified by split points, e.g., $s{p}_1=200$, $s{p}_2=1000$, $s{p}_3=3000$, and $s{p}_4=5000$ (Figure 2). For Equation (1), the partition is [0, sp₁], ($s{p}_1$, $s{p}_2$], and ($s{p}_2$, +$\infty$); for Equation (2), the partition is [0, sp₁], ($s{p}_1$, $s{p}_2$], ($s{p}_2$, $s{p}_3$], ($s{p}_3$, $s{p}_4$], and ($s{p}_4$, +$\infty$); and for Equation (3), the partition is [0, sp₃], ($s{p}_3$, $s{p}_4$], and ($s{p}_4$, +$\infty$).

The membership functions are the key to fuzzy semantic analysis and are often specified by experts, including function types (i.e., linear or non-linear functions) and parameters (i.e., split points). Note that Equations (1)–(3) are examples to show how the membership functions are related to fuzzy semantics of qualitative terms. They are not the ones used in real applications because membership functions are context- or application-dependent. That is, different languages, countries, or people likely lead to different membership functions for the same term. As a result, the user-defined functions are rather subjective and not adaptive to contexts of other users. Moreover, for interpreting fuzzy semantics of NLSR terms, it is difficult to define appropriate membership functions and select appropriate parameters for these functions. To remediate this problem, a solution is to learn membership functions from a large number of samples. Generally, for a set of terms $T$ to be interpreted along with the domain of a variable $U$, learning a membership function implies learning a fuzzy partition on domain $U$. The learned membership functions will be more objective and adaptive to contexts than the ones specified by users, as they are learned from samples that are semantically interpreted by users.

4. Methodology

Interpreting fuzzy semantics of NLSR terms from geometric representations is treated as a fuzzy classification task that involves two steps. First, a fuzzy mapping model linking a set of explanatory variables from geometric representations to a set of NLSR terms has to be developed. This process utilizes FRF to learn the membership functions of NLSR terms automatically from geometric representations, and the fuzzy partitions and combinations of explanatory variables are formed in the learned FRF model. Second, for each geometric representation, the corresponding NLSR terms and the fuzzy membership degrees are predicted by the learned FRF model. The following sub-sections will elaborate on these two steps, starting with the explanatory variables for classification. It is followed by the quantification of fuzzy semantics of NLSR terms and the procedure to build a fuzzy mapping model with FRF algorithm. Finally, a method to acquire fuzzy samples for the training and classification of FRF model is explained.

4.1. Explanatory Variables from Line-Region Geometric Representations

Explanatory variables are categorical or metric for characterizing geometric representations and building the fuzzy mapping model. A total of 19 explanatory variables from line-region geometric configurations are adopted in this study. They consist of one categorical variable that characterizes topological type (TC) based on the 9-intersection model, and other 18 metric variables including four variables characterizing splitting (IAS, OAS, ITS, and PS), eight variables characterizing closeness (OAC, OLC, IAC, ILC, OAN, OLN, IAN, and ILN), and six variables characterizing alongness (LA, PA, IPA, ILA, OPA, and OLA) of line-region geometrical representations. The values of these metric variables are continuous and in different ranges. Their validations vary from line-region configuration to configuration. For example, IAS is valid only when a line splits a region’s inner into two or more parts, and within the value range [0.0, 0.5], while OAS is valid when a line splits a region’s outer into two or more parts, and has the value range (0.0, +∞). Specific definitions of these variables can be found in [4,7], and the 18 variable abbreviations are explained in Appendix

Table A1. Abbreviations of the 18 explanatory variables.

Category	Name
Splitting	Inner Area Splitting (IAS)
	Outer Area Splitting (OAS)
	Inner Traversal Splitting (ITS)
	Perimeter Splitting (PS)
Alongness	Line Alongness (LA)
	Perimeter Alongness (PA)
	Inner Perimeter Alongness (IPA)
	Inner Line Alongness (ILA)
	Outer Perimeter Alongness (OPA)
	Outer Line Alongness (OLA)
Closeness	Outer Area Closeness (OAC)
	Outer Line Closeness (OLC)
	Outer Area Nearness (OAN)
	Outer Line Nearness (OLN)
	Inner Area Closeness (IAC)
	Inner Line Closeness (ILC)
	Inner Area Nearness (IAN)
	Inner Line Nearness (ILN)

.

4.2. Fuzzy Semantics of NLSR Terms

Exemplified in Figure 1, the semantics of NLSR terms are inherently fuzzy due to the indefinite intension or extension of NLSR terms. Semantic overlap among NLSR terms and the disparate fuzzy membership degrees of geometric representations belonging to NLSR terms are demonstrations of this fuzziness. For the first and the third sketches in Figure 1, regarding the region as a park, and the line a road, it is reasonable to describe the sketches as either “The road is in the park” or “The road runs along boundary of the park”. The two sketches overlap in semantics as they can be described by the same two NLRS terms. In the meantime, the two sketches are different in semantics as they have different membership degrees of the two terms; The first sketch in Figure 1 belongs to the term run along boundary with a larger membership degree than the third sketch, but the two sketches belong to term in with the same degrees.

Fuzzy semantics of NLSR terms can be measured by fuzzy set theory. Specifically, $T$ refers to the set of $k$ NLSR terms, and $U$ refers to the universe of line-region geometric representations. For a term $c$ in $T$ and an element $y$ in $U$, i.e., a line-region geometric representation, the membership degree of $y$ belonging to $c$ is denoted by ${\mu }_c\left(y\right)$. Therefore, a line-region geometric representation $y$ can be interpreted as $S\left(T,\mu \right)$, in which $\mu$ is a vector $\left({\mu }_1,{\mu }_2,\dots ,{\mu }_k\right)$ and each element ${\mu }_i$ ($1\le i\le k$) refers to the membership degree of the geometry $y$ belonging to the $i$-th term and confined to ${{\displaystyle \sum }}_i{\mu }_i=1$ and $0\le {\mu }_i\le 1$. The larger the degree of an element, the higher the possibility of the line-region geometry belonging to an NLSR term. The discrepancies in the membership degrees of terms demonstrate the fuzzy semantics of NLSR terms. Therefore, $S$ can be considered as the fuzzy representation of NLSR terms.

In this way, the semantic similarity (and difference) between NLSR terms can be interpreted by examining fuzzy membership degrees. Each of the elements in $\left({\mu }_1,{\mu }_2,\dots ,{\mu }_k\right)$ can take a non-zero value to measure the degree of geometric representation belonging to the $k$ term. In general, those line-region geometric representations can be reasonably assumed to be described by more than one NLSR term and be interpreted by fuzzy models as multiple NLSR terms with different membership degrees.

To use the proposed fuzzy model, a challenge is to define the membership functions for NLSR terms. Since line-region geometric representations are characterized by a set of explanatory variables, the transformation from the explanatory variables extracted from geometric representations to the membership degrees of NLSR terms is much more complicated; thus, the membership functions cannot be readily specified by users. As a result, FRF algorithm is employed in this study to learn the membership functions for NLSR terms in terms of line-region training samples. The learned FRF model is subsequently used to predict the terms and the corresponding fuzzy membership degrees for geometric representations. In the following sub-section, the training and predicting processes of FRF are introduced.

4.3. Fuzzy Random Forest

FRF is a model built with FRF algorithm [30] and a classifier composed of multiple fuzzy decision trees (FDTs). FRF can perform fuzzy classification based on FDTs more robustly and accurately than a single FDT [30]. In addition, it can eliminate the correlations among variables by introducing randomness in variable selection.

The training phase of FRF involves constructing each FDT using training samples. Each sample consists of a set of explanatory variables extracted from a line-region sketch and the corresponding NLSR terms. The classification phase of FRF applies samples to the trained FRF to obtain the aggregated votes for each NLSR term by FDTs. Each FRF consists of various FDTs [31], in which nodes are split into as many branches as possible in terms of the variables with the largest information gain. FDTs allow fuzzy-partitioned continuous variables, with each partition attached to a trapezoidal fuzzy set. For each sample in the nodes, a fuzzy membership degree can be computed in terms of the fuzzy partitions of variables in the nodes. The fuzzy membership degrees of samples are employed in both the training and classification phrases. During the training phase of each FDT, sample fuzzy membership degrees associated with NLSR terms are used to calculate the information gain in a node. During the classification phase, a fuzzy satisfaction degree in the interval [0,1] is calculated for the sample being classified into one or more leaf node(s) in each FDT. Fuzzy satisfaction degree and membership degree of NLSR terms in the leaf nodes of FRF are then utilized in the voting for NLSR terms, which is described in detail in Section 4.3.2.

In addition, the large number of FDTs is diversified in two randomization processes in the training phase. One is that the subsample set, on which a FDT is built, is randomly sampled with replacement from the original training sample set so that the training set for each FDT is different from others. The other randomization is that the variable candidate set used for splitting FDTs is a subset randomly chosen from the whole variable set so that variable candidate set for a split is different from the ones for other splits. As a result, more robust and accurate classification results can be produced in FRF model by aggregating the votes of diverse FDTs. In the following Section 4.3.1 and Section 4.3.2, details of the training and classification phases are described.

4.3.1. Training Phase

The purpose of the training is to construct a FRF model and to learn the structures of all FDTs in the FRF model. In this study, the training is mainly based on the FRF algorithm in [30] but with two adaptations: (1) replacing crisp training samples with fuzzy training samples and (2) using the method proposed by Cadenas et al. [32] to obtain fuzzy partitions of continuous variables. The detailed training steps are included in Appendix

Table A2. Steps to train a FRF model.

Input: Original fuzzy training sample set $E$, predefined tree number $n$, fuzzy partitions of variable set $P_v$. Output: FRF model.

1. Generate $n$ subsets of training samples $E_1$, $E_2$, …, $E_n$ by randomly sampling with replacement from $E$. The size of each subset $E_i$ is equal to that of $E$.

2. Build each FDT $T_i$ on $E_i$ respectively.

2.1. Start with the examples in $E_i$ with satisfaction degree value $m$ = 1.0

2.2. Choose an attribute to split the node $N$.

2.2.1. Generate a subset of available variables $V_s$ by randomly sampling without replacement. The size of the subset is the integer of the squared root of the number of available variables.

2.2.2. Calculate the information gain of node $N$ when split by each variable in $V_s$, respectively, according to the equation in Appendix Table A4.

2.2.3. Choose the variable $V_{sm}$ producing maximum information gain of node $N$ to split node $N$ into as many branches as the number of categories or fuzzy partitions of the variable.

2.3. Remove $V_{sm}$ from available variable set.

2.4. Repeat 2.2 and 2.3 on the child nodes produced in the last iteration until the stopping criteria is met.

3. Assemble all FDTs $T_1$, $T_2$, …, $T_n$ into an FRF model.

.

Essentially, the training of each FDT learns the combinations of variables to be used for fuzzy classification. The process in this study is based on the method first proposed by Janikow [31] and later used in Bonissone et al. [30], but with the adaptation of using fuzzy samples to train instead of crisp ones. In addition, the stopping criterion of training is either the number of samples at each leaf node of FDT, which is very small, or the unavailable variables that are used for splitting.

Since both categorical and fuzzy-partitioned continuous variables are involved in this study, the method proposed by Cadenas et al. [32] is employed to partition the continuous variables into several trapezoidal fuzzy sets, i.e., to pinpoint split points and form trapezoidal fuzzy sets similar to the case of NLSR term close in Figure 2. This method first uses C4.5 to obtain the crisp splits of continuous variables, and second utilizes gene algorithm [32] to optimize the fuzzy sets based on the crisp splits of continuous variables. The specific steps are shown in Appendix

Table A3. Steps for doing fuzzy partitioning of continuous variables.

Input: Crisp training sample set $E^{\prime }$, continuous variable set $V_c$, size of gene population $s$, predefined number of generations $g$, probability of mutation $p_m$ and crossover $p_c$. Output: Fuzzy partitions of $V_{co}$.

1. Build a decision tree $T_{C4.5}$ on $E^{\prime }$ using $V_c$ according to C4.5 algorithm.

2. Use the splits in $T_{C4.5}$ to generate a gene population $G$.

2.1. Code the real quantities to be added to or subtracted from each attribute’s split point in an array $A_1$. The quantity is randomly initiated decimal in the domain calculated according to the equation in Table A4.

2.2. Code randomly initiated binary values which indicate whether the corresponding quantities in $A_1$ are active or not in an array $A_2$ with 1 indicating active and 0 indicating not active.

2.3. Assemble $A_1$ and $A_2$ into an initiated gene individual.

2.4. Repeat steps 2.1., 2.2., and 2.3 until a gene population consisting $s$ gene individuals is generated.

3. Iterate evolvement of gene population $g$ times.

3.1. Do crossover on $G$.

3.1.1. Generate a set of gene individual pairs $I$ by sampling without replacement from $G$. The size of $I$ is the integer of $p_c\ast s/2$.

3.1.2. Choose a start index $l_s$ in $A_2$ for each gene individual pair $I_i$ randomly.

3.1.3. Exchange the codes after $l_s$ in $A_2$ of $I_i$.

3.1.4. Update $A_1$ for $I_i$ whose $A_2$ consists of at least a code of 1, and add these new $I_i$ to $G$.

3.2. Do mutation on $G$.

3.2.1. Generate a set of gene individuals $M$ by sampling without replacement from $G$. The size of $M$ is the integer of $p_m\ast s$.

3.2.2. Choose an index $l_m$ in $A_2$ for each gene individual $M_i$ randomly.

3.2.3. Mute the code at $l_m$ in $A_2$ from 1 to 0 or from 0 to 1.

3.2.4. Update $A_1$ for $M_i$ whose $A_2$ consists of at least a code of 1, and substitute these new $M_i$ in $G$.

3.3. Do selection on $G$.

3.3.1. Calculate the fitness of each gene individual in $G$.

3.3.1.1. Form trapezoidal fuzzy sets ${\mathrm{V}}_c^{\prime }$ according to $A_1$ and $A_2$.

3.3.1.2. For each variable $v$, each fuzzy set $f$ of variable $v$, each class $c$, calculate the probability $p_{vfc}$ according to the equation in Table A4.

3.3.1.3. For each class $c$, calculate the probability $p_{vc}={{\displaystyle \sum }}_f{p}_{vfc}$.

3.3.1.4. For each $f$, calculate the probability $p_{vf}={{\displaystyle \sum }}_c{p}_{vfc}$.

3.3.1.5. For each $f$, calculate the information gain of attribute $v$, $I_{vf}$.

3.3.1.6. For each $f$, calculate the entropy $H_{vf}$.

3.3.1.7. Calculate the information gain and entropy of attribute $v$, $Inf{o}_v={{\displaystyle \sum }}_f{I}_{vf}$, $H_v={{\displaystyle \sum }}_f{H}_{vf}$.

3.3.1.8. Calculate the fitness $F=\raisebox{1ex}{${{\displaystyle \sum }}_{v}Inf{o}_v$}\!\left/ \!\raisebox{-1ex}{${{\displaystyle \sum }}_v{H}_v$}\right.$.

3.3.2. Generate a set of gene individual pairs $S$ by sampling without replacement from $G$. The size of $S$ is the integer of $s/2$.

3.3.3. Keep gene individuals with fitness further away from 0 in each pair to substitute for all gene individuals in $G$.

4. Form trapezoidal fuzzy sets $V_c$ according to $A_1$ and $A_2$ of the gene individual with fitness furthest away from 0.

with relevant notations and equations included in Appendix

Table A4. Notations and equations.

$c$: a class.
$d_v^i$: the $i$-th child node of a node split by variable $v$.
$D$: domain of each code corresponding to a split in Array $A_1$ of a gene individual.
$e$: a sample in a node.
$Entro$: entropy of a node.
$Entr{o}_v$: a sum of all child nodes’ entropy for a node split by variable $v$.
$f_i$: the $i$-th trapezoidal fuzzy set of a variable. $t$: number of trapezoidal fuzzy sets of a continuous variable.
$f_{i1}$, $f_{i2}$, $f_{i3}$, $f_{i4}$: the $x$ value of the leftbottom, lefttop, righttop, and rightbottom point of $f_i$ respectively.
$Inf{o}_v$: information gain of a node when using variable $v$ to split the node.
$m$: satisfaction degree of a sample in a node.
$m_{ec}$: membership in class $c$ of sample $e$.
$P$: a sum of membership in all classes of all samples in a node.
$P_c$: a sum of membership in class $c$ of all samples in a node.
$P_v^{unknown}$: a sum of membership in all classes of samples with unknown value of variable $v$ in a node.
$P_{d_v^i}$: a sum of membership in all classes of all samples in $d_v^i$.
$p_{vfc}$: a sum of membership in class $c$, fuzzy set $f$ of variable $v$ of all samples in a node.
$s{p}_r$: the $r$-th split point of a variable.
$u$: the number of split points of a variable.
${\mu }_{f_i}\left(x\right)$: membership function of $f_i$.
$P_c={\displaystyle {\displaystyle \sum }_e}{m}_{ec}$	$P={\displaystyle {\displaystyle \sum }_c}{P}_c$		$Inf{o}_v=Entro-Entr{o}_v$
$Entro=-{\displaystyle {\displaystyle \sum }_c}\left(\frac{P_c}{P}\ast log\frac{P_c}{P}\right)$		$Entr{o}_v=\frac{P-P^{unknown}}{P}\frac{1}{{{\displaystyle \sum }}_{d_v^i}{P}_{d_v^i}}{\displaystyle {\displaystyle \sum }_{d_v^i}}(P_{d_v^i}\ast E_{d_v^i})$
${\mu }_{f_1}\left(x\right)=\{\begin{array}{cc}1& f_{12}\le x\le f_{13}\\ \frac{f_{13}-x}{f_{13}-f_{12}}& f_{13}\le x\le f_{14}\\ 0& f_{14}\le x\end{array}$;  ${\mu }_{f_2}\left(x\right)=\{\begin{array}{cc}\begin{array}{c}0\\ \frac{x-f_{12}}{f_{13}-f_{12}}\\ 1\end{array}& \begin{array}{c}x\le f_{12} \\ f_{12}\le x\le f_{13}\\ f_{13}\le x\le f_{23}\end{array}\\ \frac{f_{24}-x}{f_{24}-f_{23}}& f_{23}\le x\le f_{24}\\ 0& f_{24}\le x\end{array}$; ……; ${\mu }_{f_t}\left(x\right)=\{\begin{array}{cc}0& x\le f_{\left(t-1\right)3}\\ \frac{x-f_{\left(t-1\right)3}}{f_{\left(t-1\right)4}-f_{\left(t-1\right)3}}& f_{\left(t-1\right)3}\le x\le f_{\left(t-1\right)4}\\ 1& f_{t3}\le x\end{array}$
$D=\{\begin{array}{cc}\{\begin{array}{cc}\left[0,\min \left(s{p}_1,\frac{s{p}_2-s{p}_1}{2}\right)\right]& r=1\\ \left[0,\min \left(\frac{s{p}_r-s{p}_{r-1}}{2},\frac{s{p}_{r+1}-s{p}_r}{2}\right)\right]& 1<r<u\\ \left[0,\min \left(\frac{s{p}_u-s{p}_{u-1}}{2},1-s{p}_u\right)\right]& r=u\end{array}& u>1\\ \left[0, \min \left(s{p}_1, 1-s{p}_1\right)\right]& u=1\end{array}$
$p_{vfc}=\frac{{{\displaystyle \sum }}_e({\mu }_f\left(e\right)\ast m_{ec})}{{{\displaystyle \sum }}_e{\mu }_f\left(e\right)}$

.

4.3.2. Classification Phase

Once the training phase is completed, a FRF model is established to classify fuzzy samples and provide the terms and the corresponding fuzzy memberships for the samples. There are mainly two procedures for this task. First, a fuzzy sample being classified goes along the branches of each FDT in the learned FRF model from root nodes to leaf nodes with satisfaction degrees larger than zero. Second, strategies for aggregating the results of each FDT are employed to produce the final result. A good voting strategy promotes the accuracy and robustness of FRF prediction. Generally, the voting strategy is a combination of operations on the membership degrees obtained by FDTs for each sample. In this study, two voting strategies are adopted [30]: simple majority vote, denoted as SM1, and majority vote weighted by leaf and by tree, denoted as MWLT1. Let $e^{\prime }$ be the sample to be classified, $L_{ij}$ the $i$-th leaf node of the $j$-th FDT visited by $e^{\prime }$, $T$ the set of terms, $c$ a term in $T$, and ${\mu }_{ijc}$ the membership degree of term $c$ produced by $L_{ij}$, which is a sum of the memberships in term $c$ of all training samples in $L_{ij}$. Steps of both voting strategies are described as follows.

Strategy SM1 first calculates the vote of $L_{ij}$ for term $c$, i.e., $Vot{e}_{ijc}$ for each leaf node. If ${\mu }_{ijc}$ is the maximum among memberships of all terms in $L_{ij}$, $Vot{e}_{ijc}=1$; otherwise, $Vot{e}_{ijc}=0$. Second, it calculates ${{\displaystyle \sum }}_{i}Vot{e}_{ijc}$ for each FDT. Third, it calculates $Vot{e}_{jc}$ for each term and each FDT, in which $Vot{e}_{jc}$ is the vote of the $j$-th FDT for term $c$. If ${{\displaystyle \sum }}_{i}Vot{e}_{ijc}$ is the maximum among memberships of all terms, $Vot{e}_{jc}=1$; otherwise, $Vot{e}_{jc}=0$. Last, SM1 aggregates and normalizes $Vot{e}_{jc}$ by ${{\displaystyle \sum }}_{j}Vot{e}_{jc}/{{\displaystyle \sum }}_{c\in T}({{\displaystyle \sum }}_{j}Vot{e}_{jc})$ as the membership of $e^{\prime }$ belonging to term $c$.

In strategy MWLT1, the satisfaction degree of $e^{\prime }$ at each leaf node $L_{ij}$, denoted as $m_{ij}$, and OOB accuracy (accuracy of classifying out-of-bag samples) of each FDT, denoted as $oo{b}_j$ for the $j$-th FDT, are additionally employed. First, for each leaf node, $Vot{e}_{ijc}$ is calculated differently from the one in SM1. If ${\mu }_{ijc}$ is the maximum among memberships of all terms at node $L_{ij}$, $Vot{e}_{ijc}=m_{ij}$; otherwise, $Vot{e}_{ijc}=0$. Second, ${{\displaystyle \sum }}_{i}Vot{e}_{ijc}$ is calculated for each FDT and each term $c$. Third, if ${{\displaystyle \sum }}_{i}Vot{e}_{ijc}$ is the maximum for all terms, $Vot{e}_{jc}=oo{b}_j$; otherwise, $Vot{e}_{jc}=0$. Last, the normalized ${{\displaystyle \sum }}_{j}Vot{e}_{jc}/{{\displaystyle \sum }}_{c\in T}({{\displaystyle \sum }}_{j}Vot{e}_{jc})$ is considered as the membership degree of each term $c$. In comparison, strategy SM1 treats equally the leaf nodes with different satisfaction degrees and counts the votes of all FDTs equally, while strategy MWLT1 uses the weighted votes in terms of the satisfaction degree of samples at leaf nodes and the OOB accuracy of FDTs.

4.4. Fuzzy Sample Acquisition with Random Forest Algorithm

To train a robust FRF model, fuzzy training samples are required. A fuzzy sample consists of the values of the 19 explanatory variables (Section 4.1) and the fuzzy membership degrees of all terms $\mu =\left({\mu }_1,{\mu }_2,\dots ,{\mu }_k\right)$ (Section 4.2). However, it is not straightforward to collect fuzzy training samples as the assignment of fuzzy membership degrees of terms for each sample is hard and troublesome. A feasible way of acquiring fuzzy samples is to transform crisp samples into fuzzy ones by random forest (RF) algorithm [33], as it is easier to collect crisp samples than fuzzy ones.

RF algorithm [34] can train a crisp classification model by using crisp samples. The trained RF model consists of multiple crisp decision trees (CDT). RF algorithm can provide valuable information for transforming crisp samples to fuzzy ones by producing fuzzy sample matrix $FSM$ during classification, which can be used for fuzzy sample collection. $FSM$ consists of $n$ rows and $l$ columns, in which $n$ is the number of crisp samples and $l$ is the number of terms. The value of each entry in $FSM$, $FS{M}_{ij}$, refers to the votes that the $i$-th sample is classified as the $j$-th term by the RF. As

Table 1. Fuzzy sample matrix.

	${\mathit{T}}_1$	${\mathit{T}}_2$	…	${\mathit{T}}_{\mathit{l}}$
$S_{C1}$	$FS{M}_{11}$	$FS{M}_{12}$	…	$FS{M}_{1l}$
$S_{C2}$	$FS{M}_{21}$	$FS{M}_{22}$	…	$FS{M}_{2l}$
…	…	…	…	…
$S_{Cn}$	$FS{M}_{n1}$	$FS{M}_{n2}$	…	$FS{M}_{nl}$

shows, for crisp sample $S_{C1}$, the vote that it is classified as term $T_1$ is $FS{M}_{11}$. The differences among the values in the same row demonstrate the distinctions of terms in describing the same sample. Therefore, the membership degrees of a sample belonging to different terms can be approximated by the proportions of votes in the row of $FSM$, or $FS{M}_{ij}/{{\displaystyle \sum }}_{j}FS{M}_{ij}$.

In this study, the transformation of crisp samples to fuzzy ones with RF algorithm is carried out using the following procedures. First, a FR model is trained using crisp samples and RF algorithm. Second, the trained RF model is used to classify every crisp sample and to produce a fuzzy sample matrix $FSM$ (Table 1). Third, each row of $FSM$ is normalized. Finally, for each sample, the normalized entries in each row constitute a vector $\mu =\left({\mu }_1,{\mu }_2,\dots ,{\mu }_k\right)$, which represents fuzzy membership degrees of a sample belonging to every terms. The steps to train a RF can be found in Appendix

Table A5. Steps to train an RF model.

Input: original fuzzy training sample set $E$, predefined tree number $n$, variable set $P_v$. Output: RF model.

1. Generate $n$ subsets of training samples $E_1$, $E_2$, …, $E_n$ by randomly sampling with replacement from $E$. The size of each subset $E_i$ is the same with $E$.

2. Build each CDT $T_i$ on $E_i$ respectively.

2.1. Create the root node $N$ containing all examples in $E_i$

2.2. Choose an attribute to split the node $N$.

2.2.1. Generate a subset of available variables $V_s$ by randomly sampling without replacement. The size of the subset is the integer of the squared root of the number of available variables.

2.2.2. Calculate the information gain of node $N$ when split by each variable in $V_s,$ respectively.

2.2.3. Choose the variable $V_{sm}$ producing maximum information gain of node $N$ to split node $N$ into two branches.

2.3. Repeat 2.2 and 2.3 on the child nodes produced in last iteration until the stopping criteria is met.

3. Assemble all CDTs $T_1$, $T_2$, …, $T_n$ into a RF model.

.

5. Data and Experiments

In this study, three experiments are designed. The first one is to transform the crisp samples to fuzzy ones with RF algorithm, the second one is to use the fuzzy samples to train FRF models with FRF algorithm, and the third one is to obtain fuzzy interpretation of NLSR terms from human subjects. This section begins by introducing the data for the three experiments, followed by presenting the design of the three experiments.

5.1. Data

The data contains 2493 crisp samples [7] (The sample data can be available if readers send a request by email). Each sample contains a line-region sketch, a record of 19 values of the explanatory variables calculated from the sketch, and an NLSR term describing the spatial relation between the line and the region in the sketch. A total of 69 English NLSR terms are involved in the data, each attached to nearly 30 variable records at least. To collect the samples, a subject test is carried out. In the test, 41 subjects, college students with proficient English ability and different majors, are asked to choose at least one NLSR term and then draw a line and a region to match the sketch with the description of a road + NLSR term(s) + a park by using a specialized program developed with ArcEngine 10.0. The sketching process continues until each NLSR term has at least 30 line-region sketches. After verifying the usability of the sketch set, records of explanatory variable values are extracted from the sketches and the corresponding NLSR terms are attached. As a line-region sketch may be drawn for more than one synonymous NLSR term, there are a number of samples with identical variable values but different NLSR terms. In addition, values of invalid variables in some line-region configurations are set expressly to −2.

Since classification accuracy is subject to similar or identical variable values of NLSR terms, to improve classification accuracy, it is necessary to group NLSR terms of similar semantics [7]. A five-group scheme of NLSR terms to achieve this goal is thus adopted (

Table 2. Groups of NLSR terms [7]. Representative terms are in italic.

Group	NLSR Terms
1	starts and ends in
2	runs along boundary, runs along, along edge, contained in edge, encloses, enclosed by
3	in, inside, within, contained within
4	goes to, leads to, goes up to, goes through, bisects, splits, run through, pass through, comes through, cuts across, cuts through, spans, goes across, stretch over, runs across, cuts, intersect, passes, transects, traverses, crosses, break into, divides, separate, goes into, reach into, comes into, enters, runs into, ends outside, comes from, goes out of, run from, stretch from, comes out of, exits, leaves, ends in, ends on, starts in, starts outside, connected to, connects, ends at, starts just inside, ends just inside, starts near, starts just outside, ends just outside, ends near
5	near, be adjacent to, bypasses, avoids, goes away from, goes by, outside, entirely outside

). According to the grouping scheme, the 2493 samples are merged and attached to the five representative NLSR terms, namely, starts and ends in, runs along boundary, in, goes to, and near. Note that the five representative terms are used as the names of the five groups of 69 NLSR terms, as well as the five classes in the classification of FRF for convenience purposes, since each term of the group is semantically confined and approximate to each whole group of NLSR terms.

5.2. Experiment One: Fuzzifying Samples with Random Forest Algorithm

In the first experiment, RF algorithm is implemented in Visual Studio 2015 using C++, and a RF model is trained using the 2493 crisp samples. To assess the reliability of transformation, OOB accuracy of the RF model is measured according to Equations (4) and (5). Since the classification accuracy of the RF model can be influenced considerably by the number of trees, incremental number of trees are built until the classification accuracy of RF converges at a stable level. The transformation of crisp samples to fuzzy samples is then carried out following the steps described in Section 4.4.

$$f={{\displaystyle \sum }}_{e}f\left(e\right)/n$$

(4)

$$f\left(e\right)=\{\begin{array}{c}\begin{array}{cc}1& if argmax(Vot{e}_e)=c_e\end{array}\\ \begin{array}{cc}0& if argmax(Vot{e}_e)\ne c_e\end{array}\end{array}$$

(5)

in which $f$ is the OOB accuracy, $e$ is a sample in the dataset, n is the size of the dataset, $Vot{e}_e$ is the aggregated votes for sample $e$ by CDTs whose training sets do not contain sample $e$ in RF, $argmax(Vot{e}_e)$ is the class with the maximum votes, and $c_e$ is the real class of sample $e$.

5.3. Experiment Two: Building Interpretation Model

In the second experiment, two FRF models are built in Visual Studio 2015 using C++ according to the methods described in Section 4.3. The first FRF, denoted as FRF-SM1, employs voting strategy SM1, while the second FRF, denoted as FRF-MWLT1, uses voting strategy MWLT1.

To assess the validity of the interpretation model, OOB accuracy of FRF classification is defined and measured according to Equations (4) and (6). In the evaluation of OOB accuracy of FRF, for each fuzzy sample, the term with the maximum membership degree is compared with the term attached to the corresponding crisp sample. If the two terms are the same, the result of the FRF is regarded as correct. Otherwise, the result of the FRF is regarded as wrong. One special occasion is that there is more than one term with equal maximum membership degree in the results of FRF classification. In this case, the classification is regarded as correct as long as the term of the corresponding crisp sample occurs in the maximum terms. Similar to the training of RF, incremental number of trees are built until the classification accuracy of FRF converges at a stable level.

$$f\left(e\right)=\{\begin{array}{c}\begin{array}{cc}1& if argmax(Membershi{p}_e)=c_e\end{array}\\ \begin{array}{cc}0& if argmax(Membershi{p}_e)\ne c_e\end{array}\end{array}$$

(6)

in which $Membershi{p}_e$ is the aggregated memberships for sample $e$ by FDTs whose training sets do not contain sample $e$ in FRF, $argmax(Membershi{p}_e)$ is the class with the maximum membership, and $c_e$ is the real class of sample $e$ before fuzzification.

5.4. Experiment Three: Fuzzy Interpretations by Subjects

In the third experiment, a subject test with 42 participants was carried out to collect their fuzzy interpretation of NLSR terms goes to, in, near, runs along boundary, and starts and ends in. All participants are proficient in English and come from diverse studying or working backgrounds. They are asked to finish a questionnaire in which they evaluate the degree of suitability of filling each of the five NLSR terms in the sentence A road (is) + NLSR term + a park to represent three line-region sketches shown in

Table 3. Line-region sketches for evaluation of suitability.

Line-Region Sketch
No.	1	2	3

. A five-level Likert scale of suitability, i.e., very suitable, suitable, neutral, unsuitable, and very unsuitable, is used. Therefore, for each of the three line-region sketches, each subject gives five degrees of suitability for the five NLSR terms, respectively.

Next, suitability evaluation by the participants is transformed to membership degree of NLSR terms for line-region sketches. The five-level Lickert scale of suitability is first assigned the scores of 5, 4, 3, 0, and 0. The score of each of the five NLSR terms for each line-region sketch is then summed. The proportion of the score of an NLSR term in the total score of the five terms is regarded as the membership degree of the NLSR term for the line-region sketch. The membership degree thus obtained is later used as a benchmark of fuzzy interpretation of NLSR terms to contrast with results of fuzzification and classification of RF and FRF.

6. Results

6.1. Sample Fuzzification

The results of sample fuzzification on crisp samples are shown in

Table 4. Results of sample fuzzification.

Classes	Number of Samples	Percentage of Impure Samples	Percentage of Error Samples
G	1756	29.8	3.5
I	152	93.4	2.0
N	322	92.5	24.8
R	226	99.6	20.8
S	37	97.3	86.5

. The five representative terms goes to, in, near, runs along boundary, and starts and ends in, are abbreviated as G, I, N, R, and S, respectively. After fuzzification by RF algorithm, each of the 2493 samples receives its membership degrees in the five representative terms. Counting a fuzzified sample as a sample of its predicted term with the maximum membership degree, the number of samples of the five representative terms is calculated and shown in the second column of Table 4. Four types of fuzzified samples, including correct, error, pure, and impure, are differentiated. The impure samples refer to those with two or more membership degrees larger than zero in NLSR terms, and the error samples refer to those whose predicted terms with the maximum membership are not their original terms. For each representative term, the percentage of error or impure samples is calculated as the ratio of the number of error or impure samples predicted to the total number of samples.

The result, shown in Table 4 below, reveal high percentages of impure samples for classes I, N, R, and S. It demonstrates the function of the fuzzification of RF algorithm. The percentages of error samples show diverse outcomes of the classification for the five classes and indicate the accuracy loss in sample fuzzification. For class S, which has very high percentage of error samples, most crisp samples are predicted to belong to class G, while the membership in class S of those error samples is within [0.1, 0.5].

Following the above rule of identifying error and correct samples, classification accuracy of the trained RF is evaluated. The OOB accuracy of the trained RF stabilizes at 87.2% when the number of decision trees is larger than 200. Assured by the classification accuracy, fuzzified samples by RF are used to train FRFs subsequently.

6.2. Fuzzy Random Forest Classification

As illustrated in Figure 3, the median of the classification accuracy of FRF-SM1 stabilizes at about 83% when the number of trees reaches 100, while the median of the classification accuracy of FRF-MWLT1 stabilizes at about 84% when the number of trees reaches 150. During training process, the largest accuracy of FRF-SM1 is 84.86%. The largest accuracy of FRF-MWLT1 is slightly higher, at 86.01%, indicating the advantage of assigning different weights to the leaf nodes with different satisfaction degrees of samples and the votes of trees with different classification accuracy of OOB samples. Moreover, during the training process, the classification accuracy of FRF-MWLT1 is steadier than the one of FRF-SM1.

Although the classification accuracy of FRFs is slightly lower than that of RF, it still demonstrates the accuracy and robustness of FRF at establishing the fuzzy mapping between NLSR terms and line-region geometric representations. The differences between the accuracies of FRF and RF may be caused by the following. First, the quality of fuzzy samples affects the accuracy of FRF. According to the results of crisp sample fuzzification, error fuzzy samples exist in the training sample set of FRF. The presence of error fuzzy samples may decrease the accuracy of trained FRF model. Second, the learned fuzzy partitions of numeric variables and choice of fuzzy sets limit the performance of FRF.

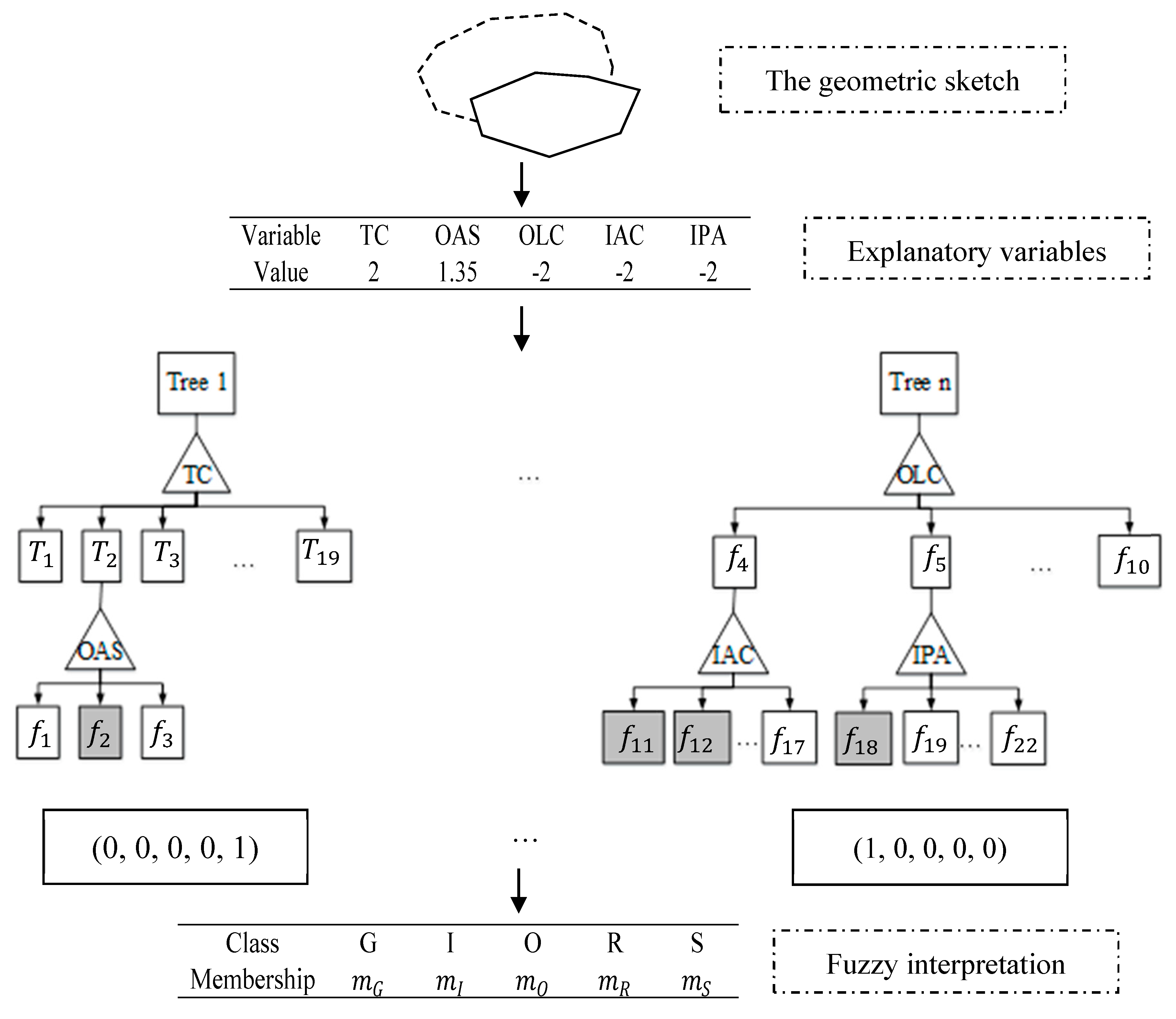
However, in this study the classification accuracy of FRF is only referred to for confirming the reliability of FRF algorithm. The membership degrees of different NLSR terms produced by FRF are significant. Take the line-region sketch and the interpreted membership degrees of NLSR terms in Figure 4 as an example. In the geometric sketch, the solid line depicts the boundary of a park, and the dotted line depicts a road. The corresponding values of relevant explanatory variables are presented in the first table in Figure 4. To attach membership degrees of NLSR terms for the sketch, the values of variables are applied to all FDTs in the established FRF model. The variables used to split each non-leaf node are enclosed by triangles such as TC, OAS, and IPA. For the categorical variable TC, there are 19 child nodes, i.e., $T_1$, …, $T_{19}$. For a metric variable, the number of child nodes is equal to the number of fuzzy partitions whose fuzzy sets are represented by $f_1$, $f_2$, …, etc. Since there may be overlap between fuzzy sets, a sample may visit more than one node in the same depth with satisfaction degrees larger than zero. Therefore, a sample may visit more than one leaf node in a tree, such as leaf nodes corresponding to $f_{11}$, $f_{12}$, $f_{18}$ in tree n. After that, according to some membership assembling strategy, the membership vector $\mu$ is calculated; for example, the two vectors below the first tree and the n-th tree. Finally, the membership degrees of each NLSR term for the geometric sketch are predicted as the result of fuzzy classification for the sample.

6.3. Subject Evaluation and Comparison

Table 5. Different types of fuzzified samples.

Fuzzy Membership (G, I, N, R, S)	Term		Type
	Original	Predicted	Correct	Error	Impure	Pure
(1.0, 0.0, 0.0, 0.0, 0.0)	G	G	√			√
(0.84, 0.0, 0.08, 0.08, 0.0)	G	G	√		√
(0.32, 0, 0.66, 0.02, 0.0)	G	N		√	√

shows the three line-region sketches used in the third experiment and

Table 6. Evaluation of suitability of the five terms.

No.	Degree of Suitability	Evaluation for Terms
		G	I	N	R	S
1	Very suitable	0	22	0	17	6
	Suitable	0	10	2	16	12
	Neutral	2	7	6	6	13
	Unsuitable	10	1	14	1	6
	Very unsuitable	30	2	20	2	5
2	Very suitable	1	0	19	7	0
	Suitable	2	0	17	10	0
	Neutral	5	0	4	11	0
	Unsuitable	11	2	1	11	5
	Very unsuitable	23	40	1	3	37
3	Very suitable	26	0	2	1	0
	Suitable	10	0	13	7	0
	Neutral	2	0	18	16	0
	Unsuitable	3	4	4	5	13
	Very unsuitable	1	38	5	13	29

shows the result of subject evaluation. The five NLSR terms, goes to, in, near, runs along boundary, and starts and ends in, are, respectively, abbreviated as G, I, N, R, and S in Table 6, and numbers below each term represent the total number of subjects who rank the term to the line-region sketch with the degree of suitability in the second column of Table 6. The result indicates that the participants rank different terms to line-region sketches with different degrees of suitability, confirming the fuzziness of semantics of terms in human cognition.

Based on the subject evaluations, membership degrees of the five NLSR terms for line-region sketches are calculated according to the transformation procedure described in Section 5.4. The results are shown in the second column of

Table 7. Examples of line-region sketches and classification results.

Line-Region Sketch	Subject Benchmark (G, I, N, R, S)	RF Classification	RF Fuzzification (G, I, N, R, S)	FRF Classification (G, I, N, R, S)
	(0.01,0.35,0.06,0.34,0.24)	R	(0.12,0.55,0,0.33,0)	(0.13,0.87,0,0,0)
	(0.09,0,0.56,0.35,0)	N	(0.02,0,0.98,0,0)	(0.11,0,0.89,0,0)
	(0.47,0,0.31,0.22,0)	G	(0.89,0,0.09,0.02,0)	(0.46,0,0.52,0.02,0)

. The results of RF classification, RF fuzzification, and FRF classification are also shown in the third to the fifth columns in Table 7.

According to Table 7, all three line-region sketches have non-zero membership degrees in multiple NLSR terms. In some NLSR terms, the membership degrees can be quite similar, e.g., the membership degree in term I (0.35) and membership in term R (0.34) for the first line-region sketch. But in crisp RF classification, the three line-region sketches are attached to single representative NLSR terms R, N, and G, respectively. In comparison, the results of FRF classification are more reasonable than those of crisp classification, as multiple non-zero membership degrees in NLSR terms are allowed. Similar membership degrees in two or more NLSR terms (e.g., the third line-region sketch in Table 7) also emerge in fuzzy classification of FRF. Although there are differences in the membership of NLSR terms between fuzzy classification and subject benchmark, possibly due to the limitations of RF fuzzification, FRF classification, and membership transformation of subject evaluation, the advantage of fuzzy classification over crisp classification is notable since the semantics of line-region geometric representations and NLSR terms can be interpreted more in full by fuzzy classification of FRF than crisp classification.

7. Discussion

This study differs from existing studies in several respects. First, fuzzy logic is introduced to interpret fuzzy semantics of NLSR terms. In existing research of building mapping model between NLSR terms and geometric representation [4,6,7], a line-region geometric representation can only be attached to a single NLSR term. The membership degree of a line-region geometric representation to an NLSR term is either zero or one. However, the semantics of human natural language are inherently fuzzy. As the semantic boundary of a concept cannot be precisely defined in natural language, using fuzzy logic to represent the semantic boundary of a concept with membership of a continuous domain [0,1] is more suitable. The proposed method in this study assigns each NLSR term a membership degree indicating the belongingness of a line-region geometric representation to the NLSR term. Therefore, a line-region geometric representation can be attached with multiple NLSR terms of varying membership degrees, which is consistent with the fuzziness of natural languages.

Second, a more accurate model is built to interpret fuzzy semantics of NLSR terms. In the research of Du et al. [22] and Liu and Shi [23], the 9-intersection model is extended to a fuzzy one to deal with uncertainty in location and boundary of spatial entities, and consequential uncertainty in topological relations. However, their research focuses on the fuzzy representation of spatial entities and formalized topological relations rather than establishing interpretation models between NLSR and geometric representation. In Wang et al. [17] and Wang [18], mapping models between non-spatial attributes in conventional GISs and natural language are developed, which enhances the representation ability of database and facilitates natural language query of non-spatial attributes. However, these methods are limited in handling natural language query involving NLSR terms. Papadias [35] proposed to process fuzzy spatial queries using configuration similarity measure. In this method, an integrated similarity measure of topology, direction, and distance among spatial entities is defined based on fuzzy sets concerning natural languages. The natural language query is processed by searching for spatial configurations with highest similarity measure. While innovative, the similarity measure is coarse because it employs only the conceptual neighborhood graph to measure similarity in topology relations, defines trapezoid membership functions subjectively to represent natural-language direction and distance relations, and uses an average combination metric as the final similarity measure. Contrary to the study by Papadias [35], this study employs FRF algorithm to learn a fuzzy mapping model to interpret fuzzy semantics of NLSR terms, and shows the trained FRF models are able to achieve good classification accuracy. Moreover, this study uses 2493 samples as training samples to allow for cognition of common people, includes a larger number of NLSR terms, i.e., 69 NLSR terms, and uses gene algorithm to optimize the fuzzy partition of numeric variables.

Employing the methodology of this study, more NLSR terms can be introduced into the fuzzy query of natural-language user interface of GIS similar to the non-spatial one in Wang [17]. A user can input “SELECT name_road FROM roadset WHERE location_road RUNS ALONG BOUNDARY OF the Olympic Park IN parkset” to search for the names of roads running along boundary of the Olympic Park in GIS database. The software interface can employ the trained FRF model to fuzzily classify the sketches formed by each road with the Olympic Park, and provide users the names of roads with membership degrees above a chosen threshold in NLSR term runs along boundary.

Some improvements and future work can be done on the basis of this study. First, in this study, fuzzy samples are yielded by fuzzifying crisp samples using RF algorithm. While the membership produced from votes for different classes is reasonable, collecting original fuzzy samples from subjects is more desirable. Second, although the trapezoid fuzzy set and fuzzy partition method [32] is effective, it is useful to explore other fuzzy sets or fuzzy partition methods, as they may provide better results. Third, for interpreting fuzzy semantics of NLSR terms, this study focuses on topological relations with little attention to other relations and contextual information. In the future, direction relation, distance relations, and contextual factors should be explored for more integrated models for complicated terms.

8. Conclusions

Facilitating the utility of the geographical information system for common people to solve routine problems is one of the purposes of geographical information research. To advance towards this goal, bridging the gap between natural language and geometric representation is critical.

Existing research into this issue tends to use crisp mapping models between NLSR terms and geometric representation. Such an approach falls short of capturing the fuzzy semantics inherent in NLSR terms. Processing a fuzzy spatial query using configuration similarity offers a better solution, but the current approach to measure semantic similarity is coarse, and its applicability may be limited. This study proposes to use the FRF algorithm to interpret the fuzzy semantics of NLSR terms. Based on a large number of fuzzy samples of line-region geometric representations and corresponding NLSR terms and variables, two FRF models with different membership aggregating strategies are built. The highest classification accuracy of two FRFs is 84.86% and 86.01%, respectively, which demonstrates good performance of the presented method.

In the future, in addition to topological relations, direction relations, and distance relations, contextual information will be introduced into models to interpret semantics of more complexed NLSR terms.