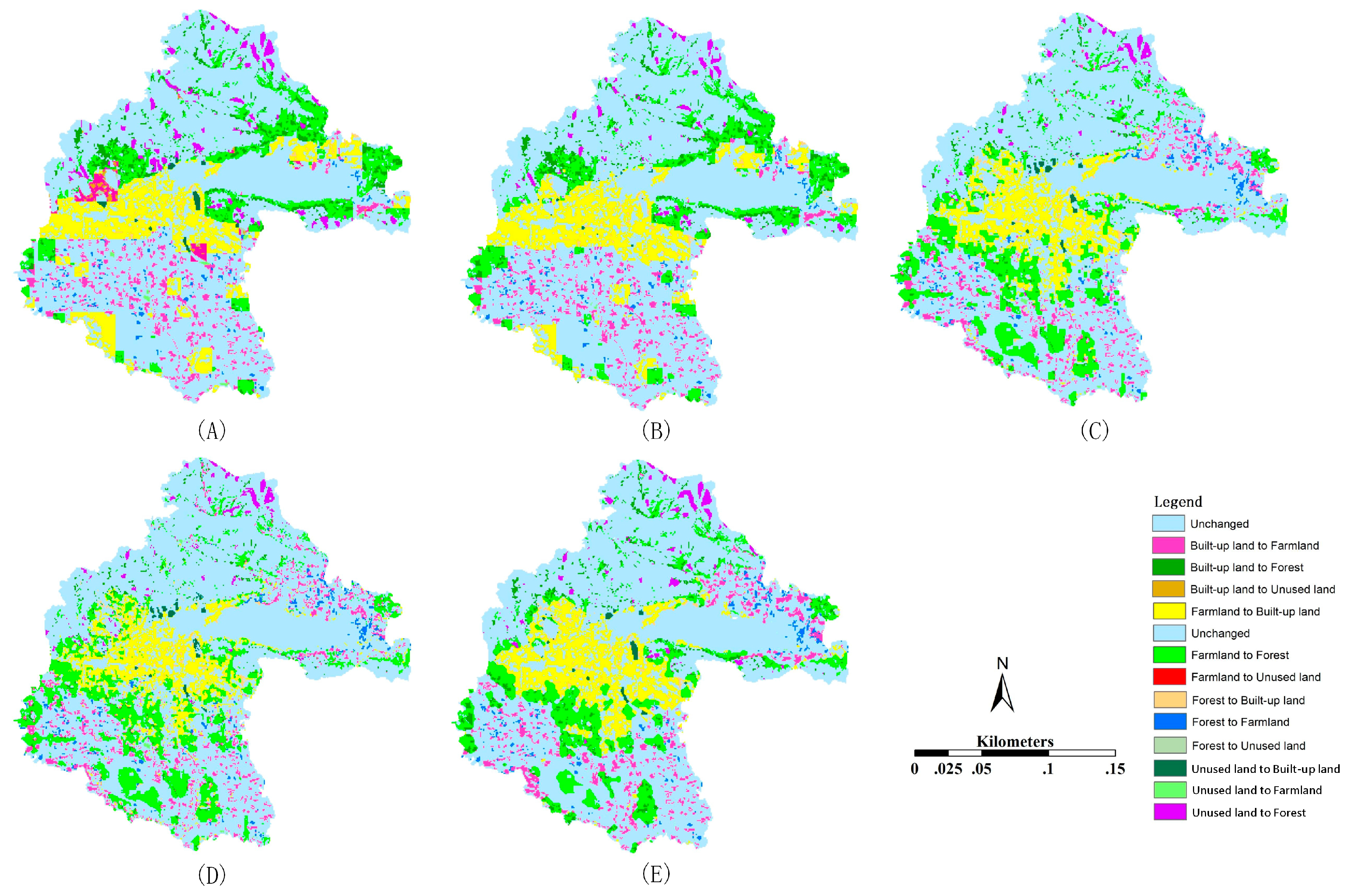
1. Introduction
Land-use allocation is a complex multi-objective optimal problem (MOOP) in which certain land-use types are allocated to proper units by considering multiple objectives [
1,
2,
3,
4,
5,
6,
7,
8]. When modeling and solving such problems, the goal is to find a set of optimal solutions that are essentially non-inferior [
9] rather than a single best solution [
10,
11]. Therefore, multi-objective land-use allocation (MOLA) is a difficult problem to solve.
The approaches to MOLA can be divided into two categories: scalarization and Pareto [
3,
5]. The goal of scalarization, the oldest and most direct approach [
3], is to transform a multi-objective problem into a single-objective problem using a priori knowledge and then solve the simpler single-objective problem [
12]. The commonly-used transformation methods include weighted sum [
13], goal programming [
14] and ε-constraint [
15]. In general, these types of methods are not able to evaluate the contributions of all the objectives to a solution and may fail to find important solutions if the transformation parameters are not properly designed [
16]. In order to get a set of optimal solutions, multiple executions of single-objective optimization are conducted by using different sets of transformation parameters such as weights. For example, Huang et al. [
17] proposed a novel approach that adaptively alters the objective weights according to the largest unexplored feasible region to produce a set of solutions. However, because multiple single-objective optimizations have to be repeatedly carried out, the whole procedure could be computationally expensive.
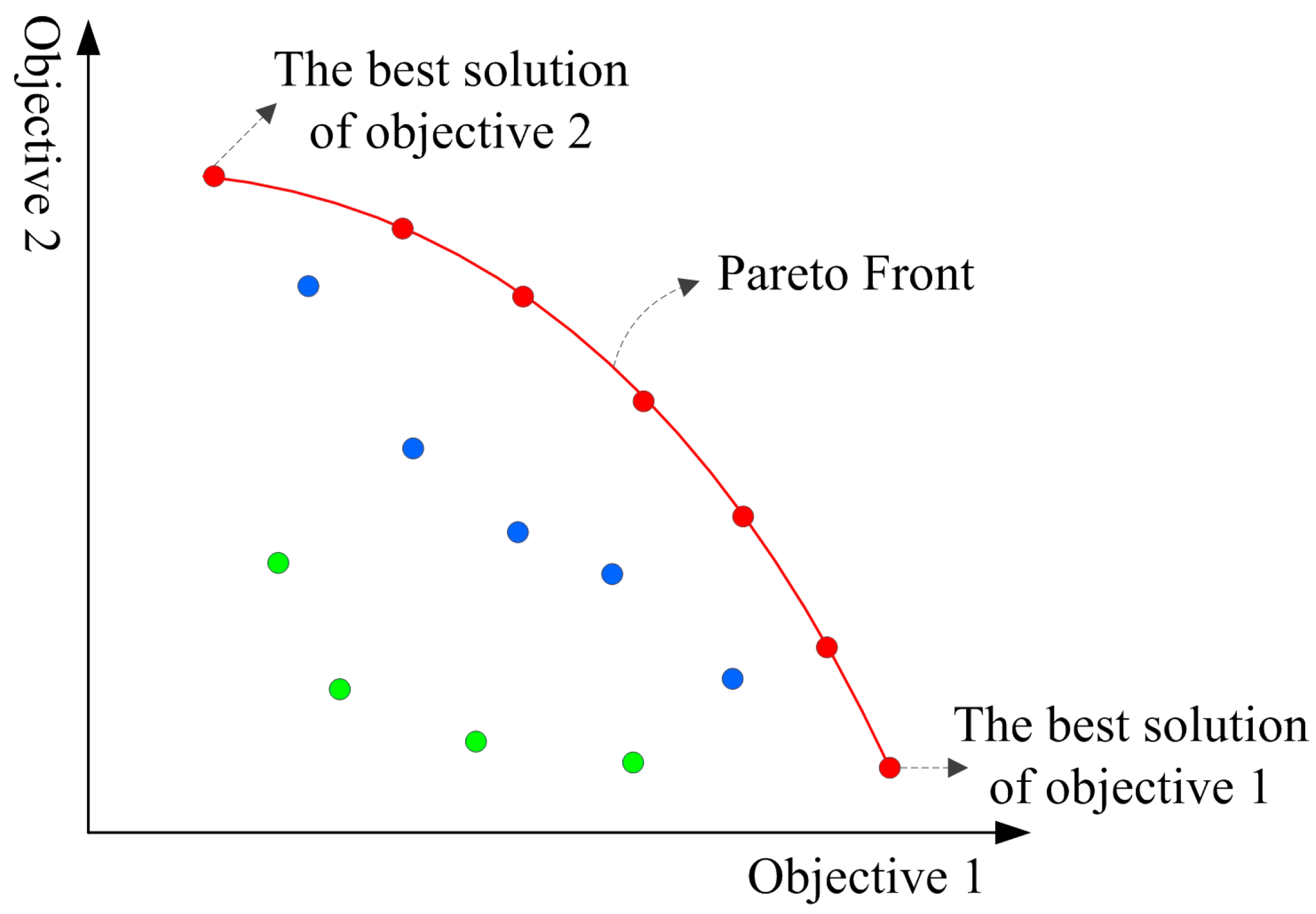
The Pareto approach originated from the concept of Pareto optimality (Pareto, 1965, originally published in 1896). A solution is Pareto optimal when no other solution is as good or better with respect to all objective functions and when it is also strictly better in at least one objective function than any other solution [
18]. A Pareto-optimal solution set or Pareto front (shown in
Figure 1) can be obtained by using the Pareto approach integrated with heuristic algorithms [
19,
20,
21,
22,
23,
24,
25], which involves constructing new solutions iteratively and preserving Pareto-optimal solutions selectively. The solutions on the Pareto front reflect different tradeoffs among the multiple objectives [
5]. Because the Pareto approach has the advantage that an entire Pareto front can be achieved by only one computation, it can better meet the requirements of multi-objective optimal decision-making.
Recently, studies on MOLA have applied some Pareto-based heuristic algorithms, including evolutionary algorithms [
7,
18,
26,
27], simulated annealing (SA) [
3] and the artificial immune system (AIS) [
28]. Duh and Brown [
3] developed a knowledge-informed Pareto simulated annealing approach (PSA) to solve the MOLA problem. Based on an initial solution set that includes the best solution of each single objective function and some random feasible solutions, PSA can obtain a Pareto front by iteratively executing the following steps: (1) new solution construction, (2) dominance assessments, (3) Pareto solution set updating, (4) objective-weight calculations and (5) new solution acceptance judgments. Meanwhile, PSA defined two knowledge-informed rules—the compactness rule and the suitability rule—to monitor the construction of new solutions. However, these rules were used only on the solutions with the largest weight values in any objective direction, which resulted in limited improvement of the qualities of all new solutions.
Huang et al. [
28] proposed an improved artificial immune system method for multi-objective land-use allocation (AIS-MOLA). Initially, based on each random solution, the mutation strategy of random exchange and the selection strategy of compromise programming [
29] were used to generate and preserve new solutions. After cloning some non-dominated solutions, new solutions were constructed using the crossover strategy. By such iterative calculations, the Pareto front can be obtained. Experiments revealed that AIS-MOLA achieved better results in both simulated and practical land-use allocation than PSA [
3]. However, because only completely random strategies were used in the phase of new solution construction and no auxiliary knowledge was imported to aid in navigating the spatial search to areas where global optima were located, we believe that there is still considerable room for improvement in the quality of the Pareto front for multi-objective land-use allocation.
Generally speaking, there is still room for improvement in the quality of the Pareto front obtained for multi-objective land-use allocation. The main reasons for this can be understood from the following two perspectives. First, the adopted heuristic algorithms have specific limitations in terms of optimization. The genetic algorithm (GA) generates new solutions (offspring) using crossover and mutation manipulations based on the parents’ solutions with good functional fitness, which can reduce the genetic diversity of the population to a certain extent. Thus, GA is usually deficient because of premature convergence, a phenomenon in which the algorithm falls into local optimal solutions and cannot escape them [
30]. The local search algorithm, for example, SA, generates new solutions by searching the adjacent space of a single solution; thus, the quality of these solutions is strongly dependent on the initial solutions and their neighborhood structures. Consequently, SA can also easily fall into locally optimal solutions. Moreover, the AI algorithm in [
28] also used the strategy of constructing new solutions from good solutions by crossover manipulation, thus introducing a defect similar to that of GA. Second, the currently-used strategies for generating new solutions lack effective inspiration by auxiliary knowledge. Effective utilization of auxiliary knowledge of natural geography or spatial structure can significantly improve the effectiveness and efficiency of spatial optimization because such knowledge is useful in reducing the scale of the search space and preventing unproductive searches [
3]. However, from the works mentioned above, it is clear that most of the solution’s neighborhood searches in a population adopted completely random strategies to construct new solutions, and auxiliary knowledge was rarely used.
Considering the above two problems, some improvements can be made from the following two aspects. To solve the first problem, we can introduce the artificial bee colony (ABC) algorithm, which is an efficient optimization algorithm that, in most cases, performs better than algorithms such as GA, AIS and particle swarm optimization (PSO) [
31,
32]. Moreover, it has been successfully used to tackle the problem of single-objective land-use allocation (SOLA) to obtain one optimal solution [
33]. For the second problem, introducing a multi-objective spatial search strategy informed by auxiliary knowledge could guide the generation of all new solutions. For example, if a type
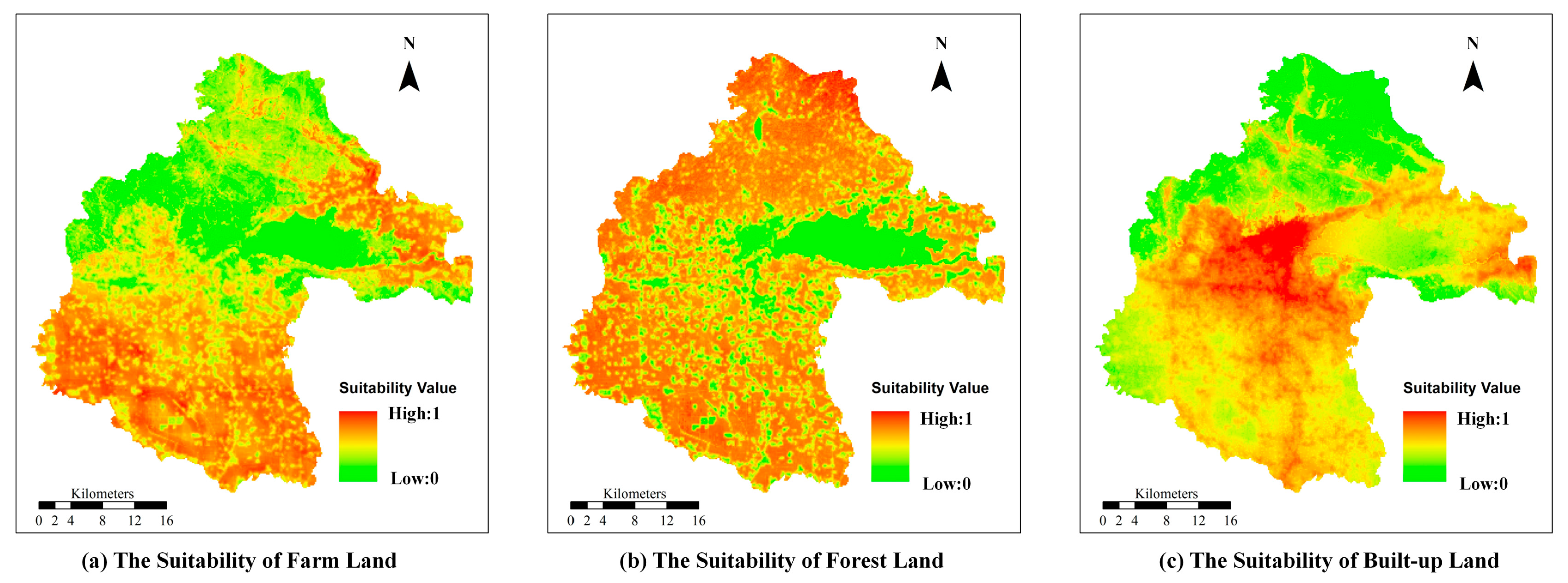
land-use needs to be allocated in a multi-objective maximization problem, auxiliary knowledge such as the neighborhood information could be used to select spatial units with increased functional values after compromising multiple objectives when the units are assigned type
. These selected units could be treated as a new size-reduced feasible solution space, which would be helpful for efficiently constructing new solutions and improving their qualities.
Therefore, to combine these two improvements and obtain better Pareto solutions of land-use allocation, this paper utilizes the ABC to solve this multi-objective spatial optimization problem and auxiliary spatial knowledge to improve ABC’s spatial search ability.
The remainder of this paper is arranged as follows.
Section 2 theoretically and briefly introduces the Pareto optimization concept, the land-use allocation model and the ABC algorithm.
Section 3 expounds on the proposed method, ABC-MOLA, in detail.
Section 4 describes both simulated and practical experiments conducted to validate the optimization ability of ABC-MOLA. Finally, a substantial discussion and the conclusion are presented in
Section 5 and
Section 6, respectively.
3. Methodology
Aiming at the three differences between Pareto-ABC and traditional ABC, this paper adopts three strategies to make the Pareto-ABC suitable for MOLA: (1) a crowding distance is used as an indicator to direct the bees’ searches to the sparse region of the Pareto front to increase the diversity of the results [
40]; the non-dominated solutions in a sparse region have higher probabilities of being selected as food sources by onlooker bees; (2) all newly-generated solutions in each iteration are added to the food-source set, which will be updated to realize the food source’s updating by the same operations as are used in the Pareto-archive maintenance process; (3) an external solution archive is used to save the Pareto optimal solutions, which will be globally updated by the Pareto-archive maintenance process described in
Section 3.3.
Moreover, a neighborhood search strategy for Pareto optimization considering auxiliary knowledge will be proposed and explicitly described in
Section 3.2; this is an important improvement of this paper for the optimization effectiveness of MOLA.
3.1. Algorithmic Procedure
In this paper, a two-dimensional matrix with
rows and
columns can be used to represent a solution [
33].
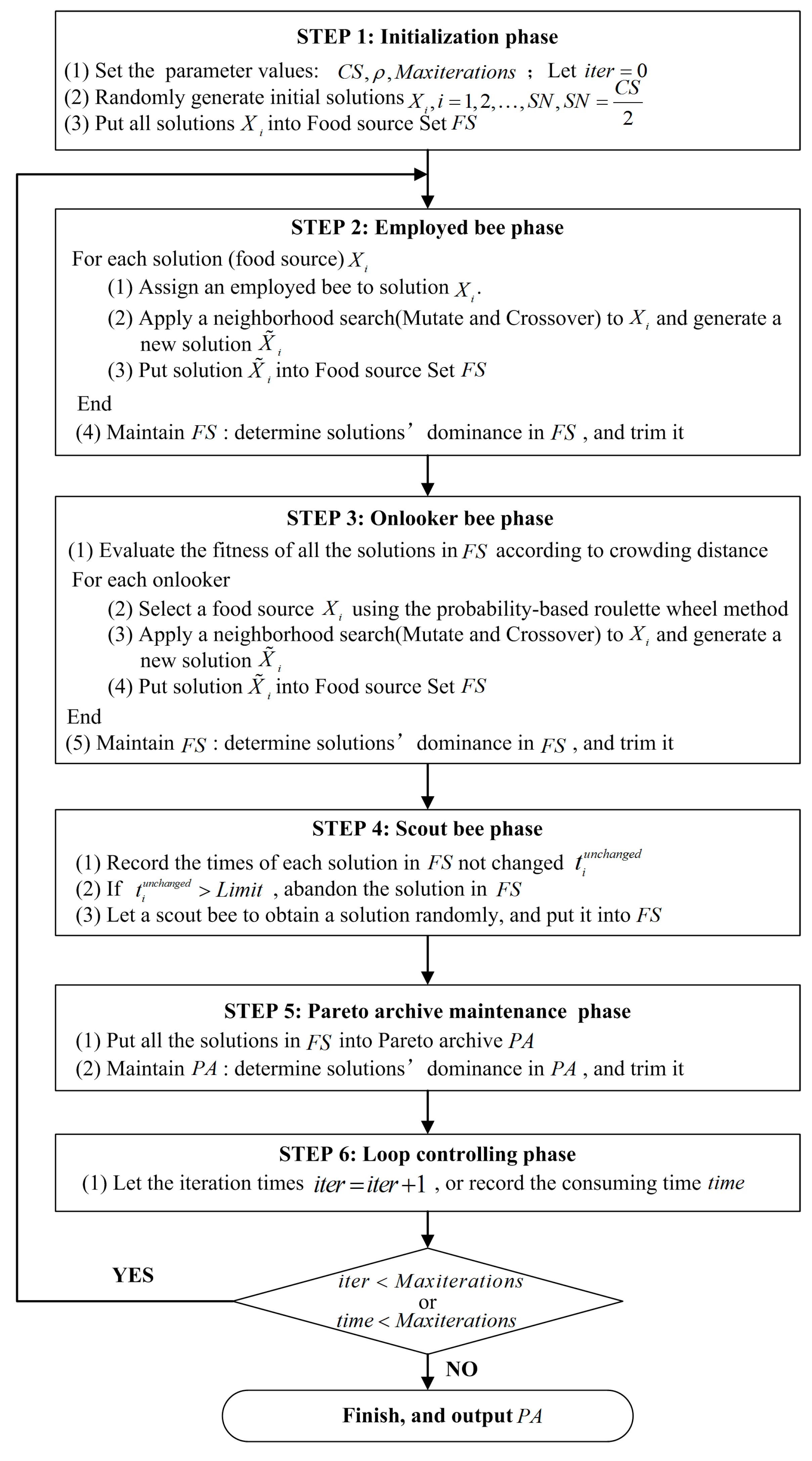
Figure 2 shows the main procedure for the ABC-MOLA algorithm.
First, all the parameter values are set and initial solutions are generated by randomly allocating a land-use type to each cell according to the planned area of each type. Then, in the employed and onlooker bee phases, new solutions are constructed using the mutation and crossover operations. In addition, the algorithm records the number of times that each solution is not updated. When this value exceeds a predefined threshold, the scout bees are activated to randomly generate a solution to replace the original. Next, all the solutions in the food-source set are added to the Pareto-solution set, and Pareto archive maintenance is conducted. Finally, when these iterative steps satisfy the convergence condition (or when the iteration time or computing time exceeds a predefined threshold), the algorithm stops.
3.2. Neighborhood Search Strategy
Bees’ neighborhood search strategies determine the optimization efficiency of the entire algorithm. Therefore, such strategies are the key parts of this study. In the ABC-MOLA algorithm, a modified mutation operator and a crossover operator are introduced to improve its spatial search capabilities.
3.2.1. Mutation Strategy
A mutation strategy, which is an iterative process, is applied to a proportion of the raster cells in the study area. During each iteration, this process allows the land-use types of a solution’s different raster cells to be exchanged to obtain a new solution with a knowledge-informed neighborhood search strategy. Then, the newly-generated solution must be compared with the original solution using the technique of compromising programming to perform the solution selection process.
Solution Selection Based on Compromising Programming
The newly-generated solution needs to be compared with the original solution xi to complete the solution-selection step. If is better than , will be replaced by , which can be notated as ; otherwise, is abandoned, and is retained. Subsequently, the next mutation will be carried out based on the better solution.
Usually, the traditional technique of Pareto-dominance judgment can be used to evaluate the two solutions’ qualities. However, if they are both non-dominated solutions, the traditional technique is no longer useful, and no helpful preference for solution selection will be given to obtain the Pareto front. Therefore, to overcome the problem, compromising programming can be introduced to evaluate two solutions during the mutation procedure.
Weighted sum, a type of compromising programming, is the most direct method to tackle a multi-objective optimization problem [
13]. It converts an
m-dimensional multi-objective problem into a single-objective problem by weighting each objective function by a nonnegative vector
. In a maximum multi-objective optimization problem, each bee searches around a food source to find a new solution with a larger value for a single objective function as shown in Formula (14).
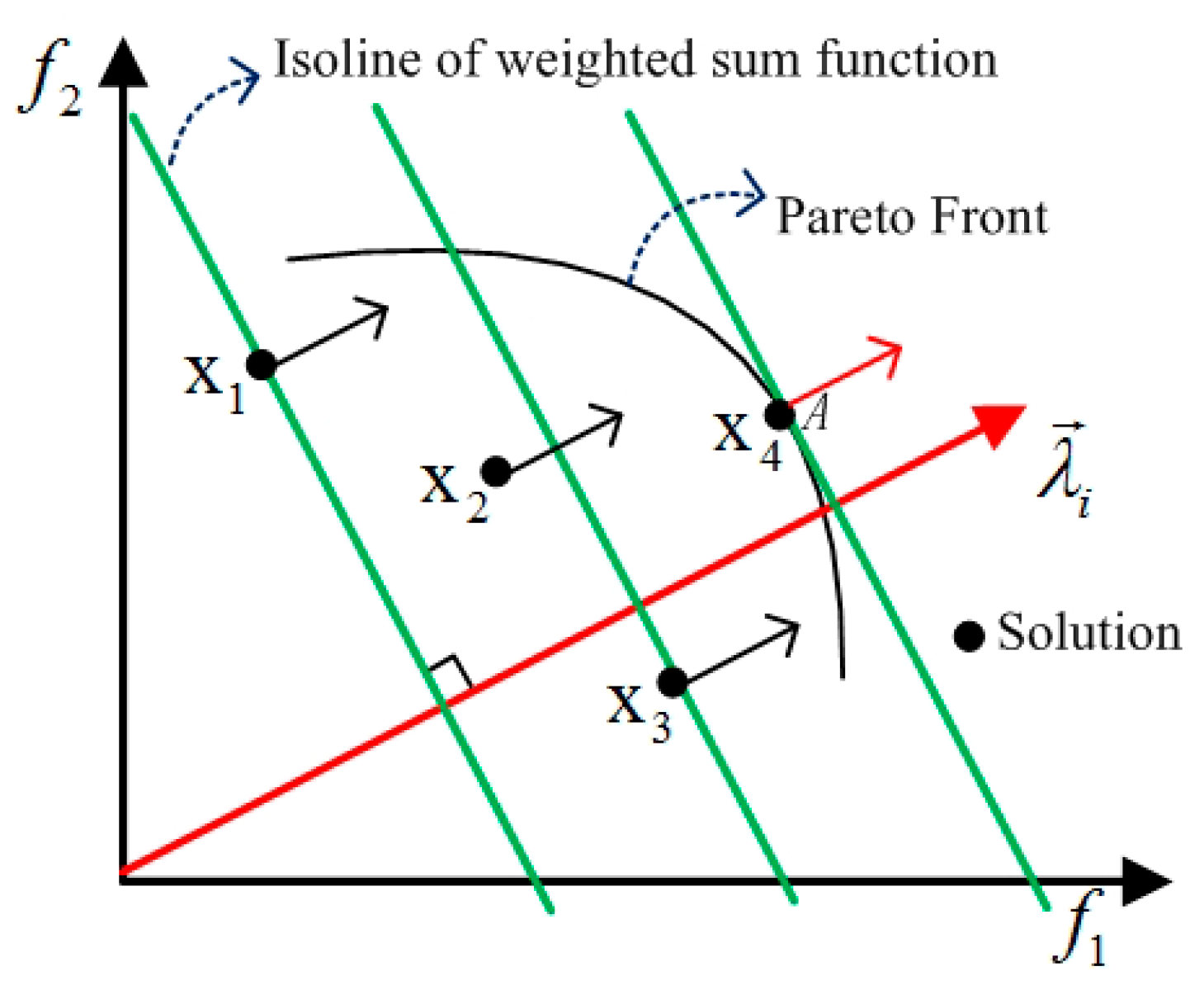
This technique is effective in guiding the spatial search in the direction of this weight vector, thus improving the mutation’s optimization efficiency. Taking as an example, the technique can be illustrated as follows.
For any two-dimensional weight vector
, the isolines of the weighted-sum function are a series of straight lines aligned perpendicularly to
, as shown in
Figure 3. According to (14), solution
is better than
and worse than
; thus, the solution retained during the mutation manipulation will move progressively further away from the origin in the direction of
, until the isoline of the solution’s weighted-sum function is tangent to the Pareto front (Point
in
Figure 3, which is an optimal solution of problem
). In the problem illustrated in
Figure 3, three mutation manipulations will be executed and the solution-selection process can be recorded as
.
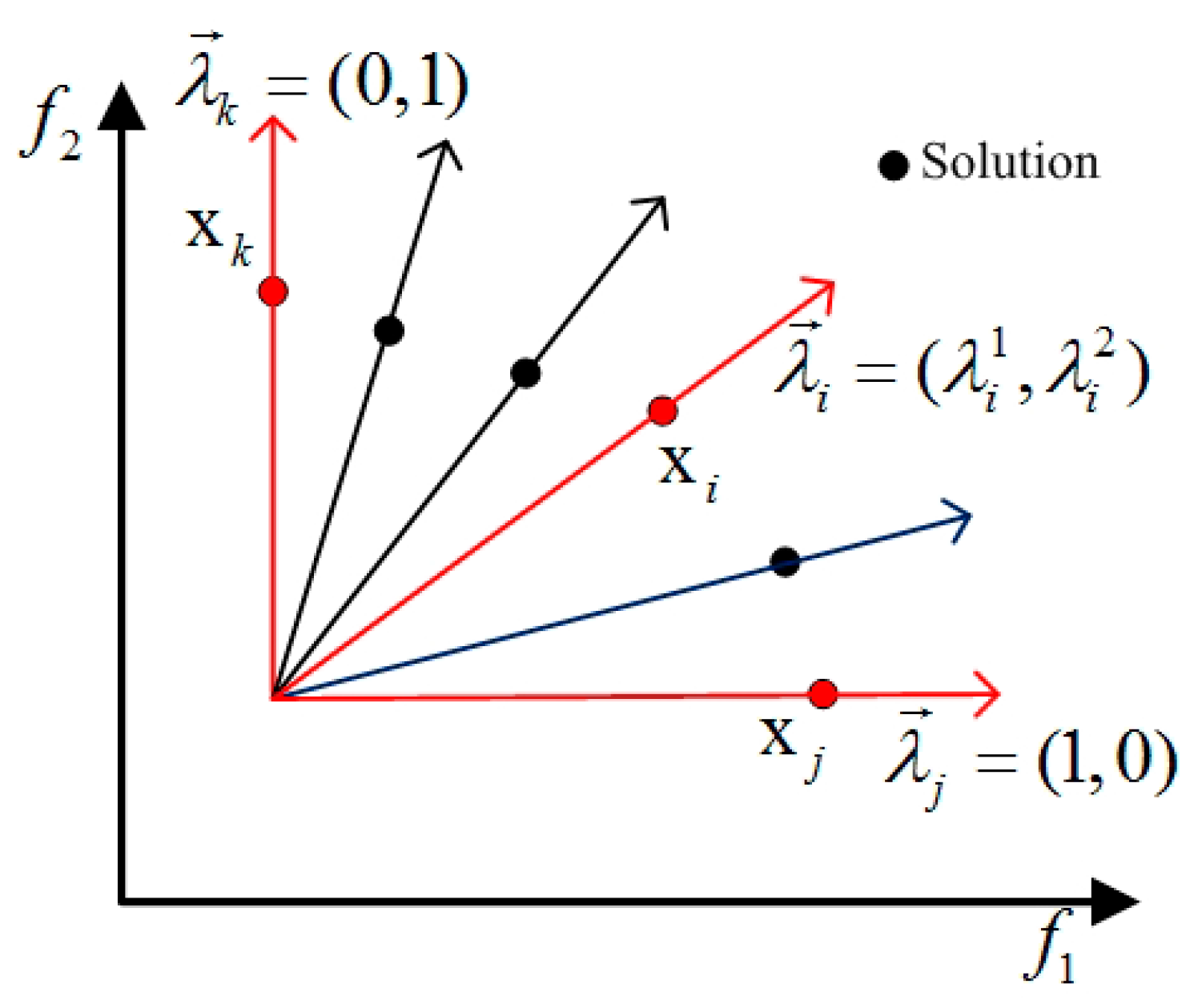
In this study, the weight vector of each solution is closely related to the spatial distribution of all solutions in the objective space, as shown in
Figure 4. The weight
of solution
in the direction of objective function
is defined by Formulas (15) and (16). Note that defining the weight vector by such a method ensures that different solutions have different optimization directions (selection preferences) during the mutation operation and further ensures the diversity of the solutions in the Pareto front.
3.2.2. Crossover Strategy
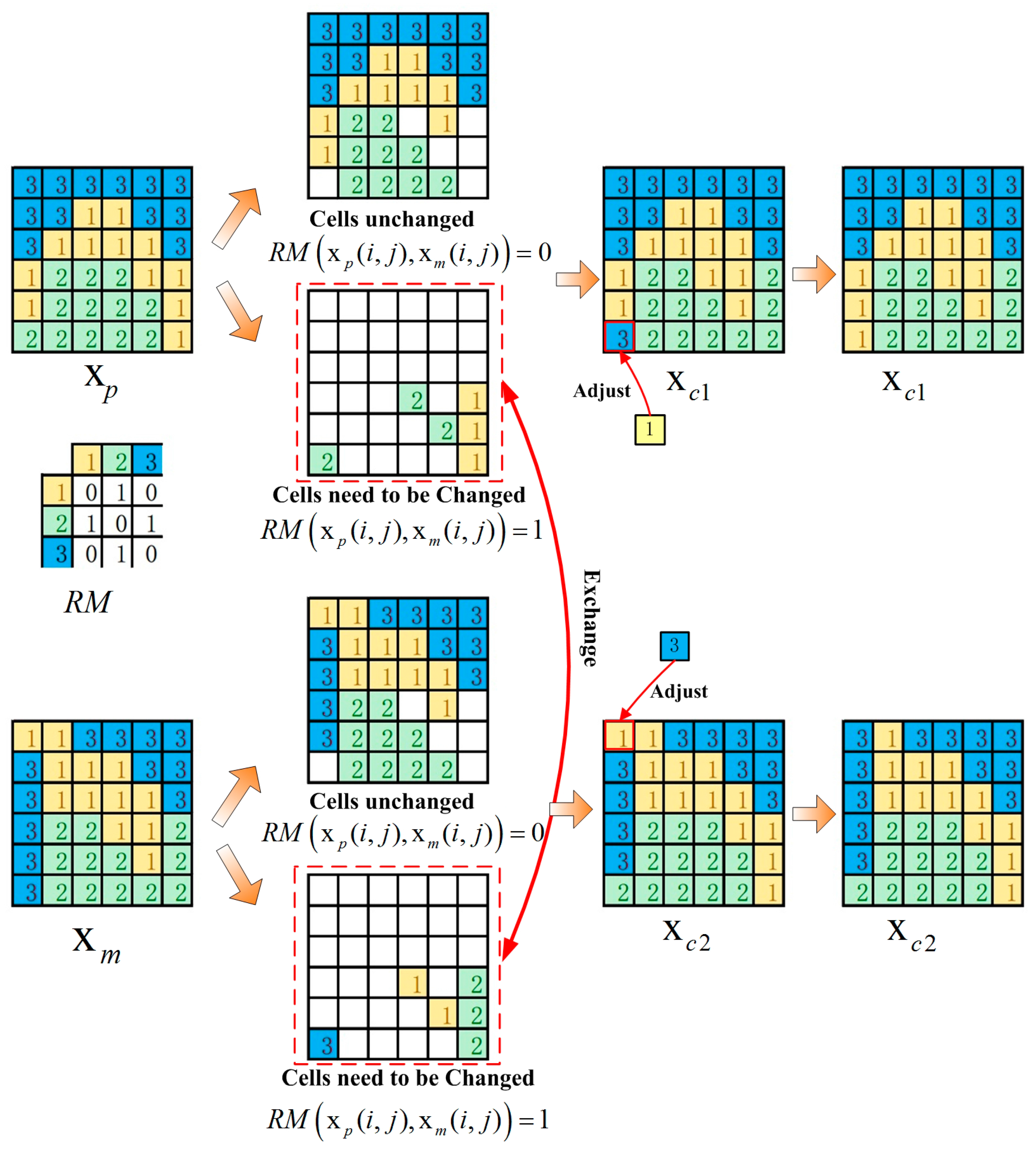
The crossover strategy is used after the mutation operation. It allows two solutions to exchange parts of their raster cells to form new solutions, which is helpful for increasing the diversity of this algorithm.
In this study, to promote the diversity of the Pareto-optimal solutions, we generate two new solutions using one crossover operation, and both solutions will take part in the process of Pareto-archive maintenance. The crossover operation is performed according to the following steps, which are also depicted in
Figure 5.
First, a solution that is different from the current food source is randomly selected, and these two solutions are duplicated as parent solutions (
and
in
Figure 5).
Then, by comparing the parent solutions, a set of raster cells with different land-use types in each parent solution is randomly selected (the two parts of solutions in the two red dotted square frames in
Figure 5). Two offspring solutions are constructed by exchanging the selected cells of the two parent solutions. Mathematically, the procedure can be represented by Formula (17):
where
is a
symmetric matrix and
is the number of land-use types that need to be allocated. When
,
is a random number in the set
; otherwise,
. Here,
,
,
and
are the land-use types of the two parents’ and two offspring’s solutions, respectively, in cell
.
Finally, after the exchange operation, the land-use types that violate the area restriction must be adjusted by random selection. The two final offspring solutions (
and
in
Figure 5) can be obtained.
3.3. Pareto-Archive Maintenance Strategy
Maintaining a Pareto-archive involves combining new solutions with the original Pareto-archive. After judging solution dominance according to the definition of Pareto dominance in
Section 2.1, non-dominated solutions will be retained. However, in ABC-MOLA, the maximum capacity of the Pareto archive is predefined. Therefore, if the quantity of non-dominated solutions exceeds the capacity, some inferior solutions with small crowding distance [
40] must be deleted.
The crowding distance
of a solution
is the average distance of its two neighboring solutions, which can be calculated by the following steps. First, all solutions in the Pareto-archive are sorted according to the values of a certain objective function. Then, the sum of the Euclidean distances between solution
and its neighboring solutions
,
in all objective directions is calculated. Finally,
is calculated according to Formula (18).
where
and
are the numbers of objectives and solutions, respectively,
is the sequence number of the reordered solutions and
and
represent the maximum and minimum values, respectively, of the objective function
for all solutions in the Pareto-archive.
In this study, the solution set of all food sources is also regarded as an archive with maximum capacity . The solution-updating strategy for this set in ABC-MOLA is the same as for the Pareto-archive.
3.4. Computational Complexity
In this paper, a solution is of rows and columns; the colony size is ; the maximum iteration number is . The mutation proportion is ; the number of objectives is ; and the quantity of land-use types to be allocated is . The ABC-MOLA algorithm’s computational time complexity can be analyzed as follows.
The main parts of the improved neighborhood search strategy’s computational complexity are listed in
Table 1, which shows that the overall complexity of neighborhood search is
. This neighborhood search complexity is governed by the solution updating procedure of mutation.
Table 2 shows the main procedures involved in the ABC-MOLA algorithm’s computational complexity. It shows that the overall complexity of ABC-MOLA is
, which is governed by the neighborhood search procedure.
5. Discussion
5.1. Sensitivity Analyses
Colony size and iteration number are two important parameters of ABC-MOLA that directly influence the quality of the Pareto front. In this section, we analyze ABC-MOLA’s sensitivity to these two parameters and demonstrate its stability while optimizing land-use allocation.
5.1.1. Impact of Iteration Number
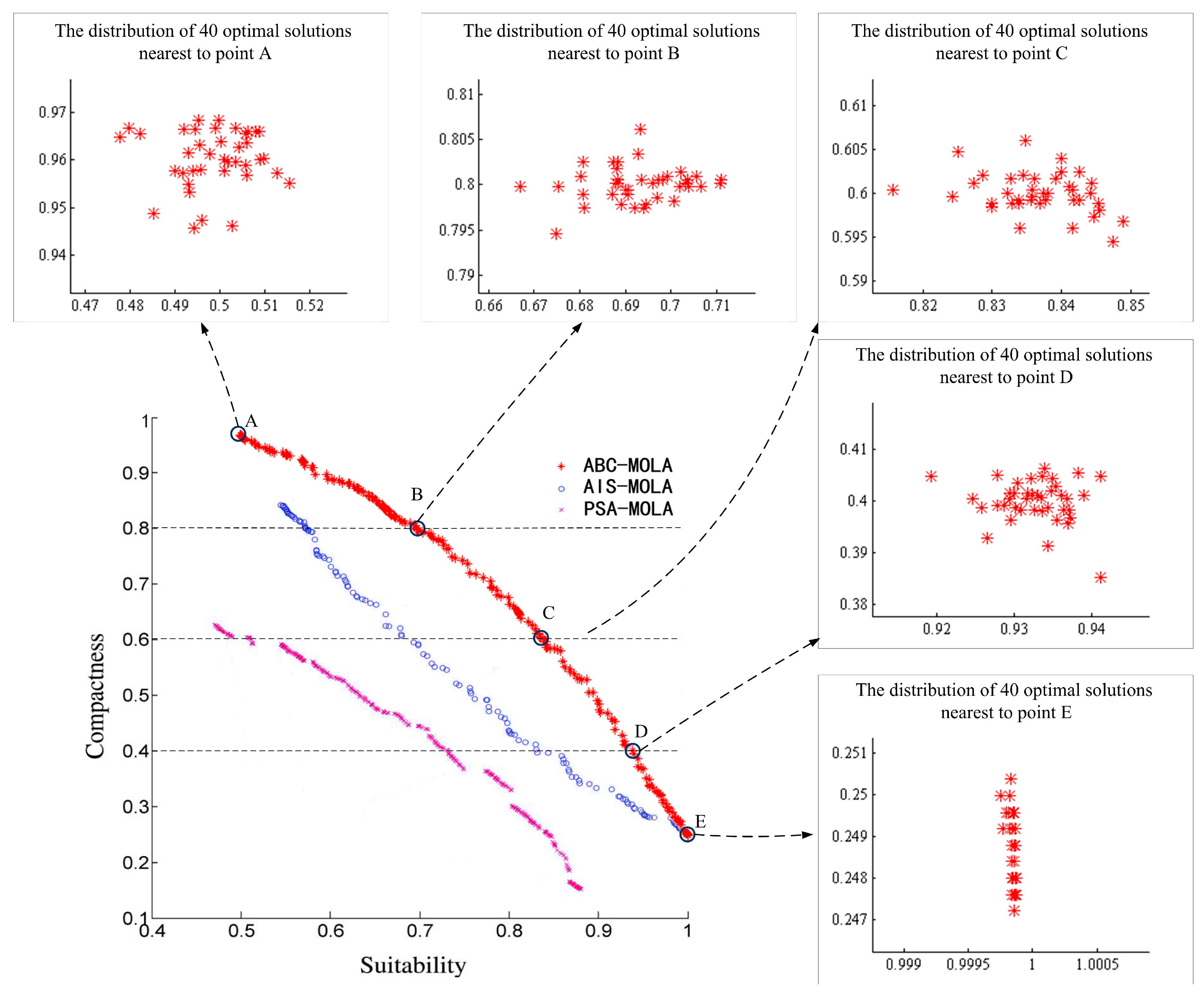
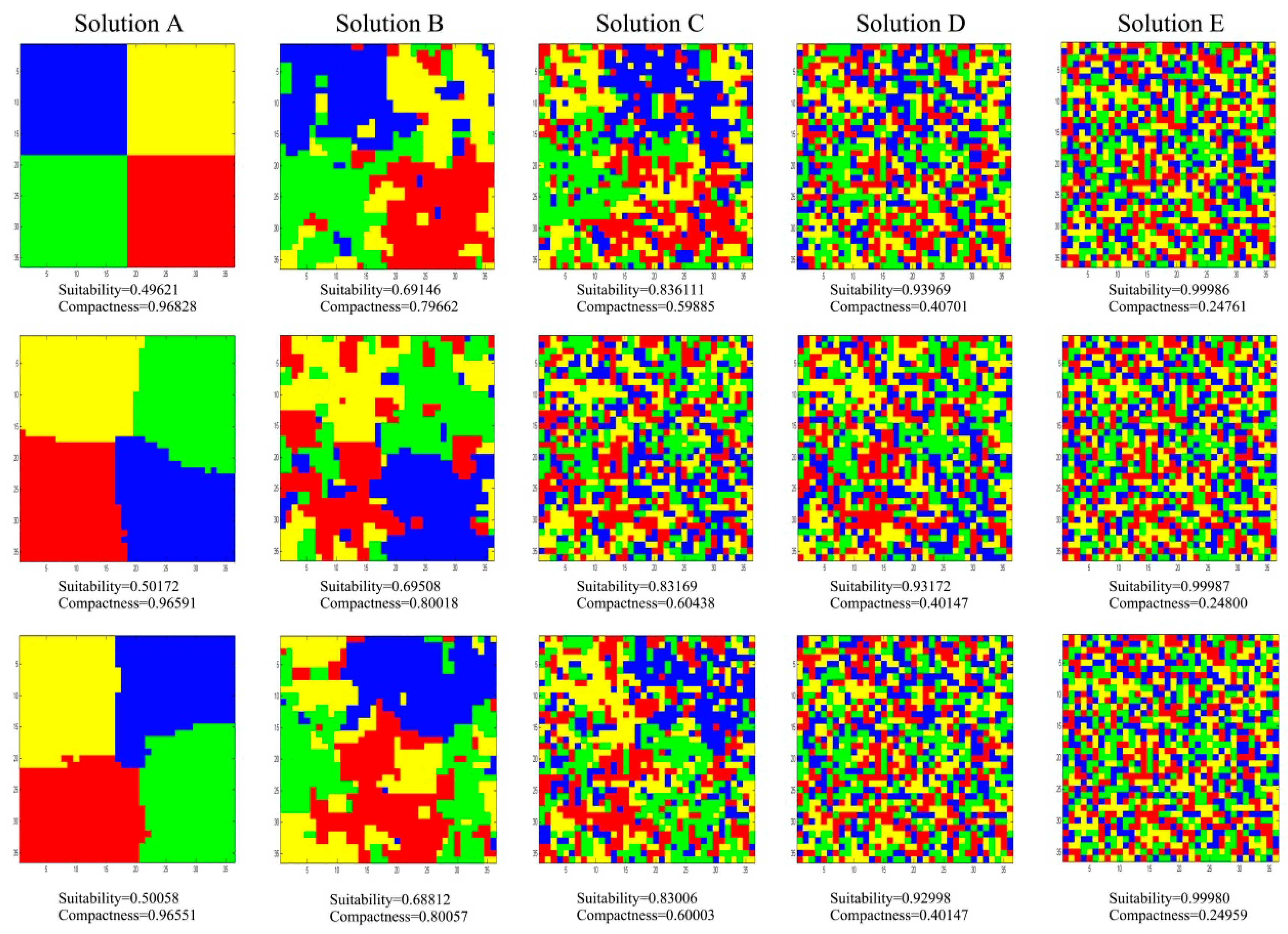
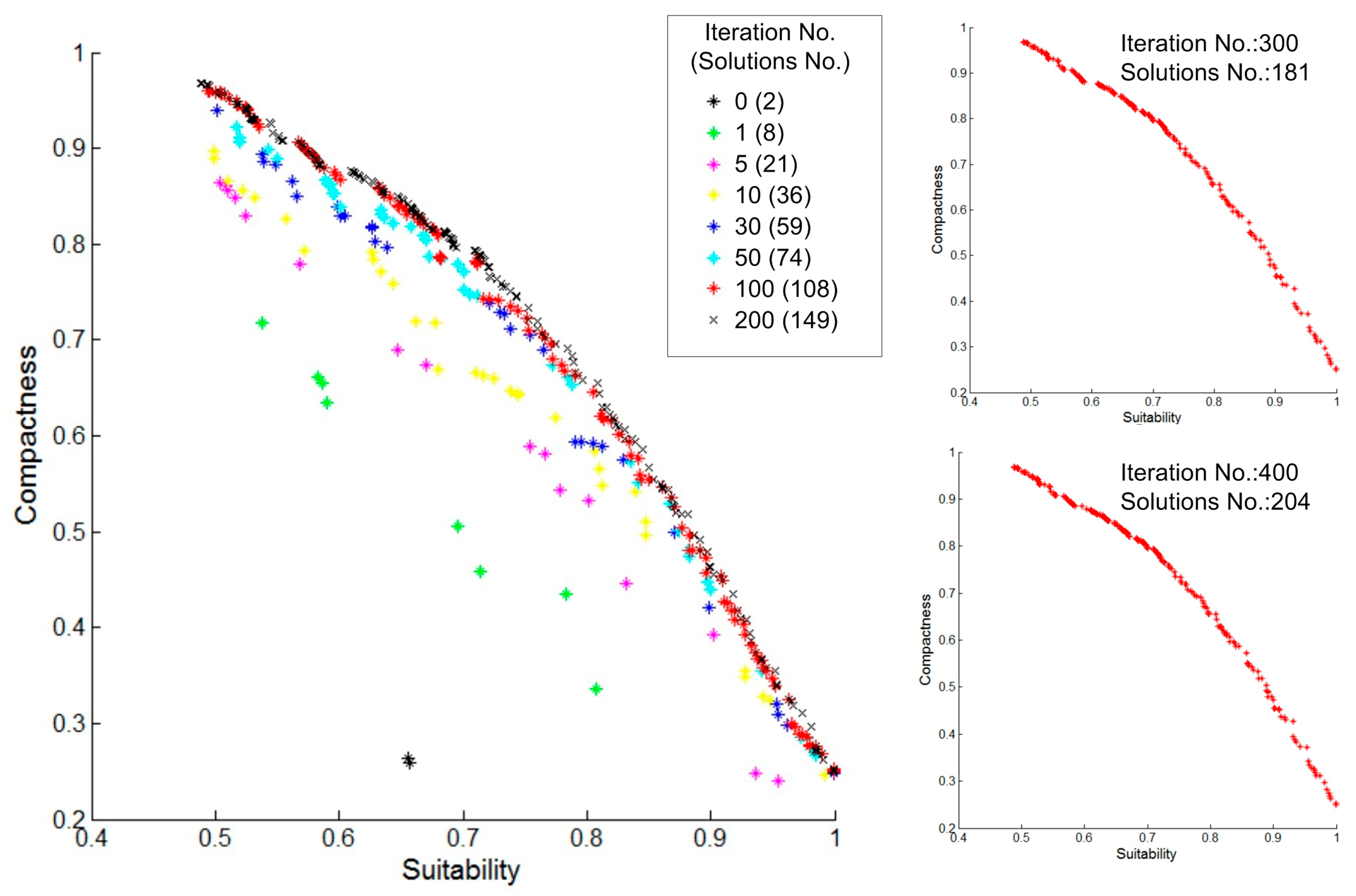
A proper number of iteration helps ensure that an optimal solution can be obtained in a reasonable time. Too much iteration prolongs the computation time, while too little prevents a set of optimal solutions from being achieved. To investigate this impact, the spatial distribution of non-dominant solutions in objective space with different numbers of iterations can be recorded with the simulated data under the condition of .
From the results shown in
Figure 15, it is evident that at the beginning of the algorithm, non-dominated solutions move quickly towards ideal solutions. By 50 iterations, the curve of the Pareto front is preliminarily formed. By approximately 100 iterations (approximately 25 s of execution time), the shape of the Pareto front tends to be stable. As the calculation continues, the number of non-dominated solutions in the Pareto-optimal solution set increases, and the newly-added solutions simply fine-tune and increase the density of the Pareto front. Therefore, we can conclude that setting the parameter
to a large value (for example, in the experiment, the iteration time is longer than 25 s or, equivalently, extending the number of iterations past 100) has little impact on the formation of the Pareto front.
5.1.2. Impact of Colony Size
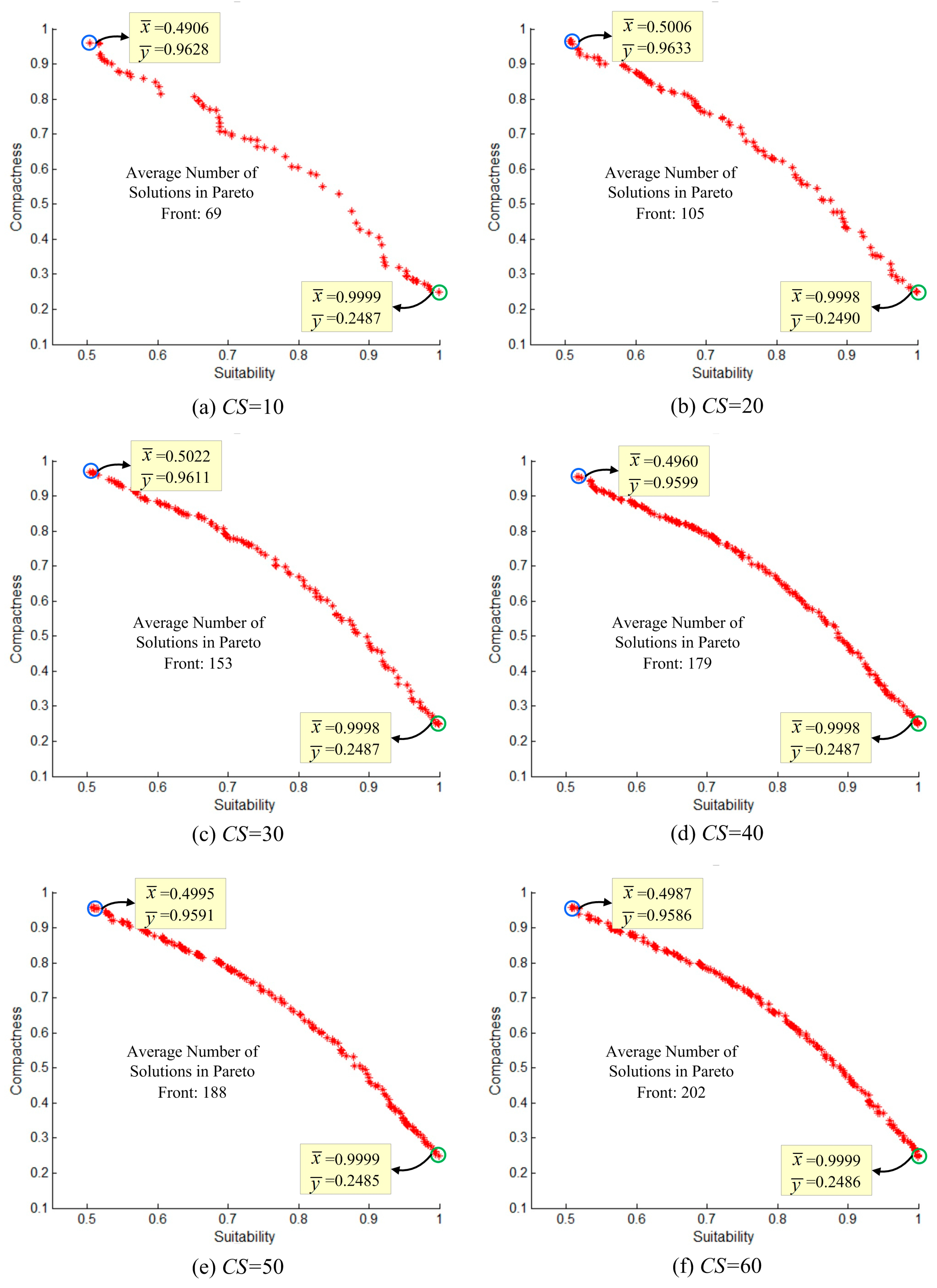
Colony size determines the quantity of solutions in each iteration. Within a certain iteration time, different Pareto fronts of different qualities can be obtained using different colony sizes. To assess this impact, six sets of calculations with different colony population sizes () were conducted with simulated data by fixing . Each set is calculated ten times.
The results (
Figure 16) indicate that the non-dominated solutions obtained by ABC-MOLA are limited in quantity and cannot form a continuous Pareto-front curve when
is too small (for example, when
in this experiment). However, as the size of the colony population
increases, the number of Pareto-optimal solutions obtained in a certain time rises dramatically, and the curves of the Pareto front, which maintain very similar spatial distributions in objective space, tend to be continuous and smooth. Therefore, the value of
has a small impact on the formation of the Pareto front when its value is relatively large (for example, when
in this experiment).
5.2. Effectiveness of the Improvements
5.2.1. Performance of Improved Search Strategies
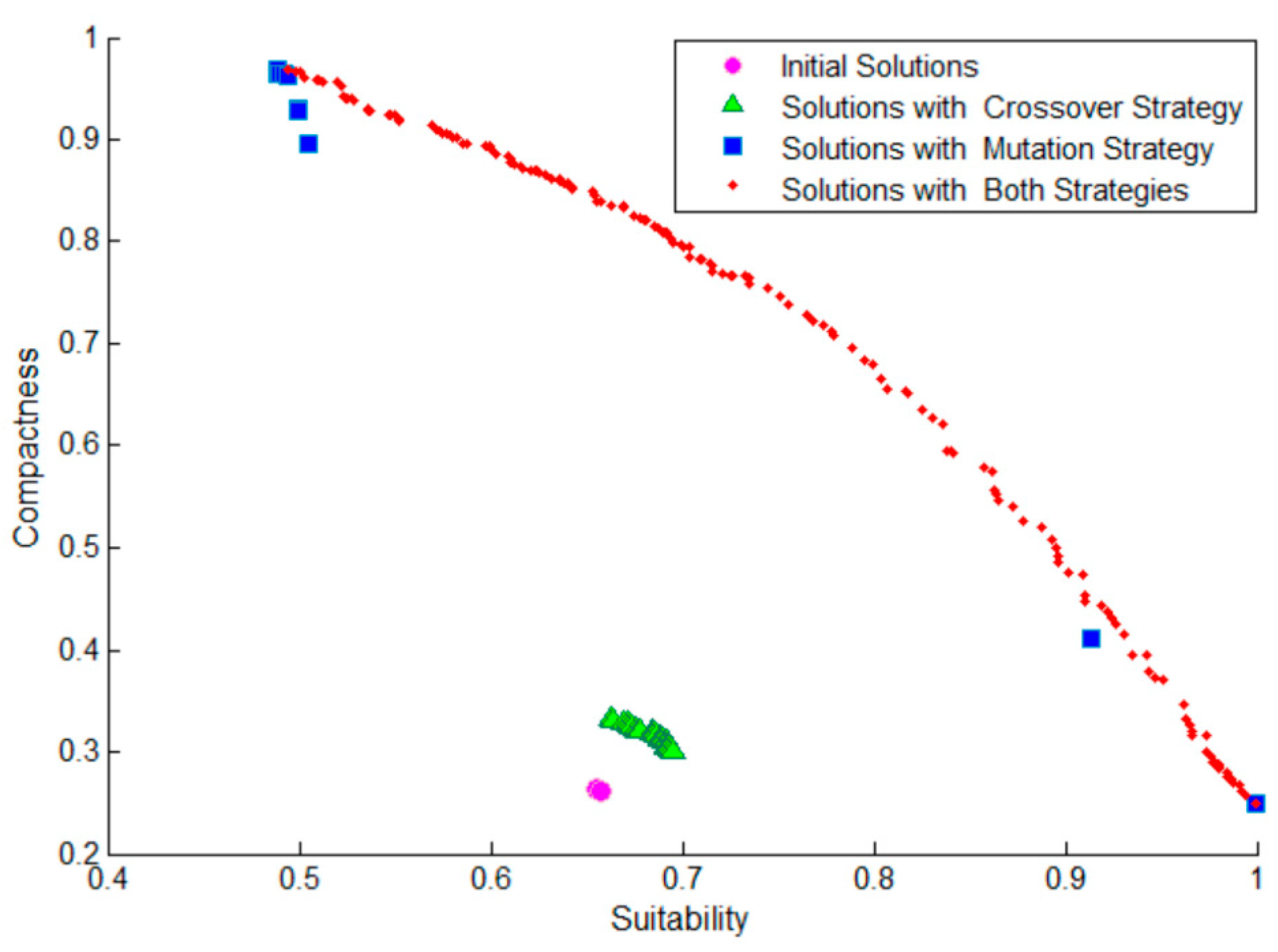
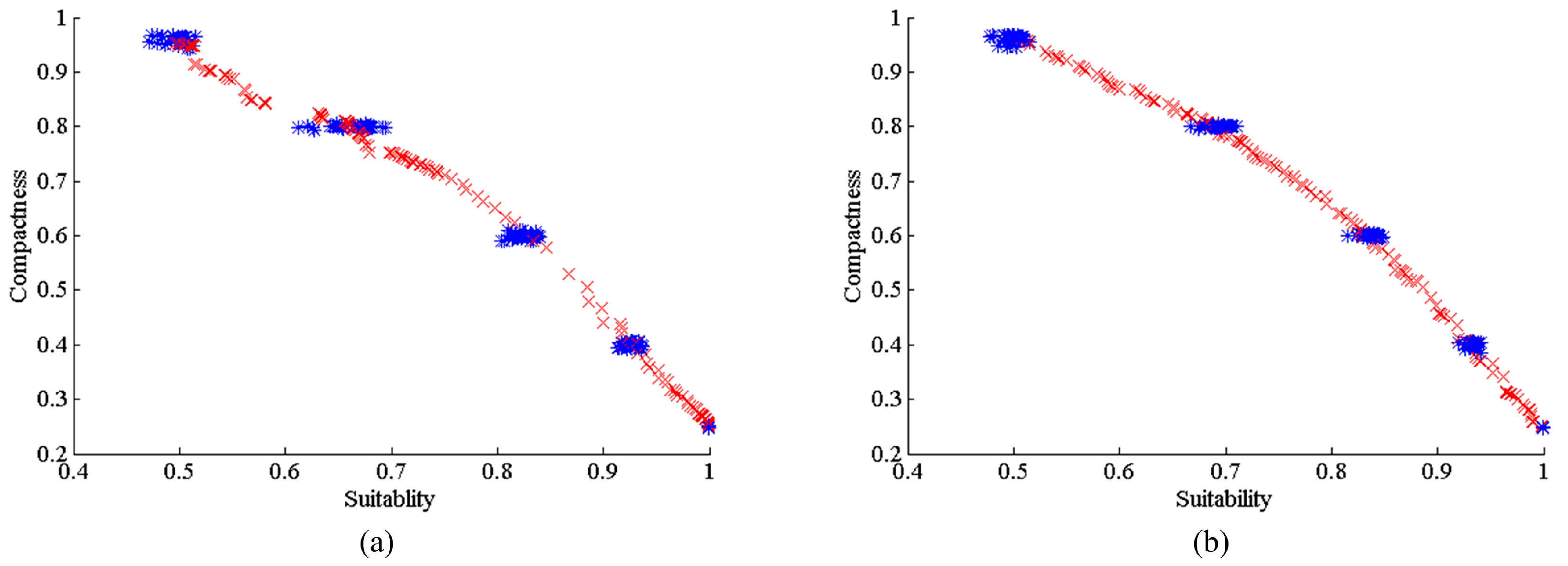
To implement the analysis of neighborhood search strategies, three combinations of neighborhood search strategies were tested: (1) the crossover operator only; (2) the mutation operator only; and (3) a combination of both crossover and mutation operators. The experimental results are shown in
Figure 17. The results reveal that after 100 iterations, when only the crossover operator is applied, a continuous and dense Pareto front can still be formed (the green triangle solutions), but with small coverage. In contrast, when only the mutation operator is used, the obtained Pareto front (the blue rectangle solutions) includes some high-quality solutions around its two end vertices, but few in between, indicating poor diversity and uniformity in the spatial distribution. However, when both the crossover and mutation operators are combined, a continuous Pareto-front curve (the red dot solutions) with a uniform distribution and wide coverage is formed in the objective space.
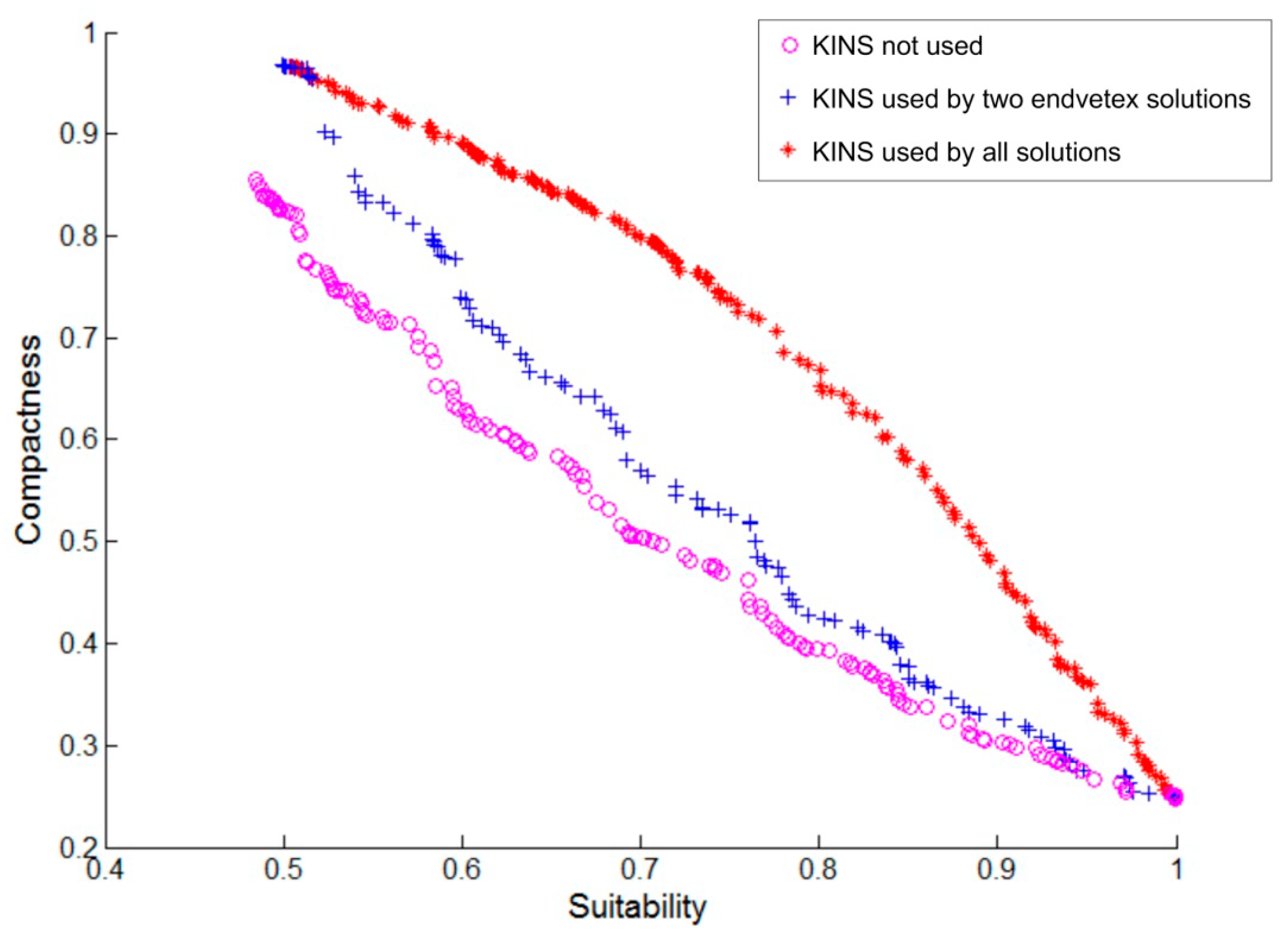
In addition, the KINS strategy was used in each new solution’s generation by neighborhood search in ABC-MOLA. To prove this method’s effectiveness, three comparison experiments based on the search, crossover and mutation operations have been carried out: (1) KINS is not used; (2) KINS is used only by the two end vertex solutions (similar to the strategy used in PSA-MOLA) [
3]; and (3) KINS is used by all solutions. The results are shown in
Figure 18. The results show that the Pareto front obtained in the first experiment has the lowest quality and is totally dominated by the other two results. The second experiment’s solutions are of similarly high quality to the third experiment’s solutions around the two end vertices of the Pareto front. However, between them, the second experiment’s solutions are totally dominated by the third experiment’s solutions. Obviously, the result of the third experiment has a better Pareto front than the others.
5.2.2. Performance of the ABC Algorithms
The proposed neighborhood search strategies (described in
Section 3.2) can be used not only by ABC, but also by many other heuristic algorithms. Here, the artificial immune system (AIS) is coupled with the improved search strategies and compared with the ABC-MOLA algorithm proposed in this paper.
The result (
Figure 19) shows that AIS achieves relatively good optimal results while using these search strategies; even better than the AIS-MOLA algorithm proposed by Huang et al. (2013). This effectively validates the portability of these strategies. However, even though the Pareto fronts obtained by AIS are very similar to ABC, they are still inferior to those obtained by ABC, regardless of the uniform distribution of the solutions or the smoothness of the Pareto front curves.
5.3. Potential Use of the Approach
The Pareto front solutions obtained by the proposed approach can be helpful for real regional planning. They can provide a set of optimal solutions for decision-makers, who can choose one solution as the final decision according to their real demands and planning preference. Furthermore, according to the Pareto front solutions’ distribution in objective space, decision-makers can quantitatively analyze one objective function’s reduction while improving the other objective functions, which could be a useful evaluation basis for final decision-making.
Besides, there are two potential uses for the approach presented in this paper. First, from the algorithmic point view, the proposed approach could theoretically be extended to handle problems with three or more objectives. From this perspective, most of the algorithm’s procedures, such as solution initialization, Pareto-archive maintenance and crossover manipulation, are extraneous to the quantity of the objectives. Only the method of determining the weight vector while using the weighted sum strategy in the mutation operation would need some improvement when processed in three or higher dimensions.
Second, from the application perspective, the proposed approach can be used to solve other MOLA problems with different objective functions. Moreover, the proposed approach could also potentially be used in other multi-objective spatial optimization problems in discrete domains—for example, zoning protected ecological areas or selecting facility locations—because these applications exhibit a high degree of similarity to MOLA in terms of problem modeling, solution representation and spatial search requirements.
5.4. Potential Limitations and Challenges
In the mutation strategy, weighted sum, the most commonly-used compromising programming technology, is adopted to evaluate two solutions’ dominance, which is efficient in seeking solutions in the convex part of Pareto front, but deficient in the concave region. Actually, the KINS proposed in this paper can be effectively coupled with the other compromising programming technology, such as weighted Tchebycheff distance, to improve its computation performance while exploring the non-convex solutions of Pareto front.
Besides, as analyzed in
Section 3.4, the algorithm’s computational complexity is the second power of the data scale. As the data scale increases in practical application, the computation time will grow dramatically. Therefore, how to solve a MOLA problem for a large area within a reasonable time is quite challenging.
5.5. Contributions
Based on Pareto theory, this paper proposed an improved ABC for MOLA, which aims to provide a set of optimal solutions for decision-makers. For the first time, this paper introduced an improved Pareto-ABC algorithm, an effective method for optimization, to solve MOLA problems and obtain satisfying solutions. ABC-MOLA could be a good way to provide decision-makers with high-quality optimal solutions. Moreover, this paper proposed a strategy that couples auxiliary knowledge of natural geography and spatial structure with the generation of all new solutions, which effectively improved the optimization performance. This strategy can be applied by many other heuristic algorithms to achieve better results. Therefore, the ABC-MOLA algorithm proposed in this paper is a beneficial and useful complement to MOLA optimization.
6. Conclusions and Future Work
The purpose of this study was to develop ABC as a new method that uses a knowledge-informed neighborhood search strategy to improve the quality of Pareto-optimal solutions for MOLA. Different from ABC for SOLA [
33] that obtains only one optimal solution under the condition of a set of predefined weights for different objectives, ABC-MOLA is able to get multiple non-dominated solutions. Similar to the main differences existing between ABC for MOOP and SOOP presented in
Section 2.3, in ABC-MOLA, different strategies for guiding the bees’ search directions in solution space and for updating solutions both locally and globally have been specifically designed.
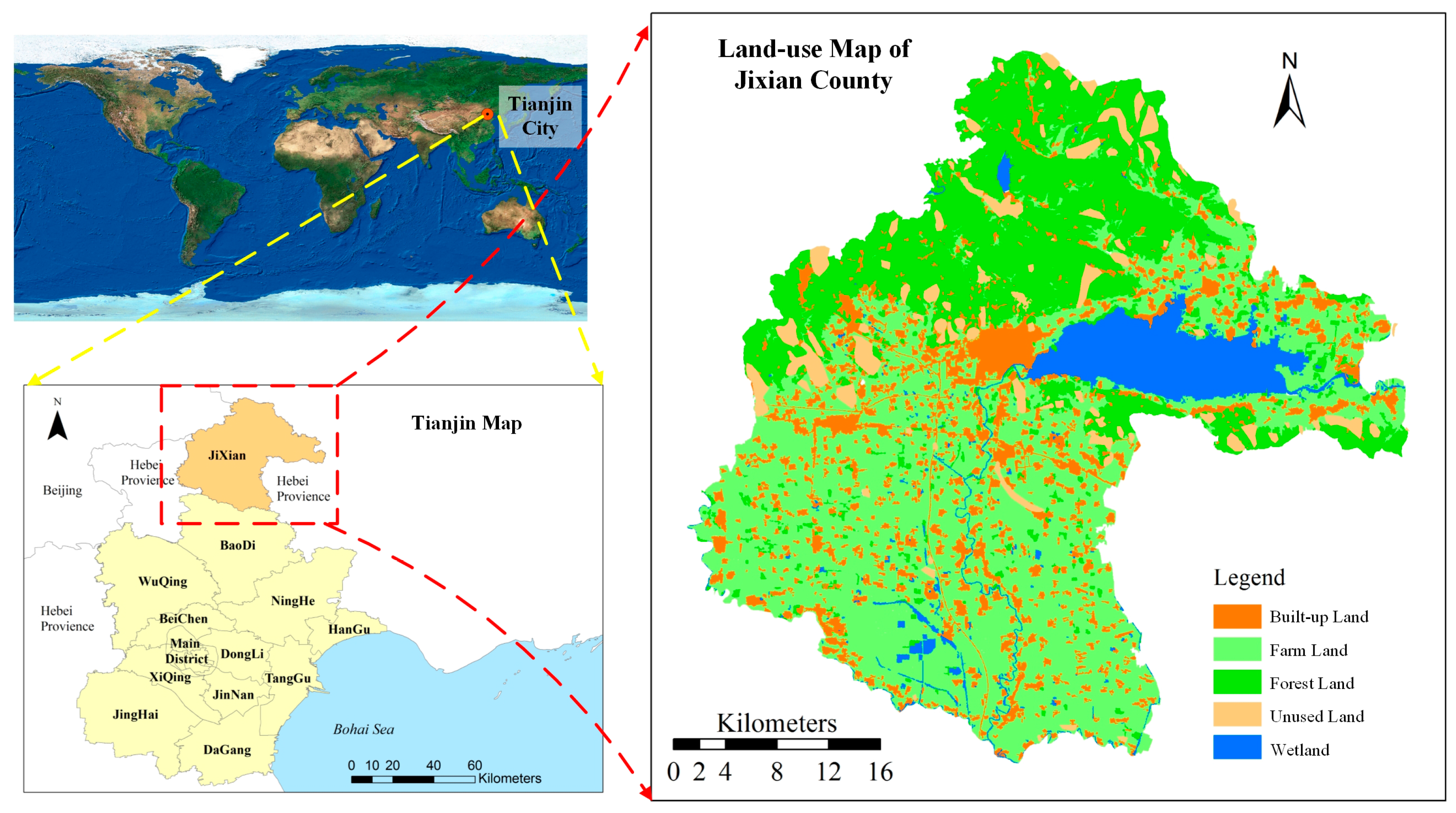
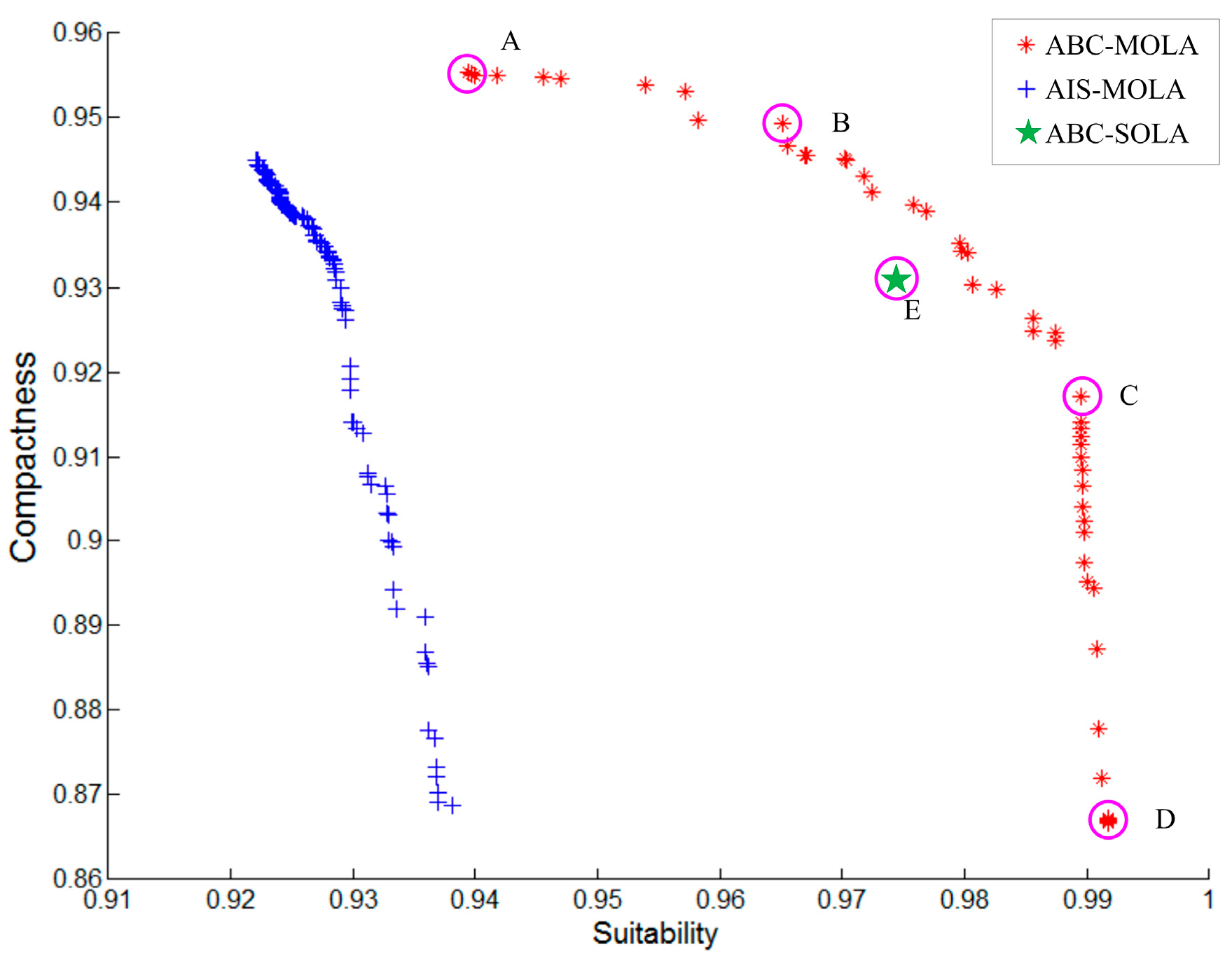
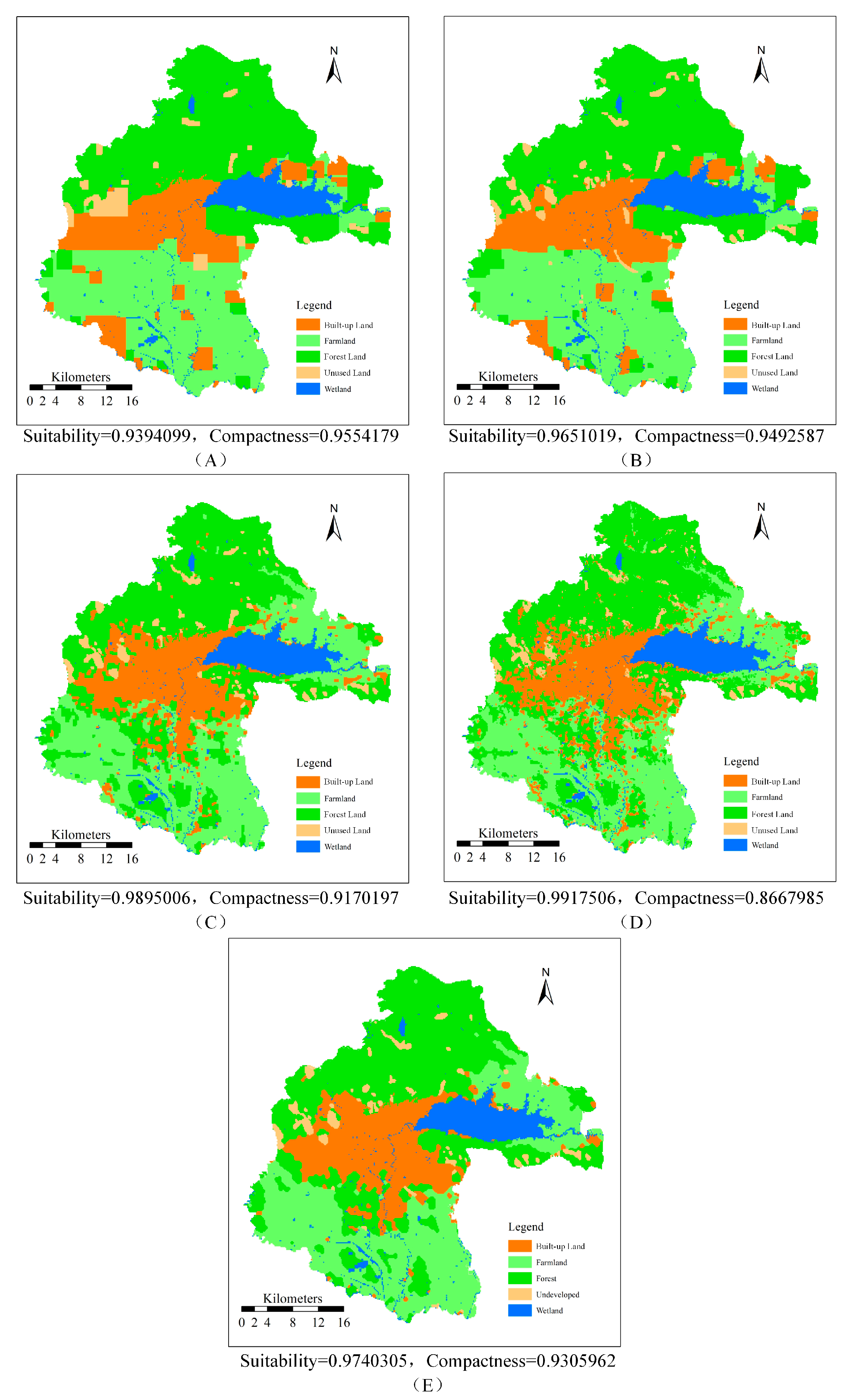
To validate the algorithm’s effectiveness, we treat the land-use allocation problem as a multi-objective spatial-combination optimization problem based on two-dimensional raster data, in which each land-use type’s area is maintained and two commonly-used objective functions, suitability and compactness, are maximized. In a series of comparison experiments, ABC-MOLA shows better optimization ability than other state-of-the-art algorithms and demonstrates good suitability for solving grid-represented land-use allocation problems in large areas.
Notably, the proposed ABC-MOLA is used to solve a land-use allocation problem with only two objectives in this paper. In the future, we plan to make further improvements to ABC-MOLA so it will be able to solve problems with three or more objectives, which are still intractable. Moreover, when solving problems that involve large areas, the calculation time required for ABC-MOLA increases dramatically. Therefore, we plan to further improve ABC-MOLA’s computational efficiency for multi-objective land-use allocation.