An Integrated Graphic Modeling System for Three-Dimensional Hydrodynamic and Water Quality Simulation in Lakes
Abstract
:1. Introduction
2. Framework of the System
2.1. Introduction to FVCOM-LAKE
2.2. System Design
2.3. System Implimentation
2.3.1. System Overview
2.3.2. Grid Generation
2.3.3. Initial and Boundary Conditions Settings
2.3.4. Driving Force and Calibration Dataset Generation
2.3.5. Modeling Running and Postprocessing
3. Case Study
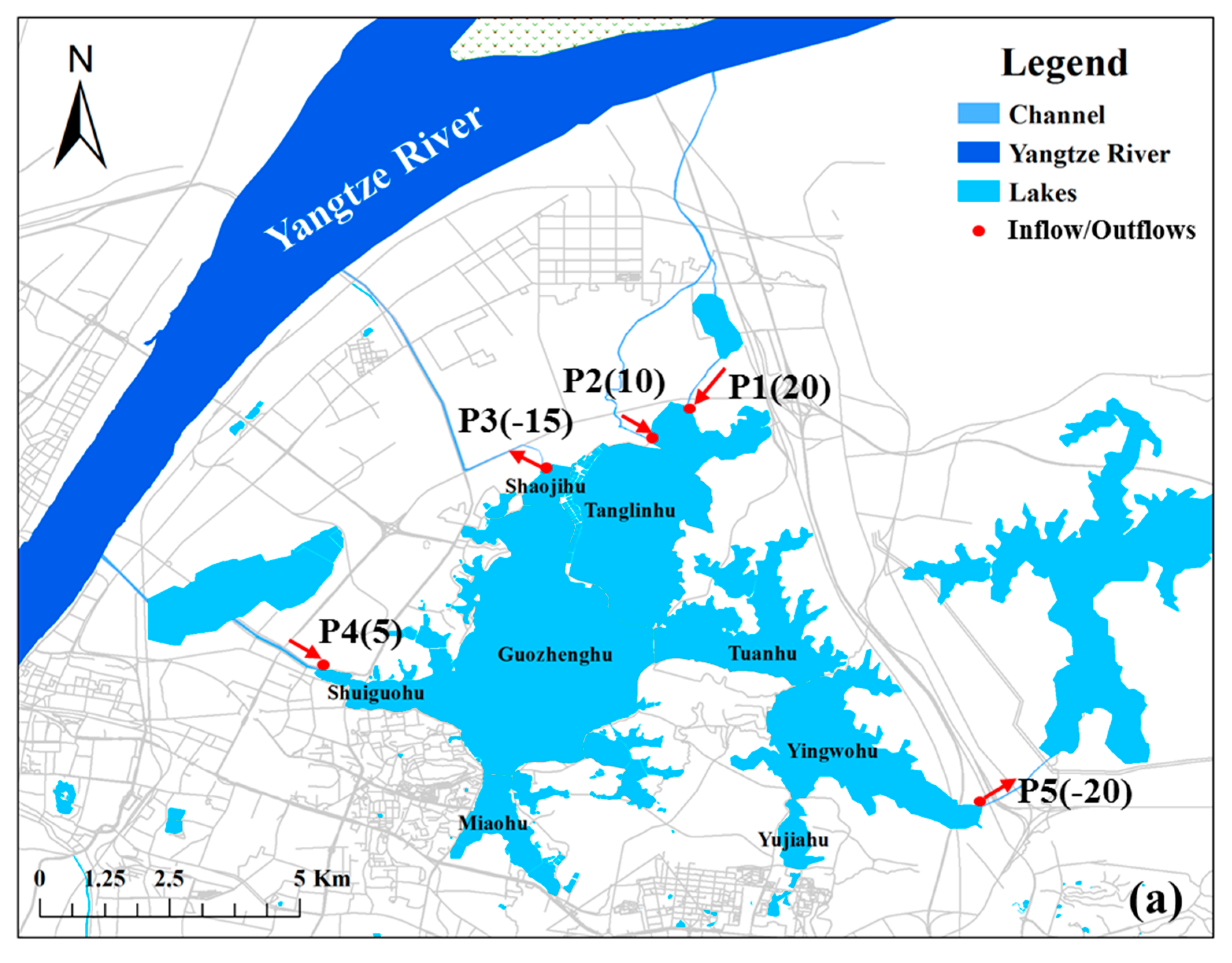
3.1. Study Area
3.2. Model Setup
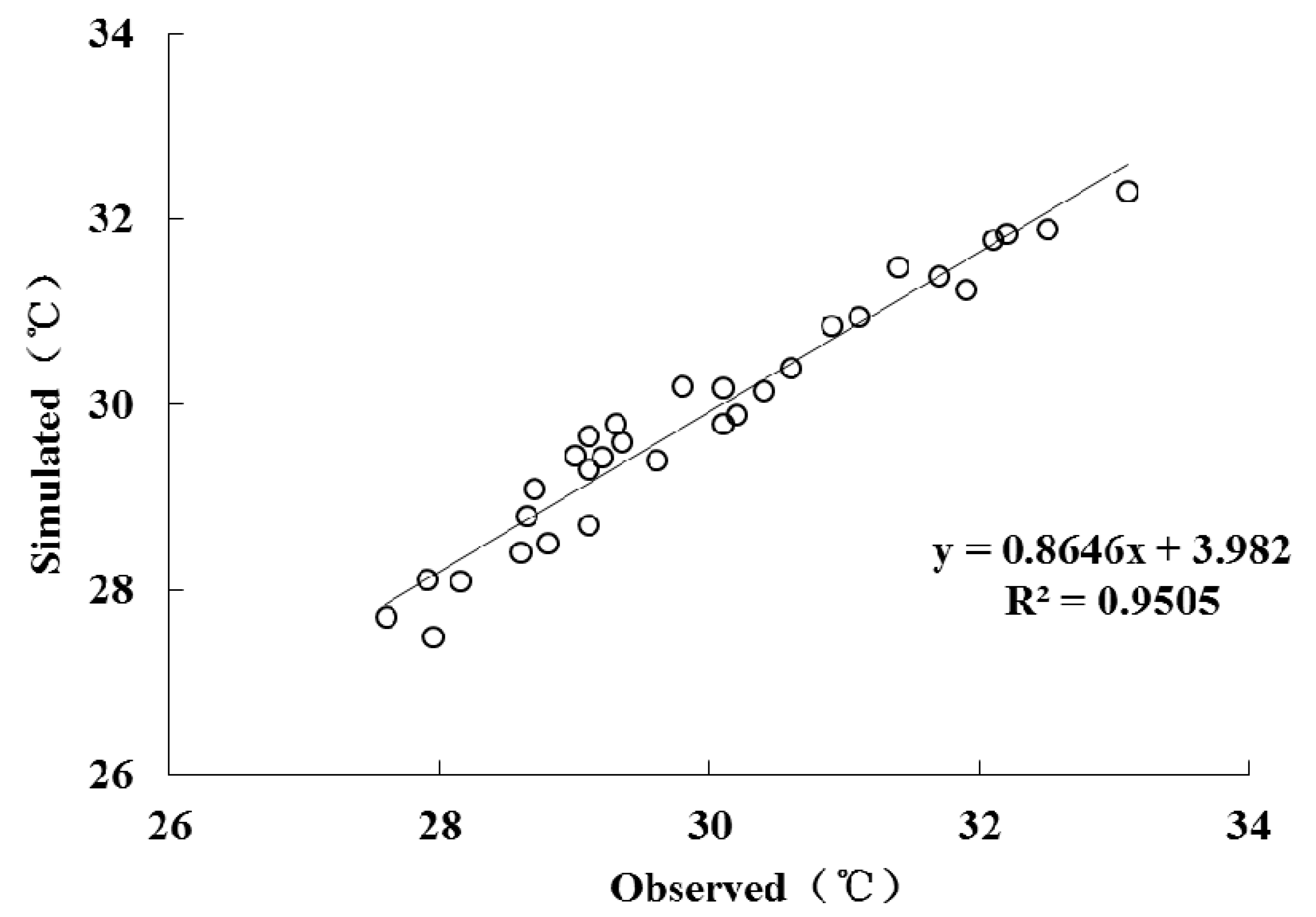
3.3. Model Calibration
3.4. Scenario Design
- (1)
- The first scenario, named S1 (Figure 7a), has three inlets, P1, P2, and P3, and two outlets, P4 and P5. P1 and P2 divert water from the Yangtze river into Tanglin bay with inflows of 20 m3 s−1 and 10 m3 s−1, respectively; P3 diverts water from Lake Shahu into Shuiguo bay with an inflow of 5 m3 s−1; P4 drains water from Yingwo bay to Lake Yanxihu with an outflow of 20 m3 s−1; and P5 drains water from Guozheng bay to the Yangtze River with an outflow of 20 m3 s−1;
- (2)
- The second scenario, named S2 (Figure 7b), has two inlets, P1 and P2, with inflows of 25 m3 s−1 and 10 m3 s−1, respectively, and three outlets, P3, P4 and P5, with outflows of 5 m3 s−1, 20 m3 s−1, and 10 m3 s−1, respectively;
- (3)
- The third scenario, named S3 (Figure 7c), only has one inlet, P3, with an inflow of 35 m3 s−1, and four outlets, P1, P2, P4 and P5, with outflows of 5 m3 s−1, 5 m3 s−1, 20 m3 s−1, and 5 m3 s−1, respectively.
4. Results and Discussions
4.1. Calibration Results
4.2. Scenario Analysis
4.2.1. Change of Lake Circulation Pattern
4.2.2. Improvement of Water Quality
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Burlakova, L.E.; Kovalenko, K.E.; Schmude, K.L.; Barbiero, R.P.; Karatayev, A.Y.; Lesht, B.M. Development of new indices of Great Lakes water quality based on profundal benthic communities. J. Gt. Lakes Res. 2018, 44, 618–628. [Google Scholar] [CrossRef]
- Huang, J.; Xu, Q.; Xi, B.; Wang, X.; Li, W.; Gao, G.; Huo, S.; Xia, X.; Jiang, T.; Ji, D.; et al. Impacts of hydrodynamic disturbance on sediment resuspension, phosphorus and phosphatase release, and cyanobacterial growth in Lake Tai. Environ. Earth Sci. 2015, 74, 3945–3954. [Google Scholar] [CrossRef]
- Nyamweya, C.; Sturludottir, E.; Tomasson, T.; Fulton, E.A.; Taabu-Munyaho, A.; Njiru, M.; Stefansson, G. Exploring Lake Victoria ecosystem functioning using the Atlantis modeling framework. Environ. Model. Softw. 2016, 86, 158–167. [Google Scholar] [CrossRef]
- Chen, C.S.; Liu, H.D.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Bravo, H.R.; McLellan, S.L.; Klump, J.V.; Hamidi, S.A.; Talarczyk, D. Modeling the fecal coliform footprint in a Lake Michigan urban coastal area. Environ. Model. Softw. 2017, 95, 401–419. [Google Scholar] [CrossRef]
- Lesser, G.R.; Roelvink, J.A.; van Kester, J.; Stelling, G.S. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Luo, X.; Li, X. Using the EFDC model to evaluate the risks of eutrophication in an urban constructed pond from different water supply strategies. Ecol. Model. 2018, 372, 1–11. [Google Scholar] [CrossRef]
- Lu, C.; Li, H.; Dai, W.; Tao, J.; Xu, F.; Cybele, S.; Zhang, X.; Guo, H. 3-D Simulation of the Suspended Sediment Transport in the Jiao jiang Estuary: Based on Validating by Remote Sensing Retrieval. J. Coast. Res. 2018, 85, 116–120. [Google Scholar] [CrossRef]
- Beletsky, D.; Hawley, N.; Rao, Y.R. Modeling summer circulation and thermal structure of Lake Erie. J. Geophys. Res. Oceans 2013, 118, 6238–6252. [Google Scholar] [CrossRef] [Green Version]
- Bai, X.; Wang, J.; Schwab, D.J.; Yang, Y.; Luo, L.; Leshkevich, G.A.; Liu, S. Modeling 1993-2008 climatology of seasonal general circulation and thermal structure in the Great Lakes using FVCOM. Ocean Model. 2013, 65, 40–63. [Google Scholar] [CrossRef]
- Shore, J.A. Modelling the circulation and exchange of Kingston Basin and Lake Ontario with FVCOM. Ocean Model. 2009, 30, 106–114. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, Y.; Huang, Q.; Gao, J. When and where to reduce nutrient for controlling harmful algal blooms in large eutrophic lake Chaohu, China? Ecol. Indic. 2018, 89, 808–817. [Google Scholar] [CrossRef]
- Gong, R.; Xu, L.; Wang, D.; Li, H.; Xu, J. Water Quality Modeling for a Typical Urban Lake Based on the EFDC Model. Environ. Model. Assess. 2016, 21, 643–655. [Google Scholar] [CrossRef]
- Liang, S.X.; Xie, J.; Sun, Z.C.; Lu, Y.P.; Liu, G.S.; Xiong, W. Development of a regional coastal management decision-aided system. Part A: Establishment of an automatic numerical simulation program. Ocean Coast. Manag. 2014, 96, 173–180. [Google Scholar] [CrossRef]
- Ng, S.M.Y.; Wai, O.W.H.; Li, Y.S.; Li, Z.L.; Jiang, Y.W. Integration of a GIS and a complex three-dimensional hydrodynamic, sediment and heavy metal transport numerical model. Adv. Eng. Softw. 2009, 40, 391–401. [Google Scholar] [CrossRef]
- Qin, R.F.; Lin, L.Z. Development of a GIS-based integrated framework for coastal seiches monitoring and forecasting: A North Jiangsu shoal case study. Comput. Geosci. 2017, 103, 70–79. [Google Scholar] [CrossRef]
- Tian, Y.; Zheng, Y.; Zheng, C.M. Development of a visualization tool for integrated surface water-groundwater modeling. Comput. Geosci. 2016, 86, 1–14. [Google Scholar] [CrossRef]
- Chen, C.S.; Huang, H.S.; Beardsley, R.C.; Liu, H.D.; Xu, Q.C.; Cowles, G. A finite volume numerical approach for coastal ocean circulation studies: Comparisons with finite difference models. J. Geophys. Res. Oceans 2007, 112, C03018. [Google Scholar] [CrossRef]
- Rego, J.L.; Li, C.Y. Storm surge propagation in Galveston Bay during Hurricane Ike. J. Mar. Syst. 2010, 82, 265–279. [Google Scholar] [CrossRef]
- Galperin, B.; Kantha, L.H.; Hassid, S.; Rosati, A. A Quasi-Equilibrium Turbulent Energy-Model for Geophysical Flows. J. Atmos. Sci. 1988, 45, 55–62. [Google Scholar] [CrossRef]
- Mellor, G.; Yamada, T. Development of a Turbulence Closure-Model for Geophysical Fluid Problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Mellor, G.; Blumberg, A. Wave breaking and ocean surface layer thermal response. J. Phys. Oceanogr. 2004, 34, 693–698. [Google Scholar] [CrossRef]
- Ambrose, J.R.B.; Wool, T.A.; Connolly, J.P.; Schanz, R.W. A Hydrodynamic and Water Quality Model: Model Theory, User’s Manual and Programmer’s Guide; U.S. Environmental Protection Agency: Athens, GA, USA, 1988; pp. 280–297.
- Zheng, L.Y.; Chen, C.S.; Zhang, F.Y. Development of water quality model in the Satilla River Estuary, Georgia. Eco. Model. 2004, 178, 457–482. [Google Scholar] [CrossRef]
- DotSpatial. Available online: https://github.com/DotSpatial/DotSpatial (accessed on 6 January 2019).
- Shewchuk, J.R. Delaunay refinement algorithms for triangular mesh generation. Comput. Geom. 2002, 22, 21–74. [Google Scholar] [CrossRef] [Green Version]
- State Environment Protection Administration (SEPA). Environmental Quality Standard for Surface Water, China; GB 3838–2002; General Administration for Quality Supervision, Inspection and Quarantine of PR China: Beijing, China, 2002; pp. 1–9. Available online: http://kjs.mee.gov.cn/hjbhbz/bzwb/shjbh/shjzlbz/200206/t20020601_66497.shtml (accessed on 6 January 2019).
- Li, Y.P.; Acharya, K.; Yu, Z.B. Modeling impacts of Yangtze River water transfer on water ages in Lake Taihu, China. Ecol. Eng. 2011, 37, 325–334. [Google Scholar] [CrossRef]
- Chen, X.; Yang, X.; Dong, X.; Liu, Q. Nutrient dynamics linked to hydrological condition and anthropogenic nutrient loading in Chaohu Lake (southeast China). Hydrobiologia 2011, 661, 223–234. [Google Scholar] [CrossRef]
- Chen, Q.W.; Tan, K.; Zhu, C.B.; Li, R.N. Development and application of a two-dimensional water quality model for the Daqinghe River Mouth of the Dianchi Lake. J. Environ. Sci. 2009, 21, 313–318. [Google Scholar] [CrossRef] [Green Version]
- Dortch, Q. The interaction between ammonium and nitrate uptake in phytoplankton. Mar. Ecol. Prog. Ser. 1990, 61, 183–201. [Google Scholar] [CrossRef]
- Geider, R.J. Respiration: Taxation without representation. In Primary Productivity and Biogeochemical Cycles in the Sea; Falkowski, P.G., Woodhead, A.D., Eds.; Plenum Press: New York, NY, USA, 1992; pp. 333–360. [Google Scholar]
- Stenstrom, M.K.; Poduska, R.A. The Effect of Dissolved-Oxygen Concentration on Nitrification. Water Res. 1980, 14, 643–649. [Google Scholar] [CrossRef]












| Bay | DO (mg L−1) | NH4 (mg L−1) | NO3 (mg L−1) | ON (mg L−1) | PO4 (mg L−1) | OP (mg L−1) | CBOD (mg L−1) | CHL (μg L−1) |
|---|---|---|---|---|---|---|---|---|
| Guozhenghu | 8.35 | 0.031 | 0.026 | 0.103 | 0.024 | 0.008 | 4.21 | 20.17 |
| Tanglinhu | 8.50 | 0.039 | 0.056 | 0.115 | 0.030 | 0.010 | 1.79 | 12.5 |
| Yingwohu | 8.67 | 0.066 | 0.022 | 0.332 | 0.017 | 0.009 | 1.42 | 21.6 |
| Tuanhu | 8.45 | 0.199 | 0.066 | 0.115 | 0.021 | 0.007 | 1.78 | 19.8 |
| Miaohu | 7.98 | 2.560 | 0.853 | 2.787 | 0.360 | 0.124 | 9.13 | 95.6 |
| Shuiguohu | 4.62 | 0.159 | 0.053 | 0.298 | 0.117 | 0.043 | 6.66 | 28.89 |
| Shaojihu | 8.70 | 0.129 | 0.043 | 0.129 | 0.054 | 0.018 | 4.95 | 22.5 |
| Yujiahu | 8.73 | 0.118 | 0.039 | 0.342 | 0.084 | 0.036 | 5.56 | 25.2 |
| Symbol | Definition | Value | Unit |
|---|---|---|---|
| Kdeox | Deoxygenation rate at 20 degree | 0.1 c | day−1 |
| knitr | Nitrification rate | 0.35 c | day−1 |
| Kresp | Phytoplankton respiration rate | 0.1 d | day−1 |
| Kdeni | Denitrification rate | 0.08 c | day−1 |
| Kgrow | Optimum phytoplankton growth rate | 1.0 c | day−1 |
| Kmort | Natural mortality rate of phytoplankton | 0.1 c | day−1 |
| Kmine1 | Organic nitrogen mineralization rate | 0.075 c | day−1 |
| Kmine2 | Organic phosphorus mineralization rate | 0.2 c | day−1 |
| KCBOD | Half-saturation constant for DO limitation of CBOD oxidation | 0.5 c | mg O2 L−1 |
| Knitr | Half-saturation constant for DO limitation of nitrification | 0.5 e | mg O2 L−1 |
| Kdnf | Half-saturation constant for DO limitation of denitrification | 0.1 c | mg O2 L−1 |
| KNO3 | Half-saturation constant for uptake of nitrate uptake | 0.014 b | mg N L−1 |
| KPO4 | Half-saturation constant for phosphorus uptake | 0.003 b | mg P L−1 |
| Tempreae | Temperature coefficient for reaeration | 1.028 c | Unitless |
| Tempnitr | Temperature coefficient of nitrification | 1.08 c | Unitless |
| Tempresp | Temperature coefficient of phytoplankton respiration | 1.08 c | Unitless |
| Tempdeni | Temperature coefficient of denitrification | 1.08 c | Unitless |
| Tempgrow | Temperature coefficient of optimum growth | 1.066 c | Unitless |
| Tempmort | Temperature coefficient of phytoplankton mortality | 1.08 c | Unitless |
| Tempmine1 | Temperature coefficient of nitrogen mineralization | 1.08 c | Unitless |
| Tempmine2 | Temperature coefficient for organic phosphorus mineralization | 1.08 c | Unitless |
| Tempsod | Temperature coefficient of sediment oxygen demand (SOD) | 1.08 c | Unitless |
| vPHY | Phytoplankton settling velocity | 0.5 a | m day−1 |
| vON | Settling velocity of particulate organic nitrogen | 0.5 a | m day−1 |
| vOP | Settling velocity of particulate organic phosphorus | 0.5 a | m day−1 |
| vCBOD | Settling velocity of CBOD | 0.5 c | m day−1 |
| SOD | Sediment oxygen demand | 0.3 c | g O2 m−2 day−1 |
| Scenario ID | Inlet & Inflow Discharge | Outlet & Outflow Discharge |
|---|---|---|
| S1 | P1: 20 m3 s−1 P2: 10 m3 s−1 P3: 5 m3 s−1 | P4: −20 m3 s−1 P5: −15 m3 s−1 |
| S2 | P1: 25 m3 s−1 P2: 10 m3 s−1 | P3: −5 m3 s−1 P4: −20 m3 s−1 P5: −10 m3 s−1 |
| S3 | P3: 35 m3 s−1 | P1: −5 m3 s−1 P2: −5 m3 s−1 P4: −20 m3 s−1 P5: −5 m3 s−1 |
| Category | Indicator | Unit |
|---|---|---|
| Hydrodynamics | Average velocity | cm s−1 |
| Velocity range | cm s−1 | |
| Proportion of stagnant water area | % | |
| Water Quality | Change in TN concentration | % |
| Change in TP concentration | % |
| Hydrodynamic Indicators | Scenarios | ||
|---|---|---|---|
| S1 | S2 | S3 | |
| Average velocity (cm s−1) | 1.9 | 1.5 | 1.3 |
| Velocity range (cm s−1) | 44 | 22 | 25 |
| Proportion of stagnant water area (%) | 2.6 | 2.3 | 2.8 |
| Water Quality Indicators | Scenarios | ||
|---|---|---|---|
| S1 | S2 | S3 | |
| Percent change in TN (%) | −35.8 | −43.2 | −17.3 |
| Percent change in TP (%) | −52.5 | −41.7 | −16.7 |
| Percentage of lake area failed to reach Class III for TN (%) | 1.32 | 1.12 | 3.85 |
| Percentage of lake area failed to reach Class III for TP (%) | 4.66 | 5.22 | 34.67 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Tian, Y. An Integrated Graphic Modeling System for Three-Dimensional Hydrodynamic and Water Quality Simulation in Lakes. ISPRS Int. J. Geo-Inf. 2019, 8, 18. https://doi.org/10.3390/ijgi8010018
Huang M, Tian Y. An Integrated Graphic Modeling System for Three-Dimensional Hydrodynamic and Water Quality Simulation in Lakes. ISPRS International Journal of Geo-Information. 2019; 8(1):18. https://doi.org/10.3390/ijgi8010018
Chicago/Turabian StyleHuang, Mutao, and Yong Tian. 2019. "An Integrated Graphic Modeling System for Three-Dimensional Hydrodynamic and Water Quality Simulation in Lakes" ISPRS International Journal of Geo-Information 8, no. 1: 18. https://doi.org/10.3390/ijgi8010018
APA StyleHuang, M., & Tian, Y. (2019). An Integrated Graphic Modeling System for Three-Dimensional Hydrodynamic and Water Quality Simulation in Lakes. ISPRS International Journal of Geo-Information, 8(1), 18. https://doi.org/10.3390/ijgi8010018





