Estimation of Physical Layer Performance in WSNs Exploiting the Method of Indirect Observations
Abstract
:1. Introduction
- we designed a new process for the monitoring of the physical layer in WSNs making use of a completely passive methodology. From data sniffed by external nodes, we first estimate the position of the nodes in the WSN by applying the Weighted Least Squares (WLS) to the method of indirect observations. The resulting information on the nodes position is then used to estimate the status of the communication links among the network nodes;
- we performed a significant number of measurements on the field to evaluate the accuracy of the proposed approach in both indoor and outdoor environments. In the experiments, the proposed method achieved an accurate estimation of the channel links status so that we could acquire the status of the channel links with an average error lower than 1 dB, which is around 5 dB lower than the error introduced without the application of the proposed method.
2. State of the Art
3. Estimation of Node Position Using Indirect Observations
3.1. Multilateration Problem
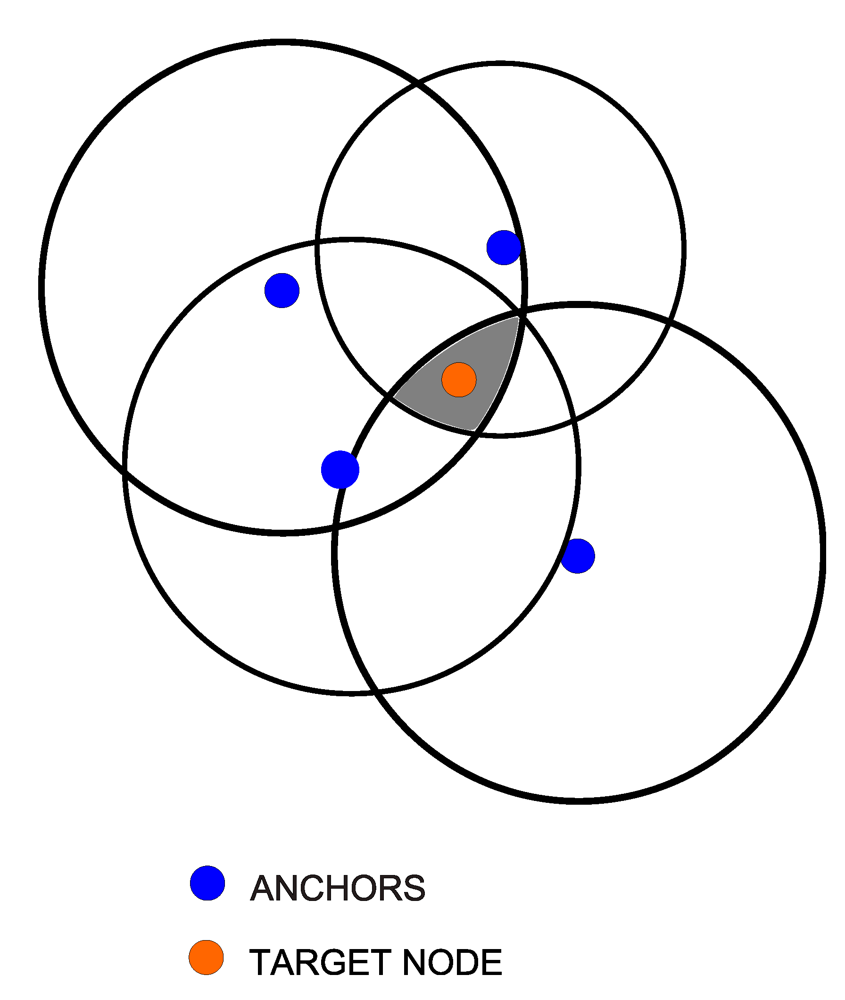
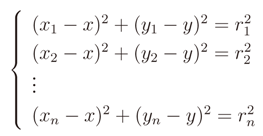
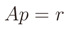
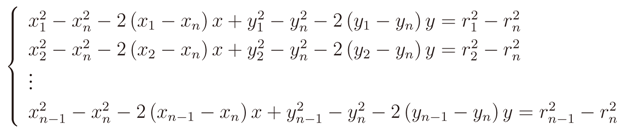
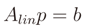
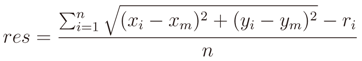
3.2. WLS Applied to the Method of Indirect Observations
 represent the obtained solution and
represent the obtained solution and  be the residual vector (the set of measures are affected by errors). We can write the following matrix equation
be the residual vector (the set of measures are affected by errors). We can write the following matrix equation
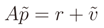
 and n for residual vector
and n for residual vector  . Hence, the system is oversized and the possible solutions are ∞n.
. Hence, the system is oversized and the possible solutions are ∞n.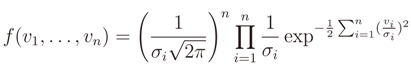
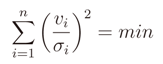
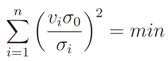
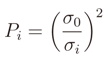
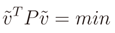
 where it is derivable, and we substitute the function by its linearization at this point. We now skip all the next mathematical passages and we give the final solution. Let A∂ represent the partial derivates of Ap in dx and dy computed at
where it is derivable, and we substitute the function by its linearization at this point. We now skip all the next mathematical passages and we give the final solution. Let A∂ represent the partial derivates of Ap in dx and dy computed at  . After the linearization we obtain the bound problem
. After the linearization we obtain the bound problem
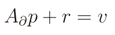
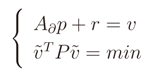
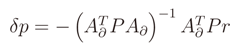
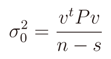
4. Proposed Method for Physical Layer Performance Estimation
4.1. Reference Scenario
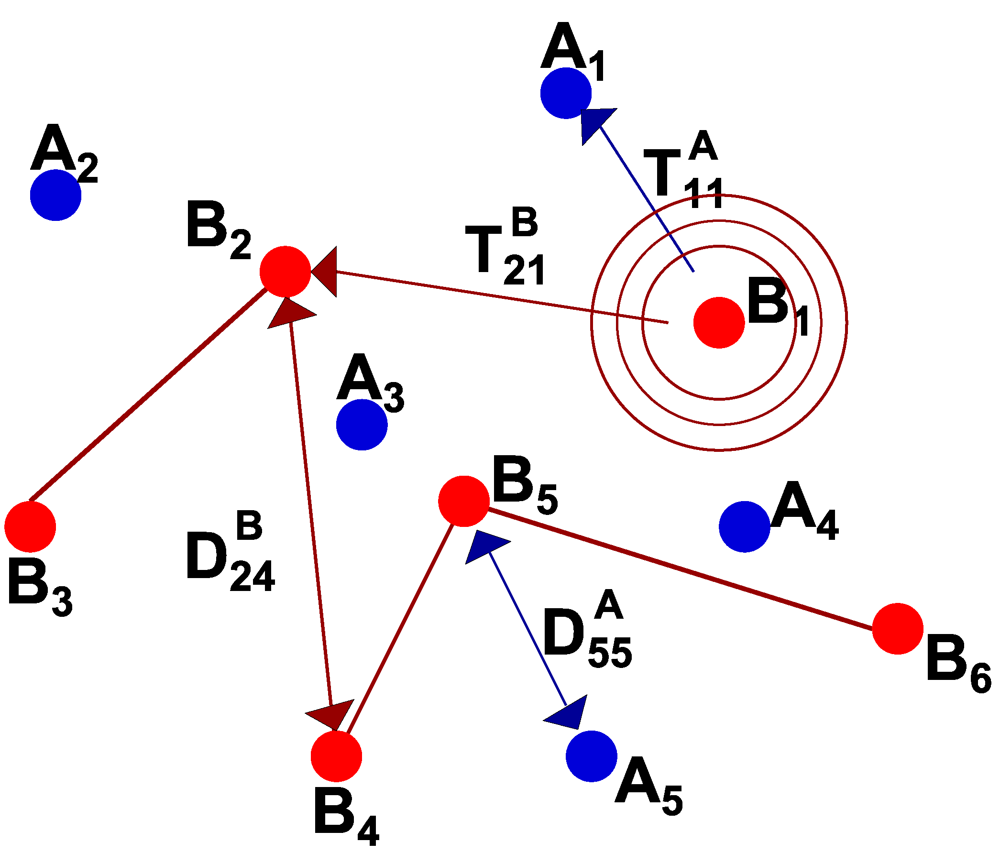
4.2. Proposed Power Estimation Algorithm

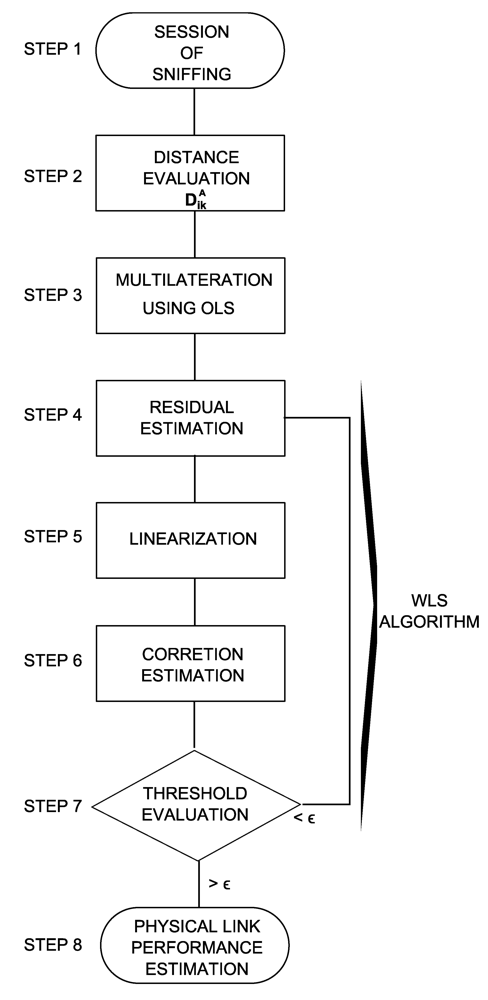
- Step 1: each anchor i measures and stores the received signal for the packets transmitted during a timeframe T and related to Sik packets per blind node k. From these measures the anchors compute the received signal power TAik.
- Step 2: on the basis of information about the ambient environment, each anchor makes use of a channel model for each of the blind nodes k, namely FAik, to estimate the distances DAik.
- Step 3: for any k, we set a vector r = DAik, for k= 1, ...,NB. We then write the system Equation (3) and apply the OLS method described in Section 3.1 to obtain the estimation of the position of each blind node. These estimations are then referred to as
.
- Step 4: for any k, we also compute the estimated residual by applying Equation (5). From this step on, we enter an interactive WLS algorithm applied to the indirect observations described in Section 3.2.
- Step 5: we compute the coefficients of matrix A∂, which represents the partial derivates of Ap in dx and dy. This is performed by a linearization of each function in the system Ap by a Taylor expansion around the point estimate in Step 3. The general equation for the linearization of a multivariable function f(X) at a point Q is: f(X) ≈ f(Q) + ▽ f|Q(X− Q)
- Step 6: we then apply Equation (14) to obtain the estimation of the correction to be applied to the initial position of each blind node k at each iteration s: δPkB,s. We compute again the new estimated position:
.
- Step 7: for any blind node k we go back for another iteration if δPkB,s< ε, where ε is a threshold set as the stop criterion. Otherwise we go ahead with the next step.
- Step 8: from the estimated position of the blinds nodes and making use of the most appropriate channel model FBjk (this is selected again on the basis of the ambient environment), the transmission power of node k seen by the blind node j is computed.
5. Experiments
5.1. Setup
- Development kit case provided by Telit Wireless Solutions. This kit is made of five ZigBee radio boards that are based on the Texas Instruments CC2530 System on Chip with the Embedded Telit Z-One ZigBee-PRO Stack. The antennas are external dipoles characterized by an omnidirectional pattern. Four modules are used to create the network under analysis whereas the fifth works as the sniffer, for which a specific firmware has been developed to correctly capture all the packets on air.
- The software used to inspect the packet content is Wireshark. To analyze the performance of the network from the Wireshark output and to conduct network discovery and commissioning, a specific tool has been developed by Telit Wireless Solution in collaboration with our lab and named SRManager Tool. In this experiment, this tool has been used to collect the RSSI values observed from the different nodes in the network.
| Scenario | Size | Description | Link type |
|---|---|---|---|
| Conference room | 6.3 m × 5.4 m | The room includes 12 desks with around 40 chairs. The room was empty when making the measurements. | LOS |
| Office room | 4.5 m × 9.5 m | The room includes 5 desks, 5 personal computers, and 4 people were working when making the measurements. | LOS |
| Small flat | around 85 m2 | The flat has 5 rooms (kitchen, living room, corridor and 2 bedrooms) with typical furniture | LOS/NLOS |
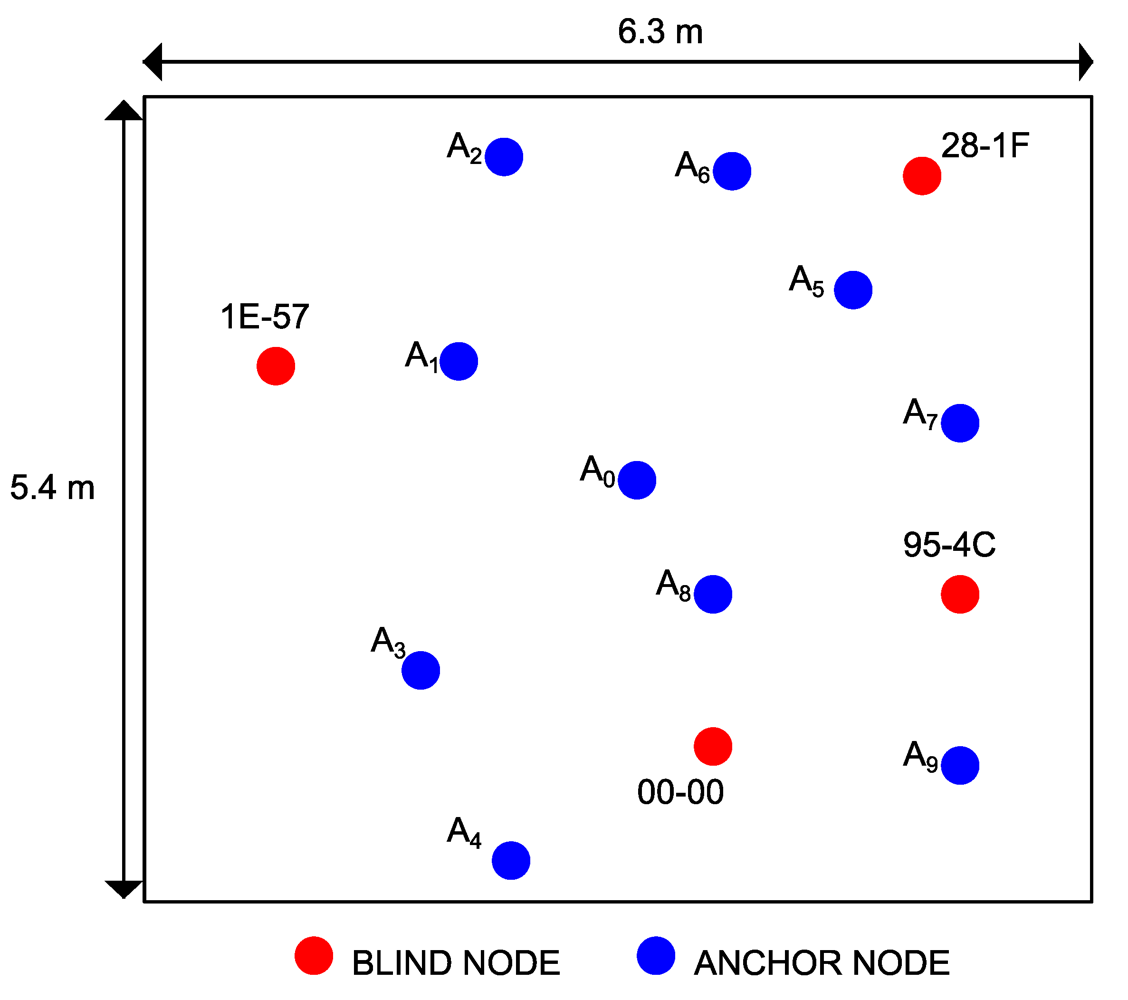

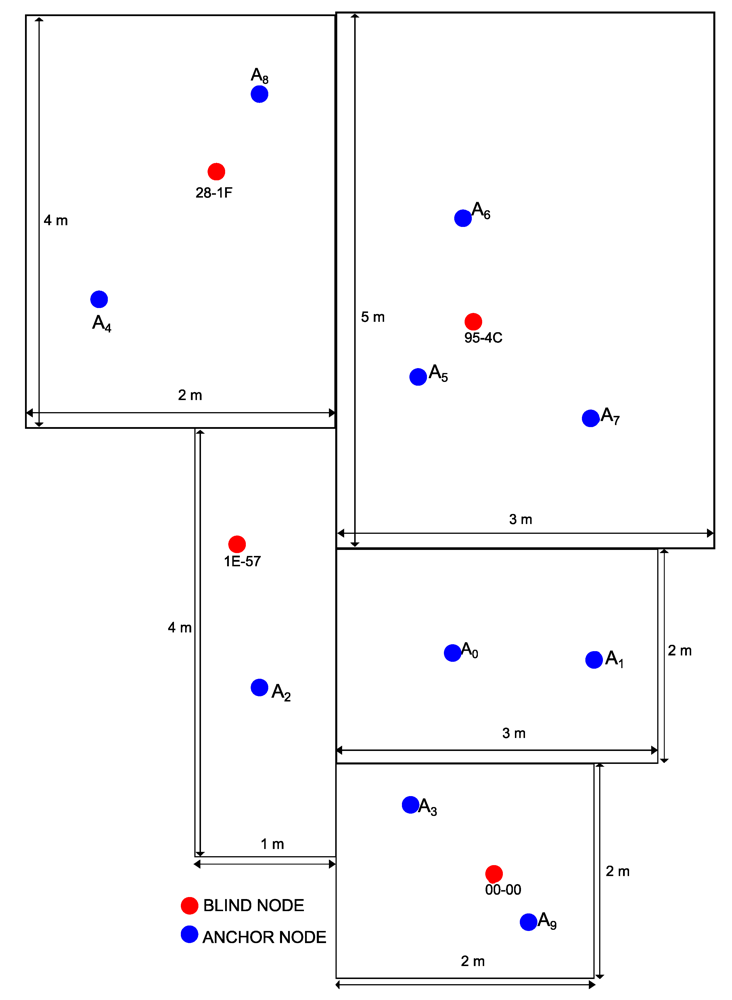
| ANCHOR | 00-00 | 28-1F | 95-4C | 1E-57 |
|---|---|---|---|---|
| Conference room | ||||
| A1 | 30.03 | 26.92 | 28.00 | 36.00 |
| A2 | 23.99 | 10.13 | 22.00 | 40.00 |
| A3 | 27.03 | 28.00 | 8.95 | 33.99 |
| A4 | 27.92 | 21.95 | 22.88 | 30.00 |
| A5 | 31.97 | 7.52 | 26.75 | 24.02 |
| A6 | 24.95 | 34.00 | 30.00 | 11.90 |
| A7 | 20.97 | 31.01 | 24.00 | 28.84 |
| A8 | 25.68 | 30.15 | 36.00 | 13.65 |
| A9 | 35.00 | 20.28 | 16.77 | 24.00 |
| A10 | 28.00 | 20.96 | 36.83 | 17.97 |
| Office room | ||||
| A1 | 24.10 | 7.63 | 34.00 | 24.35 |
| A2 | 25.62 | 42.00 | 12.50 | 33.36 |
| A3 | 29.21 | 6.20 | 39.98 | 20.31 |
| A4 | 29.27 | 14.54 | 38.00 | 25.21 |
| A5 | 23.01 | 30.00 | 20.55 | 36.45 |
| A6 | 13.60 | 30.00 | 10.85 | 43.07 |
| A7 | 27.09 | 23.03 | 21.96 | 29.59 |
| A8 | 41.96 | 15.30 | 19.63 | 21.87 |
| A9 | 33.81 | 26.26 | 21.44 | 21.96 |
| A10 | 9.60 | 34.49 | 23.53 | 28.02 |
| Flat | ||||
| A1 | 13.17 | 5.01 | 23.00 | 20.28 |
| A2 | 21.98 | -0.54 | 18.00 | 25.00 |
| A3 | 16.00 | 16.92 | 36.00 | 16.00 |
| A4 | 28.10 | 12.00 | 4.73 | 9.29 |
| A5 | -8.48 | 29.08 | 22.51 | 9.97 |
| A6 | 4.91 | 6.86 | 22.00 | 35.02 |
| A7 | 7.57 | 18.98 | -0.90 | 27.50 |
| A8 | 10.15 | 5.96 | 7.33 | 32.00 |
| A9 | -1.17 | 36.00 | 13.17 | 15.00 |
| A10 | 39.74 | -5.29 | 13.90 | 16.33 |
5.2. Propagation Models
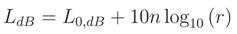
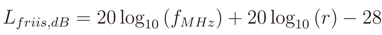
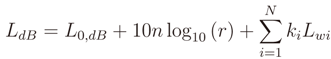
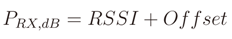
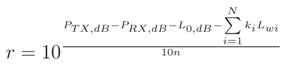
 is zero.
is zero.5.3. Analysis of Results
| Node tx | Node rx | Conference room | Office | Flat |
|---|---|---|---|---|
| 00-00 | 28-1F | 3.52 m | 3.14 m | 7.11 m |
| -00 | 95-4C | 2.20 m | 2.08 m | 5.36 m |
| -00 | 1E-57 | 3.21 m | 2.85 m | 3.87 m |
| -4C | 28-1F | 2.52 m | 1.78 m | 3.38 m |
| -1F | 1E-57 | 3.59 m | 1.11 m | 3.36 m |
| -4C | 1E-57 | 4.46 m | 2.31 m | 3.78 m |
| Node | Multilateration—Error | Proposed method-Error | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| TX | RX | RSSI | distance | RSSI | distance | RSSI | ||||
| [dB] | a.v.[m] | [%] | a.v.[dB] | [%] | a.v.[m] | [%] | a.v.[dB] | [%] | ||
| Conference room | ||||||||||
| 00-00 | 28-1F | 10 ÷ 18 | 0.25 | 7.6% | 0 | 0% | 0.33 | 10.3% | 0 | 0% |
| 00-00 | 95-4C | 18 ÷ 26 | 0.96 | 77.4% | 2 | 7.7% | 0.73 | 49.6% | 0 | 0% |
| 00-00 | 1E-57 | 12 ÷ 20 | 0.98 | 43.9% | 0 | 0% | 0.96 | 42.7% | 0 | 0% |
| 95-4C | 28-1F | 16 ÷ 24 | 0.06 | 0.7% | 0 | 0% | 0.62 | 19.7% | 0 | 0% |
| 28-1F | 1E-57 | 9 ÷ 17 | 0.04 | 1.1% | 0 | 0% | 0.33 | 10.1% | 0 | 0% |
| 95-4C | 1E-57 | 6 ÷ 14 | 1.33 | 42.5% | 0 | 0% | 0.89 | 24.9% | 0 | 0% |
| mean | 0.60 | 28.9% | 0.33 | 1.3% | 0.64 | 26.2% | 0 | 0% | ||
| variance | 0.55 | 30.9% | 0.56 | 0.1% | 0.27 | 16.6% | 0 | 0% | ||
| Office | ||||||||||
| 00-00 | 28-1F | 12 ÷ 20 | 2.52 | 44.5% | 7 | 35 % | 0.01 | 0.3% | 0 | 0% |
| 00-00 | 95-4C | 19 ÷ 27 | 2.32 | 52.7% | 10 | 37 % | 0.25 | 13.7% | 0 | 0% |
| 00-00 | 1E-57 | 14 ÷ 22 | 0.98 | 25.6% | 1 | 4.5 % | 0.57 | 25% | 0 | 0% |
| 95-4C | 28-1F | 22 ÷ 30 | 2.51 | 58.5% | 12 | 40 % | 1.3 | 42.2% | 6 | 20% |
| 28-1F | 1E-57 | 31 ÷ 39 | 1.10 | 49.8% | 9 | 23 % | 0.02 | 1.8% | 0 | 0% |
| 95-4C | 1E-57 | 18 ÷ 26 | 0.10 | 4.1% | 0 | 0 % | 0.02 | 0.9% | 0 | 0% |
| mean | 1.58 | 39.2% | 6.5 | 68.2% | 0.36 | 14.0% | 1 | 3.3% | ||
| variance | 1.01 | 20.5% | 24.3 | 59.7% | 0.51 | 16.9% | 6 | 0.5% | ||
| Flat | ||||||||||
| 00-00 | 28-1F** | –18 ÷ –10 | 0.63 | 8.1% | 2 | 20% | 0.7 | 8.9% | 0 | 0% |
| 00-00 | 95-4C** | –12 ÷ –4 | 0.51 | 8.7% | 1 | 25% | 1.31 | 19.7% | 0 | 0% |
| 00-00 | 1E-57** | –6 ÷ 2 | 1.76 | 31.3% | 8 | 400% | 0.7 | 15.3% | 0 | 0% |
| 95-4C | 28-1F* | 2 ÷ 10 | 1.68 | 33.2% | 7 | 70% | 0.23 | 6.4% | 0 | 0% |
| 28-1F | 1E-57* | 1 ÷ 9 | 1.39 | 27.7% | 9 | 100% | 0.41 | 10.2% | 0 | 0% |
| 95-4C | 1E-57** | -6 ÷2 | 1.56 | 29.2% | 10 | 50% | 1.39 | 26.9% | 2 | 100% |
| mean | 1.25 | 23.0% | 6.17 | 170.5% | 0.79 | 14.6% | 0.33 | 16.7% | ||
| variance | 0.55 | 11.5% | 14.16 | 418% | 0.47 | 7.7% | 0.67 | 13.2% | ||
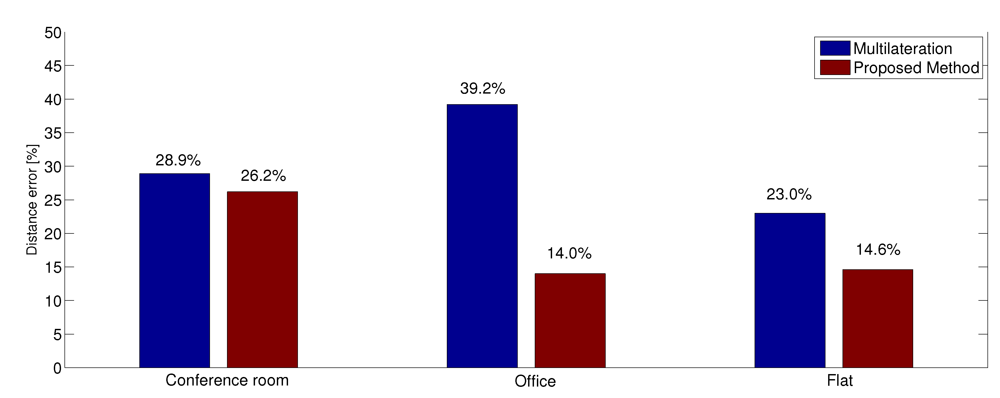


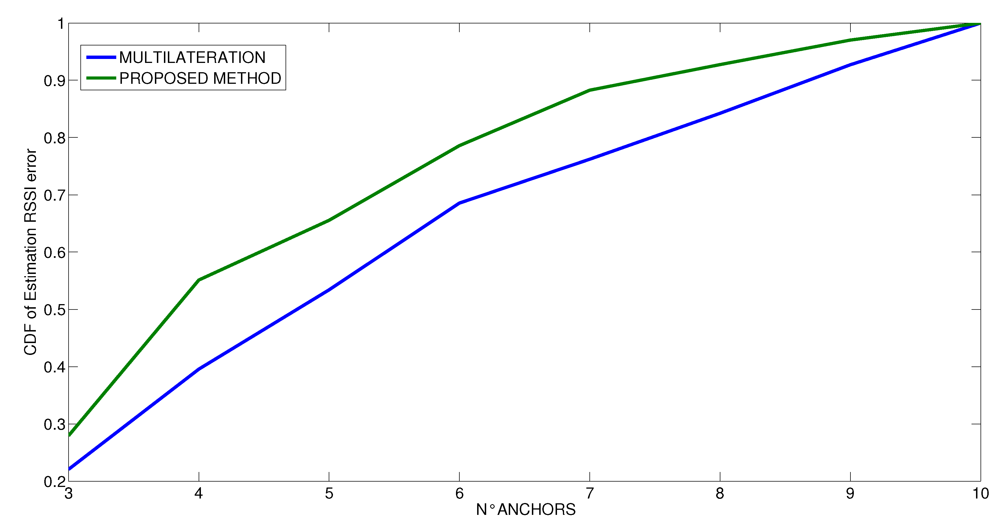
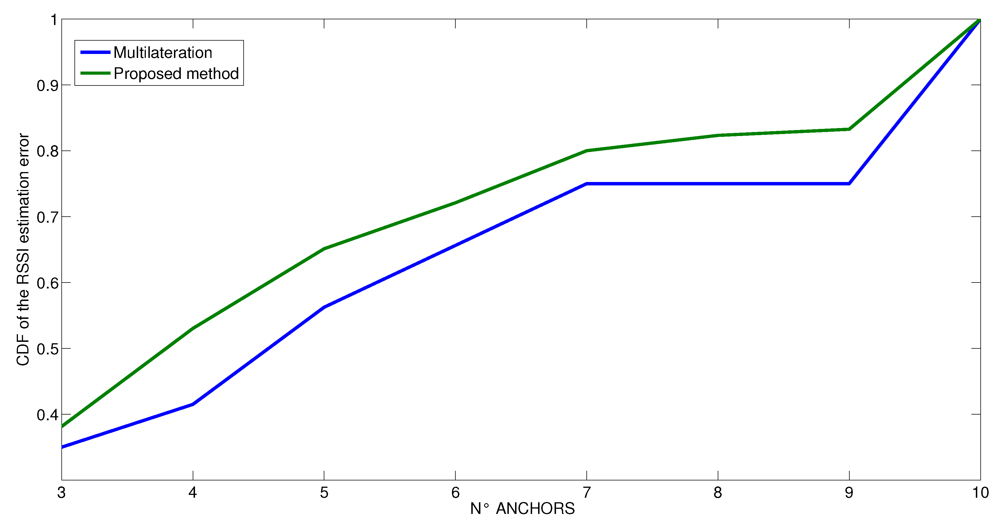
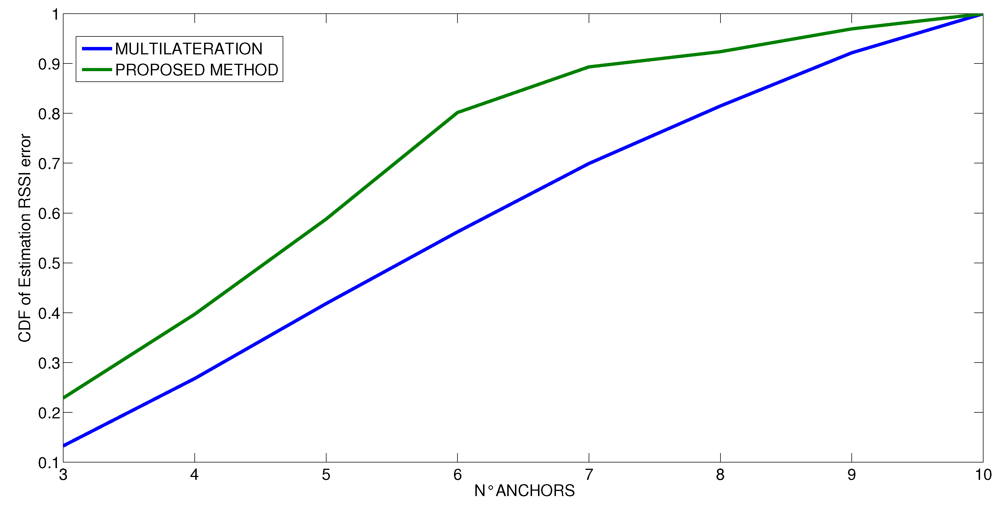
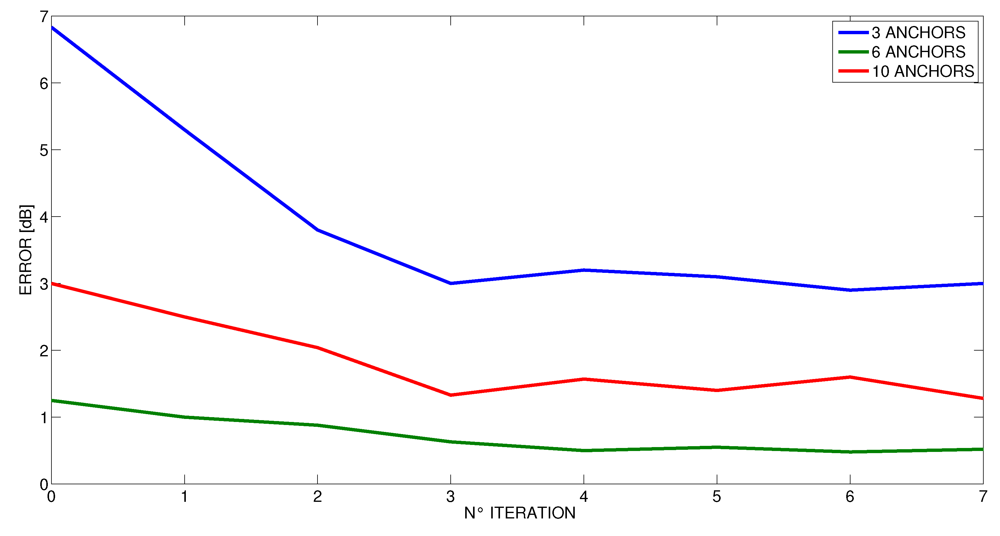
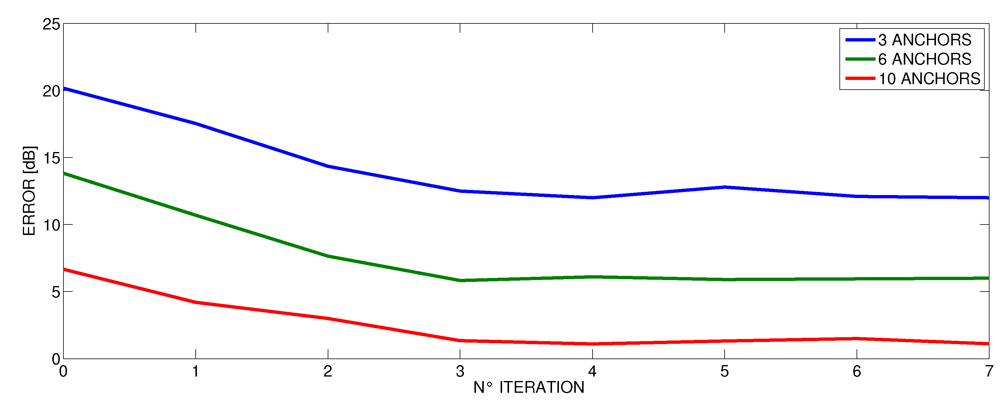
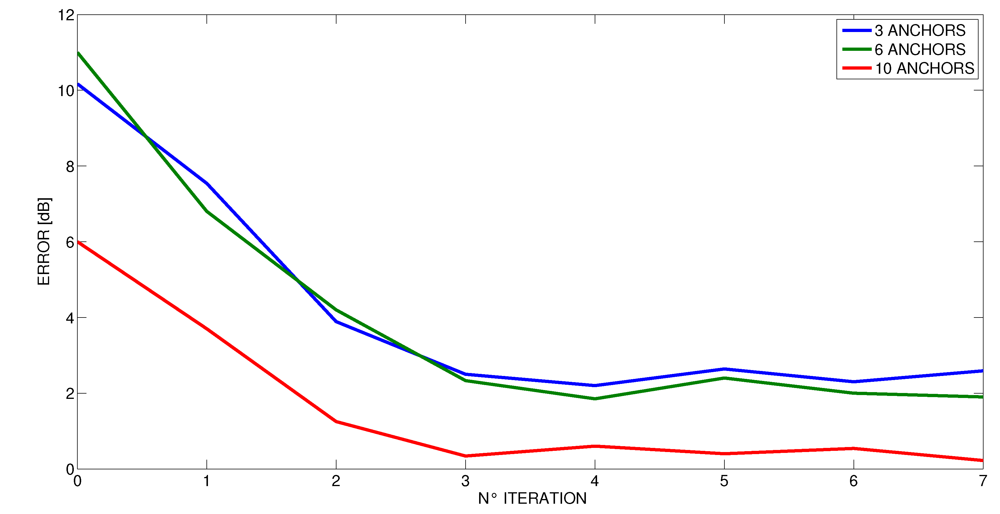
6. Conclusions
References
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. A survey on sensor networks. IEEE Commun. Mag. 2002, 40, 104–112. [Google Scholar]
- Garca-Hernndez, C.F.; Ibargengoytia-Gonzlez, P.H.; Garca-Hernndez, J.; Prez-Daz, J.A. Wireless sensor networks and applications: A survey. Int. J. Comput. Sci. Netw. Secur. 2007, 7, 264–273. [Google Scholar]
- Gill, K.; Yang, S.-H.; Yao, F.; Lu, X. A zigbee-based home automation system. IEEE Trans. Consum. Electron. 2009, 55, 422–430. [Google Scholar] [CrossRef] [Green Version]
- Alemdar, H.; Ersoy, C. Wireless sensor networks for healthcare: A survey. Comput. Netw. 2010, 54, 2688–2710. [Google Scholar]
- Han, J.; Lee, H.; Park, K.-R. Remote-controllable and energy-saving room architecture based on zigbee communication. IEEE Trans. Consum. Electron. 2009, 55, 264–268. [Google Scholar] [CrossRef]
- Lin, S.; Liu, J.; Fang, Y. ZigBee Based Wireless Sensor Networks and its Applications in Industrial. In Proceedings of the IEEE International Conference on Automation and Logistics, Jinan, China, 18–21 August 2007.
- Jiang, P.; Xia, H.; He, Z.; Wang, Z. Design of a water environment monitoring system based on wireless sensor networks. Sensors 2009, 9, 6411–6434. [Google Scholar] [CrossRef]
- Iqbal, R.; Yukimatsu, K. Intelligent transportation systems using short range wireless technologies. J. Trans. Technol. 2011, 1, 132–137. [Google Scholar] [CrossRef]
- The Internet of Things; Giusto, D.; Iera, A.; Morabito, G.; Atzori, L. (Eds.) Springer: Berlin/Heidelberg, Germany, 2010.
- Atzori, L.; Iera, A.; Morabito, G. The internet of things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- Di Caro, G.A.; Flushing, E.F. Optimal Relay Node Placement for throughput Enhancement in Wireless Sensor Networks. In Proceedings of the 50th FITCE Congress, Palermo, Italy, 31 August–3 September 2011.
- Pilloni, V.; Atzori, L. Deployment of distributed applications in wireless sensor networks. Sensors 2011, 11, 7395–7419. [Google Scholar]
- Navid, P.; Turgay, K. Improving Packet Reception Rate for Mobile Sinks in Wireless Sensor Networks. In Proceedings of the IEEE International Symposium on a World Wireless Mobile Multimedia Networks (WoWMoM) 2012, San Francisco, CA, USA, 25–28 June 2012.
- Han, X.; Cao, X.; Lloyd, E.L.; Shen, C.-C. Fault-tolerant relay node placement in heterogeneous wireless sensor networks. IEEE Trans. Mob. Comput. 2010, 9, 643–656. [Google Scholar] [CrossRef]
- Rost, S.; Balakrishnan, H. Memento: A Health Monitoring System for Wireless Sensor Networks. In Proceedings of Third Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, IEEE SECON, Reston, VA, USA, 25–28 September 2006.
- Nithya, R.; Kevin, C.; Rahul, K.; Lewis, G.; Eddie, K.; Deborah, E. Sympathy for the Sensor Network Debugger. In Proceedings of the SenSys International Conference on Embedded Networked Sensor Systems, San Diego, CA, USA, 2–4 November 2005.
- Tolle, G.; Culler, D. Design of an Application-Cooperative Management System for Wireless Sensor Networks. In Proceedings of the Second European Workshop on Wireless Sensor Networks (EWSN), Istanbul, Turkey, 31 January–2 February 2005.
- Andreas, M.; Mehul, M.; Hu, S.; Simon, K. DiMo: Distributed Node Monitoring in Wireless Sensor Networks. In Proceedings of the MSWiM International Symposium on Modeling, Analysis and Simulation of Wireless and Mobile Systems, Vancouver, BC, Canada, 27–31 October 2008.
- Jan, B.; Matthias, D.; Lennart, M.; Lothar, T. Scalable Topology Control for Deployment-Support Networks. In Proceedings of the 4th International Conference Information Processing in Sensor Networks, Los Angeles, CA, USA, 25–27 April 2005.
- Cheng, Y.; John, B.; Pter, B.; Snoeren, A.C.; Voelker, G.M.; Savage, S. Jigsaw: Solving the Puzzle of Enterprise 802.11 Analysis. In Proceedings of the Special Interest Group on Data Communication (SIGCOMM), Pisa, Italy, 11–15 September 2006.
- Lewis, G.; Nithya, R.; Jeremy, E.; Thanos, S.; Martin, L.; Deborah, E. Emstar: A software environment for developing and deploying heterogeneous sensor-actuator networks. ACM Trans. Sens. Netw. 2007, 3, 1–31. [Google Scholar]
- Rodrigo, F.; Omprakash, G.; Kyle, J.; Philip, L. Four Bit Wireless Link Estimation. In Proceedings of the Sixth Workshop on Hot Topics in Networks (HotNets VI), Atlanta, GA, USA, 14–15 November 2007.
- Kuang, X.; Shen, J. SNDS: A Distributed Monitoring and Protocol Analysis System for Wireless Sensor Network. In Proceedings of the IEEE International Conference on Networks SecurityWireless Communications and Trusted Computing, Wuhan, China, 24–25 April 2010; pp. 422–425.
- Matthias, R.; Kay, R.; Andrea, V. Passive Inspection of Sensor Networks. In Proceedings of IEEE International Conference on Distributed Computing in Sensor Systems, Santa Fe, NM, USA, 18–20 June 2007.
- Chen, B.; Georey, P.; Geo, M.; Matt, W. LiveNet: Using Passive Monitoring to Reconstruct Sensor Network Dynamics. In Proceedings of the IEEE International Conference on Distributed Computing in Sensor Systems, Santorini Island, Greece, 11–14 June 2008; pp. 79–98.
- Dan, Y. DiF: A Diagnosis Framework for Wireless Sensor Networks. In Proceedings of the IEEE International Conference on Computer Communications INFOCOM, San Diego, CA, USA, 15–19 March 2010; pp. 1–5.
- Oliveira, H.A.B.; Nakamura, E.F.; Loureiro, A.A.F. Localization systems for wireless sensor networks. IEEE Wirel. Commun. 2007, 14, 6–12. [Google Scholar]
- Wang, L.; Liu, Y.; Xu, X.; Wang, X. WSN Multilateration Algorithm Based on Landweber Iteration. In Proceedings of the IEEE The Ninth International Conference on Electronic Measurement Instruments ICEMI, Beijing, China, 16–19 August 2009; 1, pp. 250–254.
- Wang, X.; Yuan, S.; Laura, R.; Lang, W. Dynamic localization based on spatial reasoning with RSSI in wireless sensor networks for transport logistics. Sens. Actuat. 2011, 171, 421–428. [Google Scholar] [CrossRef]
- Lakafosis, V.; Tentzeris, M.M. From single to multihop: The status of wireless localization. IEEE Microw. Mag. 2009, 10, 34–41. [Google Scholar]
- Vanheel, F.; Verhaevert, J.; Laermans, E. Ingrid moerman and piet demeester. Automated linear regression tools improve RSSI WSN localization in multipath indoor environment. EURASIP J. Wirel. Commun. Netw. 2011, 38, 1–27. [Google Scholar]
- Goldberger, A.S. Econometric Theory; John Wiley & Sons: New York, NY, USA, 1964. [Google Scholar]
- Shen, Y.; Li, B.; Chen, Y. An iterative solution of weighted total least-squares adjustment. J. Geodesy 2011, 85, 229–238. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.; Jazaeri, S. Weighted total least squares formulated by standard least squares theory. J. Geodetic Sci. 2012, 2, 1–12. [Google Scholar] [CrossRef]
- Kim, E.; Kim, K. Distance estimation with weighted least squares for mobile beacon-based localization in wireless sensor networks. IEEE Signal Process. Lett. 2010, 17, 559–562. [Google Scholar] [CrossRef]
- Tarr?o, P.; Bernardos, A.M.; Casar, J.R. Weighted least squares techniques for improved received signal strength based localization. Sensors 2011, 11, 8569–8592. [Google Scholar]
- Ampeliotis, D.; Berberidis, K. Linear Least Squares Based Acoustic Source Localization Utilizing Energy Measurements. In Proceedings of the IEEE Sensor Array and Multichannel Signal Processing Workshop, Darmstadt, Germany, 21–23 July 2008; pp. 349–352.
- Homayoun, H. The indoor radio propagation channel. Proc. IEEE 1993, 81, 943–968. [Google Scholar] [CrossRef]
- Fleury, B.H.; Leuthold, P.E. Radiowave propagation in mobile communications: An overview of European research. IEEE Commun. Mag. 1996, 34, 70–81. [Google Scholar]
- Yoo, J.H.; Lee, J.H.; Cho, S.H. A Propagation Model in 2.4GHz ISM Band Using IEEE 802.15.4 Systems. In Proceedings of the Asia-Pacific Conference on Communications, Sabah, Malaysia, 2–5 October 2011; pp. 339–343.
- Yang, T.; Ikeda, M.; Mino, G.; Barolli, L.; Durresi, A.; Xhafa, F. Performance Evaluation of Wireless Sensor Networks for Mobile Sink Considering Consumed Energy Metric. In Proceedings of the International Conference on Advanced Information Networking and Applications, Perth, WA, Australia, 20–23 April 2010; pp. 245–250.
- Zvanovec, S.; Pechac, P.; Klepal, M. Wireless LAN networks design: Site survey or propagation modeling? Radioengineering 2003, 12, 42–49. [Google Scholar]
- Barsocchi, P.; Lenzi, S.; Chessa, S.; Furfari, F. Automatic virtual calibration of range-based indoor localization systems. Wirel. Commun. Mob. Comput. 2011, 12, 1546–1557. [Google Scholar]
- Barsocchi, P.; Lenzi, S.; Chessa, S.; Giunta, G. Virtual Calibration for RSSI-based Indoor Localization with IEEE 802.15.4. In Proceedings of the IEEE International Conference on Communications, Dresden, Germany, 14–18 June 2009; pp. 1–5.
- Telit ZE51 2.4 module Datasheet. Available online: http://www.telit.com/module/infopool/download.php?id=2350 (accessed on 30 June 2012).
- Sarkar, T.K.; Ji, Z.; Kim, K.; Medouri, A.; Salazar-Palma, M. A survey of various propagation models for mobile communication. IEEE Antennas Propag. Mag. 2003, 45, 51–82. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Colistra, G.; Atzori, L. Estimation of Physical Layer Performance in WSNs Exploiting the Method of Indirect Observations. J. Sens. Actuator Netw. 2012, 1, 272-298. https://doi.org/10.3390/jsan1030272
Colistra G, Atzori L. Estimation of Physical Layer Performance in WSNs Exploiting the Method of Indirect Observations. Journal of Sensor and Actuator Networks. 2012; 1(3):272-298. https://doi.org/10.3390/jsan1030272
Chicago/Turabian StyleColistra, Giuseppe, and Luigi Atzori. 2012. "Estimation of Physical Layer Performance in WSNs Exploiting the Method of Indirect Observations" Journal of Sensor and Actuator Networks 1, no. 3: 272-298. https://doi.org/10.3390/jsan1030272







