Selection Criteria in Regime Switching Conditional Volatility Models
Abstract
:1. Introduction
2. Theory: Models and Selection Criteria
2.1. Models
2.1.1. Univariate GARCH Model
2.1.2. Asymmetric Volatility Models
2.1.3. MS-GARCH Models
2.2. Selection Criteria: Information Criteria and Loss Functions
3. Design of the Experiments
3.1. Common Design: Starting Values and Numerical Method
3.2. Experiment 1: Simulation of MS-GARCH-K Processes
3.3. Experiment 2: Simulation of MS-GARCH-H Processes
3.4. Experiment 3: Simulation of LST-GARCH Processes

4. Results and Discussion
4.1. Results
4.1.1. Experiment 1
| DGP | MSE() | QLIKE() | MAE() | MSE() | QLIKE() | MAE() | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|---|
| Experiment 1 and 2 with Gaussian innovations | |||||||||
| MS-K | |||||||||
| MS-H | x | x | x | x | x | ||||
| MS-K | |||||||||
| MS-H | x | x | x | x | x | ||||
| MS-K | x | x | x | x | x | x | x | x | |
| MS-H | x | x | x | x | x | ||||
| MS-K | |||||||||
| MS-H | x | x | x | x | x | x | x | x | |
| Experiment 2 | |||||||||
| LST-G | |||||||||
| LST-G | |||||||||
| LST-G | |||||||||
| MSE() | QLIKE() | MAE() | MSE() | QLIKE() | MAE() | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|
| GARCH | 7.2 | 3.8 | 0.5 | 0 | 0 | 0 | 16.6 | 67.8 |
| GARCH-T | 4.2 | 2.1 | 0.5 | 0 | 0 | 0 | 32.2 | 31.1 |
| MSG-GARCH-H | 8.0 | 4.9 | 13.2 | 33.5 | 52.2 | 59.2 | 6.6 | 0 |
| MST-GARCH-H | 0.4 | 0.6 | 0.6 | 9 | 5.3 | 2.3 | 0.3 | 0 |
| MSG-GARCH-K | 30.7 | 46.1 | 54.3 | 49.1 | 34.2 | 34.0 | 27.1 | 0 |
| MST-GARCH-K | 40.6 | 40.6 | 29.4 | 8.4 | 8.3 | 4.5 | 1.1 | 0 |
| LST-GARCH | 1.1 | 0.9 | 0.1 | 0 | 0 | 0 | 0.4 | 0 |
| LST-GARCH-T | 1.3 | 0.2 | 0 | 0 | 0 | 0 | 1.3 | 0 |
| GJR | 0.7 | 0.4 | 0.1 | 0 | 0 | 0 | 3.8 | 0.8 |
| GJR-T | 0.7 | 0.3 | 0.1 | 0 | 0 | 0 | 5.5 | 0.1 |
| EGARCH | 3.1 | 0.1 | 0.4 | 0 | 0 | 0 | 2.0 | 0.1 |
| EGARCH-T | 2.0 | 0 | 0.8 | 0 | 0 | 0 | 2.1 | 0 |
| MSE() | QLIKE() | MAE() | MSE() | QLIKE() | MAE() | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|
| GARCH | 0.5 | 0.1 | 0 | 0 | 0 | 0 | 0 | 1.8 |
| GARCH-T | 0.2 | 0 | 0.1 | 0 | 0 | 0 | 8.2 | 82.3 |
| MSG-GARCH-H | 24.0 | 17.3 | 23.8 | 13.3 | 21.6 | 19.3 | 21.4 | 5.2 |
| MST-GARCH-H | 9.3 | 7.0 | 5.4 | 5.6 | 1.7 | 1.5 | 8.4 | 0.2 |
| MSG-GARCH-K | 36.1 | 46.1 | 49.5 | 74.6 | 72.7 | 74.4 | 42.1 | 5.4 |
| MST-GARCH-K | 21.9 | 29.4 | 19.6 | 6.5 | 4.0 | 4.8 | 12.7 | 0.1 |
| LST-GARCH | 0 | 0.1 | 0 | 0 | 0 | 0 | 0 | 0 |
| LST-GARCH-T | 0.4 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0 |
| GJR | 0.2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.1 |
| GJR-T | 0 | 0 | 0 | 0 | 0 | 0 | 3.3 | 0.5 |
| EGARCH | 6.1 | 0 | 1.6 | 0 | 0 | 0 | 0 | 0.1 |
| EGARCH-T | 1.3 | 0 | 0 | 0 | 0 | 0 | 3.7 | 4.3 |
| MSE() | QLIKE() | MAE() | MSE() | QLIKE() | MAE() | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|
| GARCH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| MSG-GARCH-H | 5.1 | 5.5 | 4.4 | 1.9 | 0.1 | 6.4 | 7.9 | |
| MST-GARCH-H | 3.2 | 4.3 | 1.3 | 0.1 | 0.1 | 0 | 1.7 | 0.2 |
| MSG-GARCH-K | 48.8 | 43.1 | 64.7 | 85.7 | 93.6 | 90.1 | 72.2 | 88.8 |
| MST-GARCH-K | 42.9 | 47.1 | 29.6 | 12.2 | 5.9 | 9.8 | 19.7 | 3.1 |
| LST-GARCH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| LST-GARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GJR | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GJR-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| EGARCH | 0 | 0 | 0 | 0.1 | 0 | 0 | 0 | 0 |
| EGARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| MSE() | QLIKE() | MAE() | MSE() | QLIKE() | MAE() | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|
| GARCH | 8.4 | 5.7 | 5.7 | 0 | 0 | 0 | 21.9 | 69.4 |
| GARCH-T | 7.3 | 5.5 | 5.9 | 0.1 | 0 | 0.1 | 43.8 | 28.8 |
| MSG-GARCH-H | 13.8 | 15.5 | 14.5 | 34.7 | 25.8 | 27.2 | 5.3 | 0 |
| MST-GARCH-H | 10.0 | 10.3 | 6.0 | 27.6 | 16.8 | 20.2 | 0.2 | 0 |
| MSG-GARCH-K | 22.2 | 34.2 | 41.7 | 30.0 | 51.9 | 45.3 | 5.0 | 0 |
| MST-GARCH-K | 14.9 | 19.7 | 16.7 | 7.4 | 5.2 | 7.0 | 0.5 | 0 |
| LST-GARCH | 3.8 | 1.7 | 1.2 | 0 | 0 | 0 | 0.2 | 0 |
| LST-GARCH-T | 4.8 | 3.3 | 1.8 | 0.2 | 0.2 | 0 | 1.0 | 0 |
| GJR | 2.3 | 1.1 | 1.5 | 0 | 0.1 | 0 | 6.9 | 1.4 |
| GJR-T | 2.2 | 2.3 | 2.1 | 0 | 0 | 0 | 9.9 | 0.1 |
| EGARCH | 5.1 | 0.5 | 1.1 | 0 | 0 | 0 | 1.9 | 0.2 |
| EGARCH-T | 5.2 | 0.2 | 1.8 | 0 | 0 | 0.1 | 3.4 | 0.1 |
4.1.2. Experiment 2
| MSE() | QLIKE() | MAE() | MSE() | QLIKE() | MAE() | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|
| GARCH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| MSG-GARCH-H | 52.3 | 46.9 | 67.8 | 12.2 | 49.8 | 7.8 | 93.6 | 99.4 |
| MST-GARCH-H | 45.7 | 45.9 | 30.2 | 7.6 | 7.6 | 2.3 | 6.3 | 5.0 |
| MSG-GARCH-K | 0.9 | 3.9 | 1.1 | 65.8 | 30.6 | 70.8 | 0.1 | 0.1 |
| MST-GARCH-K | 1 | 3.3 | 0.9 | 12.0 | 12.0 | 19.1 | 0 | 0 |
| LST-GARCH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| LST-GARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GJR | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GJR-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| EGARCH | 0.1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| EGARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| MSE() | QLIKE() | MAE() | MSE() | QLIKE() | MAE() | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|
| GARCH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| MSG-GARCH-H | 57.9 | 54.6 | 76.8 | 34.2 | 57.2 | 39.0 | 94.9 | 99.2 |
| MST-GARCH-H | 41.1 | 39.5 | 19.1 | 5.1 | 3.2 | 2.8 | 5.0 | 0.6 |
| MSG-GARCH-K | 0.7 | 3.2 | 3.7 | 53.4 | 36.8 | 54.1 | 0.1 | 0.2 |
| MST-GARCH-K | 0.2 | 2.7 | 0.4 | 7.3 | 3.3 | 4.1 | 0 | 0 |
| LST-GARCH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| LST-GARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GJR | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GJR-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| EGARCH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| EGARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| MSE() | QLIKE() | MAE() | MSE() | QLIKE() | MAE() | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|
| GARCH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| MSG-GARCH-H | 59.9 | 64.6 | 79.2 | 48.7 | 19.1 | 35.9 | 97.9 | 99.8 |
| MST-GARCH-H | 39.5 | 32.8 | 19.1 | 13.1 | 2.8 | 7.5 | 2.0 | 0 |
| MSG-GARCH-K | 0.6 | 1.8 | 1.7 | 31.2 | 73.0 | 50.0 | 0.1 | 0.2 |
| MST-GARCH-K | 0 | 0.1 | 0 | 6.9 | 5.1 | 6.6 | 0 | 0 |
| LST-GARCH | 0 | 0 | 0 | 0.1 | 0 | 0 | 0 | 0 |
| LST-GARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GJR | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GJR-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| EGARCH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| EGARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| MSE() | QLIKE() | MAE() | MSE() | QLIKE() | MAE() | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|
| GARCH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 1.3 | 21.8 |
| MSG-GARCH-H | 88.2 | 82.0 | 87.2 | 73.0 | 83.6 | 64.2 | 89.9 | 74.9 |
| MST-GARCH-H | 8.8 | 8.7 | 5.3 | 13.5 | 3.8 | 5.9 | 1.8 | 0.1 |
| MSG-GARCH-K | 3.0 | 9.3 | 7.5 | 13.2 | 12.5 | 29.7 | 6.3 | 3.0 |
| MST-GARCH-K | 0.1 | 0 | 0 | 0.2 | 0.1 | 0.2 | 0 | 0 |
| LST-GARCH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| LST-GARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GJR | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GJR-T | 0 | 0 | 0 | 0 | 0 | 0 | 0.6 | 0.1 |
| EGARCH | 0 | 0 | 0 | 0.1 | 0 | 0 | 0 | 0 |
| EGARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0.1 | 0.1 |
4.1.3. Experiment 3
| MSE() | QLIKE() | MAE() | MSE() | QLIKE() | MAE() | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|
| GARCH | 4.3 | 9.9 | 6.9 | 0.1 | 0 | 0 | 56.2 | 96.3 |
| GARCH-T | 4.0 | 8.8 | 6.4 | 0.3 | 0 | 0.2 | 2.6 | 0.2 |
| MSG-GARCH-H | 1.8 | 2.2 | 4.0 | 29.6 | 21.9 | 13.7 | 1.3 | 0 |
| MST-GARCH-H | 2.8 | 2.5 | 5.2 | 1.5 | 3.5 | 25.0 | 0 | 0 |
| MSG-GARCH-K | 1.1 | 1.9 | 2.3 | 41.8 | 61.3 | 45.2 | 4 | 0 |
| MST-GARCH-K | 4.3 | 7.5 | 6.5 | 3.9 | 3.4 | 5.1 | 0 | 0 |
| LST-GARCH | 30.9 | 32.3 | 27.3 | 7.3 | 2.5 | 1.9 | 3.5 | 0 |
| LST-GARCH-T | 16.7 | 11.1 | 18.8 | 6.0 | 4.6 | 1.9 | 0.1 | 0 |
| GJR | 14.5 | 10.0 | 9.9 | 1.4 | 1.9 | 0.9 | 26.5 | 3.3 |
| GJR-T | 14.8 | 13.5 | 11.4 | 1.1 | 0 | 0.3 | 1.0 | 0 |
| EGARCH | 2.2 | 0.2 | 0.8 | 3.9 | 0.8 | 3.0 | 8.0 | 0.2 |
| EGARCH-T | 2.6 | 0.1 | 0.5 | 3.1 | 0.1 | 2.8 | 0.4 | 0 |
| MSE() | QLIKE() | MAE() | MSE() | QLIKE() | MAE() | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|
| GARCH | 0 | 0 | 0 | 0.1 | 0 | 0 | 7.4 | 34.8 |
| GARCH-T | 0.1 | 0.4 | 0.1 | 0.2 | 0 | 0 | 0.6 | 0 |
| MSG-GARCH-H | 0 | 0.2 | 0.1 | 28.0 | 25.1 | 14.1 | 0.1 | 0 |
| MST-GARCH-H | 0 | 0.1 | 0.1 | 0.6 | 1.9 | 23.9 | 0 | 0 |
| MSG-GARCH-K | 0.1 | 0.2 | 0 | 31.9 | 58.9 | 41.8 | 0.1 | 0 |
| MST-GARCH-K | 0.1 | 0.4 | 0 | 3.2 | 4.0 | 4.2 | 0 | 0 |
| LST-GARCH | 43.4 | 63.5 | 43.1 | 10.4 | 5.3 | 3.2 | 23.4 | 1.3 |
| LST-GARCH-T | 33.0 | 19.8 | 34.5 | 8.0 | 2.3 | 1.8 | 2.0 | 0 |
| GJR | 9.7 | 6.0 | 9.2 | 1.5 | 1.2 | 1.2 | 46 | 41.3 |
| GJR-T | 11.1 | 9.3 | 10.8 | 2.7 | 0 | 0.9 | 3.0 | 0.1 |
| EGARCH | 1.4 | 0.7 | 1.3 | 5.9 | 1.2 | 4.7 | 16.3 | 22.5 |
| EGARCH-T | 1.1 | 0.4 | 0.8 | 7.5 | 2 | 4.2 | 1.1 | 0 |
| MSE() | QLIKE() | MAE() | MSE() | QLIKE() | MAE() | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|
| GARCH | 0 | 0 | 0 | 0.1 | 0 | 0 | 0 | 0.1 |
| GARCH-T | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| MSG-GARCH-H | 0 | 0 | 0 | 33.4 | 33.2 | 22.8 | 0 | 0 |
| MST-GARCH-H | 0 | 0 | 0 | 0.8 | 1.0 | 19.7 | 0 | 0 |
| MSG-GARCH-K | 0 | 0 | 0 | 30.0 | 47.3 | 37.0 | 0 | 0 |
| MST-GARCH-K | 0 | 0 | 0 | 4.4 | 5.4 | 3.9 | 0 | 0 |
| LST-GARCH | 48.0 | 62.8 | 49.5 | 7.2 | 3.8 | 2.4 | 28.9 | 1.8 |
| LST-GARCH-T | 19.6 | 26.0 | 26.3 | 8.8 | 8.4 | 6.3 | 1.3 | 0 |
| GJR | 18.1 | 5.3 | 13.5 | 6.3 | 0.8 | 3.2 | 55.8 | 92.8 |
| GJR-T | 14.3 | 5.9 | 10.7 | 8.4 | 0.1 | 4.5 | 3.1 | 0.3 |
| EGARCH | 0 | 0 | 0 | 0.4 | 0 | 5.7 | 10.9 | 5.0 |
| EGARCH-T | 0 | 0 | 0 | 0.2 | 0 | 0.2 | 0 | 0 |
4.2. Discussion
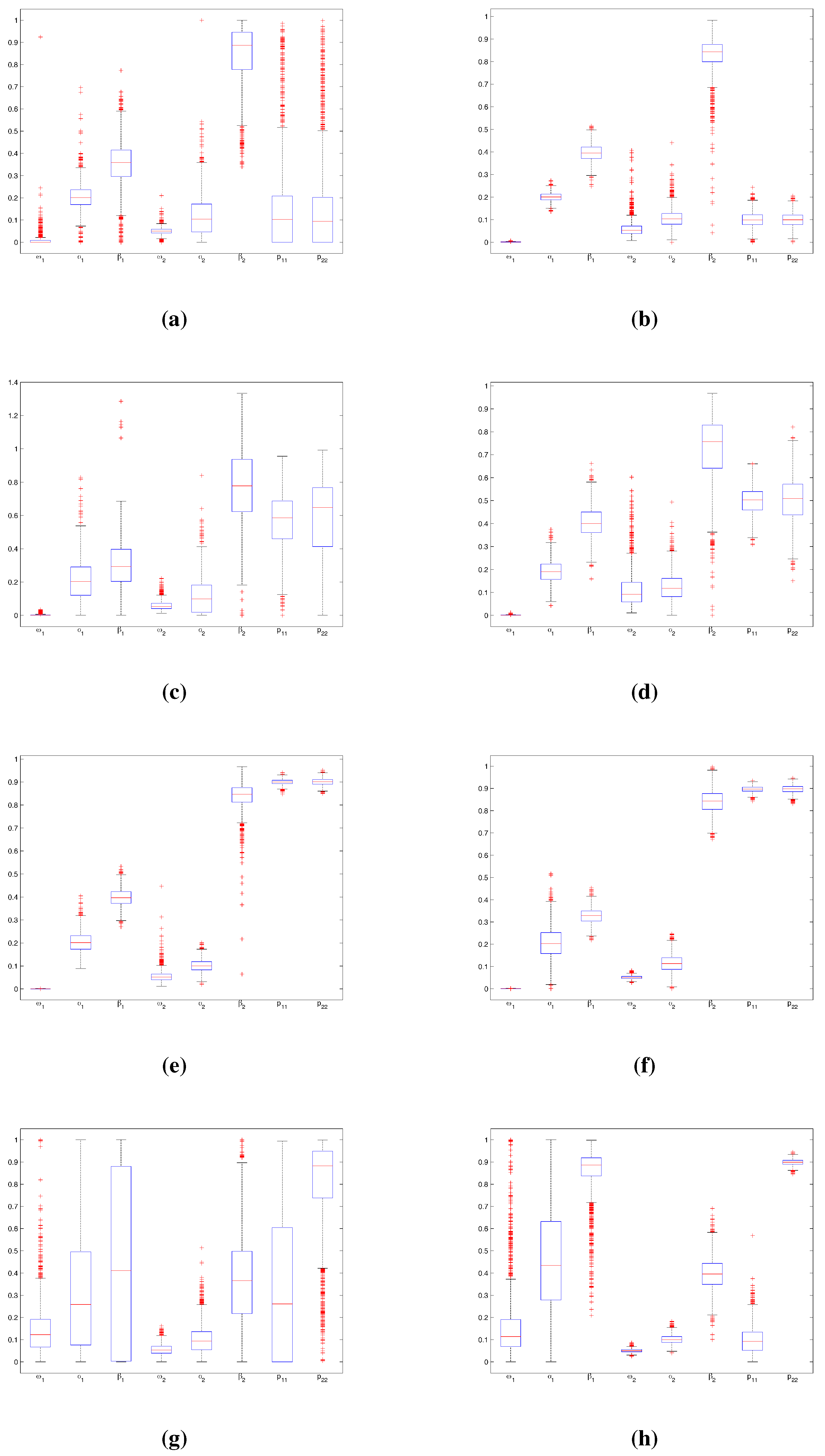


5. Conclusions
Acknowledgments
Conflicts of Interest
References
- R.F. Engle. “Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation.” Econometrica 50 (1982): 987–1007. [Google Scholar]
- T. Bollerslev. “Generalized autoregressive conditional heteroskedasticity.” J. Econom. 31 (1986): 307–327. [Google Scholar] [CrossRef]
- C.G. Lamoureux, and W.D. Lastrapes. “Persistence in Variance, Structural Change, and the GARCH Model.” J. Bus. Econ. Stat. 8 (1990): 225–34. [Google Scholar]
- G.E.P. Box. “Robustness in the strategy of scientific model building.” In Robustness in Statistics. Edited by R. L. Launer and G. N. Wilkinson. New York, NY, USA: Academic Press, 1978, pp. 201–236. [Google Scholar]
- S.F. Gray. “Modeling the conditional distribution of interest rates as a regime-switching process.” J. Financ. Econ. 42 (1996): 27–62. [Google Scholar] [CrossRef]
- G.E. Hagerud. “A Smooth Transition ARCH Model for Asset Returns.” In Working Paper Series in Economics and Finance 162. Sweden, Stockholm: Stockholm School of Economics, 1997. [Google Scholar]
- C. Francq, and J.M. Zakoïan. “Deriving the autocovariances of powers of Markov-switching GARCH models, with applications to statistical inference.” Comput. Stat. Data Anal. 52 (2008): 3027–3046. [Google Scholar] [CrossRef]
- L. Bauwens, A. Preminger, and J.V.K. Rombouts. “Theory and inference for a Markov switching GARCH model.” Econom. J. 13 (2010): 218–244. [Google Scholar] [CrossRef]
- M. Lubrano. “Smooth Transition Garch Models: A Baysian Perspective.” In Discussion Papers (REL—Recherches Economiques de Louvain) 2001032. Louvain, Belgium: Institut de Recherches Economiques et Sociales (IRES), Université Catholique de Louvain, 2001. [Google Scholar]
- F. Chan, M. McAleer, and M.C. Medeiros. “Structure and asymptotic theory for nonlinear models with GARCH errors.” EconomiA, 2015. [Google Scholar] [CrossRef]
- N. Maugeri. “Some Pitfalls in Smooth Transition Models Estimation: A Monte Carlo Study.” Comput. Econ. 44 (2014): 339–378. [Google Scholar] [CrossRef]
- M. Augustyniak. “Maximum likelihood estimation of the Markov-switching GARCH model.” Comput. Stat. Data Anal. 76 (2014): 61–75. [Google Scholar] [CrossRef]
- G. Gonzalez-Rivera. “Smooth-Transition GARCH Models.” Stud. Nonlinear Dyn. Econom. 3 (1998): 1–20. [Google Scholar]
- I. Berkes, and L. Horvàth. “The efficiency of the estimators of the parameters in GARCH processes.” Ann. Statist. 32 (2004): 633–655. [Google Scholar]
- C. Francq, and J.M. Zakoïan. “On Efficient Inference in GARCH Processes.” In Dependence in Probability and Statistics. Edited by P. Bertail, P. Soulier and P. Doukhan. New York, NY, USA: Springer, 2006, Volume 187, Lecture Notes in Statistics; pp. 305–327. [Google Scholar]
- F. Black. “Studies of stock price volatility changes.” In Proceedings of the 1976 Meetings of the American Statistical Association, Business and Economics Statistics Section, Boston, MA, USA, 23–26 August, 1976; pp. 177–181.
- Z. Ding, C.W. Granger, and R.F. Engle. “A long memory property of stock market returns and a new model.” J. Empir. Financ. 1 (1993): 83–106. [Google Scholar] [CrossRef]
- F.P. Hans, and D.V. Dijk. “Forecasting stock market volatility using (nonlinear) GARCH models.” J. Forecast. 15 (1996): 229–235. [Google Scholar]
- G.F. Loudon, W.H. Watt, and P.K. Yadav. “An empirical analysis of alternative parametric ARCH models.” J. Appl. Econom. 15 (2000): 117–136. [Google Scholar] [CrossRef]
- L.R. Glosten, R. Jagannathan, and D.E. Runkle. “On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks.” J. Financ. 48 (1993): 1779–1801. [Google Scholar] [CrossRef]
- D.B. Nelson. “Conditional Heteroskedasticity in Asset Returns: A New Approach.” Econometrica 59 (1991): 347–370. [Google Scholar] [CrossRef]
- M. Rockinger, and E. Jondeau. “Entropy densities with an application to autoregressive conditional skewness and kurtosis.” J. Econom. 106 (2002): 119–142. [Google Scholar] [CrossRef]
- J.D. Hamilton, and R. Susmel. “Autoregressive conditional heteroskedasticity and changes in regime.” J. Econom. 64 (1994): 307–333. [Google Scholar] [CrossRef]
- J. Cai. “A Markov Model of Switching-Regime ARCH.” J. Bus. Econ. Stat. 12 (1994): 309–316. [Google Scholar]
- F. Klaassen. “Improving GARCH volatility forecasts with regime-switching GARCH.” Empir. Econ. 27 (2002): 363–394. [Google Scholar] [CrossRef]
- M. Haas, S. Mittnik, and M.S. Paolella. “A New Approach to Markov-Switching GARCH Models.” J. Financ. Econom. 2 (2004): 493–530. [Google Scholar] [CrossRef]
- G.M. Gallo, and E. Otranto. “Forecasting Realized Volatility with Changing Average Volatility Levels.” Int. J. Forecast., 2015. forthcoming. [Google Scholar]
- J.D. Hamilton. “A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle.” Econometrica 57 (1989): 357–384. [Google Scholar] [CrossRef]
- J.D. Hamilton. “Nonlinearities and the Macroeconomic Effects of Oil Prices.” Macroecon. Dyn. 15 (2011): 364–378. [Google Scholar] [CrossRef]
- D. Ardia. “Bayesian estimation of a Markov-switching threshold asymmetric GARCH model with Student-t innovations.” Econom. J. 12 (2009): 105–126. [Google Scholar] [CrossRef]
- M. Haas, S. Mittnik, and M.S. Paolella. “Asymmetric multivariate normal mixture GARCH.” Comput. Stat. Data Anal. 53 (2009): 2129–2154. [Google Scholar]
- L. Hu, and Y. Shin. “Optimal Test for Markov Switching GARCH Models.” Stud. Nonlinear Dyn. Econom. 12 (2008): 3. [Google Scholar] [CrossRef]
- H. Akaike. “A New Look at the Statistical Model Identification.” In Selected Papers of Hirotugu Akaike. Edited by E. Parzen, K. Tanabe and G. Kitagawa. Springer Series in Statistics; New York, NY, USA: Springer, 1998, pp. 215–222. [Google Scholar]
- S. Kullback, and R.A. Leibler. “On Information and Sufficiency.” Ann. Math. Stat. 22 (1951): 79–86. [Google Scholar] [CrossRef]
- C.M. Hurvich, and C.L. Tsai. “Regression and Time Series Model Selection in Small Samples.” Biometrika 76 (1989): 297–307. [Google Scholar] [CrossRef]
- P.R. Hansen, and A. Lunde. “Consistent ranking of volatility models.” J. Econom. 131 (2006): 97–121. [Google Scholar] [CrossRef]
- A.J. Patton. “Volatility forecast comparison using imperfect volatility proxies.” J. Econom. 160 (2011): 246–256. [Google Scholar] [CrossRef]
- D. Guegan, and S. Rioublanc. “Regime Switching Models: Real or Spurious Long Memory ? ” Available online: http://econpapers.repec.org/paper/haljournl/halshs-00189208.htm (accessed on 13 January 2015).
- S. Frühwirth-Schnatter. Finite Mixture and Markov Switching Models. Springer Series in Statistics; New York, NY, USA: Springer, 2006. [Google Scholar]
- S. Laurent, J.V. Rombouts, and F. Violente. “Consistent ranking of multivariate volatility models.” In CORE Discussion Papers 2009002. Louvain, Belgium: Université Catholique de Louvain, Center for Operations Research and Econometrics (CORE), 2009. [Google Scholar]
- F. Chan, and M. McAleer. “Maximum likelihood estimation of STAR and STAR-GARCH models: Theory and Monte Carlo evidence.” J. Appl. Econom. 17 (2002): 509–534. [Google Scholar] [CrossRef]
- C. Brunetti, C. Scotti, R.S. Mariano, and A.H. Tan. “Markov switching GARCH models of currency turmoil in Southeast Asia.” Emerg. Mark. Rev. 9 (2008): 104–128. [Google Scholar] [CrossRef]
- K.L. Chang. “Do macroeconomic variables have regime-dependent effects on stock return dynamics? Evidence from the Markov regime switching model.” Econ. Modell. 26 (2009): 1283–1299. [Google Scholar] [CrossRef]
- 3.See [11] for example.
- 4.There are a number of expansions of these two MS-GARCH processes. For example, Gallo and Otrento [27] introduce asymmetric effects in each regime variance.
- 5.Hu and Shin [32] introduced a test procedure which tests the null hypothesis of a GARCH process against an MS-GARCH process.
- 6.For each experiment, we estimate these models: GARCH, GARCH-T, LST-GARCH, LST-GARCH-T, GJR-GARCH, GJR-GARCH-T, EGARCH, AEGARCH-T, MSG(2)-GARCH-H, MSG(2)-GARCH-K, MST(2)-GARCH-H and MST(2)-GARCH-K.
- 7.Results for are available on demand, results remain the same. We do not consider smaller sample size since in financial application, we used to study daily data.
- 9.We set , and . We generate 2000 more observations than required to minimize any starting bias.
- 10.The probabilities of being in regime . The long-run probability of the first regime: is equal to .
- 11.δ is computed as follows: .
- 12.We set , and . We generate 2000 more observations than required, to minimize any starting bias.
- 13.We generate 2000 more observations than required to minimize any starting bias.
- 14.Estimation computed with Gaussian kernel and Silverman’s rule of thumb.
- 15.Figure 3(a) is related to the 40th replication of the first and the second experiments with matrix , BIC selects the right specification when data are simulated with MSG-GARCH-H but it selects the GARCH model for data simulated with MS-GARCHG-K. Figure 3(b) is related to the 66th replication of the first and second experiments with where there is no selection problem.
- 16.Estimation computed with Gaussian kernel and Silverman’s rule of thumb.
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chuffart, T. Selection Criteria in Regime Switching Conditional Volatility Models. Econometrics 2015, 3, 289-316. https://doi.org/10.3390/econometrics3020289
Chuffart T. Selection Criteria in Regime Switching Conditional Volatility Models. Econometrics. 2015; 3(2):289-316. https://doi.org/10.3390/econometrics3020289
Chicago/Turabian StyleChuffart, Thomas. 2015. "Selection Criteria in Regime Switching Conditional Volatility Models" Econometrics 3, no. 2: 289-316. https://doi.org/10.3390/econometrics3020289
APA StyleChuffart, T. (2015). Selection Criteria in Regime Switching Conditional Volatility Models. Econometrics, 3(2), 289-316. https://doi.org/10.3390/econometrics3020289





