Evapotranspiration Analysis in Central Italy: A Combined Trend and Clustering Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Dataset
2.2. Clustering
2.3. Modeling Procedure
- The seasonal MK test assessed the overall trends over the monthly time series in Tmin, Tmax, Tmean, RHmin, RHmax, WS10, Rs, P, and ETo. It is crucial to acknowledge that the time series data for the variables under investigation may exhibit various seasonal patterns. The seasonal MK test was implemented as an alternative to the conventional MK test, taking into account the seasonality in the estimation of the MK parameters. These parameters, primarily represented by Z, were used to identify statistically significant trends, with the confidence level set at 1% based on previous studies. The Z-statistic measures how many standard deviations a data point is from the mean, with its sign indicating the direction of the trend, being positive for an increasing trend and negative for a decreasing trend. Sen’s slope β was employed to assess the slope of the linear trend. Calculated by taking the median of all possible slopes between pairs of data points, positive and negative β-values signify increasing and decreasing trends, respectively. A comprehensive description of the seasonal MK test is provided in [33,38,39].
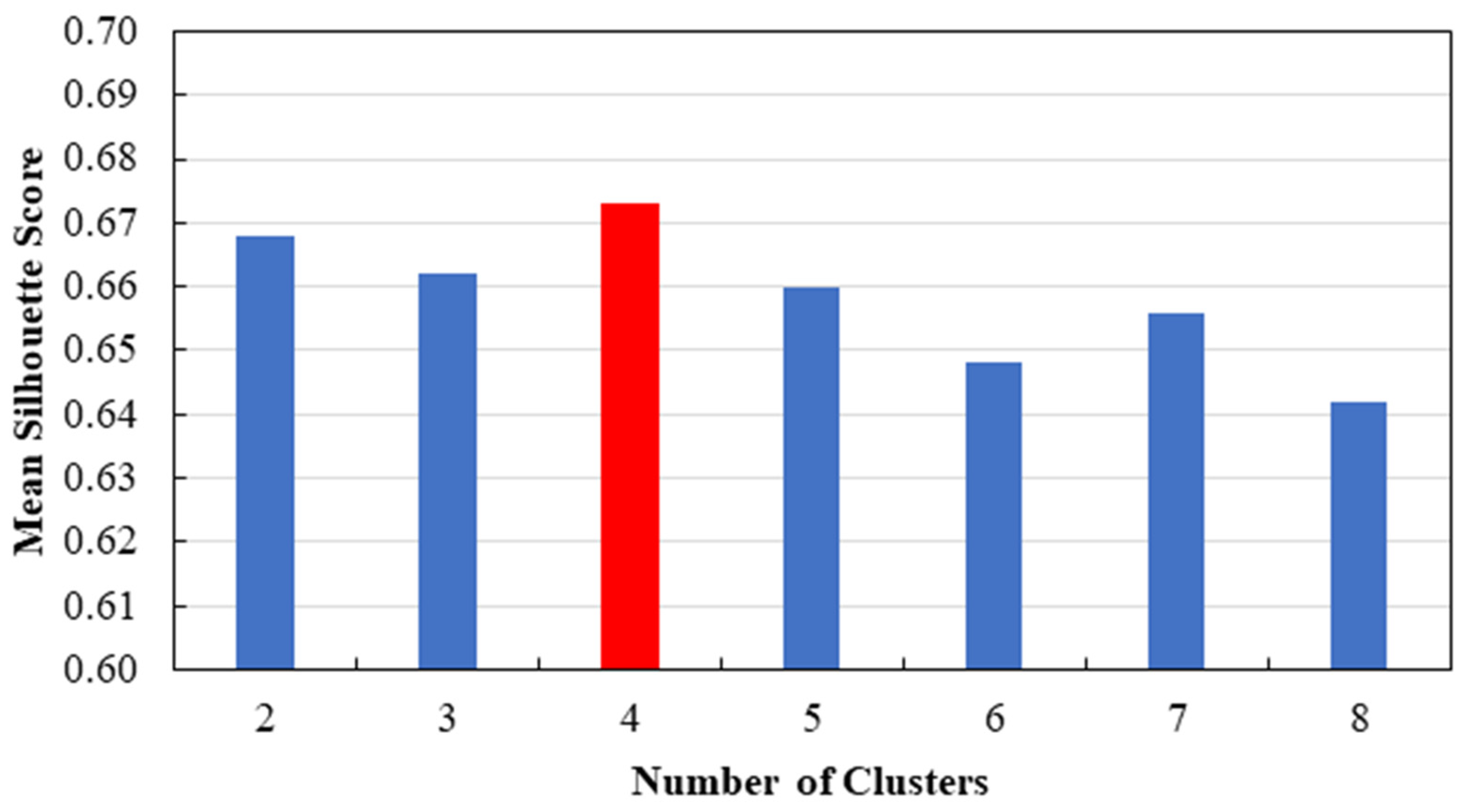
- The K-means clustering algorithm was then employed to identify homogeneous regions based on the seasonal MK parameters, Z and β, computed for each hydrological variable. The analysis of the results entailed a comparison of the distinct clusters determined by the silhouette score. The seasonal MK test parameters computed on each hydrological variable’s mean cluster time series were also discussed.
3. Results
3.1. Seasonal MK Analysis
3.2. Clustering
- –
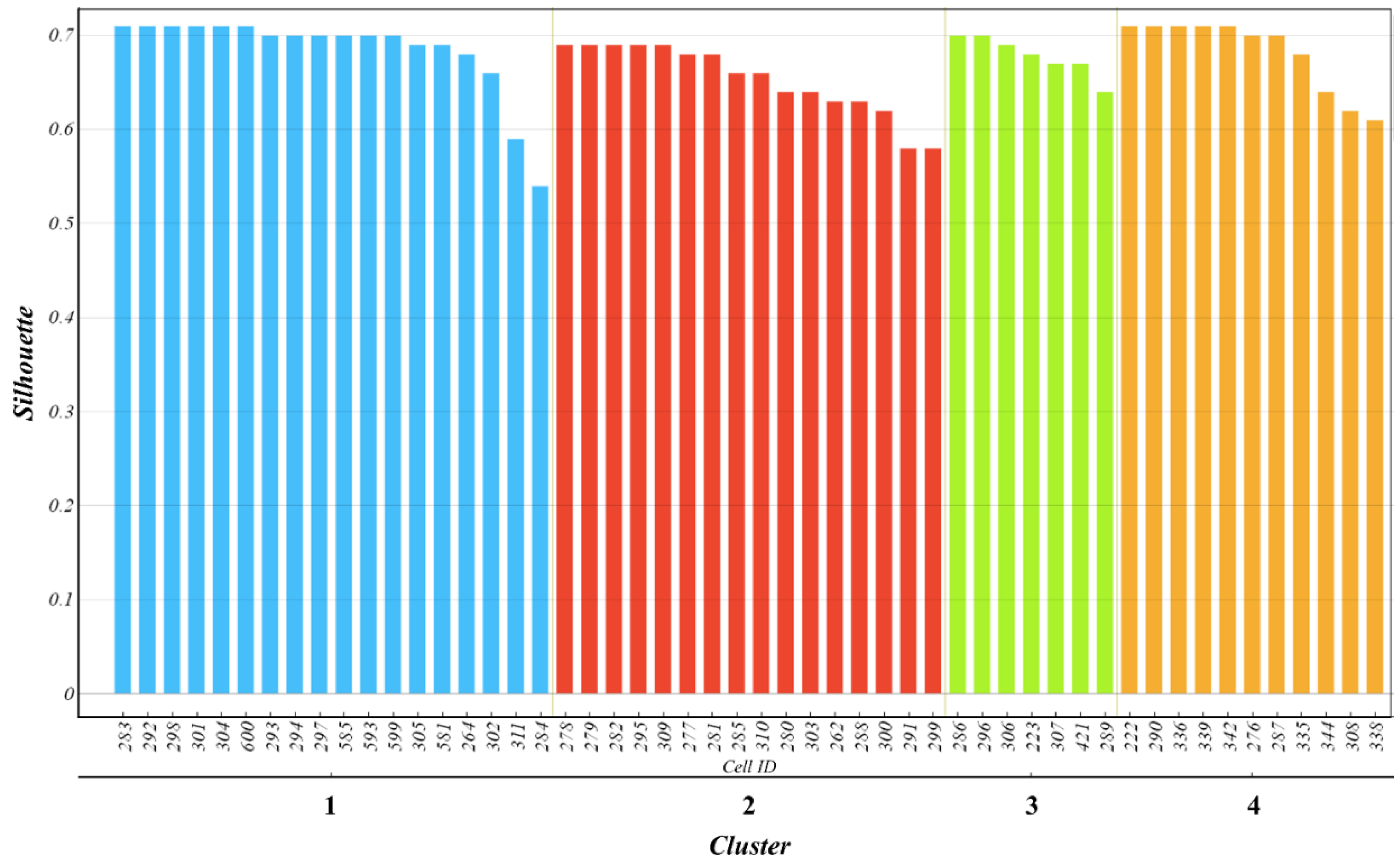
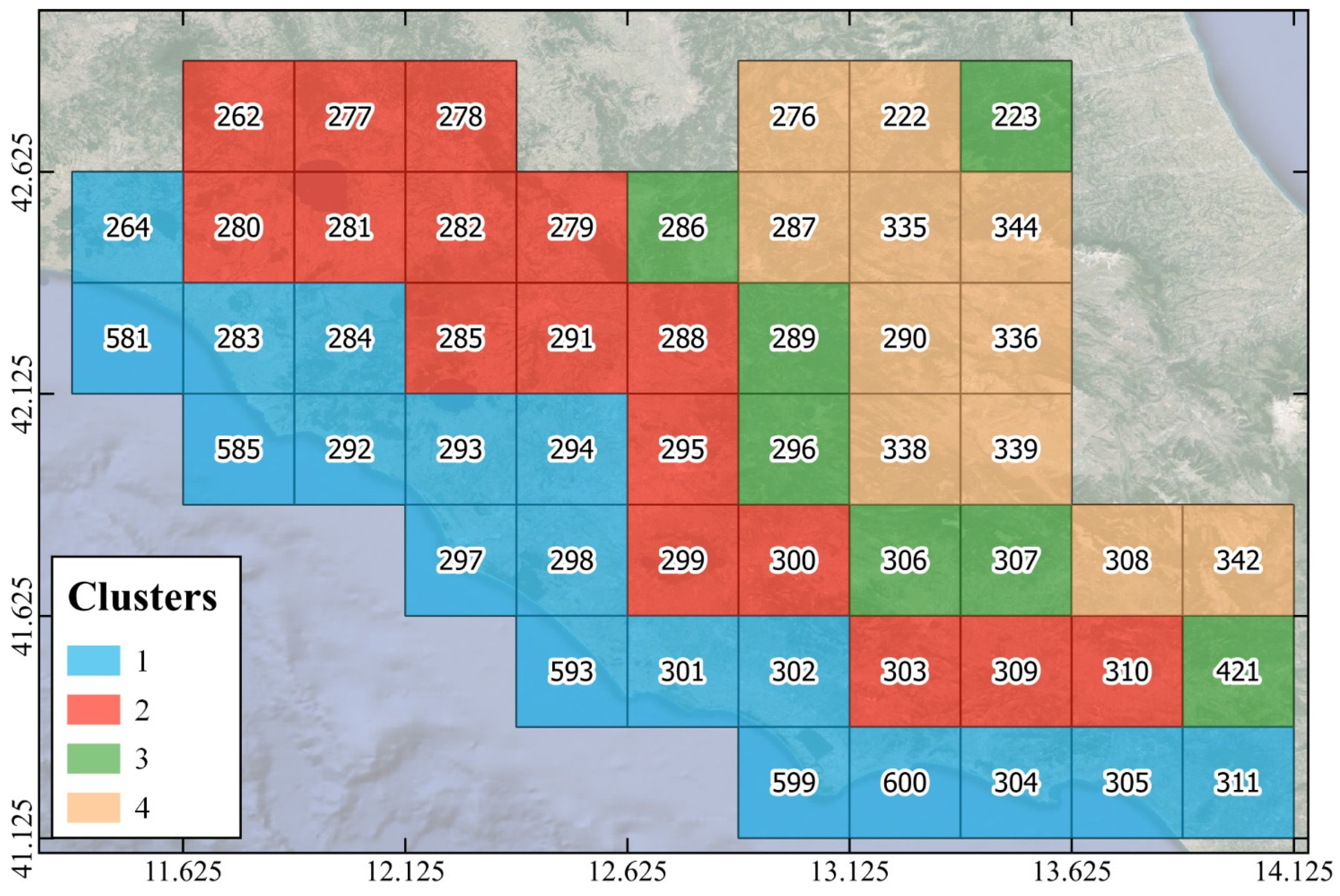
- Cluster 1 corresponded to the coastal area of Lazio, with a mean altitude of about 102 m. The proximity to the sea resulted in the highest mean values of Tmean, RHmin, WS10, Rs, and ETo among the different clusters. At the same time, cluster 1 showed the lowest CV values for air temperature, relative humidity, and ETo. However, cluster 1 also exhibited the lowest mean values of P with the highest CV, indicating a high variability in precipitation. Overall, the proximity to the sea results in higher temperatures, increased solar radiation, and elevated ETo compared with inland areas. The higher heat capacity of the sea attenuates temperatures and prevents extreme fluctuations. The reflective surface of the Tyrrhenian Sea also plays a role, cooling coastal areas by reflecting solar radiation. Additionally, enhanced evaporation rates and the presence of sea breezes contribute to the region’s overall warmer and more stable climate, distinguishing it from the potentially more variable conditions experienced inland. In terms of silhouette scores, all cells showed values greater than 0.5, with the lowest value being 0.54 for cell 284. This can be explained by the proximity of this cell to cluster 2 to the north and east.
- –
- Cluster 2 covers the hilly area of Lazio between the coastal cluster 1 and the foothill cluster 3. Compared with cluster 1, cluster 2 exhibited lower means for Tmean, WS10, Rs, and ETo and higher means for RHmax and P. At the same time, it exhibited higher CV values for air temperature, RH, and ETo. The difference between clusters 2 and 1 in Lazio lies primarily in their altitudinal variations. Cluster 2, representing the hilly area, has a higher mean altitude of about 350 m, which leads to cooler temperatures and less solar radiation compared with coastal cluster 1. The topographical and altitudinal distinctions contribute to a cooler and potentially more variable climate in the hilly areas, highlighting the significant impact of altitude on regional climate patterns. Moreover, all cells showed silhouette scores greater than 0.5, with the lowest value of 0.58 for cell 299, explained by the proximity of this cell to cluster 1 to the south and west.
- –
- Cluster 3 covers the foothills of Lazio, with a mean altitude of about 690 m, between the hilly cluster 2 and the mountainous cluster 4. It also includes cell 223, which encompasses the foothills up to the border with Abruzzo and Marche. The location of cluster 3, far from the sea and close to the Apennines, led to a further reduction in the mean values of Tmean, WS10, Rs, and ETo and a further increase in the mean value of P, which was the highest among all the clusters. Cluster 3 also showed the lowest CV related to WS10 among all clusters. The combination of its location far from the sea and its proximity to the Apennines contributes to a more stable and uniform wind speed pattern. As for the silhouette scores, all cells exhibited values exceeding 0.64, indicating a robust affiliation with cluster 3.
- –
- Cluster 4 covers the Apennine area of Lazio, with a mean altitude of about 1037 m. Consequently, this area showed the lowest means for Tmean, WS10, Rs, and ETo among all clusters. At the same time, the CV values for Tmean and ETo were the highest among all clusters. Therefore, cluster 4 experiences more fluctuations or differences in both temperature and ETo, indicating a higher degree of variability in these specific climatic parameters within this cluster. However, cluster 4 also exhibited the highest mean value of RHmax. While the coastal areas also have high humidity, the specific mechanisms at play in mountainous terrain, such as orographic uplift and cooling, contribute to even higher relative humidity levels in these regions. As with cluster 3, all cells in cluster 4 showed a silhouette score higher than 0.6, confirming a robust affiliation with cluster 4.
4. Discussion
- –
- The seasonal MK test was performed on each cell covering Lazio. The test exhibited statistically significant increasing trends in air temperature, solar radiation, and ETo while showing statistically significant decreasing trends for RH. Meanwhile, wind speed and precipitation showed both increasing and decreasing trends. However, in both cases, the trends were not statistically significant, indicating that the trends were not well-defined.
- –
- The clustering analysis based on the seasonal MK parameters led to a division of Lazio into four distinct clusters: the coastal cluster 1, the hilly cluster 2, the foothill cluster 3, and the Apennine cluster 4. Overall, a decrease in the mean values of Tmean, RHmin, WS10, Rs, and ETo was observed from the coastal area to the inland area. Nevertheless, with a decrease in temperature and solar radiation, there was a corresponding increase in the CV values of both Tmean and ETo with altitude. Indeed, the Apennine cluster 4 exhibited more pronounced fluctuations or variances in both temperature and ETo, indicating a higher degree of variability in these particular climatic variables with increasing altitude.
- –
- Finally, the seasonal MK test performed on the mean cluster time series showed statistically significant increasing trends for all clusters with respect to air temperature, solar radiation, and ETo, which were more marked for the coastal and hilly clusters 1 and 2. At the same time, statistically significant decreasing trends were observed for RH for all clusters, particularly in the hilly cluster 2.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wanniarachchi, S.; Sarukkalige, R. A Review on Evapotranspiration Estimation in Agricultural Water Management: Past, Present, and Future. Hydrology 2022, 9, 123. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Singer, M.B.; Asfaw, D.T.; Rosolem, R.; Cuthbert, M.O.; Miralles, D.G.; MacLeod, D.; Quichimbo, E.A.; Michaelides, K. Hourly potential evapotranspiration at 0.1° resolution for the global land surface from 1981-present. Sci. Data 2021, 8, 224. [Google Scholar] [CrossRef]
- Giménez, P.O.; García-Galiano, S.G. Assessing Regional Climate Models (RCMs) Ensemble-Driven Reference Evapotranspiration over Spain. Water 2018, 10, 1181. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W. Climate change impacts on the hydrological cycle. Ecohydrol. Hydrobiol. 2008, 8, 195–203. [Google Scholar] [CrossRef]
- Lee, T.-H.; Lo, M.-H.; Chiang, C.-L.; Kuo, Y.-N. The maritime continent’s rainforests modulate the local interannual evapotranspiration variability. Commun. Earth Environ. 2023, 4, 482. [Google Scholar] [CrossRef]
- Wang, X.; Liu, L. The impacts of climate change on the hydrological cycle and water resource management. Water 2023, 15, 2342. [Google Scholar] [CrossRef]
- Christidis, N.; Stott, P.A. Changes in the geopotential height at 500 hpa under the influence of external climatic forcings. Geophys. Res. Lett. 2015, 42, 10798–10806. [Google Scholar] [CrossRef]
- Blyth, E.M.; Martínez-de la Torre, A.; Robinson, E.L. Trends in evapotranspiration and its drivers in Great Britain: 1961 to 2015. Prog. Phys. Geog. 2019, 43, 666–693. [Google Scholar] [CrossRef]
- Robson, J.; Sutton, R.T.; Archibald, A.; Cooper, F.; Christensen, M.; Gray, L.J.; Holliday, N.P.; Macintosh, C.; McMillan, M.; Moat, B.; et al. Recent multivariate changes in the north Atlantic climate system, with a focus on 2005–2016. Int. J. Climatol. 2018, 38, 5050–5076. [Google Scholar] [CrossRef]
- Dong, B.; Sutton, R.T. Recent trends in summer atmospheric circulation in the north Atlantic/European region: Is there a role for anthropogenic aerosols? J. Clim. 2021, 34, 6777–6795. [Google Scholar] [CrossRef]
- Bakke, S.J.; Ionita, M.; Tallaksen, L.M. Recent European drying and its link to prevailing large-scale atmospheric patterns. Sci. Rep. 2023, 13, 21921. [Google Scholar] [CrossRef] [PubMed]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1948; p. 202. [Google Scholar]
- Sen, Z. Innovative trend analysis methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F. Forecasting evapotranspiration in different climates using ensembles of recurrent neural networks. Agric. Water Manag. 2021, 255, 107040. [Google Scholar] [CrossRef]
- Chaouche, K.; Neppel, L.; Dieulin, C.; Pujol, N.; Ladouche, B.; Martin, E.; Salas, D.; Caballero, Y. Analyses of precipitation, temperature and evapotranspiration in a French Mediterranean region in the context of climate change. C. R. Geosci. 2010, 342, 234–243. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of trends in reference evapotranspiration data in a humid climate. Hydrolog. Sci. J. 2014, 59, 165–180. [Google Scholar] [CrossRef]
- Elferchichi, A.; Giorgio, G.A.; Lamaddalena, N.; Ragosta, M.; Telesca, V. Variability of Temperature and Its Impact on Reference Evapotranspiration: The Test Case of the Apulia Region (Southern Italy). Sustainability 2017, 9, 2337. [Google Scholar] [CrossRef]
- Tomas-Burguera, M.; Santiago Beguería Sergio, M. Vicente-Serrano Climatology and trends of reference evapotranspiration in Spain. Int. J. Clim. 2021, 41, E1860–E1874. [Google Scholar] [CrossRef]
- Bouregaa, T. Spatiotemporal trends of reference evapotranspiration in Algeria. Theor. Appl. Clim. 2024, 155, 581–598. [Google Scholar] [CrossRef]
- Pandey, B.K.; Khare, D. Identification of trend in long term precipitation and reference evapotranspiration over Narmada River basin (India). Glob. Planet. Chang. 2018, 161, 172–182. [Google Scholar] [CrossRef]
- Jerin, J.N.; Islam, H.M.T.; Islam, A.R.M.T.; Shahid, S.; Hu, Z.; Badhan, M.A.; Chu, R.; Elbeltagi, A. Spatiotemporal trends in reference evapotranspiration and its driving factors in Bangladesh. Theor. Appl. Climatol. 2021, 144, 793–808. [Google Scholar] [CrossRef]
- Xu, S.; Yu, Z.; Yang, C.; Ji, X.; Zhang, K. Trends in evapotranspiration and their responses to climate change and vegetation greening over the upper reaches of the Yellow River Basin. Agric. For. Meteorol. 2018, 263, 118–129. [Google Scholar] [CrossRef]
- Li, Y.; Yao, N.; Chau, H.W. Influences of removing linear and nonlinear trends from climatic variables on temporal variations of annual reference crop evapotranspiration in Xinjiang, China. Sci. Total Environ. 2017, 592, 680–692. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.; Gong, Y.; Zheng, W.; Zou, J.; Zhang, M.; Zhang, Z.; Qin, J.; Liu, J.; Quan, B. Spatial-temporal variations of terrestrial evapotranspiration across China from 2000 to 2019. Sci. Total Environ. 2022, 825, 153951. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; He, H.; Dong, K.; Li, X. Trends in reference evapotranspiration and their causative factors in the West Liao River basin, China. Agric. For. Meteorol. 2017, 232, 106–117. [Google Scholar] [CrossRef]
- Solaimani, S.; Bararkhanpour Ahmadi, S. Evaluation of TerraClimate gridded data in investigating the changes of reference evapotranspiration in different climates of Iran. J. Hydrol. Reg. Stud. 2024, 52, 101678. [Google Scholar] [CrossRef]
- Al-Hasani, A.A.J.; Shahid, S. Spatial distribution of the trends in potential evapotranspiration and its influencing climatic factors in Iraq. Theor. Appl. Climatol. 2022, 150, 677–696. [Google Scholar] [CrossRef]
- Xing, W.; Wang, W.; Shao, Q.; Yu, Z.; Yang, T.; Fu, J. Periodic fluctuation of reference evapotranspiration during the past five decades: Does evaporation paradox really exist in China. Sci. Rep. 2016, 6, 39503. [Google Scholar] [CrossRef] [PubMed]
- Masanta, S.K.; Vemavarapu, S.V. Regionalization of evapotranspiration using fuzzy dynamic clustering approach. Part 1: Formation of regions in India. Int. J. Climatol. 2020, 40, 3514–3530. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, Z.; Jiang, H.; Sun, S. Estimating daily reference evapotranspiration based on limited meteorological data using deep learning and classical machine learning methods. J. Hydrol. 2020, 591, 125286. [Google Scholar] [CrossRef]
- Di Nunno, F.; De Matteo, M.; Izzo, G.; Granata, F. Spatio-temporal analysis of reference evapotranspiration in Veneto: A combined clustering and trends analysis approach. Sustainability 2023, 15, 11091. [Google Scholar] [CrossRef]
- Parisse, B.; Alilla, R.; Pepe, A.G.; De Natale, F. MADIA-Meteorological variables for Agriculture: A Dataset for the Italian Area. Data Brief 2023, 46, 108843. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F. Spatio-temporal analysis of drought in Southern Italy: A combined clustering-forecasting approach based on SPEI index and Artificial Intelligence algorithms. Stoch. Environ. Res. Risk Assess. 2023, 37, 2349–2375. [Google Scholar] [CrossRef]
- Callahan, C.; Bridge, H. Data Mining of Rare Alleles to Assess Biogeographic Ancestry. In Proceedings of the Systems and Information Engineering Design Symposium (SIEDS), Charlottesville, VA, USA, 29–30 April 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Demsar, J.; Curk, T.; Erjavec, A.; Gorup, C.; Hocevar, T.; Milutinovic, M.; Mozina, M.; Polajnar, M.; Toplak, M.; Staric, A.; et al. Orange: Data Mining Toolbox in Python. J. Mach. Learn. Res. 2013, 14, 2349–2353. Available online: http://jmlr.org/papers/v14/demsar13a.html (accessed on 1 March 2024).
- Hirsch, R.M.; Slack, J.R. A Nonparametric Trend Test for Seasonal Data with Serial Dependence. Water Resour. Res. 1984, 20, 727–732. [Google Scholar] [CrossRef]
- Di Nunno, F.; de Marinis, G.; Granata, F. Analysis of SPI index trend variations in the United Kingdom -A cluster-based and bayesian ensemble algorithms approach. J. Hydrol. Reg. Stud. 2024, 52, 101717. [Google Scholar] [CrossRef]
- Shahfahad; Talukdar, S.; Ghose, B.; Islam, A.R.M.T.; Hasanuzzaman, M.; Ahmed, I.A.; Praveen, B.; Asif; Paarcha, A.; Rahman, A.; et al. Predicting long term regional drought pattern in Northeast India using advanced statistical technique and wavelet-machine learning approach. Model. Earth Syst. Environ. 2024, 10, 1005–1026. [Google Scholar] [CrossRef]
- Aschale, T.M.; Peres, D.J.; Palazzolo, N.; Sciuto, G.; Cancelliere, A. Run analysis of potential evapotranspiration and soil moisture for investigating flash droughts in Sicily. In Proceedings of the EGU23, the 25th EGU General Assembly, Vienna, Austria, 23–28 April 2023. EGU-13360. [Google Scholar] [CrossRef]
- Liuzzo, L.; Noto, L.V.; Arnone, E.; Caracciolo, D.; La Loggia, G. Modifications in Water Resources Availability Under Climate Changes: A Case Study in a Sicilian Basin. Water Resour. Manag. 2015, 29, 1117–1135. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S.; Aeini, A.; Talaee, P.H.; Mohammadi, K. Trend analysis of reference evapotranspiration in the western half of Iran. Agric. For. Meteorol. 2011, 151, 128–136. [Google Scholar] [CrossRef]
- Aschale, T.M.; Peres, D.J.; Gullotta, A.; Sciuto, G.; Cancelliere, A. Trend Analysis and Identification of the Meteorological Factors Influencing Reference Evapotranspiration. Water 2023, 15, 470. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F. Future trends of reference evapotranspiration in Sicily based on CORDEX data and Machine Learning algorithms. Agric. Water Manag. 2023, 280, 108232. [Google Scholar] [CrossRef]
- Singer, M.; Asfaw, D.; Rosolem, R.; Cuthbert, M.O.; Miralles, D.G.; Miguitama, E.Q.; MacLeod, D.; Michaelides, K. Hourly Potential Evapotranspiration (hPET) at 0.1degs Grid Resolution for the Global Land Surface from 1981-Present; University of Bristol: Bristol, UK, 2020. [Google Scholar] [CrossRef]



| Cluster | Mean Silhouette | Mean Longitude | Mean Latitude | Mean Altitude (m a.s.l.) |
|---|---|---|---|---|
| 1 | 0.684 | 12.542 | 41.750 | 102.472 |
| 2 | 0.653 | 12.563 | 42.188 | 350.401 |
| 3 | 0.679 | 13.286 | 42.071 | 691.120 |
| 4 | 0.682 | 13.386 | 42.273 | 1037.745 |
| Statistics | Cluster | Tmin | Tmax | Tmean | RHmin | RHmax | WS10 | Rs | P | ETo |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 1 | 13.37 | 18.87 | 16.12 | 0.62 | 0.88 | 3.23 | 15.84 | 79.45 | 86.85 |
| 2 | 9.43 | 18.87 | 14.15 | 0.55 | 0.91 | 2.05 | 15.40 | 86.16 | 81.06 | |
| 3 | 7.27 | 16.82 | 12.04 | 0.55 | 0.91 | 1.52 | 15.15 | 96.69 | 73.40 | |
| 4 | 5.55 | 14.40 | 9.97 | 0.56 | 0.92 | 1.48 | 15.04 | 90.81 | 68.29 | |
| Standard deviation | 1 | 5.42 | 5.77 | 5.59 | 0.04 | 0.03 | 0.56 | 7.07 | 64.35 | 44.35 |
| 2 | 5.87 | 7.18 | 6.51 | 0.10 | 0.03 | 0.29 | 6.98 | 57.83 | 49.57 | |
| 3 | 5.95 | 7.05 | 6.48 | 0.08 | 0.04 | 0.15 | 6.74 | 58.39 | 45.78 | |
| 4 | 6.11 | 7.19 | 6.63 | 0.08 | 0.04 | 0.19 | 6.63 | 49.02 | 43.90 | |
| CV | 1 | 0.41 | 0.31 | 0.35 | 0.07 | 0.03 | 0.17 | 0.45 | 0.81 | 0.51 |
| 2 | 0.62 | 0.38 | 0.46 | 0.17 | 0.04 | 0.14 | 0.45 | 0.67 | 0.61 | |
| 3 | 0.82 | 0.42 | 0.54 | 0.15 | 0.04 | 0.10 | 0.45 | 0.60 | 0.62 | |
| 4 | 1.10 | 0.50 | 0.66 | 0.15 | 0.04 | 0.13 | 0.44 | 0.54 | 0.64 |
| Seasonal MK | Cluster | Tmin | Tmax | Tmean | RHmin | RHmax | WS10 | Rs | P | ETo |
|---|---|---|---|---|---|---|---|---|---|---|
| Z | 1 | 9.47 | 9.04 | 9.65 | −5.04 | −8.91 | 0.56 | 4.44 | 0.21 | 9.47 |
| 2 | 9.84 | 8.96 | 9.84 | −6.38 | −13.11 | 0.81 | 3.87 | 0.50 | 9.52 | |
| 3 | 9.07 | 8.11 | 9.06 | −6.09 | −12.79 | 1.17 | 2.86 | 1.04 | 8.60 | |
| 4 | 9.03 | 7.02 | 8.35 | −5.17 | −11.18 | 1.08 | 2.75 | 1.54 | 7.98 | |
| β | 1 | 0.34 | 0.32 | 0.33 | −0.01 | −0.01 | 0.01 | 0.12 | 0.23 | 1.48 |
| 2 | 0.40 | 0.42 | 0.40 | −0.01 | −0.01 | 0.01 | 0.11 | 0.52 | 1.43 | |
| 3 | 0.40 | 0.39 | 0.39 | −0.01 | −0.01 | 0.01 | 0.09 | 1.53 | 0.94 | |
| 4 | 0.42 | 0.36 | 0.39 | −0.01 | −0.01 | 0.01 | 0.09 | 2.10 | 0.83 | |
| p-value | 1 | ≤0.01 | ≤0.01 | ≤0.01 | ≤0.01 | ≤0.01 | 0.57 | ≤0.01 | 0.83 | ≤0.01 |
| 2 | ≤0.01 | ≤0.01 | ≤0.01 | ≤0.01 | ≤ 0.01 | 0.42 | ≤0.01 | 0.62 | ≤0.01 | |
| 3 | ≤0.01 | ≤0.01 | ≤0.01 | ≤0.01 | ≤ 0.01 | 0.24 | ≤0.01 | 0.30 | ≤0.01 | |
| 4 | ≤0.01 | ≤0.01 | ≤0.01 | ≤0.01 | ≤ 0.01 | 0.28 | ≤0.01 | 0.12 | ≤0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Nunno, F.; Diodato, N.; Bellocchi, G.; Tricarico, C.; de Marinis, G.; Granata, F. Evapotranspiration Analysis in Central Italy: A Combined Trend and Clustering Approach. Climate 2024, 12, 64. https://doi.org/10.3390/cli12050064
Di Nunno F, Diodato N, Bellocchi G, Tricarico C, de Marinis G, Granata F. Evapotranspiration Analysis in Central Italy: A Combined Trend and Clustering Approach. Climate. 2024; 12(5):64. https://doi.org/10.3390/cli12050064
Chicago/Turabian StyleDi Nunno, Fabio, Nazzareno Diodato, Gianni Bellocchi, Carla Tricarico, Giovanni de Marinis, and Francesco Granata. 2024. "Evapotranspiration Analysis in Central Italy: A Combined Trend and Clustering Approach" Climate 12, no. 5: 64. https://doi.org/10.3390/cli12050064










