Climate Risks and Stock Market Volatility over a Century in an Emerging Market Economy: The Case of South Africa
Abstract
1. Introduction
2. Brief Discussion of Stock Return Volatility Literature of South Africa
3. Forecasting Models
3.1. Classical Models
3.2. NoVaS-Type Models
3.2.1. GARCH-NoVaS Model
3.2.2. GARCHX-NoVaS Model
4. Model Evaluation
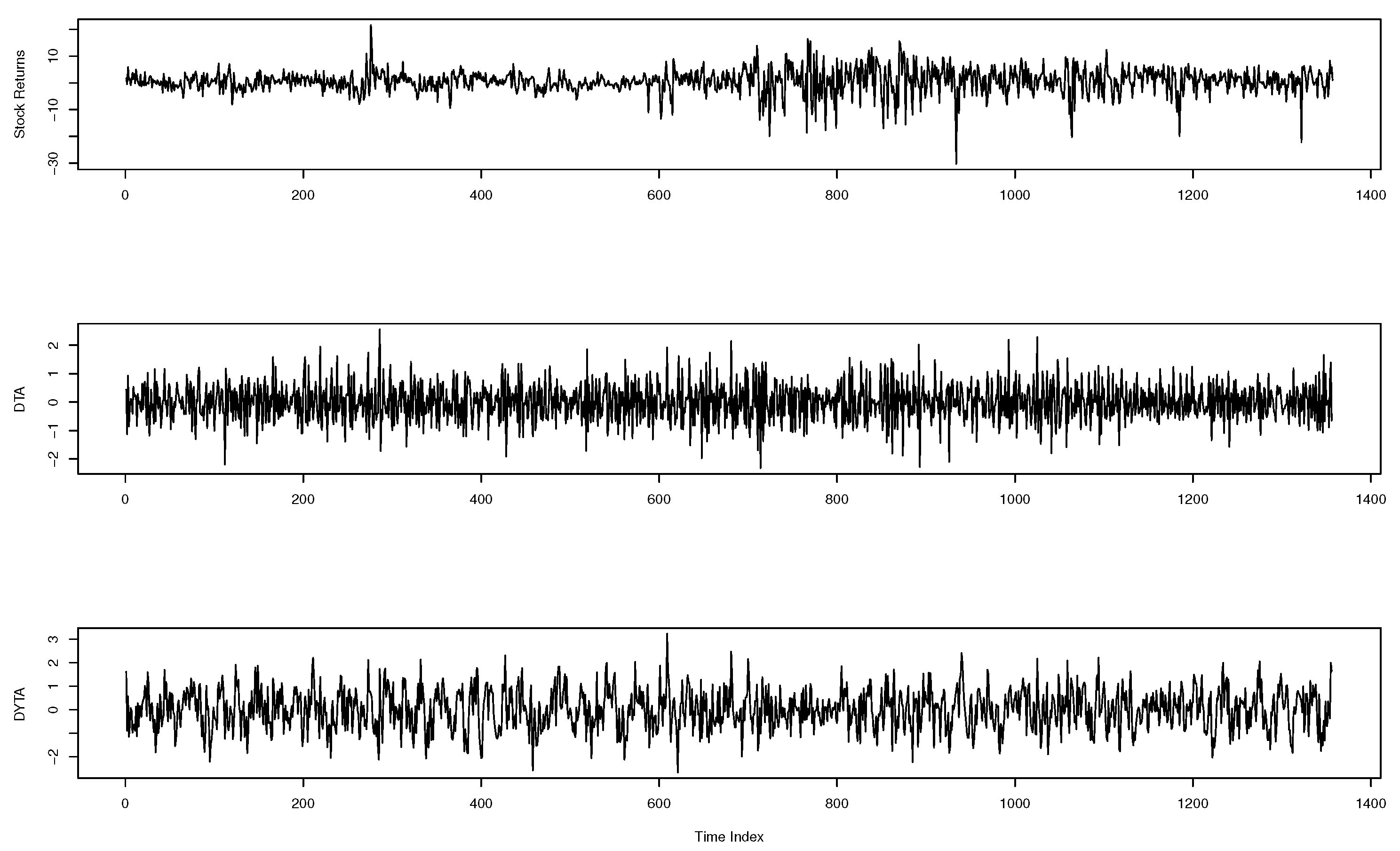
5. Data
6. Empirical Results
- Stage-1 model: we apply the GARCH and GARCH-NoVaS models to compute predictions. These two models are the benchmark for classical and model-free type methods.
- Stage-2 model: we add OR and GS to the model. This results in GARCHX and GARCHX-NoVaS models with two covariates.
- Stage-3 model: we take DTA or DYTA data into account based on Stage 2 models. Meanwhile, we keep including OR and GS as exogenous variables.
- Stage-4 model: we estimate the volatilities of DTA and DYTA by means of GARCH or NoVaS models and then use the estimates as additional covariates. In order to simplify notation, we denote the volatility of DTA/DYTA estimated by a GARCH model as DTAV1/DYTAV1, while we use DTAV2/DYTAV2 to denote the volatility of DTA/DYTA as estimated by means of a NoVaS model.
- The effects of OR and GS: the role of fundamentals- and sentiments-based information is revealed by the comparison of the Stage-1 and -2 models in Table 1. Taking the GARCH model as the benchmark, the Stage-2 GARCH model performs better when we use the SSPE statistic to evaluate 6- and 12-step-ahead predictions (moving window of size 500). The results of the CW test corroborate that the MSPE of the GARCH Stage-2 model is significantly smaller in a statistical sense than that of the benchmark model. However, for the moving window with 240 observations, the benchmark model beats the Stage-2 GARCH model. One reason may be that the sample size is not large enough to obtain a satisfactory estimation of the GARCHX model. However, OR and GS are also statistically beneficial to the predictions when we study the NoVaS method. Moreover, this improvement can also be observed for the 240-moving window.
- The effects of DTA/DYTA: the results that we report in Table 2 show that, for GARCH-type models, with a 500- or 240-moving window, the improvement in SSPE brought about by including DTA or DYTA in the models is negligible. Actually, the Stage-2 GARCH model outperforms the Stage-3 GARCH model, irrespective of whether we study DTA or DYTA, for 1-, 3-, and 6-step-ahead predictions. The corresponding CW tests are not significant. The NoVaS-type models, however, can utilize climate information to yield more accurate forecasts. For example, the GARCHX-NoVaS-3-DTA model is better than the corresponding Stage-2 NoVaS model when we use a 500-moving window. The corresponding CW test also implies that we can reject the null hypothesis. However, the gain in forecast accuracy is hardly visible for predictions based on a 240-moving window, but it is still statistically significant at a significance level of 0.05. According to our results, DTA is more useful when the moving window size is 500, and DYTA is more useful for a 240-moving window.
- The effects of volatilities of DTA/DYTA: according to Table 3, the volatility of DTA and DYTA is almost useless in improving the forecast accuracy of the GARCHX models, and almost all CW tests when applied to the corresponding Stage-3 and -4 models cannot reject the null hypothesis. Interestingly, the NoVaS-type models produce some forecasting benefits after including the volatility of DTA or DYTA, especially for long prediction horizons and a short moving window. For two types of volatility, DTAV1 and DYTAV2, the forecasts are slightly more accurate than their counterparts estimated by the NoVaS model.
- The effects of applying the model-free NoVaS prediction technique: it is evident from Table 1, Table 2 and Table 3 that the NoVaS-type models are much better than the corresponding GARCH models for all four stages, and, hence, our work adds to the general literature on stock return volatility forecasting in South Africa that has primarily relied on the GARCH framework. More importantly, when we add climate risks to the NoVaS model, we observe that forecasting performance improves. The classical GARCH model, however, fails to take advantage of the information embedded in these covariates. All in all, the combination of the temperate anomaly and its volatility captured by a GARCH model gives the best model (Stage-4 NoVaS) due to its large MSE accuracy and robustness. Our findings thus corroborate the importance of climate risks in driving historical second-moment movements of an emerging stock market, i.e., South Africa, just like what was detected for the US and other advanced economies by [14,64]. In the process, we confirm that the role of physical risks due to changes in the temperature anomaly and its volatility acting as proxies of rare disaster events can be associated with the theoretical idea of the predictive relationship between asset market volatility and disaster risks.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mehra, R.; Prescott, E.C. The equity premium: A puzzle. J. Monet. Econ. 1985, 15, 145–161. [Google Scholar] [CrossRef]
- Rietz, T.A. The equity risk premium a solution. J. Monet. Econ. 1988, 22, 117–131. [Google Scholar] [CrossRef]
- Barro, R.J. Rare disasters and asset markets in the twentieth century. Q. J. Econ. 2006, 121, 823–866. [Google Scholar] [CrossRef]
- Wachter, J.A. Can time-varying risk of rare disasters explain aggregate stock market volatility? J. Financ. 2013, 68, 987–1035. [Google Scholar] [CrossRef]
- Tsai, J.; Wachter, J.A. Disaster risk and its implications for asset pricing. Annu. Rev. Financ. Econ. 2015, 7, 219–252. [Google Scholar] [CrossRef]
- Sundaresan, S. Emergency Preparation and Uncertainty Persistence. Manag. Sci. 2023. [Google Scholar] [CrossRef]
- Shiller, R.J. Do stock prices move too much to be justified by subsequent changes in dividends? Am. Econ. Rev. 1981, 75, 421–436. [Google Scholar]
- Shiller, R.J. The use of volatility measures in assessing market efficiency. J. Financ. 1981, 36, 291–304. [Google Scholar]
- Bernanke, B.S. Nonmonetary effects of the financial crises in the propagation of the Great Depression. Am. Econ. Rev. 1983, 73, 257–276. [Google Scholar]
- Schwert, G.W. Why does stock market volatility change over time? J. Financ. 1989, 44, 1115–1153. [Google Scholar] [CrossRef]
- Balvers, R.; Du, D.; Zhao, X. Temperature shocks and the cost of equity capital: Implications for climate change perceptions. J. Bank. Financ. 2017, 77, 18–34. [Google Scholar] [CrossRef]
- Donadelli, M.; Jüppner, M.; Paradiso, A.; Ghisletti, M. Tornado activity, house prices, and stock returns. N. Am. J. Econ. Financ. 2020, 52, 101162. [Google Scholar] [CrossRef]
- Balcilar, M.; Gabauer, D.; Gupta, R.; Pierdzioch, C. Climate Risks and Forecasting Stock Market Returns in Advanced Economies over a Century. Mathematics 2023, 11, 2077. [Google Scholar] [CrossRef]
- Bonato, M.; Çepni, O.; Gupta, R.; Pierdzioch, C. Climate risks and state-level stock market realized volatility. Journal of Financial Markets 2023, 66, 100854. [Google Scholar] [CrossRef]
- Salisu, A.A.; Pierdzioch, C.; Gupta, R.; Van Eyden, R. Climate risks and US stock-market tail risks: A forecasting experiment using over a century of data. Int. Rev. Financ. 2023, 23, 228–244. [Google Scholar] [CrossRef]
- Giglio, S.; Kelly, B.; Stroebel, J. Climate finance. Annu. Rev. Financ. Econ. 2021, 13, 15–36. [Google Scholar] [CrossRef]
- Stroebel, J.; Wurgler, J. What do you think about climate finance? J. Financ. Econ. 2021, 142, 487–498. [Google Scholar] [CrossRef]
- van Benthem, A.A.; Crooks, E.; Giglio, S.; Schwob, E.; Stroebel, J. The effect of climate risks on the interactions between financial markets and energy companies. Nat. Energy 2022, 7, 690–697. [Google Scholar] [CrossRef]
- Ćorić, B. Economic disasters: A new data set. Financ. Res. Lett. 2021, 39, 101612. [Google Scholar] [CrossRef]
- Ćorić, B.; Šimić, V. Economic disasters and aggregate investment. Empir. Econ. 2021, 61, 3087–3124. [Google Scholar] [CrossRef]
- Bansal, R.; Kiku, D.; Ochoa, M. Price of Long-Run Temperature Shifts in Capital Markets; National Bureau of Economic Research: Cambridge, MA, USA, 2021. [Google Scholar]
- Bansal, R.; Ochoa, M.; Kiku, D. Climate change and growth risks. In Climate Change Economics: The Role of Uncertainty and Risk; The Role of Uncertainty and Risk in Climate Change, Economics; Chari, V.V., Litterman, R., Eds.; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Mensi, W.; Hammoudeh, S.; Reboredo, J.C.; Nguyen, D.K. Do global factors impact BRICS stock markets? A quantile regression approach. Emerg. Mark. Rev. 2014, 19, 1–17. [Google Scholar] [CrossRef]
- Mensi, W.; Hammoudeh, S.; Yoon, S.M.; Nguyen, D.K. Asymmetric linkages between BRICS stock returns and country risk ratings: Evidence from dynamic panel threshold models. Rev. Int. Econ. 2016, 24, 1–19. [Google Scholar] [CrossRef]
- Poon, S.H.; Granger, C.W.J. Forecasting volatility in financial markets: A review. J. Econ. Lit. 2003, 41, 478–539. [Google Scholar] [CrossRef]
- Rapach, D.E.; Strauss, J.K.; Wohar, M.E. Forecasting stock return volatility in the presence of structural breaks. In Forecasting in the Presence of Structural Breaks and Model Uncertainty; Emerald Group Publishing Limited: Leeds, UK, 2008. [Google Scholar]
- Donadelli, M.; Jüppner, M.; Riedel, M.; Schlag, C. Temperature shocks and welfare costs. J. Econ. Dyn. Control 2017, 82, 331–355. [Google Scholar] [CrossRef]
- Donadelli, M.; Grüning, P.; Jüppner, M.; Kizys, R. Global temperature, R&D expenditure, and growth. Energy Econ. 2021, 104, 105608. [Google Scholar]
- Donadelli, M.; Jüppner, M.; Paradiso, A.; Schlag, C. Computing macro-effects and welfare costs of temperature volatility: A structural approach. Comput. Econ. 2021, 58, 347–394. [Google Scholar] [CrossRef]
- Donadelli, M.; Jüppner, M.; Vergalli, S. Temperature variability and the macroeconomy: A world tour. Environ. Resour. Econ. 2022, 83, 221–259. [Google Scholar] [CrossRef]
- Sheng, X.; Gupta, R.; Cepni, O. Persistence of state-level uncertainty of the United States: The role of climate risks. Econ. Lett. 2022, 215, 110500. [Google Scholar] [CrossRef]
- Cepni, O.; Gupta, R.; Liao, W.; Ma, J. Climate risks and forecastability of the weekly state-level economic conditions of the United States. Int. Rev. Financ. 2024, 24, 154–162. [Google Scholar] [CrossRef]
- Salisu, A.A.; Gupta, R. Commodity prices and forecastability of international stock returns over a century: Sentiments versus fundamentals with focus on South Africa. Emerg. Mark. Financ. Trade 2022, 58, 2620–2636. [Google Scholar] [CrossRef]
- Degiannakis, S.; Filis, G.; Arora, V. Oil prices and stock markets: A review of the theory and empirical evidence. Energy J. 2018, 39, 85–130. [Google Scholar] [CrossRef]
- Smyth, R.; Narayan, P.K. What do we know about oil prices and stock returns? Int. Rev. Financ. Anal. 2018, 57, 148–156. [Google Scholar] [CrossRef]
- Salisu, A.A.; Pierdzioch, C.; Gupta, R.; Gabauer, D. Forecasting stock-market tail risk and connectedness in advanced economies over a century: The role of gold-to-silver and gold-to-platinum price ratios. Int. Rev. Financ. Anal. 2022, 83, 102300. [Google Scholar] [CrossRef]
- Huang, D.; Kilic, M. Gold, platinum, and expected stock returns. J. Financ. Econ. 2019, 132, 50–75. [Google Scholar] [CrossRef]
- Moolman, E.; Du Toit, C. An econometric model of the South African stock market: Economics. S. Afr. J. Econ. Manag. Sci. 2005, 8, 77–91. [Google Scholar] [CrossRef][Green Version]
- Mangani, R. Modelling return volatility on the JSE securities exchange of South Africa. Afr. Financ. J. 2008, 10, 55–71. [Google Scholar]
- Samouilhan, N.; Shannon, G. Forecasting volatility on the JSE. Investig. Anal. J. 2008, 37, 19–28. [Google Scholar] [CrossRef]
- Babikir, A.; Gupta, R.; Mwabutwa, C.; Owusu-Sekyere, E. Structural breaks and GARCH models of stock return volatility: The case of South Africa. Econ. Model. 2012, 29, 2435–2443. [Google Scholar] [CrossRef]
- Chinzara, Z. Macroeconomic uncertainty and conditional stock market volatility in South Africa. S. Afr. J. Econ. 2011, 79, 27–49. [Google Scholar] [CrossRef]
- Mandimika, N.Z.; Chinzara, Z. Risk–return trade-off and behaviour of volatility on the south african stock market: Evidence from both aggregate and disaggregate data. S. Afr. J. Econ. 2012, 80, 345–366. [Google Scholar] [CrossRef]
- Afuecheta, E.; Pérez Ruiz, D.A.; Utazi, C.; Nwosu, C. On the flexibility of GARCH-family models with an application to the BRICS stock indices. Commun. Stat. Case Stud. Data Anal. Appl. 2016, 2, 44–77. [Google Scholar] [CrossRef][Green Version]
- Sigauke, C. Volatility modeling of the JSE all share index and risk estimation using the Bayesian and frequentist approaches. Econ. Manag. Financ. Mark. 2016, 11, 33–48. [Google Scholar]
- Cakan, E.; Gupta, R. Does the US macroeconomic news make the South African stock market riskier? J. Dev. Areas 2017, 51, 15–27. [Google Scholar]
- Cheteni, P. Stock market volatility using GARCH models: Evidence from South Africa and China stock markets. J. Econ. Behav. Stud. 2017, 8, 237–245. [Google Scholar] [CrossRef] [PubMed]
- Naik, P.K.; Gupta, R.; Padhi, P. The relationship between stock market volatility and trading volume: Evidence from South Africa. J. Dev. Areas 2018, 52, 99–114. [Google Scholar] [CrossRef]
- Muzindutsi, P.F.; Obalade, A.A.; Gaston, R.T. Financial crisis and stock return volatility of the JSE general mining index: GARCH modelling approach. J. Account. Manag. 2020, 10, 115–124. [Google Scholar]
- Dwarika, N.; Moores-Pitt, P.; Chifurira, R. Volatility dynamics and the risk-return relationship in South Africa: A GARCH approach. Investig. Manag. Financ. Innov. 2021, 18, 106–117. [Google Scholar] [CrossRef]
- Kaseke, F.; Ramroop, S.; Mwambi, H. A comparative analysis of the volatility nature of cryptocurrency and JSE market. Investig. Manag. Financ. Innov. 2022, 19, 23–39. [Google Scholar] [CrossRef]
- Gupta, R.; Nel, J.; Pierdzioch, C. Drivers of Realized Volatility for Emerging Countries with a Focus on South Africa: Fundamentals versus Sentiment. Mathematics 2023, 11, 1371. [Google Scholar] [CrossRef]
- Ben Nasr, A.; Boutahar, M.; Trabelsi, A. Fractionally integrated time varying GARCH model. Stat. Methods Appl. 2010, 19, 399–430. [Google Scholar] [CrossRef]
- Ben Nasr, A.; Ajmi, A.N.; Gupta, R. Modelling the volatility of the Dow Jones Islamic Market World Index using a fractionally integrated time-varying GARCH (FITVGARCH) model. Appl. Financ. Econ. 2014, 24, 993–1004. [Google Scholar] [CrossRef][Green Version]
- Bhowmik, R.; Wang, S. Stock market volatility and return analysis: A systematic literature review. Entropy 2020, 22, 522. [Google Scholar] [CrossRef]
- Muguto, L.; Muzindutsi, P.F. A comparative analysis of the nature of stock return volatility in BRICS and G7 markets. J. Risk Financ. Manag. 2022, 15, 85. [Google Scholar] [CrossRef]
- Segnon, M.; Gupta, R.; Wilfling, B. Forecasting stock market volatility with regime-switching GARCH-MIDAS: The role of geopolitical risks. Int. J. Forecast. 2023, 40, 29–43. [Google Scholar] [CrossRef]
- Bouri, E.; Gupta, R.; Pierdzioch, C.; Salisu, A.A. El Niño and forecastability of oil-price realized volatility. Theor. Appl. Climatol. 2021, 144, 1173–1180. [Google Scholar] [CrossRef]
- Demirer, R.; Gupta, R.; Nel, J.; Pierdzioch, C. Effect of rare disaster risks on crude oil: Evidence from El Niño from over 145 years of data. Theor. Appl. Climatol. 2022, 147, 691–699. [Google Scholar] [CrossRef]
- Gupta, R.; Pierdzioch, C. Climate risks and forecastability of the realized volatility of gold and other metal prices. Resour. Policy 2022, 77, 102681. [Google Scholar] [CrossRef]
- Bonato, M.; Çepni, O.; Gupta, R.; Pierdzioch, C. El Niño, La Niña, and forecastability of the realized variance of agricultural commodity prices: Evidence from a machine learning approach. J. Forecast. 2023, 42, 785–801. [Google Scholar] [CrossRef]
- Gupta, R.; Pierdzioch, C. Climate Risk and the Volatility of Agricultural Commodity Price Fluctuations: A Forecasting Experiment. In Behavioral Finance and Asset Prices: The Influence of Investor’s Emotions; Bourghelle, D., Grandin, P., Jawadi, F., Rozin, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2023; Chapter 2. [Google Scholar]
- Nel, J.; Gupta, R.; Wohar, M.E.; Pierdzioch, C. Climate Risks and Predictability of Commodity Returns and Volatility: Evidence from over 750 Years of Data. Forthcoming in Climate Change Economics. Available online: https://www.up.ac.za/media/shared/61/WP/wp_2022_42.zp224084.pdf (accessed on 15 January 2024).
- Del Fava, S.; Gupta, R.; Pierdzioch, C.; Rognone, L. Forecasting international financial stress: The role of climate risks. J. Int. Financ. Mark. Inst. Money 2024, 92, 101975. [Google Scholar] [CrossRef]
- Politis, D.N. A normalizing and variance-stabilizing transformation for financial time series. In Recent Advances and Trends in Nonparametric Statistics; Elsevier Inc.: Amsterdam, The Netherlands, 2003; pp. 335–347. [Google Scholar]
- Gulay, E.; Emec, H. Comparison of forecasting performances: Does normalization and variance stabilization method beat GARCH (1, 1)-type models? Empirical Evidence from the Stock Markets. J. Forecast. 2018, 37, 133–150. [Google Scholar] [CrossRef]
- Wu, K.; Karmakar, S. Model-free time-aggregated predictions for econometric datasets. Forecasting 2021, 3, 920–933. [Google Scholar] [CrossRef]
- Wu, K.; Karmakar, S. A model-free approach to do long-term volatility forecasting and its variants. Financ. Innov. 2023, 9, 1–38. [Google Scholar] [CrossRef]
- Wu, K.; Karmakar, S. GARHCX-NoVaS: A Model-free Approach to Incorporate Exogenous Variables. arXiv 2023, arXiv:2308.13346. [Google Scholar]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Francq, C.; Thieu, L.Q. QML inference for volatility models with covariates. Econom. Theory 2019, 35, 37–72. [Google Scholar] [CrossRef]
- Wuertz, D.; RUnit, S.; Chalabi, M.Y. Package ‘fGarch’; Technical Report, working Paper/Manual, 09.11. 2013. Available online: https://CRAN.R-project.org/package=fGarch (accessed on 15 January 2024).
- Sucarrat, G. garchx: Flexible and robust garch-x modelling. R J. 2021, 13, 267–291. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Clark, T.E.; West, K.D. Approximately normal tests for equal predictive accuracy in nested models. J. Econom. 2007, 138, 291–311. [Google Scholar] [CrossRef]
- Chudý, M.; Karmakar, S.; Wu, W.B. Long-term prediction intervals of economic time series. Empir. Econ. 2020, 58, 191–222. [Google Scholar] [CrossRef]
- Karmakar, S.; Chudý, M.; Wu, W.B. Long-term prediction intervals with many covariates. J. Time Ser. Anal. 2022, 43, 587–609. [Google Scholar] [CrossRef]
- McLeod, A.I.; Li, W.K. Diagnostic checking ARMA time series models using squared-residual autocorrelations. J. Time Ser. Anal. 1983, 4, 269–273. [Google Scholar] [CrossRef]
- Chan, K.S.; Ripley, B.; Chan, M.K.S.; Chan, S. Package ‘TSA’, R Package Version 1.31. 2022. Available online: https://CRAN.R-project.org/package=TSA (accessed on 15 January 2024).
- Bonato, M.; Çepni, O.; Gupta, R.; Pierdzioch, C. Climate risks and realized volatility of major commodity currency exchange rates. J. Financ. Mark. 2023, 62, 100760. [Google Scholar] [CrossRef]
| Ratio of Squared Errors | p-Value of CW-Test | |||||||
|---|---|---|---|---|---|---|---|---|
| Prediction Step | 1 | 3 | 6 | 12 | 1 | 3 | 6 | 12 |
| Moving window size 500: | ||||||||
| GARCH (Benchmark) | 1.000 | 1.000 | 1.000 | 1.000 | ||||
| GARCH-NoVaS | 0.998 | 0.957 | 0.883 | 0.746 | ||||
| GARCHX-2 | 1.000 | 1.004 | 0.998 | 0.987 | 0.087 | 0.036 | 0.014 | 0.003 |
| GARCHX-NoVaS-2 | 0.995 | 0.959 | 0.881 | 0.732 | 0.061 | 0.032 | 0.000 | 0.000 |
| Moving window size 240: | ||||||||
| GARCH (Benchmark) | 1.000 | 1.000 | 1.000 | 1.000 | ||||
| GARCH-NoVaS | 1.070 | 1.025 | 0.908 | 0.684 | ||||
| GARCHX-2 | 1.023 | 1.060 | 1.092 | 1.059 | 0.449 | 0.401 | 0.349 | 0.030 |
| GARCHX-NoVaS-2 | 0.990 | 0.934 | 0.842 | 0.644 | 0.041 | 0.000 | 0.000 | 0.000 |
| Ratio of Squared Errors | p-Value of CW-Test | |||||||
|---|---|---|---|---|---|---|---|---|
| Prediction Step | 1 | 3 | 6 | 12 | 1 | 3 | 6 | 12 |
| Moving window size 500: | ||||||||
| GARCHX-2 (Benchmark) | 1.000 | 1.000 | 1.000 | 1.000 | ||||
| GARCHX-NoVaS-2 | 0.994 | 0.956 | 0.882 | 0.742 | ||||
| GARCHX-3-DTA | 1.000 | 1.000 | 1.005 | 0.996 | 0.386 | 0.309 | 0.986 | 0.102 |
| GARCHX-NoVaS-3-DTA | 1.004 | 0.947 | 0.878 | 0.732 | 0.894 | 0.001 | 0.013 | 0.000 |
| GARCHX-3-DYTA | 1.000 | 1.001 | 1.003 | 1.004 | 0.940 | 0.917 | 0.943 | 0.806 |
| GARCHX-NoVaS-3-DYTA | 0.997 | 0.955 | 0.882 | 0.734 | 0.525 | 0.143 | 0.187 | 0.001 |
| Moving window size 240: | ||||||||
| GARCHX-2 (Benchmark) | 1.000 | 1.000 | 1.000 | 1.000 | ||||
| GARCHX-NoVaS-2 | 0.967 | 0.882 | 0.771 | 0.608 | ||||
| GARCHX-3-DTA | 1.002 | 1.003 | 1.006 | 0.996 | 0.837 | 0.787 | 0.929 | 0.154 |
| GARCHX-NoVaS-3-DTA | 0.968 | 0.887 | 0.772 | 0.602 | 0.234 | 0.473 | 0.240 | 0.042 |
| GARCHX-3-DYTA | 1.004 | 1.009 | 1.009 | 1.010 | 0.994 | 0.998 | 0.976 | 0.847 |
| GARCHX-NoVaS-3-DYTA | 0.963 | 0.888 | 0.770 | 0.601 | 0.070 | 0.723 | 0.192 | 0.023 |
| Ratio of Squared Errors | p-Value of CW-Test | |||||||
|---|---|---|---|---|---|---|---|---|
| Prediction Step | 1 | 3 | 6 | 12 | 1 | 3 | 6 | 12 |
| Moving window size 500: | ||||||||
| GARCHX-3-DTA (Benchmark) | 1.000 | 1.000 | 1.000 | 1.000 | ||||
| GARCHX-NoVaS-3-DTA | 1.004 | 0.948 | 0.874 | 0.734 | ||||
| GARCHX-4-DTAV1 | 1.001 | 1.000 | 0.995 | 0.992 | 0.576 | 0.298 | 0.037 | 0.014 |
| GARCHX-NoVaS-4-DTAV1 | 1.001 | 0.960 | 0.881 | 0.749 | 0.156 | 0.991 | 0.721 | 0.960 |
| GARCHX-4-DTAV2 | 1.000 | 0.999 | 0.993 | 0.990 | 0.419 | 0.103 | 0.001 | 0.002 |
| GARCHX-NoVaS-4-DTAV2 | 0.999 | 0.962 | 0.876 | 0.743 | 0.081 | 0.993 | 0.404 | 0.808 |
| GARCHX-3-DYTA (Benchmark) | 1.000 | 1.000 | 1.000 | 1.000 | ||||
| GARCHX-NoVaS-3-DYTA | 0.997 | 0.953 | 0.879 | 0.731 | ||||
| GARCHX-4-DYTAV1 | 1.000 | 1.000 | 0.998 | 0.999 | 0.974 | 0.371 | 0.144 | 0.357 |
| GARCHX-NoVaS-4-DYTAV1 | 1.005 | 0.957 | 0.885 | 0.740 | 0.961 | 0.647 | 0.797 | 0.801 |
| GARCHX-4-DYTAV2 | 1.000 | 0.999 | 1.002 | 0.997 | 0.891 | 0.205 | 0.823 | 0.133 |
| GARCHX-NoVaS-4-DYTAV2 | 1.003 | 0.957 | 0.887 | 0.740 | 0.926 | 0.581 | 0.882 | 0.808 |
| Moving window size 240: | ||||||||
| GARCHX-3-DTA (Benchmark) | 1.000 | 1.000 | 1.000 | 1.000 | ||||
| GARCHX-NoVaS-3-DTA | 0.966 | 0.884 | 0.766 | 0.603 | ||||
| GARCHX-4-DTAV1 | 1.003 | 1.003 | 0.999 | 1.015 | 0.789 | 0.811 | 0.269 | 0.923 |
| GARCHX-NoVaS-4-DTAV1 | 0.973 | 0.880 | 0.756 | 0.585 | 0.762 | 0.091 | 0.008 | 0.005 |
| GARCHX-4-DTAV2 | 1.001 | 1.000 | 1.001 | 1.003 | 0.700 | 0.481 | 0.477 | 0.516 |
| GARCHX-NoVaS-4-DTAV2 | 0.977 | 0.882 | 0.761 | 0.585 | 0.941 | 0.176 | 0.066 | 0.008 |
| GARCHX-3-DYTA (Benchmark) | 1.000 | 1.000 | 1.000 | 1.000 | ||||
| GARCHX-NoVaS-3-DYTA | 0.960 | 0.880 | 0.763 | 0.593 | ||||
| GARCHX-4-DYTAV1 | 1.000 | 1.001 | 0.997 | 0.994 | 0.879 | 0.691 | 0.069 | 0.184 |
| GARCHX-NoVaS-4-DYTAV1 | 0.965 | 0.867 | 0.752 | 0.562 | 0.777 | 0.002 | 0.053 | 0.001 |
| GARCHX-4-DYTAV2 | 1.001 | 1.001 | 1.004 | 1.005 | 0.945 | 0.864 | 0.861 | 0.640 |
| GARCHX-NoVaS-4-DYTAV2 | 0.967 | 0.872 | 0.752 | 0.580 | 0.853 | 0.012 | 0.026 | 0.020 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, K.; Karmakar, S.; Gupta, R.; Pierdzioch, C. Climate Risks and Stock Market Volatility over a Century in an Emerging Market Economy: The Case of South Africa. Climate 2024, 12, 68. https://doi.org/10.3390/cli12050068
Wu K, Karmakar S, Gupta R, Pierdzioch C. Climate Risks and Stock Market Volatility over a Century in an Emerging Market Economy: The Case of South Africa. Climate. 2024; 12(5):68. https://doi.org/10.3390/cli12050068
Chicago/Turabian StyleWu, Kejin, Sayar Karmakar, Rangan Gupta, and Christian Pierdzioch. 2024. "Climate Risks and Stock Market Volatility over a Century in an Emerging Market Economy: The Case of South Africa" Climate 12, no. 5: 68. https://doi.org/10.3390/cli12050068
APA StyleWu, K., Karmakar, S., Gupta, R., & Pierdzioch, C. (2024). Climate Risks and Stock Market Volatility over a Century in an Emerging Market Economy: The Case of South Africa. Climate, 12(5), 68. https://doi.org/10.3390/cli12050068







