Characteristics of Vortices around Forward Swept Wing at Low Speeds/High Angles of Attack
Abstract
:1. Introduction
- In the first section, we provide an introduction.
- The second section introduces the wing model used in this study.
- The third section outlines the methodologies employed, including computational fluid dynamics, computational mesh generation, and computational conditions.
- In the fourth section, we present and discuss the numerical results, including flowfield visualizations.
- The theoretical hypothesis is then discussed based on the numerical results.
- Finally, the fifth section presents the conclusions of this study.
2. Wing Models
3. Numerical Simulation
3.1. Computational Fluid Dynamics
3.2. Computational Conditions
4. Results
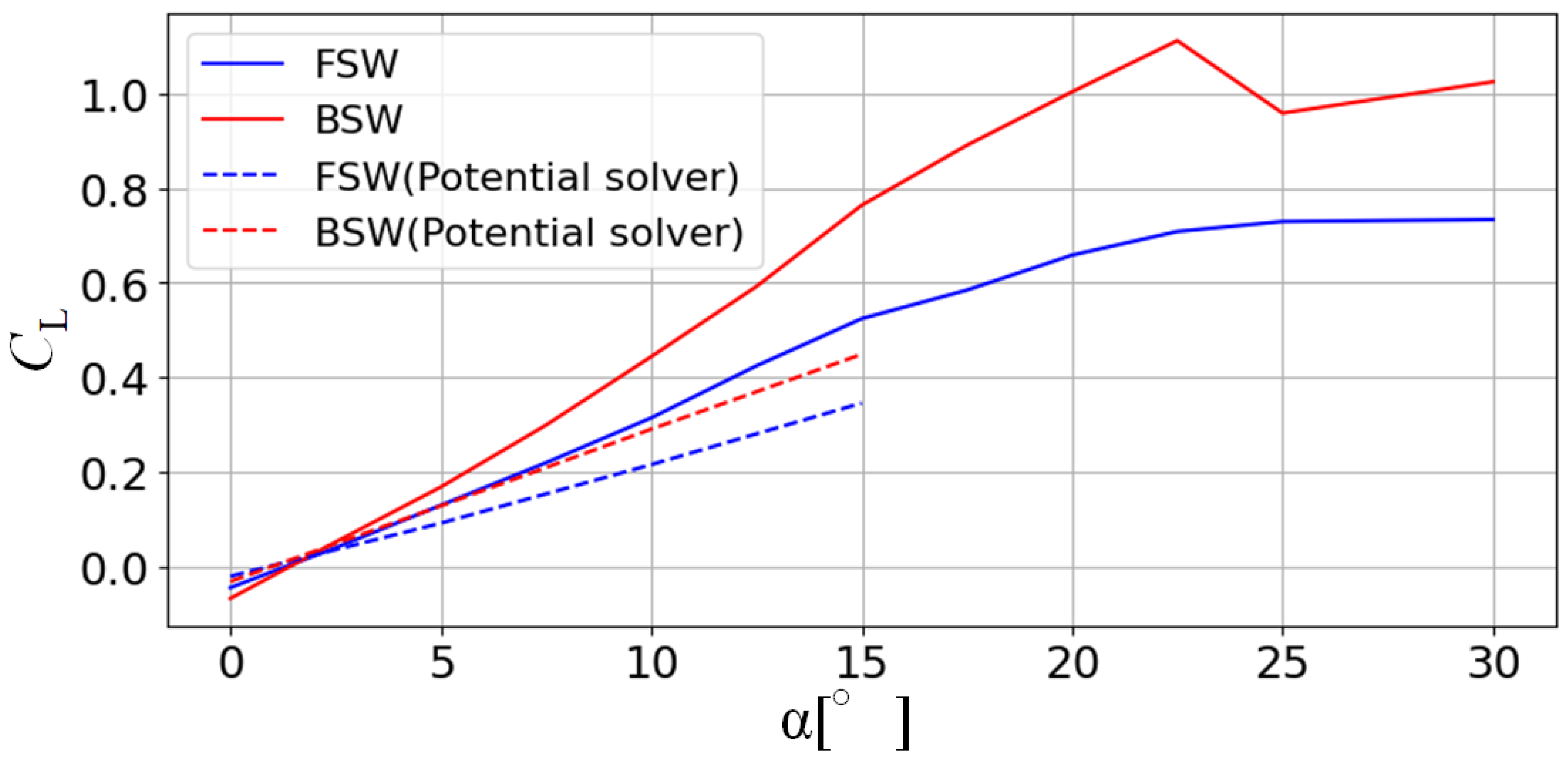
4.1. Comparisons of Lift Characteristics
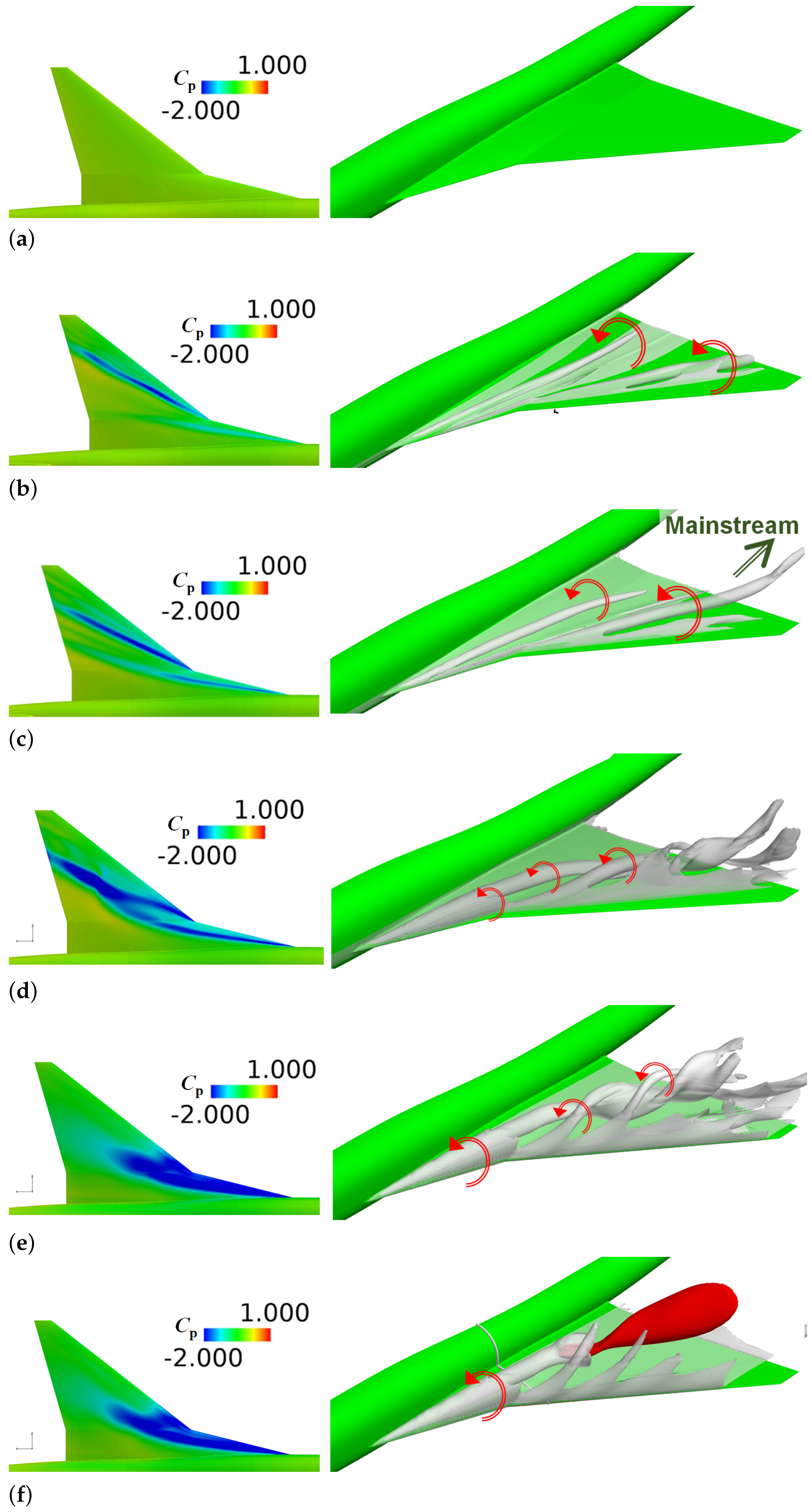
4.2. Comparisons of Separation Vortex Behavior
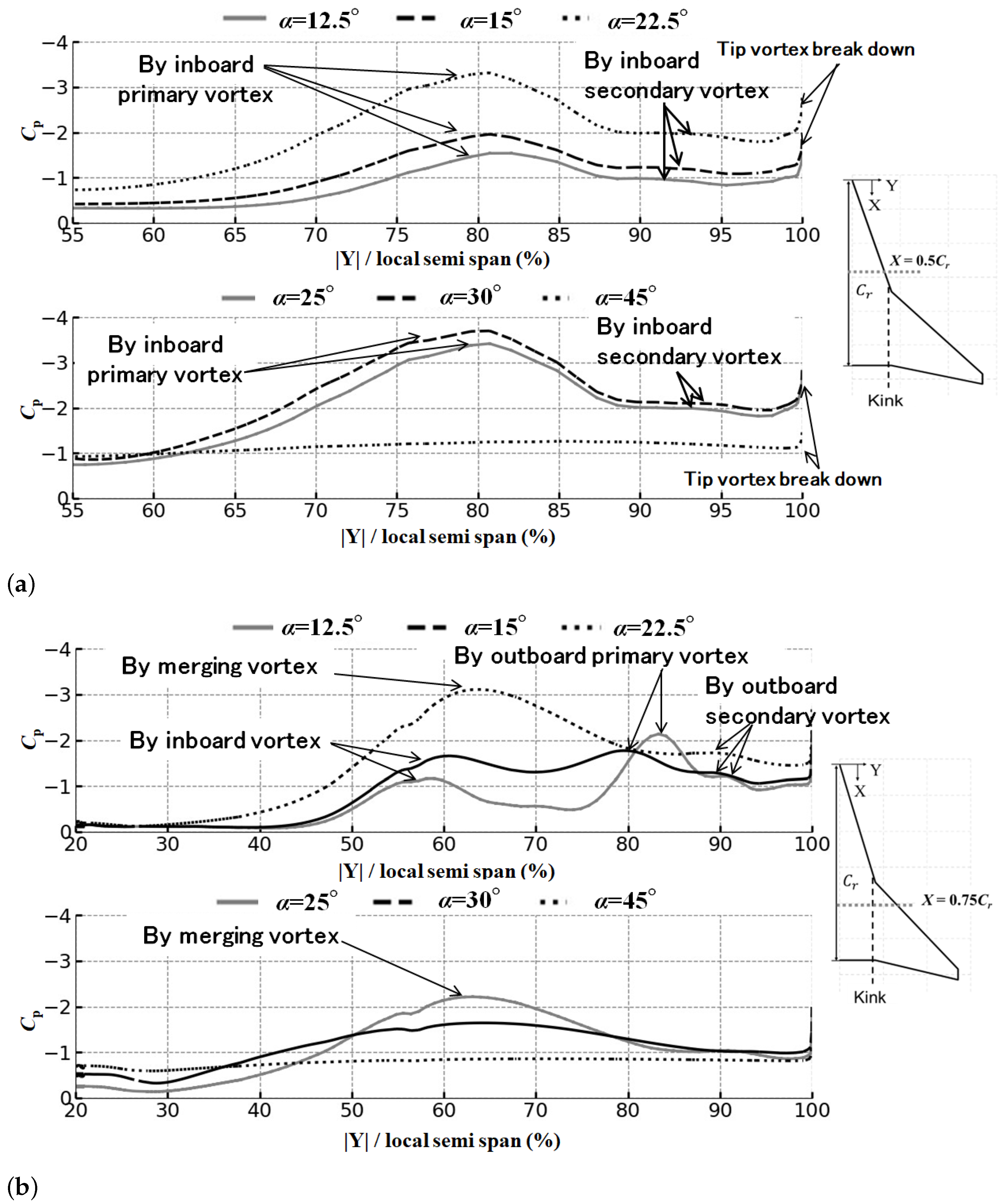
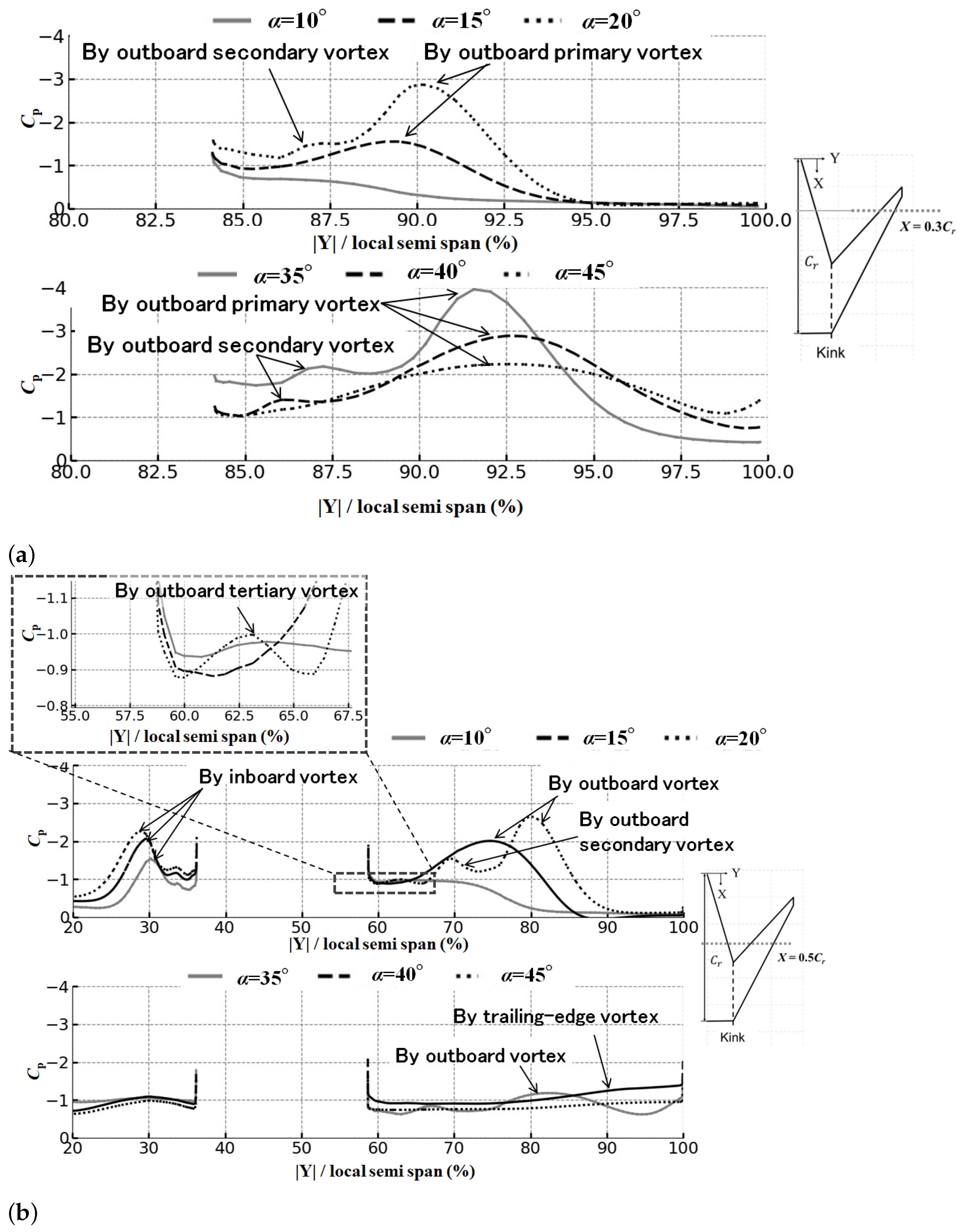
4.3. Observation of Span-Wise Surface Pressure
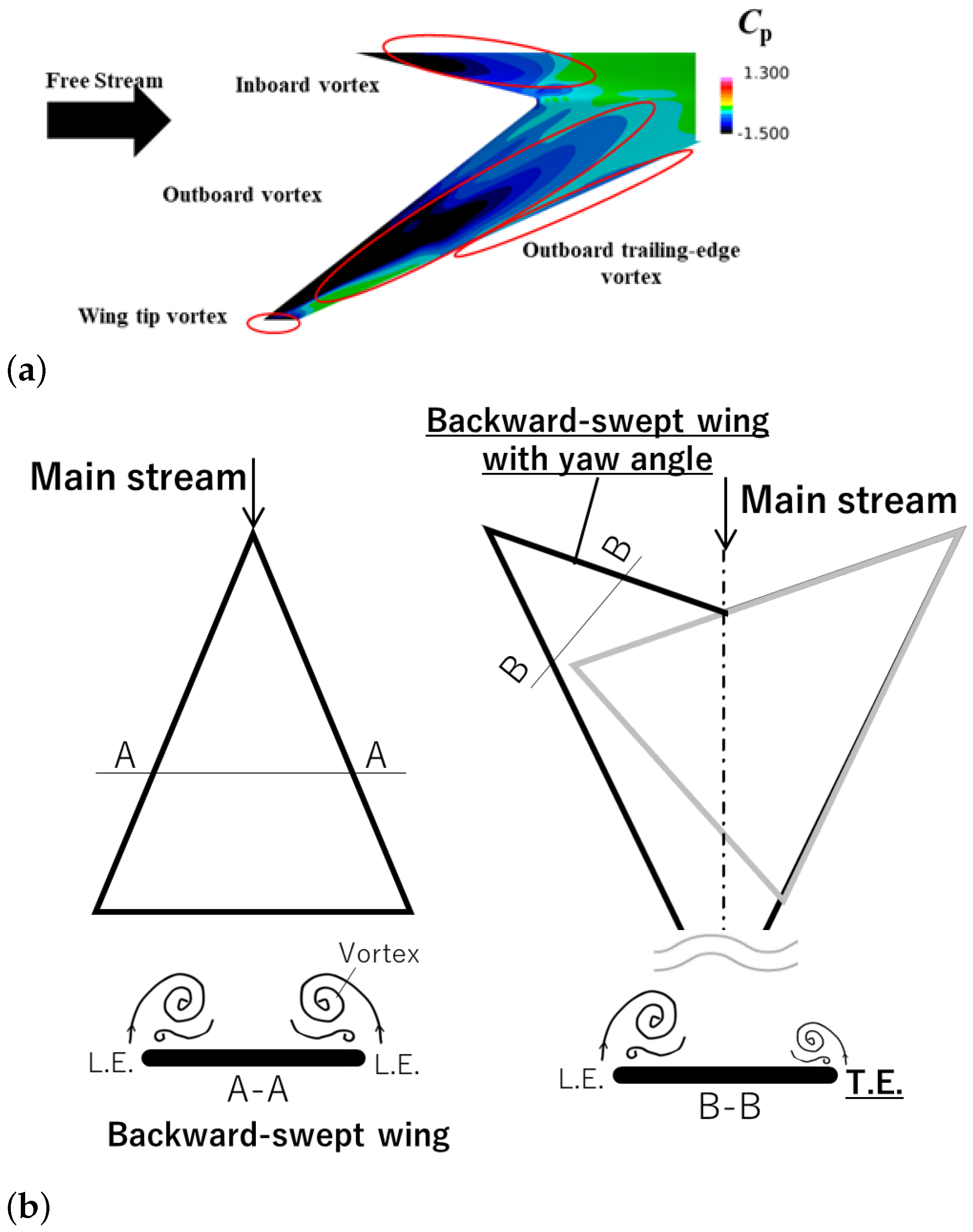
4.4. Hypothesis of Trailing-Edge Vortex in FSW
- A forward-swept wing can be regarded as a delta wing with a yaw angle of incidence, resulting in a flow structure where the leading-edge separation vortices on both sides are biased.
- The leading edge of this delta wing with a yaw angle generates the leading edge vortex similar to a normal backward-swept wing. However, a lateral vortex emerges from the leading edge on the trailing side of the main flow, corresponding to the trailing edge of the forward-swept wing, known as the trailing edge vortex.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
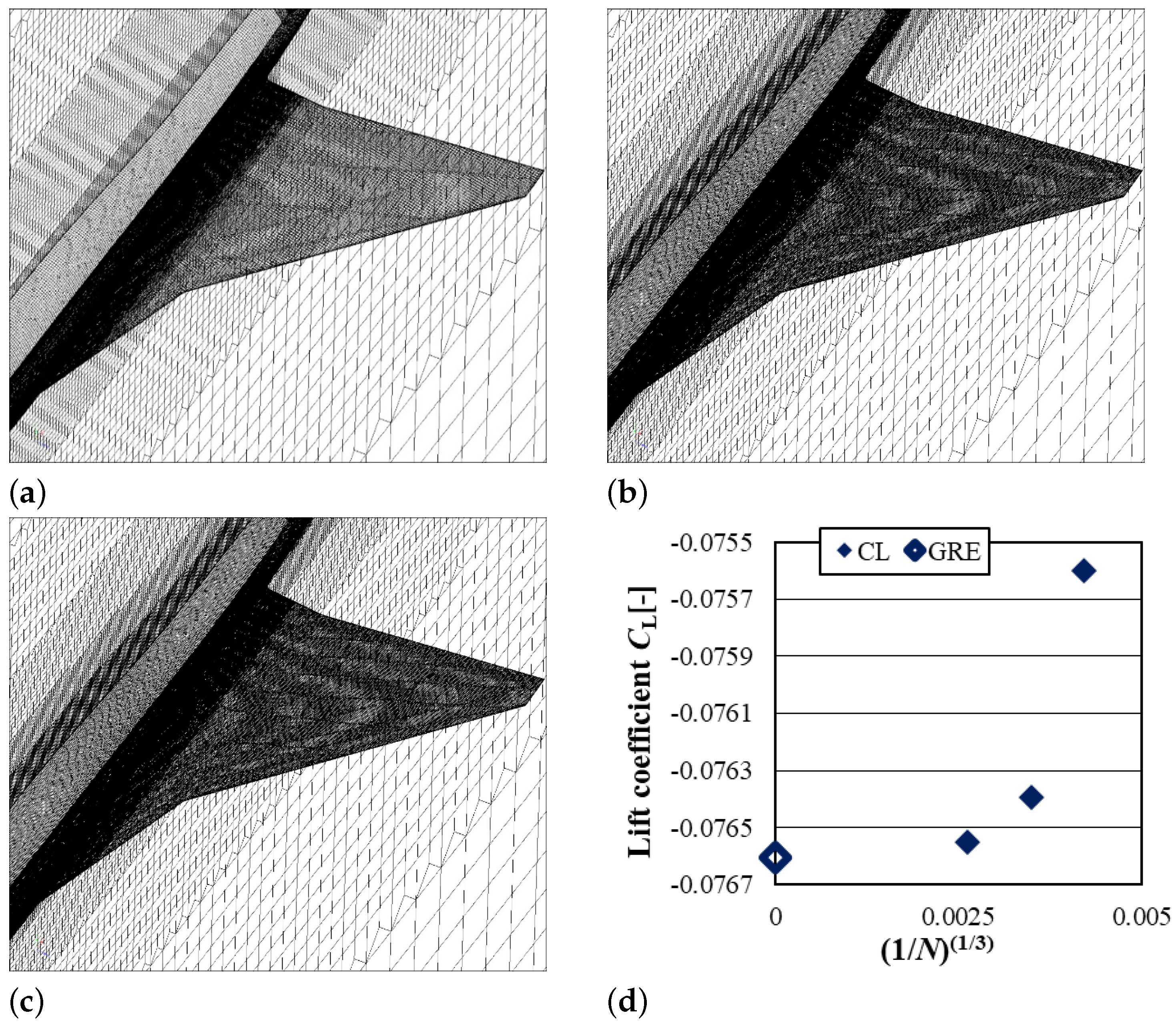
Appendix A. Grid Dependency Study
References
- Kishi, Y.; Kanazaki, M.; Makino, Y. Supersonic Forward-Swept Wing Design Using Multifidelity Efficient Global Optimization. J. Aircr. 2022, 59, 1027–1040. [Google Scholar]
- Rongrong, X.; Zhengyin, Y.; Kun, Y.; Gang, W. Composite material structure optimization design and aeroelastic analysis on forward swept wing. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2019, 233, 4679–4695. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Yu, S.C.M.; Chien, A.; Yang, S.X. Aerodynamic Characteristics of Canard-Forward Swept Wing Aircraft Configurations. J. Aircr. 2013, 50, 378–387. [Google Scholar] [CrossRef]
- Razak, K.; Snyder, M., Jr. A Review of the Planform Effects on the Low-Speed Aerodynamic Characteristics of Triangular and Modified Triangular Wings; NASA–CR–421; NASA: Washington, DC, USA, 1966. [Google Scholar]
- Saltzman, E.J.; Hicks, J.W.; Luke, S. In-Flight Lift-Drag Characteristics for a Forward-Swept Wing Aircraft and Comparisons with Contemporary Aircraft; NASA–TP–3414; NASA: Washington, DC, USA, 1994. [Google Scholar]
- Horinouchi, S. Conceptual design of a low boom SSBJ. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. AIAA 2005-1018. [Google Scholar]
- Shima, E.; Kitamura, K. Parameter-free simple low-dissipation AUSM-family scheme for all speeds. AIAA J. 2011, 49, 1693–1709. [Google Scholar] [CrossRef]
- Burg, C. Higher order variable extrapolation for unstructured finite volume RANS flow solvers. In Proceedings of the 17th AIAA Computational Fluid Dynamics Conference, Toronto, ON, Canada, 6–9 June 2005. AIAA 2005-4999. [Google Scholar]
- Sharov, D.; Nakahashi, K. Reordering of hybrid unstructured grids for lower-upper symmetric Gauss–Seidel computations. AIAA J. 1998, 36, 484–486. [Google Scholar] [CrossRef]
- Dacles-Mariani, J.; Zilliac, G.G.; Chow, J.S.; Bradshaw, P. Numerical/experimental study of a wingtip vortex in the near field. AIAA J. 1995, 33, 1561–1568. [Google Scholar] [CrossRef]
- Hashimoto, A.; Murakami, K.; Aoyama, T.; Ishiko, K.; Hishida, M.; Sakashita, M.; Lahur, P. Toward the fastest unstructured CFD code’FaSTAR’. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. AIAA 2012-1075. [Google Scholar]
- Richardson, L.F. IX. The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam. Philos. Trans. R. Soc. Math. Phys. Character 1911, 210, 307–357. [Google Scholar]
- Hashimoto, A.; Murakami, K.; Aoyama, T.; Yamamoto, K.; Murayama, M.; Lahur, P.R. Drag prediction on NASA common research model using automatic hexahedra grid-generation method. J. Aircr. 2014, 51, 1172–1182. [Google Scholar] [CrossRef]
- Cenko, A.; Tinoco, E.; Dyer, R.; DeJongh, J. PAN AIR applications to weapons carriage and separation. J. Aircr. 1981, 18, 128–134. [Google Scholar] [CrossRef]
- Lei, Z. Flow simulation of an supersonic transport configuration at low-speed and high-lift conditions. J. Aircr. 2008, 45, 1514–1521. [Google Scholar] [CrossRef]
- Mitchell, A.M.; Morton, S.A.; Forsythe, J.R.; Cummings, R.M. Analysis of delta-wing vortical substructures using detached-eddy simulation. AIAA J. 2006, 44, 964–972. [Google Scholar] [CrossRef]
- Kwak, D.; Shirotake, M.; Rinoie, K. Vortex Behaviors over a Cranked Arrow Wing Configuration at High Angles of Attack. In Proceedings of the 24th International Congress of the Aeronautical Sciences, Yokohama, Japan, 29 August–3 September 2004. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanazaki, M.; Setoguchi, N. Characteristics of Vortices around Forward Swept Wing at Low Speeds/High Angles of Attack. Aerospace 2023, 10, 790. https://doi.org/10.3390/aerospace10090790
Kanazaki M, Setoguchi N. Characteristics of Vortices around Forward Swept Wing at Low Speeds/High Angles of Attack. Aerospace. 2023; 10(9):790. https://doi.org/10.3390/aerospace10090790
Chicago/Turabian StyleKanazaki, Masahiro, and Nao Setoguchi. 2023. "Characteristics of Vortices around Forward Swept Wing at Low Speeds/High Angles of Attack" Aerospace 10, no. 9: 790. https://doi.org/10.3390/aerospace10090790
APA StyleKanazaki, M., & Setoguchi, N. (2023). Characteristics of Vortices around Forward Swept Wing at Low Speeds/High Angles of Attack. Aerospace, 10(9), 790. https://doi.org/10.3390/aerospace10090790






