Analysis and Design of Bat-Like Flapping-Wing Aircraft
Abstract
:1. Introduction
2. Aerodynamic Modeling and Analysis of Bat-Like Flapping Aircraft
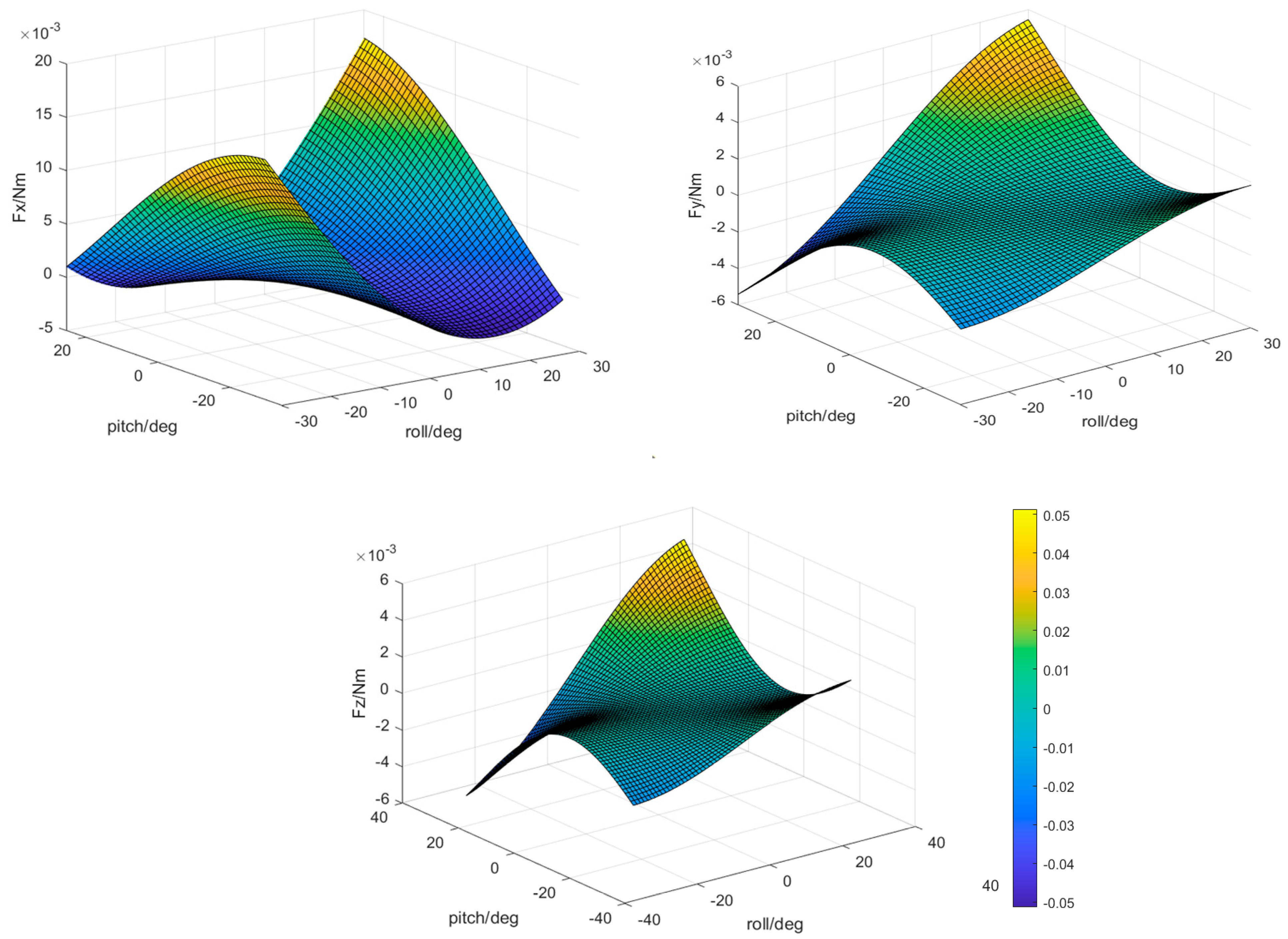
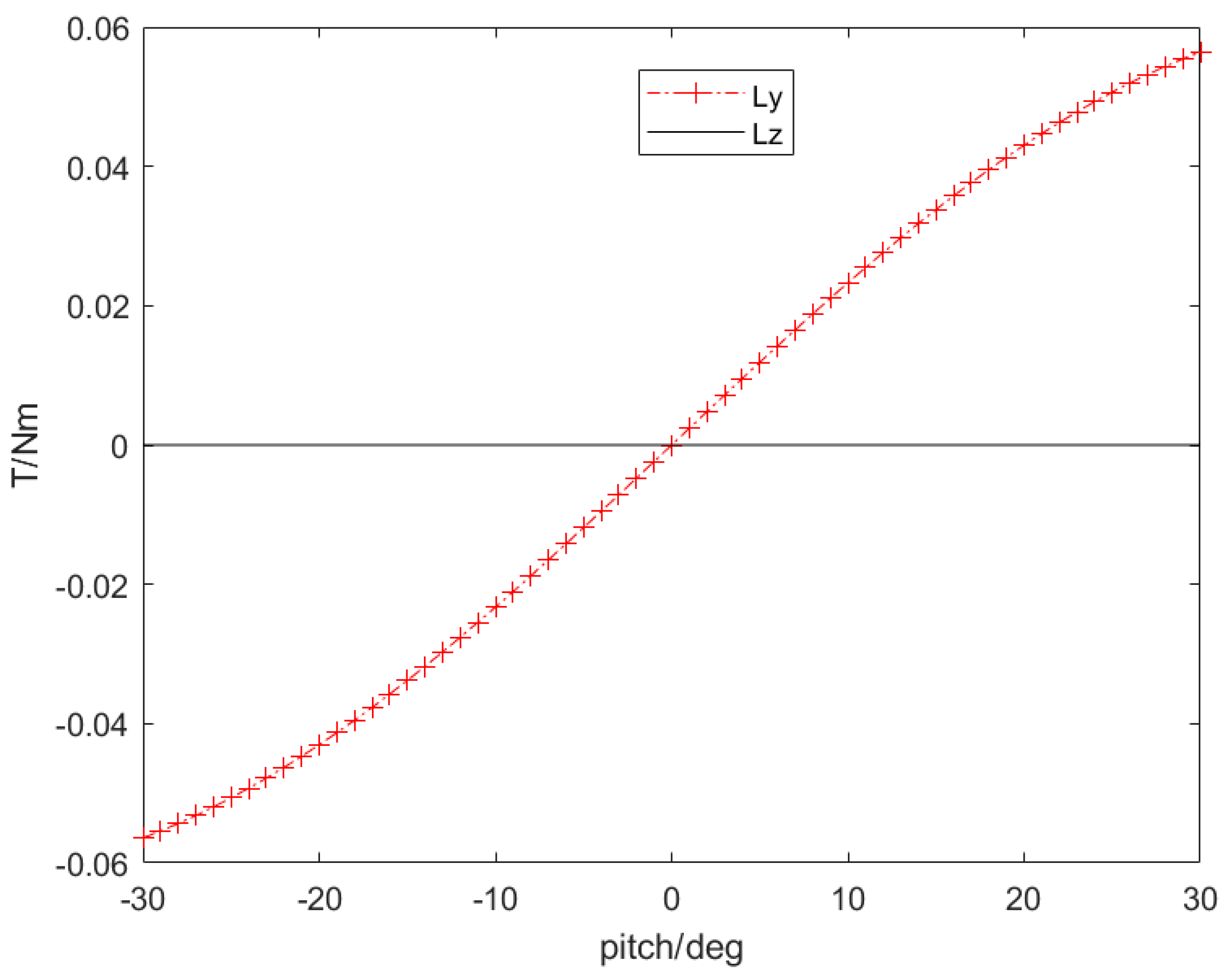
2.1. Rigid Swing Aerodynamic Model
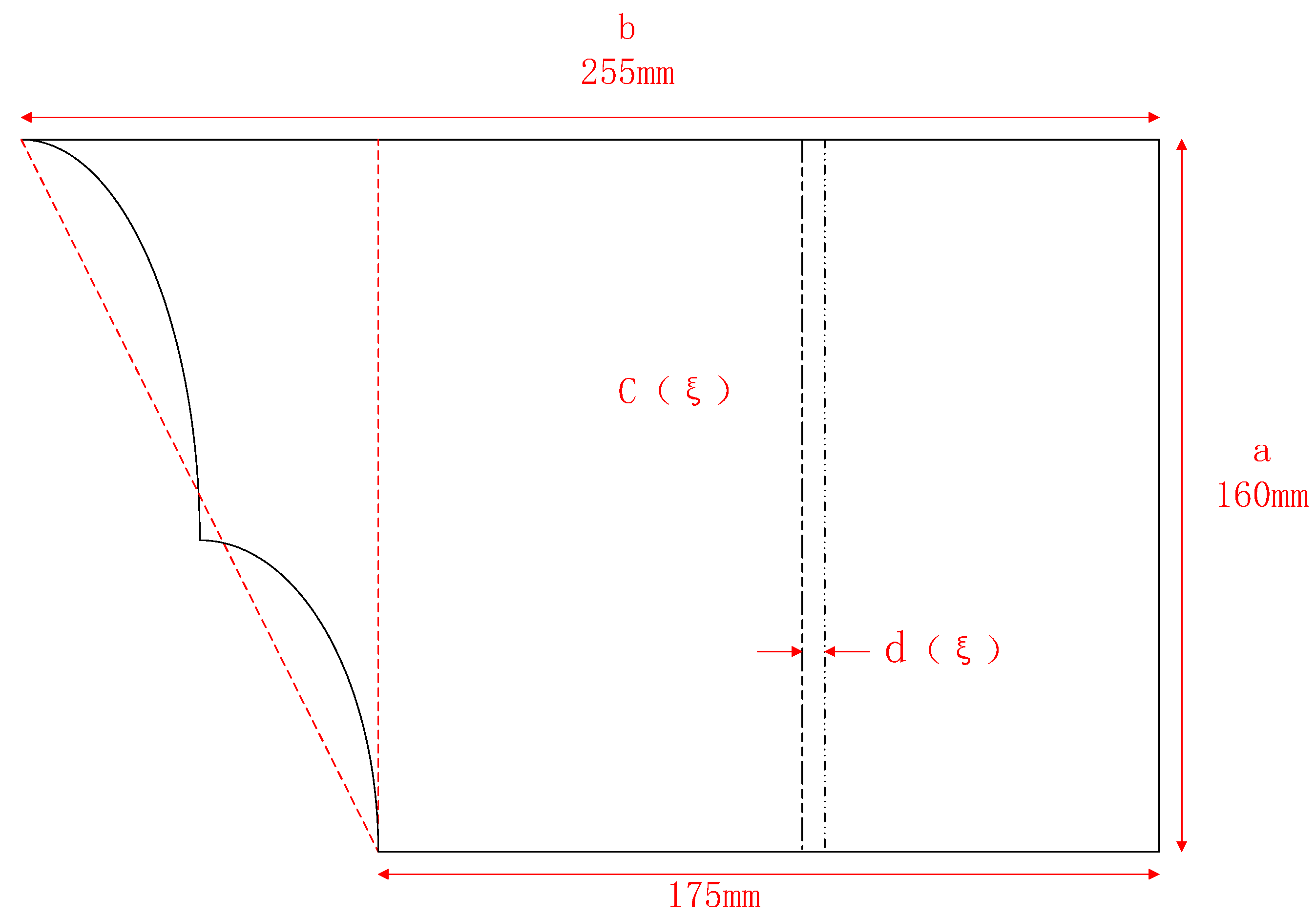
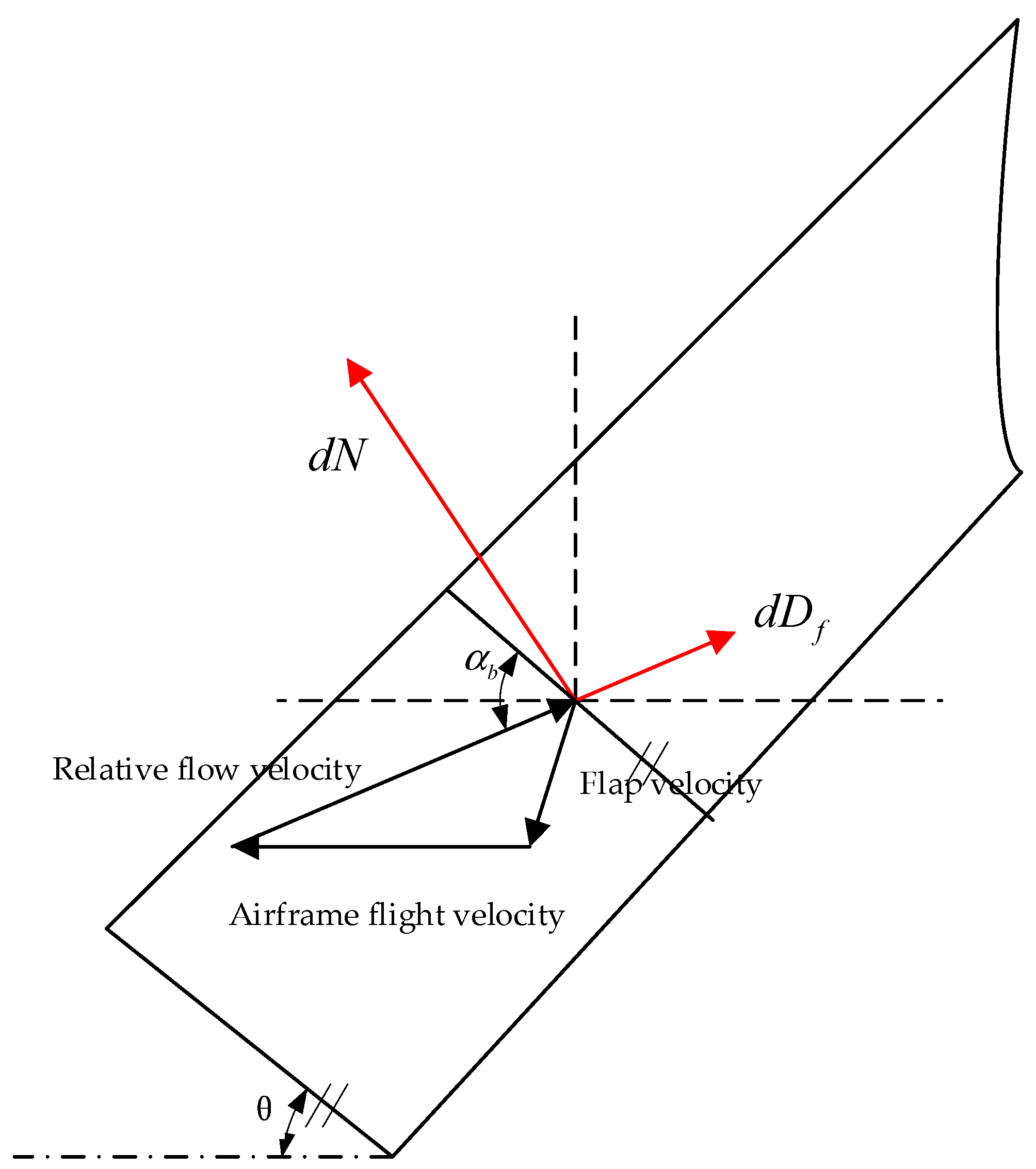
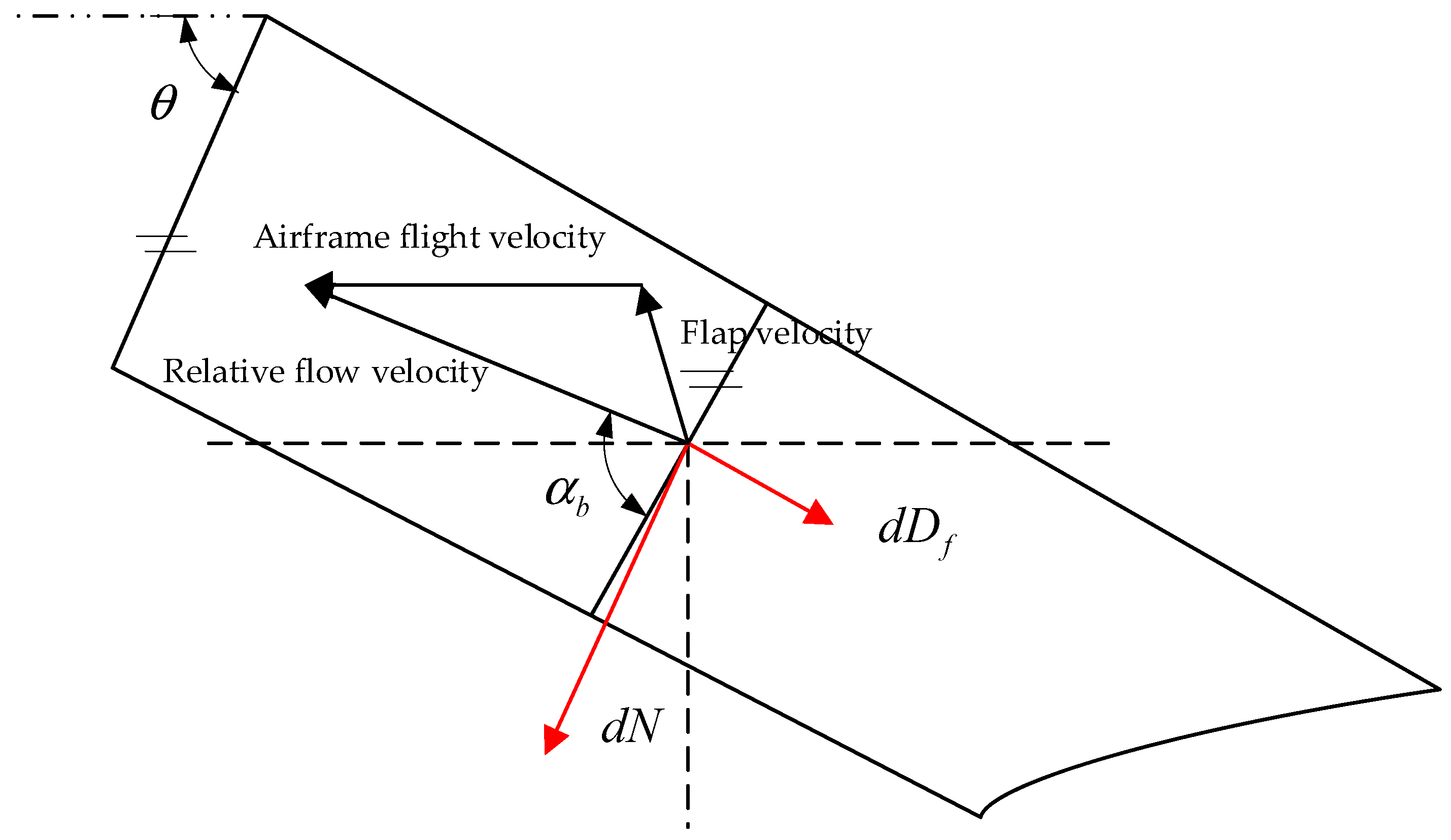
2.2. Tail Deformation Aerodynamic Model
- (1)
- We ignore the influence of disturbing airflow in other directions than the relative incoming flow;
- (2)
- We ignore the impact of attitude changes on the aerodynamic force of the wing or tail during flight;
- (3)
- We treat the flapping of the wings and the movement of the tail as internal movements and ignore the influence of inertial forces;
- (4)
- We ignore the effect of atmospheric density changes caused by flight altitude and the effect of the Earth’s curvature caused by flight distance.
3. Aerodynamic Analysis of the Bat-Imitation Flapping-Wing Aircraft
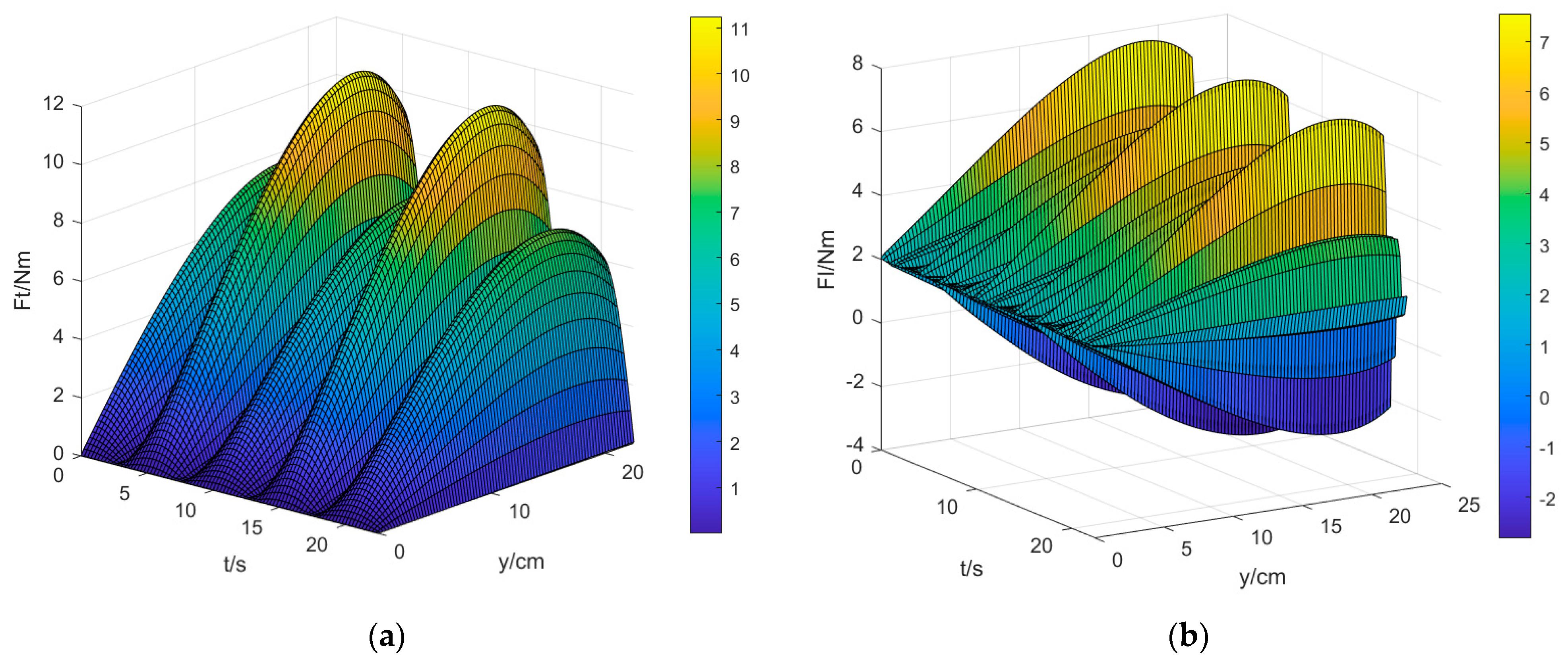
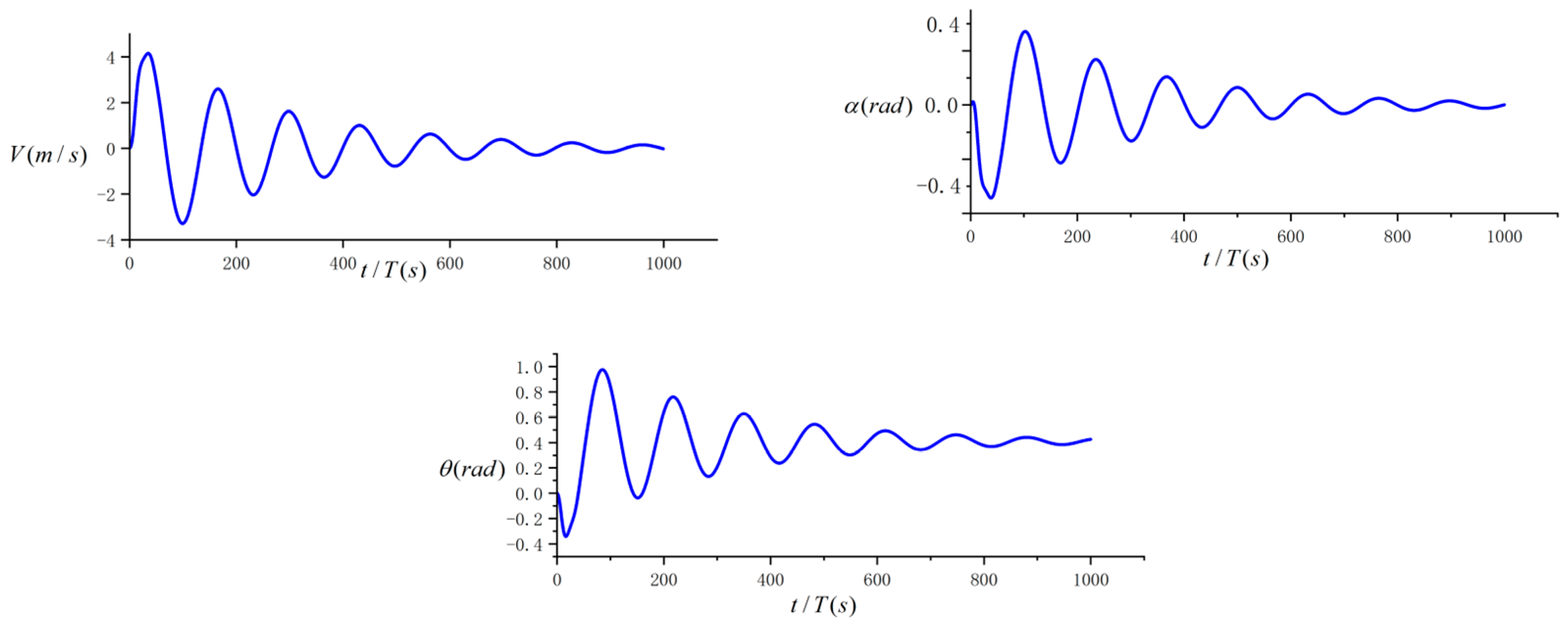
3.1. Rigid Swing Aerodynamic Response
3.2. Aerodynamic Response of Tail Wing Pitch Angle
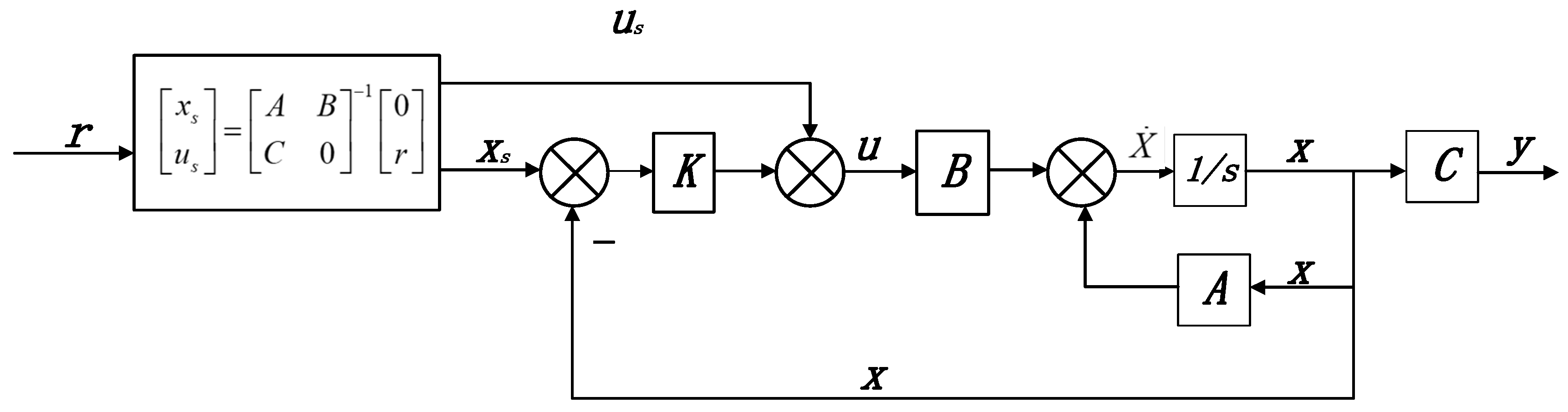
4. Design of Longitudinal Channel Controller for a Bat-like Ornithopter
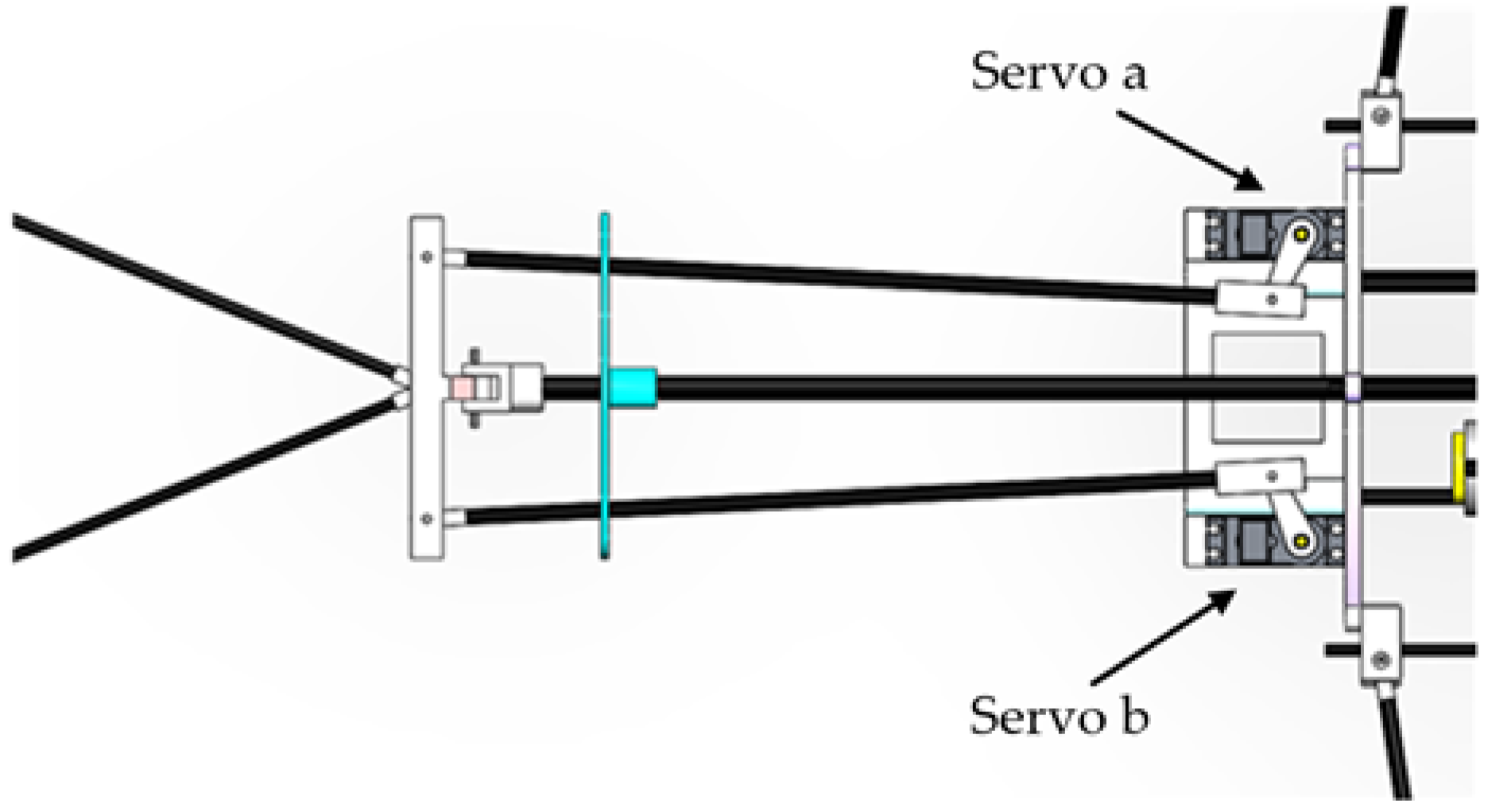
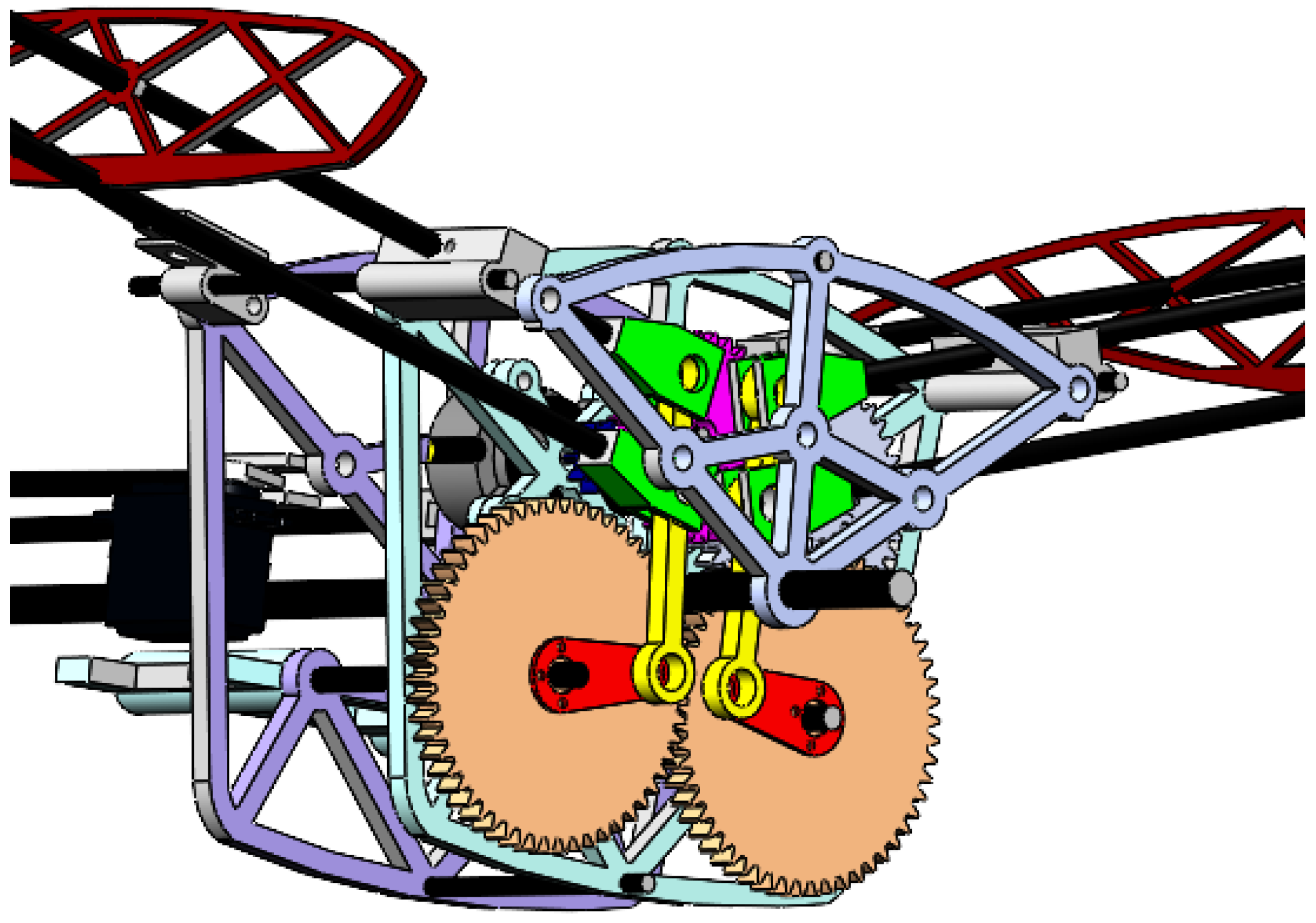
4.1. Kinematic and Dynamic Modeling
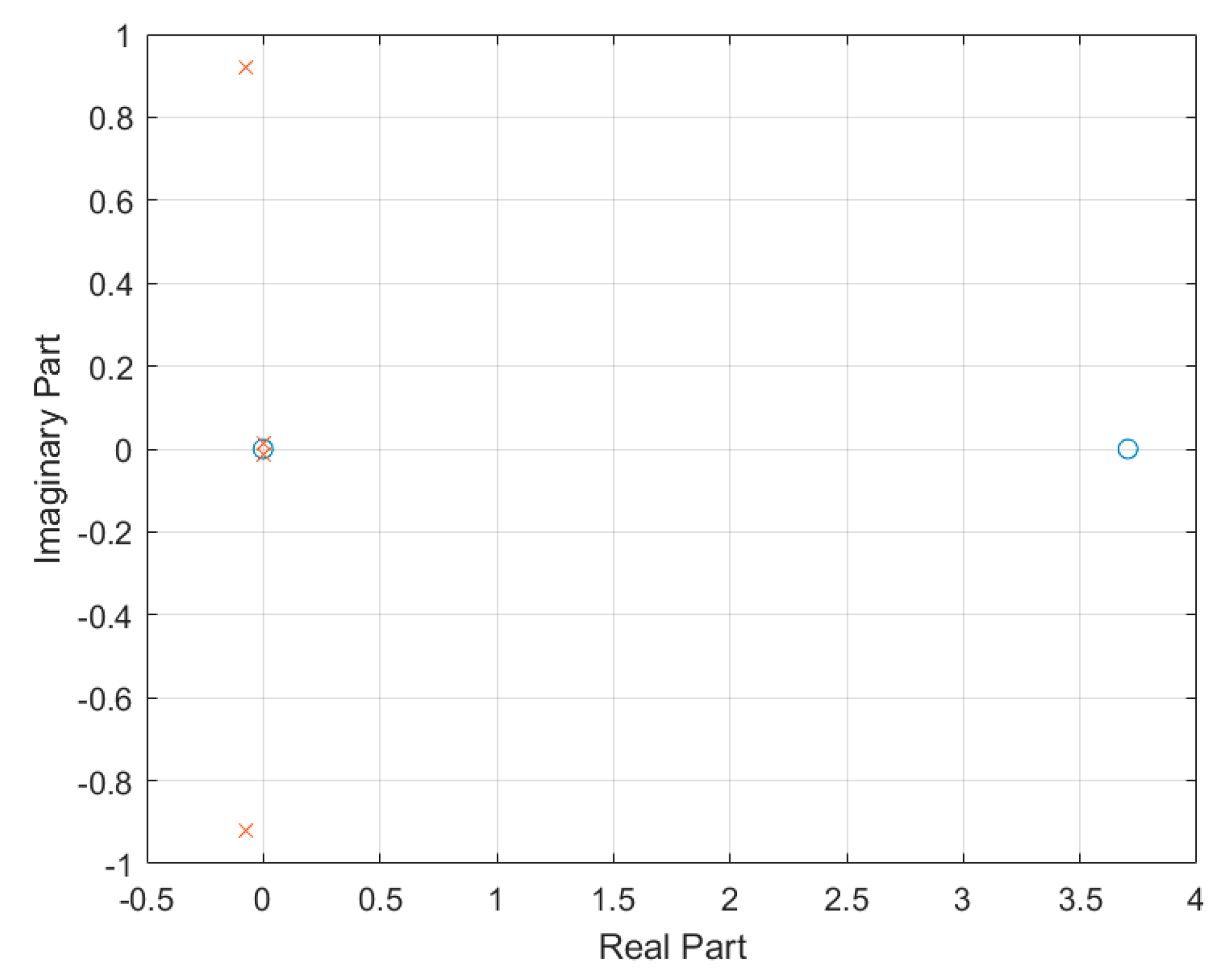
4.2. System Stability Analysis
4.3. Longitudinal Pitch Angle Control Based on LQR
- (1)
- The system is reversible (m = p), stable, and has no variable zero at the origin.
- (2)
- The system has at least n − 2p different LHP zero points.
5. Simulation and Flight Test
5.1. Simulation Analysis
- The expected value of the pitch angle is given as .
- The dynamic expected pitch angle values are given , , , ,
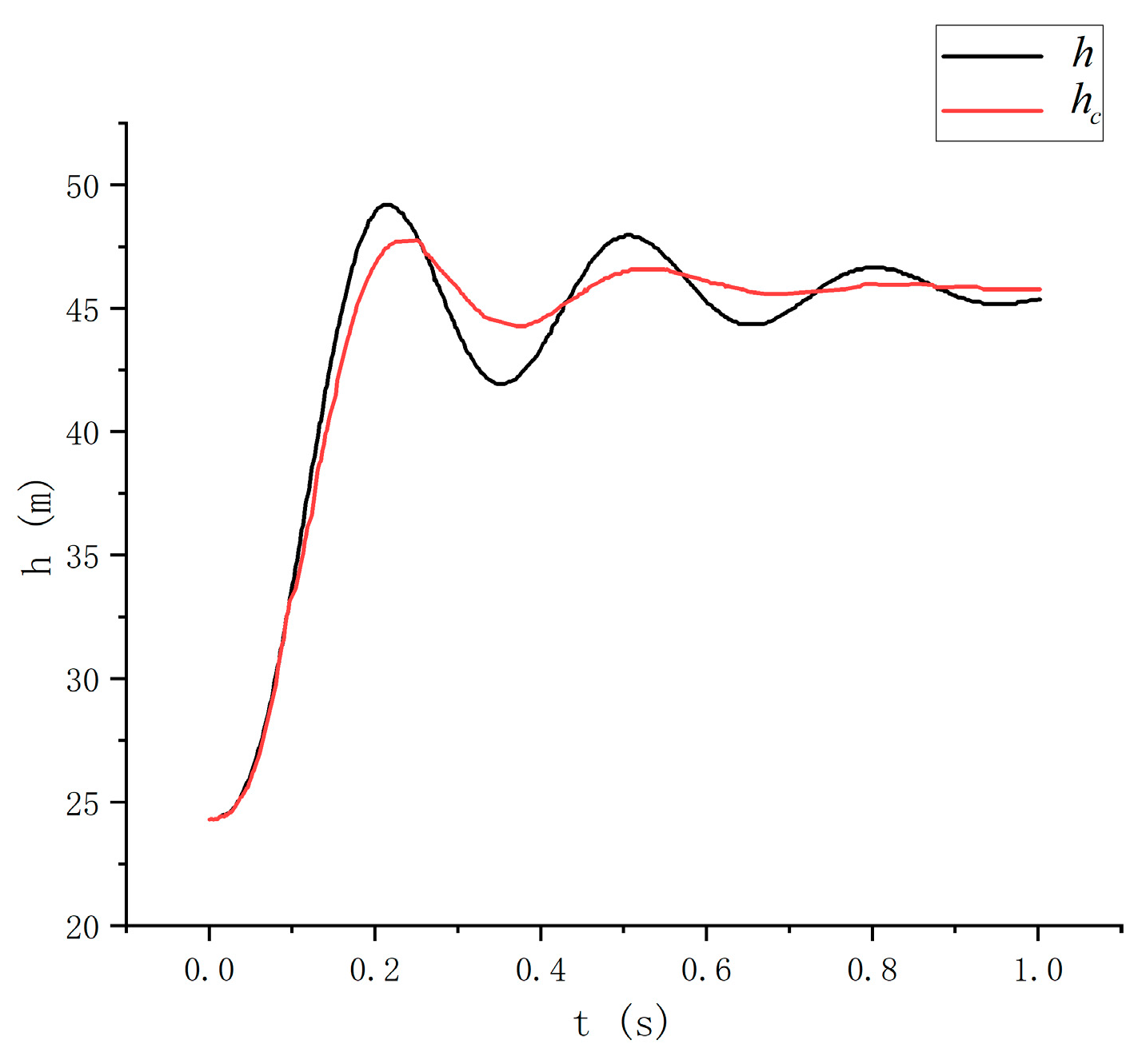
5.2. Altitude Control
5.3. Altitude Control Simulation Analysis
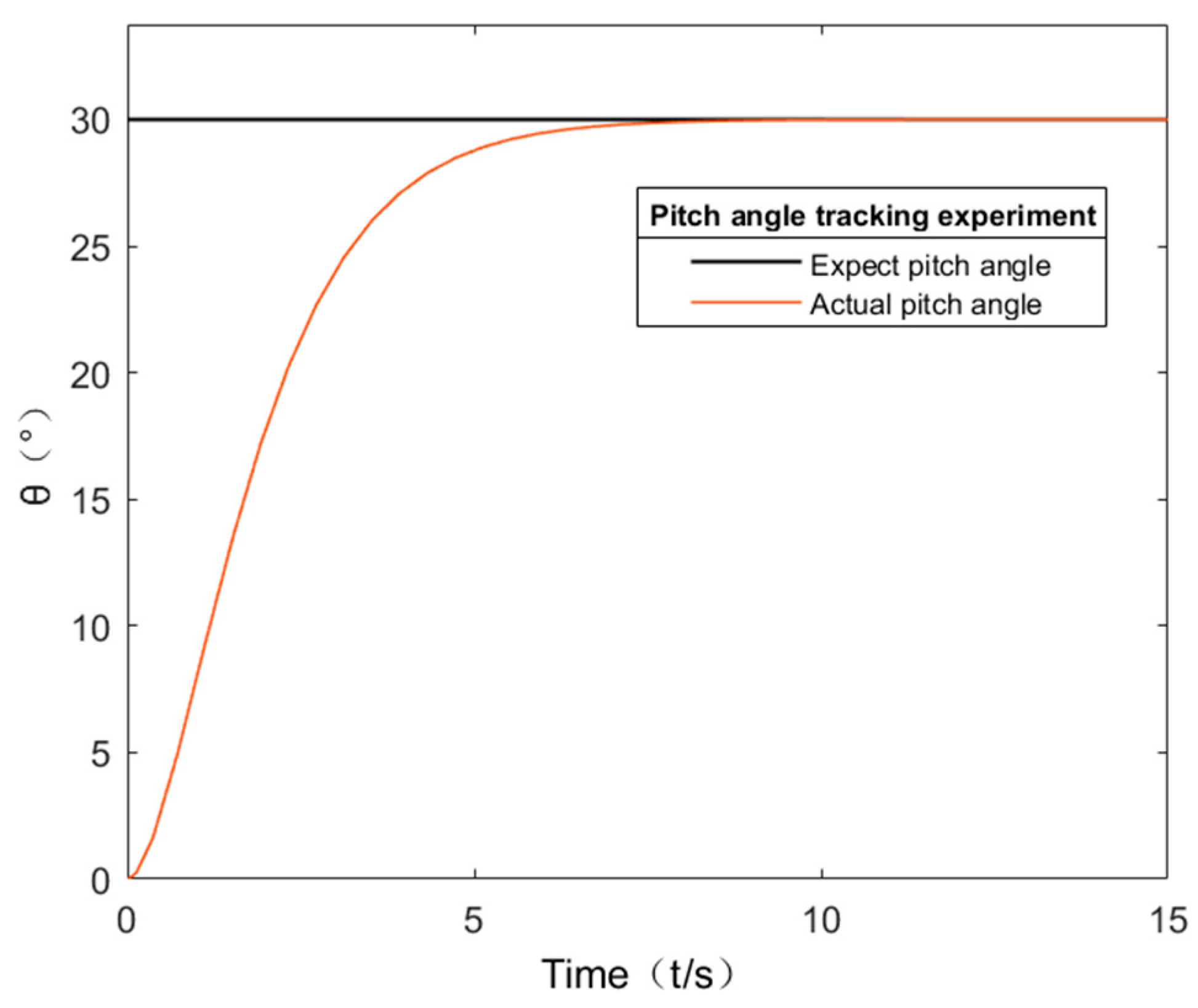
5.4. Flight Test
6. Conclusions
7. Future Work
- (1)
- Completing the lateral channel modeling and controller design of our bat-like flapping aircraft;
- (2)
- Improving the airfoil shape and structure, adding a folding wing device, reducing the resistance in the upswing phase of the rigid swing, and increasing the overall lift in the cycle.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, M. Aerodynamics of animal flight. Acta Aerodyn. Sin. 2018, 36, 122–128. [Google Scholar]
- Tanaka, H.; Okada, H.; Shimasue, Y.; Liu, H. Flexible flapping wings with self-organized microwrinkles. Bioinspiration Biomim. 2015, 10, 046005. [Google Scholar] [CrossRef] [PubMed]
- Riskin, D.K.; Willis, D.J.; Iriarte-Díaz, J.; Hedrick, T.L.; Kostandov, M.; Chen, J.; Laidlaw, D.H.; Breuer, K.S.; Swartz, S.M. Quantifying the complexity of bat wing kinematics. J. Theor. Biol. 2008, 254, 604–615. [Google Scholar] [CrossRef] [PubMed]
- Azuma, A. The Biokinetics of Flying and Swimming; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Yu, Y.; Guan, Z. Learning from bat: Aerodynamics of actively morphing wing. Theor. Appl. Mech. Lett. 2015, 5, 13–15. [Google Scholar] [CrossRef]
- Guan, Z.; Yu, Y. Aerodynamic mechanism of forces generated by twisting model-wing in bat flapping flight. Appl. Math. Mech. 2014, 35, 1607–1618. [Google Scholar] [CrossRef]
- Guan, Z.; Yu, Y. Aerodynamics and mechanisms of elementary morphing models for flapping wing in forward flight of bat. Appl. Math. Mech. 2015, 36, 669–680. [Google Scholar] [CrossRef]
- Joshi, V.; Jaiman, R.K.; Ollivier-Gooch, C. A variational flexible multibody formulation for partitioned fluid–structure interaction: Application to bat-inspired drones and unmanned air-vehicles. Comput. Math. Appl. 2020, 80, 2707–2737. [Google Scholar] [CrossRef]
- Fan, X.; Swartz, S.; Breuer, K. Power requirements for bat-inspired flapping flight with heavy, highly articulated and cambered wings. J. R. Soc. Interface 2022, 19, 20220315. [Google Scholar] [CrossRef]
- Wagter, C.D.; Tijmons, S.; Remes, B.D.W.; de Croon, G.C. Autonomous Flight of a 20-gram Flapping Wing MAV with a 4-gram Onboard Stereo Vision System. In Proceedings of the IEEE International Conference on Robotics & Automation, Hong Kong, China, 31 May–7 June 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Ramezani, A.; Shi, X.; Chung, S.-J.; Hutchinson, S. Bat Bot (B2), A Biologically Inspired Flying Machine. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3219–3226. [Google Scholar]
- Hedrick, T.L.; Cheng, B.; Deng, X. Wingbeat time and the scaling of passive rotational damping in flapping flight. Science 2009, 324, 252–255. [Google Scholar] [CrossRef]
- Hoff, J.; Ramezani, A.; Chung, S.-J.; Hutchinson, S. Reducing Versatile Bat Wing Conformations to a 1-DoF Machine. In Proceedings of the Biomimetic and Biohybrid Systems 6th International Conference, Living Machines 2017, Stanford, CA, USA, 26–28 July 2017; pp. 181–192. [Google Scholar]
- Hoff, J.; Ramezani, A.; Chung, S.J.; Hutchinson, S. Optimizing the structure and movement of a robotic bat with biological kinematic synergies. Int. J. Robot. Res. 2017, 37, 1233–1252. [Google Scholar] [CrossRef]
- Ramezani, A.; Chung, S.J.; Hutchinson, S. A biomimetic robotic platform to study flight specializations of bats. Sci. Robot. 2017, 2, eaal2505. [Google Scholar] [CrossRef] [PubMed]
- Bahlman, J.W.; Swartz, S.M.; Breuer, K.S. Breuer Design and characterization of a multi-articulated robotic bat wing. Bioinspiration Biomim. 2013, 8, 016009. [Google Scholar] [CrossRef] [PubMed]
- Bunget, G. BATMAV—A Bio-Inspired Micro-Aerial Vehicle for Flapping Flight; The Graduate Faculty of North Carolina State University: Raleigh, NC, USA, 2010. [Google Scholar]
- Zhang, X.; Zhou, C. Numerical Investigation on the Aerodynamic Characteristics of a Forward Flight Flapping Airfoil with Nonsymmetrical Plunging Motion. Inf. Technol. J. 2011, 10, 258–266. [Google Scholar]
- Dickinson, M.H.; Lehmann, F.O.; Sane, S.P. Wing rotation and the aerodynamic basis of insect flight. Science 1999, 284, 1954. [Google Scholar] [CrossRef]
- Lambregts, A.A. TECS Generalized Airplane Control System Design–An Update, Advances in Aerospace Guidance, Navigation and Control: Selected Papers of the Second CEAS Specialist Conference on Guidance, Navigation and Control; Springer: Berlin/Heidelberg, Germany, 2013; pp. 503–534. [Google Scholar]
- Wu, S.; Guo, S. Optimum flight trajectory guidance based on total energy control of aircraft. J. Guid. Control Dyn. 1994, 17, 291–296. [Google Scholar] [CrossRef]
- Warkentin, J.; DeLaurier, J. Experimental aerodynamic study of tandem flapping membrane wings. J. Aircr. 2007, 44, 1653–1661. [Google Scholar] [CrossRef]
- Zakaria, M.Y.; Taha, H.E.; Hajj, M.R. Design optimization of flapping ornithopters: The pterosaur replica in forward flight. J. Aircr. 2016, 53, 48–59. [Google Scholar] [CrossRef]
- Zakaria, M.Y.; Allen, D.W.; Woolsey, C.A.; Hajj, M.R. Lift and drag of flapping membrane wings at high angles of attack. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Washington, DC, USA, 13–17 June 2016; p. 3554. [Google Scholar]
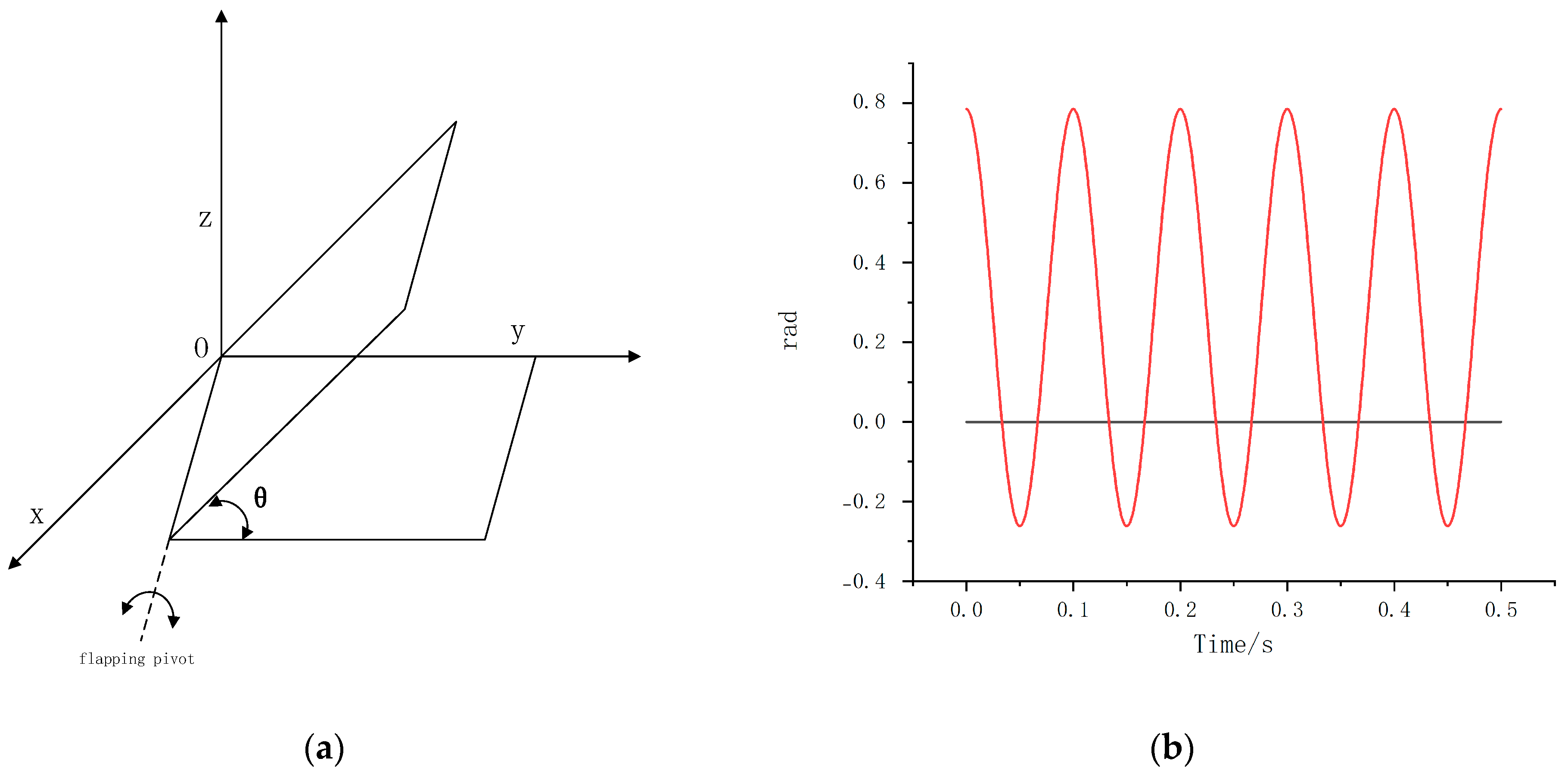

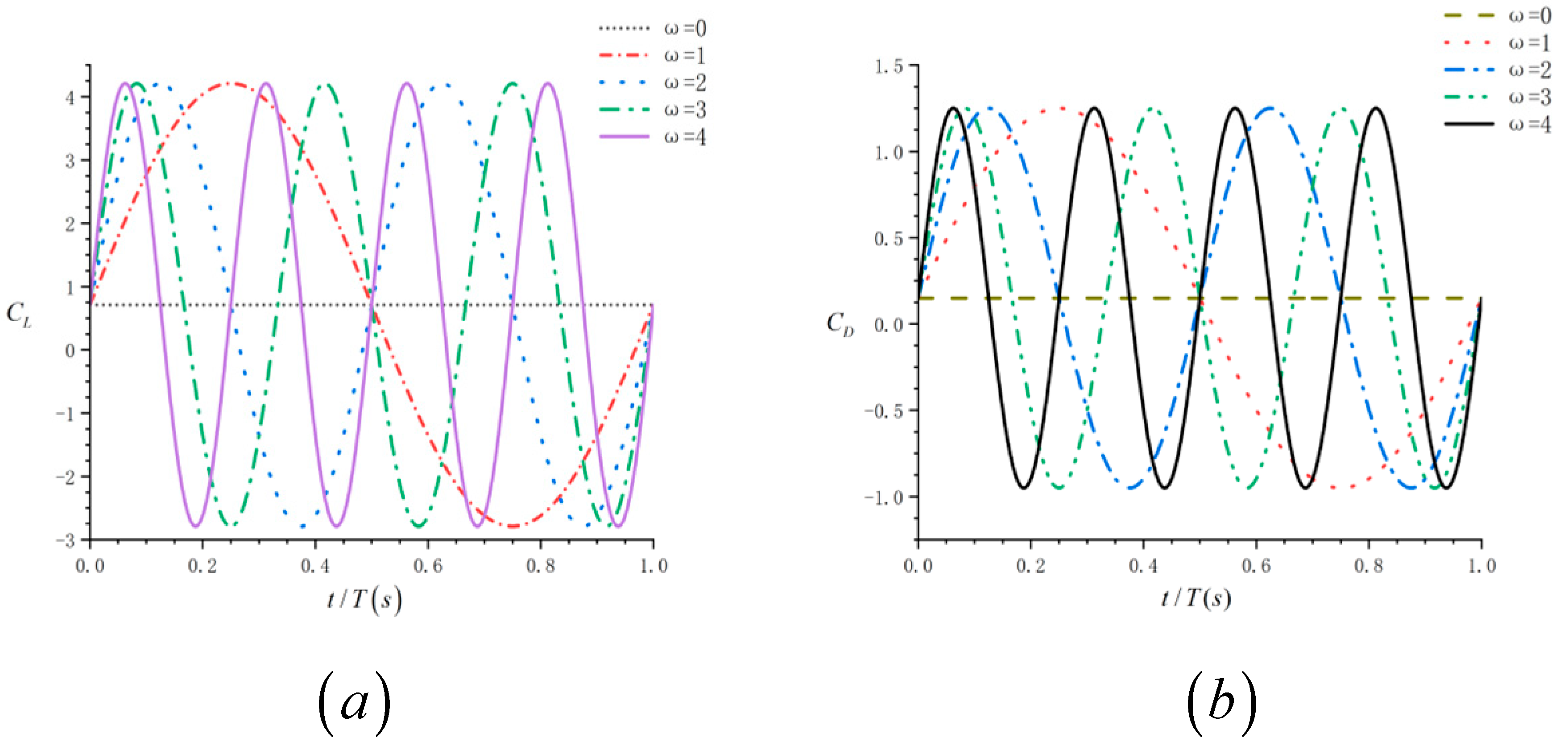
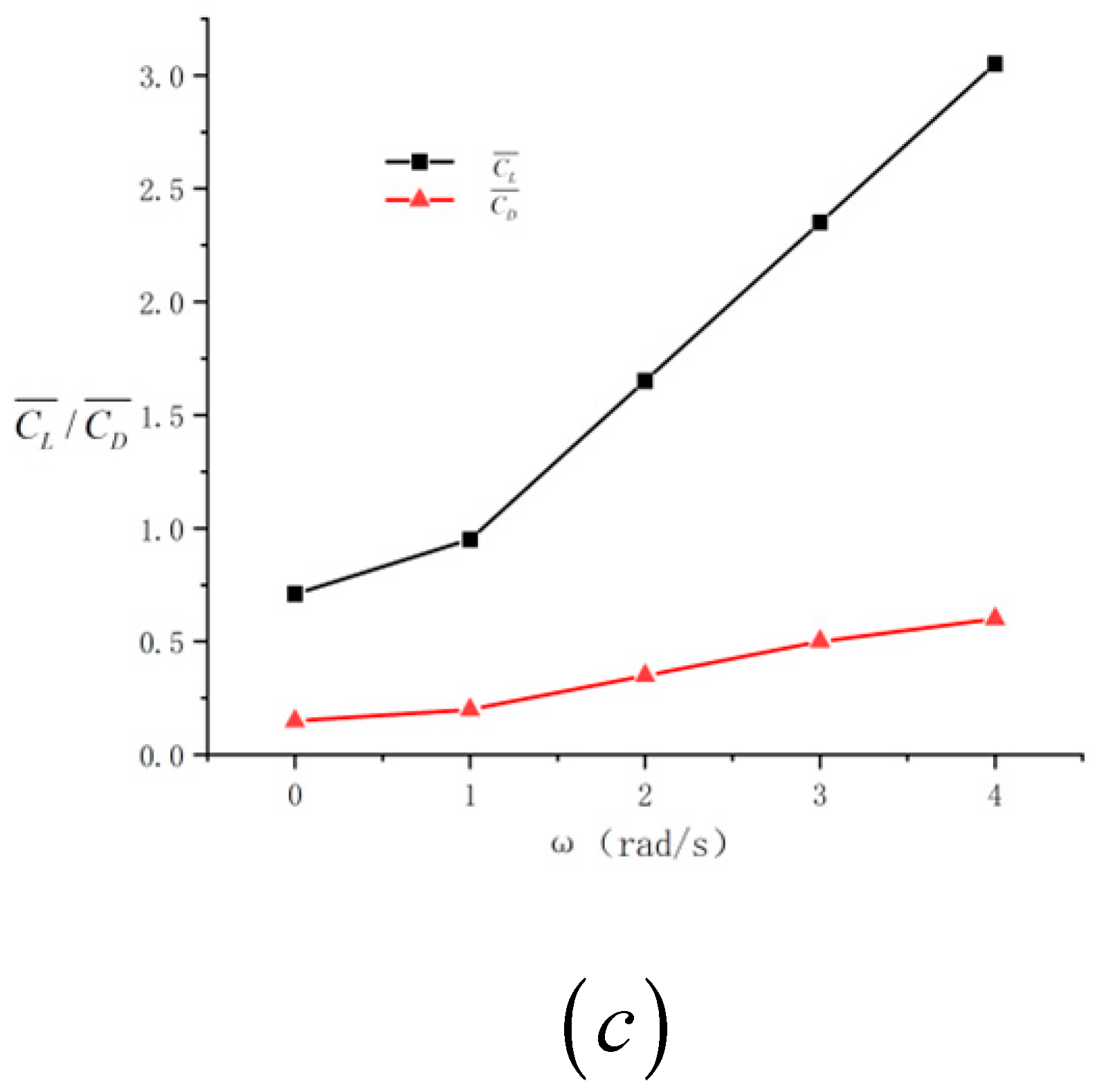
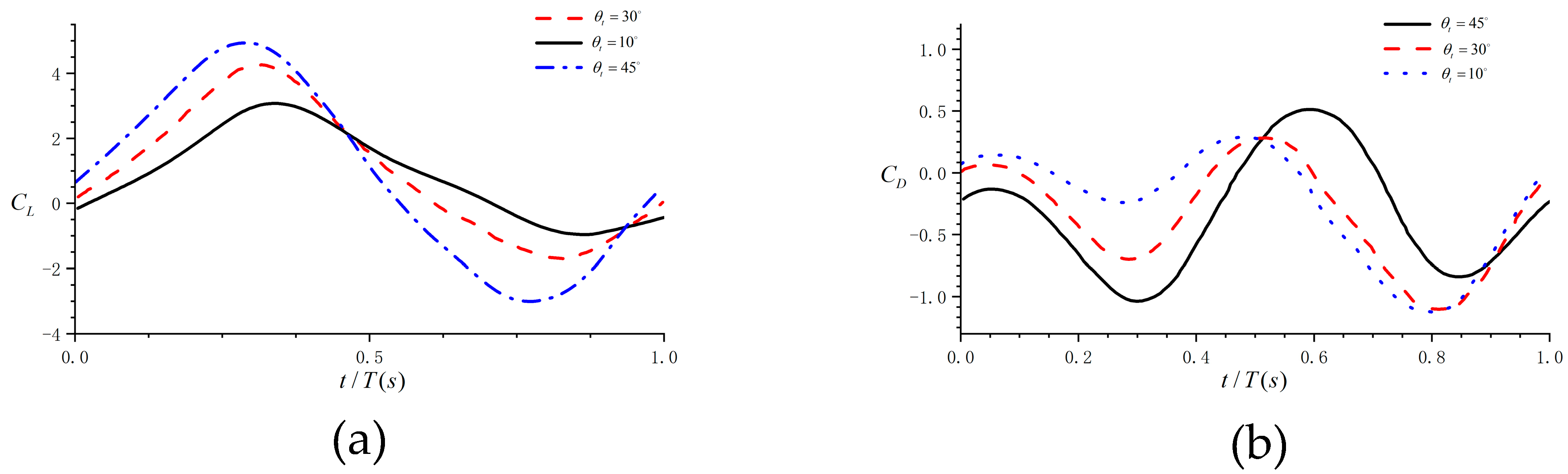
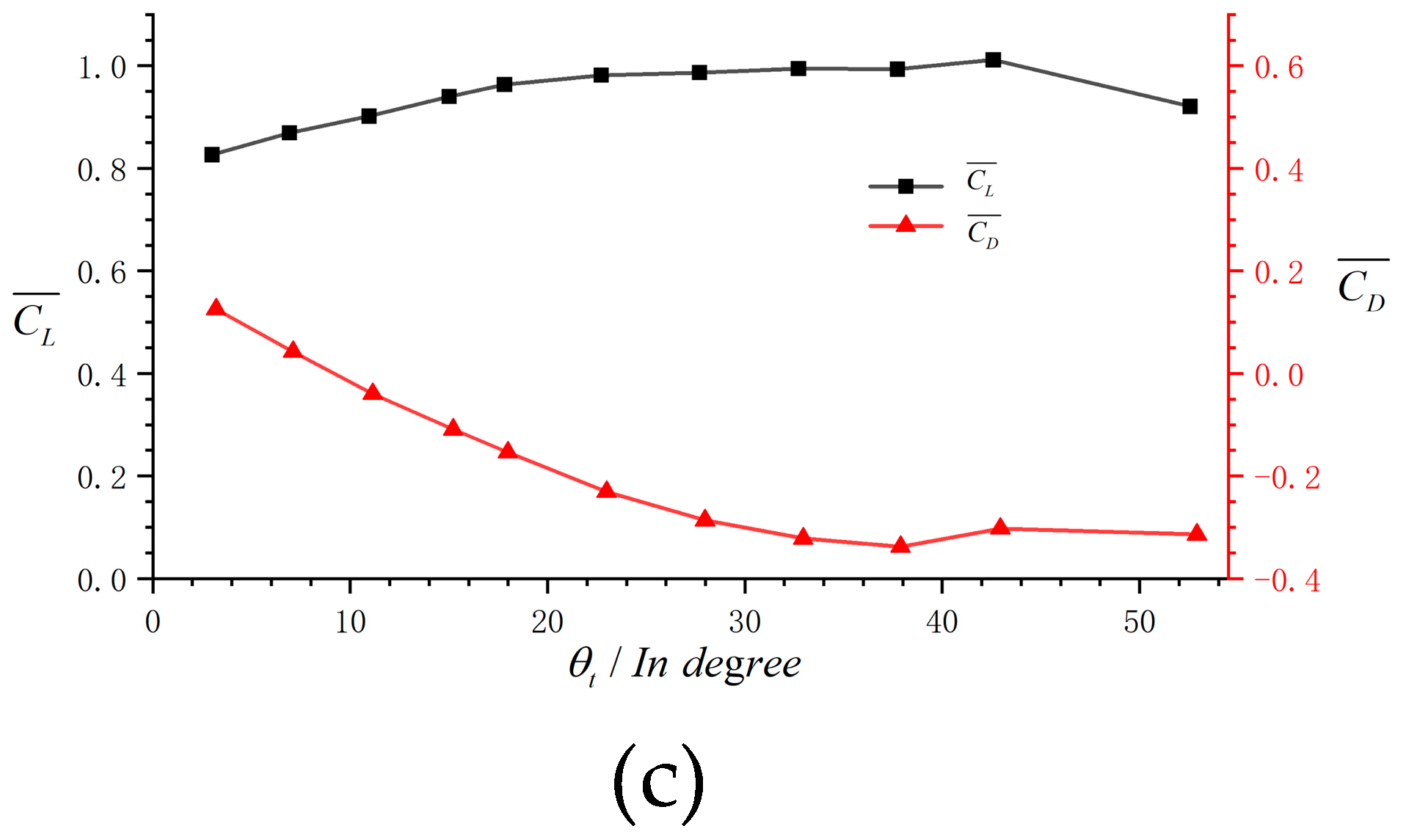





| Parameter Name | Parameter Value |
|---|---|
| Initial flight speed | 5 m/s |
| Initial flight angle of attack | 13° |
| Flapping frequency | 10 Hz |
| Maximum twist angle of trailing edge | ±7° |
| Upshot amplitude | 45° |
| Down shot amplitude | 15° |
| SP (cm) | C (cm) | AR | |
|---|---|---|---|
| 35 | 4.7 | 7.44 | 13.4 |
| Variable | Definition | Variable | Definition |
|---|---|---|---|
| T | Thrust | Yaw velocity | |
| Y | Lateral force | Angle of attack | |
| D | Drag | Sideslip angle | |
| L1 | Lift | Roll | |
| p | Pitch velocity | Pitch | |
| q | Roll velocity | Yaw |
| External Force | ||
| External Moment | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Pei, X.; Wu, G.; Bai, Y. Analysis and Design of Bat-Like Flapping-Wing Aircraft. Aerospace 2024, 11, 325. https://doi.org/10.3390/aerospace11040325
Wang F, Pei X, Wu G, Bai Y. Analysis and Design of Bat-Like Flapping-Wing Aircraft. Aerospace. 2024; 11(4):325. https://doi.org/10.3390/aerospace11040325
Chicago/Turabian StyleWang, Fan, Xinbiao Pei, Guangxin Wu, and Yue Bai. 2024. "Analysis and Design of Bat-Like Flapping-Wing Aircraft" Aerospace 11, no. 4: 325. https://doi.org/10.3390/aerospace11040325





