Constructive Aerodynamic Interference in a Network of Weakly Coupled Flutter-Based Energy Harvesters
Abstract
:1. Introduction
Aeroelastic Energy Harvesting
2. Materials and Methods
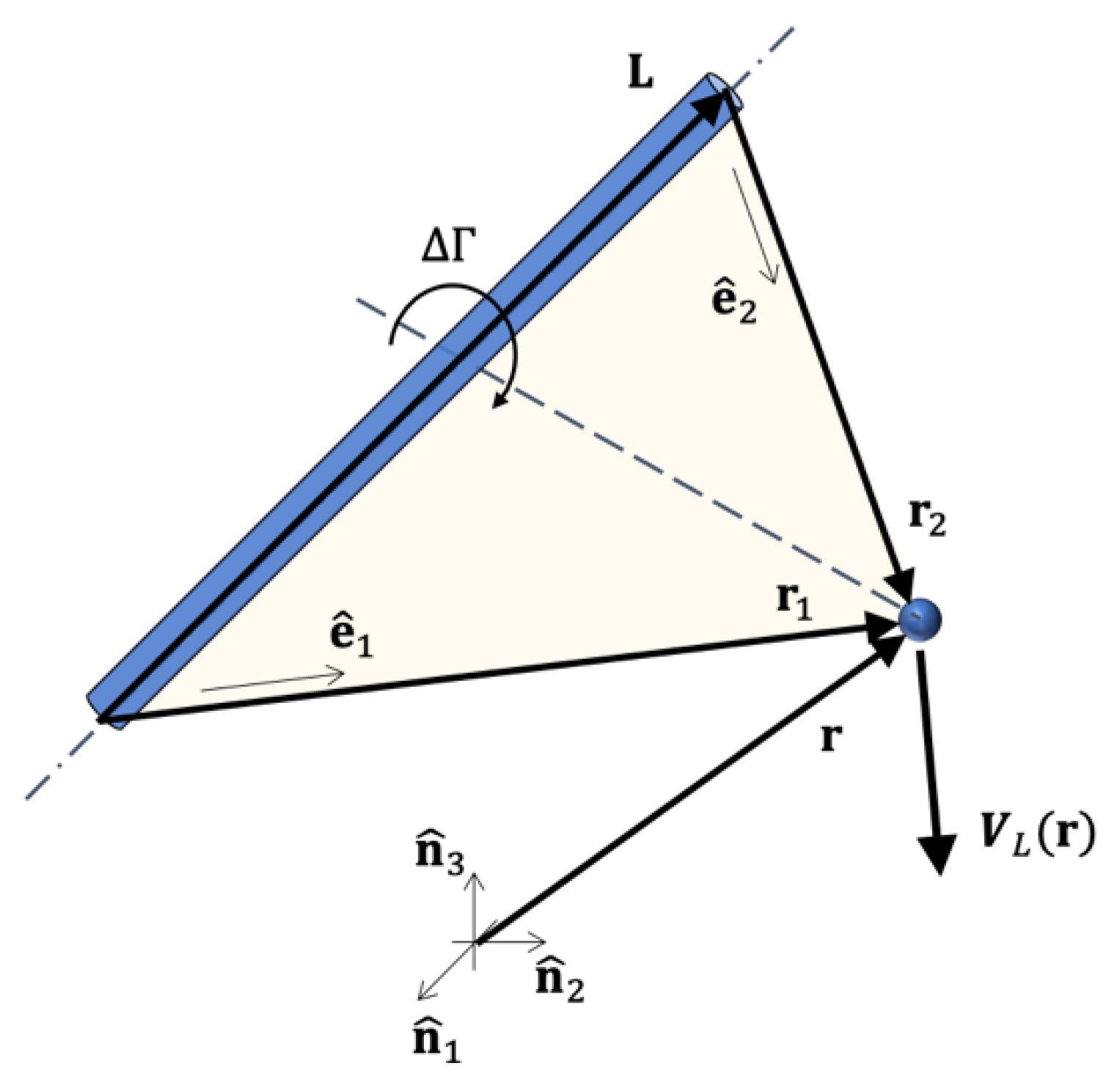
2.1. Aerodynamic Model
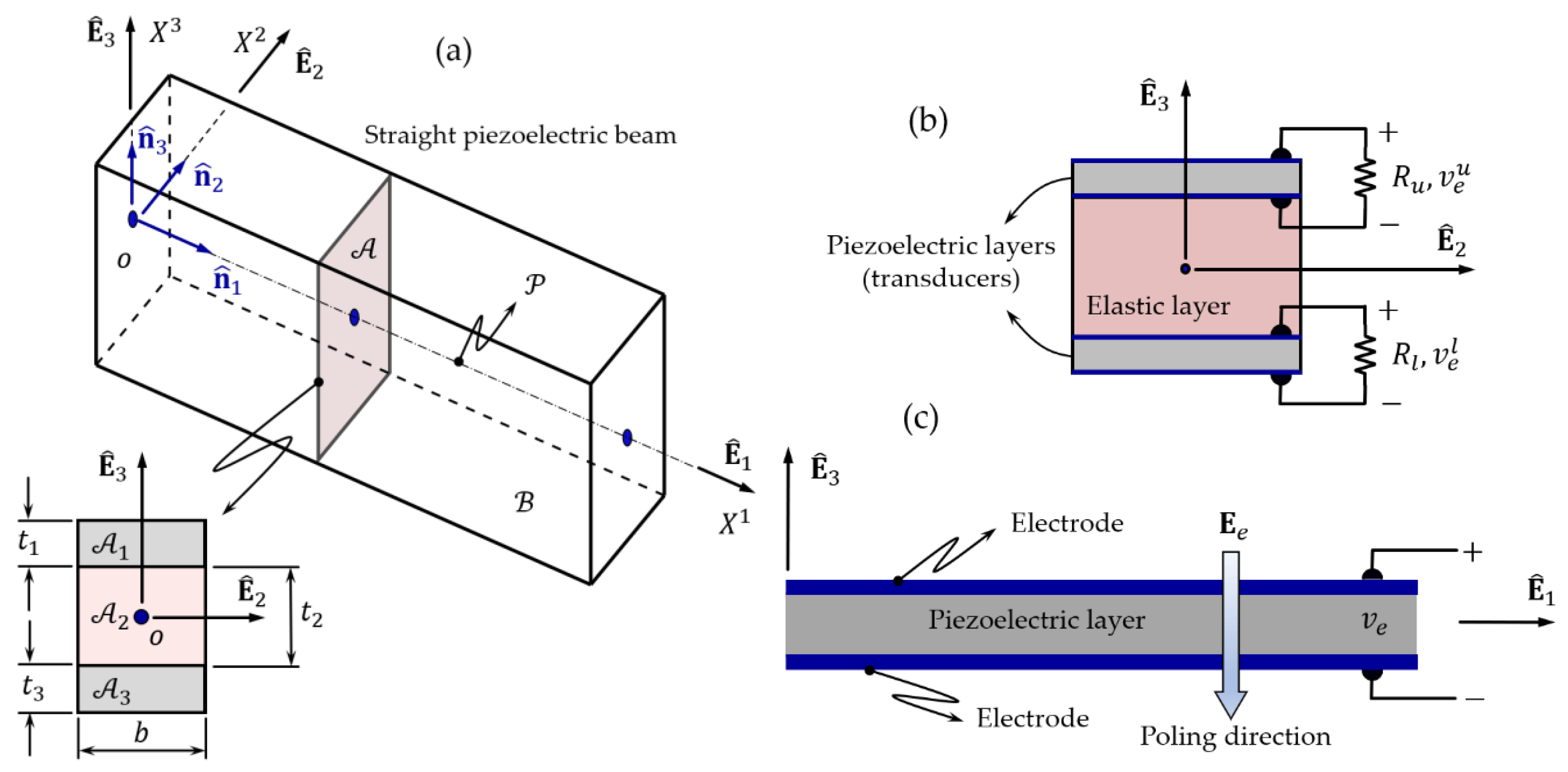
2.2. Structural Model
Discretized Dynamic Formulation (Finite-Element Model)
- (i)
- Obtain the structure’s natural frequencies and eigenvectors (mode shapes):
- Express the nodal degrees of freedom as .
- Replace this expression into the linear, undamped, and homogeneous version of Equation (22) to obtain the generalized eigenvalue problem .
- Solve the eigenvalue problem by obtaining the natural frequencies and associated eigenvectors (free-vibration modes).
- (ii)
- Obtain the actual response:
- Express the nodal degrees of freedom as a linear combination of the free-vibration modes; that is to say, , where is a column vector whose components are the modal coordinates, and is the modal matrix, whose columns are the eigenvectors such that .
- Replace this expression into Equation (22) and solve for the modal weights .
- Recover the vector of physical coordinates from the modal coordinates .
2.3. Communication between Models and Numerical Integration
Co-Simulation Strategy
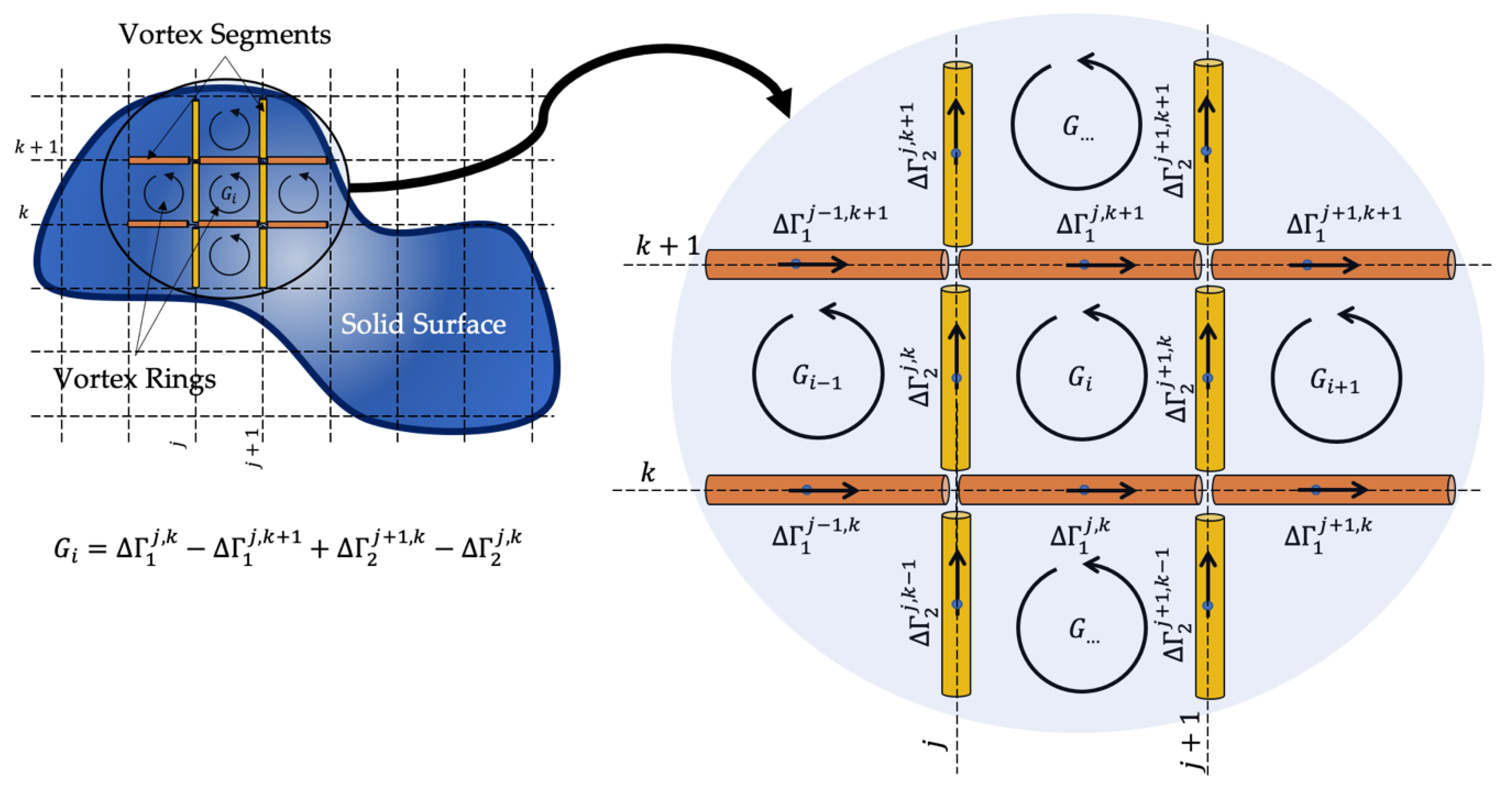
- The configurations of the wakes are updated. The new position of each node of the vortex segments in the wakes is estimated within the UVLM module according to Equation (14). Throughout the rest of the procedure for the current time step, and until convergence is achieved, the wake configuration remains frozen.
- The current fluid flow variables (velocity field, pressure distribution, and aerodynamic loads) are solved within the UVLM module. The current aerodynamic loads computed at the control points of the aerodynamic grid are transferred to the nodal points of the structural FEM mesh by means of Equation (25). With , the response of each harvester in the array is computed through Equation (23).
- The computed state of the structure (nodal displacements and velocities) is transferred to the aerodynamic mesh through Equation (22). With the updated configuration a new prediction or correction of the aerodynamic loads is obtained.
- Steps 2 and 3 are repeated until a convergence criterion is met. This criterion requires that the infinite norm of the relative error of the computed displacements between two consecutive iterations is less than .
- With the converged configuration of the structure, Step 3 is repeated one last time to obtain the final (converged) estimate of the aerodynamic loads.
3. Numerical Results
3.1. Verification of the Numerical Model
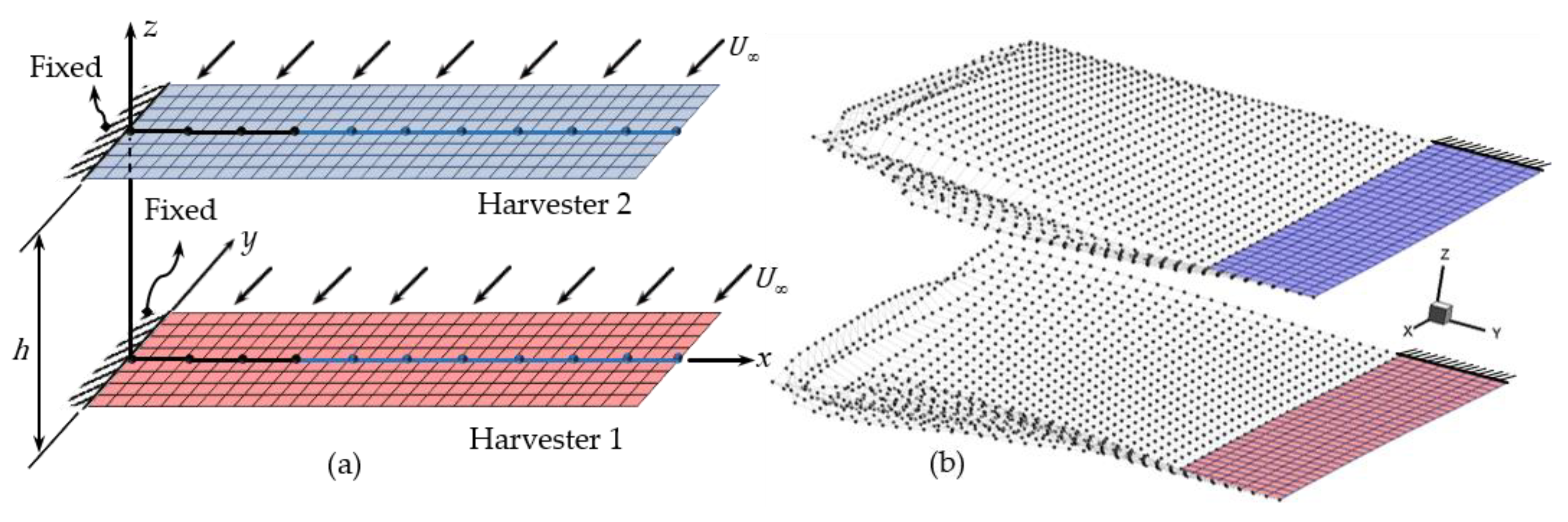
3.2. Case Study: Two Aerodynamically Coupled Harvesters
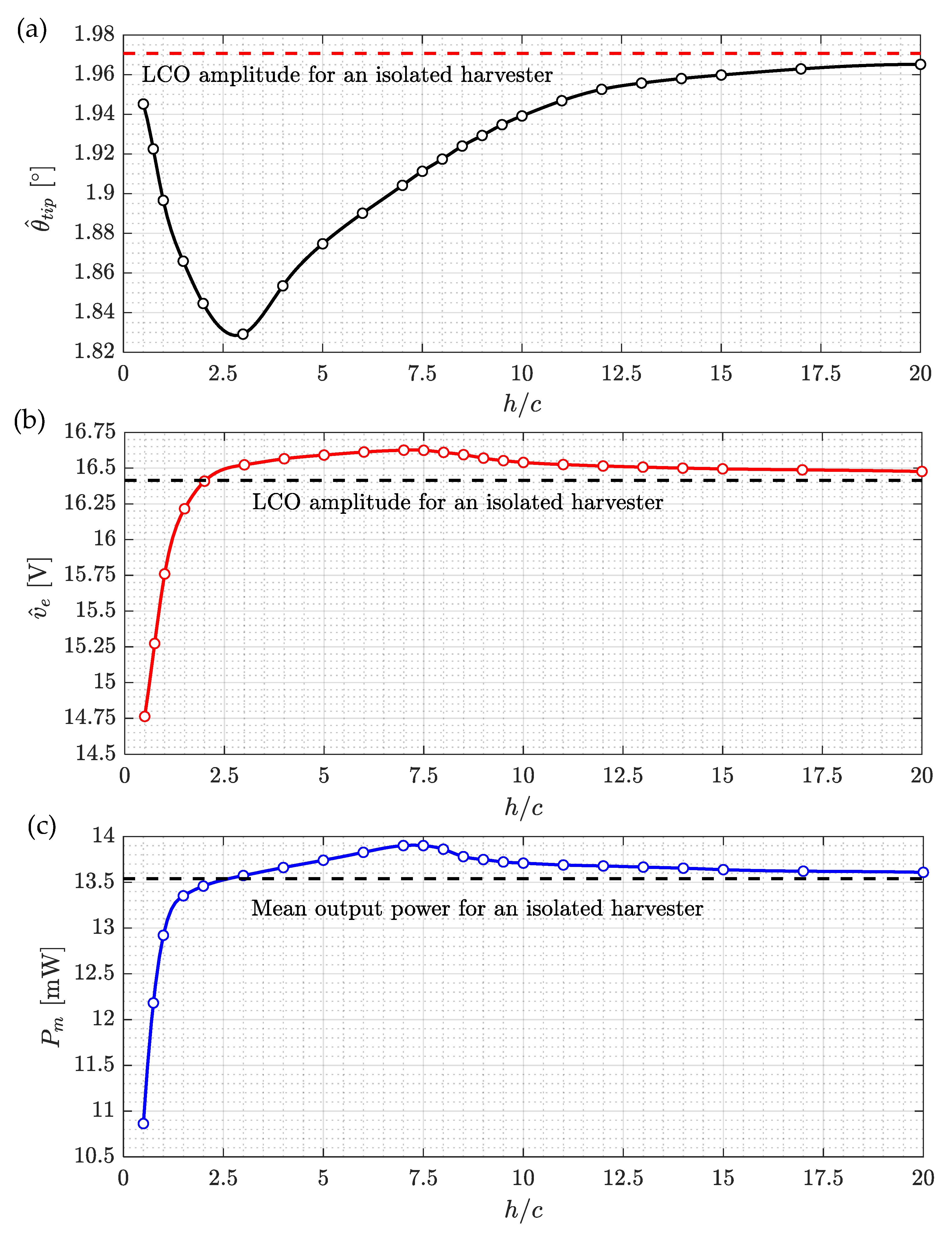
3.2.1. Influence of the Separation Distance
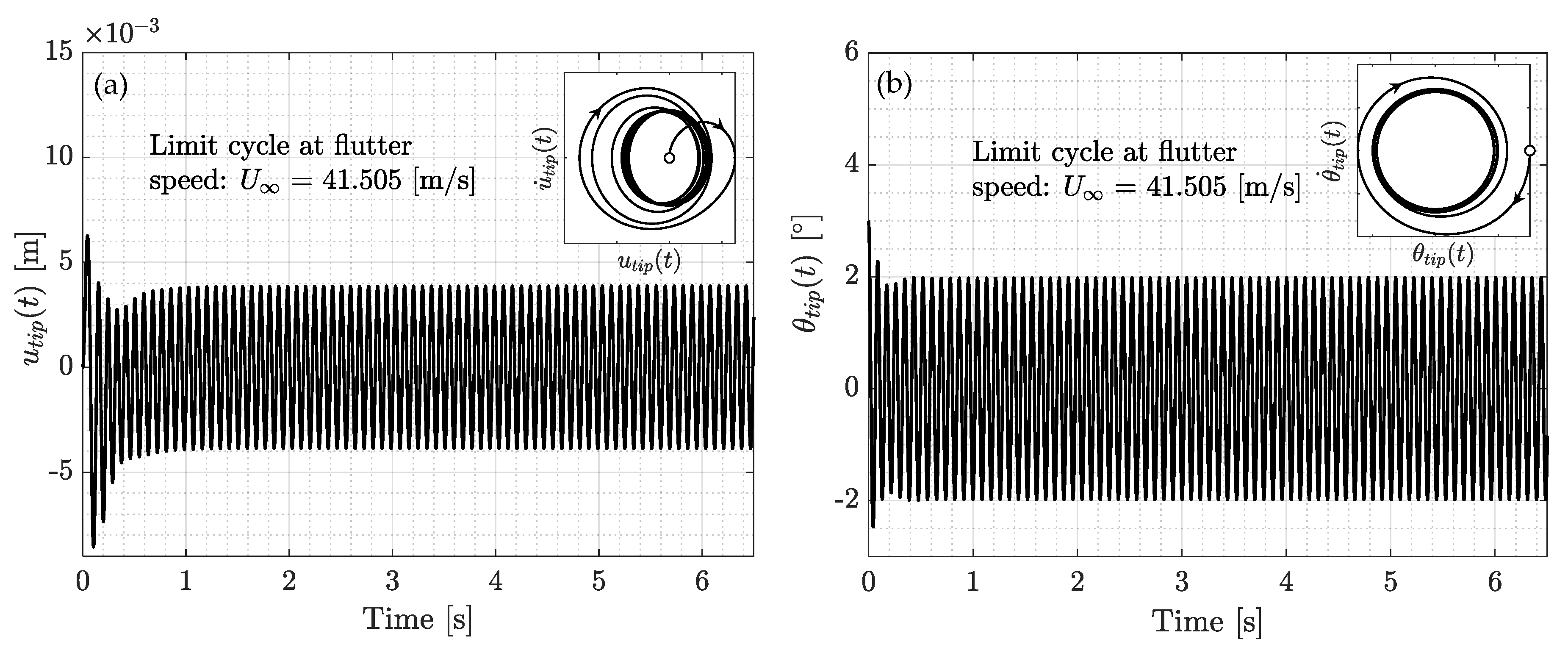
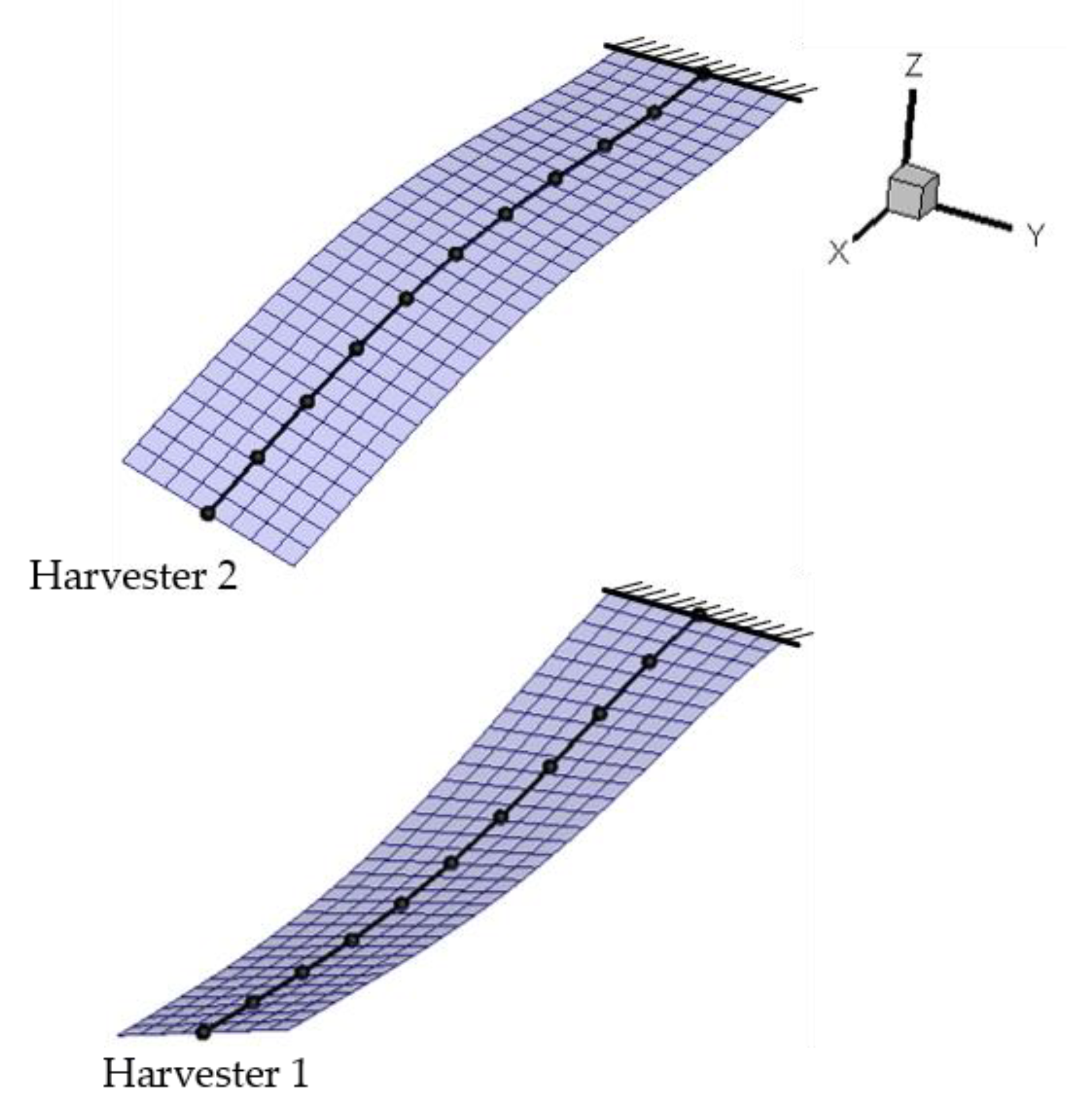
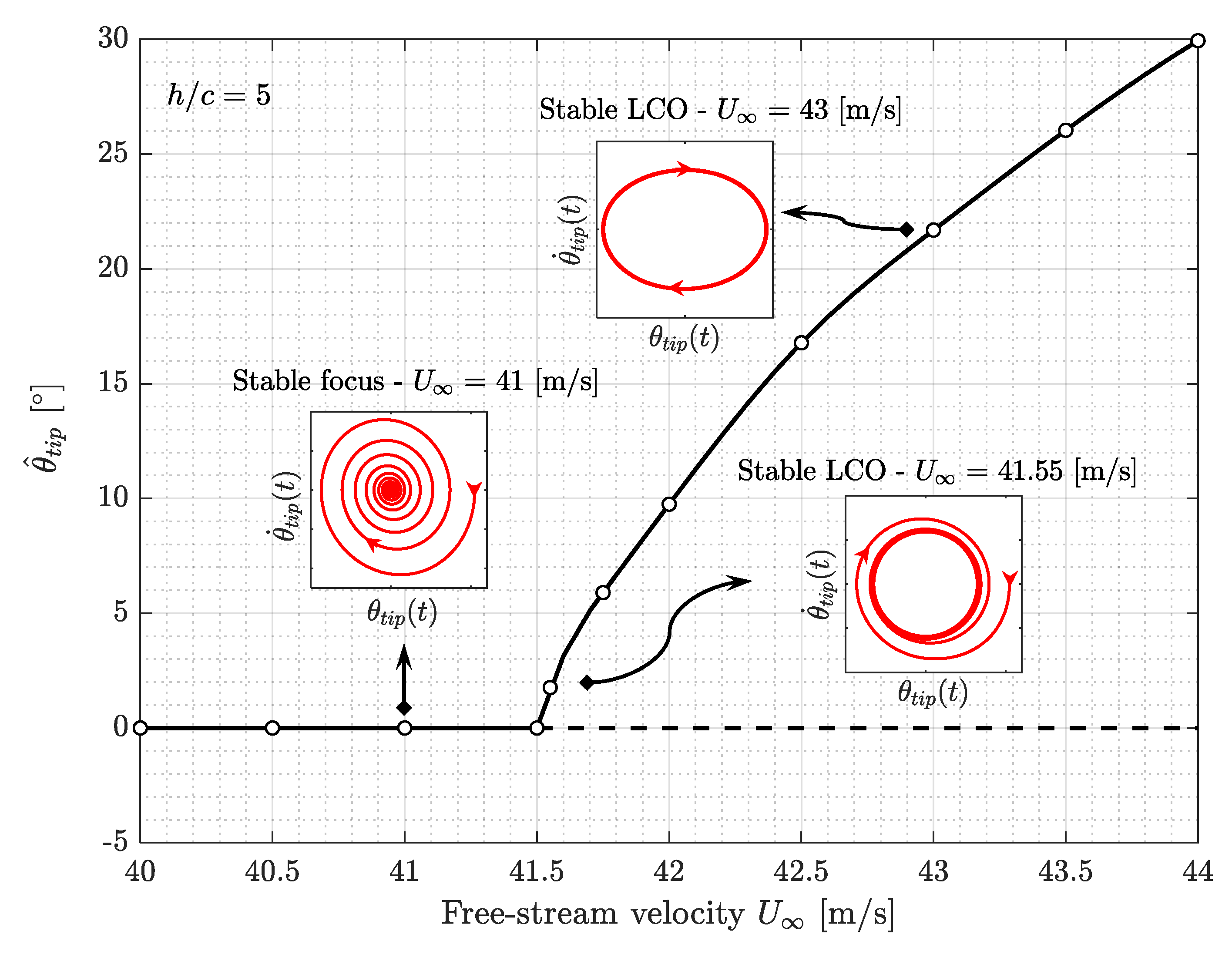
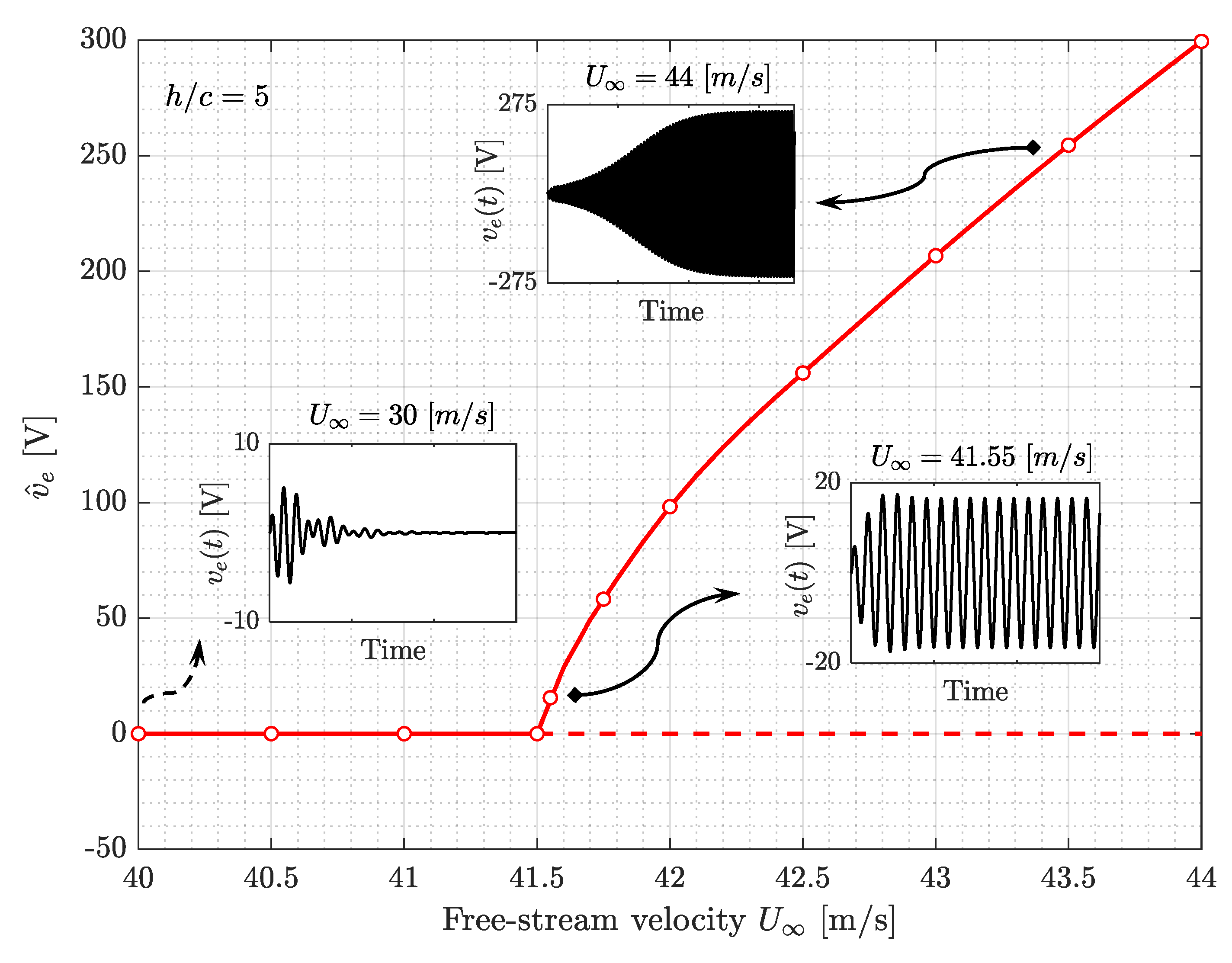
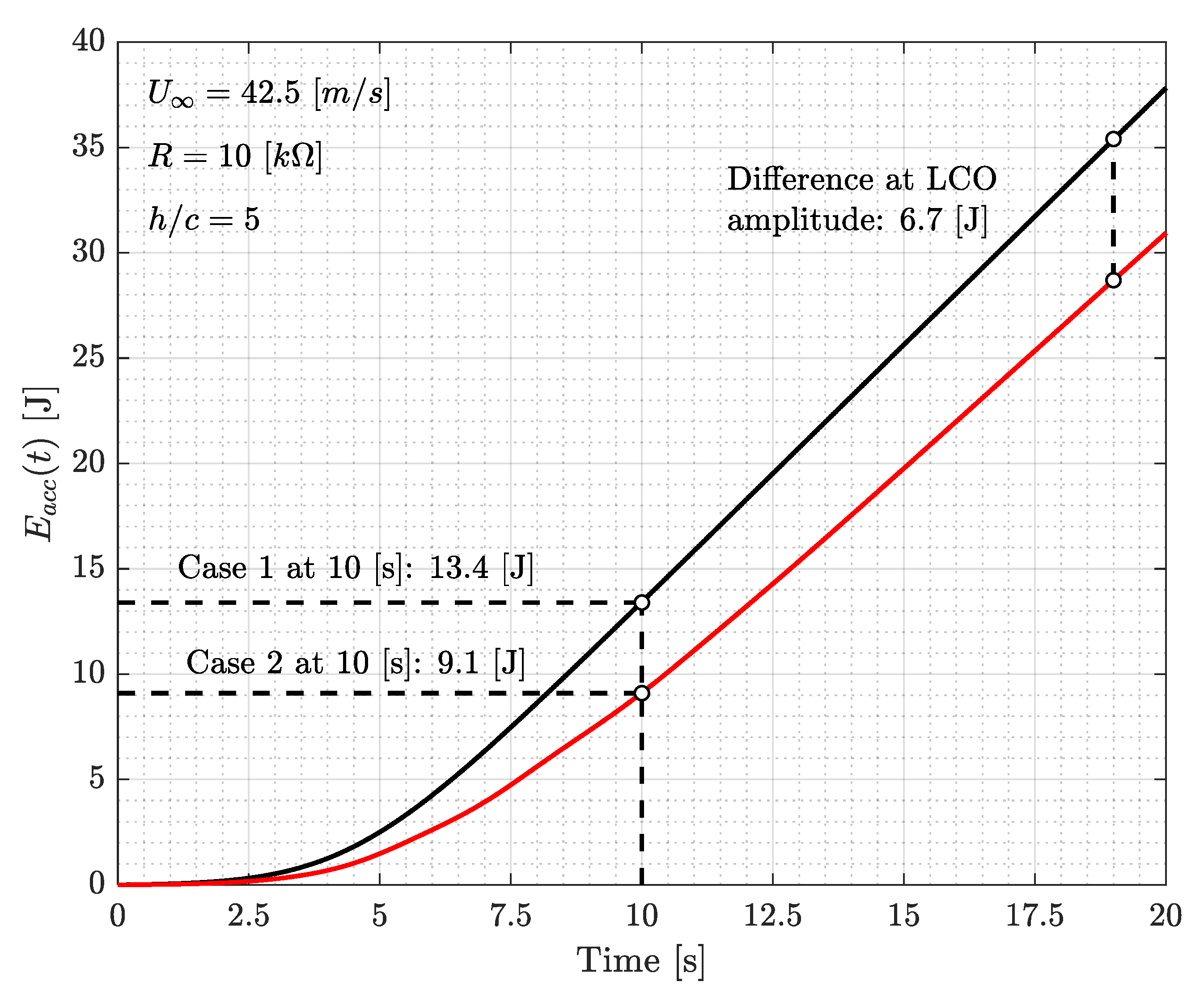
3.2.2. Postcritical Response Analysis
- Case 1: A deg rotation of the free tip is imposed to both harvesters in a symmetrical configuration.
- Case 2: A deg rotation of the free tip is imposed only to the bottom harvester (Harvester 1).
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hodges, D.H.; Pierce, G.A. Introduction to Structural Dynamics and Aeroelasticity; Cambridge University Press: Cambridge, UK, 2011; ISBN 9780511997112. [Google Scholar]
- Rostami, A.B.; Armandei, M. Renewable energy harvesting by vortex-induced motions: Review and benchmarking of technologies. Renew. Sustain. Energy Rev. 2017, 70, 193–214. [Google Scholar] [CrossRef]
- Bryant, M.; Garcia, E. Development of an aeroelastic vibration power harvester. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 8–12 March 2009; p. 728812. [Google Scholar] [CrossRef]
- Dias, J.A.C.; De Marqui, C.; Erturk, A. Three-degree-of-freedom hybrid piezoelectric-inductive aeroelastic energy harvester exploiting a control surface. AIAA J. 2014, 53, 394–404. [Google Scholar] [CrossRef] [Green Version]
- Doarée, O.; Michelin, S. Piezoelectric coupling in energy-harvesting fluttering flexible plates: Linear stability analysis and conversion efficiency. J. Fluids Struct. 2011, 27, 1357–1375. [Google Scholar] [CrossRef] [Green Version]
- Erturk, A.; Vieira, W.G.R.; De Marqui, C.; Inman, D.J. On the energy harvesting potential of piezoaeroelastic systems. Appl. Phys. Lett. 2010, 96. [Google Scholar] [CrossRef]
- Safaei, M.; Sodano, H.A.; Anton, S.R. A review of energy harvesting using piezoelectric materials: State-of-the-art a decade later (2008–2018). Smart Mater. Struct. 2019, 28. [Google Scholar] [CrossRef]
- Elahi, H.; Eugeni, M.; Gaudenzi, P. A review on mechanisms for piezoelectric-based energy harvesters. Energies 2018, 11, 1850. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-performance piezoelectric energy harvesters and their applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef] [Green Version]
- Bae, J.-S.; Inman, D.J. Aeroelastic characteristics of linear and nonlinear piezo-aeroelastic energy harvester. J. Intell. Mater. Syst. Struct. 2013, 25, 401–416. [Google Scholar] [CrossRef]
- Wu, Y.; Li, D.; Xiang, J.; Da Ronch, A. Piezoaeroelastic energy harvesting based on an airfoil with double plunge degrees of freedom: Modeling and numerical analysis. J. Fluids Struct. 2017, 74, 111–129. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Nayfeh, A.H.; Hajj, M.R. Modeling and analysis of piezoaeroelastic energy harvesters. Nonlinear Dyn. 2012, 67, 925–939. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Ghommem, M.; Nuhait, A.O.; Hajj, M.R. Nonlinear analysis and enhancement of wing-based piezoaeroelastic energy harvesters. J. Sound Vib. 2014, 333, 166–177. [Google Scholar] [CrossRef]
- Sousa, V.C.; de M Anicézio, M.; De Marqui, C., Jr.; Erturk, A. Enhanced aeroelastic energy harvesting by exploiting combined nonlinearities: Theory and experiment. Smart Mater. Struct. 2011, 20, 094007. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Hu, H.Y. Aeroelastic analysis of a non-linear airfoil based on unsteady vortex lattice model. J. Sound Vib. 2004, 276, 491–510. [Google Scholar] [CrossRef]
- Dos Santos, C.R.; Marques, F.D.; Hajj, M.R. The effects of structural and aerodynamic nonlinearities on the energy harvesting from airfoil stall-induced oscillations. JVC J. Vib. Control 2019, 25, 1991–2007. [Google Scholar] [CrossRef]
- Bao, C.; Dai, Y.; Wang, P.; Tang, G. A piezoelectric energy harvesting scheme based on stall flutter of airfoil section. Eur. J. Mech. B Fluids 2019, 75, 119–132. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Hajj, M.R.; Nayfeh, A.H. Sensitivity analysis of piezoaeroelastic energy harvesters. J. Intell. Mater. Syst. Struct. 2012, 23, 1523–1531. [Google Scholar] [CrossRef]
- Bryant, M.; Fang, A.; Garcia, E. Self-powered smart blade: Helicopter blade energy harvesting. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 7–11 March 2010; p. 764317. [Google Scholar] [CrossRef]
- Elahi, H.; Eugeni, M.; Gaudenzi, P. Design and performance evaluation of a piezoelectric aeroelastic energy harvester based on the limit cycle oscillation phenomenon. Acta Astronaut. 2019, 157, 233–240. [Google Scholar] [CrossRef]
- Eugeni, M.; Elahi, H.; Fune, F.; Lampani, L.; Mastroddi, F.; Romano, G.P.; Gaudenzi, P. Numerical and experimental investigation of piezoelectric energy harvester based on flag-flutter. Aerosp. Sci. Technol. 2020, 97, 105634. [Google Scholar] [CrossRef]
- Elahi, H.; Eugeni, M.; Fune, F.; Lampani, L.; Mastroddi, F.; Romano, G.P.; Gaudenzi, P. Performance evaluation of a piezoelectric energy harvester based on flag-flutter. Micromachines 2020, 11, 933. [Google Scholar] [CrossRef]
- Zhu, D.; Tudor, M.J.; Beeby, S.P. Strategies for increasing the operating frequency range of vibration energy harvesters: A review. Meas. Sci. Technol. 2010, 21. [Google Scholar] [CrossRef]
- Zhu, D.; Beeby, S.; Tudor, J.; White, N.; Harris, N. A novel miniature wind generator for wireless sensing applications. In Proceedings of the IEEE Sensors, Kona, HI, USA, 1–4 November 2010; pp. 1415–1418. [Google Scholar]
- Hu, G.; Wang, J.; Su, Z.; Li, G.; Peng, H.; Kwok, K.C.S. Performance evaluation of twin piezoelectric wind energy harvesters under mutual interference. Appl. Phys. Lett. 2019, 115, 1–5. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Scanlon, J.M.; McDowell, E.; Hajj, M.R. Performance enhancement of piezoelectric energy harvesters from wake galloping. Appl. Phys. Lett. 2013, 103, 033903. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Yang, Y. An impact-based broadband aeroelastic energy harvester for concurrent wind and base vibration energy harvesting. Appl. Energy 2018, 212, 233–243. [Google Scholar] [CrossRef]
- Bibo, A.; Abdelkefi, A.; Daqaq, M.F. Modeling and characterization of a piezoelectric energy harvester under combined aerodynamic and base excitations. J. Vib. Acoust. Trans. ASME 2015, 137. [Google Scholar] [CrossRef]
- Hafezi, M.; Mirdamadi, H.R. A novel design for an adaptive aeroelastic energy harvesting system: Flutter and power analysis. J. Braz. Soc. Mech. Sci. Eng. 2019, 41. [Google Scholar] [CrossRef]
- Bryant, M.; Mahtani, R.L.; Garcia, E. Wake synergies enhance performance in aeroelastic vibration energy harvesting. J. Intell. Mater. Syst. Struct. 2012, 23, 1131–1141. [Google Scholar] [CrossRef]
- McCarthy, J.M.; Deivasigamani, A.; Watkins, S.; John, S.J.; Coman, F.; Petersen, P. On the visualisation of flow structures downstream of fluttering piezoelectric energy harvesters in a tandem configuration. Exp. Therm. Fluid Sci. 2014, 57, 407–419. [Google Scholar] [CrossRef]
- Deivasigamani, A.; Mccarthy, J.; John, S.; Watkins, S.; Coman, F. Proximity effects of piezoelectric energy harvesters in fluid flow. In Proceedings of the 29th Congress of the International Council of the Aeronautical Science, St. Petersburg, Russia, 7–12 September 2014. [Google Scholar]
- Roccia, B.A.; Verstraete, M.L.; Ceballos, L.R.; Balachandran, B.; Preidikman, S. Computational study on aerodynamically coupled piezoelectric harvesters. J. Intell. Mater. Syst. Struct. 2020, 31, 1578–1593. [Google Scholar] [CrossRef]
- Kirschmeier, B.; Bryant, M. Experimental investigation of wake-induced aeroelastic limit cycle oscillations in tandem wings. J. Fluids Struct. 2018, 81, 309–324. [Google Scholar] [CrossRef]
- McCarthy, J.M.; Watkins, S.; Deivasigamani, A.; John, S.J. Fluttering energy harvesters in the wind: A review. J. Sound Vib. 2016, 361, 355–377. [Google Scholar] [CrossRef]
- Katz, J.; Plotkin, A. Low-speed aerodynamics, second edition. J. Fluids Eng. 2004, 126, 293–294. [Google Scholar] [CrossRef] [Green Version]
- Van Garrel, A. Development of a Wind Turbine Aerodynamics Simulation Module; Energy research Centre of the Netherlands ECN: Petten, The Netherlands, 2003. [Google Scholar]
- Chopra, I.; Sirohi, J. Smart Structures Theory; Cambridge University Press: Cambridge, UK, 2013; ISBN 9781139025164. [Google Scholar]
- Auricchio, F.; Carotenuto, P.; Reali, A. On the geometrically exact beam model: A consistent, effective and simple derivation from three-dimensional finite-elasticity. Int. J. Solids Struct. 2008, 45, 4766–4781. [Google Scholar] [CrossRef] [Green Version]
- Hassanpour, S.; Heppler, G.R. Approximation of infinitesimal rotations in calculus of variations. J. Guid. Control. Dyn. 2016, 39, 703–710. [Google Scholar] [CrossRef]
- Andersen, L.; Nielsen, S.R.K. Elastic Beams in Three Dimensions; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2008. [Google Scholar]
- Reddy, J.N. An Introduction to Nonlinear Finite Element Analysis, 2nd ed.; Oxford University Press: Oxford, UK, 2010; ISBN 978-0199641758. [Google Scholar]
- Lerch, R. Simulation of piezoelectric devices by two- and three-dimensional finite elements. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1990, 37, 233–247. [Google Scholar] [CrossRef]
- Allik, H.; Hughes, T.J.R. Finite element method for piezoelectric vibration. Int. J. Numer. Methods Eng. 1970, 2, 151–157. [Google Scholar] [CrossRef]
- Brannon, R. Rotation Reflection and Frame Changes Orthogonal Tensors in Computational Engineering Mechanics; IOP Publishing: Bristol, UK, 2018. [Google Scholar]
- Przemieniecki, J.S. Theory of Matrix Structural Analysis; Courier Corporation: North Chelmsford, Chelmsford, MA, USA, 1985; ISBN 0486649482. [Google Scholar]
- Beltramo, E.; Balachandran, B.; Preidikman, S. Three-dimensional formulation of a strain-based geometrically nonlinear piezoelectric beam for energy harvesting. J. Intell. Mater. Syst. Struct. 2020. submitted. [Google Scholar]
- Preidikman, S. Numerical Simulations of Interactions among Aerodynamics, Structural Dynamics, and Control Systems. Ph.D. Thesis, Department of Engineering Science and Mechanics, Virginia Polytechnic Inst. and State University, Blacksburg, VA, USA, 1998. [Google Scholar]
- Konstandinopoulos, P.; Mook, D.T.; Nayfeh, A. A Numerical Method for General, Unsteady Aerodynamics; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 1981. [Google Scholar]
- Roccia, B.A.; Preidikman, S.; Massa, J.C.; Mook, D.T. Modified unsteady vortex-lattice method to study flapping wings in hover flight. AIAA J. 2013, 51, 2628–2642. [Google Scholar] [CrossRef] [Green Version]
- Carnahan, B.; Luther, H.A. Applied Numerical Methods; Wiley: New York, NY, USA, 1969. [Google Scholar] [CrossRef]
- Roccia, B.A.; Preidikman, S.; Balachandran, B. Computational dynamics of flapping wings in hover flight: A co-simulation strategy. AIAA J. 2017, 55, 1806–1822. [Google Scholar] [CrossRef]
- De Marqui, C.; Erturk, A.; Inman, D.J. Piezoaeroelastic modeling and analysis of a generator wing with continuous and segmented electrodes. J. Intell. Mater. Syst. Struct. 2010, 21, 983–993. [Google Scholar] [CrossRef]
- De Marqui, C.; Vieira, W.G.R.; Erturk, A.; Inman, D.J. Modeling and analysis of piezoelectric energy harvesting from aeroelastic vibrations using the doublet-lattice method. J. Vib. Acoust. Trans. ASME 2011, 133. [Google Scholar] [CrossRef] [Green Version]







| Property | Value |
|---|---|
| Piezoceramic transducers | |
| Material | PZT-5A |
| Length [mm] | 400 |
| Thickness [mm] | 0.5 |
| Width [mm] | 240 |
| Electrical resistance ( [kΩ] | 10 |
| Substrate | |
| Young’s modulus [Gpa] | 70 |
| Constant [rad/s] | 0.1635 |
| Constant [s/rad] | 4.1711 × 10−4 |
| Mass density [kg/m3] | 2750 |
| Length [mm] | 800 |
| Thickness [mm] | 2 |
| Thickness [mm] | 3 |
| Airflow | |
| Air density [kg/m3] | 1.225 |
| Reynolds Number | |
| Characteristic | Present Model | De Marqui et al. | Error |
|---|---|---|---|
| (Bending) [Hz] | 1.6336 | 1.68 | 2.76% |
| (Bending) [Hz] | 10.2050 | 10.46 | 2.48% |
| (Torsion) [Hz] | 16.8463 | 16.66 | 1.11% |
| (Bending) [Hz] | 27.0155 | 27.74 | 2.61% |
| (Torsion) [Hz] | 48.0711 | 48.65 | 1.20% |
| Flutter Frequency [Hz] | 11.55 | 11.47 | 0.70% |
| Flutter Speed [m/s] | 41.05 | 40.5 | 1.35% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beltramo, E.; Pérez Segura, M.E.; Roccia, B.A.; Valdez, M.F.; Verstraete, M.L.; Preidikman, S. Constructive Aerodynamic Interference in a Network of Weakly Coupled Flutter-Based Energy Harvesters. Aerospace 2020, 7, 167. https://doi.org/10.3390/aerospace7120167
Beltramo E, Pérez Segura ME, Roccia BA, Valdez MF, Verstraete ML, Preidikman S. Constructive Aerodynamic Interference in a Network of Weakly Coupled Flutter-Based Energy Harvesters. Aerospace. 2020; 7(12):167. https://doi.org/10.3390/aerospace7120167
Chicago/Turabian StyleBeltramo, Emmanuel, Martín E. Pérez Segura, Bruno A. Roccia, Marcelo F. Valdez, Marcos L. Verstraete, and Sergio Preidikman. 2020. "Constructive Aerodynamic Interference in a Network of Weakly Coupled Flutter-Based Energy Harvesters" Aerospace 7, no. 12: 167. https://doi.org/10.3390/aerospace7120167










