Using Grey Incidence Analysis Approach in Portfolio Selection
Abstract
:1. Introduction
2. Previous Research
3. Methodology
4. Empirical Results
4.1. Data Description and Rationale for Used Factors
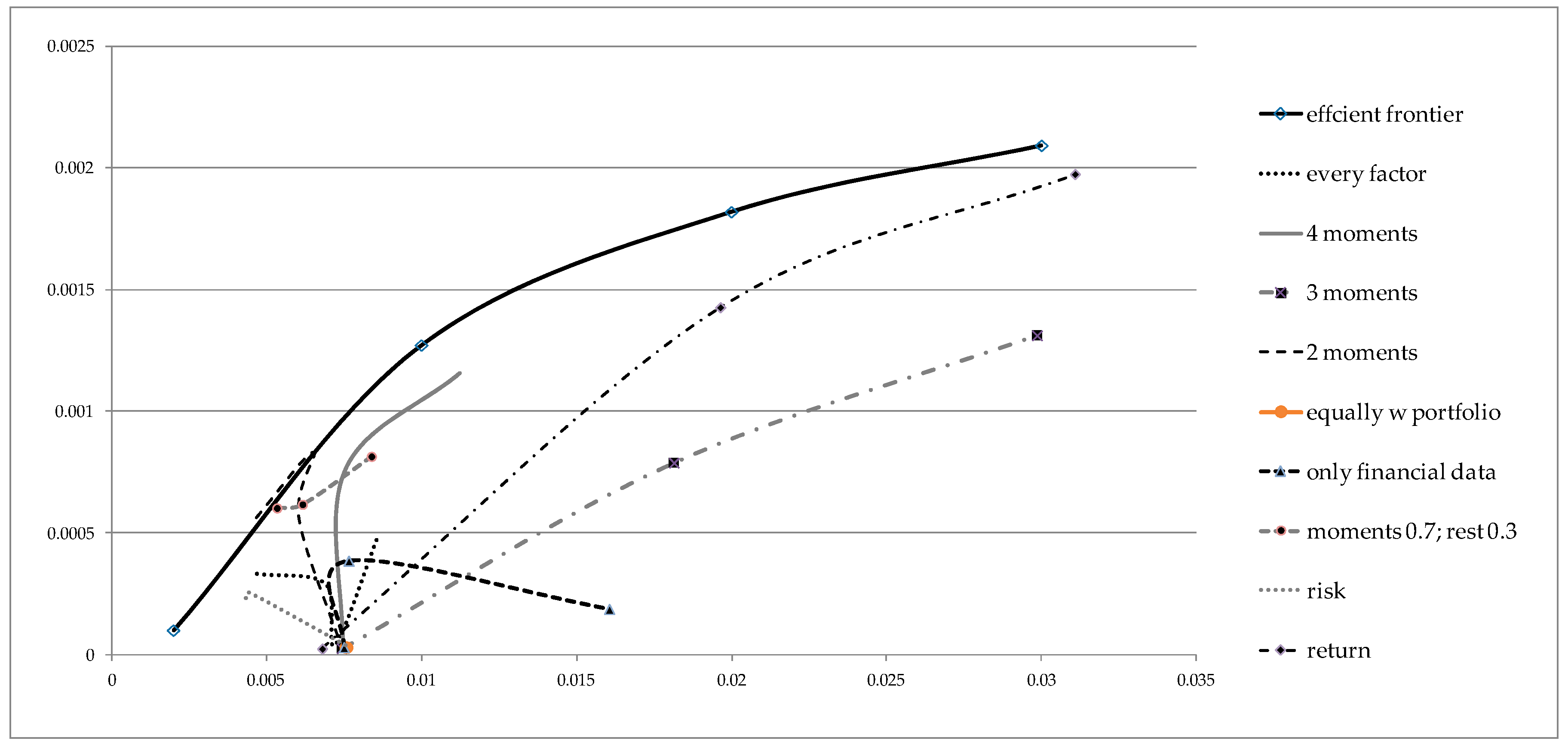
4.2. Results in Sample
5. Backtesting Portfolio Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Return Distribution: | Market: | Financial Ratios: |
|---|---|---|
| Expected return (ER) + Standard deviation (SD) − Coefficient of asymmetry (CA) + Coefficient of skewness (CS) − | Trading volume (TV) − Number of transactions (NT) − | Book to market ratio (BM) + Price to earnings ratio (PE) + Return on assets (ROA) + Return on equity (ROE) + Earnings per share (EPS) + Total business efficiency ratio (TBR) + Asset turnover ratio (ATR) + Dividends per share (DPS) + |
| ADPL h | ADRS p | ADRS2 p | ARNT l | ATGR j | ATLN o | ATPL k | AUHR j |
| BD62 b | BLJE a | CKML b | DDJH p | DLKV i | ERNT f | HDEL i | HHLD l |
| HMST l | HT m | HUPZ l | IGH q | INA d | INGR p | IPKK b | JDGT k |
| JDPL k | JMNC b | JNAF k | KOEI g | KRAS b | LEDO b | LHRC l | LKPC k |
| LKRI k | LPLH k | LRH l | MAIS l | MDKA j | OPTE m | PLAG l | PODR b |
| PTKM e | RIVP l | RIZO f | SAPN e | SLRS l | THNK i | TPNG k | TUHO l |
| ULPL k | ULJN h | VART c | VIRO b | VLEN h | ZB n | ZVZD b | - |
| Stock. | p = 0.5 | 2 mom | 4 mom | 3 mom | Only Financial | 0.7 mom; 0.3 other | Risk | Return |
|---|---|---|---|---|---|---|---|---|
| ADPL | 24 | 6 | 7 | 12 | 26 | 9 | 10 | 12 |
| ADRS | 18 | 21 | 17 | 26 | 35 | 20 | 13 | 34 |
| ADRS2 | 34 | 17 | 10 | 19 | 34 | 14 | 14 | 38 |
| ARNT | 26 | 22 | 18 | 25 | 24 | 22 | 24 | 32 |
| ATGR | 21 | 18 | 13 | 17 | 36 | 15 | 20 | 19 |
| ATLN | 3 | 14 | 9 | 14 | 6 | 2 | 18 | 5 |
| ATPL | 38 | 4 | 1 | 8 | 40 | 6 | 37 | 2 |
| AUHR | 33 | 35 | 43 | 43 | 38 | 43 | 30 | 49 |
| BD62 | 36 | 49 | 47 | 52 | 14 | 46 | 43 | 51 |
| BLJE | 49 | 53 | 52 | 21 | 5 | 52 | 54 | 48 |
| CKML | 17 | 2 | 29 | 5 | 37 | 27 | 2 | 26 |
| DDJH | 53 | 51 | 48 | 53 | 43 | 49 | 48 | 53 |
| DLKV | 52 | 32 | 16 | 29 | 32 | 34 | 40 | 23 |
| ERNT | 32 | 16 | 21 | 18 | 31 | 25 | 21 | 28 |
| HDEL | 39 | 46 | 44 | 48 | 50 | 45 | 45 | 41 |
| HHLD | 43 | 44 | 37 | 45 | 55 | 39 | 39 | 43 |
| HMST | 12 | 5 | 20 | 3 | 15 | 18 | 11 | 6 |
| HT | 45 | 8 | 4 | 6 | 20 | 17 | 9 | 39 |
| HUPZ | 46 | 31 | 55 | 47 | 18 | 54 | 33 | 40 |
| IGH | 47 | 48 | 49 | 50 | 42 | 50 | 52 | 27 |
| INA | 14 | 15 | 19 | 15 | 25 | 19 | 17 | 16 |
| INGR | 51 | 39 | 27 | 37 | 33 | 38 | 46 | 22 |
| IPKK | 30 | 38 | 39 | 39 | 45 | 36 | 35 | 37 |
| JDGT | 28 | 11 | 46 | 27 | 19 | 44 | 6 | 33 |
| JDPL | 41 | 47 | 42 | 51 | 44 | 41 | 47 | 47 |
| JMNC | 27 | 50 | 51 | 34 | 9 | 48 | 51 | 21 |
| JNAF | 8 | 12 | 33 | 4 | 11 | 26 | 4 | 17 |
| KOEI | 11 | 13 | 6 | 13 | 28 | 5 | 12 | 11 |
| KRAS | 15 | 23 | 14 | 24 | 17 | 13 | 16 | 30 |
| LEDO | 55 | 55 | 54 | 49 | 54 | 55 | 55 | 55 |
| LHRC | 9 | 3 | 3 | 7 | 21 | 3 | 26 | 3 |
| LKPC | 6 | 19 | 15 | 16 | 8 | 8 | 7 | 14 |
| LKRI | 4 | 29 | 26 | 28 | 7 | 16 | 27 | 10 |
| LPLH | 5 | 20 | 34 | 23 | 4 | 23 | 8 | 13 |
| LRH | 7 | 9 | 5 | 11 | 12 | 4 | 3 | 8 |
| MAIS | 13 | 24 | 12 | 20 | 22 | 11 | 23 | 20 |
| MDKA | 2 | 25 | 28 | 22 | 2 | 12 | 15 | 7 |
| OPTE | 54 | 37 | 31 | 36 | 49 | 42 | 42 | 42 |
| PLAG | 10 | 10 | 11 | 9 | 16 | 7 | 5 | 9 |
| PODR | 16 | 33 | 22 | 33 | 10 | 21 | 25 | 44 |
| PTKM | 50 | 52 | 53 | 54 | 48 | 53 | 50 | 52 |
| RIVP | 42 | 7 | 2 | 10 | 3 | 10 | 22 | 18 |
| RIZO | 31 | 43 | 40 | 46 | 51 | 40 | 34 | 50 |
| SAPN | 23 | 34 | 36 | 38 | 27 | 31 | 31 | 24 |
| SLRS | 22 | 27 | 41 | 35 | 13 | 35 | 28 | 31 |
| THNK | 48 | 54 | 50 | 55 | 41 | 51 | 49 | 54 |
| TPNG | 19 | 30 | 23 | 31 | 39 | 24 | 19 | 45 |
| TUHO | 1 | 1 | 8 | 2 | 1 | 1 | 1 | 4 |
| ULPL | 29 | 41 | 24 | 41 | 23 | 28 | 38 | 25 |
| ULJN | 40 | 45 | 45 | 44 | 52 | 47 | 44 | 29 |
| VART | 25 | 36 | 30 | 32 | 46 | 30 | 32 | 35 |
| VIRO | 35 | 42 | 38 | 42 | 47 | 37 | 36 | 46 |
| VLEN | 44 | 40 | 32 | 40 | 30 | 33 | 41 | 15 |
| ZB | 37 | 26 | 25 | 30 | 53 | 29 | 29 | 36 |
| ZVZD | 20 | 28 | 35 | 1 | 29 | 32 | 53 | 1 |
References
- Ang, Andrew, and Geert Bekaert. 2002. International Asset allocation With Regime Shifts. Review of Financial Studies 15: 1137–87. [Google Scholar] [CrossRef]
- Arditti, Fred, and Haim Levy. 1975. Portfolio efficiency analysis in three moments: The multiperiod case. The Journal of Finance 303: 797–809. [Google Scholar] [CrossRef]
- Arditti, Fred. 1967. Risk and the Required Return on Equity. The Journal of Finance 22: 19–36. [Google Scholar] [CrossRef]
- Athayde, Gustavo, and Renato Galvão Flôres. 1997. A CAPM with Higher Moments: Theory and Econometrics. Discussion Paper EPGE-FGV. Rio de Janeiro: EPGE/FGV. [Google Scholar]
- Banz, Rolf. 1981. The relationship between return and market value of common stocks. Journal of Financial Economics 9: 3–18. [Google Scholar] [CrossRef] [Green Version]
- Basu, Sanjoy. 1977. The Investment Performance of Common Stocks in Relation to their Price to Earnings Ratio: A Test of the Efficient Markets Hypothesis. The Journal of Finance 32: 663–82. [Google Scholar] [CrossRef]
- Briec, Walter, Kristiaan Kerstens, and Octave Jokung. 2006. Mean-variance-skewness portfolio performance gauging: A general shortage function and dual approach. Management Science 531: 135–49. [Google Scholar] [CrossRef]
- Campbell, John, and Robert Shiller. 1988. The dividend-price ratio and expectations of future dividends and discount factors. Review of Financial Studies 1: 195–228. [Google Scholar] [CrossRef]
- Campbell, John. 1987. Stock returns and the term structure. Journal of Financial Economics 18: 373–99. [Google Scholar] [CrossRef]
- Cremers, Jan-Hein, Mark Kritzman, and Sebastian Page. 2003. Portfolio Formation with Higher Moments and Plausible Utility. In Revere Street Working Paper Series in Financial Economics 272-12. Cambridge: State Street Associates. [Google Scholar]
- Chen, Hsing-Hung. 2008. Stock selection using data envelopment analysis. Industrial Management & Data Systems 108: 1255–68. [Google Scholar] [CrossRef]
- Chen, Kung, and Shimerda Thomas. 1981. An Empirical Analysis of Useful Financial Ratios. Financial Management 10: 51–60. [Google Scholar] [CrossRef]
- Datar, Vinay, Narayan Naik, and Robert Radcliffe. 1998. Liquidity and stock returns: An alternative test. Journal of Financial Markets 12: 203–19. [Google Scholar] [CrossRef]
- Deng, Ju-Long. 1982. Control problems of Grey Systems. Systems and Control Letters 5: 288–94. [Google Scholar] [CrossRef]
- Deng, Ju-Long. 1989. Introduction to Grey System Theory. The Journal of Grey Systems 1: 1–24. [Google Scholar]
- Dia, Mohamm. 2007. A Portfolio Selection Methodology Based on Data Envelopment Analysis. INFOR: Information Systems and Operational Research 47: 71–79. [Google Scholar] [CrossRef]
- Dimitropoulos, Panagiotis, and Dimitrios Asteriou. 2009. The Relationship between Earnings and Stock Returns: Empirical Evidence from the Greek Capital Market. International Journal of Economics and Finance 11: 40–50. [Google Scholar] [CrossRef]
- Edirisinghe, Nalin Chanaka, and Xin Zhang. 2007. Generalized DEA model of fundamental analysis and its application to portfolio optimization. Journal of Banking & Finance 31: 3311–35. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1988. Dividend yields and expected stock returns. Journal of Financial Economics 22: 3–25. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1992. The Cross-Section of Expected Stock Returns. The Journal of Finance 47: 427–65. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1993. Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1995. Size and Book-to-Market Factors in Earnings and Returns. The Journal of Finance 50: 131–55. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1996. Multifactor Explanations of Asset Pricing Anomalies. The Journal of Finance 51: 55–84. [Google Scholar] [CrossRef] [Green Version]
- Fama, Eugene F., and William Schwert. 1977. Asset returns and inflation. Journal of Financial Economics 5: 115–46. [Google Scholar] [CrossRef]
- Gardijan, Margareta, and Tihana Škrinjarić. 2015. Estimating investor preferences towards portfolio return distribution in investment funds. Croatian Operational Research Review 62: 1–16. [Google Scholar] [CrossRef]
- Guidolin, Massimo, and Allan Timmermann. 2007. Asset allocation under multivariate regime switching. Journal of Economic Dynamics and Control 31: 3503–44. [Google Scholar] [CrossRef]
- Guidolin, Massimo, and Allan Timmermann. 2008. International Asset allocation under Regime Switching, Skew, and Kurtosis Preferences. The Review of Financial Studies 21: 889–935. [Google Scholar] [CrossRef]
- Huang, Kuang Yu, and Chuen-Jiuan Jane. 2008. An Automatic Stock Market Forecasting and Portfolio Selection Mechanism Based on VPRS, ARX and Grey System. Paper presented at IEEE Asia-Pacific Services Computing Conference, Yilan, Taiwan, December 9–12. [Google Scholar]
- Huang, Kuang Yu, Chuen-Jiuan Jane, and Ting-Cheng Chang. 2008. A RS Model for Stock Market Forecasting and Portfolio Selection Allied with Weight Clustering and Grey System Theories. Paper presented at IEEE Congress on Evolutionary Computation, CEC 2008, Hong Kong, China, June 1–6; pp. 1240–46. [Google Scholar] [CrossRef]
- Hur, Seok-Kyun, Chune Young Chung, and Chang Liu. 2018. Is Liquidity Risk Priced? Theory and Evidence. Sustainability 10: 1809. [Google Scholar] [CrossRef]
- Hur, Seok-Kyun, and Chune Young Chung. 2018. A novel measure of liquidity premium: Application to the Korean stock market. Applied Economics Letters 25: 211–15. [Google Scholar] [CrossRef]
- Hwang, Soosung, and Stephen Satchell. 1999. Modeling emerging market risk premia using higher moments. International Journal of Finance and Economics 44: 271–96. [Google Scholar] [CrossRef]
- Jane, Chuen-Jiuan, and Yu Kuang Huang. 2013. A Fusion Model for Stock selection Based on Decision Tree, Artificial Neural Network and Grey Relational Analysis. International Journal of Kansei Information 4: 115–22. [Google Scholar]
- Jondeau, Eric, and Michael Rockinger. 2006. Optimal portfolio allocation under higher moments. European Financial Management 121: 29–55. [Google Scholar] [CrossRef]
- Jurczenko, Emmanuel, and Bertrand Maillet. 2005. The Four-moment Capital Asset Pricing Model: Between Asset Pricing and Asset Allocation. In Multi-Moment Asset Allocation and Pricing Models. New York: John Wiley and Sons. [Google Scholar]
- Knight, John, and Stephen Satchell. 2002. Performance Measurement in Finance. Oxford: Elsevier Science Ltd. [Google Scholar]
- Korzeniewski, Jerzy. 2018. Efficient Stock Portfolio Construction by Means of Clustering. Folia Oeconomica 1: 85–92. [Google Scholar] [CrossRef]
- Kothari, Smitu P., and Jay Shanken. 1997. Book-to-market, dividend yield, and expected market returns: A time series analysis. Journal of Financial Economics 44: 169–203. [Google Scholar] [CrossRef]
- Kroll, Yoram, Haim Levy, and Harry Markowitz. 1984. Mean-Variance Versus Direct Utility Maximization. The Journal of Finance 39: 47–61. [Google Scholar] [CrossRef]
- Kuo, Yiyo, Taho Yang, and Guan-Wei Huang. 2008. The use of a grey-based Taguchi method for optimizing multi-response simulation problems. Engineering Optimization 40: 517–28. [Google Scholar] [CrossRef]
- Lewellen, Jonathan. 2004. Predicting returns with financial ratios. Journal of Financial Economics 742: 209–35. [Google Scholar] [CrossRef]
- Li, Hong-Yi, Chu Zhang, and Di Zhao. 2010. Stock Investment Value Analysis Model Based on AHP and Grey Relational Degree. Management Science and Engineering 4: 1–6. [Google Scholar]
- Liu, Sifeng, and Yi Lin. 2006. Grey Information Theory and Practical Applications. New York: Springer. [Google Scholar]
- Liu, Sifeng, and Yi Lin. 2010. Grey Systems, Theory and Applications. Berlin/Heidelberg: Springer. [Google Scholar]
- Liu, Sifeng, Yingjie Yang, and Jeffery Forrest. 2016. Grey Data Analysis: Methods, Models and Applications. Singapore: Springer Science + Business Media. [Google Scholar]
- Liu, Weimin. 2006. A liquidity-augmented capital asset pricing model. Journal of Financial Economics 823: 631–71. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio Selection. The Journal of Finance 7: 77–91. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1959. Portfolio Selection: Efficient Diversification of Investments. New York: Wiley. [Google Scholar]
- Ministry of Finance. 2018. Available online: https://www.mfin.hr (accessed on 13 December 2018).
- Mohammadi Pour, Rahmatollah, Zhaleh Alavimoghadam, and Adel Fatemi. 2016. Comparison of Selected Performance of Portfolio Investment Companies by Using of Grey Forecasting and Johnson’s Index in Tehran Stock Exchange Market. Advances in Mathematical Finance & Applications 1: 15–28. [Google Scholar]
- Muhammad, Noor, and Frank Scrimgeour. 2014. Stock Returns and Fundamentals in the Australian Market. Asian Journal of Finance & Accounting 6: 271–90. [Google Scholar] [CrossRef]
- Müller, Sigrid, and Mark Machina. 1987. Moment preferences and polynomial utility. Economics Letters 23: 349–53. [Google Scholar] [CrossRef]
- Palepu, Krishna, and Paul Healy. 2010. Business Analysis & Valuation: Using Financial Statements, 4th ed. Nashville: South-Western College Pub. [Google Scholar]
- Pástor, Ľuboš, and Robert Stambaugh. 2003. Liquidity risk and expected stock returns. Journal of Political Economy 1113: 642–85. [Google Scholar] [CrossRef]
- Pulley, Lawrence. 1981. A General Mean-Variance Approximation to Expected Utility for Short Holding Periods. Journal of Financial and Quantitative Analysis 16: 361–73. [Google Scholar] [CrossRef]
- Reinganum, Marc. 1981. Misspecification of asset pricing: Empirical anomalies based on earnings yields and market values. Journal of Financial Economics 9: 19–46. [Google Scholar] [CrossRef]
- Salardini, Firoozeh. 2013. An AHP-GRA method for asset allocation: A case study of investment firms on Tehran Stock Exchange. Decision Science Letters 2: 275–80. [Google Scholar] [CrossRef]
- Shiller, Robert. 2005. Irrational Exuberance, 2nd ed. Princeton: Princeton University Press. [Google Scholar]
- Singh, Arjun, and Raymond Schmidgall. 2002. Analysis of financial ratios commonly used by US lodging financial executives. Journal of Retail & Leisure Property 2: 201–13. [Google Scholar] [CrossRef]
- Steuer, Ralph, Yue Qi, and Markus Hirschberger. 2008. Portfolio Selection in the Presence of Multiple Criteria. In Handbook of Financial Engineering. New York: Springer Science, pp. 3–24. [Google Scholar]
- Škrinjarić, Tihana. 2018a. Revisiting Herding Investment Behavior on the Zagreb Stock Exchange: A Quantile Regression Approach. Econometric Research in Finance 3: 119–62. [Google Scholar]
- Škrinjarić, Tihana. 2018b. Testing for Seasonal Affective Disorder on Selected CEE and SEE Stock Markets. Risks 6: 140. [Google Scholar] [CrossRef]
- Vidović, Jelena. 2013. Investigation of Stock Illiquidity on Central and South East European markets in Naive Portfolio Framework. Economic Thought and Practice 22: 537–50. [Google Scholar]
- Wei, Guiwu. 2011. Grey Relational Analysis Model for Dynamic Hybrid Multiple Attribute Decision Making. Knowledge-Based Systems 24: 672–79. [Google Scholar] [CrossRef]
- Wu, Liansheng. 2000. A Survey and An Analysis of Investor’s Demands for Listed Companies’ Accounting Information. Economic Research Journal 4: 41–48. [Google Scholar]
- ZSE. 2018. Available online: https://www.zse.hr (accessed on 1 November 2018).
| 1 | Liquid in terms of number of transactions. Although research exists on how (il)liquidity affects stock returns, here we include more liquid stocks due to having more data to make calculations with. In 2017, in total 93 stocks were traded on ZSE. Problems with liquidity are not something new for ZSE. Namely, as Škrinjarić (2018a) states: in the period from September 2014 until May 2018, there were only 9 stocks which were traded at least 90% of the time, 17 with 75%, 25 with 60% and 37 with 30% of the whole period. The usual approach is to pick the liquid stocks which have been traded most frequently in a period. More details can be seen in Škrinjarić (2018b) or Vidović (2013). |
| 2 | Moreover, we do not choose to invest only in the best stock, due to diversification possibilities within Modern Portfolio Theory. |
| 3 | Sharpe ratio was calculated based upon the 91 day Treasury bill interest rate of the Ministry of Finance (2018) in Croatia which was equal to 0.36% in the observed period. |
| 4 | Values of 1 and 2 were chosen based upon Guidolin and Timmermann (2008) who used 2, 5 and 10; Ang and Bekaert (2002) where authors used 5 and 10. Guidolin and Timmermann (2007) showed that the results of ranking are robust if the coefficient is in the interval (0, 20]. Additionally, we calculated Certainty Equivalent for values 5 and 10 and the rankings remained the same. Quadratic utility function was chosen for the calculation of Certainty Equivalent due to results in Pulley (1981), Kroll et al. (1984) and Cremers et al. (2003) who compared the rankings of the quadratic utility function to other functional forms of investor’s utility and the results showed that the differences were nonsignificant. |
| 5 | Maximization of portfolio return problems were chosen since these portfolios could have enabled an investor to achieve the best results in terms of return series. Other 3 scenarios from Table 3 are omitted, but are available upon request; the portfolio values have similar relations one to another. |


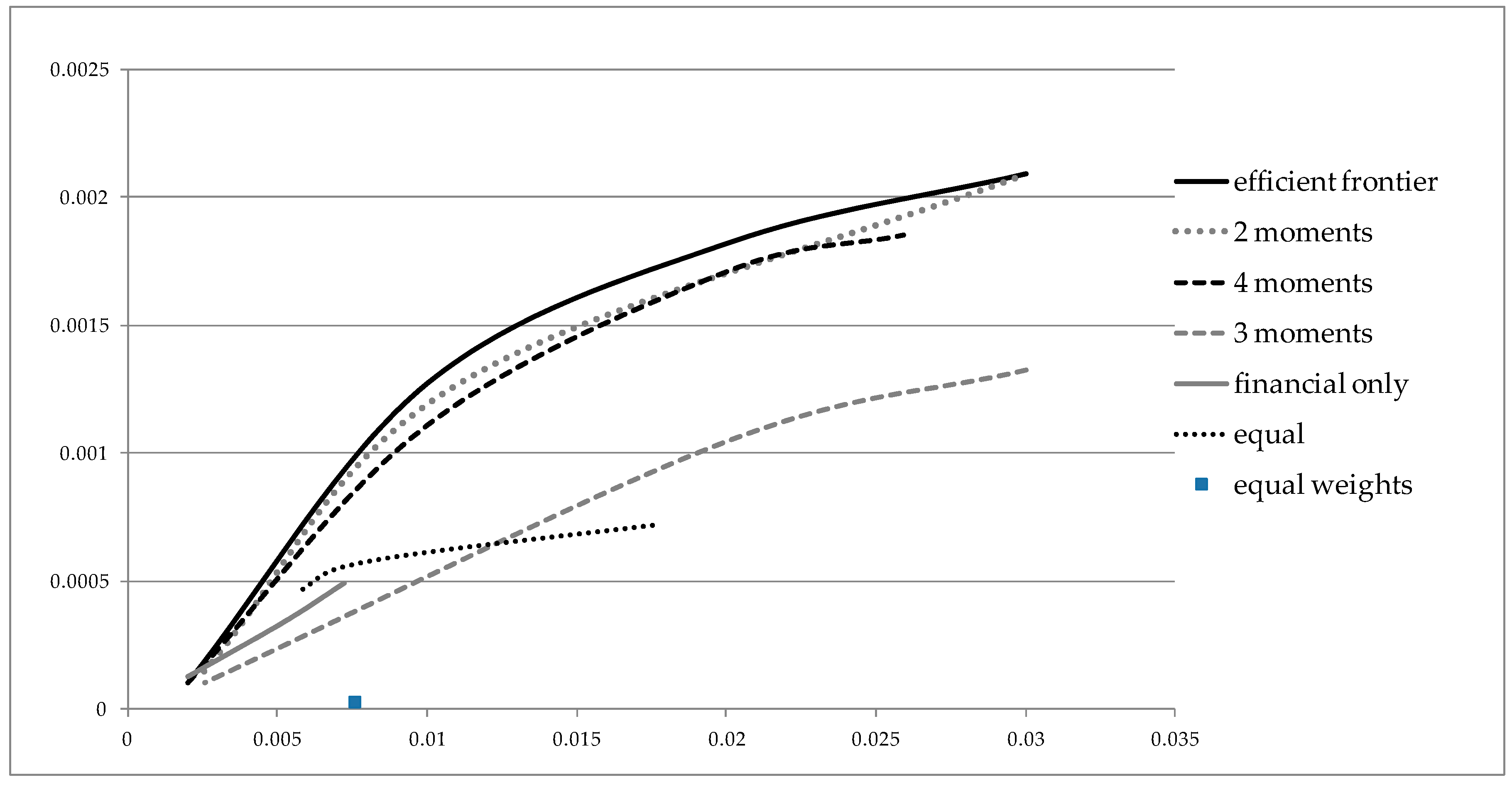
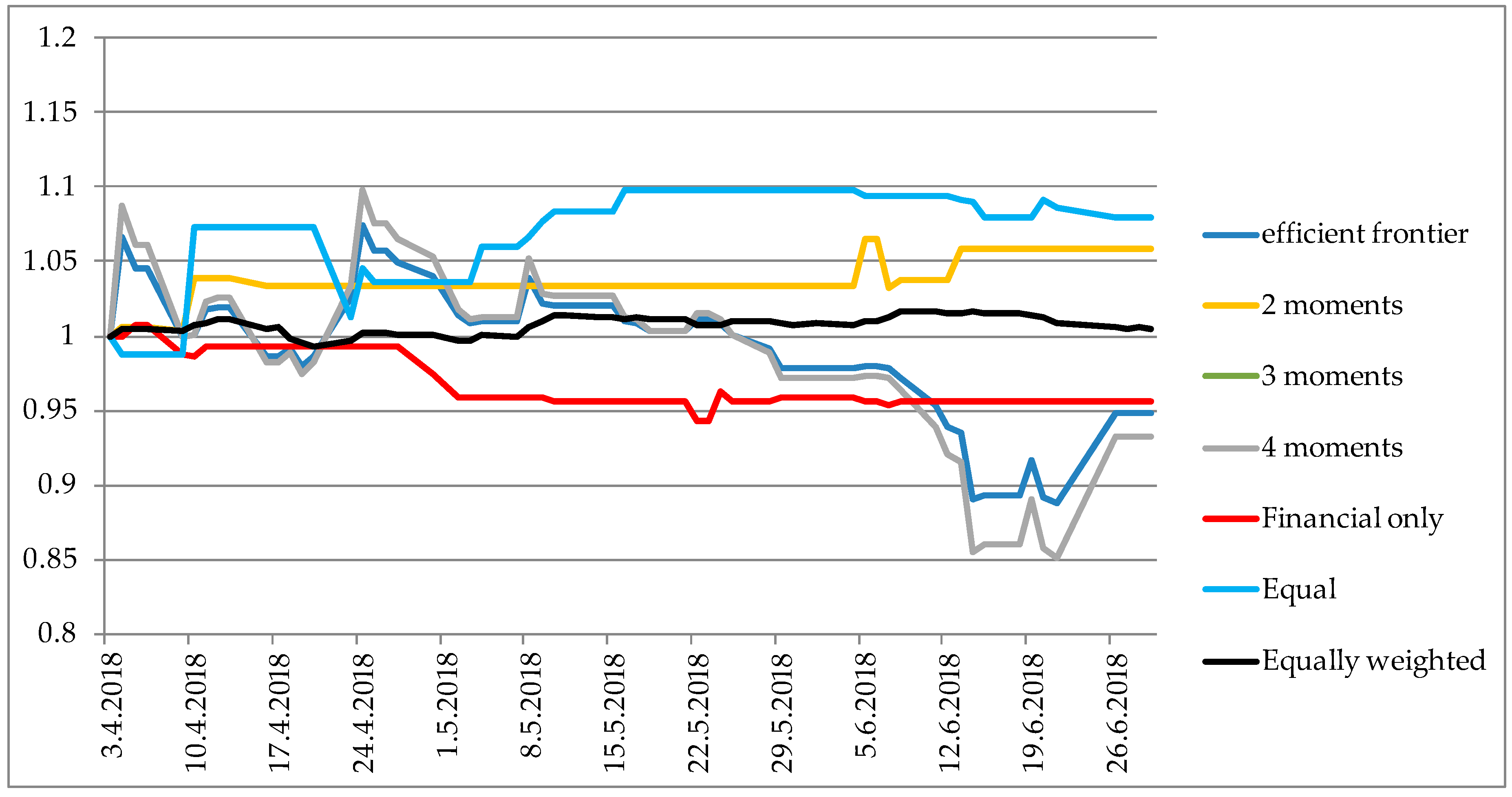
| Factor | Average | Min | Max |
|---|---|---|---|
| SD | 0.020 | 0.003 | 0.073 |
| CS | 23.570 | 3.194 | 127.755 |
| TV | 637,612.691 | 800.000 | 7,892,835.000 |
| NT | 2914.218 | 260.000 | 16,276.000 |
| ER | 0.000 | −0.003 | 0.003 |
| CA | 0.722 | −6.847 | 9.195 |
| BM | 2.923 | 0.001 | 78.930 |
| PE | 5.121 | −30.875 | 79.841 |
| ROA | 0.428 | −2.230 | 26.362 |
| ROE | −0.343 | −50.453 | 68.125 |
| EPS | 1584.294 | 0.028 | 45,894.157 |
| TBR | 1.047 | 0.201 | 2.673 |
| ATR | 7.926 | 0.007 | 208.657 |
| DPS | 41.831 | 0.000 | 1649.937 |
| Stock | p = 0.5 | Stock | p = 0.5 |
|---|---|---|---|
| ADPL | 0.5303 | KRAS | 0.5418 |
| ADRS | 0.5401 | LEDO | 0.4358 |
| ADRS2 | 0.5213 | LHRC | 0.5535 |
| ARNT | 0.5276 | LKPC | 0.569 |
| ATGR | 0.5364 | LKRI | 0.5771 |
| ATLN | 0.5886 | LPLH | 0.5746 |
| ATPL | 0.518 | LRH | 0.5652 |
| AUHR | 0.5224 | MAIS | 0.5454 |
| BD62 | 0.5205 | MDKA | 0.5889 |
| BLJE | 0.4855 | OPTE | 0.4592 |
| CKML | 0.5406 | PLAG | 0.5526 |
| DDJH | 0.461 | PODR | 0.5417 |
| DLKV | 0.4702 | PTKM | 0.4829 |
| ERNT | 0.5224 | RIVP | 0.511 |
| HDEL | 0.5152 | RIZO | 0.5229 |
| HHLD | 0.5104 | SAPN | 0.533 |
| HMST | 0.5458 | SLRS | 0.5356 |
| HT | 0.4984 | THNK | 0.4873 |
| HUPZ | 0.4959 | TPNG | 0.5398 |
| IGH | 0.4874 | TUHO | 0.6111 |
| INA | 0.5435 | ULPL | 0.5248 |
| INGR | 0.4778 | ULJN | 0.514 |
| IPKK | 0.5242 | VART | 0.5281 |
| JDGT | 0.5255 | VIRO | 0.521 |
| JDPL | 0.5139 | VLEN | 0.5076 |
| JMNC | 0.5269 | ZB | 0.5198 |
| JNAF | 0.5537 | ZVZD | 0.5389 |
| KOEI | 0.5477 |
| Portfolio | Realized Return (%) | Standard Deviation (%) | Sharpe Ratio | Certainty Equivalent (CE) | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 mom | 4 mom | |||||
| Efficient frontier | Min risk | 0.827 | 0.462 | 1.399 | 0.008 | 0.008 | 0.347 | 1.777 |
| Portfolio 1 | 0.827 | 0.462 | 1.788 | 0.008 | 0.008 | 0.347 | 1.777 | |
| Portfolio 2 | −3.567 | 3.455 | −1.032 | −0.036 | −0.037 | −0.679 | −0.880 | |
| Max return | −5.152 | 4.520 | −1.140 | −0.053 | −0.054 | −0.766 | −1.038 | |
| 2 moments | Min risk | 0.941 | 0.797 | 1.181 | 0.009 | 0.009 | 0.442 | 1.724 |
| Portfolio 1 | 1.382 | 0.713 | 1.937 | 0.014 | 0.014 | −0.084 | 1.194 | |
| Portfolio 2 | 2.024 | 0.755 | 2.681 | 0.020 | 0.020 | 0.143 | 1.695 | |
| Max return | 5.917 | 1.388 | 4.262 * | 0.059 | 0.059 | −0.194 | −1.081 | |
| 3 moments | Min risk | 0.197 | 0.591 | 0.333 | −0.044 | −0.044 | 0.025 | 0.594 |
| Portfolio 1 | −2.660 | 1.067 | −2.493 | −0.018 | −0.018 | 0.714 | 1.778 | |
| Portfolio 2 | −1.792 | 0.746 | −2.403 | −0.027 | −0.027 | 0.747 * | 1.845 * | |
| Max return | −4.367 | 1.817 | −2.403 | −0.002 | −0.002 | 0.721 | 1.819 | |
| 4 moments | Min risk | −0.223 | 0.952 | −0.235 | −0.002 | −0.002 | 0.304 | −0.178 |
| Portfolio 1 | 2.790 | 0.951 | 2.935 | 0.028 | 0.028 | −0.927 | −1.336 | |
| Portfolio 2 | −0.563 | 2.597 | −0.217 | −0.006 | −0.006 | −0.590 | −0.850 | |
| Max return | −6.778 | 5.960 | −1.137 | −0.070 | −0.071 | −0.784 | −1.057 | |
| Financial only | Min risk | 0.311 | 0.615 | 0.506 | −0.044 | −0.044 | −0.850 | −1.353 |
| Portfolio 1 | 0.196 | 0.383 | 0.512 | 0.002 | 0.002 | −0.851 | −1.352 | |
| Portfolio 2 | 0.161 | 0.319 * | 0.505 | 0.002 | 0.002 | −0.848 | −1.343 | |
| Max return | −4.367 | 1.817 | −2.403 | 0.003 | 0.003 | 0.721 | 1.819 | |
| Equal | Min risk | −1.677 | 0.812 | −2.065 | −0.017 | −0.017 | −1.395 | −2.722 |
| Portfolio 1 | 1.371 | 1.017 | 1.349 | 0.014 | 0.014 | −1.456 | −2.713 | |
| Portfolio 2 | 3.888 | 1.684 | 2.309 | 0.039 | 0.039 | −0.751 | −1.010 | |
| Max return | 7.977 * | 3.065 | 2.602 | 0.079 * | 0.079 * | 0.262 | 0.793 | |
| Equal weights | ||||||||
| - | 0.470 | 0.593 | 0.793 | 0.005 | 0.005 | −0.441 | 0.135 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Škrinjarić, T.; Šego, B. Using Grey Incidence Analysis Approach in Portfolio Selection. Int. J. Financial Stud. 2019, 7, 1. https://doi.org/10.3390/ijfs7010001
Škrinjarić T, Šego B. Using Grey Incidence Analysis Approach in Portfolio Selection. International Journal of Financial Studies. 2019; 7(1):1. https://doi.org/10.3390/ijfs7010001
Chicago/Turabian StyleŠkrinjarić, Tihana, and Boško Šego. 2019. "Using Grey Incidence Analysis Approach in Portfolio Selection" International Journal of Financial Studies 7, no. 1: 1. https://doi.org/10.3390/ijfs7010001
APA StyleŠkrinjarić, T., & Šego, B. (2019). Using Grey Incidence Analysis Approach in Portfolio Selection. International Journal of Financial Studies, 7(1), 1. https://doi.org/10.3390/ijfs7010001






