First-Year Mathematics and Its Application to Science: Evidence of Transfer of Learning to Physics and Engineering
Abstract
:1. Introduction
2. Literature Review
2.1. Transfer in Science/Engineering Educational Research
2.2. Quantitative Measures of Transfer
- (i)
- A student gave the correct answers in both sections. His or her transfer score was 2, and it is assumed that transfer of learning occurred;
- (ii)
- A student gave the wrong answer in a mathematics question; however, he or she answered correctly on its corresponding non-mathematics question. A score of 1 was given, as it was considered that to some extent, transfer of learning had occurred;
- (iii)
- If students gave a right answer in a mathematics section, but did not get the corresponding question in non-mathematics section, a score of 0 was awarded;
- (iv)
- If students answered incorrectly in both questions, a score of 0 was given.
- Can transfer of mathematics learning be observed in the biology, molecular bioscience, engineering, and physics exam performances?
- How is transfer related to overall attainment in mathematics and science/engineering courses?
- What are the relationships between general educational attainment (university entrance rank), mathematics attainment, science/engineering attainment, and the transfer of learning between mathematics and science/engineering?
3. Materials and Methods
3.1. The Mathematics and Science Courses Examined and Their Assessment
3.2. Operationalisation of the Transfer of Mathematics
3.3. Demonstration of Calculation of the Transfer Scores and the Transfer Index
3.4. ATAR-Adjusted Transfer Index
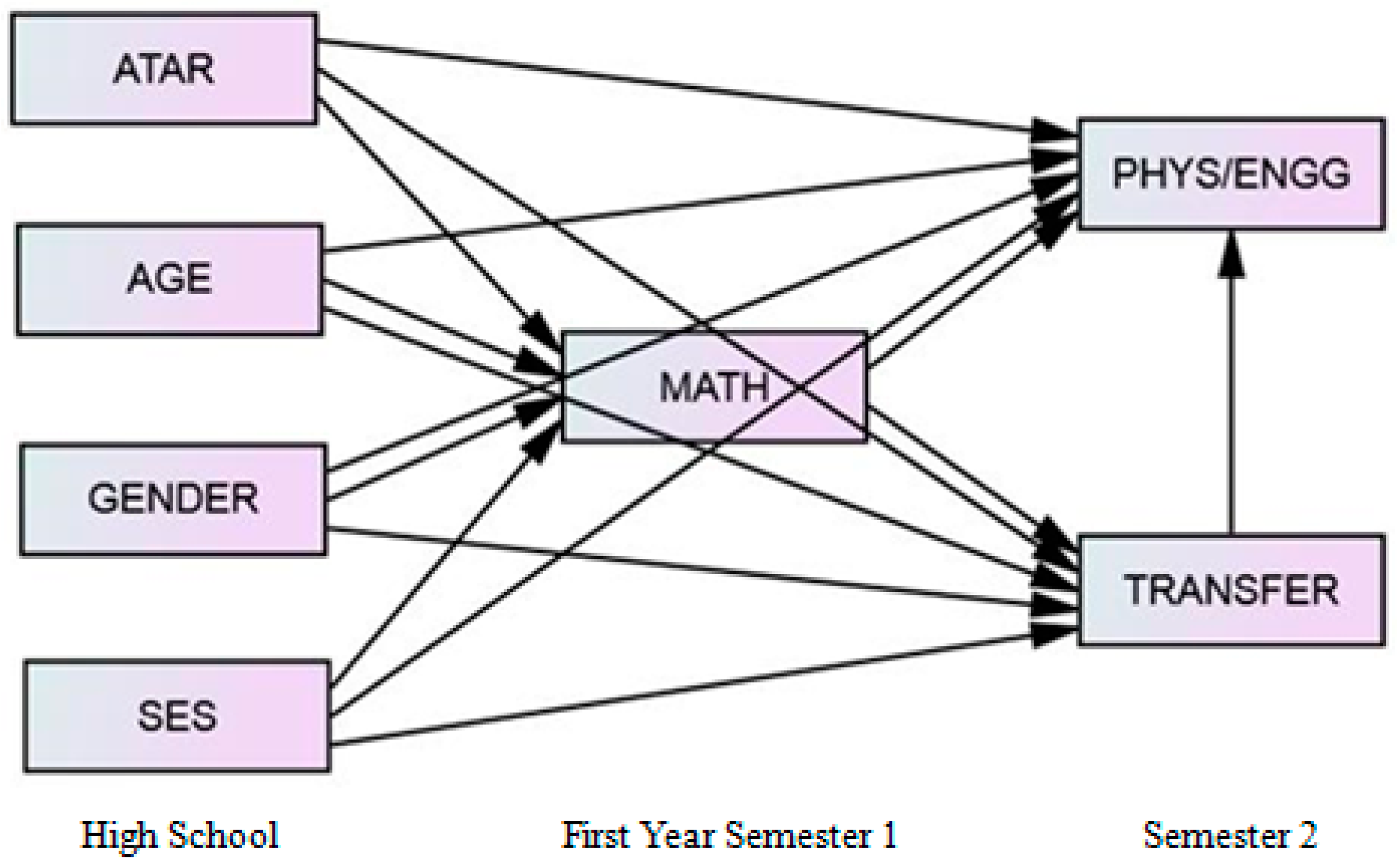
3.5. Modeling the Relationships between Transfer and Attainment in Mathematics and Science/Engineering
4. Results
4.1. Can Transfer of Mathematics Learning be Observed in Biology, Molecular Bioscience, Engineering and Physics Exam Performance?
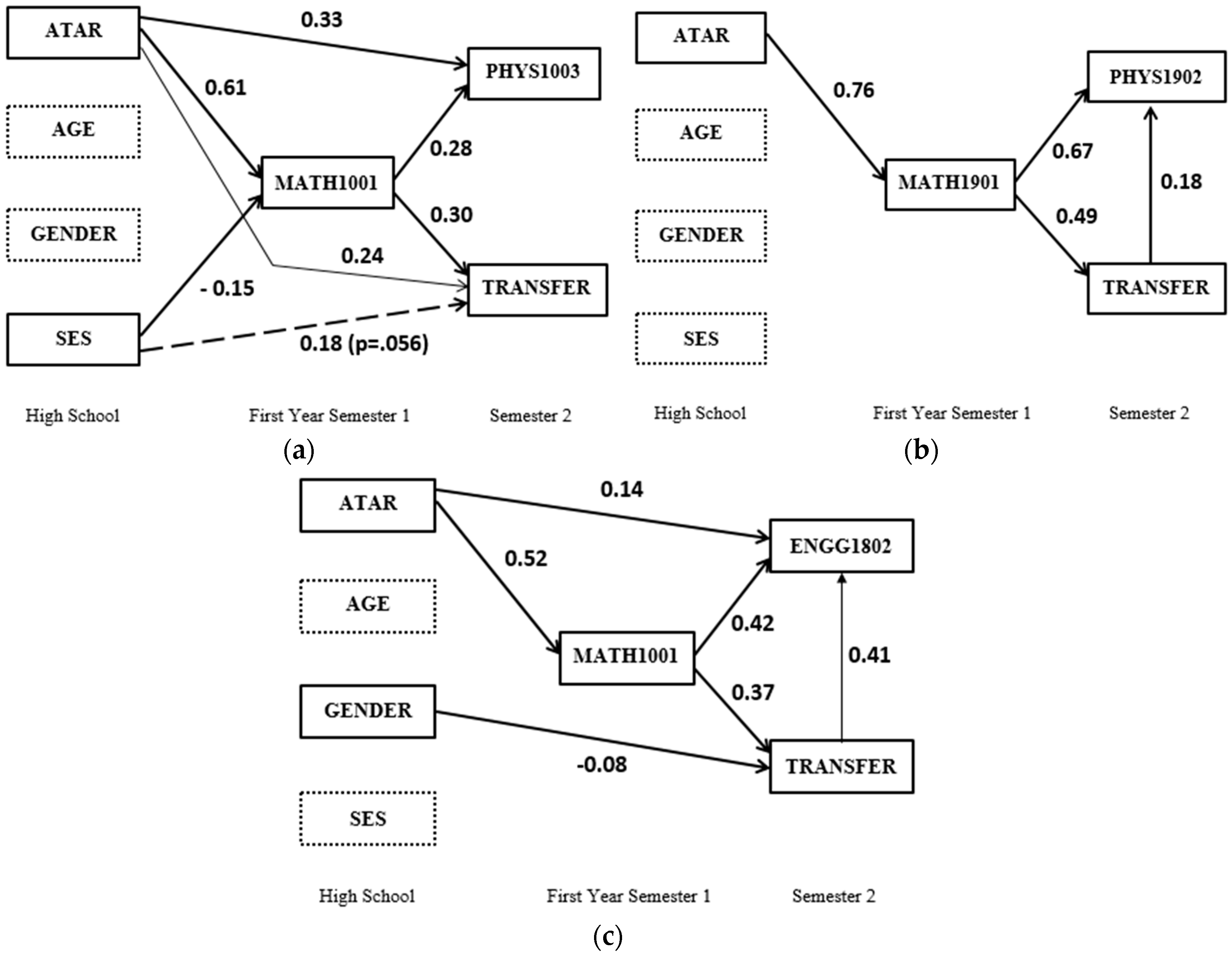
4.2. How Is Transfer Related to Overall Attainment in Mathematics and Physics/Engineering Courses?
4.3. What Are the Relationships between General Educational Attainment (University Entrance Rank), Mathematics Attainment, Physics/Engineering Attainment, and the Transfer of Learning between Mathematics and Physics/Engineering?
5. Discussion
5.1. Transfer from Mathematics to Science
5.2. Relationships between Transfer and Educational Attainment
5.3. Strengths, Limitations, and Insights for Future Transfer Research
5.4. Implications for Teaching and Learning Science
Author Contributions
Conflicts of Interest
References
- Australian Industry Group. Lifting Our Science, Technology, Engineering and Maths (STEM) Skills. 2013. Available online: http://www.utas.edu.au/__data/assets/pdf_file/0005/368546/lifting_our_stem_skills_13.pdf (accessed on 28 November 2017).
- Office of the Chief Scientist. Mathematics, Engineering & Science in the National Interest. 2012. Available online: http://www.chiefscientist.gov.au/2012/05/mes-report/ (accessed on 28 November 2008).
- Stokke, A. What to Do about Canada’s Declining Math Scores. 2015. Available online: https://www.cdhowe.org/sites/default/files/attachments/research_papers/mixed/commentary_427.pdf (accessed on 28 November 2017).
- Government of India. Annual Report 2013–14; Department of Science and Technology: New Delhi, India, 2014. Available online: http://www.dst.gov.in/annual-report-2013-14-0 (accessed on 28 November 2017).
- Science Council of Japan. Nihon no Tenbou—Rigaku Kougaku Karano Teigen (Prospects of Japan: Suggestions from science and engineering). 2010. Available online: http://www.scj.go.jp/ja/info/kohyo/pdf/kohyo-21-tsoukai-3.pdf (accessed on 28 November 2017).
- The Royal Society. Vision for Science and Mathematics Education. 2014. Available online: https://royalsociety.org/education/policy/vision/ (accessed on 28 November 2017).
- National Research Council. The Mathematical Sciences in 2025; National Academies Press: Washington, DC, USA, 2013. [Google Scholar]
- U.S. Congress Joint Economic Committee. STEM Education: Preparing for the Jobs of the Future. 2012. Available online: https://www.jec.senate.gov/public/index.cfm/democrats/2012/4/stem-education-preparing-jobs-of-the-future (accessed on 28 November 2017).
- Massachusetts Institute of Technology. Strategic Plan 2011–2016: From Imagination to Impact. 2010. Available online: http://odge.mit.edu/wp-content/uploads/2012/09/ODGE-Strategic-Plan-web.pdf (accessed on 28 November 2017).
- U.S. Department of Education. STEM 2026: A Vision for Innovation in STEM Education. 2016. Available online: https://innovation.ed.gov/files/2016/09/AIR-STEM2026_Report_2016.pdf (accessed on 28 November 2017).
- Bransford, J.D.; Brown, A.L.; Cocking, R.R. How People Learn: Brain, Mind, Experience, and School; National Academy Press: Washington, DC, USA, 1999. [Google Scholar]
- Mayer, R.E.; Wittrock, M.C. Problem-solving transfer. In Handbook of Educational Psychology; Berliner, D.C., Calfee, R.C., Eds.; Simon & Schuster Macmillan: New York, NY, USA, 1996. [Google Scholar]
- Thorndike, E.L.; Woodworth, R.S. The influence of improvement in one mental function upon the efficiency of other functions. Psychol. Rev. 1901, 8, 247–261. [Google Scholar]
- Karakok, G. Students’ Transfer of Learning of Eigenvalues and Eigenvectors: Implementation of Actor-Oriented Transfer Framework; ProQuest LLC: Ann Arbor, MI, USA, 2009. [Google Scholar]
- Lobato, J.; Rhodehamel, B.; Hohensee, C. “Noticing” as an alternative transfer of learning process. J. Learn. Sci. 2012, 21, 433–482. [Google Scholar] [CrossRef]
- Bock, D.D.; Deprez, J.; Dooren, W.V.; Roelens, M.; Verschaffel, L. Abstract or concrete examples in learning mathematics? A replication and elaboration of Kaminski, Sloutsky, and Heckler’s study. J. Res. Math. Educ. 2011, 42, 109–126. [Google Scholar] [CrossRef]
- Fyfe, E.R.; McNeil, N.M.; Borjas, S. Benefits of “concreteness fading” for children’s mathematics understanding. Learn. Instr. 2015, 35, 104–120. [Google Scholar] [CrossRef]
- McNeil, N.; Fyfe, E. “Concreteness fading” promotes transfer of mathematical knowledge. Learn. Instr. 2012, 22, 440–448. [Google Scholar] [CrossRef]
- Siler, S.; Willow, K. Individual differences in the effect of relevant concreteness on learning and transfer of a mathematical concept. Learn. Instr. 2014, 33, 170–181. [Google Scholar] [CrossRef]
- Barnett, S.M.; Ceci, S.J. When and where do we apply what we learn? A taxonomy for far transfer. Psychol. Bull. 2002, 128, 612–637. [Google Scholar] [CrossRef] [PubMed]
- Nakakoji, Y.; Wilson, R. Transfer of mathematical learning to science: An integrative review. Manuscript in preparation.
- Jackson, D.; Johnson, E. A hybrid model of mathematics support for science students emphasizing basic skills and discipline relevance. Int. J. Math. Educ. Sci. Technol. 2013, 44, 846–864. [Google Scholar] [CrossRef]
- Matthews, K.; Hodgson, Y.; Varsavsky, C. Factors influencing students’ perceptions of their quantitative skills. Int. J. Math. Educ. Sci. Technol. 2013, 44, 782–795. [Google Scholar] [CrossRef]
- Rylands, L.; Simbag, V.; Matthews, K.; Coady, C.; Belward, S. Scientists and mathematicians collaborating to build quantitative skills in undergraduate science. Int. J. Math. Educ. Sci. Technol. 2013, 44, 834–845. [Google Scholar] [CrossRef]
- Becker, K.; Park, K. Effects of integrative approaches among science, technology, engineering, and mathematics (STEM) subjects on students’ learning: A preliminary meta-analysis. J. STEM Educ. 2011, 12, 23–37. [Google Scholar]
- Anderton, R.; Hine, G.; Joyce, C. Secondary school mathematics and science matters: Academic performance for secondary students transitioning into university allied health and science courses. Int. J. Innov. Sci. Math. Educ. 2017, 25, 34–47. [Google Scholar]
- Sadler, P.M.; Tai, R.H. The two high-school pillars supporting college science. Science 2007, 317, 457–458. [Google Scholar] [CrossRef] [PubMed]
- Sazhin, S. Teaching mathematics to engineering students. Int. J. Eng. Ed. 1998, 14, 145–152. [Google Scholar]
- Bransford, J.D.; Schwartz, D.L. Rethinking transfer: A simple proposal with multiple implications. Rev. Res. Educ. 1999, 24, 61–100. [Google Scholar]
- Detterman, D.K. The case for the prosecution: Transfer as an epiphenomenon. In Transfer on Trial: Intelligence, Cognition, and Instruction; Detterman, D.K., Sternberg, R.J., Eds.; Ablex Publishing Corporartion: Norwood, NJ, USA, 1993. [Google Scholar]
- Gruber, H.; Law, L.; Mandl, H.; Renkl, A. Situated learning and transfer. In Learning in Humans and Machines: Towards an Interdisciplinary Learning Science; Reimann, P., Spada, H., Eds.; Elsevier Science Ltd.: Oxford, UK, 1995. [Google Scholar]
- Hatano, G.; Greeno, J.G. Commentary: Alternative perspectives on transfer and transfer studies. Int. J. Educ. Res. 1999, 31, 645–654. [Google Scholar] [CrossRef]
- Sternberg, R.J.; Frensch, P.A. Mechanisms of transfer. In Transfer on Trial: Intelligence, Cognition, and Instruction; Detterman, D.K., Sternberg, R.J., Eds.; Ablex Publishing Corporartion: Norwood, NJ, USA, 1993. [Google Scholar]
- Potgieter, M.; Harding, A.; Engelbrecht, J. Transfer of algebraic graphical thinking between mathematics and chemistry. J. Res. Sci. Teach. 2008, 45, 197–218. [Google Scholar] [CrossRef]
- Britton, S.; New, P.B.; Sharma, M.D.; Yardley, D. A case study of the transfer of mathematics skills by university students. Int. J. Math. Educ. Sci. Technol. 2005, 36, 1–13. [Google Scholar] [CrossRef]
- Roberts, A.L.; Sharma, M.D.; Britton, S.; New, P.B. An index to measure the ability of first year science students to transfer mathematics. Int. J. Math. Educ. Sci. Technol. 2007, 38, 429–448. [Google Scholar] [CrossRef]
- Arbuckle, J.L. IBM® SPSS® Amos™ 22 User’s Guide. 2013. Available online: http://www.uni-paderborn.de/fileadmin/imt/softwarelizenzen/spss/IBM_SPSS_Amos_User_Guide-22.pdf (accessed on 28 November 2017).
- Byrne, B.M. Structural Equation Modeling with AMOS: Basic Concepts, Applications, and Programming; Routledge: New York, NY, USA, 2010. [Google Scholar]
- Champagne, A.B.; Klopfer, L.E. A causal model of students’ achievement in a college physics course. J. Res. Sci. Teach. 1982, 19, 299–309. [Google Scholar] [CrossRef]
- Dehipawala, S.; Shekoyan, V.; Yao, H. Using mathematics review to enhance problem solving skills in general physics classes. In Proceedings of the 2014 Zone 1 Conference of the American Society for Engineering Education, University of Bridgeport, CT, USA, 3–5 April 2014. [Google Scholar]
- Taub, G.E.; Floyd, R.G.; Keith, T.Z.; McGrew, K.S. Effects of general and broad cognitive abilities on mathematical achievement. Sch. Psychol. Q. 2008, 23, 187–198. [Google Scholar] [CrossRef]
- Deary, I.J.; Strand, S.; Smith, P.; Fernandes, C. Intelligence and educational achievement. Intelligence 2007, 35, 13–21. [Google Scholar] [CrossRef]
- Australian Government. How much of the Variation in Literacy and Numeracy Can be Explained by School Performance? 2008. Available online: https://archive.treasury.gov.au/documents/1421/HTML/docshell.asp?URL=05%20How%20much%20of%20the%20variation%20in%20Literacy%20and%20Numeracy%20can%20be%20explained%20by%20School%20Performance.htm (accessed on 28 November 2017).
- Haskell, R.E. Transfer of Learning: Cognition, Instruction and Reasoning; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Nakakoji, Y.; Wilson, R.; Poladian, L. Mixed methods research on the nexus between mathematics and science. Int. J. Innov. Sci. Math. Educ. 2014, 22, 61–76. [Google Scholar]
- Van Someren, M.W.; Barnard, Y.F.; Sandberg, J.A.C. The Think Aloud Method: A Practical Guide to Modelling Cognitive Processes; Academic Press: San Diego, CA, USA, 1994. [Google Scholar]

| Context: When and Where Transferred from and to | |||||
|---|---|---|---|---|---|
| Near ←―――――――――――――――――――――――――――――――――――――→ Far | |||||
| Knowledge domain | Mouse vs. rat | Biology vs. botany | Biology vs. economics | Science vs. history | Science vs. art |
| Physical context | Same room at school | Different room at school | School vs. research lab | School vs. home | School vs. the beach |
| Temporal context | Same session | Next day | Weeks later | Months later | Years later |
| Functional context | Both clearly academic | Both academic but one nonevaluative | Academic vs. filling in tax forms | Academic vs. informal questionnaire | Academic vs. at play |
| Social context | Both individual | Individual vs. pair | Individual vs. small group | Individual vs. large group | Individual vs. society |
| Modality | Both written, same format | Both written, multiple choice vs. essay | Book learning vs. oral exam | Lecture vs. wine testing | Lecture vs. wood carving |
| No | Formulae to Measure Transfer |
|---|---|
| 1 | Transfer rating = z-score for first attempted component − z-score for mathematics |
| 2 | Transfer index = the sum of transfer scores ÷ the number of paired questions × 50 |
| Semester 1 Course Codes & Names | MATH1901 | MATH1001 | |
|---|---|---|---|
| Semester 2 Course Codes & Names | Differential Calculus (Advanced) | Differential Calculus | |
| PHYS1902 | Physics 1B (Advanced) | 67 | 27 |
| PHYS1003 | Physics 1 (Regular) | 28 | 136 |
| ENGG1802 | Engineering Mechanics | 44 | 382 |
| MBLG1901 | Molecular Biology and Genetics (Advanced) | 33 | 72 |
| MBLG1001 | Molecular Biology and Genetics | 53 | 190 |
| BIOL1902 | Living Systems (Advanced) | 12 | 20 |
| BIOL1002 | Living Systems | 6 | 55 |
| Total Enrolment for Combination of Two Courses | 243 | 882 | |
| Math score | 1 | 0 | 1 | 0 |
| Non-math score | 1 | 1 | 0 | 0 |
| Transfer score | 2 | 1 | 0 | 0 |
| Transfer Index | Min | Max | n | Mean | Mode | SD | SE of Mean | |
|---|---|---|---|---|---|---|---|---|
| MATH1901 Differential Calculus (Advanced) | PHYS1902 Physics 1B (Advanced) | 2.5 | 95.0 | 67 | 48.69 | 26.25/92.50 * | 28.29 | 3.46 |
| PHYS1003 Physics 1 (Regular) | 0.0 | 95.0 | 28 | 47.02 | 43.50/68.50 * | 26.30 | 4.97 | |
| ENGG1802 Engineering Mechanics | 22.5 | 100.0 | 44 | 67.28 | 70.00 | 20.93 | 3.16 | |
| MATH1001 Differential Calculus | PHYS1902 Physics 1B (Advanced) | 7.5 | 85.0 | 27 | 50.49 | 69.17 | 19.41 | 3.74 |
| PHYS1003 Physics 1 (Regular) | 0.0 | 100.0 | 136 | 30.15 | 0.00 | 28.76 | 2.47 | |
| ENGG1802 Engineering Mechanics | 0.0 | 100.0 | 382 | 74.79 | 77.50 | 18.18 | 0.93 | |
| Transfer Indices | MATH Final Marks | n | PHYS/ENGG Final Marks | n | ATAR | n | |
|---|---|---|---|---|---|---|---|
| MATH1001 (Norm) & PHYS1003(Reg) | TI | 0.477 * | 136 | 0.447 * | 136 | 0.423 * | 100 |
| ATAR Adj TI | 0.186 | 100 | 0.147 | 100 | |||
| MATH1001 (Norm) & PHYS1902 (Adv) | TI | 0.759 * | 27 | 0.753 * | 27 | 0.355 | 22 |
| ATAR Adj TI | 0.483 | 22 | 0.619 * | 22 | |||
| MATH1001 (Norm) & ENGG1802 | TI | 0.505 * | 382 | 0.711 * | 382 | 0.361 * | 255 |
| ATAR Adj TI | 0.239 * | 255 | 0.479 * | 255 | |||
| MATH1901 (Adv) & PHYS1003 (Reg) | TI | 0.495 | 28 | 0.706 * | 28 | 0.494 | 24 |
| ATAR Adj TI | 0.032 | 24 | 0.489 | 24 | |||
| MATH1901 (Adv) & PHYS1902 (Adv) | TI | 0.497 * | 67 | 0.537 * | 67 | 0.438 * | 57 |
| ATAR Adj TI | 0.368 | 57 | 0.474 * | 57 | |||
| MATH1901(Adv) & ENGG1802 | TI | 0.488 * | 44 | 0.541 * | 44 | 0.315 | 39 |
| ATAR Adj TI | 0.400 | 39 | 0.500 * | 39 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakakoji, Y.; Wilson, R. First-Year Mathematics and Its Application to Science: Evidence of Transfer of Learning to Physics and Engineering. Educ. Sci. 2018, 8, 8. https://doi.org/10.3390/educsci8010008
Nakakoji Y, Wilson R. First-Year Mathematics and Its Application to Science: Evidence of Transfer of Learning to Physics and Engineering. Education Sciences. 2018; 8(1):8. https://doi.org/10.3390/educsci8010008
Chicago/Turabian StyleNakakoji, Yoshitaka, and Rachel Wilson. 2018. "First-Year Mathematics and Its Application to Science: Evidence of Transfer of Learning to Physics and Engineering" Education Sciences 8, no. 1: 8. https://doi.org/10.3390/educsci8010008
APA StyleNakakoji, Y., & Wilson, R. (2018). First-Year Mathematics and Its Application to Science: Evidence of Transfer of Learning to Physics and Engineering. Education Sciences, 8(1), 8. https://doi.org/10.3390/educsci8010008





