Bayesian Framework for Multi-Wave COVID-19 Epidemic Analysis Using Empirical Vaccination Data
Abstract
:1. Introduction
2. Materials
2.1. Source of Data
2.2. Data Description
3. Methods
3.1. Epidemiological Model
3.2. Model for the Reported Cases
3.3. Bayesian Framework
3.4. Prior Specification
3.5. Markov Chain Monte Carlo (Mcmc) with No-U-Turn Sampler (NUTS)
| Algorithm 1 Complete modeling framework |
|
4. Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maier, B.F.; Brockmann, D. Effective containment explains sub-exponential growth in confirmed cases of recent COVID-19 outbreak in Mainland China. Science 2020, 368, 742–746. [Google Scholar] [CrossRef] [Green Version]
- Gompertz, B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1825, 115, 513–585. [Google Scholar]
- Brauer, F. Compartmental Models in Epidemiology. In Mathematical Epidemiology; Brauer, F., Driessche, P.V.D., Wu, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 1945, pp. 19–79. [Google Scholar] [CrossRef]
- Blackwood, J.C.; Childs, L.M. An introduction to compartmental modeling for the budding infectious disease modeler. Lett. Biomath. 2018, 5, 195–221. [Google Scholar] [CrossRef]
- Dehning, J.; Zierenberg, J.; Spitzner, F.P.; Wibral, M.; Neto, J.P.; Wilczek, M.; Priesemann, V. Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science 2020, 369, eabb9789. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; Heesterbeek, H.; Klinkenberg, D.; Hollingsworth, T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet 2020, 395, 931–934. [Google Scholar] [CrossRef]
- Borchering, R.K.; Viboud, C.; Howerton, E.; Smith, C.P.; Truelove, S.; Runge, M.C.; Reich, N.G.; Contamin, L.; Levander, J.; Salerno, J.; et al. Modeling of Future COVID-19 Cases, Hospitalizations, and Deaths, by Vaccination Rates and Nonpharmaceutical Intervention Scenarios-United States, April-September 2021. Morb. Mortal. Wkly. Rep. 2021, 70, 719–724. [Google Scholar] [CrossRef]
- Jaffe-Hoffman, M. Netanyahu: A Small Shot for a Person, a Huge Step toward the Health of Us All. 2020. Available online: https://www.jpost.com/health-science/netanyahu-to-kick-off-israels-covid-19-vaccination-campaign-on-saturday-652628 (accessed on 20 December 2020).
- El Koufi, A.; Adnani, J.; Bennar, A.; Yousfi, N. Analysis of a Stochastic SIR Model with Vaccination and Nonlinear Incidence Rate. Int. J. Differ. Equ. 2019, 2019, 9275051. [Google Scholar] [CrossRef] [Green Version]
- Cui, Q.; Qiu, Z.; Ding, L. An SIR epidemic model with vaccination in a patchy environment. Math. Biosci. Eng. 2017, 14, 1141–1157. [Google Scholar] [CrossRef] [Green Version]
- Pfizer and BioNTech Conclude Phase 3 Study of COVID-19 Vaccine Candidate, Meeting All Primary Efficacy Endpoints. 2020. Available online: https://www.businesswire.com/news/home/20201118005595/en/ (accessed on 18 November 2020).
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Ser. Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar] [CrossRef] [Green Version]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef] [Green Version]
- He, S.; Peng, Y.; Sun, K. SEIR modeling of the COVID-19 and its dynamics. Nonlinear Dyn. 2020, 101, 1667–1680. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165–174. [Google Scholar] [CrossRef]
- Rajagopal, K.; Hasanzadeh, N.; Parastesh, F.; Hamarash, I.I.; Jafari, S.; Hussain, I. A fractional-order model for the novel coronavirus (COVID- 19) outbreak. Nonlinear Dyn. 2020, 101, 711–718. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar] [CrossRef]
- Lai, C.C.; Hsu, C.Y.; Jen, H.H.; Yen, A.M.F.; Chan, C.C.; Chen, H.H. The Bayesian Susceptible-Exposed-Infected-Recovered model for the outbreak of COVID-19 on the Diamond Princess Cruise Ship. Stoch. Environ. Res. Risk Assess. Vol. 2021, 35, 1319–1333. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Ji, Y. Semiparametric Bayesian inference for the transmission dynamics of COVID-19 with a state-space model. Contemp. Clin. Trials 2020, 97, 106146. [Google Scholar] [CrossRef]
- Park, S.W.; Bolker, B.M.; Champredon, D.; Earn, D.J.; Li, M.; Weitz, J.S.; Grenfell, B.T.; Dushoff, J. Reconciling early-outbreak preliminary estimates of the basic reproductive number and its uncertainty: A new framework and applications to the novel coronavirus (2019-nCoV) outbreak. J. R. Soc. Interface 2020, 17, 20200144. [Google Scholar] [CrossRef]
- Yang, H.; Lee, J. Variational Bayes method for ordinary differential equation models. arXiv 2021, arXiv:2011.09718. [Google Scholar]
- Mansour, N.A.; Saleh, A.I.; Badawy, M.; Ali, H.A. Accurate detection of Covid-19 patients based on Feature Correlated Naïve Bayes (FCNB) classification strategy. J. Ambient Intell. Humaniz. Comput. 2021, 142, 1–33. [Google Scholar] [CrossRef]
- Butcher, R.; Fenton, N. Extending the range of symptoms in a Bayesian Network for the Predictive Diagnosis of COVID-19. medRxiv 2020. [Google Scholar] [CrossRef]
- Terwangne, C.d.; Laouni, J.; Jouffe, L.; Lechien, J.R.; Bouillon, V.; Place, S.; Capulzini, L.; Machayekhi, S.; Ceccarelli, A.; Saussez, S.; et al. Predictive Accuracy of COVID-19 World Health Organization (WHO) Severity Classification and Comparison with a Bayesian-Method-Based Severity Score (EPI-SCORE). Pathogens 2020, 9, 880. [Google Scholar] [CrossRef]
- Vitalea, V.; D’Ursoa, P.; Giovanni, L.D. Spatio-temporal Object-Oriented Bayesian Network modelling of the COVID-19 Italian outbreak data. Spat. Stat. 2021, 140, 100529. [Google Scholar] [CrossRef] [PubMed]
- Lawson, A.B.; Kim, J. Space-time covid-19 Bayesian SIR modeling in South Carolina. PLoS ONE 2021, 16, e0242777. [Google Scholar] [CrossRef] [PubMed]
- Hao, X.; Cheng, S.; Wu, D.; Wu, T.; Lin, X.; Wang, C. Reconstruction of the full transmission dynamics of COVID-19 in Wuhan. Nature 2020, 584, 420–424. [Google Scholar] [CrossRef] [PubMed]
- Bhaduri, R.; Kundu, R.; Purkayastha, S.; Kleinsasser, M.; Beesley, L.J.; Mukherjee, B. Extending the susceptible-exposed-infected-removed (seir) model to handle the high false negative rate and symptom-based administration of covid-19 diagnostic tests: Seir-fansy. MedRxiv 2020, 9, 24. [Google Scholar] [CrossRef]
- Bherwani, H.; Anjum, S.; Kumar, S.; Gautam, S.; Gupta, A.; Kumbhare, H.; Anshul, A.; Kumar, R. Understanding COVID-19 transmission through Bayesian probabilistic modeling and GIS-based Voronoi approach: A policy perspective. Environ. Dev. Sustain. 2021, 23, 5846–5864. [Google Scholar] [CrossRef]
- Mbuvha, R.; Tshilidzi, M. Bayesian inference of COVID-19 spreading rates in South Africa. PLoS ONE 2020, 15, e0237126. [Google Scholar] [CrossRef] [PubMed]
- Salvadore, F.; Fiscon, G.; Paci, P. Integro-differential approach for modeling the COVID-19 dynamics - Impact of confinement measures in Italy. Comput. Biol. Med. 2021, 139, 105013. [Google Scholar] [CrossRef]
- Beira, M.J.; Sebastião, P.J. A differential equations model fitting analysis of COVID 19 epidemiological data to explain multi wave dynamics. Sci. Rep. 2021, 11, 16312. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Cot, C.; Sannino, F. Multiwave pandemic dynamics explained: How to tame the next wave of infectious diseases. Sci. Rep. 2021, 11, 6638. [Google Scholar] [CrossRef] [PubMed]
- Cot, C.; Cacciapaglia, G.; Islind, A.S.; Óskarsdóttir, M.; Sannino, F. Impact of US vaccination strategy on COVID 19 wave dynamics. Sci. Rep. 2021, 11, 10960. [Google Scholar] [CrossRef]
- Chen, Y.C.; Lu, P.E.; Chang, C.S.; Liu, T.H. A Time-dependent SIR model for COVID-19 with undetectable infected persons. IEEE Trans. Netw. Sci. Eng. 2020, 7, 3279–3294. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Cuomo-Dannenburg, G.; et al. Report 9: Impact of Nonpharmaceutical Interventions (NPIs) to Reduce COVID19 Mortality and Healthcare Demand; Imperial College London: London, UK, 2020. [Google Scholar] [CrossRef]
- Head, M. Israel Was a Leader in the COVID Vaccination Race—So Why Are Cases Spiralling There? 2021. Available online: https://theconversation.com/israel-was-a-leader-in-the-covid-vaccination-race-so-why-are-cases-spiralling-there-166945 (accessed on 8 September 2021).
- Israel Confirms First Coronavirus Case as Cruise Ship Returnee Diagnosed. 2020. Available online: https://www.timesofisrael.com/israel-confirms-first-coronavirus-case-as-cruise-ship-returnee-diagnosed/ (accessed on 21 February 2020).
- Coronavirus: Infected Israelis hit 707 as Emergency Orders Roll Out. 2020. Available online: https://www.jpost.com/Breaking-News/529-Israelis-have-been-diagnosed-with-coronavirus-Health-Ministry-621536 (accessed on 24 December 2020).
- Ynet. Malls and Markets Reopen after Israel Lifts Coronavirus Restrictions. 2020. Available online: https://www.ynetnews.com/article/BkjylNW9U (accessed on 7 May 2020).
- Ganot, S. Israel Is Now World’s Worst in Daily COVID-19 Infections Per Capita. 2021. Available online: https://themedialine.org/life-lines/israel-is-now-worlds-worst-in-daily-covid-19-infections-per-capita/ (accessed on 9 February 2021).
- Thousands in Israel Protest Netanyahu’s Coronavirus Response. 2020. Available online: https://www.france24.com/en/20200719-thousands-in-israel-protest-government-s-coronavirus-response (accessed on 19 July 2020).
- Third Coronavirus Lockdown Rules—Everything You Need to Know. Available online: https://www.jpost.com/israel-news/coronavirus-third-lockdown-rules-everything-you-need-to-know-653072 (accessed on 24 December 2020).
- Jaffe-Hoffman, M. Everything You Need to Know about Israel’s Green Passport Program. 2021. Available online: https://www.jpost.com/israel-news/everything-you-need-to-know-about-israels-green-passport-program-659437 (accessed on 28 February 2021).
- Israel logs Indian COVID Variant, Sees Some Vaccine Efficacy against It. 2021. Available online: https://www.ynetnews.com/health_science/article/By2OjehUu (accessed on 20 April 2021).
- Golan, A.; AP; ILH. Israel’s 4th COVID Wave Sees Surge in New Cases, with 81 Hospitalized. 2021. Available online: https://www.israelhayom.com/2021/07/13/israels-4th-covid-wave-sees-surge-in-new-cases-with-81-hospitalized/ (accessed on 13 July 2021).
- Britton, T.; O’Neill, P.D. Bayesian inference for stochastic epidemics in populations with random social structure. Scand. J. Stat. 2002, 29, 375–390. [Google Scholar] [CrossRef]
- Chauhan, S.; Misra, O.P.; Dhar, J. Stability Analysis of SIR Model with Vaccination. Am. J. Comput. Appl. Math. 2014, 4, 17–23. [Google Scholar] [CrossRef]
- Bayes, T.; Price, R. An Essay towards solving a Problem in the Doctrine of Chance. By the late Rev. Mr. Bayes, communicated by Mr. Price, in a letter to John Canton, A. M. F. R. S. Philos. Trans. R. Soc. Lond. 1763, 53, 370–418. [Google Scholar] [CrossRef]
- Lange, K.L.; Little, R.J.A.; Taylor, J.M.G. Robust statistical modeling using the t Distribution. J. Am. Stat. Assoc. 1989, 84, 881–896. [Google Scholar] [CrossRef] [Green Version]
- Wilting, J.; Priesemann, V. Inferring collective dynamical states from widely unobserved systems. Nat. Commun. 2018, 9, 2325. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.; Lin, Q.; Ran, J.; Musa, S.S.; Yang, G.; Wang, W.; Lou, Y.; Gao, D.; Yang, L.; He, D.; et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. Int. J. Infect. Dis. 2020, 92, 214–217. [Google Scholar] [CrossRef] [Green Version]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Ann. Intern. Med. 2020, 172, 577–582. [Google Scholar] [CrossRef] [Green Version]
- Petherick, A.; Kira, B.; Cameron-Blake, E.; Tatlow, H.; Hallas, L.; Hale, T.; Phillips, T.; Webster, S.; Anania, J.; Ellen, L.; et al. Variation in Government Responses to COVID-19. In BSG Working Paper Series; Blavatnik School of Government, University of Oxford: Oxford, UK, 2021. [Google Scholar]
- Smith, A.; Roberts, G. Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods. J. R. Stat. Soc. Ser. B 1993, 55, 3–23. [Google Scholar] [CrossRef]
- Neal, R.M. Probabilistic Inference Using Markov Chain Monte Carlo Methods; Department of Computer Science, University of Toronto: Toronto, ON, Canada, 1993. [Google Scholar]
- Taylor, B.M.; Diggle, P.J. INLA or MCMC? A tutorial and comparative evaluation for spatial prediction in log-Gaussian Cox processes. J. Stat. Comput. Simul. 2014, 84, 2266–2284. [Google Scholar] [CrossRef] [Green Version]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Hastings, W. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–108. [Google Scholar] [CrossRef]
- Neal, R.M. MCMC Using Hamiltonian Dynamics; Chapman & Hall/CRC Press: New York, NY, USA, 2011; Volume 2, pp. 113–162. [Google Scholar] [CrossRef] [Green Version]
- Girolami, M.; Ben, C. Riemann manifold Langevin and Hamiltonian Monte Carlo methods. J. R. Stat. Soc. Ser. B 2011, 73, 123–214. [Google Scholar] [CrossRef]
- Neal, R.M. An improved acceptance procedure for the hybrid Monte Carlo algorithm. J. Comput. Phys. 1994, 111, 194–203. [Google Scholar] [CrossRef] [Green Version]
- Hoffman, M.D.; Gelman, A. The No-U-turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar] [CrossRef]
- Neal, R.M. Slice sampling. Ann. Stat. 2003, 31, 705–767. [Google Scholar] [CrossRef]
- Israel’s Virus Death Toll Hits 600; Outdoor Cultural Performances Set to Resume. 2020. Available online: https://www.timesofisrael.com/israels-virus-death-toll-hits-600-as-ministers-approve-raft-of-restrictions/ (accessed on 9 August 2020).
- School Is Back in Session for Grades 1–4 as Lockdown Eased; Synagogues Reopen. 2020. Available online: https://www.timesofisrael.com/school-is-back-in-session-for-grades-1-4-as-lockdown-eased-synagogues-reopen/ (accessed on 1 November 2020).
- Israel Drops Indoor Mask Mandate as COVID Infection Rates Plummet. 2021. Available online: https://www.ynetnews.com/health_science/article/By5zU6SiO (accessed on 15 June 2021).
- Malkov, E. Simulation of coronavirus disease 2019 (COVID-19) scenarios with possibility of reinfection. Chaos Solitons Fractals 2020, 139, 110296. [Google Scholar] [CrossRef] [PubMed]
- Nanduri, S.; Pilishvili, T.; Derado, G.; Soe, M.M.; Dollard, P.; Wu, H.; Li, Q.; Bagchi, S.; Dubendris, H.; Link-Gelles, R.; et al. Effectiveness of Pfizer-BioNTech and Moderna Vaccines in Preventing SARS-CoV-2 Infection Among Nursing Home Residents Before and During Widespread Circulation of the SARS-CoV-2 B.1.617.2 (Delta) Variant—National Healthcare Safety Network, 1 March–1 August 2021. Morb. Mortal. Wkly. Rep. 2021, 70, 1163–1166. [Google Scholar] [CrossRef]
- Goldberg, Y.; Mandel, M.; Bar-On, Y.M.; Bodenheimer, O.; Freedman, L.; Haas, E.J.; Milo, R.; Alroy-Preis, S.; Ash, N.; Huppert, A. Waning Immunity after the BNT162b2 Vaccine in Israel. N. Engl. J. Med. 2021, 385, e85. [Google Scholar] [CrossRef]
- Sharov, K.S. Creating and applying SIR modified compartmental model for calculation of COVID-19 lockdown efficiency. Chaos Solitons Fractals 2020, 141, 110295. [Google Scholar] [CrossRef]
- Valba, O.V.; Avetisov, V.A.; Gorsky, A.S.; Nechaev, S.K. Evaluating Ideologies of Coronacrisis-Related Self-Isolation and Frontiers Closing by SIR Compartmental Epidemiological Model. Beacon: J. Stud. Ideol. Ment. 2020, 3, 020210318. [Google Scholar]
- Nenchev, V. Optimal quarantine control of an infectious outbreak. Chaos Solitons Fractals 2020, 138, 110139. [Google Scholar] [CrossRef] [PubMed]


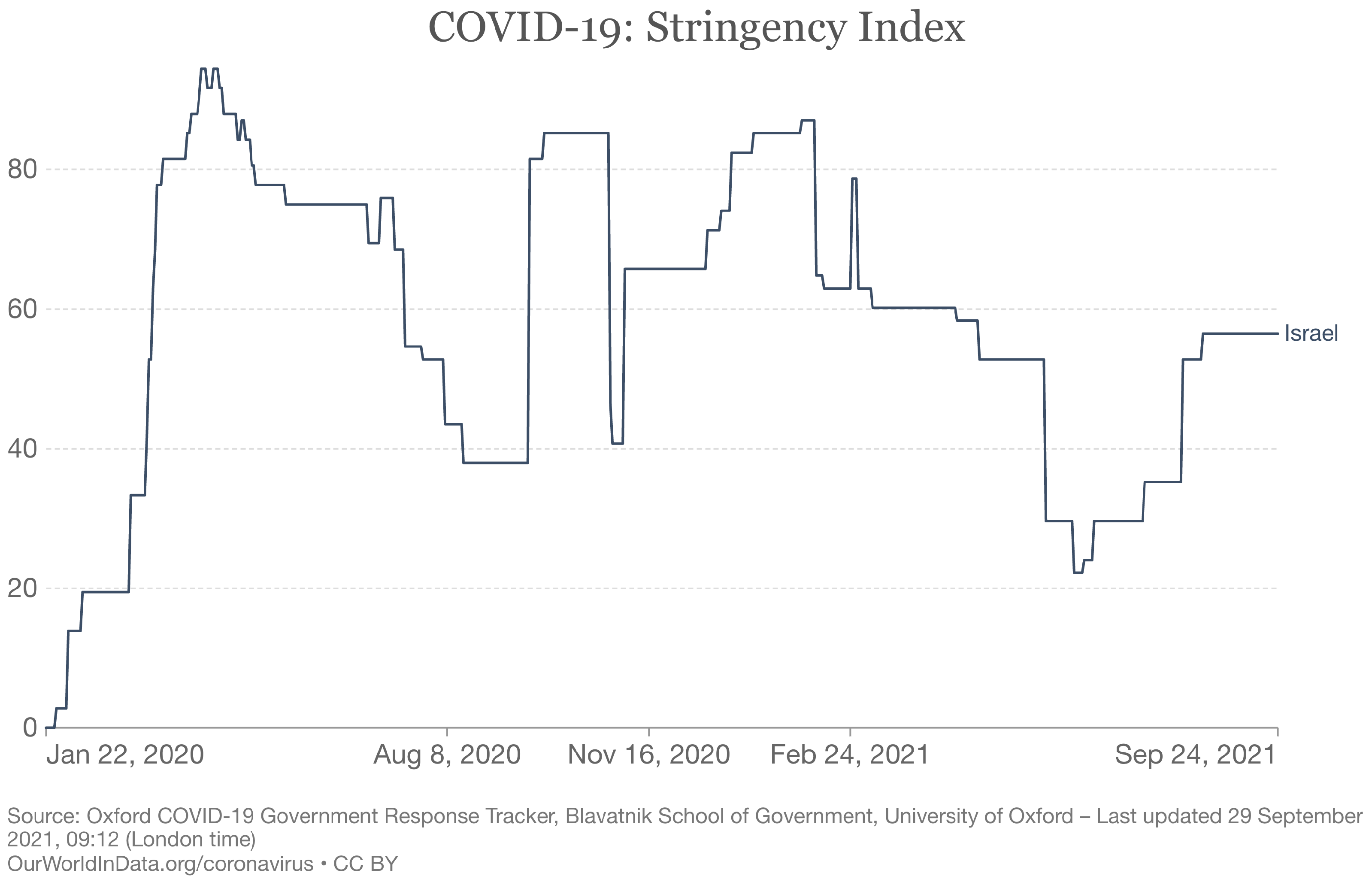

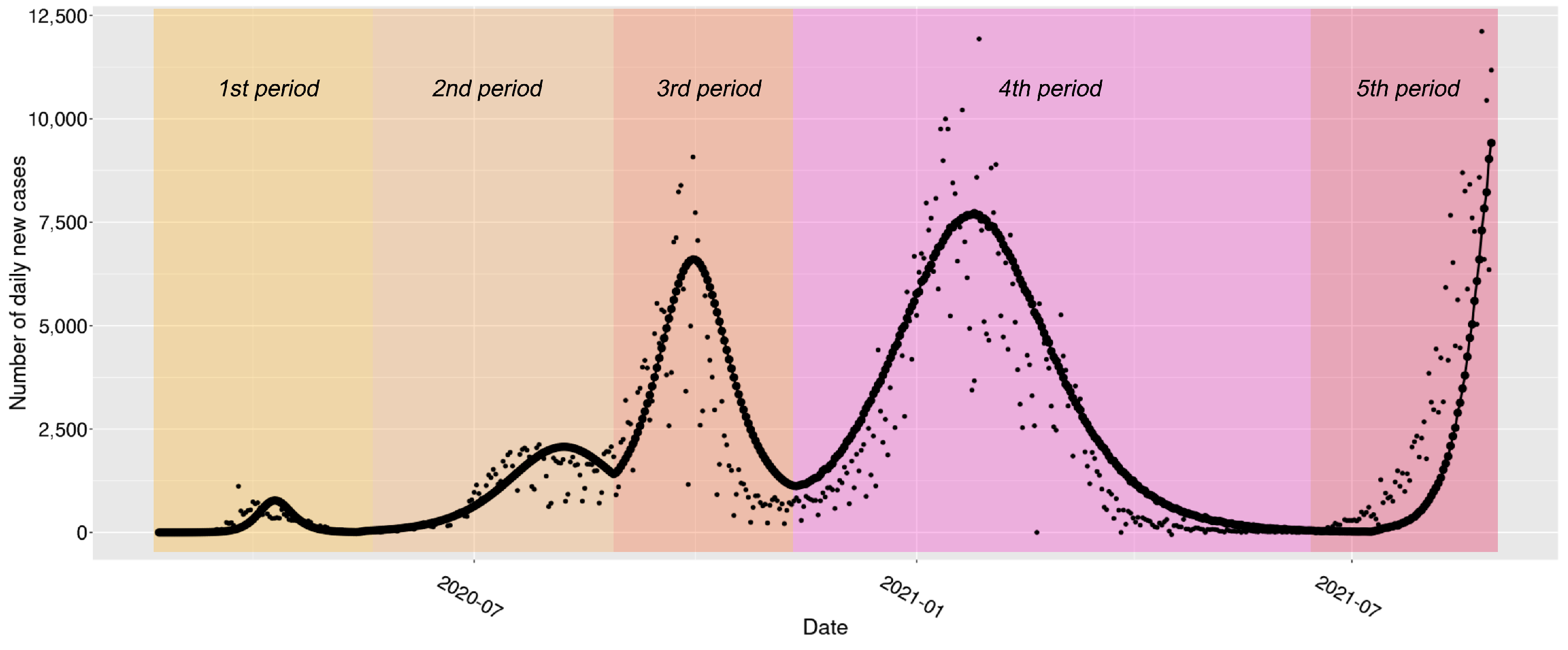

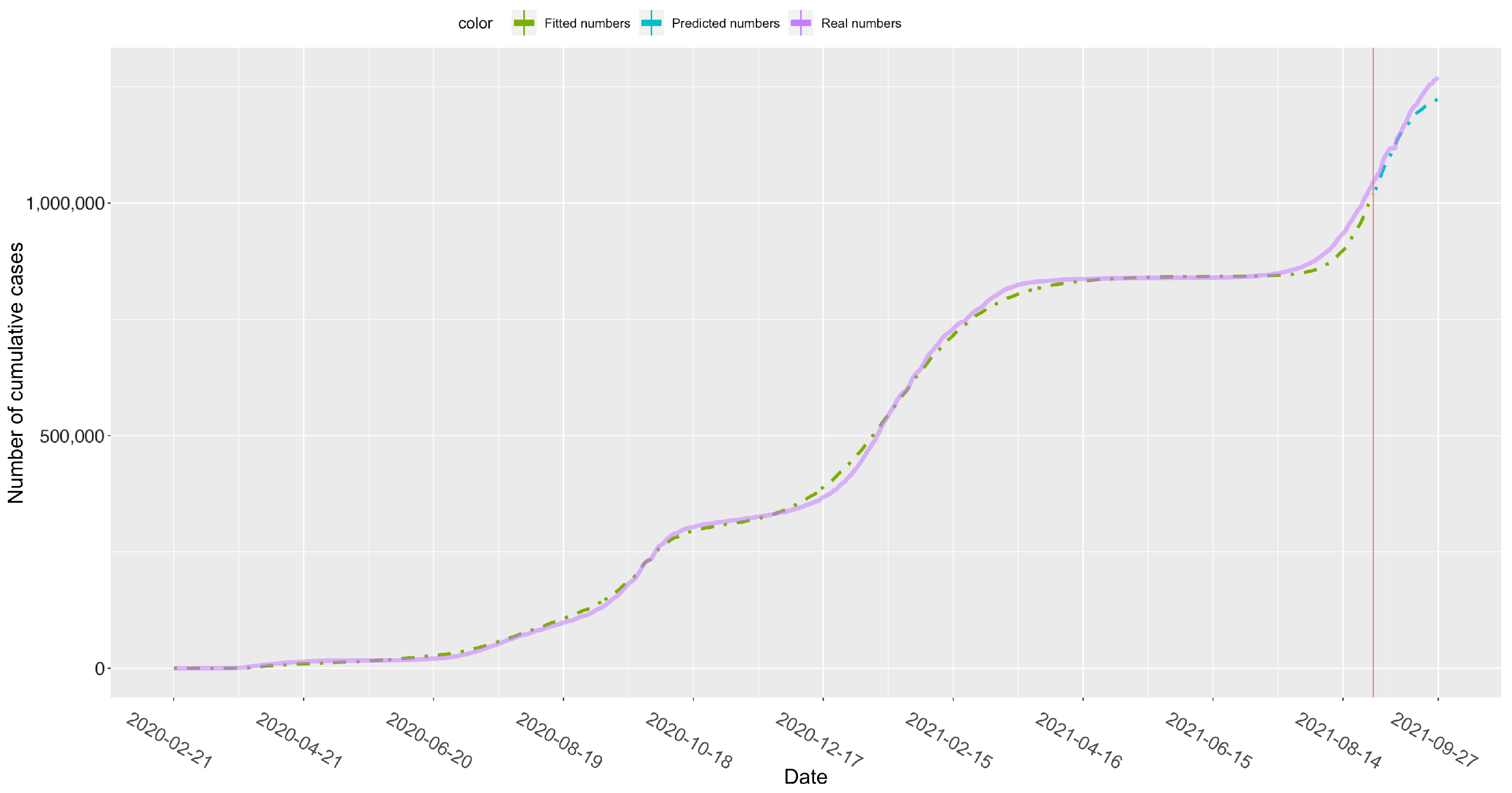

| Parameter | Interpretation | Prior |
|---|---|---|
| Initial transmission rate | LogNormal(log(0.4), 0.5) | |
| Transmission rate after the 1st change point | LogNormal(log(0.4), 0.5) | |
| Transmission rate after the 2nd change point | LogNormal(log(0.4), 0.5) | |
| Transmission rate after the 3rd change point | LogNormal(log(0.4), 0.5) | |
| Transmission rate after the 4th change point | LogNormal(log(0.4), 0.5) | |
| Initial infectious rate | LogNormal(log(1/5), 0.5) | |
| Infectious rate after the 1st change point | LogNormal(log(1/5), 0.5) | |
| Infectious rate after the 2nd change point | LogNormal(log(1/5), 0.5) | |
| Infectious rate after the 3rd change point | LogNormal(log(1/5), 0.5) | |
| Infectious rate after the 4th change point | LogNormal(log(1/5), 0.5) | |
| Recovery rate | LogNormal(log(1/8), 0.2) | |
| D | Reporting delay | LogNormal(log(8), 0.2) |
| Initial number of infected | HalfCauchy(100) | |
| Initial number of exposed | HalfCauchy(100) | |
| The 1st change point | Normal(7 May 2020, 3) | |
| The 2nd change point | Normal(17 Aug 2020, 3) | |
| The 3rd change point | Normal(31 Oct 2020, 3) | |
| The 4th change point | Normal(20 Jun 2021, 3) | |
| Weekly modulation amplitude | Beta(4.39, 1.88) | |
| Weekly modulation phase | VonMises(0, 0.01) | |
| The proportion of cases reported | Beta(1, 2) | |
| Scale factor | HalfCauchy(10) | |
| Effective rate of the first dose | Normal(0.52,0.01) | |
| Effective rate of the second dose | Normal(0.95,0.01) |
| Parameter | Mean | Standard Deviation | 95% Confidence Interval |
|---|---|---|---|
| 0.62 | 0.07 | [0.50, 0.76] | |
| 0.34 | 0.04 | [0.28, 0.45] | |
| 0.36 | 0.05 | [0.25, 0.45] | |
| 0.49 | 0.07 | [0.37, 0.64] | |
| 1.02 | 0.13 | [0.82, 1.31] | |
| 1.05 | 0.42 | [0.47, 2.09] | |
| 0.32 | 0.11 | [0.16, 0.59] | |
| 1.83 | 0.63 | [0.94, 3.35] | |
| 0.33 | 0.04 | [0.25, 0.42] | |
| 1.26 | 0.49 | [0.57, 2.45] | |
| 0.31 | 0.05 | [0.23, 0.41] | |
| D | 7.68 | 0.92 | [5.72, 9.30] |
| 1.51 | 1.87 | [0.05, 6.45] | |
| 1.59 | 2.02 | [0.04, 6.94] | |
| 8 May 2020 | 0.94 | [6 May 2020, 10 May 2020] | |
| 20 August 2020 | 0.68 | [19 August 2020, 22 August 2020] | |
| 1 November 2020 | 1.51 | [28 October 2020, 4 November 2020] | |
| 16 June 2021 | 1.63 | [13 June 2021, 20 June 2021] | |
| 0.58 | 0.06 | [0.47, 0.69] | |
| 3.71 | 2.72 | [1.74, 8.60] | |
| 0.20 | 0.01 | [0.18, 0.22] | |
| 19.79 | 0.89 | [18.11, 21.64] | |
| 0.52 | 0.03 | [0.47, 0.57] | |
| 0.95 | 0.01 | [0.93, 0.97] | |
| 2.03 | 0.24 | [1.64, 2.56] | |
| 1.10 | 0.01 | [1.07, 1.13] | |
| 1.17 | 0.04 | [1.11, 1.24] | |
| 1.59 | 0.04 | [1.50, 1.68] | |
| 3.33 | 0.32 | [2.79, 4.03] | |
| 1.10 | 0.43 | [0.48, 2.12] | |
| 3.50 | 1.14 | [1.70, 6.12] | |
| 0.61 | 0.20 | [0.30, 1.07] | |
| 3.11 | 0.40 | [2.38, 3.93] | |
| 0.91 | 0.35 | [0.41, 1.75] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Tang, Y. Bayesian Framework for Multi-Wave COVID-19 Epidemic Analysis Using Empirical Vaccination Data. Mathematics 2022, 10, 21. https://doi.org/10.3390/math10010021
Xu J, Tang Y. Bayesian Framework for Multi-Wave COVID-19 Epidemic Analysis Using Empirical Vaccination Data. Mathematics. 2022; 10(1):21. https://doi.org/10.3390/math10010021
Chicago/Turabian StyleXu, Jiawei, and Yincai Tang. 2022. "Bayesian Framework for Multi-Wave COVID-19 Epidemic Analysis Using Empirical Vaccination Data" Mathematics 10, no. 1: 21. https://doi.org/10.3390/math10010021






