Optimizing Costs in a Reliability System under Markovian Arrival of Failures and Reposition by K-Policy Inspection
Abstract
:1. Introduction
1.1. Contributions
1.2. Organization
2. The Model
2.1. Definitions
2.2. Asumptions of the Model
- The online unit is submitted to shocks governed by the with initial vector c and order
- The standby units are submitted to shocks governed by the with initial vector d and order
- The inspections occur following the with initial vector h and order
- All the MAPs are independent.
2.3. Macro-States of the System
2.3.1. Transition
2.3.2. Transition
2.3.3. Transition
2.3.4. Transition
3. Cycles of the System, Performance Measures and Costs
3.1. Distribution of the Up and Down Periods
3.2. Costs by Cycles
3.3. Performance Measures
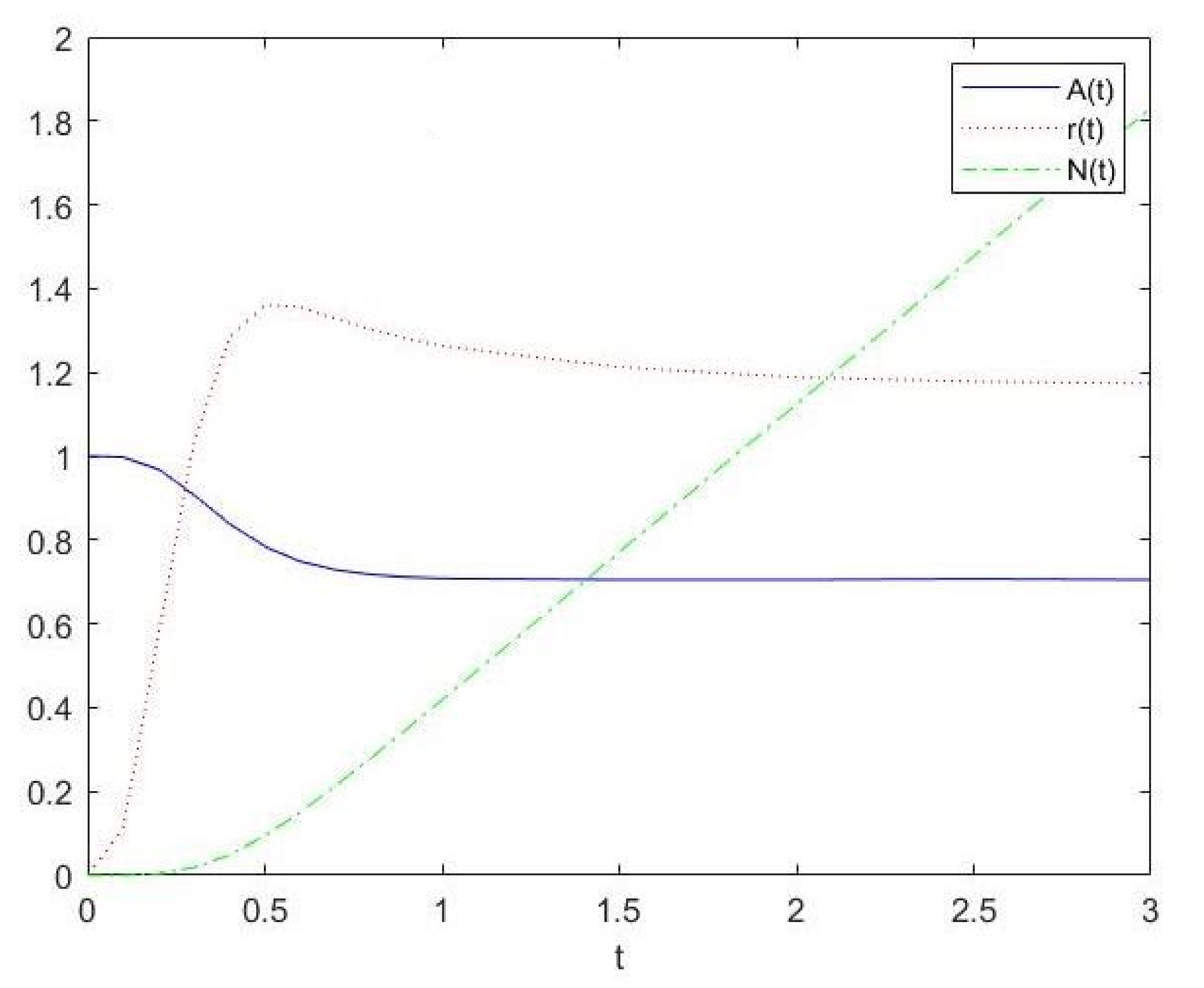
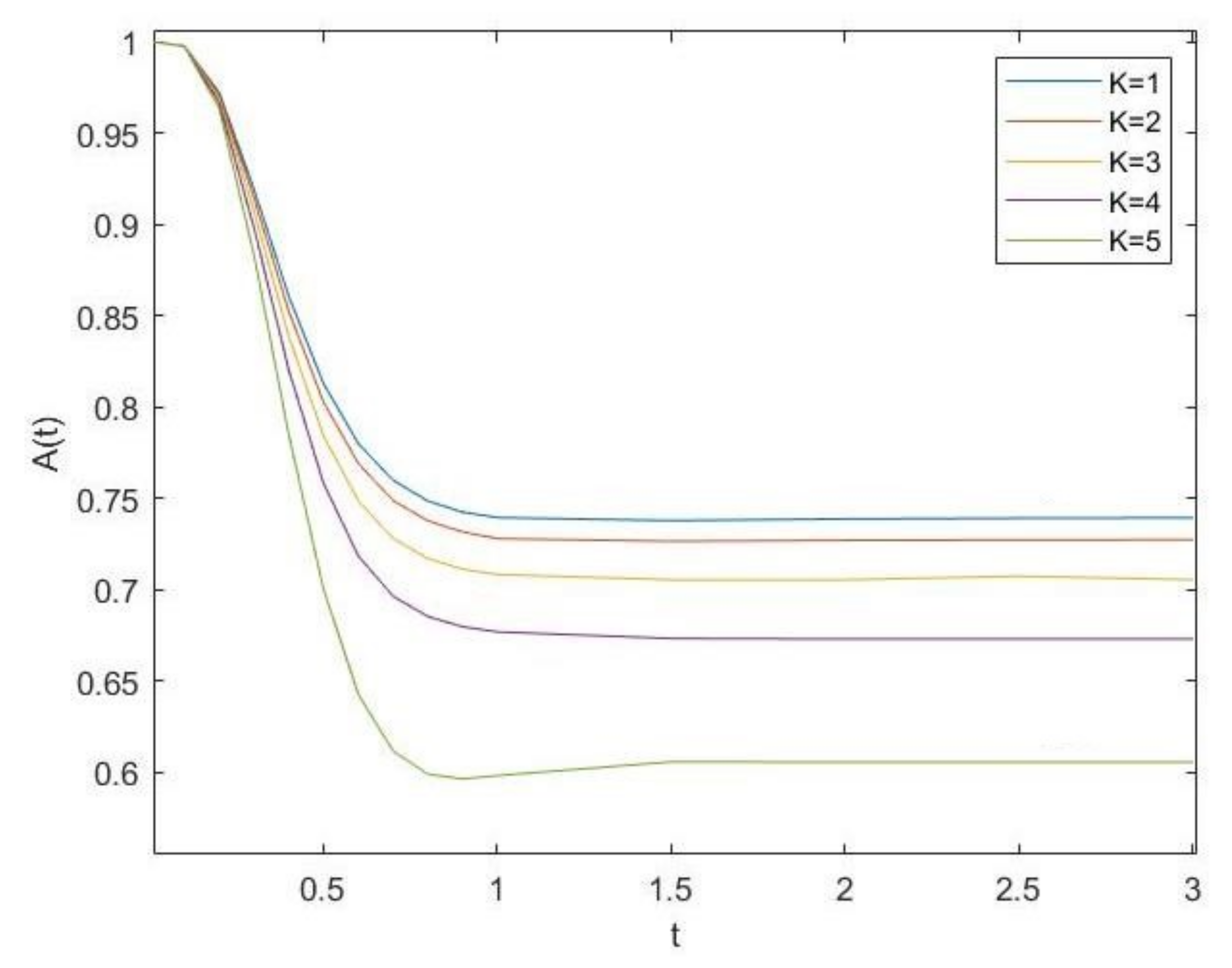
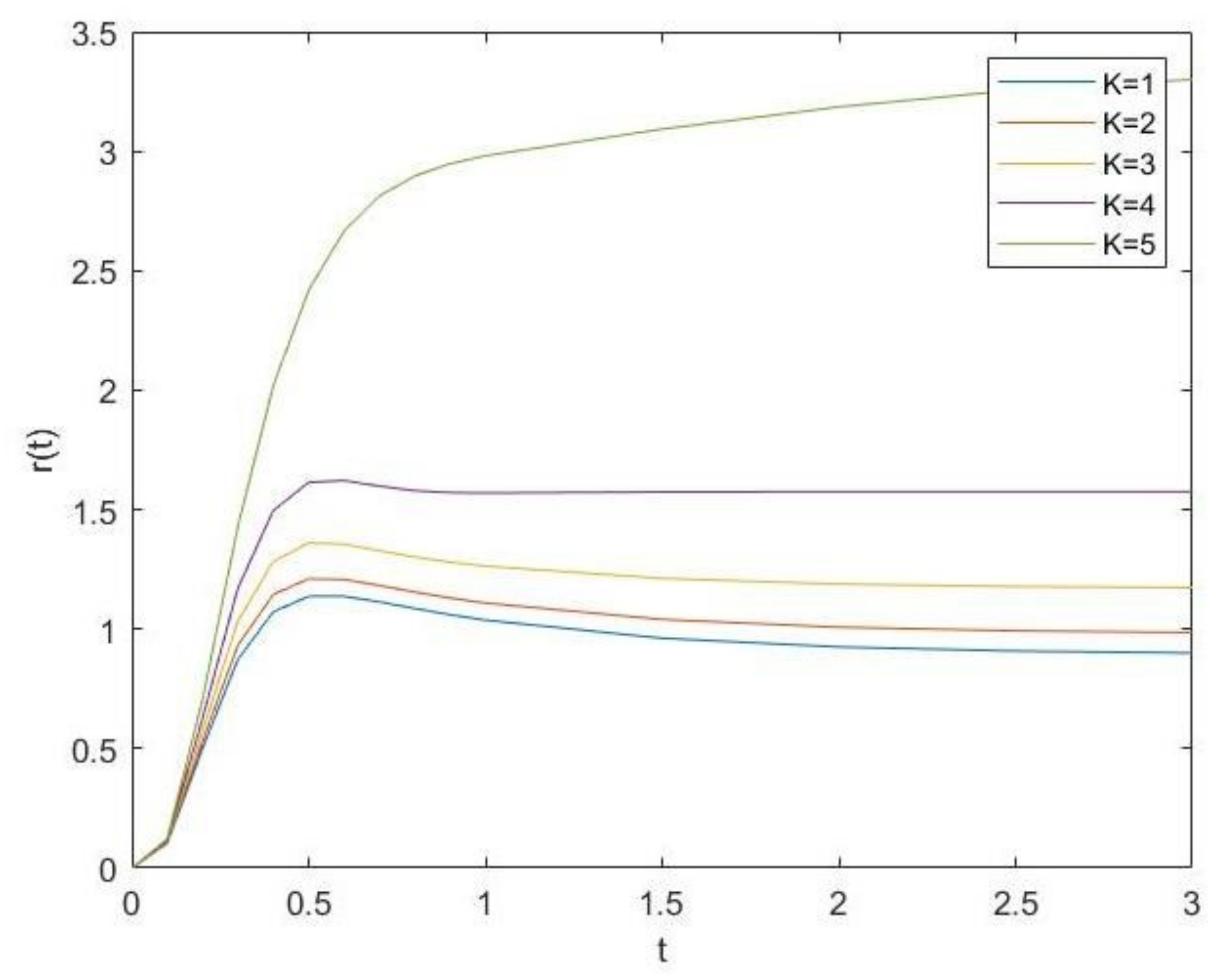
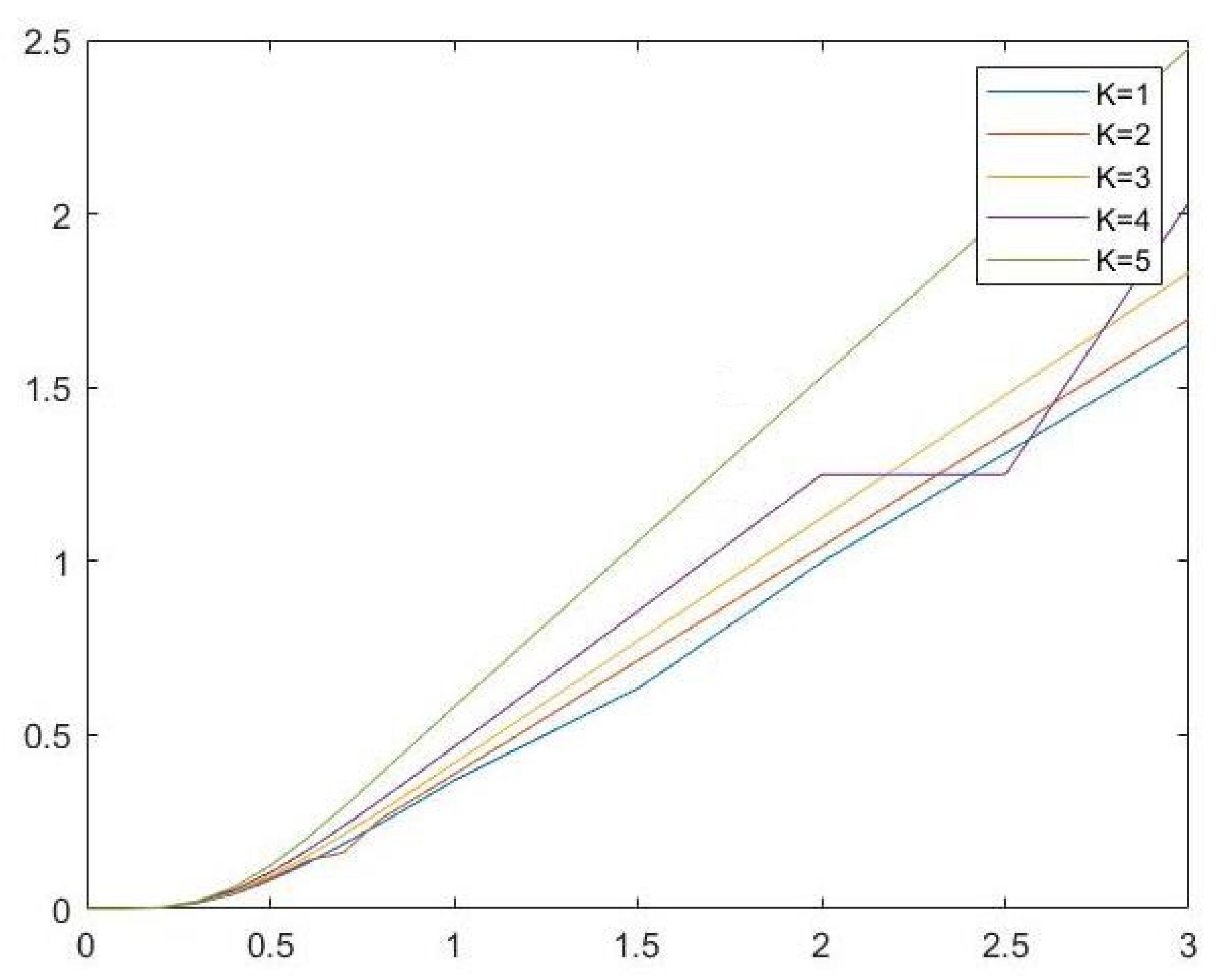
4. Numerical Example
| Arrival of shocks to online unit | |||
| Arrival of shocks to the standby units | |||
| Occurrence of an inspection |
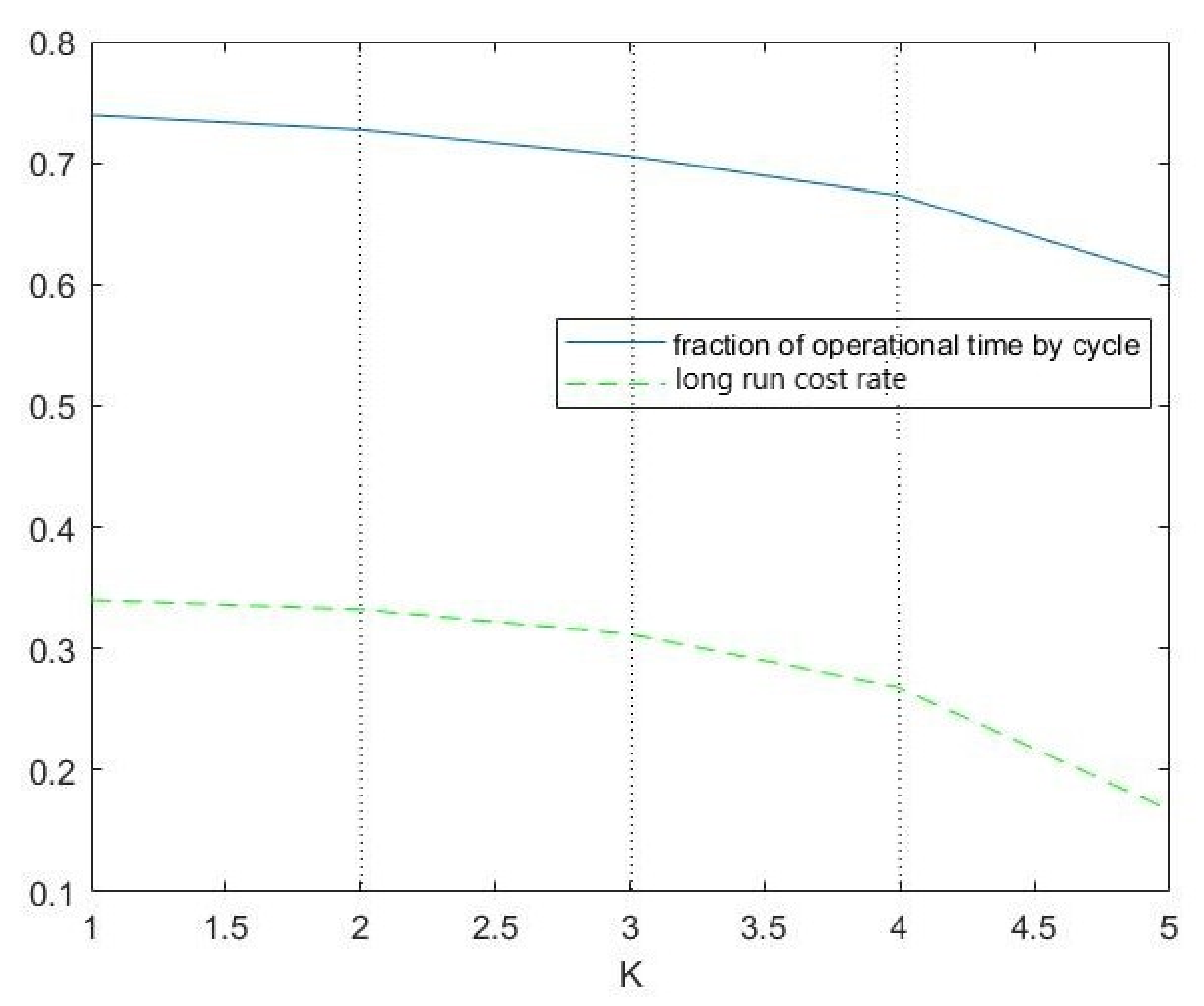
- Performance measures for
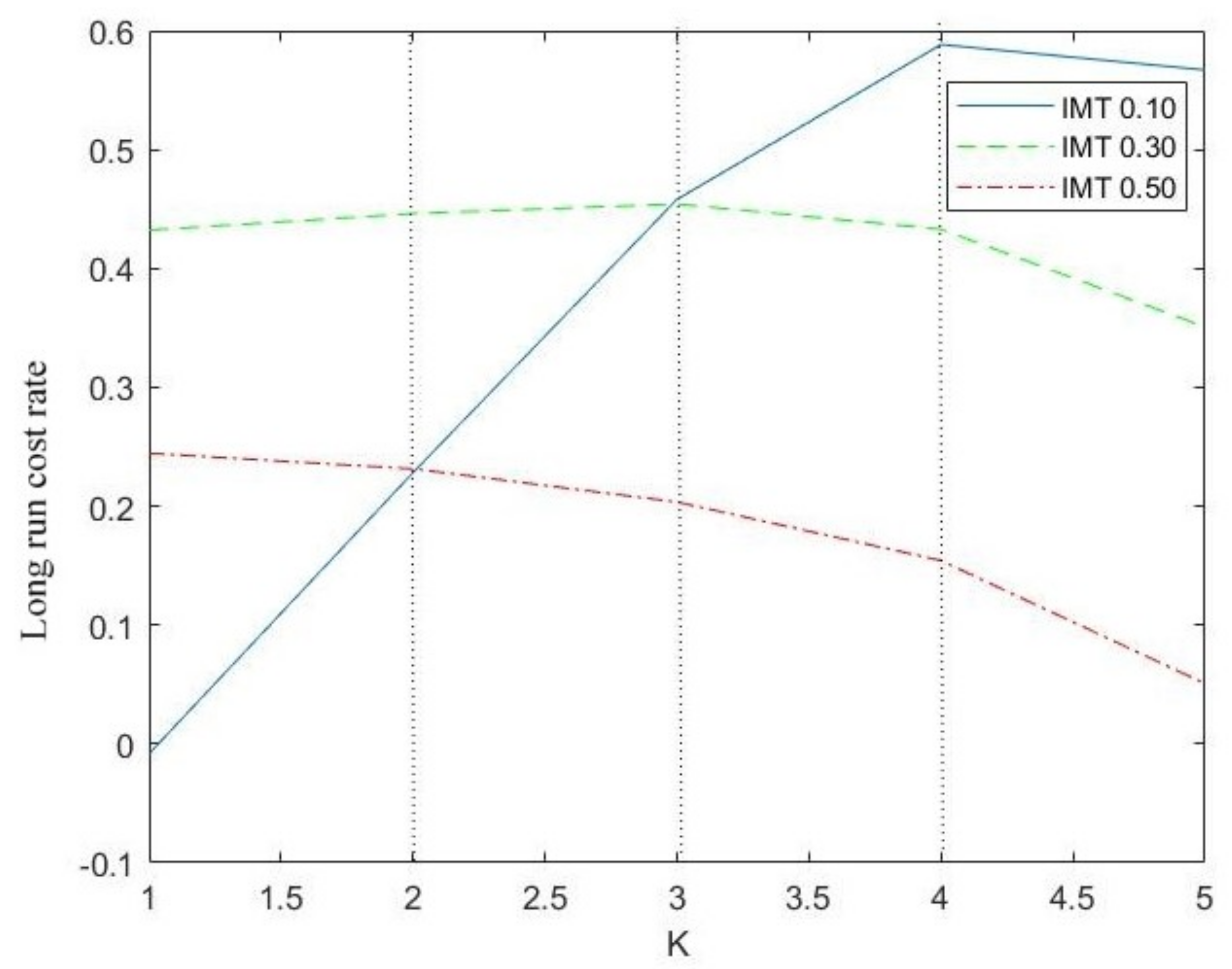
- Comparing performance measures
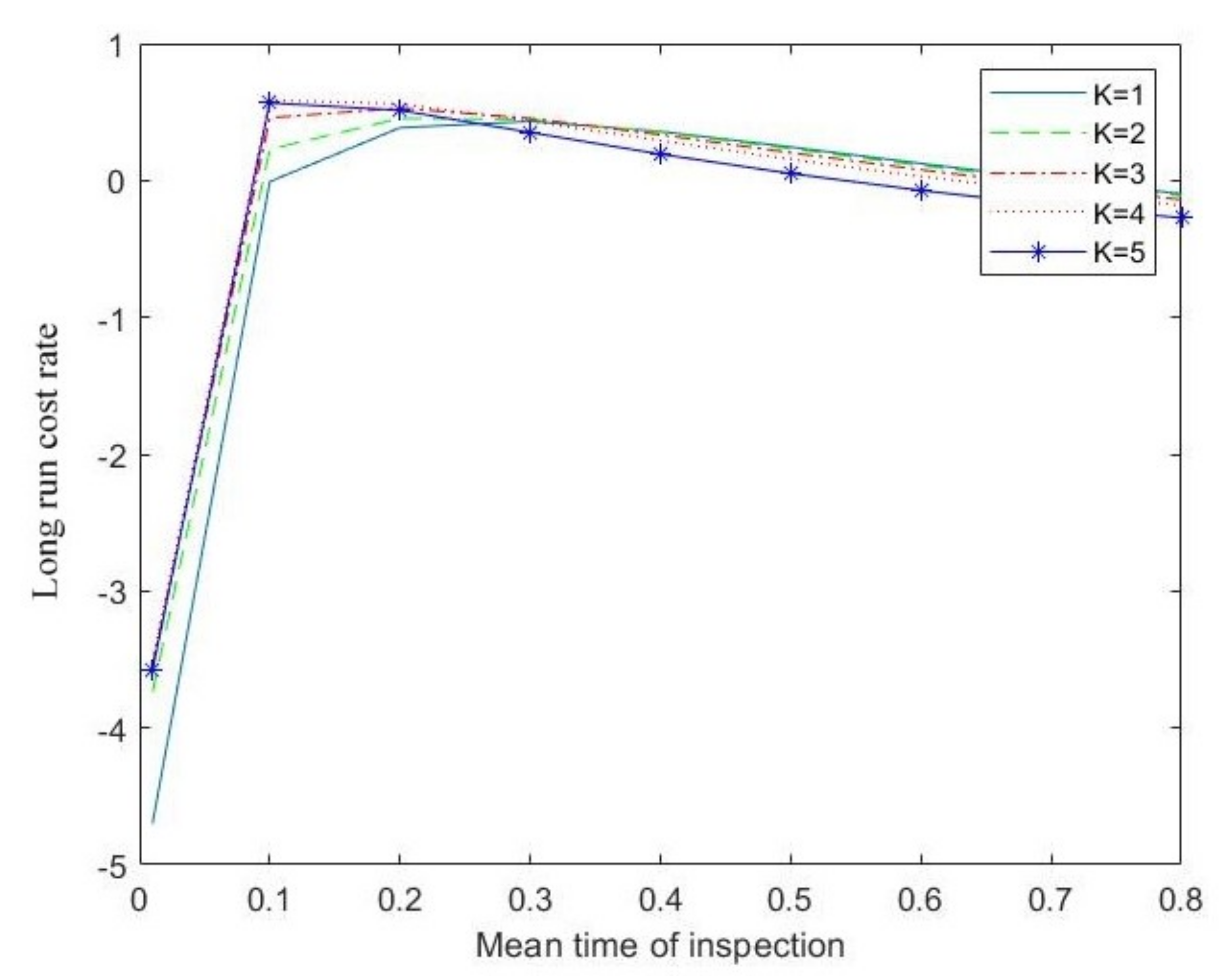
- Availability and the long-run cost rate in terms of the inspection times
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| shock arrival process for online unit | |
| shock arrival process for standby units | |
| inspection arrival process | |
| identity matrix of order r | |
| column vector of 1’s of order r | |
| generator of the process under policy K | |
| steady state vector associated with the macro-state i | |
| steady state vector | |
| A | steady state availability |
| rate of occurrence of failures for online unit | |
| rate of occurrence of failures for standby units | |
| v | rate of occurrence of failures for the system |
| distribution of the up period of the system, | |
| distribution of the down period of the system, | |
| length of a cycle of the system | |
| expected length of the up period of the system | |
| expected length of the down period of the system | |
| expected length of a cycle of the system | |
| cost per inspection | |
| cost per every unit replacement | |
| cost by operational unit time | |
| cost by nonoperational unit time | |
| cost due to the starting-up of the system | |
| expected cost during an up period | |
| expected cost during a down period | |
| expected cost per inspection, depending on the number of replacements, | |
| in the up period | |
| expected number of inspections in the up period | |
| long-run cost rate | |
| availability of the system in time t | |
| reliability of the system in time t | |
| mean number of replacements of the system | |
| failure rate of the system in time t |
References
- Levitin, G.; Finkelstein, M.; Dai, Y. Redundancy optimization for series-parallel phased mission systems exposed to random shocks. Reliab. Eng. Syst. Saf. 2017, 167, 554–560. [Google Scholar] [CrossRef]
- Ruiz-Castro, J.E. A complex multi-state k-out-of-n: G system with preventive maintenance and loss of units. Reliab. Eng. Syst. Saf. 2020, 197, 106797. [Google Scholar] [CrossRef]
- Ruiz-Castro, J.E. Optimizing a Multi-State Cold-Standby System with Multiple Vacations in the Repair and Loss of Units. Mathematics 2021, 9, 913. [Google Scholar] [CrossRef]
- Wang, G.J.; Zhang, Y.L. Optimal repair-replacement policies for a system with two types of failures. Eur. J. Oper. Res 2013, 226, 500–506. [Google Scholar] [CrossRef]
- Badía, F.G.; Berrada, M.D.; Lee, H. An study of cost effective maintenance policies: Age replacement versus replacement after N minimal repairs. Reliab. Eng. Syst. Saf. 2020, 201, 106949. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Wang, G.J. A deteriorating cold standby repairable system with priority in use. Eur. J. Oper. Res 2007, 183, 278–295. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Wang, G.J. A geometric process repair model for a repairable cold standby system with priority in use and repair. Reliab. Eng. Syst. Saf. 2009, 94, 1782–1787. [Google Scholar] [CrossRef]
- Leung, K.N.F.; Zhang, Y.L.; Lai, K.K. Analysis for a two-dissimilar-component cold standby repairable system with repair priority. Reliab. Eng. Syst. Saf. 2011, 96, 1542–1551. [Google Scholar] [CrossRef]
- Yuang, I.; Meng, S.-Y. Reliability analysis of a warm standby repairable system with priority in use. Appl. Math. Model. 2011, 35, 4295–4303. [Google Scholar] [CrossRef]
- Cha, J.H.; Finkelstein, M.; Levitin, G. On preventive maintenance of systems with lifetimes dependent on a random shock process. Reliab. Eng. Syst. Saf. 2017, 168, 90–97. [Google Scholar] [CrossRef]
- Azaron, A.; Katagiri, H.; Sakawa, M.; Modarres, M. Reliability function of a class of time-dependent systems with standby redundancy. Eur. J. Oper. Res 2005, 64, 376–386. [Google Scholar] [CrossRef]
- Azaron, A.; Katagiri, H.; Kato, K.; Sakawa, M. Reliability evaluation of multi-component cold-standby redundant systems. Appl. Math. Comput. 2006, 173, 137–149. [Google Scholar] [CrossRef]
- Dieulle, L. Reliability of several component sets with inspections at random times. Eur. J. Oper. Res. 2002, 139, 96–114. [Google Scholar] [CrossRef]
- Csenki, A. On the three-state weather model of transmission line failures. Proc. Inst. Mech. Eng. O J. Risk Reliab. 2007, 139, 217–228. [Google Scholar] [CrossRef]
- Montoro-Cazorla, D.; Pérez-Ocón, R. Shock and wear degradating systems under three types of repair. Appl. Math. Comput. 2012, 218, 11727–11737. [Google Scholar] [CrossRef]
- Montoro-Cazorla, D.; Pérez-Ocón, R. A shock and wear system under environmental conditions subject to internal failures, repair and replacement three types of repair. Reliab. Eng. Syst. Saf. 2012, 99, 55–61. [Google Scholar] [CrossRef]
- Montoro-Cazorla, D.; Pérez-Ocón, R. A warmstandby system under shocks and repair governed by a MAPs. Reliab. Eng. Syst. Saf. 2016, 152, 331–338. [Google Scholar] [CrossRef]
- Baolian, L.; Cui, L.; Wen, Y.; Shen, J. A cold standby repairable system with working vacations and vacation interruption following Markovian arrival process. Reliab. Eng. Syst. Saf. 2015, 142, 1–8. [Google Scholar]
- Baolian, L.; Wen, Y.; Kang, S.; Qiu, Q. A multiple warm standby repairable system under N-policy with multiple vacations following Markovian arrival process. Commun. Stat.-Theory Methods 2020, 49, 3609–3634. [Google Scholar]
- Li, H.; Huang, C.G.; Guedes Soares, C. A Real-Time Inspection and Opportunistic Maintenance Strategies for Floating Offshore Wind Turbines. Ocean Eng. 2022, 256, 111433. [Google Scholar] [CrossRef]
- Montoro-Cazorla, D.; Pérez-Ocón, R. Constructing a Markov process for modelling a reliability system under multiple failures and replacements. Reliab. Eng. Syst. Saf. 2018, 173, 34–47. [Google Scholar] [CrossRef]
- Chakravarthy, S.R. Maintenance of a deteriorating single system with Markovian arrivals and random shocks. Eur. J. Oper. Res. 2012, 222, 508–522. [Google Scholar] [CrossRef]
- Castro, I.T. A model imperfect preventive maintenance with dependent failure modes. Eur. J. Oper. Res. 2009, 196, 217–224. [Google Scholar] [CrossRef]
- Castro, I.T.; Barros, A.; Grall, A. Age-based preventive maintenance for passive components submitted to stress corrosion cracking. Math. Comput. Model. 2011, 54, 598–609. [Google Scholar] [CrossRef]
- Huynh, K.T.; Barros, A.; Bérenguer, C.; Castro, I.T. A periodic inspection and replacement policy for systems subject to competing failure modes due to degradation and traumatic events. Reliab. Eng. Syst. Saf. 2011, 96, 497–508. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Qiu, Q.; Wang, H. Joint optimization of condition-based and age-based replacement policy and inventory policy for a two-unit series system. Reliab. Eng. Syst. Saf. 2021, 205, 107251. [Google Scholar] [CrossRef]
- Ouaret, S.; Kennéa, J.P.; Gharbi, A. Production and replacement policies for a deteriorating manufacturing system under random demand and quality. Eur. J. Oper. Res. 2018, 264, 623–636. [Google Scholar] [CrossRef]
- Zhai, Q.; Peng, R.; Xing, L.; Yang, J. Reliability of demand-based warm standby systems subject to fault level coverage. Appl. Stoch. Model. Bus. Ind. 2015, 31, 380–393. [Google Scholar] [CrossRef]
- Liu, X.; Yang, T.; Pei, J.; Liao, H.; Pohl, E.A. Replacement and inventory control for a multi-customer product service system with decreasing replacement costs. Eur. J. Oper. Res. 2019, 273, 561–574. [Google Scholar] [CrossRef]
- Distefano, S.; Longo, F.; Trivedi, K.S. Investigating dynamic reliability and availability through state-space models. Comput. Math. Appl. 2012, 64, 3701–3716. [Google Scholar] [CrossRef] [Green Version]
- Bellman, R. Introduction to Matrix Analysis; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Neuts, M.F. Matrix-Geometric Solutions in Stochastic Models—An Algorithm Approach; John Hopkins, University Press: Baltimore, MD, USA, 1981. [Google Scholar]

| t | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||||
| 0 | |||||||||||
| 0 | 0 |
| Policy | A | CT | |||
|---|---|---|---|---|---|
| Policy | A | ||||
|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montoro-Cazorla, D.; Pérez-Ocón, R. Optimizing Costs in a Reliability System under Markovian Arrival of Failures and Reposition by K-Policy Inspection. Mathematics 2022, 10, 1918. https://doi.org/10.3390/math10111918
Montoro-Cazorla D, Pérez-Ocón R. Optimizing Costs in a Reliability System under Markovian Arrival of Failures and Reposition by K-Policy Inspection. Mathematics. 2022; 10(11):1918. https://doi.org/10.3390/math10111918
Chicago/Turabian StyleMontoro-Cazorla, Delia, and Rafael Pérez-Ocón. 2022. "Optimizing Costs in a Reliability System under Markovian Arrival of Failures and Reposition by K-Policy Inspection" Mathematics 10, no. 11: 1918. https://doi.org/10.3390/math10111918






