Introducing Two Parsimonious Standard Power Mixture Models for Bimodal Proportional Data with Application to Loss Given Default
Abstract
:1. Introduction
2. Data and Benchmark Model
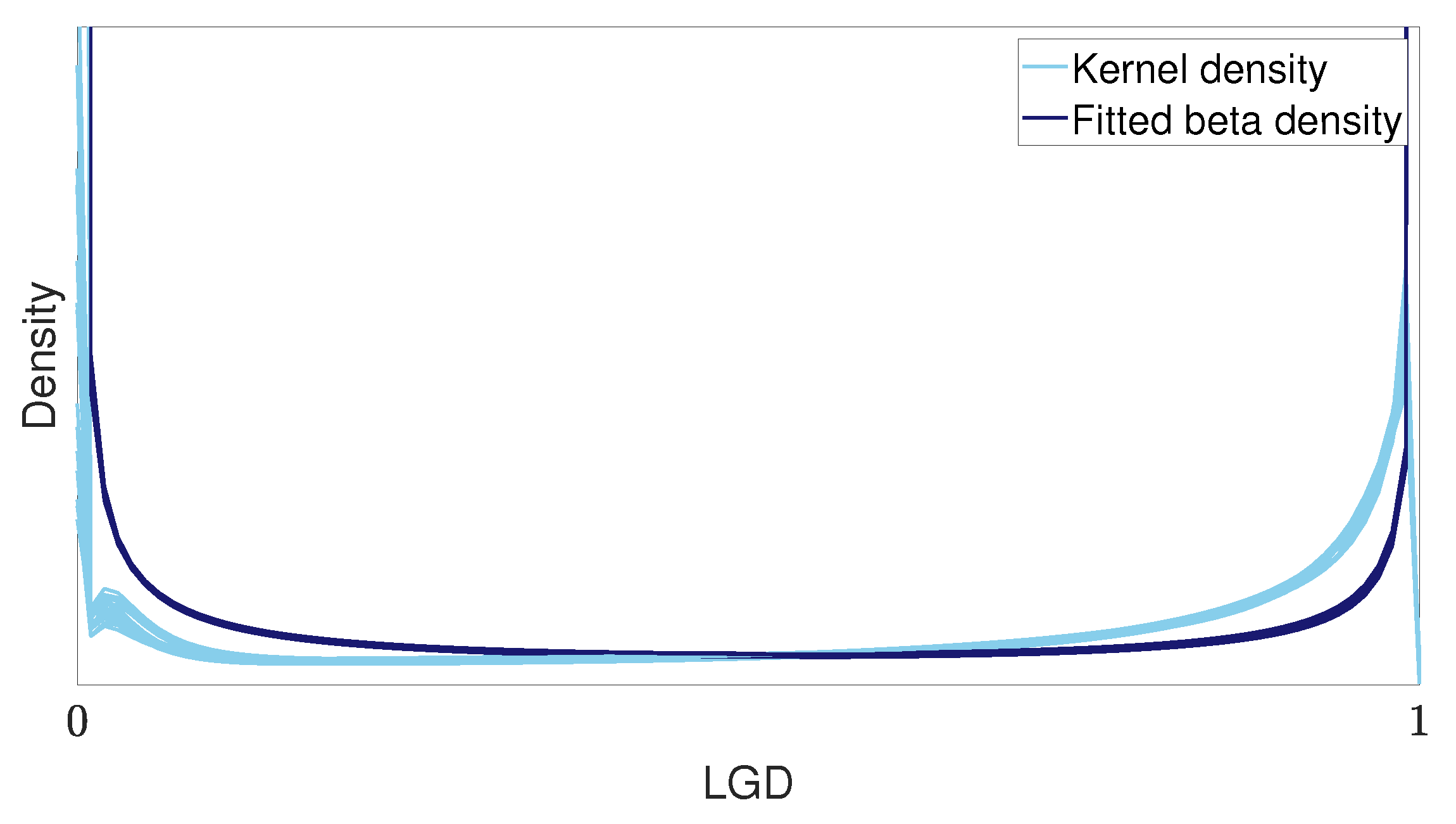
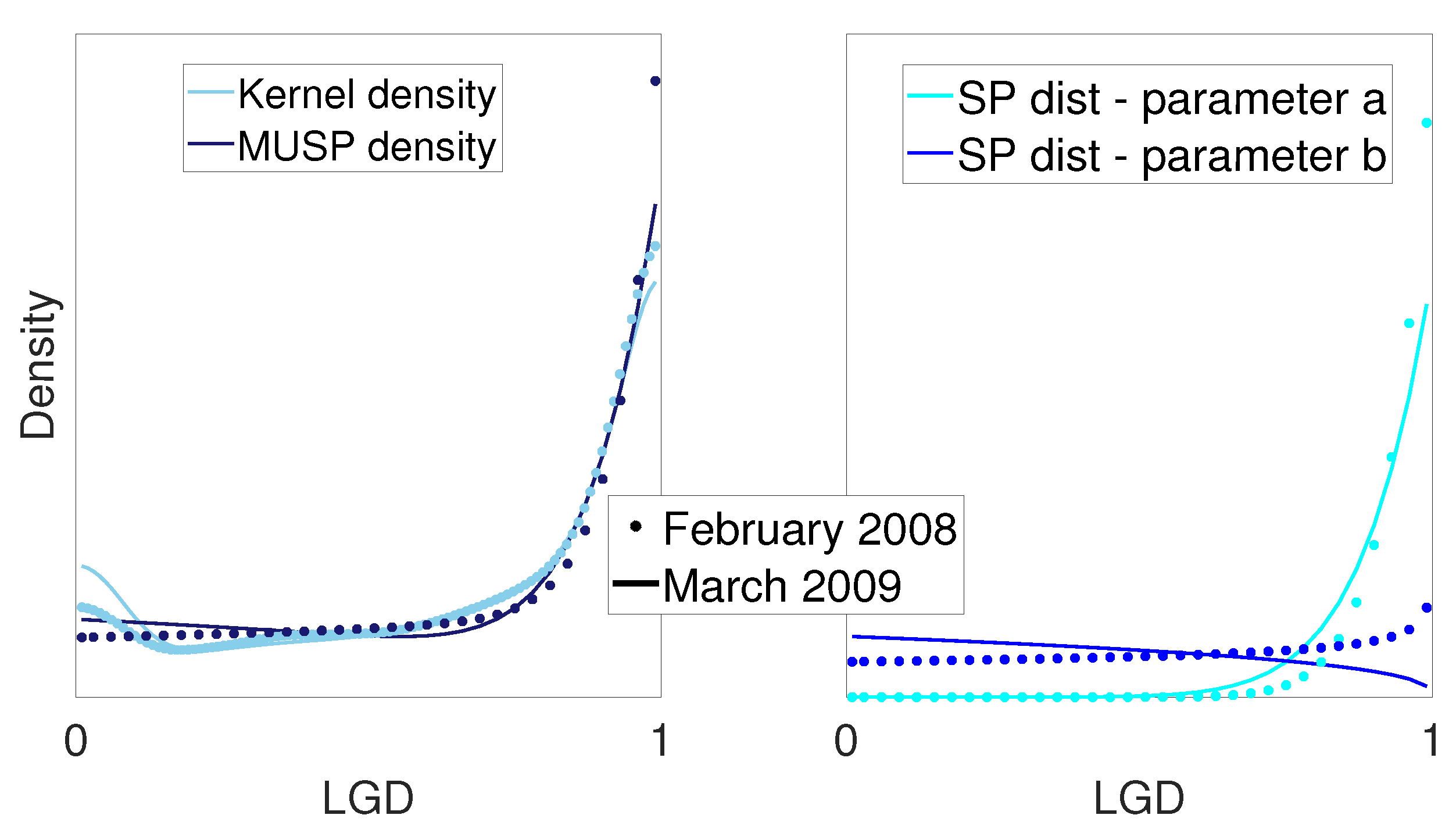
2.1. Zero-One Inflated Beta Distribution
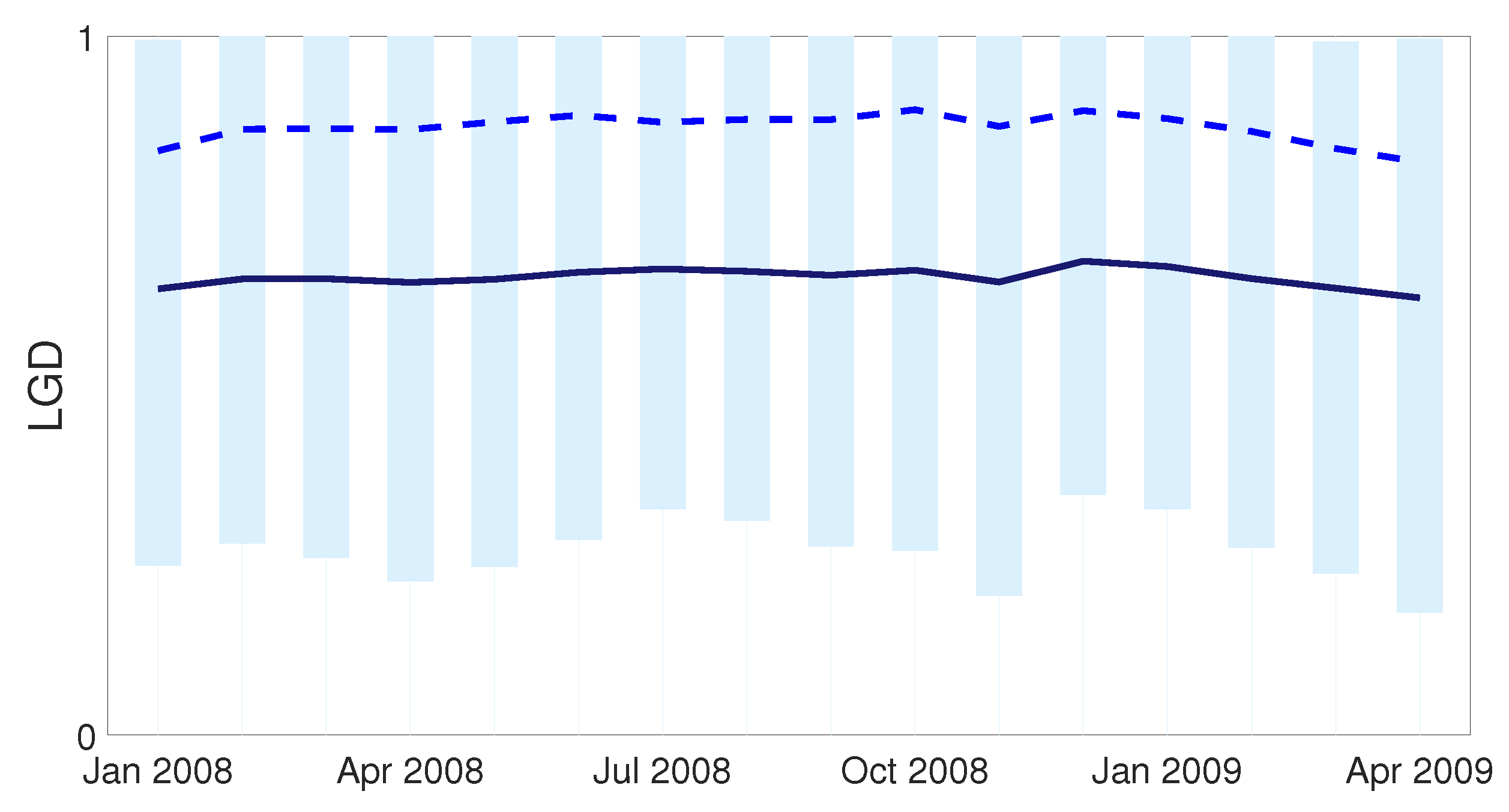
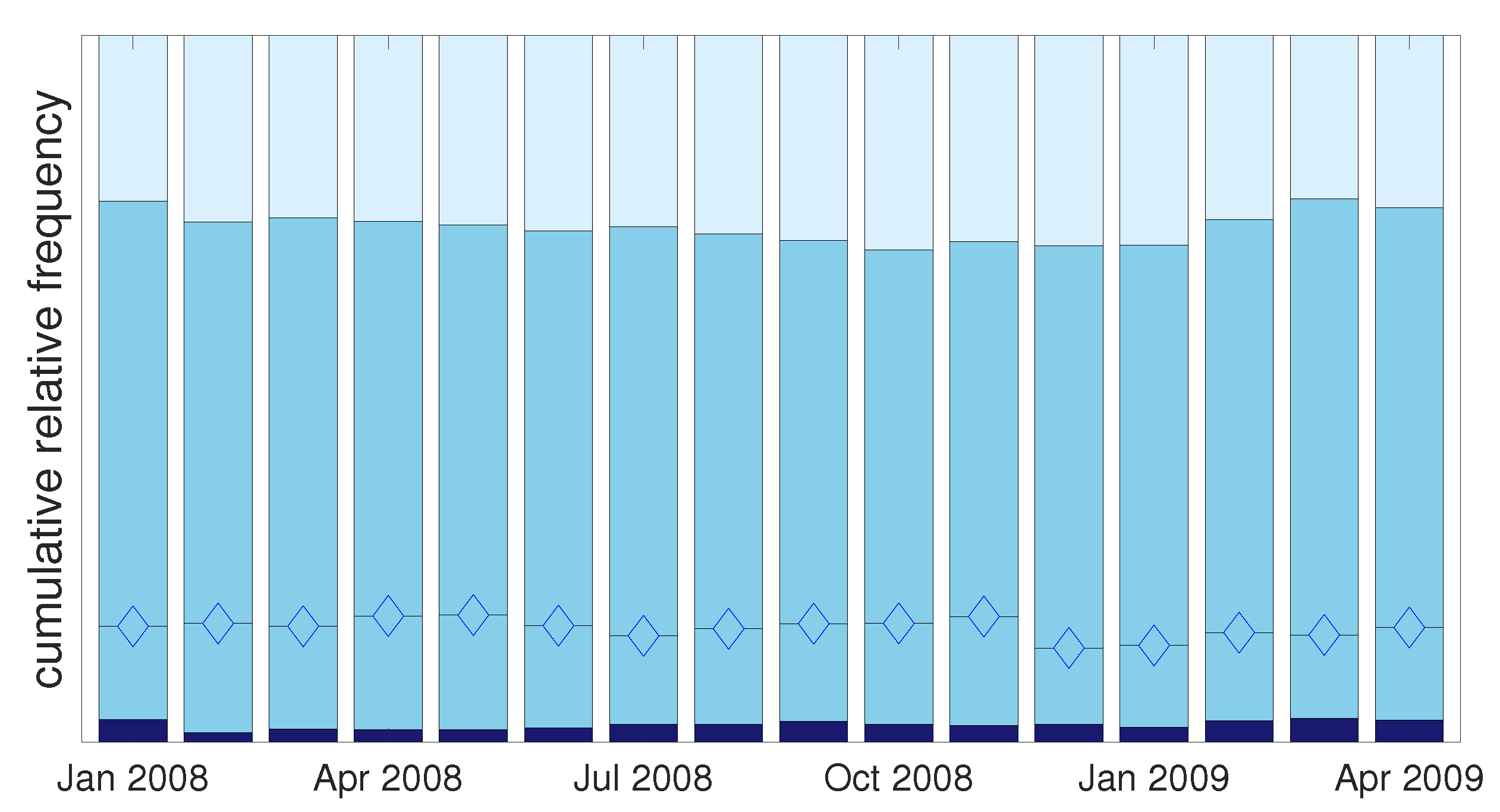
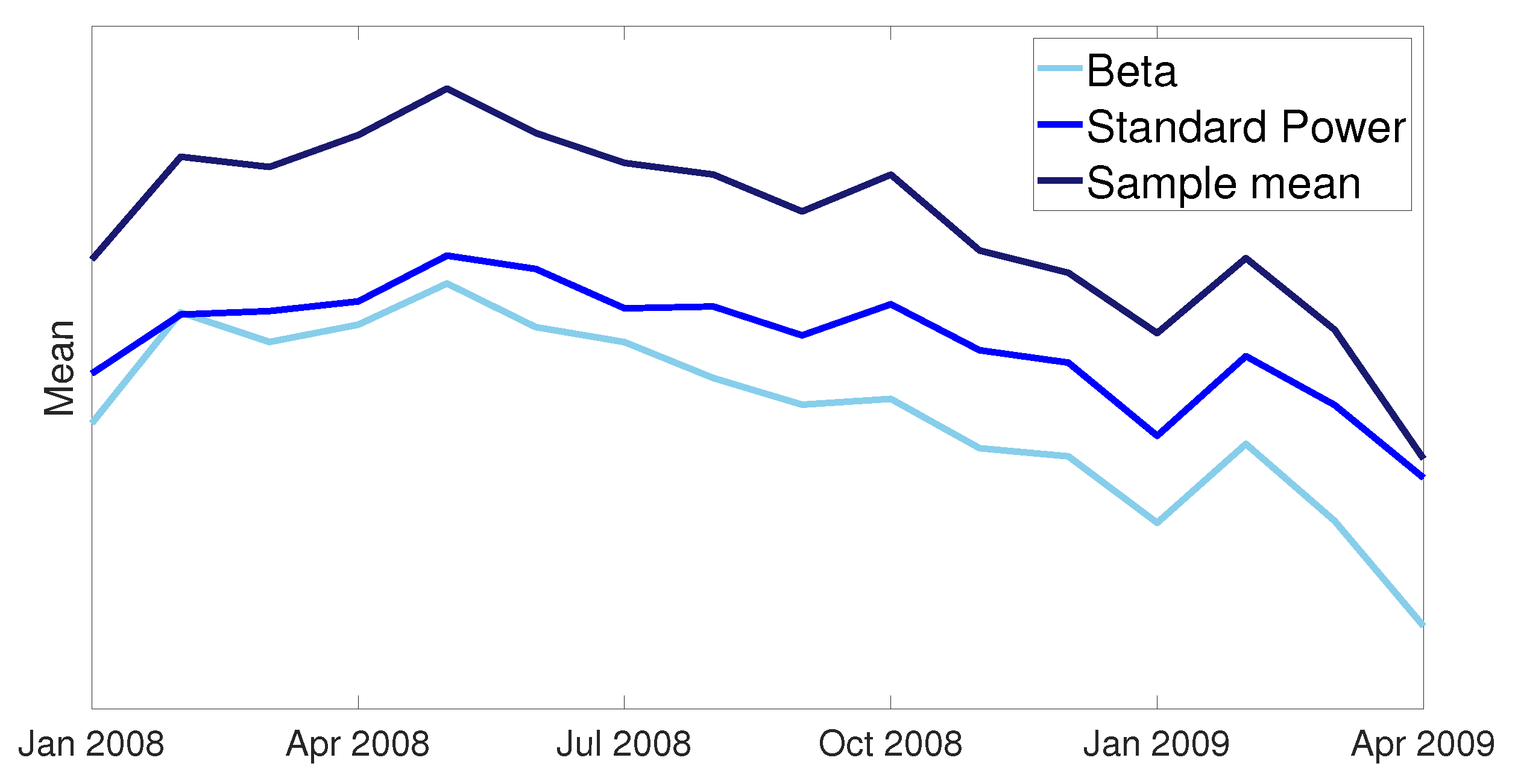
2.2. Data
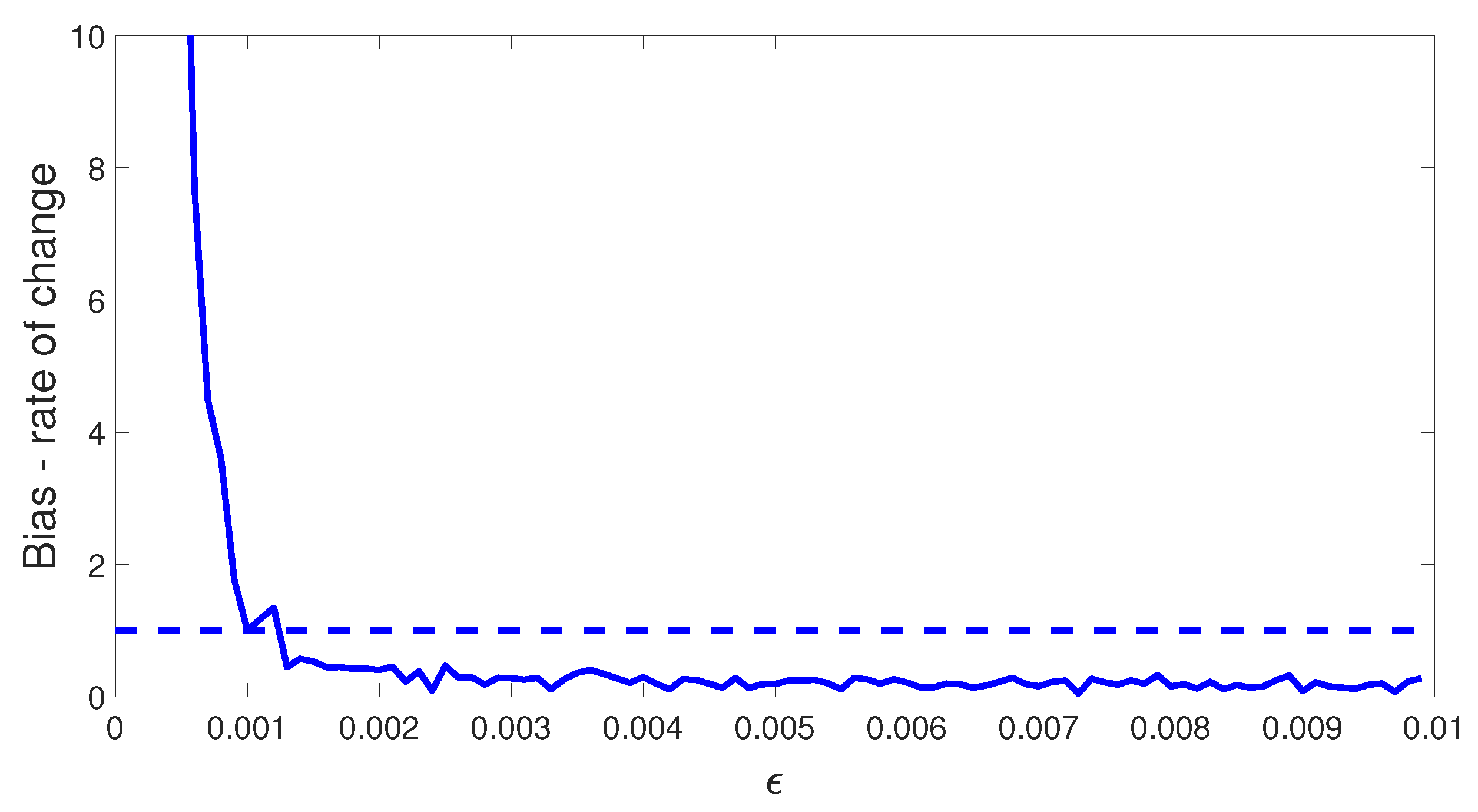
2.3. Selection of a Rounding Threshold
2.4. Fitting the Benchmark Model
3. New Proposed Models
3.1. Inflated Mixed Standard Power Distribution
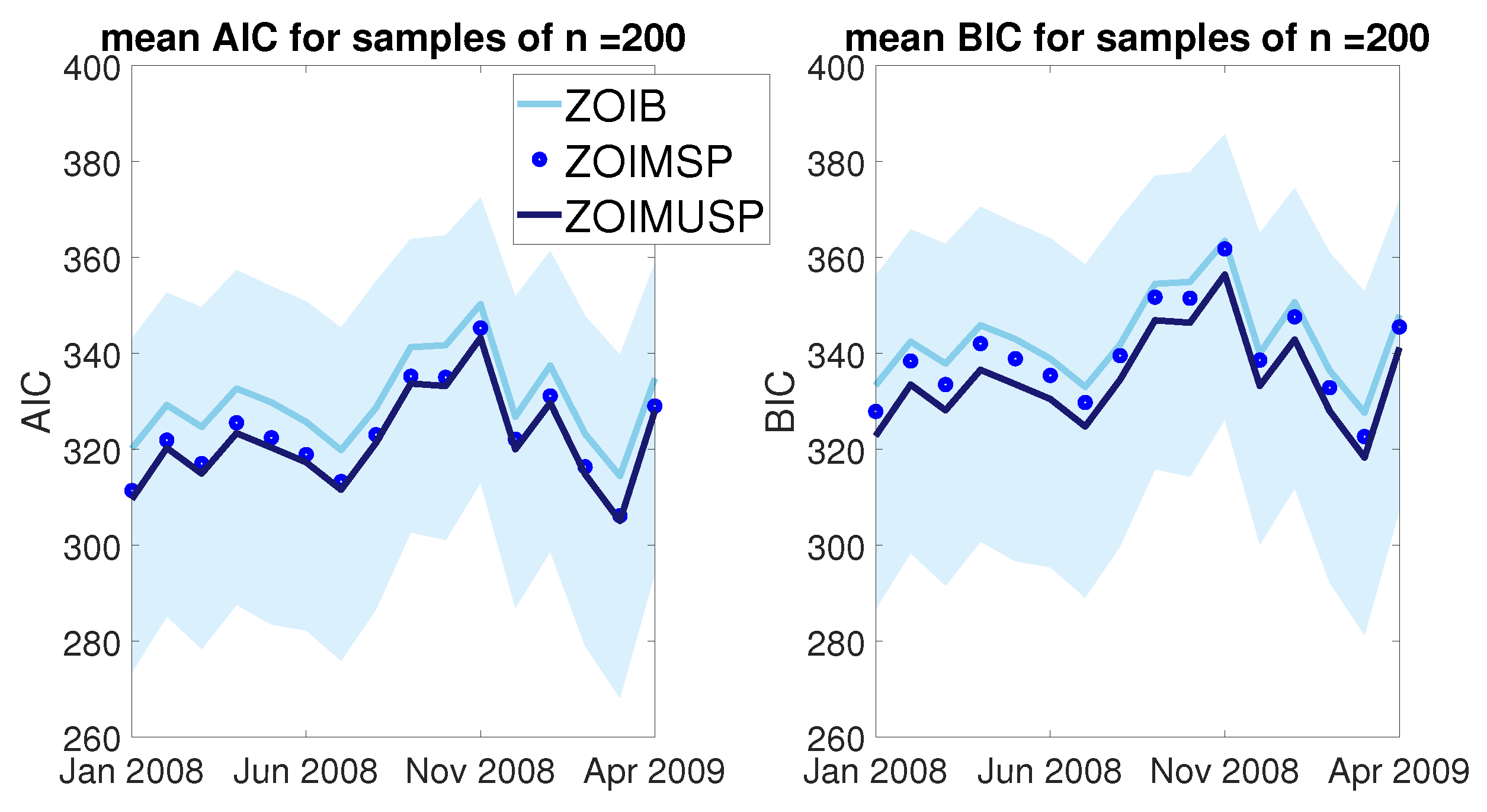
3.2. Model Performance Based on Information Criteria
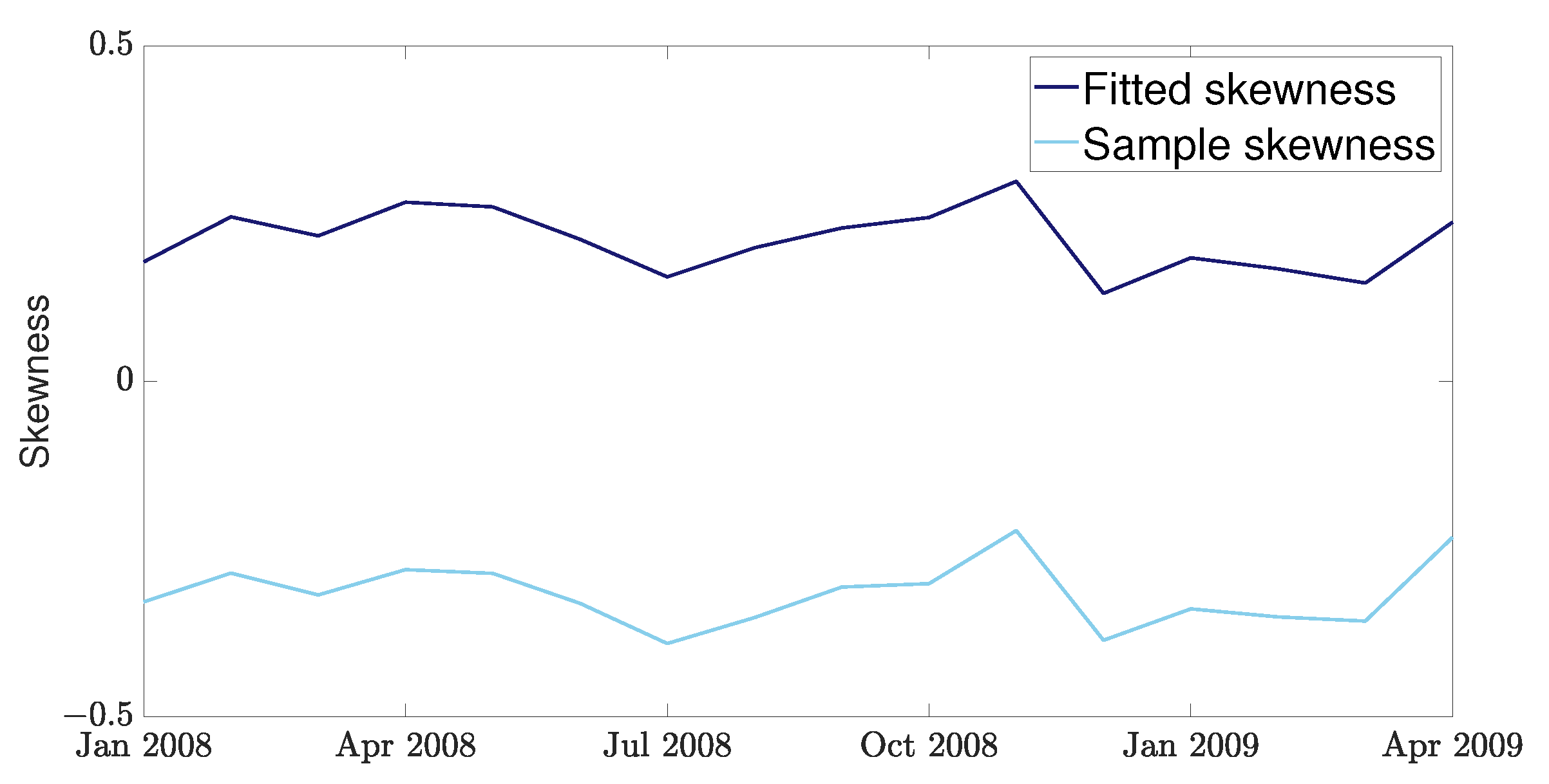
3.3. Model Performance Based on Empirical Bias
3.4. Model Performance for Small Samples
- For month j, obtain a sample by sampling observations with a replacement from .
- Fit a model on to obtain the estimator .
- Calculate the statistics and from Equations (8) and (9) with inputs , , n and the number of parameters k.
- Repeat steps 1–3 above B times to obtain , and
4. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramalho, E.; Ramalho, J.; Coelho, L. Exponential Regression of Fractional-Response Fixed-Effects Models with an Application to Firm Capital Structure. J. Econom. Methods 2016, 7, 20150019. [Google Scholar] [CrossRef]
- Falls, L.W. The beta distribution—A statistical model for world cloud cover. J. Geophys. Res. 1974, 79, 1261–1264. [Google Scholar] [CrossRef] [Green Version]
- Kousathanas, A.; Keightley, P.D. A comparison of models to infer the distribution of fitness effects of new mutations. Genetics 2013, 193, 1197–1208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stewart, J. The Beta Distribution as a Model of Behavior in Consumer Goods Markets. Manag. Sci. 1979, 25, 813–821. [Google Scholar] [CrossRef]
- Tasche, D. The single risk factor approach to capital charges in case of correlated loss given default rates. arXiv 2004, arXiv:condmat/0402390. [Google Scholar] [CrossRef]
- Damme, G.V. A generic framework for stochastic Loss-Given-Default. J. Comput. Appl. Math. 2011, 235, 2523–2550. [Google Scholar] [CrossRef] [Green Version]
- Farinelli, S.; Shkolnikov, M. Two models of stochastic loss given default. J. Credit. Risk 2012, 8, 3–20. [Google Scholar] [CrossRef] [Green Version]
- Simone, R. On finite mixtures of Discretized Beta model for ordered responses. TEST 2022, 31, 828–855. [Google Scholar] [CrossRef]
- Simone, R.; Tutz, G. Modelling uncertainty and response styles in ordinal data. Stat. Neerl. 2018, 72, 224–245. [Google Scholar] [CrossRef]
- James, S.A.; West, C.L.; Davey, R.P.; Dicks, J.L.; Roberts, I.N. Prevalence and Dynamics of Ribosomal DNA Micro-heterogeneity Are Linked to Population History in Two Contrasting Yeast Species. Sci. Rep. 2016, 6, 28555. [Google Scholar] [CrossRef] [PubMed]
- Memmel, C.; Sachs, A.; Stein, I. Contagion at the Interbank Market with Stochastic LGD. SSRN 2794059. 2011. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2794059 (accessed on 1 November 2022). [CrossRef]
- Basel Committee on Banking Supervision. An Explanatory Note on the Basel II IRB Risk Weight Functions; Technical Report; Bank for International Settlements: Basel, Switzerland, 2004; Available online: http://www.bis.org/bcbs/irbriskweight.htm (accessed on 28 September 2022).
- Ospina, R.; Ferrari, S.L.P. Inflated beta distributions. Stat. Pap. 2008, 51, 111–126. [Google Scholar] [CrossRef] [Green Version]
- Calabrese, R.; Zenga, M. Bank loan recovery rates: Measuring and nonparametric density estimation. J. Bank. Financ. 2010, 34, 903–911. [Google Scholar] [CrossRef]
- Basel Committee on Banking Supervision. Guidance on Paragraph 468 of the Framework Document; Technical Report; Bank for International Settlements: Basel, Switzerland, 2005; Available online: https://www.bis.org/publ/bcbs115.htm (accessed on 28 September 2022).
- Jones, M. Kumaraswamy’s distribution: A beta-type distribution with some tractability advantages. Stat. Methodol. 2009, 6, 70–81. [Google Scholar] [CrossRef]
- Kumaraswamy, P. A generalized probability density function for double-bounded random processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- Cribari-Neto, F.; Santos, J. Inflated Kumaraswamy distributions. An. Acad. Bras. CiêNcias 2019, 91, e20180955. [Google Scholar] [CrossRef] [PubMed]
- Leemis, L.M.; McQueston, J. Univariate Distribution Relationships. Am. Stat. 2008, 62, 45–53. [Google Scholar] [CrossRef]
- Ribeiro, M. A Zero-One Inflated Mixture Model for Loss Given Default Data: The Beta Distribution Case. In Proceedings of the XIV Conference on Credit Scoring and Credit Control, Edinburgh, Scotland, 29 May 2015. [Google Scholar]
- Ribeiro, M.; Louzada, F.; Henrique, G.; Pereira, A.; Moreira, F.; Calabrese, R. Inflated Mixture Models: Applications to Multimodality in Loss Given Default. SSRN 2634919. 2015. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2634919 (accessed on 1 November 2022). [CrossRef]
- Schröder, C.; Rahmann, S. A hybrid parameter estimation algorithm for beta mixtures and applications to methylation state classification. Algorithms Mol. Biol. 2017, 12, 21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bishop, C.M. Pattern Recognition and Machine Learning, 5th ed.; Information Science and Statistics; Springer: New York, NY, USA, 2007. [Google Scholar]
- Van Reenen, M.; Westerhuis, J.A.; Reinecke, C.J.; Venter, J.H. Metabolomics variable selection and classification in the presence of observations below the detection limit using an extension of ERp. BMC Bioinform. 2017, 18, 83. [Google Scholar] [CrossRef] [PubMed]







| Bernoulli | Beta | |||
|---|---|---|---|---|
| Month | ||||
| 200801 | 0.266 | 0.881 | 0.303 | 0.653 |
| 200802 | 0.277 | 0.952 | 0.27 | 0.658 |
| 200803 | 0.276 | 0.934 | 0.277 | 0.646 |
| 200804 | 0.281 | 0.938 | 0.26 | 0.66 |
| 200805 | 0.286 | 0.939 | 0.255 | 0.643 |
| 200806 | 0.297 | 0.932 | 0.271 | 0.63 |
| 200807 | 0.296 | 0.916 | 0.298 | 0.626 |
| 200808 | 0.305 | 0.92 | 0.281 | 0.636 |
| 200809 | 0.319 | 0.908 | 0.277 | 0.655 |
| 200810 | 0.329 | 0.922 | 0.266 | 0.65 |
| 200811 | 0.316 | 0.925 | 0.256 | 0.682 |
| 200812 | 0.323 | 0.922 | 0.317 | 0.634 |
| 200901 | 0.318 | 0.933 | 0.311 | 0.672 |
| 200902 | 0.291 | 0.896 | 0.302 | 0.643 |
| 200903 | 0.265 | 0.872 | 0.319 | 0.651 |
| 200904 | 0.274 | 0.889 | 0.297 | 0.698 |
| Bernoulli | Beta | Standard Power | |||
|---|---|---|---|---|---|
| Month | |||||
| 200801 | 0.393 | 0.596 | 0.94 (0.019) | 0.525 (0.009) | 0.54 (0.008) |
| 200802 | 0.428 | 0.616 | 1.003 (0.02) | 0.521 (0.009) | 0.52 (0.007) |
| 200803 | 0.418 | 0.617 | 0.962 (0.02) | 0.51 (0.009) | 0.519 (0.008) |
| 200804 | 0.438 | 0.602 | 0.972 (0.021) | 0.509 (0.009) | 0.516 (0.008) |
| 200805 | 0.444 | 0.605 | 0.966 (0.021) | 0.493 (0.009) | 0.501 (0.008) |
| 200806 | 0.437 | 0.634 | 0.931 (0.019) | 0.488 (0.009) | 0.505 (0.018) |
| 200807 | 0.417 | 0.65 | 0.959 (0.018) | 0.508 (0.008) | 0.518 (0.007) |
| 200808 | 0.435 | 0.645 | 0.916 (0.018) | 0.496 (0.008) | 0.518 (0.007) |
| 200809 | 0.452 | 0.641 | 0.918 (0.019) | 0.506 (0.009) | 0.527 (0.008) |
| 200810 | 0.466 | 0.651 | 0.891 (0.018) | 0.489 (0.009) | 0.517 (0.008) |
| 200811 | 0.466 | 0.627 | 0.887 (0.019) | 0.503 (0.009) | 0.532 (0.008) |
| 200812 | 0.427 | 0.698 | 0.891 (0.018) | 0.508 (0.009) | 0.537 (0.008) |
| 200901 | 0.429 | 0.692 | 0.897 (0.016) | 0.533 (0.009) | 0.562 (0.008) |
| 200902 | 0.41 | 0.636 | 0.898 (0.016) | 0.507 (0.007) | 0.534 (0.007) |
| 200903 | 0.377 | 0.613 | 0.867 (0.014) | 0.514 (0.008) | 0.552 (0.006) |
| 200904 | 0.4 | 0.609 | 0.832 (0.014) | 0.527 (0.008) | 0.578 (0.007) |
| ZOIB | ZOISP | |||
|---|---|---|---|---|
| Month | AIC | BIC | AIC | BIC |
| 200801 | 13240 | 13268 | 13248 (0.06%) | 13269 (0.01%) |
| 200802 | 13418 | 13446 | 13416 (−0.01%) | 13437 (−0.07%) |
| 200803 | 12535 | 12563 | 12537 (0.02%) | 12558 (−0.04%) |
| 200804 | 12852 | 12880 | 12852 (0%) | 12873 (−0.05%) |
| 200805 | 13174 | 13202 | 13174 (0%) | 13195 (−0.05%) |
| 200806 | 12263 | 12291 | 12272 (0.07%) | 12293 (0.02%) |
| 200807 | 13817 | 13846 | 13820 (0.02%) | 13841 (−0.04%) |
| 200808 | 13900 | 13929 | 13918 (0.13%) | 13939 (0.07%) |
| 200809 | 14171 | 14199 | 14186 (0.11%) | 14207 (0.06%) |
| 200810 | 14699 | 14727 | 14730 (0.21%) | 14751 (0.16%) |
| 200811 | 15578 | 15606 | 15613 (0.22%) | 15634 (0.18%) |
| 200812 | 13102 | 13130 | 13133 (0.24%) | 13154 (0.18%) |
| 200901 | 15142 | 15170 | 15172 (0.2%) | 15194 (0.16%) |
| 200902 | 18403 | 18432 | 18443 (0.22%) | 18465 (0.18%) |
| 200903 | 17309 | 17338 | 17384 (0.43%) | 17406 (0.39%) |
| 200904 | 18401 | 18431 | 18526 (0.68%) | 18548 (0.63%) |
| MSP | MUSP | ||||
|---|---|---|---|---|---|
| Month | |||||
| 200801 | 14.727 (0.722) | 0.892 (0.05) | 0.338 (0.02) | 13.618 (0.518) | 0.378 (0.007) |
| 200802 | 14.945 (0.753) | 0.798 (0.04) | 0.324 (0.02) | 13.047 (0.527) | 0.407 (0.007) |
| 200803 | 12.81 (0.601) | 0.879 (0.057) | 0.382 (0.023) | 11.983 (0.463) | 0.428 (0.008) |
| 200804 | 12.609 (0.615) | 0.82 (0.051) | 0.367 (0.024) | 11.575 (0.437) | 0.438 (0.008) |
| 200805 | 13.932 (0.676) | 0.769 (0.041) | 0.352 (0.021) | 12.447 (0.476) | 0.447 (0.008) |
| 200806 | 13.755 (0.717) | 0.739 (0.038) | 0.327 (0.021) | 12.329 (0.473) | 0.438 (0.008) |
| 200807 | 14.305 (0.726) | 0.768 (0.036) | 0.315 (0.019) | 12.466 (0.463) | 0.415 (0.007) |
| 200808 | 14.586 (0.747) | 0.761 (0.036) | 0.308 (0.02) | 12.522 (0.457) | 0.414 (0.007) |
| 200809 | 13.918 (0.713) | 0.816 (0.046) | 0.329 (0.022) | 12.318 (0.492) | 0.406 (0.008) |
| 200810 | 11.369 (0.561) | 1.041 (0.076) | 0.451 (0.024) | 11.522 (0.427) | 0.439 (0.008) |
| 200811 | 12.026 (0.581) | 0.974 (0.066) | 0.397 (0.023) | 11.827 (0.452) | 0.407 (0.008) |
| 200812 | 9.182 (0.439) | 1.411 (0.107) | 0.515 (0.02) | 11.651 (0.48) | 0.403 (0.008) |
| 200901 | 7.001 (0.415) | 1.873 (0.329) | 0.584 (0.063) | 10.77 (0.428) | 0.391 (0.008) |
| 200902 | 13.489 (0.551) | 0.911 (0.046) | 0.36 (0.019) | 12.641 (0.402) | 0.394 (0.006) |
| 200903 | 9.698 (0.392) | 1.375 (0.078) | 0.488 (0.015) | 12.241 (0.421) | 0.383 (0.006) |
| 200904 | 8.164 (0.32) | 1.708 (0.087) | 0.515 (0.012) | 12.455 (0.471) | 0.344 (0.007) |
| ZOIB | ZOIMSP | ZOIMUSP | ||||
|---|---|---|---|---|---|---|
| Month | AIC | BIC | AIC | BIC | AIC | BIC |
| 200801 | 13240 | 13268 | 12822 (−3.2%) | 12858 (−3.1%) | 12825 (−3.1%) | 12853 (-3.1%) |
| 200802 | 13418 | 13446 | 13047 (−2.8%) | 13082 (−2.7%) | 13063 (−2.6%) | 13091 (−2.6%) |
| 200803 | 12535 | 12563 | 12156 (−3%) | 12190 (−3%) | 12155 (−3%) | 12183 (−3%) |
| 200804 | 12852 | 12880 | 12489 (−2.8%) | 12524 (−2.8%) | 12492 (−2.8%) | 12520 (−2.8%) |
| 200805 | 13174 | 13202 | 12791 (−2.9%) | 12826 (−2.8%) | 12801 (−2.8%) | 12829 (−2.8%) |
| 200806 | 12263 | 12291 | 11952 (−2.5%) | 11987 (−2.5%) | 11961 (−2.5%) | 11988 (−2.5%) |
| 200807 | 13817 | 13846 | 13458 (−2.6%) | 13494 (−2.5%) | 13476 (−2.5%) | 13505 (−2.5%) |
| 200808 | 13900 | 13929 | 13588 (−2.2%) | 13624 (−2.2%) | 13606 (−2.1%) | 13634 (−2.1%) |
| 200809 | 14171 | 14199 | 13852 (−2.2%) | 13887 (−2.2%) | 13858 (−2.2%) | 13887 (−2.2%) |
| 200810 | 14699 | 14727 | 14328 (−2.5%) | 14363 (−2.5%) | 14326 (−2.5%) | 14355 (−2.5%) |
| 200811 | 15578 | 15606 | 15269 (−2%) | 15304 (−1.9%) | 15267 (−2%) | 15295 (−2%) |
| 200812 | 13102 | 13130 | 12812 (−2.2%) | 12847 (−2.2%) | 12813 (−2.2%) | 12841 (−2.2%) |
| 200901 | 15142 | 15170 | 14717 (−2.8%) | 14753 (−2.8%) | 14735 (−2.7%) | 14763 (−2.7%) |
| 200902 | 18403 | 18432 | 17928 (−2.6%) | 17965 (−2.5%) | 17929 (−2.6%) | 17958 (−2.6%) |
| 200903 | 17309 | 17338 | 16779 (−3.1%) | 16816 (−3%) | 16787 (−3%) | 16817 (−3%) |
| 200904 | 18401 | 18431 | 18007 (−2.1%) | 18043 (−2.1%) | 18039 (−2%) | 18068 (−2%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Larney, J.; Grobler, G.L.; Allison, J.S. Introducing Two Parsimonious Standard Power Mixture Models for Bimodal Proportional Data with Application to Loss Given Default. Mathematics 2022, 10, 4520. https://doi.org/10.3390/math10234520
Larney J, Grobler GL, Allison JS. Introducing Two Parsimonious Standard Power Mixture Models for Bimodal Proportional Data with Application to Loss Given Default. Mathematics. 2022; 10(23):4520. https://doi.org/10.3390/math10234520
Chicago/Turabian StyleLarney, Janette, Gerrit Lodewicus Grobler, and James Samuel Allison. 2022. "Introducing Two Parsimonious Standard Power Mixture Models for Bimodal Proportional Data with Application to Loss Given Default" Mathematics 10, no. 23: 4520. https://doi.org/10.3390/math10234520






