Classification of Alzheimer’s Disease and Mild-Cognitive Impairment Base on High-Order Dynamic Functional Connectivity at Different Frequency Band
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Data Acquisition
2.3. Data Preprocessing
2.4. Features Selection
| Algorithm 1: SFS |
| Then, the output will be: |
| Where the selected features are |
| In the initialization (where k is the size of the subset). |
| In the termination, the size is is the number of desired features. |
2.5. SVM Classifier
2.6. Evaluation Matrices
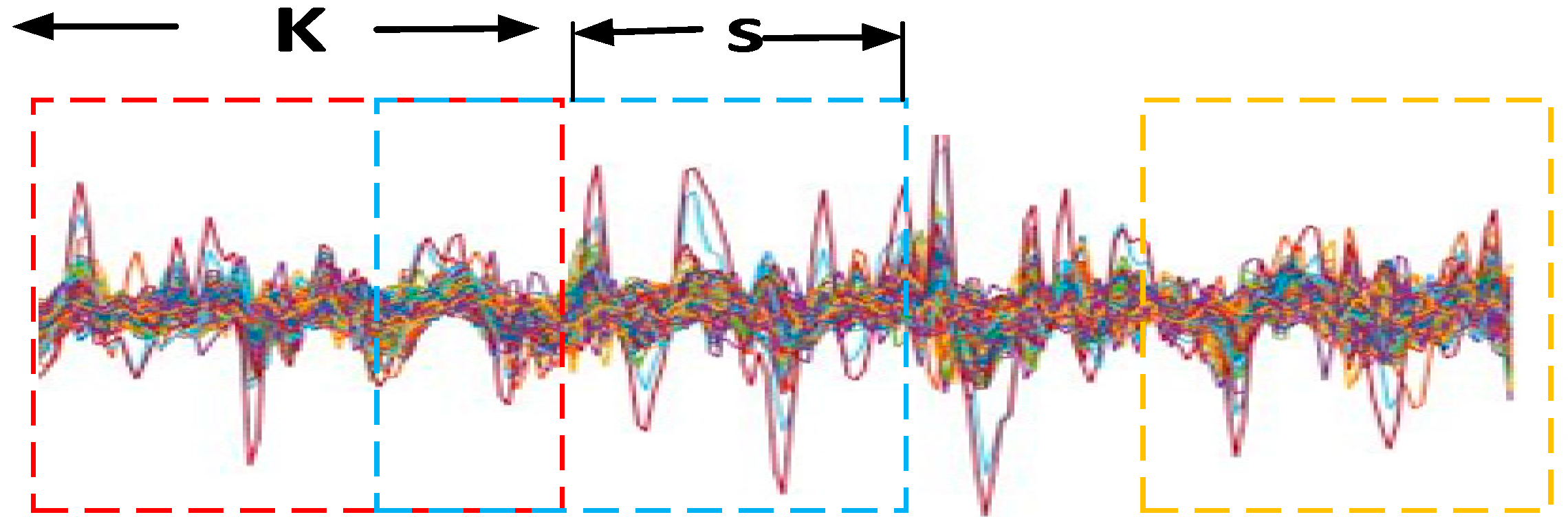
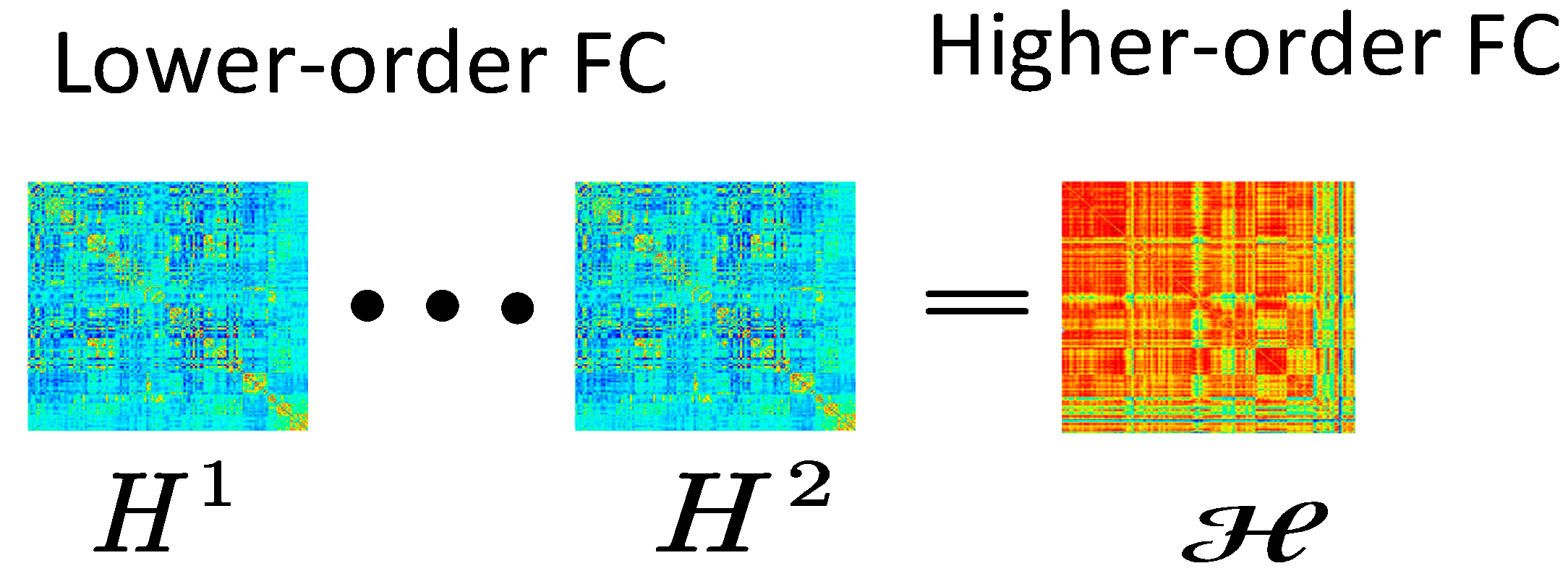
2.7. Higher-Order Dynamic Functional Network Construction
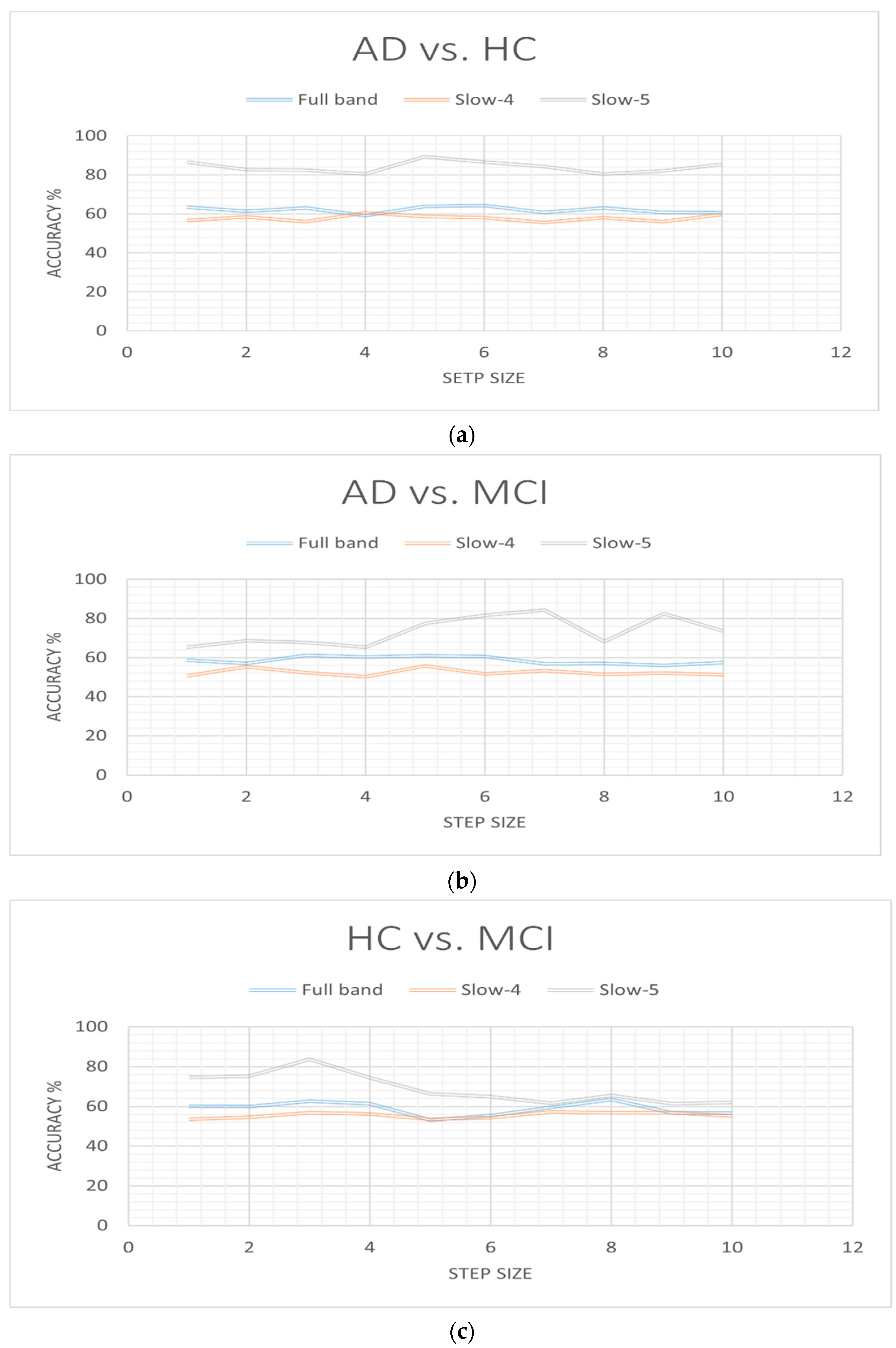
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ju, R.; Hu, C.; Zhou, P.; Li, Q. Early Diagnosis of Alzheimer’s Disease Based on Resting-State Brain Networks and Deep Learning. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019, 16, 244–257. [Google Scholar] [CrossRef]
- Zhou, T.; Thung, K.; Zhu, X.; Shen, D. Effective feature learning and fusion of multimodality data using stage-wise deep neural network for dementia diagnosis. Hum. Brain Mapp. 2018, 40, 1001–1016. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Zheng, X.; Li, Y.; Zhang, Q.; Ying, S. Multimodal Neuroimaging Feature Learning With Multimodal Stacked Deep Polynomial Networks for Diagnosis of Alzheimer’s Disease. IEEE J. Biomed. Health Inform. 2018, 22, 173–183. [Google Scholar] [CrossRef]
- Huettel, S.A.; Song, A.W.; McCarthy, G. Functional Magnetic Resonance Imaging, 2nd ed.; Sinauer Associates: Sunderland, MA, USA, 2004. [Google Scholar]
- Ogawa, S.; Lee, T.M.; Kay, A.R.; Tank, D.W. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc. Natl. Acad. Sci. USA 1990, 87, 9868–9872. [Google Scholar] [CrossRef] [Green Version]
- Herculano-Houzel, S. The remarkable, yet not extraordinary, human brain as a scaled-up primate brain and its associated cost. Proc. Natl. Acad. Sci. USA 2012, 109, 10661–10668. [Google Scholar] [CrossRef] [Green Version]
- Qi, S.; Meesters, S.; Nicolay, K.; Romeny, B.M.T.H.; Ossenblok, P. The influence of construction methodology on structural brain network measures: A review. J. Neurosci. Methods 2015, 253, 170–182. [Google Scholar] [CrossRef]
- Weng, S.-J.; Wiggins, J.L.; Peltier, S.J.; Carrasco, M.; Risi, S.; Lord, C.; Monk, C.S. Alterations of Resting State Functional Connectivity in the Default Network in Adolescents with Autism Spectrum Disorders. Brain Res. 2010, 1313, 202. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Zhang, S.; Li, Y.; Zhang, J.; Yang, L.; Fang, Y. Low-Rank Sparse Subspace for Spectral Clustering. IEEE Trans. Knowl. Data Eng. 2019, 31, 1532–1543. [Google Scholar] [CrossRef]
- Khazaee, A.; Ebrahimzadeh, A.; Babajani-Feremi, A. Identifying patients with Alzheimer’s disease using resting-state fMRI and graph theory. Clin. Neurophysiol. Off. J. Int. Fed. Clin. Neurophysiol. 2015, 126, 2132–2141. [Google Scholar] [CrossRef]
- Wee, C.Y.; Yap, P.T.; Shen, D.; Alzheimer’s Disease Neuroimaging Initiative. Prediction of Alzheimer’s disease and mild cognitive impairment using cortical morphological patterns. Hum. Brain Mapp. 2013, 34, 3411–3425. [Google Scholar] [CrossRef] [Green Version]
- Sanaat, A.; Zaidi, H. Depth of Interaction Estimation in a Preclinical PET Scanner Equipped with Monolithic Crystals Coupled to SiPMs Using a Deep Neural Network. Appl. Sci. 2020, 10, 4753. [Google Scholar] [CrossRef]
- Roshani, M.; Sattari, M.A.; Muhammad Ali, P.J.; Roshani, G.H.; Nazemi, B.; Corniani, E.; Nazemi, E. Application of GMDH neural network technique to improve measuring precision of a simplified photon attenuation based two-phase flowmeter. Flow Meas. Instrum. 2020, 75, 101804. [Google Scholar] [CrossRef]
- Azizi, A.; Tahmid, I.A.; Waheed, A.; Mangaokar, N.; Pu, J.; Javed, M.; Reddy, C.K.; Viswanath, B. T-Miner: A Generative Approach to Defend Against Trojan Attacks on DNN-based Text Classification. In Proceedings of the 30th USENIX Security Symposium (USENIX Security 21), Vancouver, BC, Canada, 11–13 August 2021. [Google Scholar]
- Kudela, M.; Harezlak, J.; Lindquist, M.A. Assessing uncertainty in dynamic functional connectivity. NeuroImage 2017, 149, 165–177. [Google Scholar] [CrossRef] [Green Version]
- Zuo, X.-N.; Di Martino, A.; Kelly, C.; Shehzad, Z.E.; Gee, D.G.; Klein, D.F.; Castellanos, F.X.; Biswal, B.B.; Milham, M.P. The oscillating brain: Complex and reliable. NeuroImage 2010, 49, 1432–1445. [Google Scholar] [CrossRef] [Green Version]
- Mascali, D.; DiNuzzo, M.; Gili, T.; Moraschi, M.; Fratini, M.; Maraviglia, B.; Serra, L.; Bozzali, M.; Giove, F. Intrinsic Patterns of Coupling between Correlation and Amplitude of Low-Frequency fMRI Fluctuations Are Disrupted in Degenerative Dementia Mainly due to Functional Disconnection. PLoS ONE 2015, 10, e0120988. [Google Scholar] [CrossRef]
- Allen, E.A.; Damaraju, E.; Plis, S.M.; Erhardt, E.B.; Eichele, T.; Calhoun, V.D. Tracking whole-brain connectivity dynamics in the resting state. Cereb. Cortex 2014, 24, 663–676. [Google Scholar] [CrossRef]
- Chang, C.; Glover, G.H. Time-frequency dynamics of resting-state brain connectivity measured with fMRI. NeuroImage 2010, 50, 81–98. [Google Scholar] [CrossRef] [Green Version]
- Lindquist, M.A.; Xu, Y.; Nebel, M.B.; Caffo, B.S. Evaluating dynamic bivariate correlations in resting-state fMRI: A comparison study and a new approach. NeuroImage 2014, 101, 531–546. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, H.; Chen, X.; Lee, S.-W.; Shen, D. Hybrid High-order Functional Connectivity Networks Using Resting-state Functional MRI for Mild Cognitive Impairment Diagnosis. Sci. Rep. 2017, 7, 6530. [Google Scholar] [CrossRef] [Green Version]
- Yan, C.; Zang, Y. DPARSF: A MATLAB toolbox for “pipeline” data analysis of resting-state fMRI. Front. Syst. Neurosci. 2010, 4, 13. [Google Scholar] [CrossRef] [Green Version]
- Song, X.-W.; Dong, Z.-Y.; Long, X.-Y.; Li, S.-F.; Zuo, X.-N.; Zhu, C.-Z.; He, Y.; Yan, C.-G.; Zang, Y.-F. REST: A toolkit for resting-state functional magnetic resonance imaging data processing. PLoS ONE 2011, 6, e25031. [Google Scholar] [CrossRef]
- Chen, R.-C.; Dewi, C.; Huang, S.-W.; Caraka, R.E. Selecting critical features for data classification based on machine learning methods. J. Big Data 2020, 7, 52. [Google Scholar] [CrossRef]
- Aha, D.W.; Bankert, R.L. A Comparative Evaluation of Sequential Feature Selection Algorithms. In Learning from Data: Artificial Intelligence and Statistics V; Fisher, D., Lenz, H.-J., Eds.; Lecture Notes in Statistics; Springer: New York, NY, USA, 1996; pp. 199–206. ISBN 978-1-4612-2404-4. [Google Scholar]
- Muni, D.P.; Pal, N.R.; Das, J. Genetic programming for simultaneous feature selection and classifier design. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2006, 36, 106–117. [Google Scholar] [CrossRef]
- Ghayab, H.R.A.; Li, Y.; Abdulla, S.; Diykh, M.; Wan, X. Classification of epileptic EEG signals based on simple random sampling and sequential feature selection. Brain Inform. 2016, 3, 85–91. [Google Scholar] [CrossRef] [Green Version]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, Y.; Zhou, L.; Yuan, H.; Shen, D. Alzheimer’s Disease Neuroimaging Initiative Multimodal classification of Alzheimer’s disease and mild cognitive impairment. NeuroImage 2011, 55, 856–867. [Google Scholar] [CrossRef] [Green Version]
- Collij, L.E.; Heeman, F.; Kuijer, J.P.A.; Ossenkoppele, R.; Benedictus, M.R.; Möller, C.; Verfaillie, S.C.J.; Sanz-Arigita, E.J.; van Berckel, B.N.M.; van der Flier, W.M.; et al. Application of Machine Learning to Arterial Spin Labeling in Mild Cognitive Impairment and Alzheimer Disease. Radiology 2016, 281, 865–875. [Google Scholar] [CrossRef] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 2010, 52, 1059–1069. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; Gao, Y.; Wee, C.-Y.; Li, G.; Shen, D. Alzheimer’s Disease Neuroimaging Initiative High-order resting-state functional connectivity network for MCI classification. Hum. Brain Mapp. 2016, 37, 3282–3296. [Google Scholar] [CrossRef] [Green Version]
- Sakoğlu, U.; Pearlson, G.D.; Kiehl, K.A.; Wang, Y.M.; Michael, A.M.; Calhoun, V.D. A method for evaluating dynamic functional network connectivity and task-modulation: Application to schizophrenia. Magn. Reson. Mater. Phys. Biol. Med. 2010, 23, 351–366. [Google Scholar] [CrossRef] [Green Version]
- Hinrichs, C.; Singh, V.; Xu, G.; Johnson, S.C. Predictive markers for AD in a multi-modality framework: An analysis of MCI progression in the ADNI population. NeuroImage 2011, 55, 574–589. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Chen, Z.; Gong, G.; Evans, A. Neuronal networks in Alzheimer’s disease. Neurosci. Rev. J. Bringing Neurobiol. Neurol. Psychiatry 2009, 15, 333–350. [Google Scholar] [CrossRef]
- Challis, E.; Hurley, P.; Serra, L.; Bozzali, M.; Oliver, S.; Cercignani, M. Gaussian process classification of Alzheimer’s disease and mild cognitive impairment from resting-state fMRI. NeuroImage 2015, 112, 232–243. [Google Scholar] [CrossRef] [Green Version]
- de Vos, F.; Koini, M.; Schouten, T.M.; Seiler, S.; van der Grond, J.; Lechner, A.; Schmidt, R.; de Rooij, M.; Rombouts, S.A.R.B. A comprehensive analysis of resting state fMRI measures to classify individual patients with Alzheimer’s disease. NeuroImage 2018, 167, 62–72. [Google Scholar] [CrossRef] [Green Version]



| Group | MCI | AD | HC |
|---|---|---|---|
| Nos. of Subjects | 61 | 35 | 35 |
| Male/Female | 33/28 | 23/12 | 14/21 |
| Age | 72.80 ± 7.9 | 75.65 ± 8.61 | 77.83 ± 6.17 |
| FAQ score | 2.74 ± 3.71 | 4.46 ± 4.01 | 0.33 ± 0.78 |
| CDR | 0.5 | 0.7 ± 0.3 | 0 |
| MMSE score | 26.42 ± 3.75 | 19.59 ± 4.56 | 29.13 ± 1.20 |
| Group | Frequency Band | Classifiers | AUC | ACC | SEN | SPE |
|---|---|---|---|---|---|---|
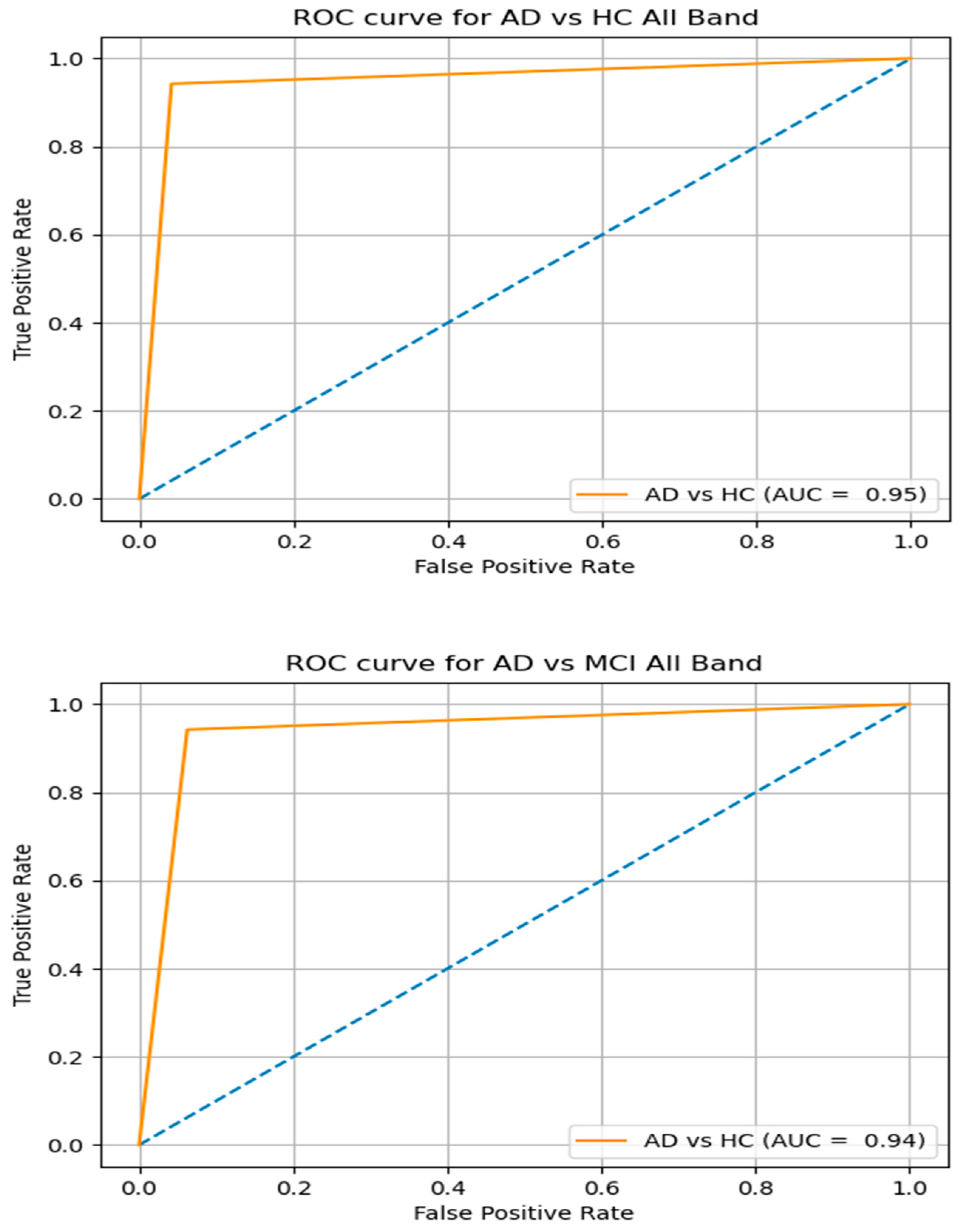
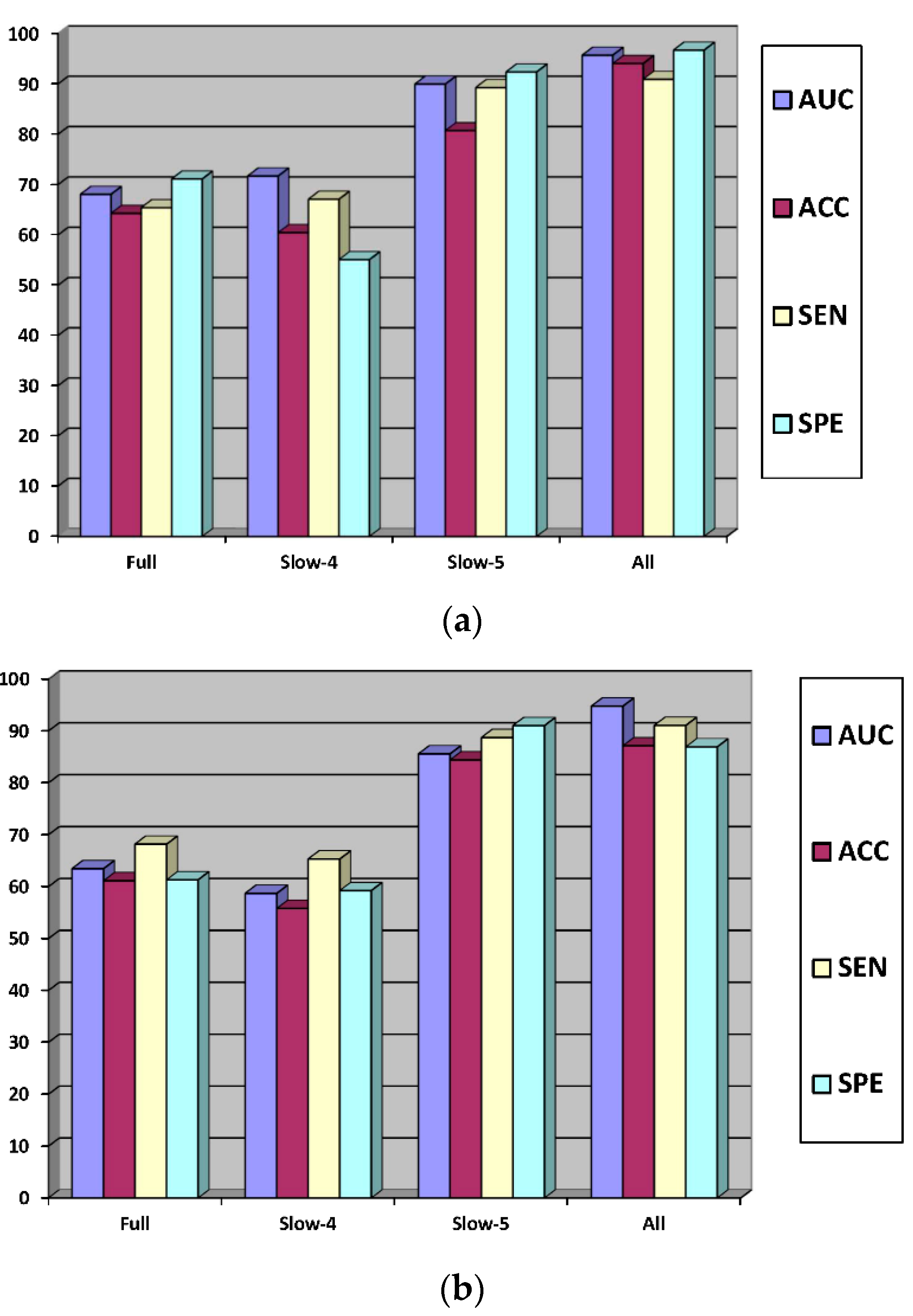
| AD vs. HC | Full band | SVM | 68.10 | 64.33 | 65.45 | 71.15 |
| Slow-4 | 71.74 | 60.50 | 67.13 | 55.12 | ||
| Slow-5 | 80.77 | 89.30 | 92.41 | 88.90 | ||
| All | 95.74 | 94.10 | 90.95 | 96.75 | ||
| AD vs. MCI | Full band | SVM | 63.45 | 61.13 | 68.17 | 61.30 |
| Slow-4 | 58.70 | 55.80 | 65.31 | 59.23 | ||
| Slow-5 | 85.57 | 84.40 | 88.71 | 91.01 | ||
| All | 94.77 | 87.14 | 91.05 | 86.91 | ||
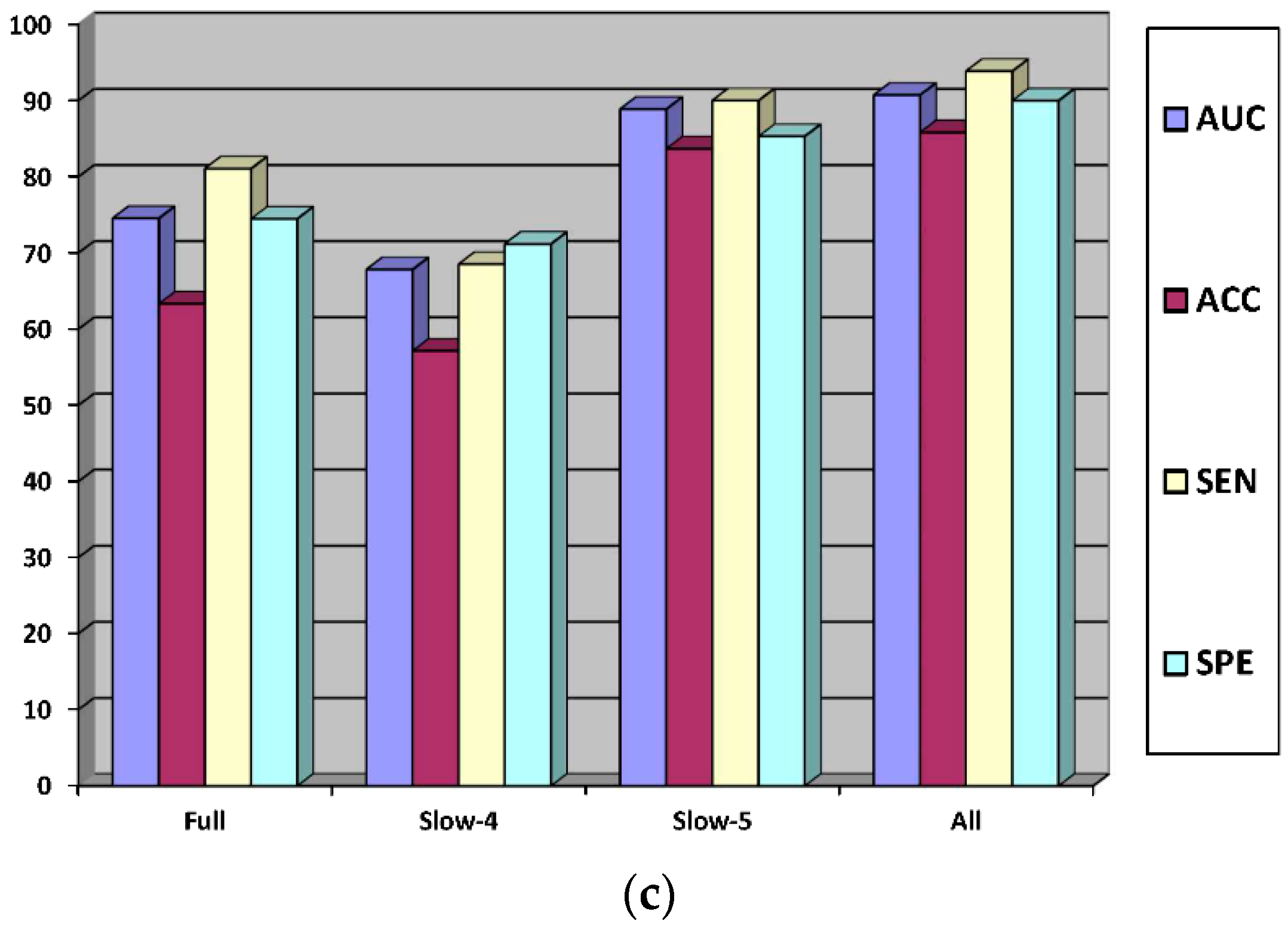
| HC vs. MCI | Full band | SVM | 74.57 | 63.35 | 81.09 | 74.50 |
| Slow-4 | 67.85 | 57.17 | 68.54 | 71.20 | ||
| Slow-5 | 88.90 | 83.71 | 90.03 | 85.33 | ||
| All | 90.75 | 85.85 | 93.89 | 90.01 |
| Reference | Methods | No of Subjects | Group | ACC | SEN | SPE |
|---|---|---|---|---|---|---|
| Challis et al. [39] | Covariance, 82 ROIs, logistic regression, Bayesian Gaussian Process | 20 HC/50 MCI/27 AD | AD vs. MCI | 0.8 | 0.7 | 0.9 |
| MCI vs. NC | 0.75 | 1.00 | 0.5 | |||
| de Vos et al. [40] | Amplitude of low frequency fluctuation | 173 HC/27 AD | 0.76 | 0.71 | 0.82 | |
| Sparse partial correlation FCNs, 70 ROIs | 0.75 | 0.79 | 0.71 | |||
| Sparse partial correlation dynamic FCNs, 70 ROIs | 0.78 | 0.83 | 0.73 | |||
| khazaee et al. [10] | graph measure | 20 AD/20 HC | AD vs. HC | 90.00 | ||
| Our method | HoD-FCN (Full band, slow-4, slow-5) | 35 HC/61 MCI/35 AD | AD vs. HC | 94.1 | 90.95 | 96.75 |
| AD vs. MCI | 87.14 | 91.05 | 86.91 | |||
| HC vs. MCI | 85.85 | 93.89 | 90.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khatri, U.; Kwon, G.-R. Classification of Alzheimer’s Disease and Mild-Cognitive Impairment Base on High-Order Dynamic Functional Connectivity at Different Frequency Band. Mathematics 2022, 10, 805. https://doi.org/10.3390/math10050805
Khatri U, Kwon G-R. Classification of Alzheimer’s Disease and Mild-Cognitive Impairment Base on High-Order Dynamic Functional Connectivity at Different Frequency Band. Mathematics. 2022; 10(5):805. https://doi.org/10.3390/math10050805
Chicago/Turabian StyleKhatri, Uttam, and Goo-Rak Kwon. 2022. "Classification of Alzheimer’s Disease and Mild-Cognitive Impairment Base on High-Order Dynamic Functional Connectivity at Different Frequency Band" Mathematics 10, no. 5: 805. https://doi.org/10.3390/math10050805






