Multiaxial Strength Criterion Model of Concrete Based on Random Forest
Abstract
:1. Introduction
2. Strength Criterion of Concrete
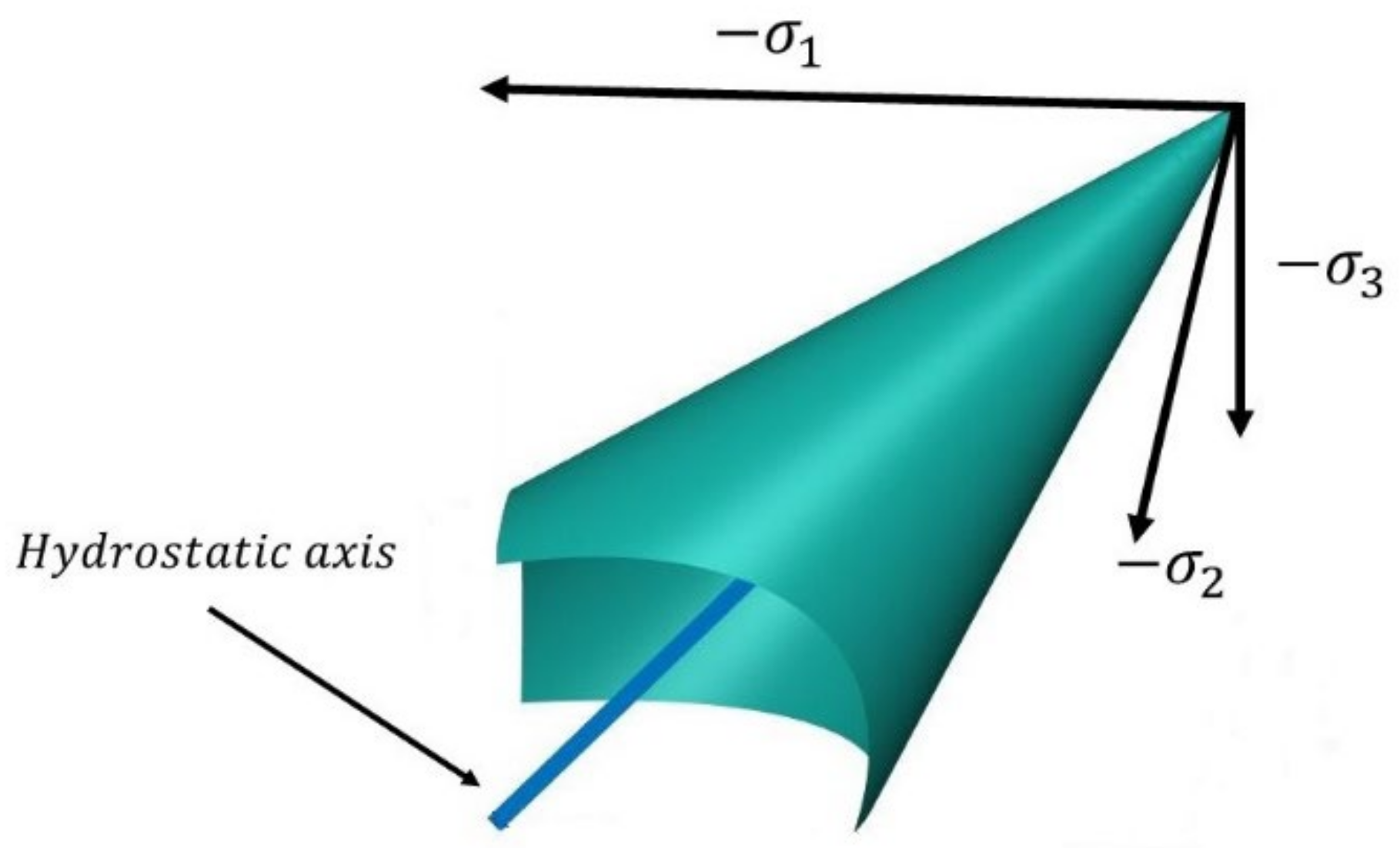
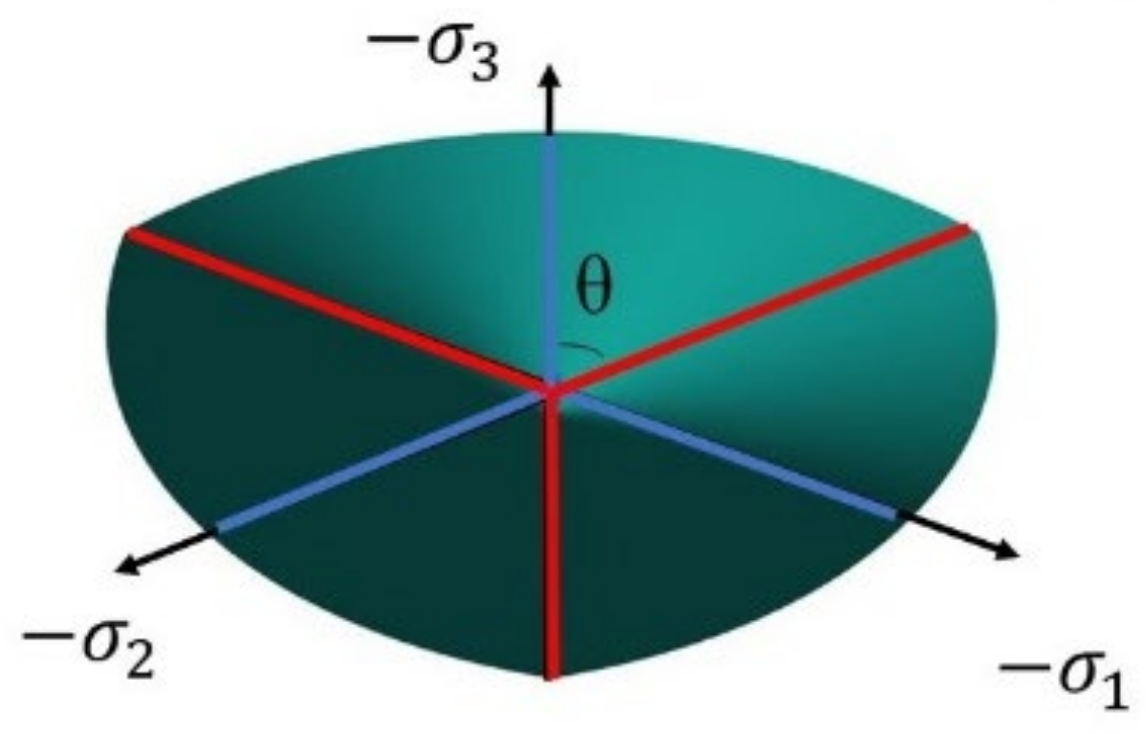
2.1. Failure Curve Surface
- (1)
- The surface is continuous, smooth and convex;
- (2)
- For the same hydrostatic pressure, , where is located on the pull meridian and on the pressure meridian;
- (3)
- Threefold symmetry of the hydrostatic pressure axis;
- (4)
- The deviatoric plane shape is gradually convex and full from an approximate triangle to nearly round.
2.2. Typical Strength Criterion
3. Multiaxial Strength Criterion for Concrete Based on Machine Learning
3.1. Machine Learning Approach
3.2. Comparative Analysis with Typical Multiaxial Strength Criterion
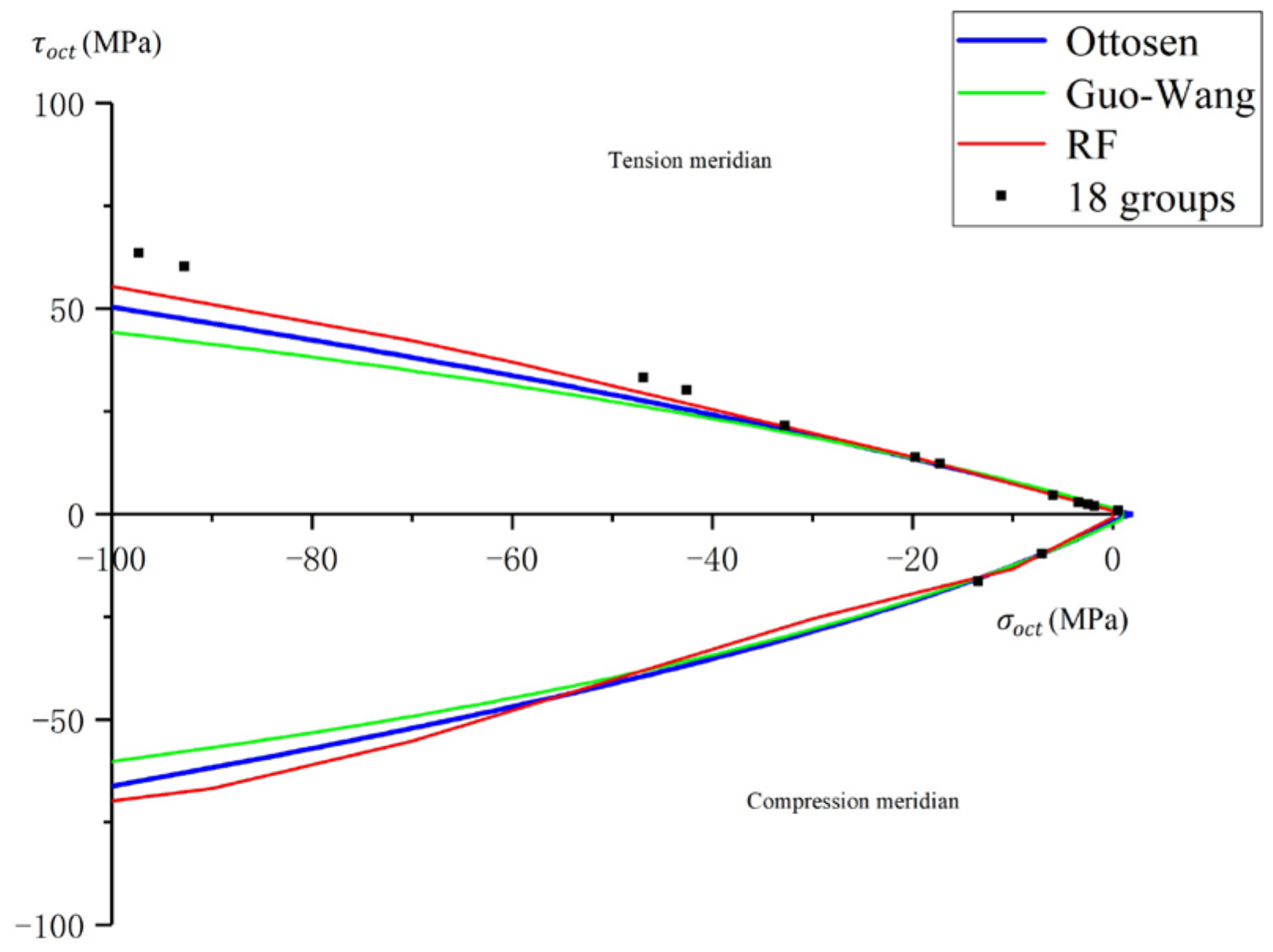
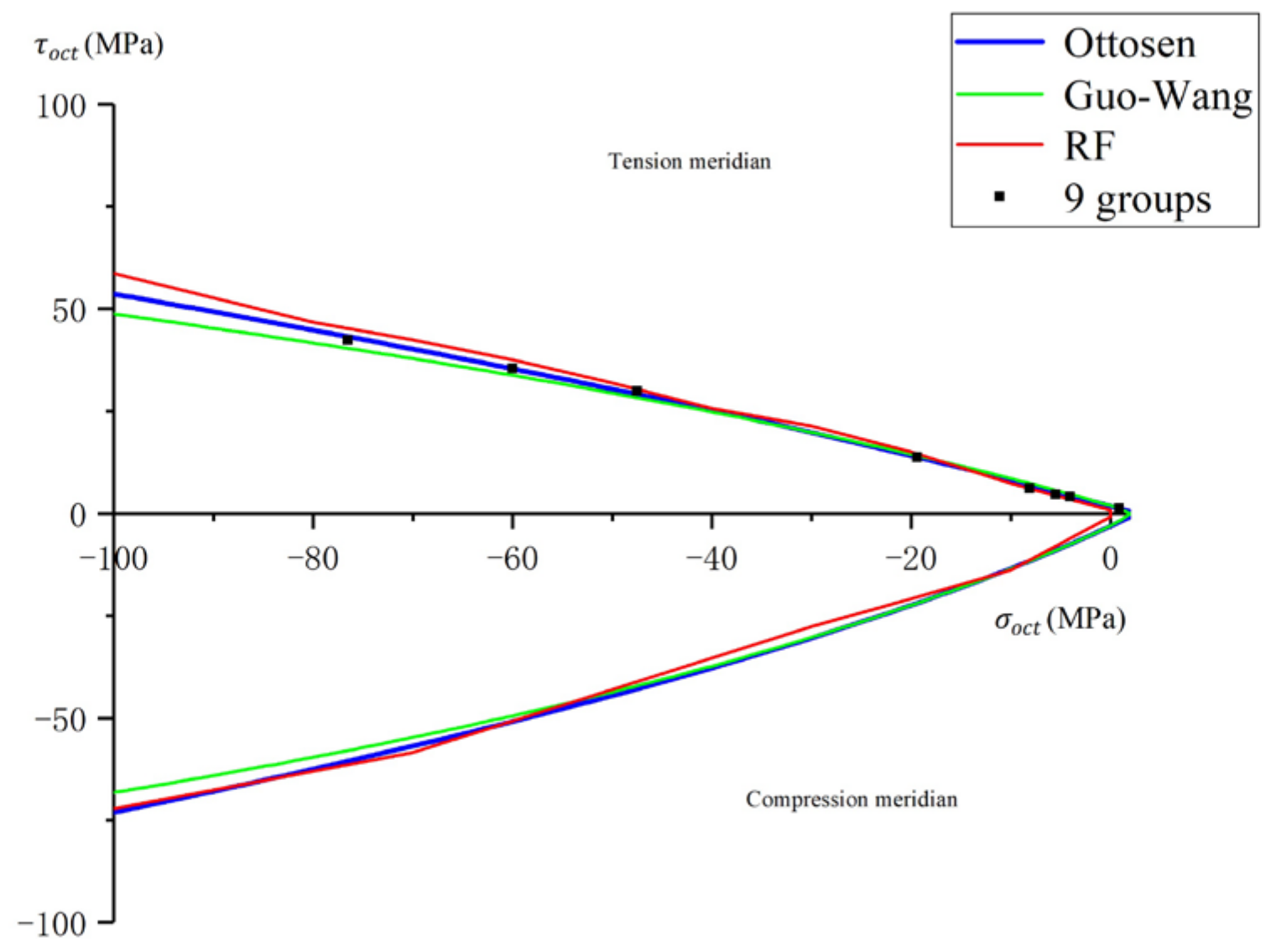
3.2.1. Accuracy Analysis of the Strength Criterion
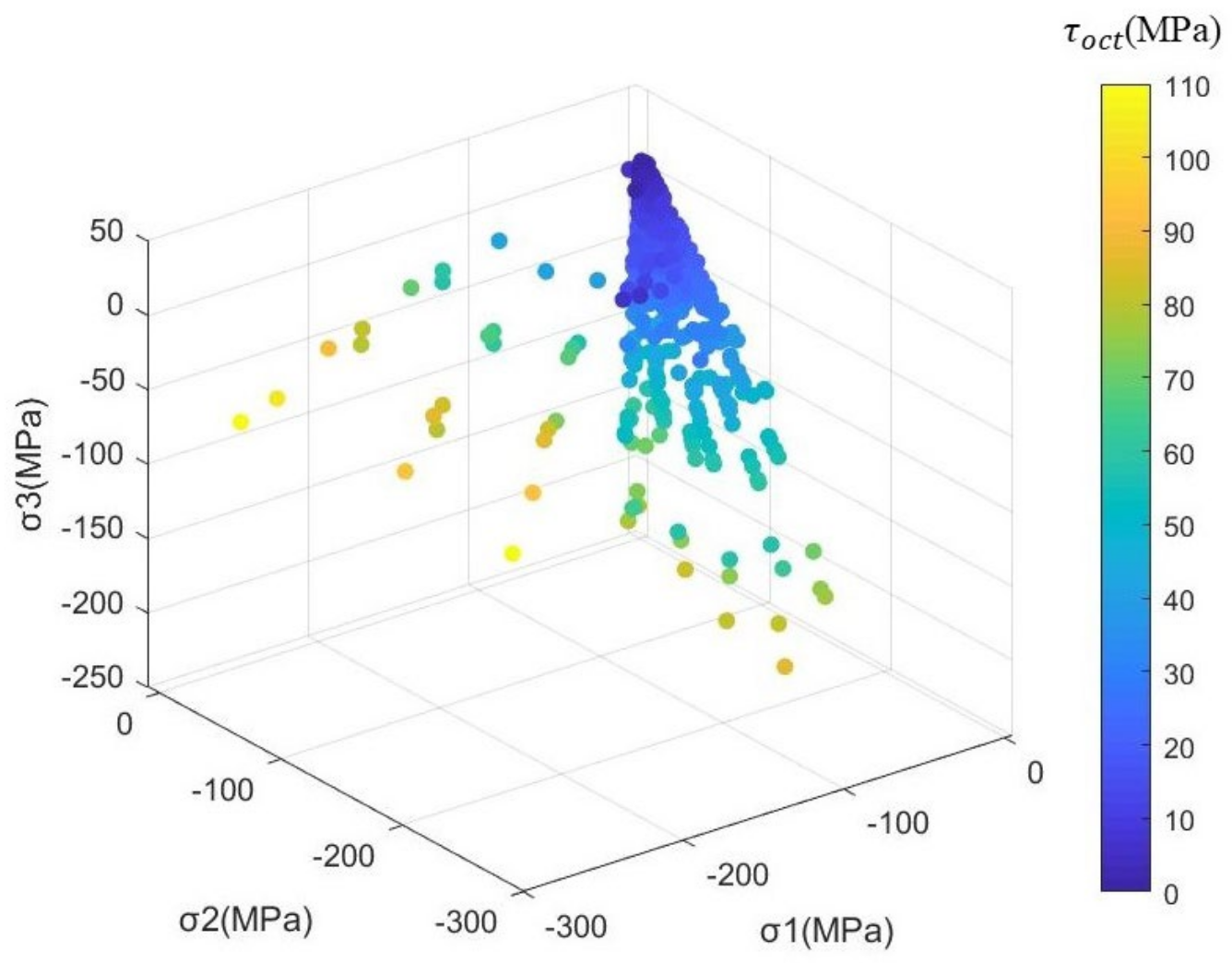
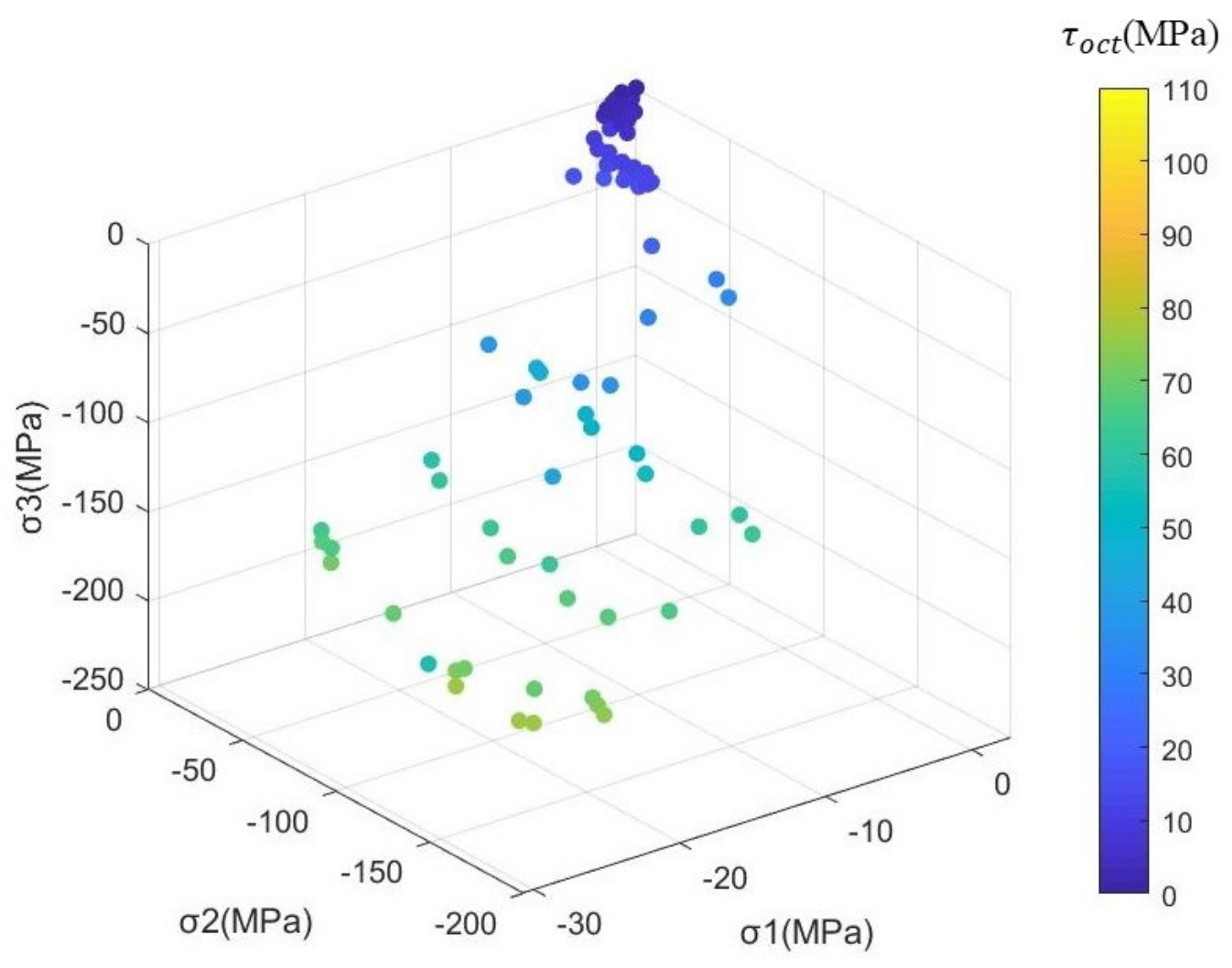
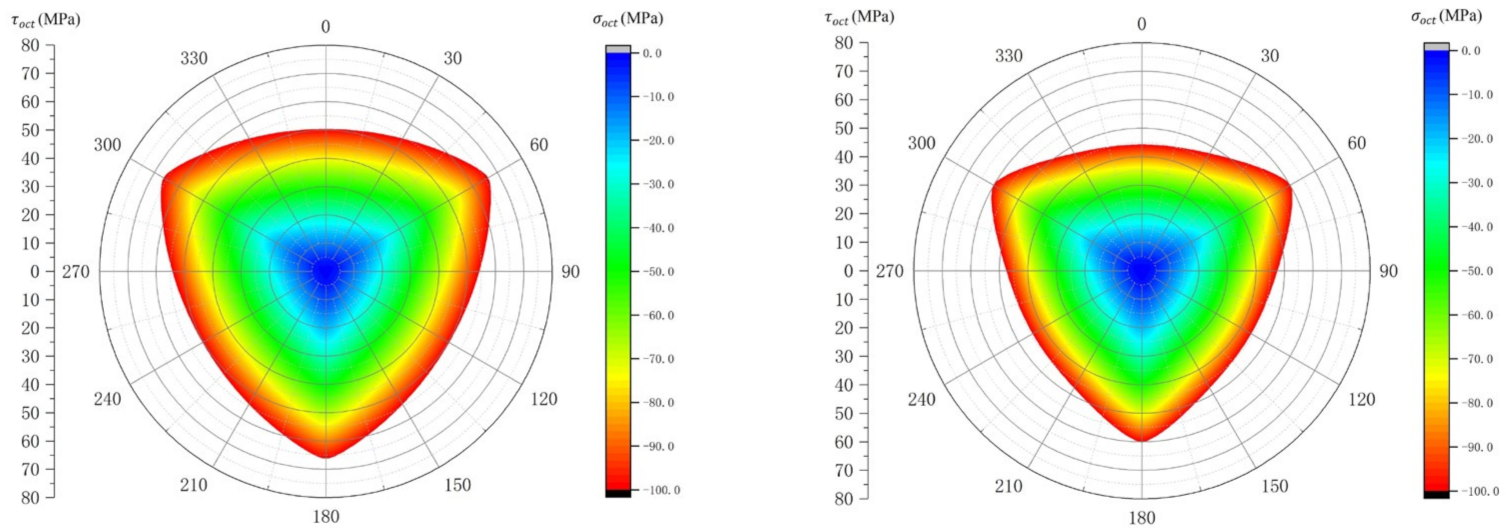
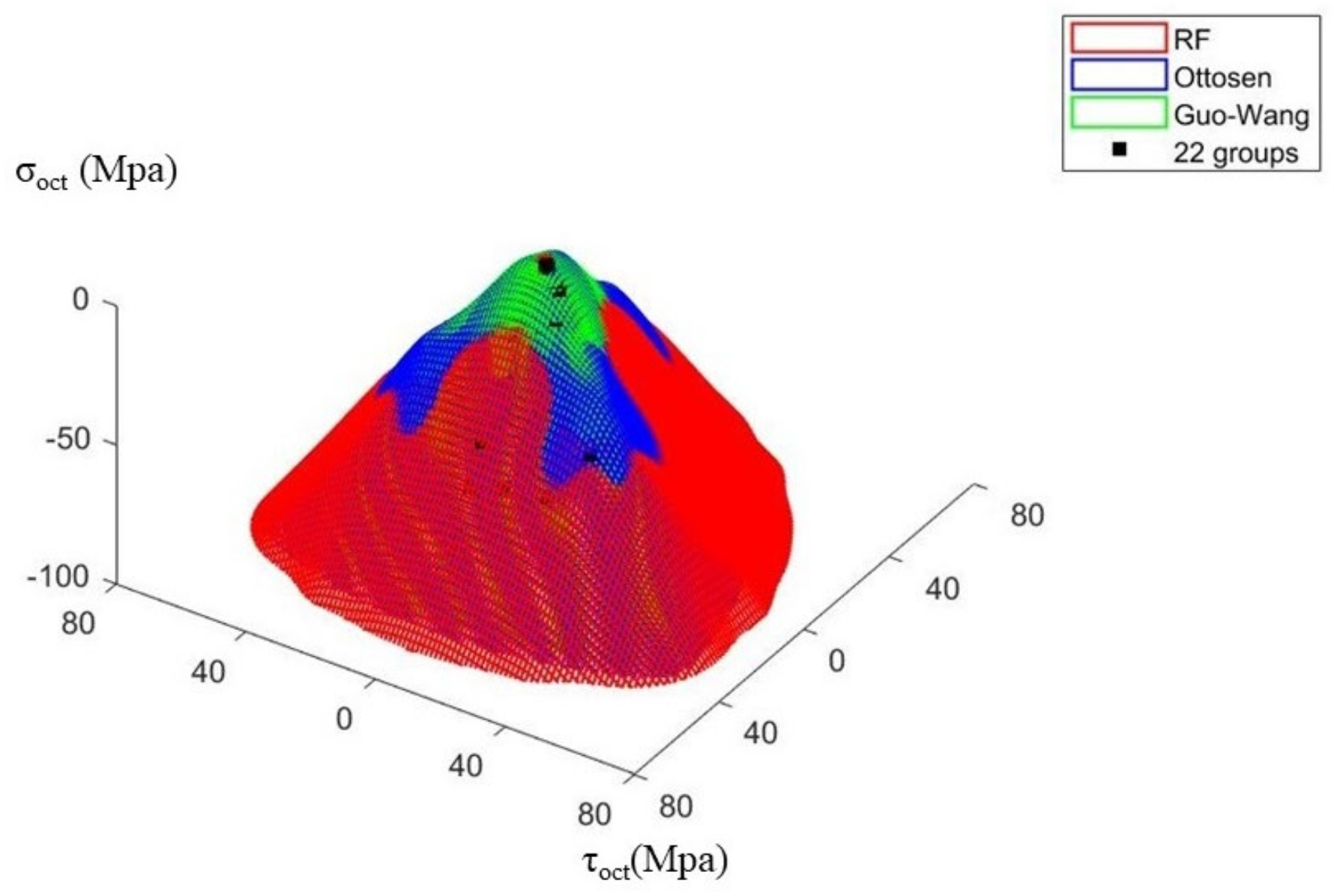
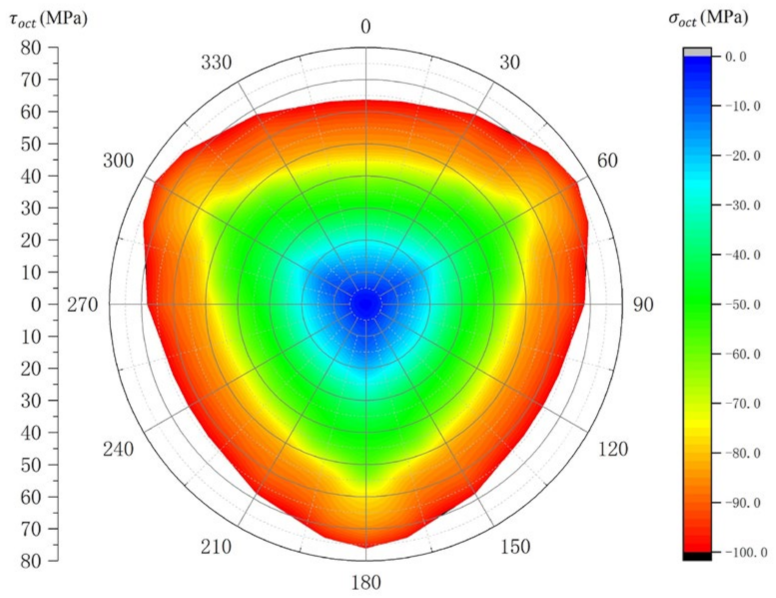
3.2.2. Rationality Analysis of the Failure Curve Surface
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, W.F. Plasticity in Reinforced Concrete; McGraw-Hill: New York, NY, USA, 1982. [Google Scholar]
- Bresler, B.; Pister, K.S. Strength of concrete under combined stresses. J. Proc. 1958, 55, 321–345. [Google Scholar]
- William, K.J.; Warnke, E.P. Constitutive Models for the Triaxial Behavior of Concrete; ETH: Zurich, Switzerland, 1975; Volume 19, pp. 1–30. [Google Scholar]
- Ottosen, N.S. A failure criterion for concrete. J. Eng. Mech. 1977, 103, 527–535. [Google Scholar] [CrossRef]
- Hesieh, S.S.; Ting, E.C.; Chen, W.F. An elasticity-fracture model for concrete. In Proceeding of 3rd Engineering Mechanics Division, Special Conference ASCE, Austin, TX, USA, 17–19 September 1979; pp. 437–440. [Google Scholar]
- Kotsovos, M.D. A mathematical description of the strength properties of concrete under generalized stress. Mag. Concr. Res. 1979, 31, 151–158. [Google Scholar] [CrossRef]
- Podgorski, J. General failure criterion for isotropic media. J. Eng. Mech. 1984, 111, 188–201. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, C. Research on Strength and Failure Criterion of Concrete under Multi-axial Stress. China Civ. Eng. J. 1991, 3, 1–14. (In Chinese) [Google Scholar]
- Jiang, J.-J. Nonliner Finite Element Analysis of Reinforced Concrete Structures; Shanxi Science and Technology Publishing House: Xi’an, China, 1994. (In Chinese) [Google Scholar]
- Liu, X.; Yang, Z. Failure mechanism criterion for multiaxial strength of concrete after exposure to normal and high temperatures. Constr. Build. Mater. 2016, 125, 105–118. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Z. Evaluation of several multiaxial failure criteria for concrete after freeze-thaw (F-T) cycles. Constr. Build. Mater. 2017, 142, 233–247. [Google Scholar] [CrossRef]
- Zhou, J.; Pan, J.; Leung, C.K.Y.; Li, Z. Experimental study on mechanical behavior of high performance concrete under multi-axial compressive stress. Sci. China (Technol. Sci.) 2014, 57, 2514–2522. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Wang, Y.B.; Zhao, Y.Z.; Li, G.Q.; Lyu, Y.F.; Li, H. Experimental study on ultra-high performance concrete under triaxial compression. Constr. Build. Mater. 2020, 263, 120225. [Google Scholar] [CrossRef]
- Yu, Z.; Huang, Q.; Xie, X.; Xiao, N. Experimental study and failure criterion analysis of plain concrete under combined compression-shear stress. Constr. Build. Mater. 2018, 179, 198–206. [Google Scholar] [CrossRef]
- Kim, J.I.; Kim, D.K.; Feng, M.Q.; Yazdani, F. Application of Neural Networks for Estimation of Concrete Strength. J. Mater. Civ. Eng. 2004, 16, 257–264. [Google Scholar] [CrossRef]
- Wu, N.J. Predicting the Compressive Strength of Concrete Using an RBF-ANN Model. Appl. Sci. 2021, 11, 6382. [Google Scholar] [CrossRef]
- El Asri, Y.; Aicha, M.B.; Zaher, M.; Alaoui, A.H. Prediction of compressive strength of self-compacting concrete using four machine learning technics. Mater. Today Proc. 2022, 57, 859–866. [Google Scholar] [CrossRef]
- Ikumi, T.; Galeote, E.; Pujadas, P.; de la Fuente, A.; López-Carreño, R.D. Neural network-aided prediction of post-cracking tensile strength of fibre-reinforced concrete. Comput. Struct. 2021, 256, 106640. [Google Scholar] [CrossRef]
- Zhao, Z. Failure Criterion of Concrete under Triaxial Stresses Using Neural Networks. Comput.-Aided Civ. Infrastruct. Eng. 2002, 17, 68–73. [Google Scholar] [CrossRef]
- Babanajad, S.K.; Gandomi, A.H.; Alavi, A.H. New prediction models for concrete ultimate strength under true-triaxial stress states: An evolutionary approach. Adv. Eng. Softw. 2017, 110, 55–68. [Google Scholar] [CrossRef]
- Reuter, U.; Sultan, A.; Reischl, D.S. A comparative study of machine learning approaches for modeling concrete failure surfaces. Adv. Eng. Softw. 2018, 116, 67–79. [Google Scholar] [CrossRef]
- Shang, H.-S.; Song, Y.-P. Triaxial compressive strength of air-entrained concrete after freeze–thaw cycles. Cold Reg. Sci. Technol. 2013, 90–91, 33–37. [Google Scholar] [CrossRef]
- Zhou, W.; Feng, P.; Lin, H. Constitutive relations of coral aggregate concrete under uniaxial and triaxial compression. Constr. Build. Mater. 2020, 251, 118957. [Google Scholar] [CrossRef]
- Shang, H.; Song, Y.; Ou, J. Behavior of air-entrained concrete after freeze-thaw cycles. Cold Reg. Sci. Technol. 2013, 89, 1–6. [Google Scholar] [CrossRef]
- Shi, L.; Wang, L.; Song, Y.; Shen, L. Dynamic multiaxial strength and failure criterion of dam concrete. Constr. Build. Mater. 2014, 66, 181–191. [Google Scholar] [CrossRef]
- IWHR. Chinese Translation and Collection of Strength and Failure of Concrete; China Hydraulic Press: Beijing, China, 1982. (In Chinese) [Google Scholar]
- Ma, G.; Zeng, W. Calculation of Three-Dimensional Stress Concrete with a New Three-Parameter Criterion; Proceedings of the Second Symposium on Basic Theory and Application of Concrete Structures: Beijing, China, 1990; p. 7. (In Chinese) [Google Scholar]
- Song, Y.; Zhao, G.; Peng, F. Strength of lightweight concrete under triaxial compression. J. Hydraul. Eng. 1993, 6, 10–16. (In Chinese) [Google Scholar]
- Mills, L.L.; Zimmerman, R.M. Compressive strength of plain concrete under multiaxial loading conditions. ACI J. Proc. 1970, 67, 802–807. [Google Scholar]
- Rukhaiyar, S.; Sajwan, G.; Samadhiya, N.K. Strength Behavior of Plain Cement Concrete Subjected to True Triaxial Compression; NRC Research Press: Ottawa, ON, Canada, 2017; p. 45. [Google Scholar]
- Wang, C.; Guo, Z.; Zhang, X. Strength test of concrete under biaxial and triaxial compression. China Civ. Eng. J. 1987, 1, 15–27. (In Chinese) [Google Scholar]
- Shang, H.-S.; Ji, G.-J. Mechanical behaviour of different types of concrete under multiaxial compression. Mag. Concr. Res. 2014, 66, 870–876. [Google Scholar] [CrossRef]
- Song, Y. The Multiaxial Strength of Large Aggregate Concrete after Freeze-Thaw Cycles and Failure Criteria in Octahedral Stress Space, Final Report to NNSFC. 2009. Available online: http://npd.nsfc.gov.cn/ (accessed on 10 December 2015). (In Chinese)
- Rong, C.; Shi, Q.; Zhang, T.; Zhao, H. New failure criterion models for concrete under multiaxial stress in compression. Constr. Build. Mater. 2018, 161, 432–441. [Google Scholar] [CrossRef]
- Lee, S.-K.; Song, Y.-C.; Han, S.-H. Biaxial behavior of plain concrete of nuclear containment building. Nucl. Eng. Des. 2003, 227, 143–153. [Google Scholar] [CrossRef]
- Yu, Z.; Sun, X.; Li, F. Experimental Analysis and Failure Criterion of Plain Concrete Subjected to Biaxial Loading under Fixed Lateral Loading. Adv. Civ. Eng. 2019, 2019, 7059475. [Google Scholar] [CrossRef]
- He, Z.-J.; Song, Y.-P. Multiaxial tensile-compressive strengths and failure criterion of plain high-performance concrete before and after high temperatures. Constr. Build. Mater. 2010, 24, 498–504. [Google Scholar] [CrossRef]
- He, Z.; Song, Y. Multiaxial tension and compression properties of high-strength and high-performance concrete. Eng. Mech. 2010, 27, 190–195. (In Chinese) [Google Scholar]
- Kalifa, P.; Menneteau, F.D.; Quenard, D. Spalling and pore pressure in HPC at high temperatures. Cem. Concr. Res. 2000, 30, 1915–1927. [Google Scholar] [CrossRef]
- Hampel, T.; Speck, K.; Scheerer, S.; Ritter, R.; Curbach, M. High-Performance Concrete under Biaxial and Triaxial Loads. J. Eng. Mech. 2009, 135, 1274–1280. [Google Scholar] [CrossRef]
- Zhou, J.; Pan, J.; Ma, H.; Zhao, J.; Li, Z. Behavior of high-performance concrete under multiaxial tensile-compressive loading. Constr. Build. Mater. 2020, 260, 119887. [Google Scholar] [CrossRef]
- Zhou, J.; Pan, J.; Yao, S.; Zhao, J.; Zhang, Z. Experimental study on triaxial tension and compression properties of high-strength and high-performance concrete. Eng. Mech. 2018, 35, 144–150. (In Chinese) [Google Scholar]
- Zhou, J.; Pan, J.; Zhang, L.; Zhao, J.; Li, Z. Experimental study on mechanical behavior of high-strength high-performance concrete under biaxial loading. Constr. Build. Mater. 2020, 258, 119681. [Google Scholar] [CrossRef]
- Wang, L.; Song, Y. A four-parameter multiaxial strength criterion for lightweight aggregate concrete. China Civ. Eng. J. 2005, 7, 27–33. (In Chinese) [Google Scholar]
- Chen, X.; Zheng, D.; Wu, X.; Li, C. A Review of Three Common Concrete Multiaxial Strength Criteria from 2010 to 2020. Arch. Comput. Methods Eng. 2022. [Google Scholar] [CrossRef]
- Yan, Z.H.; Zeng, L. The BP Neural Network with MATLAB. In Proceedings of the International Conference on Electrical, Control and Automation Engineering (ECAE), Hong Kong, China, 1–2 December 2013; pp. 565–569. [Google Scholar]
- Nasir, V.; Kooshkbaghi, M.; Cool, J.; Sassani, F. Cutting tool temperature monitoring in circular sawing: Measurement and multi-sensor feature fusion-based prediction. Int. J. Adv. Manuf. Technol. 2021, 112, 2413–2424. [Google Scholar] [CrossRef]
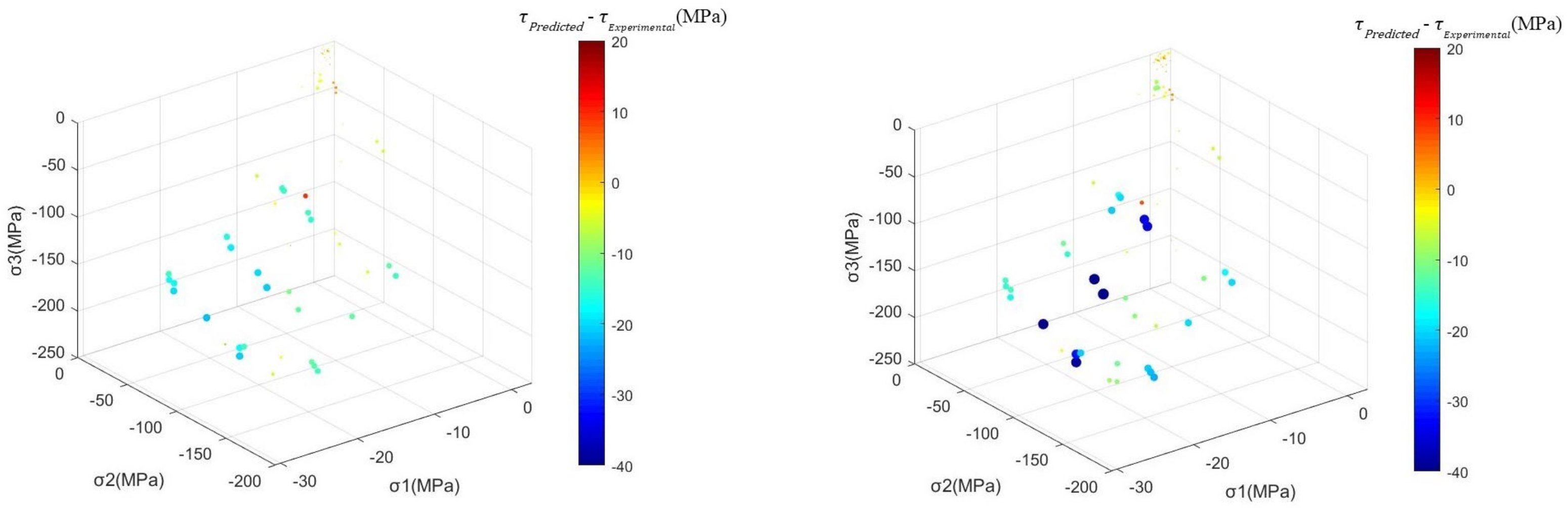
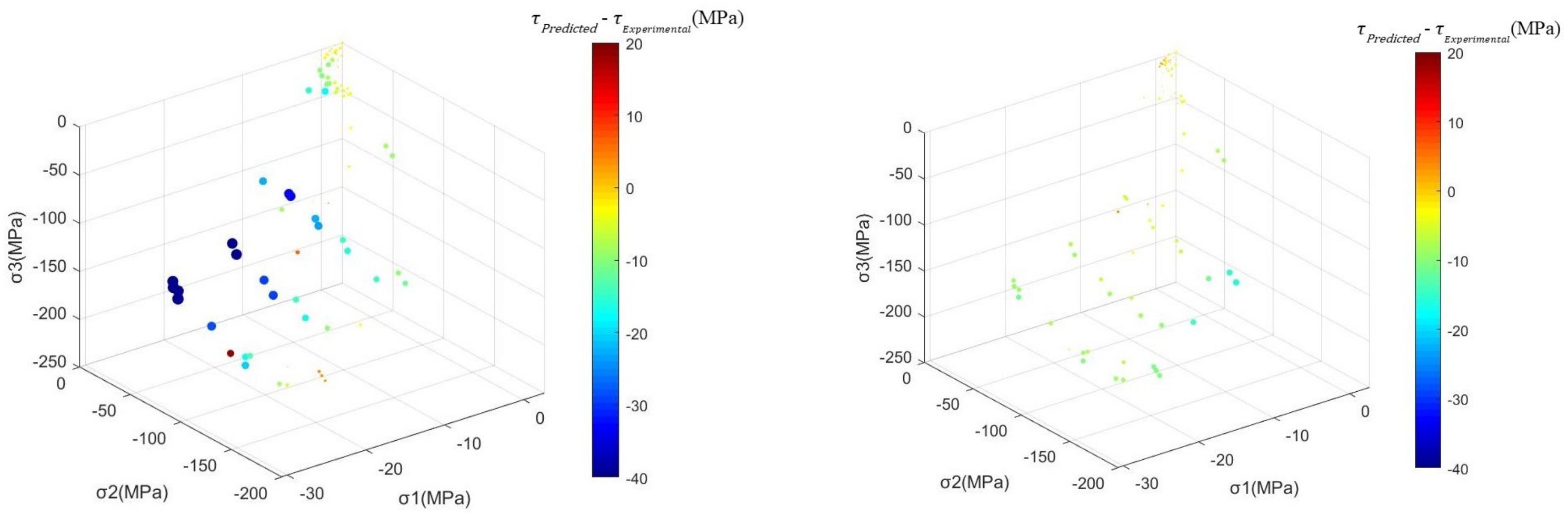
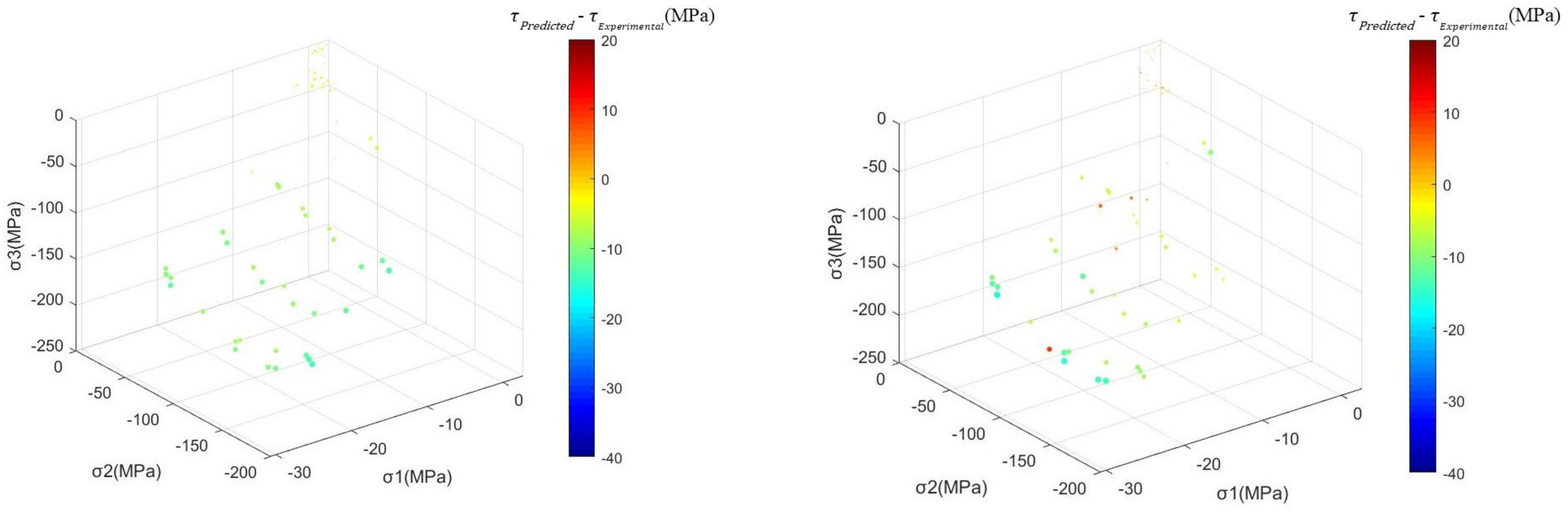



| Guo Wang | Ottosen | DP | RF | RBF | BP | |
|---|---|---|---|---|---|---|
| MAE | 9.25 | 5.9 | 11.18 | 4.07 | 4.62 | 4.59 |
| RMSE | 14.52 | 9.07 | 16.66 | 6.01 | 6.51 | 6.09 |
| R | 0.92 | 0.97 | 0.87 | 0.99 | 0.99 | 0.99 |
| Guo Wang | Ottosen | RF | |
|---|---|---|---|
| MAE | 11.46 | 7.50 | 4.88 |
| RMSE | 16.70 | 10.52 | 6.81 |
| R | 0.91 | 0.98 | 0.99 |
| Guo Wang | Ottosen | RF | |
|---|---|---|---|
| MAE | 3.44 | 1.66 | 1.93 |
| RMSE | 5.66 | 2.77 | 3.04 |
| R | 0.94 | 0.98 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Zheng, D.; Liu, Y.; Wu, X.; Jiang, H.; Qiu, J. Multiaxial Strength Criterion Model of Concrete Based on Random Forest. Mathematics 2023, 11, 244. https://doi.org/10.3390/math11010244
Chen X, Zheng D, Liu Y, Wu X, Jiang H, Qiu J. Multiaxial Strength Criterion Model of Concrete Based on Random Forest. Mathematics. 2023; 11(1):244. https://doi.org/10.3390/math11010244
Chicago/Turabian StyleChen, Xingqiao, Dongjian Zheng, Yongtao Liu, Xin Wu, Haifeng Jiang, and Jianchun Qiu. 2023. "Multiaxial Strength Criterion Model of Concrete Based on Random Forest" Mathematics 11, no. 1: 244. https://doi.org/10.3390/math11010244





