Estimation of Coefficient of Variation Using Calibrated Estimators in Double Stratified Random Sampling
Abstract
:1. Introduction
2. Linear Moments and Proposed Families of CV Estimators
2.1. Linear Moments
2.2. First Proposed Family of CV Estimators
2.3. Second Proposed Family of CV Estimators
3. Numerical Illustrations
- Step 1: Using from stratum , select a random sample with size .
- Step 2: Using a random sample in step 1, calculate the mean square errors (MSEs).
- Step 3: Replicate Step 1 and Step 2, times, and then
- Step 4: Calculate the percentage relative efficiency (PRE) as
3.1. COVID-19 Data (Population-1)
3.2. Apple Data: Population-2 and Population-3
3.3. Discussion of Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Watson, D.J. The estimation of leaf area in field crops. J. Agric. Sci. 1937, 27, 474–483. [Google Scholar] [CrossRef]
- Cochran, W.G. The estimation of the yields of cereal experiments by sampling for the ratio of grain to total produce. J. Agric. Sci. 1940, 30, 262–275. [Google Scholar] [CrossRef]
- Zaman, T.; Bulut, H. Modified ratio estimators using robust regression methods. Commun. Stat. Theory Methods 2019, 48, 2039–2048. [Google Scholar] [CrossRef]
- Shahzad, U.; Al-Noor, N.H.; Hanif, M.; Sajjad, I. An exponential family of median based estimators for mean estimation with simple random sampling scheme. Commun. Stat. Theory Methods 2021, 50, 4890–4899. [Google Scholar] [CrossRef]
- Gagnon, F.; Lee, H.; Rancourt, E.; Särndal, C.E. Estimating the variance of the generalized regression estimator in the presence of imputation for the generalized estimation system. In Proceedings of the Survey Methods Section; Statistical Society of Canada: Ottawa, ON, Canada, 1997; pp. 151–156. [Google Scholar]
- Sorensen, J.B. The use and misuse of the coefficient of variation in organizational demography research. Sociol. Methods Res. 2002, 30, 475–491. [Google Scholar] [CrossRef]
- Wilson, C.A.; Payton, M.E. Modelling the coefficient of variation in factorial experiments. Commun. Stat. Theory Methods 2002, 31, 436–476. [Google Scholar] [CrossRef]
- Faber, D.S.; Korn, H. Applicability of the coefficient of variation method for analyzing synaptic plasticity. Biophys. J. 1991, 60, 1288–1294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Banik, S.; Kibria, B.G. Estimating the population coefficient of variation by confidence intervals. Commun. Stat. Simul. Comput. 2011, 40, 1236–1261. [Google Scholar] [CrossRef]
- Yosboonruang, N.; Niwitpong, S.-A.; Niwitpong, S. Measuring the dispersion of rain-fall using Bayesian confidence intervals for coefficient of variation of delta-lognormal distribution: A study from Thailand. PeerJ 2019, 7, e7344. [Google Scholar] [CrossRef]
- Tian, L. Inferences on the common coefficient of variation. Stat. Med. 2005, 24, 2213–2220. [Google Scholar] [CrossRef]
- Mahmoudvand, R.; Hassani, H.; Wilson, R. Is the sample coefficient of variation a good estimator for the population coefficient of variation? World Appl. Sci. J. 2007, 2, 519–522. [Google Scholar]
- La-Ongkaew, M.; Niwitpong, S.-A.; Niwitpong, S. Confidence intervals for the difference between the coefficients of variation of Weibull distributions for analyzing wind speed dispersion. PeerJ 2021, 9, e11676. [Google Scholar] [CrossRef] [PubMed]
- Särndal, C.E.; Swensson, B.; Wretman, J. Model Assisted Survey Sampling; Springer: New York, NY, USA, 1992. [Google Scholar]
- Hosking, J.R. L-moments: Analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. Ser. B Methodol. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Deville, J.C.; Särndal, C.E. Calibration estimators in survey sampling. J. Am. Stat. Assoc. 1992, 87, 376–382. [Google Scholar] [CrossRef]
- Koyuncu, N. Calibration estimator of population mean under stratified ranked set sampling design. Commun. Stat. Theory Methods 2018, 47, 5845–5853. [Google Scholar] [CrossRef]
- Shahzad, U.; Ahmad, I.; Almanjahie, I.; Al-Noor, N.H.; Hanif, M. A new class of L-moments based calibration variance Estimators. Comput. Mater. Contin. 2021, 66, 3013–3028. [Google Scholar] [CrossRef]
- Shahzad, U.; Ahmad, I.; Almanjahie, I.; Hanif, M.; Al-Noor, N.H. L-moments and calibration based variance estimators under double stratified random sampling scheme: An application of COVID-19 pandemic. Sci. Iran. 2021; in press. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Landweher, J.M.; Matales, N.C.; Wallis, J.R. Probability weighted moments: Definition and relation to parameters of several distributions expressible in inverse form. Water Resour. Res. 1979, 15, 1049–1054. [Google Scholar] [CrossRef] [Green Version]
- Hosking, J.R.M.; Wallis, J. A comparison of unbiased and plotting-position estimators of L-moments. Water Resour. Res. 1995, 31, 2019–2025. [Google Scholar] [CrossRef]
- Elamir, E.A.H.; Seheult, A.H. Trimmed L-moments. Comput. Stat. Data Anal. 2003, 43, 299–314. [Google Scholar] [CrossRef]
- Bhushan, S.; Kumar, A.; Akhtar, M.T.; Lone, S.A. Logarithmic type predictive estimators under simple random sampling. AIMS Math. 2022, 7, 11992–12010. [Google Scholar] [CrossRef]
- Bhushan, S.; Kumar, A. Predictive estimation approach using difference and ratio type estimators in ranked set sampling. J. Comput. Appl. Math. 2022, 410, 114214. [Google Scholar] [CrossRef]


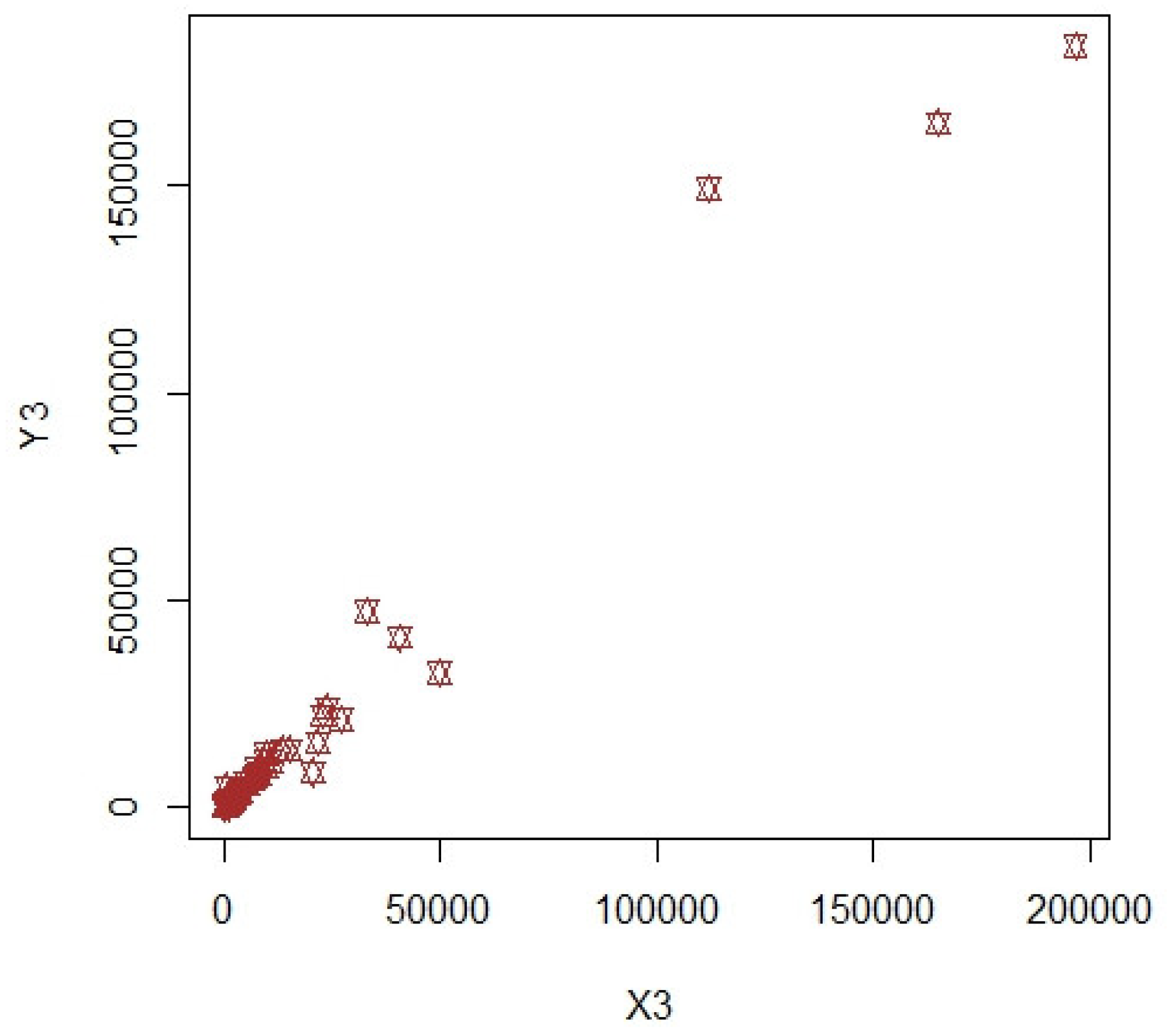
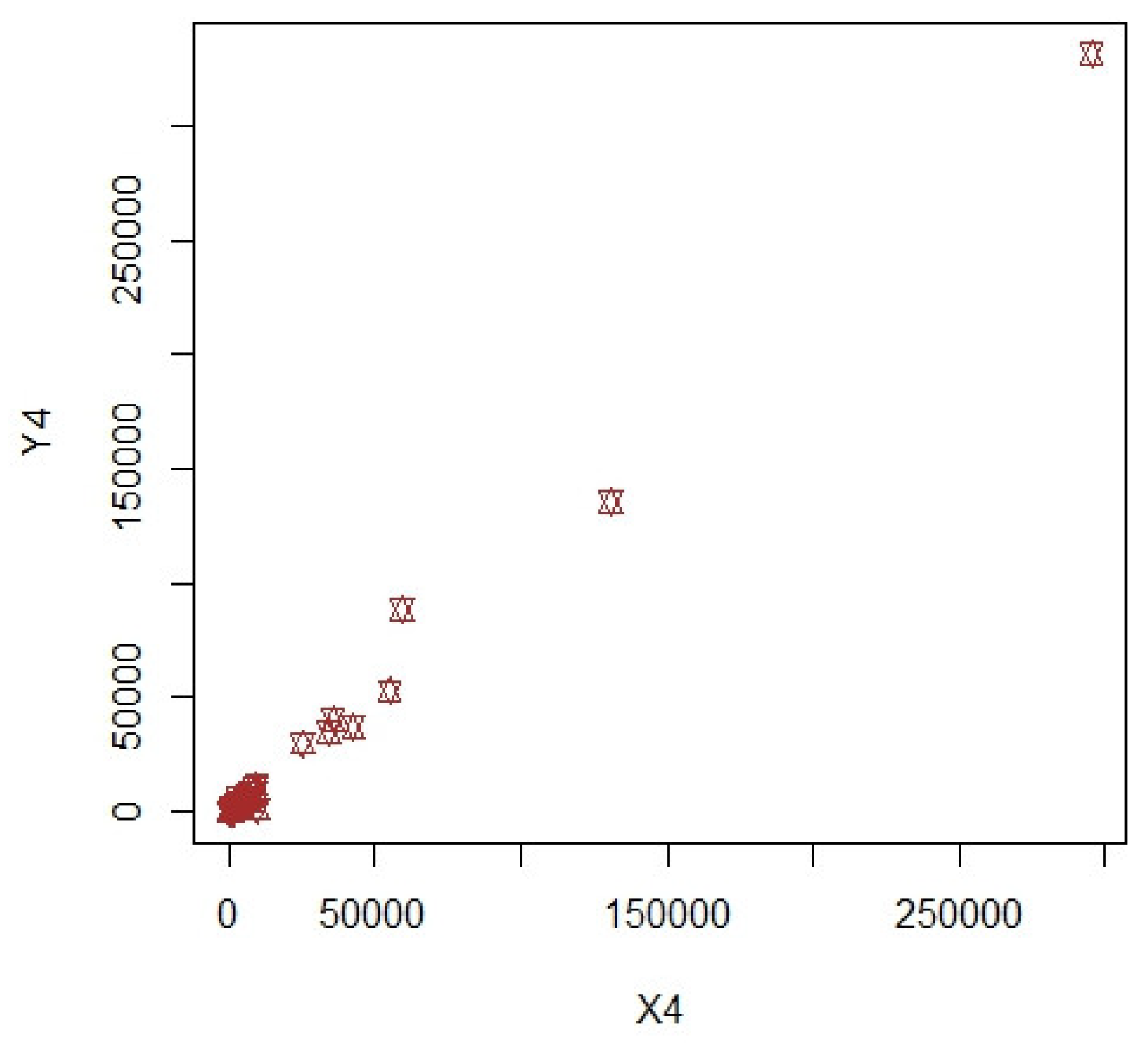
| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| L-Moments | ||||
| TL-Moments | ||||
| L-Moments | ||||
| TL-Moments | ||||
| L-Moments | ||||
| TL-Moments | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahzad, U.; Ahmad, I.; García-Luengo, A.V.; Zaman, T.; Al-Noor, N.H.; Kumar, A. Estimation of Coefficient of Variation Using Calibrated Estimators in Double Stratified Random Sampling. Mathematics 2023, 11, 252. https://doi.org/10.3390/math11010252
Shahzad U, Ahmad I, García-Luengo AV, Zaman T, Al-Noor NH, Kumar A. Estimation of Coefficient of Variation Using Calibrated Estimators in Double Stratified Random Sampling. Mathematics. 2023; 11(1):252. https://doi.org/10.3390/math11010252
Chicago/Turabian StyleShahzad, Usman, Ishfaq Ahmad, Amelia V. García-Luengo, Tolga Zaman, Nadia H. Al-Noor, and Anoop Kumar. 2023. "Estimation of Coefficient of Variation Using Calibrated Estimators in Double Stratified Random Sampling" Mathematics 11, no. 1: 252. https://doi.org/10.3390/math11010252






