Mean-Square Stability of Uncertain Delayed Stochastic Systems Driven by G-Brownian Motion

Abstract

This paper investigates the mean-square stability of uncertain time-delay stochastic systems driven by G-Brownian motion, which are commonly referred to as G-SDDEs. To derive a new set of sufficient stability conditions, we employ the linear matrix inequality (LMI) method and construct a Lyapunov–Krasovskii function under the constraint of uncertainty bounds. The resulting sufficient condition does not require any specific assumptions on the G-function, making it more practical. Additionally, we provide numerical examples to demonstrate the validity and effectiveness of the proposed approach.

1. Introduction

In general, dynamic changes are intrinsically linked to both the current and previous states. Fundamentally, the designated system feature is defined as a time delay, wherein mechanisms encompassing such a functionality are termed time-delay systems (TDS). In view of the widespread applications of time delay in various technical domains such as engineering technology, mechanics, cybernetics and biomedicine, the research scope of TDS has gained prominence among researchers. Specifically, comprehensive research on TDS stability revealed a critical issue pertaining to control theory, which has been assessed in various monographs [1,2,3,4,5,6,7,8,9,10,11,12,13]. For example, in [14], Zhao and Zhu discussed a neutral stochastic highly nonlinear time-delay system with a nonlinear growth condition. In addition, closer studies revealed discrepancies relating to the memory length in numerous practical systems, which highlights the lack of mandates concerning fixed delay. Subsequently, the aspect of time-delay variation warrants both theoretical and practical evaluation [15]. Likewise, the prevalence of random factors and disturbances could potentially result in system instability. Through extensive studies on stochastic delay differential equations (SDDE) from several literary sources, valuable research findings have been obtained [14,15,16,17,18,19,20]. In particular, the research focus of SDDE stability is divided into two categories: the first method extends the Lyapunov stability theorem and LaSalle invariant principle of TDS to SDDE, while the second approach employs the stochastic Lyapunov stability theorem to derive the stability criterion. With the emergence of the linear matrix inequality (LMI) toolbox, research domains on SDDE stability have gradually advanced [21]. Furthermore, prominent scholars have begun to leverage LMI to ascertain SDDE stability and to derive the system stability conditions [22,23,24]. For instance, Zhu [25] first solved the stabilization problem of stochastic nonlinear delay systems by using event-triggered feedback control and the LMI tool.

Subsequently, Peng [26,27] formulated the concepts of G-Gaussian expectation (GGE) and G-Brownian motion (GBM) on the topic of sublinear expectation space, thereby providing a novel aspect for upcoming investigations. In the presence of model uncertainty, the discipline of stochastic calculus typically poses serious concerns. Evidently, Peng [28] adopted the basic theory of time-consistent G-expectation to introduce the GGE and GBM and diligently utilized both concepts to establish the relevant integral. Furthermore, Ren and Yuan et al. [29,30,31,32] assessed the stability of stochastic differential equations under G expectation and attained multiple results. Zhu and Huang [33] studied the p-moment exponential stability of a class of stochastic time-delay nonlinear systems (SDNS) driven by G-Brownian motion. Fei and Fei [34] attempted to provide the criteria for delay-dependent stability of G-SDDEs with highly nonlinear coefficients.

In accordance with an accurate mathematical model, both the classical and modern control theories aid in constructing the control system. In the realm of practical engineering, multiple ambiguities such as measurement interference, aging of system components, wear, unmodeled dynamics of the system and system linearization approximation can possibly lead to system errors or uncertain system parameters [35,36]. Subsequently, the obtained mathematical model fails to accurately delineate the controlled system and to maintain optimal system performance, thereby compromising the overall stability of the resultant control system.

According to the aforementioned discussion, the distinct lack of relevant literature pertaining to the concurrent stability analysis of both probability and coefficient uncertainty is evident. In this study, we propose a novel method for obtaining sufficient conditions for system stability using LMI. By analyzing the uncertainty of system coefficients and the disturbance of G-Brownian motion on the system, our sufficient conditions do not require specific assumptions on the G function, making them more practical and easy to implement. Ideally, this paper strives to conduct an extensive analysis on the subject of G-SDDE to address the specified issues.

The primary contributions of this research are encapsulated as follows:

(1)

This study investigates the stability criterion of G-SDDEs in the context of coefficient uncertainty, offering a comprehensive understanding of how variable coefficients impact system stability.

(2)

Unlike previous research that typically imposes specialized conditions on the G function within their premises, our study innovatively addresses the G function without imposing any specific constraints. This approach, while offering a broader understanding, undeniably introduces considerable challenges to our research.

Consider the following system:

$$\left\{\begin{array}{cc}dx(t)& =[A(t)x(t)+B(t)x(t-\tau (t))]dt+[C_{ij}(t)x(t)+D_{ij}(t)x(t-\tau (t))]d{〈w^i,w^j〉}_t,\\ & +[Ej(t)x(t)+Fj(t)x(t-\tau (t)]d{w}_t^j,\hfill \\ x(t)=& \phi (t) t\in [-{\tau }_M,0],\hfill \end{array}\right.$$

(1)

where $0\le \tau (t)\le {\tau }_M$, $\dot{\tau }(t)⩽d<1$; $w_s$ stands for an n-dimensional G-Brownian motion defined in the G-expectation space; $A(t),B(t),C_{ij}(t),D_{ij}(t),E_j(t),F_j(t)\in R^{n\times n}$, $A(t)=A+\mathsf{\Delta }A(t),B(t)=B+\mathsf{\Delta }B(t),C_{ij}(t)=C_{ij}+\mathsf{\Delta }{C}_{ij}(t),D_{ij}(t)=D_{ij}+\mathsf{\Delta }{D}_{ij}(t),E_j(t)=E_j+\mathsf{\Delta }{E}_j(t),F_j(t)=F_j+\mathsf{\Delta }{F}_j(t)$ ; $[A(t)B(t)C_{ij}(t)D_{ij}(t)E_j(t)F_j(t)]=HK(t)[Z_1{Z}_2{Z}_3{Z}_4{Z}_5{Z}_6]$ and $K^T(t)K(t)\le I$; and I is a unit matrix. $A,B,C_{ij},D_{ij},E_j,F_j\in R^{n\times n}$ are real constant matrices.

The current paper is summarized as follows: Section 2 presents mathematical concepts. In Section 3, as the main part of this work, the stability of G-SDDE is proved using LMI. Section 4 gives some numerical examples and simulation results.

2. Definitions and Preliminaries

In this section, we introduce some notations and preliminaries about sublinear expectations and G-Brownian motion; more details concerning this section can be found in [26,37].

Definition 1 

([27]). Let Ω be the space of all $R^n$-valued continuous functions with $w_0=0$, equipped with the distance

$$\begin{array}{c}\hfill \rho (w^1,w^2)=\sum _{i=1}^{\infty }\frac{1}{2^i}[(max\left|w_t^1-w_t^2\right|)\wedge 1]\end{array}$$

Then, $(\mathrm{\Omega },\rho )$ is a metric space. H is assumed to be a linear space of real valued functions, which is defined on Ω.

Definition 2 

([27]). A function $\widehat{E}:H\to R$ is called a sublinear expectation; if $\forall X,Y\in H$, $C\in R$ and $\lambda ⩾0$, it satisfies the following properties:

(1) 

Monotonicity: If $X,Y\in H$ and $X\ge Y$, then $\widehat{E}X\ge \widehat{E}Y$.

(2) 

Maintaining constants: $\widehat{E}(C)=C$.

(3) 

Subadditivity: $\widehat{E}(X+Y)\le \widehat{E}(X)+\widehat{E}(Y)$.

(4) 

Positive homogeneity: $\widehat{E}(\lambda X)=\lambda \widehat{E}(X)$.

Definition 3 

([28]). For any fixed $T>0$, let ${\mathrm{\Omega }}_T=C_0([0,T];R^n)$ be the space of $R^n$-valued continuous paths on [0, T ] with $w_0=0$, endowed with the supremum norm, and $B_t(w)=w_t$ be the canonical process. $C_{b,Lip}(R^{d\times n})$ denotes the set of bounded Lipschitz functions on $R^{d\times n}$.

Definition 4 

([28]). (G-normal distributions) The monotonic and sublinear function $G:S(d)\to R$ is defined by

$$\begin{array}{c}\hfill Lip({\mathrm{\Omega }}_T)=\left\{\phi (B_{t_1},\cdots ,B_{t_n}):n⩾1,t_1,\cdots ,t_n\in [0,T],\phi \in C_{b,Lip}(R^{d\times n})\right\}\end{array}$$

where $S(d)$ denotes the set of $d\times d$ symmetric matrices. Note that there is a bounded and closed subset ${\rm Y}\subset S^{+}(d)$ such that

$$\begin{array}{c}\hfill G(A)=\frac{1}{2}\underset{\mathrm{O}\in {\rm Y}}{sup}tr[\mathrm{O}A],A\subset S(d).\end{array}$$

where $S^{+}(d)$ denotes the set of $d\times d$ positive-definite symmetric matrices.

Remark 1. 

$G(·)$ has the following properties:

(1) $G(A+B)\le G(A)+G(B)$.

(2) $G(\lambda A)=\lambda G(A),\lambda \ge 0$.

(3) If $A\le B$, then $G(A)\le G(B)$.

Definition 5 

([28]). For each $V\in C^{1,2}(R_{+}\times R^n;R)$, define an operator L, which is called a G-Lyapunov function:

$$LV(t,x(t))={\partial }_{t}V(t,x(t))+〈{\partial }_{x}V(t,x(t)),f(t,x_1,x_2)〉+G(〈{\partial }_{x}V(t,x(t)),g(t,x_1,x_2)〉$$

$$+〈{\partial }_{xx}^{2}V(t,x(t))h(t,x_1,x_2),h(t,x_1,x_2)〉).$$

where $〈{\partial }_{x}V(t,x),g(t,x_1,x_2)〉+〈{\partial }_{xx}^{2}V(t,x)h(t,x_1,x_2),h(t,x_1,x_2)〉$ is a symmetric matrix in $S^n$, with the form

$$〈{\partial }_{x}V(t,x),g(t,x_1,x_2)〉+〈{\partial }_{xx}^{2}V(t,x)h(t,x_1,x_2),h(t,x_1,x_2)〉:=$$

$${[〈{\partial }_{x}V(t,x),g_{ij}(t,x_1,x_2)+g_{ji}(t,x_1,x_2)〉+〈{\partial }_{xx}^{2}V(t,x)h_i(t,x_1,x_2),h_j(t,x_1,x_2)〉]}_{ij}^n$$

where $x_1=x(t)$, $x_2=x(t-\tau (t))$, $f(t,x_1,x_2)\stackrel{\mathsf{\Delta }}{=}A(t)x(t)+B(t)x(t-\tau (t))$, $g(t,x_1,x_2)\stackrel{\mathsf{\Delta }}{=}{C}_{ij}(t)x(t)+D_{ij}(t)x(t-\tau (t))$, $h(t,x_1,x_2)\stackrel{\mathsf{\Delta }}{=}{E}_j(t)x(t)+F_j(t)x(t-\tau (t))$.

Definition 6 

([38]). (1) For fixed $p>1$, the space $M_G^{p,0}([0,T])$ of simple processes is defined by

$$\begin{array}{c}\hfill M_G^{p,0}=\left\{{\eta }_t(\omega ):=\sum _{j=0}^{N-1}{\xi }_j(\omega )I_{[t_j,t_{j+1}]};{\xi }_j(\omega )\in L_G^p({\mathrm{\Omega }}_{t_j}),\forall N⩾1,0=t_0<t_1<\dots <t_N=T,j=0,1,\dots ,N-1\right\}\end{array}$$

where $L_G^p({\mathrm{\Omega }}_{t_j})=\left\{\xi \in L_G^1({\mathrm{\Omega }}_{t_j}):\widehat{E}({\left|\xi \right|}^p)<\infty \right\}$

(2) For every ${\eta }_t(\omega ):={\displaystyle \sum _{j=0}^{N-1}}{\xi }_j(\omega )I_{[t_j,t_{j+1}]}\in M_G^{p,0}([0,T])$, its Bochner integral is defined by ${\int }_0^t{\eta }_t(\omega )dt={\sum }_{j=0}^{N-1}{\xi }_j(\omega )(t_{j+1}-t_j)$.

(3) Let $\widehat{E}(\eta )=\frac{1}{T}{\int }_0^T\widehat{E}(\eta )dt=\frac{1}{T}{\sum }_{j=0}^{N-1}{\xi }_j(\omega )(t_{j+1}-t_j)$. For each $p>1$, let $M_G^{p,0}([0,T])$ be the completion of $M_G^{p,0}([0,T])$ under the following norm:

$${∥\eta ∥}_{M_G^p([0,T])}=\frac{1}{T}{({\int }_0^T\widehat{E}({\eta }_s^p)dt)}^{\frac{1}{p}}={(\frac{1}{T}{\sum }_{j=0}^{N-1}E{\left|{\xi }_j(\omega )\right|}^P(t_{j+1}-t_j))}^{\frac{1}{p}}$$

Definition 7 

([38]). Define the Ito integral by $I(\eta )={\int }_0^T{\eta }_{t}d{w}_t$ for ${\eta }_t(\omega )dt={\sum }_{j=0}^{N-1}{\xi }_j(\omega )I_{(t_{j+1}-t_j)}\in M_G^{p,0}([0,T])$.

Definition 8 

([39]). The trivial solution of System (1) is said to be asymptotically stable in mean square, if there exists a ${\sigma }_0>0$ such that

$$\underset{t\to \infty }{lim}\widehat{E}{\left|x(t;t_0,x_0)\right|}^2=0$$

whenever $\widehat{E}{\left|x_0\right|}^2<{\sigma }_0.$

Assumption A1 

($1^{\prime }$). Let $A(t),B(t),C_{ij}(t),D_{ij}(t)$ satisfy the following conditions:

(1) 

$A^T(t)=A(t),B^T(t)=B(t)$.

(2) 

$C_{ij}^T(t)=C_{ij}(t)=C_{ji}(t),D_{ij}(t)=-D_{ji}(t)$(${D_{ij}}^T(t)=D_{ij}(t)=D_{ji}(t)$).

Remark 2. 

While the coefficient matrix’s Assumption 1 and Assumption $1^{\prime }$ appear to be strictly constrained, they serve a convenient purpose in proving Theorem 2, 3 and 4. These proofs do not require any special assumptions about the G function, which is often necessary in [30,34]. A special assumption about the G function is made in [26], while in our study, the treatment of the G function involves the proposition of specific conditions for the study of the G function itself. Furthermore, Assumption 1’ is more universally applicable than Assumption 1, making it an essential consideration in the research. It is worth noting that these assumptions play a significant role in the results obtained.

Lemma 1 

([39]). If $V\in C^{1,2}(R_{+}\times R^n;R)$ satisfies the following conditions, then system (1) is mean-square exponentially stable:

(1) 

For all $(t,x)\in R_{+}\times R^n$, we have $LV(t,x)\le 0$.

(2) 

There exist positive constants $C_1$ and $C_2$ such that $C_1{\left|x\right|}^2\le V(t,x)\le C_2{\left|x\right|}^2$.

Lemma 2 

([39]). If there exists $V\in C^{1,2}(R_{+}\times R^n;R)$, satisfying the following properties:

(1) 

$\forall (t,x)\in R_{+}\times R^n$, there exist a constant $\lambda >0$ such that

$$LV(t,x)\le -\lambda V(t,x(t)),$$

(2) 

There exist constants $C_1,C_2>0$ such that

$$C_1{\left|x\right|}^2\le V(t,x)\le C_2{\left|x\right|}^2,$$

then system (1) is mean-square exponentially stable.

Lemma 3 

([25]). (Schur complement) For known real matrices ${\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2$ and ${\mathrm{\Omega }}_3,$ where ${\mathrm{\Omega }}_1={\mathrm{\Omega }}_1^T,$${\mathrm{\Omega }}_2={\mathrm{\Omega }}_2^T,$ then the following conditions are equivalent to each other:

(1) 

$\left[\begin{array}{cc}{\mathrm{\Omega }}_1& {\mathrm{\Omega }}_3\\ {\mathrm{\Omega }}_3^T& {\mathrm{\Omega }}_2\end{array}\right]<0$.

(2) 

${\mathrm{\Omega }}_1<0,{\mathrm{\Omega }}_2-{\mathrm{\Omega }}_3^T{\mathrm{\Omega }}_1^{-1}{\mathrm{\Omega }}_3<0$.

(3) 

${\mathrm{\Omega }}_2<0,{\mathrm{\Omega }}_1-{\mathrm{\Omega }}_3^T{\mathrm{\Omega }}_2^{-1}{\mathrm{\Omega }}_3<0$.

Lemma 4 

([21]). For a symmetric matrix Σ and real matrices M and N, the following matrix inequality holds:

$$\mathrm{\Sigma }+MKN+N^T{K}^T{M}^T<0,$$

if and only if the following matrix inequality is met:

$$\mathrm{\Sigma }+\epsilon M{M}^T+{\epsilon }^{-1}{N}^{T}N<0,$$

where $K^{T}K\le I$ and given scalar $\epsilon >0$.

3. Existence and Uniqueness Theorem

The G-SDDEs in (1) can be rewritten in an equivalent form:

$$\begin{array}{c}\hfill x(t)=x(0)+{\int }_0^{t}f(s,x_1,x_2)ds+{\int }_0^{t}g(s,x_1,x_2)d{〈w^i,w^j〉}_s+{\int }_0^{t}h(s,x_1,x_2)d{w}_s^j,\end{array}$$

(2)

where $f,g$ and h satisfy the following Lipschitz condition hold:

Assumption A2. 

For $f,g,h\in M_G^{P,0}(R_{+};R^n)$, assume that there exist constants $L_1,L_2,L_3,L_4,L_5>0$ and $L_4>L_5$, such that we have the following conditions:

(1) 

$\left|f(s,x_1,x_2)-f(s,{\overline{x}}_1,{\overline{x}}_2)\right|\vee \left|\mathrm{g}(s,x_1,x_2)-g(s,{\overline{x}}_1,{\overline{x}}_2)\right|\le L_1(\left|x_1-{\overline{x}}_1\right|+\left|x_2-{\overline{x}}_2\right|).$

(2) 

$\left|h(s,x_1,x_2)-h(s,{\overline{x}}_1,{\overline{x}}_2)\right|\le L_2(\left|x_1-{\overline{x}}_1\right|+\left|x_2-{\overline{x}}_2\right|).$

(3) 

$\left|f(s,0,0)\right|\vee \left|g(s,0,0)\right|\le L_3$ and $\left|h(s,0,0)\right|\le L_3.$

(4) 

$g^T(s,x_1,x_2)x(s)⩽-L_4{x}_1^T(t)x_1(t)+L_5{x}_2^T(t)x_2(t)$

Theorem 1. 

Let $f,g$ and h satisfy Assumption 2; then, there is a unique solution $x(t)$ of Equation (2), which belongs to $M_{G,l}^{P,0}(R_{+};R^n)$.

Proof. 

Using $H\ddot{o}lde{r}^{\prime }s$ inequality and Assumption 2, we can prove Theorem 1 by employing similar steps to those used in [40]. □

4. Main Results

In this section, we derive certain conditions that can be used to ensure the mean-square stability of the trivial solutions of System (1). By doing so, we aim to establish a comprehensive understanding of the system’s behavior and to identify the underlying factors that contribute to its stability. Specifically, we will explore various techniques, including the application of Assumption 1, Assumption $1^{\prime }$ and Assumption 2 to demonstrate how these conditions can be met. Additionally, we will draw upon similar methodologies utilized in prior research studies, such as [25], to strengthen our findings and to validate our conclusions. Overall, this section provides a valuable contribution to the literature and serves as an important step towards understanding the system’s dynamics.

Theorem 2. 

Assuming Assumption 1 holds, for a scalar $0<d<1$ and $\forall \epsilon >0$, the uncertain time-delay system (1) can achieve mean-square stability if there exist positive definite matrices $P_i=P_i^T>0$, $Q_i=Q_i^T>0$ and $R_i=R_i^T>0$ for $i=1,\cdots ,n$, satisfying the following linear matrix inequality (LMI):

$$\begin{array}{c}\hfill \left(\begin{array}{cccccc}{Q}_i+P_{i}A+A^T{P}_i+{\epsilon }^{-1}{Z}_1{Z}_1^T& P_{i}B& A^T{P}_i+{\epsilon }^{-1}{Z}_1{Z}_1^T& \epsilon H^T{P}_i& \epsilon H^T{P}_i& 0\\ *& -(1-d)Q_i+{\epsilon }^{-1}{Z}_2{Z}_2^T& 0& 0& \epsilon H^T{P}_i& 0\\ *& *& -P_i& 0& 0& 0\\ *& *& *& -\epsilon I& 0& 0\\ *& *& *& *& -\epsilon I& 0\\ *& *& *& *& *& -R_i\end{array}\right)<0,\end{array}$$

(3)

$$\begin{array}{c}\hfill \left(\begin{array}{cccccccc}{P}_i{C}_{ii}+C_{ii}^T{P}_i+{\epsilon }^{-1}{Z}_3{Z}_3^T& 0& E_i^T{P}_i+{\epsilon }^{-1}{Z}_3{Z}_5^T& \epsilon H^T{P}_i& 0& 0& 0& 0\\ *& -R_i^2& F_i^T{P}_i& 0& \epsilon H^T{P}_i& Z_6& R_i& 0\\ *& *& -P_i+{\epsilon }^{-1}{Z}_5{Z}_5^T& 0& \epsilon H^T{P}_i& 0& 0& 0\\ *& *& *& -\epsilon I& 0& 0& 0& 0\\ *& *& *& *& -\epsilon I& 0& 0& 0\\ *& *& *& *& *& -\epsilon I& 0& 0\\ *& *& *& *& *& *& -\epsilon I& 0\\ *& *& *& *& *& *& *& -R_i\end{array}\right)<0.\end{array}$$

(4)

Proof. 

Using the following Lyapunov–Krasovskii candidate function

$$\begin{array}{c}\hfill V(t,x(t))=x^T(t)P_{i}x(t)+{\int }_{t-\tau (t)}^t{x}^T(s)Q_{i}x(s)ds,\end{array}$$

(5)

for $V(t,x(t))$, we have

$$\begin{array}{cc}LV(t,x(t))& =x^T(t)Q_{i}x(t)-(1-\dot{\tau }(t))x^T(t-\tau (t))Q_{i}x(t-\tau (t))+〈2P_{i}x(t),A(t)x(t)+B(t)x(t-\tau (t))〉\\ & +G(〈2P_{i}x(t),(C_{ij}(t)+C_{ji}(t))x(t)+(D_{ij}(t)+D_{ji}(t))x(t-\tau (t))〉\\ & +〈2P_i(E_i(t)x(t)+F_i(t)x(t-\tau (t))),E_j(t)x(t)+F_j(t)x(t-\tau (t))〉)\\ & =x^T(t)[Q_i+2P_{i}A(t)]x(t)+2x^T(t)P_{i}B(t)x(t-\tau (t))-(1-\dot{\tau }(t))x^T(t-\tau (t))Q_{i}x(t-\tau (t))\\ & +2G(\mathrm{\Theta }).\end{array}$$

where

$$\mathrm{\Theta }:=(x^T(t)[P_i(C_{ij}(t)+C_{ji}(t))]x(t)+x^T(t)E_j^T(t)P_i{E}_i(t)x(t)$$

$$+x^T(t)E_j(t)P_i{F}_i(t)x(t-\tau (t))+x^T(t-\tau (t))F_j^T(t)P_i{F}_i(t)x(t-\tau (t))+x^T(t-\tau (t))F_j^T(t)P_i{E}_i{(t)x(t))}_{ij=1}^n$$

$$={\left([x^T(t)x^T(t-\tau (t))]\left(\begin{array}{cc}{P}_i(C_{ij}(t)+C_{ji}(t))+E_j^T(t)P_i{E}_i(t)& E_j^T(t)P_i{F}_i(t)\\ F_j^T(t)P_i{E}_i(t)& F_j^T(t)P_i{F}_i(t)\end{array}\right)\left[\begin{array}{c}x(t)\\ x(t-\tau (t))\end{array}\right]\right)}_{i,j=1}^n$$

$$={\left[{\phi }^T(t){\mathrm{\Lambda }}_{ij}\phi (t)\right]}_{n\times n}$$

$${\phi }^T(t)=[x^T(t)x^T(t-\tau (t))],{\mathrm{\Lambda }}_{ij}=\left(\begin{array}{cc}{P}_i(C_{ij}(t)+C_{ji}(t))+E_j^T(t)P_i{E}_i(t)& E_j^T(t)P_i{F}_i(t)\\ F_j^T(t)P_i{E}_i(t)& F_j^T(t)P_i{F}_i(t)\end{array}\right).$$

$$LV(t,x(t))\le x^T(t)[Q_i+P_{i}A(t)+A(t)P_i+A^T(t)P_{i}A(t)]x(t)+x^T(t)P_{i}B(t)x(t-\tau (t))$$

$$+x^T(t-\tau (t))B(t)P_{i}x(t)-(1-d)x^T(t-\tau (t))Q_{i}x(t-\tau (t))+2G(\mathrm{\Theta })$$

$$={\phi }^T(t)\left(\begin{array}{cc}{Q}_i+P_{i}A(t)+A(t)P_i+A^T(t)P_{i}A(t)& P_{i}B(t)\\ *& -(1-d)Q_i\end{array}\right)\phi (t)+2G(\mathrm{\Theta })$$

.

Using Lemma 3, we have

$$\left(\begin{array}{cc}{Q}_i+P_{i}A(t)+A^T(t)P_i+A^T(t)P_{i}A(t)& P_{i}B(t)\\ *& -(1-d)Q_i\end{array}\right)<0,$$

which is equivalent to

$${\mathrm{\Sigma }}_1=\left(\begin{array}{ccc}{Q}_i+P_{i}A(t)+A^T(t)P_i& P_{i}B(t)& A^T(t)P_i\\ *& -(1-d)Q_i& 0\\ *& *& -P_i\end{array}\right)<0.$$

Using Lemma 4, we can obtain

$${\mathrm{\Sigma }}_1={\mathrm{\Omega }}_1+{\mathrm{\Pi }}_{1}K(t){\mathrm{\Gamma }}_1+{\mathrm{\Gamma }}_1^{T}K{(t)}^T{\mathrm{\Pi }}_1^T<0,$$

if and only if there is a constant $\epsilon$ fulfilling the next inequality

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_1+\epsilon {\mathrm{\Pi }}_1^T{\mathrm{\Pi }}_1+{\epsilon }^{-1}{\mathrm{\Gamma }}_1{{\mathrm{\Gamma }}_1}^T<0,\end{array}$$

(6)

where

$${\mathrm{\Omega }}_1=\left(\begin{array}{ccc}{Q}_i+P_{i}A+A^T{P}_i& P_{i}B& A^T{P}_i\\ *& -(1-d)Q_i& 0\\ *& *& -P_i\end{array}\right),{\mathrm{\Pi }}_1=\left(\begin{array}{ccc}{P}_{i}H& P_{i}H& 0\\ 0& 0& 0\\ P_{i}H& 0& 0\end{array}\right),{\mathrm{\Gamma }}_1=\left(\begin{array}{ccc}{Z}_1& 0& 0\\ 0& Z_2& 0\\ Z_1& 0& 0\end{array}\right).$$

${\mathrm{\Omega }}_1+\epsilon {\mathrm{\Pi }}_1^T{\mathrm{\Pi }}_1+{\epsilon }^{-1}{\mathrm{\Gamma }}_1{{\mathrm{\Gamma }}_1}^T={\mathrm{\Phi }}_1+{\mathrm{\Phi }}_2<0$ is equivalent to

$$\left(\begin{array}{ccccc}{Q}_i+P_{i}A+A^T{P}_i+{\epsilon }^{-1}{Z}_1{Z}_1^T& P_{i}B& A^T{P}_i+{\epsilon }^{-1}{Z}_1{Z}_1^T& \epsilon H^T{P}_i& \epsilon H^T{P}_i\\ *& -(1-d)Q_i+{\epsilon }^{-1}{Z}_2{Z}_2^T& 0& 0& \epsilon H^T{P}_i\\ *& *& -P_i& 0& 0\\ *& *& *& -\epsilon I& 0\\ *& *& *& *& -\epsilon I\end{array}\right)<0,$$

which is equivalent to

$$\left(\begin{array}{cccccc}{Q}_i+P_{i}A+A^T{P}_i+{\epsilon }^{-1}{Z}_1{Z}_1^T& P_{i}B& A^T{P}_i+{\epsilon }^{-1}{Z}_1{Z}_1^T& \epsilon H^T{P}_i& \epsilon H^T{P}_i& 0\\ *& -(1-d)Q_i+{\epsilon }^{-1}{Z}_2{Z}_2^T& 0& 0& \epsilon H^T{P}_i& 0\\ *& *& -P_i& 0& 0& 0\\ *& *& *& -\epsilon I& 0& 0\\ *& *& *& *& -\epsilon I& 0\\ *& *& *& *& *& -R_i\end{array}\right)<0$$

where

$${\mathrm{\Phi }}_1=\left(\begin{array}{ccc}{Q}_i+P_{i}A+A^T{P}_i+{\epsilon }^{-1}{Z}_1{Z}_1^T& P_{i}B& A^T{P}_i+{\epsilon }^{-1}{Z}_1{Z}_1^T\\ *& -(1-d)Q_i+{\epsilon }^{-1}{Z}_2{Z}_2^T& 0\\ *& *& -P_i+{\epsilon }^{-1}{Z}_1{Z}_1^T\end{array}\right),$$

$${\mathrm{\Phi }}_2=\left(\begin{array}{ccc}2\epsilon H^T{P}_i^{2}H& \epsilon H^T{P}_i^{2}H& 0\\ *& \epsilon H^T{P}_i^{2}H& 0\\ *& *& 0\end{array}\right).$$

Noting that ${\mathrm{\Lambda }}_{ii}$ is a symmetric matrix, ${\mathrm{\Lambda }}_{ii}<0$ is equivalent to

$${\mathrm{\Sigma }}_2=\left(\begin{array}{ccc}{P}_i{C}_{ii}(t)+C_{ii}^T(t)P& 0& E_i^T(t)P_i\\ *& 0& F_i^T(t)P\\ *& *& -P_i\end{array}\right)<0$$

using Lemma 4 again, ${\mathrm{\Sigma }}_2<0$ is equivalent to

$${\mathrm{\Sigma }}_2={\mathrm{\Omega }}_2+{\mathrm{\Pi }}_{2}K(t){\mathrm{\Gamma }}_2+{\mathrm{\Gamma }}_2^T{K}^T(t){\mathrm{\Pi }}_2^T<0$$

if and only if there is a constant $\epsilon$, meeting the upcoming inequality

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_2+\epsilon {\mathrm{\Pi }}_2^T{\mathrm{\Pi }}_2+{\epsilon }^{-1}{\mathrm{\Gamma }}_2{{\mathrm{\Gamma }}_2}^T<0,\end{array}$$

(7)

where

$${\mathrm{\Sigma }}_2=\left(\begin{array}{ccc}{P}_i{C}_{ii}+C_{ii}^T{P}_i& 0& E_i^T{P}_i\\ *& 0& F_i^{T}P\\ *& *& -P_i\end{array}\right),{\mathrm{\Pi }}_2=\left(\begin{array}{ccc}{P}_{i}H& 0& 0\\ 0& 0& 0\\ 0& P_{i}H& P_{i}H\end{array}\right),{\mathrm{\Gamma }}_2=\left(\begin{array}{ccc}{Z}_3& 0& 0\\ 0& Z_6& 0\\ Z_5& 0& 0\end{array}\right)$$

${\mathrm{\Omega }}_2+\epsilon {\mathrm{\Pi }}_2^T{\mathrm{\Pi }}_2+{\epsilon }^{-1}{\mathrm{\Gamma }}_2{{\mathrm{\Gamma }}_2}^T={\mathrm{\Phi }}_3+{\mathrm{\Phi }}_4<0$ is equivalent to

$$\left(\begin{array}{cccccc}{P}_i{C}_{ii}+C_{ii}^T{P}_i+{\epsilon }^{-1}{Z}_3{Z}_3^T& 0& E_i^T{P}_i+{\epsilon }^{-1}{Z}_3{Z}_5^T& \epsilon H^T{P}_i& 0& 0\\ *& Z_6{Z}_6^T& F_i^T{P}_i& 0& \epsilon H^T{P}_i& 0\\ *& *& -P_i+{\epsilon }^{-1}{Z}_5{Z}_5^T& 0& \epsilon H^T{P}_i& 0\\ *& *& *& -\epsilon I& 0& 0\\ *& *& *& *& -\epsilon I& 0\\ *& *& *& *& *& -\epsilon I\end{array}\right)<0$$

which is equivalent to

$$\left(\begin{array}{cccccccc}{P}_i{C}_{ii}+C_{ii}^T{P}_i+{\epsilon }^{-1}{Z}_3{Z}_3^T& 0& E_i^T{P}_i+{\epsilon }^{-1}{Z}_3{Z}_5^T& \epsilon H^T{P}_i& 0& 0& 0& 0\\ *& -R_i^2& F_i^T{P}_i& 0& \epsilon H^T{P}_i& Z_6& R_i& 0\\ *& *& -P_i+{\epsilon }^{-1}{Z}_5{Z}_5^T& 0& \epsilon H^{T}P& 0& 0& 0\\ *& *& *& -\epsilon I& 0& 0& 0& 0\\ *& *& *& *& -\epsilon I& 0& 0& 0\\ *& *& *& *& *& -\epsilon I& 0& 0\\ *& *& *& *& *& *& -\epsilon I& 0\\ *& *& *& *& *& *& *& -R_i\end{array}\right)<0$$

where

$${\mathrm{\Phi }}_3=\left(\begin{array}{ccc}{P}_i{C}_{ii}+C_{ii}^T{P}_i+{\epsilon }^{-1}{Z}_3{Z}_3^T& 0& E_i^T{P}_i+{\epsilon }^{-1}{Z}_3{Z}_5^T\\ *& Z_6{Z}_6^T& F_i^T{P}_i\\ *& *& -P_i+{\epsilon }^{-1}{Z}_5{Z}_5^T\end{array}\right),{\mathrm{\Phi }}_4=\left(\begin{array}{ccc}\epsilon H^T{P}^{2}H& 0& 0\\ *& \epsilon H^T{P}^{2}H& \epsilon H^T{P}^{2}H\\ *& \epsilon H^T{P}^{2}H& \epsilon H^T{P}^{2}H\end{array}\right).$$

Next, according to the properties of function $G(·)$ and ${\mathrm{\Lambda }}_{ii}<0$, and as we know that $\mathrm{O}$ is a positive definite matrix, we have

$$\begin{array}{c}\hfill G(\mathrm{\Theta })=\frac{1}{2}\underset{\mathrm{O}\in {\rm Y}}{sup}tr(\mathrm{O}\mathrm{\Theta })⩽\frac{1}{2}\underset{\mathrm{O}\in {\rm Y}}{sup}{\lambda }_{max}(\mathrm{O})\sum _{i=1}^{n}tr({\mathrm{\Lambda }}_{ii})<0,\end{array}$$

where ${\lambda }_{max}(\mathrm{O})$ denotes the largest eigenvalue of $\mathrm{O}$ and $tr(·)$ denotes the trace of the corresponding matrix.

Finally, we obtain

$$LV<0.$$

Noting that $P_i$ and $Q_i$ are positive definite matrices, there exist constants $C_1$ and $C_2$ such that

$$\begin{array}{c}\hfill C_1{\left|x\right|}^2\le V(t,x(t))\le C_2{\left|x\right|}^2.\end{array}$$

Therefore, System (1) is mean-square stable. □

Theorem 3. 

Assuming $\tau (t)=0$ and Assumption 1 holds, $\epsilon >0$, the uncertain System (1) can achieve mean-square stability by finding positive definite matrices $P_i=P_i^T>0$, $Q_i=Q_i^T>0$ and $R_i=R_i^T>0$ for $i=1,\cdots ,n$, satisfying the following linear matrix inequality (LMI):

$$\left(\begin{array}{cccc}{Q}_i+PA+A^{T}P+\epsilon Z_1{Z}_1^T& 0& \epsilon H^{T}P& 0\\ *& -P_i& 0& 0\\ *& *& -\epsilon I& 0\\ *& *& *& -R_i\end{array}\right)<0,$$

$$\left(\begin{array}{cccccc}{C}_{ii}^T{P}_i+P_i{C}_{ii}+\epsilon Z_3{Z}_3^T& 0& E_i^T{P}_i+\epsilon Z_5{Z}_5^T& \epsilon H^T{P}_i& 0& 0\\ *& -R_i^2& 0& 0& R_i& 0\\ *& *& -P_i& 0& 0& \epsilon H^{T}P\\ *& *& *& -\epsilon I& 0& 0\\ *& *& *& *& -\epsilon I& 0\\ *& *& *& *& *& -\epsilon I\end{array}\right)<0.$$

Proof. 

Obviously, the proof process refers to Theorem 2, and Lemmas 3 and 4 are also needed. □

Theorem 4. 

Assuming both Assumption $1^{\prime }$ and Assumption 2 hold, and $\forall \epsilon >0$, the mean-square stability of the uncertain time-delay system in (1) can be guaranteed if there exist positive definite matrices $P_i=P_i{}^T>0$, $Q_i=Q_i{}^T>0$ and $R_i=R_i{}^T>0$ for $i=1,\cdots ,n$ that satisfy the following linear matrix inequality (LMI):

$$\begin{array}{c}\hfill \left(\begin{array}{cccccc}{Q}_i+P_{i}A+A^T{P}_i+{\epsilon }^{-1}{Z}_1{Z}_1^T& P_{i}B& A^T{P}_i+{\epsilon }^{-1}{Z}_1{Z}_1^T& \epsilon H^T{P}_i& \epsilon H^T{P}_i& 0\\ *& -(1-d)Q_i+{\epsilon }^{-1}{Z}_2{Z}_2^T& 0& 0& \epsilon H^T{P}_i& 0\\ *& *& -P_i& 0& 0& 0\\ *& *& *& -\epsilon I& 0& 0\\ *& *& *& *& -\epsilon I& 0\\ *& *& *& *& *& -R_i\end{array}\right)<0,\end{array}$$

(8)

$$\begin{array}{c}\hfill \left(\begin{array}{ccccccc}-R_i^2& 0& E_i^{T}P& R_i& 0& 0& 0\\ *& -R_i^2& F_i^T{P}_i& 0& H^T{P}_i& 0& R_i\\ *& *& -P_i+{\epsilon }^{-1}{Z}_5{Z}_5^T+{\epsilon }^{-1}{Z}_6{Z}_6^T& 0& 0& H^T{P}_i& 0\\ *& *& *& -\epsilon I& 0& 0& 0\\ *& *& *& *& -\epsilon I& 0& 0\\ *& *& *& *& *& -\epsilon I& 0\\ *& *& *& *& *& *& -\epsilon I\end{array}\right)<0.\end{array}$$

(9)

Proof. 

Consider the same Lyapunov–Krasovskii candidate function as (5).

According to Remark 2, we have $G({\mathrm{\Theta }}_{ij})⩽G({\mathrm{\Theta }}_{ij}^1)+G({\mathrm{\Theta }}_{ij}^2)$, considering $G({\mathrm{\Theta }}_{ij}^1)$ and $G({\mathrm{\Theta }}_{ij}^2)$, respectively.

$${\mathrm{\Theta }}_{ij}:=〈2P_{i}x(t),(C_{ij}(t)+C_{ji}(t))x(t)+(D_{ij}(t)+D_{ji}(t))x(t-\tau (t))〉+〈2P_i(E_i(t)x(t)+F_i(t)x(t-\tau (t))),$$

$$E_j(t)x(t)+F_j(t)x(t-\tau (t))〉$$

$$\begin{array}{c}{\mathrm{\Theta }}_{ij}^1:=〈2P_{i}x(t),(C_{ij}(t)+C_{ji}(t))x(t)+(D_{ij}(t)+D_{ji}(t))x(t-\tau (t))〉\hfill \\ {\mathrm{\Theta }}_{ij}^2:=〈2P_i(E_i(t)x(t)+F_i(t)x(t-\tau (t))),E_j(t)x(t)+F_j(t)x(t-\tau (t))〉\hfill \end{array}$$

Based on (4) in Assumption 2, we can obtain

$${\mathrm{\Theta }}_{ij}^1⩽-L_4{x}^T(t)x(t)+L_5{x}^T(t-\tau (t))x(t-\tau (t)):={\mathrm{\Theta }}^3$$

which implies

$$G({\mathrm{\Theta }}_{ij}^1)⩽G({\mathrm{\Theta }}_{ij}^1-{\mathrm{\Theta }}^3)+G({\mathrm{\Theta }}^3)<0,$$

noting that

$$G({\mathrm{\Theta }}_{ij}^1-{\mathrm{\Theta }}^3)=\frac{1}{2}\underset{\mathrm{O}\in {\rm Y}}{sup}tr(\mathrm{O}{({\mathrm{\Theta }}_{ij}^1-{\mathrm{\Theta }}^3)}_{i,j=1}^n)⩽\frac{1}{2}\underset{\mathrm{O}\in {\rm Y}}{sup}{\lambda }_{max}(\mathrm{O})\sum _{i=1}^{n}tr({\mathrm{\Theta }}_{ii}^1-{\mathrm{\Theta }}^3)⩽0.$$

On the other hand,

$$\left(\begin{array}{ccc}{\mathrm{\Theta }}^3& \dots & {\mathrm{\Theta }}^3\\ ⋮& \ddots & ⋮\\ {\mathrm{\Theta }}^3& \cdots & {\mathrm{\Theta }}^3\end{array}\right)=\left(\begin{array}{ccc}{\phi }^T(t)\left(\begin{array}{cc}-L_4& 0\\ & L_5\end{array}\right)\phi (t)& \dots & {\phi }^T(t)\left(\begin{array}{cc}-L_4& 0\\ & L_5\end{array}\right)\phi (t)\\ ⋮& \ddots & ⋮\\ {\phi }^T(t)\left(\begin{array}{cc}-L_4& 0\\ & L_5\end{array}\right)\phi (t)& \cdots & {\phi }^T(t)\left(\begin{array}{cc}-L_4& 0\\ & L_5\end{array}\right)\phi (t)\end{array}\right)$$

due to $L_4>L_5$, can be easily obtained

$$tr({\phi }^T(t)\left(\begin{array}{cc}-L_4& 0\\ *& L_5\end{array}\right)\phi (t))<0.$$

Therefore, we obtain

$$G({\mathrm{\Theta }}^3)=\frac{1}{2}\underset{\mathrm{O}\in {\rm Y}}{sup}tr(\mathrm{O}{({\mathrm{\Theta }}^3)}_{i,j=1}^n)⩽\frac{1}{2}\underset{\mathrm{O}\in {\rm Y}}{sup}{\lambda }_{max}(\mathrm{O})ntr({\mathrm{\Theta }}^3)<0$$

and we know ${\mathrm{\Theta }}_{ii}^2={\phi }^T(t)\left(\begin{array}{cc}{E}_i^T(t)P_i{E}_i(t)& E_i^T(t)P_i{F}_i(t)\\ F_i^T(t)P_i{E}_i(t)& F_i^T(t)P_i{E}_i(t)\end{array}\right)\phi (t)$, so we only need the following to hold:

$$\left(\begin{array}{cc}{E}_i^T(t)P_i{E}_i(t)& E_i^T(t)P_i{F}_i(t)\\ F_i^T(t)P_i{E}_i(t)& F_i^T(t)P_i{E}_i(t)\end{array}\right)<0$$

which is equivalent to

$$\left(\begin{array}{ccc}0& 0& E_i^T(t)P_i\\ *& 0& F_i^T(t)P_i\\ *& *& -P_i\end{array}\right)<0$$

Using Lemma 4, we can show that it is equivalent to

$$\left(\begin{array}{ccccccc}-R_i^2& 0& E_i^{T}P& R_i& 0& 0& 0\\ *& -R_i^2& F_i^T{P}_i& 0& H^T{P}_i& 0& R_i\\ *& *& -P_i+{\epsilon }^{-1}{Z}_5{Z}_5^T+{\epsilon }^{-1}{Z}_6{Z}_6^T& 0& 0& H^T{P}_i& 0\\ *& *& *& -\epsilon I& 0& 0& 0\\ *& *& *& *& -\epsilon I& 0& 0\\ *& *& *& *& *& -\epsilon I& 0\\ *& *& *& *& *& *& -\epsilon I\end{array}\right)<0$$

Hence,

$$G({\mathrm{\Theta }}_{ij})⩽G({\mathrm{\Theta }}_{ij}^1)+G({\mathrm{\Theta }}_{ij}^2)<0$$

the rest follows the same proof process as in Theorem 2, and we obtain

$$\left(\begin{array}{cccccc}{Q}_i+P_{i}A+A^T{P}_i+{\epsilon }^{-1}{Z}_1{Z}_1^T& P_{i}B& A^T{P}_i+{\epsilon }^{-1}{Z}_1{Z}_1^T& \epsilon H^T{P}_i& \epsilon H^T{P}_i& 0\\ *& -(1-d)Q_i+{\epsilon }^{-1}{Z}_2{Z}_2^T& 0& 0& \epsilon H^T{P}_i& 0\\ *& *& -P_i& 0& 0& 0\\ *& *& *& -\epsilon I& 0& 0\\ *& *& *& *& -\epsilon I& 0\\ *& *& *& *& *& -R_i\end{array}\right)<0$$

This ends the proof. □

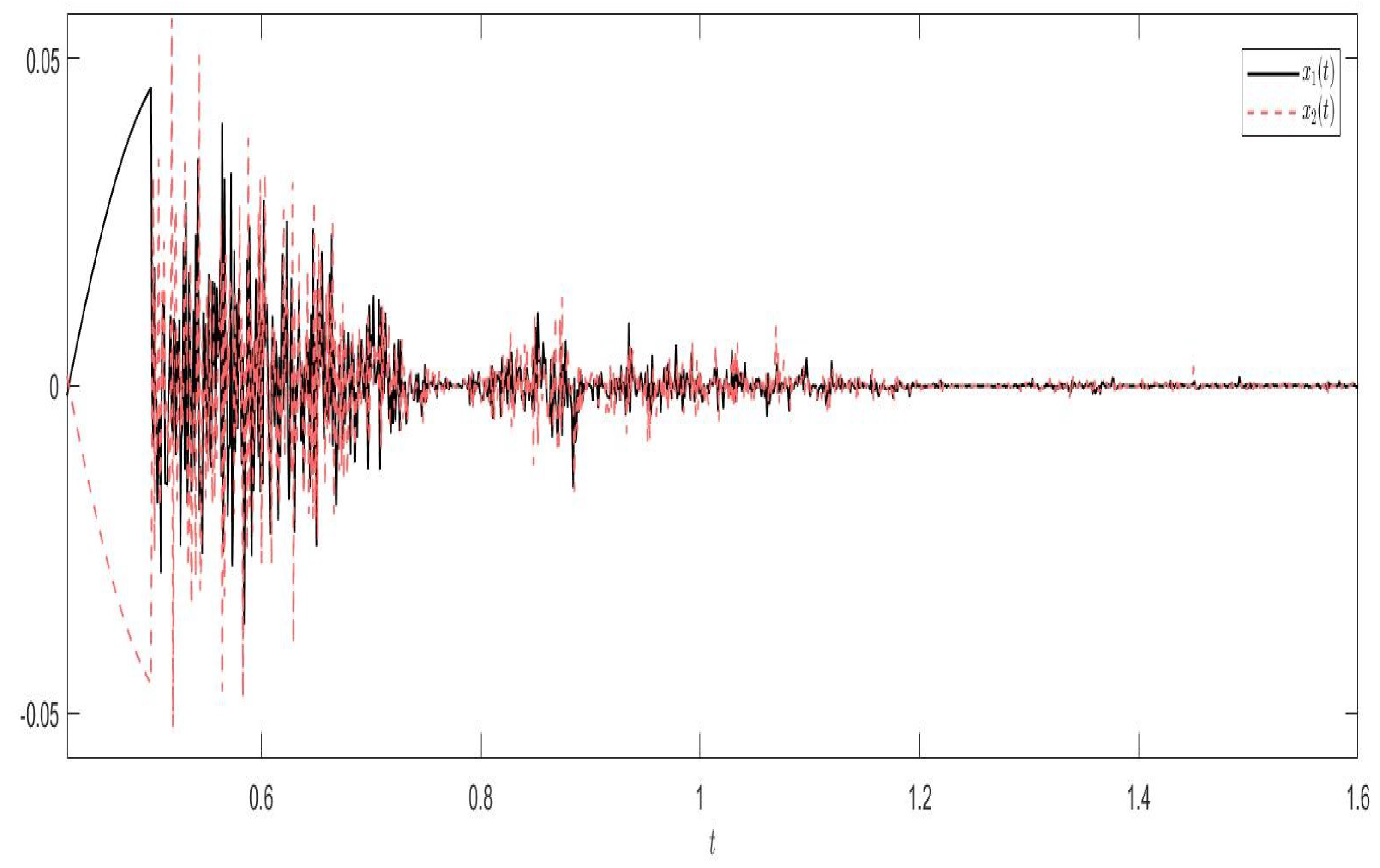
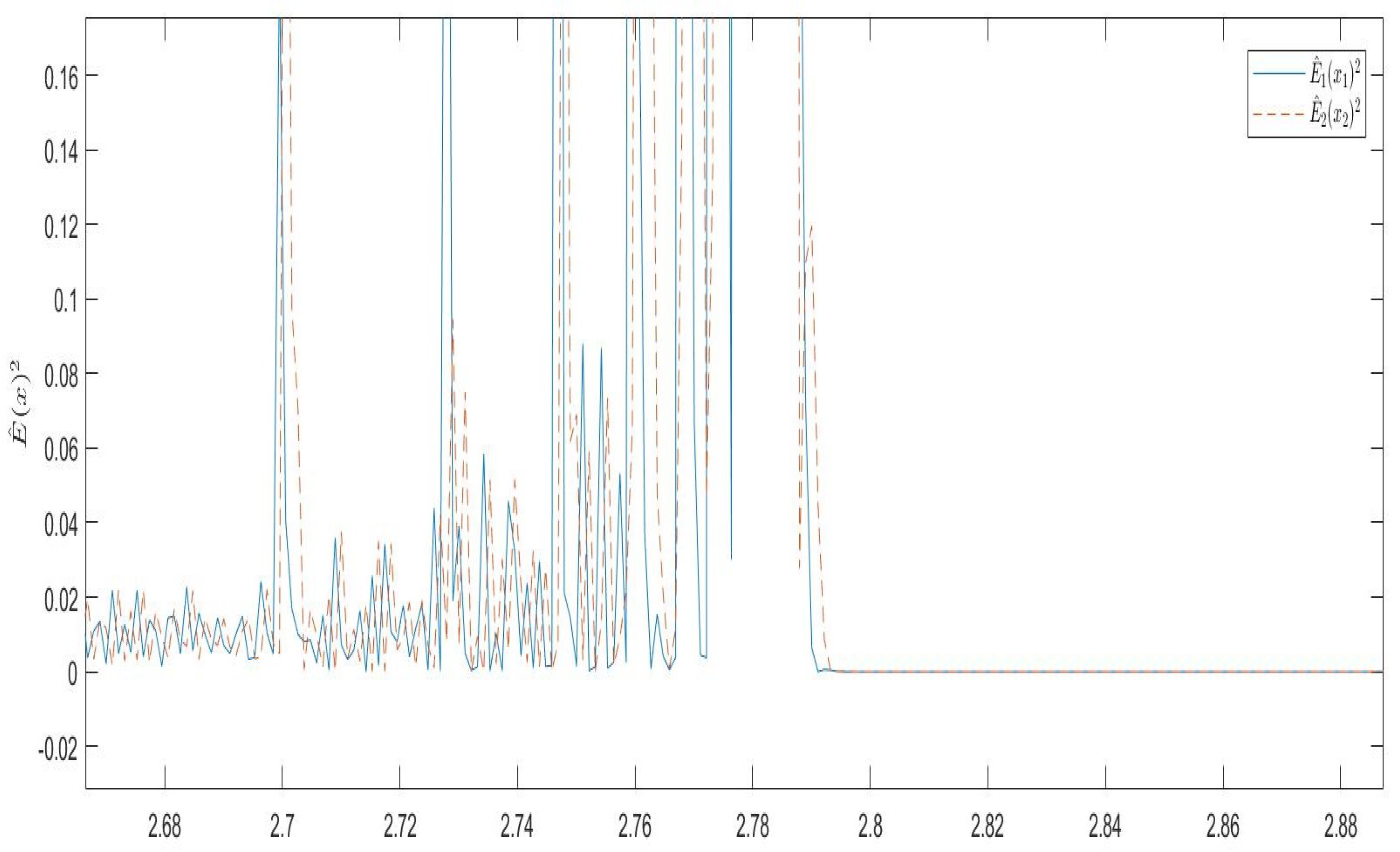
5. Numerical Examples

Example 1. 

Consider the following two-dimensional G-SDDE. Let ${\phi }_1(t)=-0.05+0.1sin(10t),{\phi }_2(t)=0.05-0.1sin(10t),\tau (t)=0.5sin(t),\epsilon =1$ and the corresponding coefficient matrices be as follows:

$$A=\left(\begin{array}{cc}-0.65& 0.5\\ 0.5& -0.65\end{array}\right),B=\left(\begin{array}{cc}0.3& 0.05\\ 0.05& 0.05\end{array}\right),C_{11}=\left(\begin{array}{cc}-10& 0\\ 0& -10\end{array}\right),C_{12}=C_{21}=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right)$$

$$C_{22}=\left(\begin{array}{cc}-5& 1\\ 1& -5\end{array}\right),E_1=\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right),E_2=\left(\begin{array}{cc}0.3& 0\\ 0& 0.3\end{array}\right),F_1=\left(\begin{array}{cc}0.2& 0\\ 0& 0.2\end{array}\right),F_2=\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right)$$

$$Z_1=\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right),Z_2=\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right),Z_3=\left(\begin{array}{cc}-10& 0\\ 0& -10\end{array}\right),Z_5=\left(\begin{array}{cc}-0.05& 0\\ 0& -0.05\end{array}\right),H=\left(\begin{array}{cc}0.02& 0\\ 0& 0.02\end{array}\right),$$

$$Z_6=\left(\begin{array}{cc}-10& 0\\ 0& -10\end{array}\right)$$

Moreover, let

$${\rm Y}=\left\{{\rm Y}=\left(\begin{array}{cc}{\mathrm{O}}_{11}& {\mathrm{O}}_{12}\\ {\mathrm{O}}_{21}& {\mathrm{O}}_{22}\end{array}\right):{\mathrm{O}}_{11}\in [4,5],{\mathrm{O}}_{12}\in [1,2],{\mathrm{O}}_{22}\in [4,5]\right\}$$

Through the MATLAB LMI toolbox, the upcoming possible solution can be derived for the LMI in (3) and (4):

$$P_1=\left(\begin{array}{cc}14.0741& 0.3062\\ 0.3062& 17.0813\end{array}\right),Q_1=\left(\begin{array}{cc}6.0347& -2.3100\\ -2.3100& 6.9992\end{array}\right),R_1=\left(\begin{array}{cc}1.6820& -0.0129\\ -0.0129& 1.6820\end{array}\right)$$

$$P_2=\left(\begin{array}{cc}11.6163& 1.6701\\ 1.6701& 11.6163\end{array}\right),Q_2=\left(\begin{array}{cc}9.8632& -0.6683\\ -0.6683& 9.8632\end{array}\right),R_2=\left(\begin{array}{cc}1.9385& 0.0174\\ 0.0174& 1.9385\end{array}\right).$$

By using the Euler method [41], we choose the step size $h=0.001$ and $w_1(t)\sim N(0,[9,10]t),w_2(t)\sim N(0,[10,11]t)$ to simulate the numerical solution $x_1(t)$, $x_2(t)$ and $\widehat{E}{(x_1(t))}^2$, $\widehat{E}{(x_2(t))}^2$ for the system in Example 1 and Example 2, which are shown in Figure 1, Figure 2, Figure 3 and Figure 4, respectively.

Example 2. 

Consider the following two-dimensional G-SDDE. Let ${\phi }_1(t)=-0.05+0.1sin(10t),$${\phi }_2(t)=0.05-0.1sin(10t),\tau (t)=0.5sin(t),\epsilon =1$ and the corresponding coefficient matrices be as follows:

$$A=\left(\begin{array}{cc}-1.5& 0.5\\ 0.5& -1.5\end{array}\right),B=\left(\begin{array}{cc}0.35& 0.05\\ 0.05& 0.35\end{array}\right),C_{11}=\left(\begin{array}{cc}-10& 0\\ 0& -10\end{array}\right),C_{12}=C_{21}=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right)$$

$$C_{22}=\left(\begin{array}{cc}-5& 1\\ 1& -5\end{array}\right),E_1=\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right),E_2=\left(\begin{array}{cc}0.3& 0\\ 0& 0.3\end{array}\right),F_1=\left(\begin{array}{cc}0.2& 0\\ 0& 0.2\end{array}\right),F_2=\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right)$$

$$Z_1=\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right),Z_2=\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right),Z_3=\left(\begin{array}{cc}-10& 0\\ 0& -10\end{array}\right),Z_5=\left(\begin{array}{cc}-0.05& 0\\ 0& -0.05\end{array}\right),H=\left(\begin{array}{cc}0.02& 0\\ 0& 0.02\end{array}\right),$$

$$Z_6=\left(\begin{array}{cc}-10& 0\\ 0& -10\end{array}\right),D_{11}=\left(\begin{array}{cc}-10& 0\\ 0& -10\end{array}\right),D_{12}=D_{21}=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right),D_{22}=\left(\begin{array}{cc}-5& 1\\ 1& -5\end{array}\right).$$

Using the MATLAB LMI toolbox, it is possible to derive a potential solution for the LMI in (8) and (9), as shown below:

$$P_1=\left(\begin{array}{cc}3.3450& -0.1392\\ -0.1392& 3.3450\end{array}\right),Q_1=\left(\begin{array}{cc}2.7255& 1.0822\\ 1.0822& 2.7255\end{array}\right),R_1=\left(\begin{array}{cc}1.8680& -0.0135\\ -0.0135& 1.8680\end{array}\right)$$

$$P_2=\left(\begin{array}{cc}9.5265& 1.7550\\ 1.7550& 9.5265\end{array}\right),Q_2=\left(\begin{array}{cc}8.6448& 4.1045\\ 4.1045& 8.6448\end{array}\right),R_2=\left(\begin{array}{cc}2.1565& 0.0064\\ 0.0064& 2.1565\end{array}\right).$$

By selecting sufficiently large constants $L_4$ and $L_5$, we can verify that the following condition holds:

$$〈2P_{i}x(t),(C_{ij}(t)+C_{ji}(t))x(t)+(D_{ij}(t)+D_{ji}(t))x(t-\tau (t))〉⩽-L_4{x}^T(t)x(t)+L_5{x}^T(t-\tau (t))x(t-\tau (t)).$$

6. Conclusions

This paper primarily investigates the mean-square stability of G-SDDE and presents three sufficient conditions for the stability of time-delay systems using the Lyapunov function. Through Theorems 2–4 and numerical examples, we can directly use MATLAB calculations to preliminarily determine the stability of G-SDDE systems when obtaining system parameters, without the need for additional proof, thus reducing the practical workload. These extensions will enhance our understanding of G-SDDE stability and improve our ability to design effective control strategies for these systems. In the future, we will also extend our work to the case of intermittent control, impulse control and cooperative control [11,12,13].