Nonlinear Oscillations of a Composite Stepped Piezoelectric Cantilever Plate with Aerodynamic Force and External Excitation

Abstract

Axially moving wing aircraft can better adapt to the flight environment, improve flight performance, reduce flight resistance, and improve flight distance. This paper simplifies the fully unfolded axially moving wing into a stepped cantilever plate model, analyzes the structural nonlinearity of the system, and studies the influence of aerodynamic nonlinearity on system vibration. The model is affected by aerodynamic forces, piezoelectric excitation, and in-plane excitation. Due to Hamilton’s principle of least action, the mathematical model is established based on Reddy’s higher-order shear deformation theory, and using Galerkin’s method, the governing dimensionless partial differential equations of the system are simplified to two nonlinear ordinary differential equations, and then a study of the influence of the various engineering parameters on the nonlinear oscillations and frequency responses of this model is conducted by the method of multiple scales. It was found that the different values of $a_5$, $a_6$, $b_6$ and $b_8$ can change the shape of the amplitude–frequency response curve and size of the plate, while different symbols $a_7$ and $b_7$ can change the rigidity of the model. The excitations greatly impact the nonlinear dynamic responses of the plate.

1. Introduction

The aspect ratio of the wing can optimize its performance under radically different flight conditions. Thus, axially moving wing aircraft can better adapt to the flight environment, improve flight performance, reduce flight resistance, and improve flight distance [1,2,3]. At present, the aircraft wings used in civil and military aviation are still the fixed wing aircraft type. However, more flight requirements are set for traditional aircraft, such as in the process of take-off, landing, and cruising; the aircraft is required to have a high aspect ratio, light weight, and high flexibility to improve the low-speed performance, landing performance, and cruising lift-to-drag ratio of the aircraft. If the retractable wing is fully expanded and maintained in a stable state during takeoff, landing, and cruising of the aircraft, it not only maintains a fixed-wing configuration but also meets the requirements of improving the low-speed performance, landing performance, and cruising lift-to-drag of the aircraft. If the axially moving wing is fully expanded, which can be simplified to a stepped cantilever plate model, the nonlinear analysis of the structure and further aerodynamic nonlinearity influence on the system vibration can be considered, as it can provide some effective strategies for restraining the flutter of the structures and further control research on system stability, with high value in engineering applications.

Compared with the traditional fixed wing, the axial retractable wing can meet higher flight requirements; therefore, the research on the axial retractable wing has received extensive attention from relevant scholars: during its deploying and retreating, it is simplified into axial moving beam, plate, and shell models. In 2017, Zhang et al. [4] investigated the nonlinear dynamic behaviors when deploying a cantilevered thin shell subjected to the aerodynamic force in subsonic airflow. In 2022, Zhang et al. [5] studied the stability and vibration of the telescopic cantilevered laminated composite rectangular plate subjected to the first-order aerodynamic force and in-plane excitation using theoretical, numerical, and experimental methods. In 2022, Liu [6] analyzed the nonlinear dynamics of an axially moving composite laminated cantilever beam in supersonic airflow, and nonlinear dynamic modeling and numerical simulations analysis were carried out. Moreover, Zhang and co-workers performed studies on axially moving structures, such as belts [7,8], beams [9,10,11], and plates [12,13,14,15,16,17].

At the same time, there also several other excellent studies on axially moving wing aircraft, which mainly focused on design, manufacturing, test flight, and experimentation. In 1998, researchers [18] designed an axially moving wing. A wind tunnel experiment was used to test the small-scale model of this aircraft. In 2003, the Virginia Tech AE/ME Morphing design team [19] invented another axially moving wing aircraft by varying the sweep angle. In 2005, Henry [20] described an axially moving variable-span morphing wing (VSMW), which could be used to change the flight direction with a variable wingspan. In 2018, Jin and Li [21] used a numerical method to investigate the dynamic behavior and stability of a variable-span wing subjected to supersonic aerodynamic loads to make use of morphing technology for flutter suppression. All of the work mentioned above is about the wing during deployment and retraction; there is no work related to the retractable wing, which is fully expanded and maintained in a stable state, and the stepped cantilever plate was chosen as the model for the first time.

Although in current studies the fully deployable system is simplified into a stepped cantilever plate model, the theoretical foundation for the study of the stepped cantilever plate model has not yet been laid. Meanwhile, a series of studies on rectangular plates have been reported. For instance, in 2012, Amabili et al. [22] performed numerous experiments and numerical simulations to examine the large-amplitude vibrations of plates with concentrated masses. Also, in 2010 and 2014, Zhang et al. [23,24] carried out nonlinear dynamics analysis by deploying a rectangular cantilever plate and a simply supported thin rectangular plate, which were made of orthotropic and angle-ply composite laminates, respectively.

Piezoelectric fiber composite material [25,26] is the crystal material in which a voltage appears between two ends under pressure. Compared to traditional piezoelectric ceramics, the piezoelectric fiber composite material overcomes the defects in toughness and has excellent flexibility and piezoelectric properties. In addition, it is thin and light, can be bent greatly and is thus easily subjected to torsion, is easy to paste, and is especially suitable for the spacecraft rigid-flexible coupling structure. Therefore, regular symmetric cross-ply laminates with n layers are chosen for the plate. A layer of the PVDF (Poly Vinyli Dene Fluoride) piezoelectric materials is embedded in the middle of two adjacent fiber-reinforced composite materials. The PVDF piezoelectric materials act as actuators. The composite stepped piezoelectric cantilever plate can be chosen as a model of the axially moving wings and has theoretical and practical significance for our study.

At present, a great number of valuable research results have been obtained by researchers who have performed research on piezoelectric composite laminates and piezoelectric functionally gradient plates from the perspectives of experimental analysis [27,28], static conditions [29,30], and dynamics [31], as well as on the control of piezoelectric beams, plates, and shell structures [32,33,34]. Similarly, reference [35] studied the nonlinear dynamic characteristics of composite laminated plates under different loads and boundary conditions, and reference [36] studied the static and dynamic stability of composite cylindrical shells. The research methods of these articles have guiding significance for the research in this paper.

In detail, the main work in this study is as follows: the nonlinear behavior of the piezoelectric stepped rectangular cantilever plates made of composite laminated materials is studied. Additionally, the primary parameter resonance and 1:3 internal resonance are discussed. The mathematical models are formulated based on the pneumatic elastic piston theory [37] and the higher-order shear deformation theory [38]. The nonlinear governing partial differential equations and the ordinary differential equations of motion can be obtained by using Hamilton’s principle and Galerkin’s method, respectively. Subsequently, the average equations can be acquired by using the multiple scales method. Then, for the nonlinear oscillations of the model governed by various engineering parameters, the periodic, almost periodic, and chaotic motions of this model are studied by the numerical simulation method. Based on the numerical simulation, the influence of the nonlinear piston aerodynamic force, piezoelectric excitations, and in-plane excitations on the bifurcation behaviors is discussed. This research will contribute to a better understanding of the mechanical design and safety of stepped plate-type structures made of PVDF piezoelectric materials as actuators.

2. Equations of Nonlinear Oscillations

The composite stepped piezoelectric cantilever plate is chosen as the model of the axially moving wing. Regular symmetric cross-ply laminates with n layers are chosen for the plate. A layer of the PVDF piezoelectric material is embedded in the middle of two adjacent fiber-reinforced composite materials. It is assumed that different layers of the symmetric cross-ply composite laminated piezoelectric stepped cantilever plate are perfectly bonded to each other. The PVDF piezoelectric materials act as actuators. As Figure 1 shows, the length and width of model is a and b, respectively. The plate is divided into two regions, namely, $o_1$ and $o_2$. The thickness of the stepped left zone is $h_1-h_2$, and the remaining part of the plate has a thickness of $h_{2 }$. In the $x$ direction at $x=0$, the model’s in-plane excitations are presented in the $F=F_0+F_1{\cos \mathsf{\Omega }}_{1}t$ form. In the Z-axis direction, the transversal aerodynamics loading is $\mathsf{\Delta }p$. The structural damping force is $\gamma \frac{dw}{dt}$. OXYZ is used as the Cartesian coordinate system.

The lamina constitutive relationship of the kth layer coupling the direct and converse piezoelectric equations is given by

$${\left\{\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\tau }_{xy}\end{array}\right\}}_k={\left[\begin{array}{ccc}{Q}_{11}& Q_{12}& 0\\ Q_{21}& Q_{22}& 0\\ 0& 0& Q_{66}\end{array}\right]}_k{\left\{\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\gamma }_{xy}\end{array}\right\}}_k-{\left[\begin{array}{ccc}0& 0& e_{31}\\ 0& 0& e_{32}\\ 0& 0& 0\end{array}\right]}_k{\left\{\begin{array}{c}{E}_x\\ E_y\\ E_z\end{array}\right\}}_k$$

(1a)

$${\left\{\begin{array}{c}{\tau }_{yx}\\ {\tau }_{zx}\end{array}\right\}}_k={\left[\begin{array}{cc}{Q}_{44}& 0\\ 0& Q_{55}\end{array}\right]}_k{\left\{\begin{array}{c}{\gamma }_{yz}\\ {\gamma }_{zx}\end{array}\right\}}_k$$

(1b)

where $Q_{ij}\left(i=1,2,4,5,6;j=1,2,4,5,6\right)$ are elastic moduli of this model, which is given as follows

$$Q_{11}=Q_{22}=\frac{E}{1-{\nu }^2}$$

(1c)

$$Q_{12}=Q_{21}=\frac{\nu E}{1-{\nu }^2}$$

(1d)

$$Q_{44}=Q_{55}=Q_{66}=\frac{E}{2\left(1-\nu \right)}$$

(1e)

where E represent Young’s modulus, and ν represent Poisson’s ratio.

According to the third-order Piston Theory, the transversal aerodynamics loading can be expressed as

$$\Delta p_i=-\frac{4q_d\gamma }{M_{\infty }}\left(\frac{\partial w_{0i}}{\partial x}+\frac{\partial w_{0i}}{\partial y}+\frac{1}{{\nu }_a}\frac{\partial w_{0i}}{\partial t}\right)$$

(2)

where $q_d$ represents the dynamic pressure, $q_d=\frac{1}{2}{\rho }_{air}{\nu }_a^2$, ${\rho }_{air}$ denotes the air density, the airflow supersonic speed is expressed by ${\nu }_a$, and $M_{\infty }$ represents the Mach number, $\gamma =\frac{M_{\infty }}{\sqrt{M_{\infty }^2-1}}$ (note: typical value of $\gamma =1.4$).

The displacements of an arbitrary point in the direction of $\mathrm{x}$,$y$, and $z$ can be represented by $\left(u_i,v_i,w_i\right)$, and the displacement of any point on the mid-plane is represented by $\left(u_{0i},v_{0i},w_{0i}\right)$; the mid-plane rotations can be expressed by $\left({\phi }_{xi},{\phi }_{yi}\right)$, and the rotation normal of the mid-plane on the $x$ and $y$ axes is represented by $\left({\phi }_{xi},{\phi }_{yi}\right)$.

Based on Reddy’s third-order shear deformation theory, the displacement fields of the stepped plate are derived and can be divided into two plates, which are expressed as

$$u_i=u_{0i}\left(x,y,t\right)+z_i{\phi }_{xi}\left(x,y,t\right)-z_i^3\frac{4}{3h^2}\left({\phi }_{xi}+\frac{\partial w_{0i}}{\partial x}\right)$$

(3a)

$$v_i=v_{0i}\left(x,y,t\right)+z_i{\phi }_{yi}\left(x,y,t\right)-z_i^3\frac{4}{3h^2}\left({\phi }_{yi}+\frac{\partial w_{0i}}{\partial y}\right)$$

(3b)

$$w_i=w_{0i}\left(x,y,t\right)$$

(3c)

According to the von Karman strain–displacement relationship, the relationships of strain and displacement are expressed by Equations (4a) and (4b)

$${\epsilon }_{xxi}=\frac{\partial u_i}{\partial x}+\frac{1}{2}{\left(\frac{\partial w_{0i}}{\partial x}\right)}^2, {\epsilon }_{yyi}=\frac{\partial v_i}{\partial y}+\frac{1}{2}{\left(\frac{\partial w_{0i}}{\partial y}\right)}^2$$

(4a)

$${\gamma }_{xzi}=\frac{\partial u_i}{\partial z}+\frac{\partial w_{0i}}{\partial x},{\gamma }_{yzi}=\frac{\partial v_i}{\partial z}+\frac{\partial w_{0i}}{\partial y},{\gamma }_{xyi}=\frac{\partial u_i}{\partial y}+\frac{\partial v_i}{\partial x}+\frac{\partial w_{0i}}{\partial x}\frac{\partial w_{0i}}{\partial y}$$

(4b)

Equations (4a) and (4b) can be substituted into Equations (3a)–(3c) to obtain Equations (5a) and (5b)

$$\left\{\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\gamma }_{xy}\end{array}\right\}=\left\{\begin{array}{c}{\epsilon }^0\end{array}\right\}+z\left\{\begin{array}{c}{\epsilon }^1\end{array}\right\}+z^3 \left\{\begin{array}{c}{\epsilon }^3\end{array}\right\}$$

(5a)

$$\left\{\begin{array}{c}{\gamma }_{yz}\\ {\gamma }_{zx}\end{array}\right\}=\left\{\begin{array}{c}{\gamma }^0\end{array}\right\}+z^2 \left\{\begin{array}{c}{\gamma }^2\end{array}\right\}$$

(5b)

in which

$$\left\{\begin{array}{c}{\epsilon }^0\end{array}\right\}=\left\{\begin{array}{c}\frac{\partial u_{0i}}{\partial x}+\frac{1}{2}{\left(\frac{\partial w_{0i}}{\partial x}\right)}^2\\ \frac{\partial v_{0i}}{\partial y}+\frac{1}{2}{\left(\frac{\partial w_{0i}}{\partial y}\right)}^2\\ \frac{\partial v_{0i}}{\partial x}+\frac{\partial u_{0i}}{\partial y}+\frac{\partial w_{0i}}{\partial x}\frac{\partial w_{0i}}{\partial y}\end{array}\right\}, \left\{\begin{array}{c}{\epsilon }^1\end{array}\right\}=\left\{\begin{array}{c}-\frac{{\partial }^2{w}_{0i}}{\partial x_2}\\ -\frac{{\partial }^2{w}_{0i}}{\partial y_2}\\ -2\frac{{\partial }^2{w}_{0i}}{\partial x\partial y}\end{array}\right\}, \left\{\begin{array}{c}{\gamma }^0\end{array}\right\}=\left\{\begin{array}{c}{\phi }_{yi}+\frac{\partial w_{0i}}{\partial y}\\ {\phi }_{xi}+\frac{\partial w_{0i}}{\partial x}\end{array}\right\},$$

(5c)

$$\left\{\begin{array}{c}{\epsilon }^3\end{array}\right\}=-c_1\left\{\begin{array}{c}\frac{\partial {\phi }_{xi}}{\partial x}+\frac{{\partial }^2{w}_{0i}}{\left(\partial x^2\right)}\\ \frac{\partial {\phi }_{0i}}{\partial y}+\frac{{\partial }^2{w}_{0i}}{\left(\partial y^2\right)}\\ \frac{\partial {\phi }_{0i}}{\partial y}+\frac{\partial {\phi }_{0i}}{\partial x}+2\frac{{\partial }^2{w}_{0i}}{\partial x\partial y}\end{array}\right\},\left\{\begin{array}{c}{\gamma }^2\end{array}\right\}=-c_2\left\{\begin{array}{c}{\phi }_{yi}+\frac{\partial w_{0i}}{\partial y}\\ {\phi }_{xi}+\frac{\partial w_{0i}}{\partial x}\end{array}\right\},$$

(5d)

$$c_1=\frac{4}{3h^2},c_2=3c_1$$

(5e)

The internal force and moment resultants can be computed from the formulas below:

$$\left(N_{xxi},N_{yyi},N_{xyi}\right)={\displaystyle \sum }_{k=1}^N{\int }_{z_k}^{z_{k+1}}\left({\sigma }_{xxi},{\sigma }_{yyi},{\tau }_{xyi}\right)\mathrm{dz}$$

(6a)

$$\left(M_{xxi},M_{yyi},M_{xyi}\right)={\displaystyle \sum }_{k=1}^N{\int }_{z_k}^{z_{k+1}}\left({\sigma }_{xxi},{\sigma }_{yyi},{\tau }_{xyi}\right)\mathrm{zdz}$$

(6b)

$$\left(P_{xxi},P_{yyi},P_{xyi}\right)={\displaystyle \sum }_{k=1}^N{\int }_{z_k}^{z_{k+1}}\left({\sigma }_{xxi},{\sigma }_{yyi},{\tau }_{xyi}\right)z^3\mathrm{dz}$$

(6c)

$$\left(R_{xxi},R_{yyi}\right)={\displaystyle \sum }_{k=1}^N{\int }_{z_k}^{z_{k+1}}\left({\tau }_{zxi},{\tau }_{zyi}\right)z^2\mathrm{dz}$$

(6d)

$$\left(Q_{xxi},Q_{yyi}\right)={\displaystyle \sum }_{k=1}^N{\int }_{z_k}^{z_{k+1}}\left({\tau }_{zxi},{\tau }_{zyi}\right)\mathrm{dz}$$

(6e)

Substituting constitutive Equations (1a)–(1e) into internal force and bending moment (6a)–(6e), Equations (7a)–(7d) is obtained

$$\left\{\begin{array}{c}{N}_{xxi}\\ N_{yyi}\\ N_{xyi}\end{array}\right\}=\left[\begin{array}{ccc}{A}_{11}& A_{12}& 0\\ A_{21}& A_{22}& 0\\ 0& 0& A_{66}\end{array}\right]\left\{\begin{array}{c}{\epsilon }^0\end{array}\right\}-\left\{\begin{array}{c}{N}_x^p\\ N_y^p\\ 0\end{array}\right\}$$

(7a)

$$\left\{\begin{array}{c}{M}_{xxi}\\ M_{yyi}\\ M_{xyi}\end{array}\right\}=\left\{\begin{array}{ccc}{D}_{11}& D_{12}& 0\\ D_{21}& D_{22}& 0\\ 0& 0& D_{66}\end{array}\right\}\left\{\begin{array}{c}{\epsilon }^1\end{array}\right\}+\left\{\begin{array}{ccc}{F}_{11}& F_{12}& 0\\ F_{21}& F_{22}& 0\\ 0& 0& F_{66}\end{array}\right\}\left\{\begin{array}{c}{\epsilon }^3\end{array}\right\}$$

(7b)

$$\left\{\begin{array}{c}{P}_{xxi}\\ P_{yyi}\\ P_{xyi}\end{array}\right\}=\left\{\begin{array}{ccc}{F}_{11}& F_{12}& 0\\ F_{21}& F_{22}& 0\\ 0& 0& F_{66}\end{array}\right\}\left\{\begin{array}{c}{\epsilon }^1\end{array}\right\}+\left\{\begin{array}{ccc}{H}_{11}& H_{12}& 0\\ H_{21}& H_{22}& 0\\ 0& 0& H_{66}\end{array}\right\}\left\{\begin{array}{c}{\epsilon }^3\end{array}\right\}$$

(7c)

$$\left\{\begin{array}{c}\begin{array}{c}{Q}_{xxi}\\ Q_{yyi}\end{array}\end{array}\right\}=\left\{\begin{array}{cc}{A}_{44}& 0\\ 0& A_{55}\end{array}\right\}\left\{\begin{array}{c}{\gamma }^0\end{array}\right\}+\left\{\begin{array}{cc}{D}_{44}& 0\\ 0& D_{55}\end{array}\right\}\left\{\begin{array}{c}{\gamma }^2\end{array}\right\}$$

(7d)

in which

$$N_x^p=N_x^p{{\displaystyle \sum }}_{k=1}^N{\int }_{z_k}^{z_{k+1}}{e}_{31}{E}_Z\mathrm{dz},N_y^p={{\displaystyle \sum }}_{k=1}^N{\int }_{z_k}^{z_{k+1}}{e}_{32}{E}_Z\mathrm{dz},$$

(7e)

where $e_{31}$ and $e_{32}$ are piezoelectric coefficients; according to the lamination theory, the shear stiffness coefficients are $A_{ij}$, $B_{ij}$, $D_{ij}$, $E_{ij}$, $F_{ij}$, and $H_{ij}$ and are defined as follows:

$$(A_{ij}, B_{ij}, D_{ij}, E_{ij},F_{ij}, H_{ij})={{\displaystyle \sum }}_{k=1}^N{\int }_{z_k}^{z_{k+1}}{Q}_{ij}^k\left(1,\mathrm{z},z^2,z^3,z^4,z^6\right)\mathrm{dz},\left(i,j=1,2,6\right),$$

(7f)

$$(A_{ij},D_{ij},F_{ij})={{\displaystyle \sum }}_{k=1}^N{\int }_{z_k}^{z_{k+1}}{Q}_{ij}^k\left(1,\mathrm{z},z^4\right)\mathrm{dz},\left(i,j=4,5\right),$$

(7g)

$$I_i={\displaystyle \sum }_{k=1}^N{\rho }^{\left(k\right)}{Z}^i\mathrm{dz},\left(i=0,1,2,\dots ,6\right)$$

(7h)

$$J_i=I_i-c_1{I}_{i+2},K_2=I_2-2c_1{I}_4+c_1^2{I}_6$$

(7i)

The nonlinear governing equations for the two regions and of the system according to Hamilton’s principle are given by Equations (8a)–(8e) and (9a)–(9e)

For the inner plate O₁:

$$\begin{array}{c}{A}_{11}\frac{{\partial }^2{u}_{01}}{\partial x_1^2}+A_{66}\frac{{\partial }^2{u}_{01}}{\partial y_1^2}+\left(A_{12}+A_{66}\right)\frac{{\partial }^2{v}_{01}}{\partial x_1\partial y_1}+A_{11}\frac{\partial w_{01}}{\partial x_1}\frac{{\partial }^2{w}_{01}}{\partial x_1^2}+\\ A_{66}\frac{\partial w_{01}}{\partial x_1}\frac{{\partial }^2{w}_{01}}{\partial y_1^2}+(A_{12}+A_{66})\frac{\partial w_{01}}{\partial y_1}\frac{{\partial }^2{w}_{01}}{\partial x_1\partial y_1}=I_0{\ddot{u}}_{01}+\left(I_1-c_1{I}_3\right){\ddot{\phi }}_{x1}-c_1{I}_3\frac{\partial {\ddot{w}}_{01}}{\partial x_1}\end{array}$$

(8a)

$$\begin{array}{c}{A}_{22}\frac{{\partial }^2{v}_{01}}{\partial y_1^2}+A_{66}\frac{{\partial }^2{v}_{01}}{\partial x_1^2}+\left(A_{21}+A_{66}\right)\frac{{\partial }^2{u}_{01}}{\partial x_1\partial y_1}+A_{66}\frac{\partial w_{01}}{\partial y_1}\frac{{\partial }^2{w}_{01}}{\partial x_1^2}+\\ A_{22}\frac{\partial w_{01}}{\partial y_1}\frac{{\partial }^2{w}_{01}}{\partial y_1^2}+(A_{21}+A_{66})\frac{\partial w_{01}}{\partial x_1}\frac{{\partial }^2{w}_{01}}{\partial x_1\partial y_1}=I_0{\ddot{v}}_{01}+\left(I_1-c_1{I}_3\right){\ddot{\phi }}_{y1}-c_1{I}_3,\end{array}$$

(8b)

$$\begin{array}{c}{A}_{11}\frac{\partial u_{01}}{\partial x_1}\frac{{\partial }^2{w}_{01}}{\partial x_1^2}+A_{21}\frac{\partial u_{01}}{\partial x}\frac{{\partial }^2{w}_{01}}{\partial y_1^2}+2A_{66}\frac{\partial u_{01}}{\partial y_1}\frac{{\partial }^2{w}_{01}}{\partial x_1\partial y_1}+A_{11}\frac{{\partial }^2{u}_{01}}{\partial x_1^2}\frac{\partial w_{01}}{\partial x_1}\\ +(A_{21}+A_{66})\frac{{\partial }^2{u}_{01}}{\partial x_1\partial y_1}\frac{\partial w_{01}}{\partial y_1}+A_{66}\frac{{\partial }^2{v}_{01}}{\partial x_1^2}\frac{\partial w_{01}}{\partial y_1}+(A_{12}+A_{66})\frac{{\partial }^2{v}_{01}}{\partial x_1\partial y_1}\frac{\partial w_{01}}{\partial x_1}\\ +A_{22}\frac{{\partial }^2{v}_{01}}{\partial y_1^2}\frac{\partial w_{01}}{\partial y_1}+\frac{3}{2}{A}_{11}{\left(\frac{\partial w_{01}}{\partial x_1}\right)}^2\frac{{\partial }^2{w}_{01}}{\partial x_1^2}+(\frac{1}{2}{A}_{21}+A_{66}){\left(\frac{\partial w_{01}}{\partial x_1}\right)}^2\frac{{\partial }^2{w}_{01}}{\partial y_1^2}\\ +(A_{12}+A_{21}+4A_{66})\frac{\partial w_{01}}{\partial x_1}\frac{\partial w_{01}}{\partial y_1}\frac{{\partial }^2{w}_{01}}{\partial x_1\partial y_1}+\frac{3}{2}{A}_{11}{\left(\frac{\partial w_{01}}{\partial x_1}\right)}^2\frac{{\partial }^2{w}_{01}}{\partial y_1^2}+(\frac{1}{2}{A}_{21}\\ +A_{66}){\left(\frac{\partial w_{01}}{\partial x_1}\right)}^2\frac{{\partial }^2{w}_{01}}{\partial x_1^2}+\left(A_{55}-2c_2{D}_{55}-c_2^2{F}_{55}-N_x^p\cos \left({\mathsf{\Omega }}_{2}t\right)\right)\frac{{\partial }^2{w}_{01}}{\partial x_1^2}\\ +\left(A_{44}-2c_2{D}_{44}-c_2^2{F}_{44}-N_y^p\cos \left({\mathsf{\Omega }}_{3}t\right)\right)\frac{{\partial }^2{w}_{01}}{\partial y_1^2}-c_1^2{H}_{11}\frac{{\partial }^4{w}_{01}}{\partial x_1^4}\\ -c_1^2(H_{21}-4H_{66}-H_{12})\frac{{\partial }^4{w}_{01}}{\partial x_1^2\partial y_1^2}+(A_{55}-2c_2{D}_{55}-c_2^2{F}_{44})\frac{\partial {\phi }_{x1}}{\partial x_1}-c_1^2{H}_{22}\frac{{\partial }^4{w}_{01}}{\partial y_1^4}\\ +(A_{44}-2c_2{D}_{44}+c_2^2{F}_{44})\frac{\partial {\phi }_{y1}}{\partial y_1}+c_1(F_{12}+2F_{66}-c_1{H}_{12}-2c_1{H}_{66})\frac{{\partial }^3{\phi }_{y1}}{\partial x_1^2\partial y_1}\\ +c_1(F_{11}-c_1{H}_{11})\frac{{\partial }^3{\phi }_{x1}}{\partial x_1^3}+c_1(F_{12}+2F_{66}-c_1{H}_{21}-2c_1{H}_{66})\frac{{\partial }^3{\phi }_{y1}}{\partial x_1\partial y_1^2}\\ +c_1(F_{22}-c_1{H}_{22})\frac{{\partial }^3{\phi }_{y1}}{\partial y_1^3}+\mathsf{\Delta }p-\gamma {\dot{w}}_{01}+(F_0+F_1\cos \left({\mathsf{\Omega }}_{1}t\right))\\ =I_0{\ddot{w}}_{01}-c_1^2{I}_6\left(\frac{{\partial }^2{\ddot{w}}_{01}}{\partial x_1^2}+\frac{{\partial }^2{\ddot{w}}_{01}}{\partial y_1^2}\right)+c_1{I}_3\left(\frac{\partial {\ddot{u}}_{01}}{\partial x_1}+\frac{\partial {\ddot{v}}_{01}}{\partial y_1}\right)+c_1{J}_4\left(\frac{{\partial }^2{\ddot{\phi }}_{x_1}}{\partial x_1}+\frac{{\partial }^2{\ddot{\phi }}_{y_1}}{\partial y_1}\right),\\ (D_{11}-2c_1{F}_{11}-c_1^2{H}_{11})\frac{{\partial }^2{\phi }_{x1}}{\partial x_1^2}+(D_{12}+D_{66}-c_1^2{H}_{66}-2c_1{F}_{66}+c_1^2{F}_{12})\frac{{\partial }^2{\phi }_{y1}}{\partial x_1\partial y_1}\\ (D_{66}-2c_1{F}_{66}-c_1^2{H}_{66})\frac{{\partial }^2{\phi }_{x1}}{\partial y_1^2}+\left(2c_2{D}_{55}-A_{55}-c_2^2{F}_{55}\right){\phi }_{x1}\\ -c_1(F_{11}-c_1{H}_{11})\frac{{\partial }^3{w}_{01}}{\partial x_1^3}-\left(c_2^2{F}_{55}-2c_2{D}_{55}+A_{55}\right)\frac{\partial w_{01}}{\partial x_1}\\ -c_1(2F_{66}+F_{12}-2c_1{H}_{66}-c_1{H}_{12})\frac{{\partial }^3{w}_{01}}{\partial x_1\partial y_1^2}\end{array}$$

(8c)

$$=(I_1-c_1{I}_3){\ddot{u}}_{01}+\left(I_2-2c_1{I}_4+c_1^2{I}_6\right){\ddot{\phi }}_{x_1}-c_1\left(I_4-c_1{I}_6\right)\frac{\partial {\ddot{w}}_{01}}{\partial x_1},$$

(8d)

$$\begin{array}{c}(D_{22}-2c_1{F}_{22}+c_1^2{H}_{22})\frac{{\partial }^2{\phi }_{x1}}{\partial y_1^2}-c_1\left(F_{22}-c_1{H}_{22}+A_{55}\right)\frac{{\partial }^3{w}_{01}}{\partial y_1^3}\\ +(D_{21}+D_{66}+c_1^2{H}_{66}+c_1^2{H}_{21}-2c_1{F}_{66}-2c_1{F}_{21})\frac{{\partial }^2{\phi }_{x1}}{\partial x_1\partial y_1}\\ +(D_{66}-2c_1{F}_{66}+c_1^2{H}_{66})\frac{{\partial }^2{\phi }_{y1}}{\partial x_1^2}+\left(2c_2{D}_{44}-c_2^2{F}_{44}-A_{44}\right){\phi }_{y1}\\ -\left(c_2^2{F}_{44}-2c_2{D}_{44}+A_{44}\right)\frac{\partial w_{01}}{\partial y_1}-c_1\left(2F_{66}+F_{12}-2c_1{H}_{66}-c_1{H}_{21}\right)\frac{{\partial }^3{w}_{01}}{\partial x_1^2\partial y_1}\\ =(I_1-c_1{I}_3){\ddot{v}}_{01}+\left(I_2-2c_1{I}_4+c_1^2{I}_6\right){\ddot{\phi }}_{y1}-c_1\left(I_4-c_1{I}_6\right)\frac{\partial {\ddot{w}}_{01}}{\partial y_1},\end{array}$$

(8e)

where

$$I_1^{*}=(I_1-c_1{I}_3),I_2^{*}=\left(I_2-2c_1{I}_4+c_1^2{I}_6\right),I_3^{*}=(I_4-c_1{I}_6).$$

(8f)

For the outer plate $O_2$:

$$\begin{array}{c}{A}_{11}\frac{{\partial }^2{u}_{02}}{\partial x_2^2}+A_{66}\frac{{\partial }^2{u}_{02}}{\partial y_2^2}+\left(A_{12}+A_{66}\right)\frac{{\partial }^2{v}_{02}}{\partial x_2\partial y_2}+A_{11}\frac{\partial w_{02}}{\partial x_{21}}\frac{{\partial }^2{w}_{01}}{\partial x_2^2}\\ A_{66}\frac{\partial w_{02}}{\partial x_2}\frac{{\partial }^2{w}_{02}}{\partial y_2^2}+\left(A_{12}+A_{66}\right)\frac{\partial w_{02}}{\partial y_2}\frac{{\partial }^2{w}_{02}}{\partial x_2\partial y_2}\\ =I_2{\ddot{u}}_{02}+\left(I_1-c_1{I}_3\right){\ddot{\phi }}_{x_2}-c_1{I}_3\frac{\partial {\ddot{w}}_{02}}{\partial x_2},\end{array}$$

(9a)

$$\begin{array}{c}{A}_{22}\frac{{\partial }^2{v}_{02}}{\partial y_2^2}+A_{66}\frac{{\partial }^2{v}_{02}}{\partial x_2^2}+\left(A_{21}+A_{66}\right)\frac{{\partial }^2{u}_{02}}{\partial x_2\partial y_2}\\ A_{66}\frac{\partial w_{02}}{\partial y_2}\frac{{\partial }^2{w}_{02}}{\partial x_2^2}+A_{22}\frac{\partial w_{02}}{\partial y_2}\frac{{\partial }^2{w}_{02}}{\partial y_2^2}+\left(A_{21}+A_{66}\right)\frac{\partial w_{02}}{\partial x_2}\frac{{\partial }^2{w}_{02}}{\partial x_2\partial y_2}\\ =I_2{\ddot{v}}_{02}+\left(I_1-c_1{I}_3\right){\ddot{\phi }}_{y_2}-c_1{I}_3\frac{\partial {\ddot{w}}_{02}}{\partial y_2}\end{array}$$

(9b)

$$\begin{array}{c}{A}_{11}\frac{\partial u_{02}}{\partial x_2}\frac{{\partial }^2{w}_{02}}{\partial x_2^2}+A_{21}\frac{\partial u_{02}}{\partial x_2}\frac{{\partial }^2{w}_{02}}{\partial y_1^2}+2A_{66}\frac{\partial u_{02}}{\partial y_2}\frac{{\partial }^2{w}_{02}}{\partial x_2\partial y_2}+A_{11}\frac{{\partial }^2{u}_{01}}{\partial x_2^2}\frac{\partial w_{02}}{\partial x_2}\\ +\left(A_{21}+A_{66}\right)\frac{{\partial }^2{u}_{02}}{\partial x_2\partial y_2}\frac{\partial w_{02}}{\partial y_2}+A_{66}\frac{{\partial }^2{v}_{02}}{\partial x_2^2}\frac{\partial w_{02}}{\partial y_2}+\left(A_{12}+A_{66}\right)\frac{{\partial }^2{v}_{02}}{\partial x_2\partial y_2}\frac{\partial w_{02}}{\partial x_2}\\ +A_{22}\frac{{\partial }^2{v}_{02}}{\partial y_2^2}\frac{\partial w_{02}}{\partial y_2}+\frac{3}{2}{A}_{11}{\left(\frac{\partial w_{02}}{\partial x_2}\right)}^2\frac{{\partial }^2{w}_{02}}{\partial x_2^2}+\left(\frac{1}{2}{A}_{21}+A_{66}\right){\left(\frac{\partial w_{02}}{\partial x_2}\right)}^2\frac{{\partial }^2{w}_{02}}{\partial y_2^2}\\ +\left(A_{12}+A_{21}+4A_{66}\right)\frac{\partial w_{02}}{\partial x_2}\frac{\partial w_{02}}{\partial y_2}\frac{{\partial }^2{v}_{02}}{\partial x_2\partial y_2}+\frac{3}{2}{A}_{11}{\left(\frac{\partial w_{02}}{\partial y_2}\right)}^2\frac{{\partial }^2{w}_{02}}{\partial y_2^2}\\ +\left(\frac{1}{2}{A}_{12}+A_{66}\right){\left(\frac{\partial w_{02}}{\partial y_2}\right)}^2\frac{{\partial }^2{w}_{02}}{\partial x_2^2}-c_1^2{H}_{11}\frac{{\partial }^4{w}_{02}}{\partial x_2^4}\\ +\left(A_{55}-2c_2{D}_{55}+c_2^2{F}_{55}-N_x^p\cos \left({\mathsf{\Omega }}_{2}t\right)\right)\frac{{\partial }^2{w}_{02}}{\partial x_2^2}\\ +\left(A_{44}-2c_2{D}_{44}+c_2^2{F}_{44}-N_x^p\cos \left({\mathsf{\Omega }}_{3}t\right)\right)\frac{{\partial }^2{w}_{02}}{\partial y_2^2}\\ -c_1^2(H_{21}+4H_{11}+H_{12})\frac{{\partial }^4{w}_{02}}{\partial x_2^2\partial y_2^2}+c_1\left(F_{11}-c_1{H}_{11}\right)\frac{{\partial }^3{\phi }_{x2}}{\partial x_2^3}\\ +\left(A_{55}-2c_2{D}_{55}+c_2^2{F}_{55}\right)\frac{\partial {\phi }_{x2}}{\partial x_2}-c_1^2{H}_{22}\\ +c_1\left(F_{12}+2F_{66}-c_1{H}_{21}-2c_1{H}_{66}\right)\frac{{\partial }^3{\phi }_{x2}}{\partial x_2\partial y_2^2}\\ +\left(A_{44}-2c_2{D}_{44}+c_2^2{F}_{44}\right)\frac{\partial {\phi }_{y2}}{\partial y_2}\\ +c_1\left(F_{22}+2F_{66}-c_1{H}_{21}-2c_1{H}_{66}\right)\frac{{\partial }^3{\phi }_{y2}}{\partial x_2\partial y_2^2}\\ +c_1\left(F_{22}-c_1{H}_{22}\right)\frac{{\partial }^3{\phi }_{y2}}{\partial y_2^3}+\Delta p-\gamma {\dot{w}}_{02}+(F_0+F_1\cos \left({\mathsf{\Omega }}_{1}t\right))\\ =I_0{\ddot{w}}_{02}-c_1^2{I}_6(\frac{{\partial }^2{\ddot{w}}_{02}}{\partial x_2^2}+\frac{{\partial }^2{\ddot{w}}_{02}}{\partial y_2^2})+c_1{I}_3(\frac{\partial {\ddot{u}}_{02}}{\partial x_2}+\frac{\partial {\ddot{v}}_{02}}{\partial y_2})+c_1{J}_4(\frac{\partial {\ddot{\phi }}_{x2}}{\partial x_2}+\frac{\partial {\ddot{\phi }}_{y2}}{\partial y_2}),\end{array}$$

(9c)

$$\begin{array}{c}\left(D_{11}+2c_1{F}_{11}-c_1^2{H}_{11}\right)\frac{{\partial }^2{\phi }_{x2}}{\partial x_2^2}-c_1\left(F_{11}-c_1{H}_{11}\right)\frac{{\partial }^3{w}_{02}}{\partial x_2^3}\\ +\left(D_{12}+D_{66}+c_1^2{H}_{66}-2c_1{F}_{66}+c_1^2{F}_{12}\right)\frac{{\partial }^2{\phi }_{y2}}{\partial x_2\partial y_2}\\ +\left(D_{66}-2c_1{F}_{66}+c_1^2{H}_{66}\right)\frac{{\partial }^2{\phi }_{x2}}{\partial y_2^2}+\left(2c_2{D}_{55}-A_{55}-c_2^2{F}_{22}\right){\phi }_{x2}\\ -\left(c_2^2{F}_{55}-2c_2{D}_{55}+A_{55}\right)\frac{\partial {\phi }_{02}}{\partial x_2}-c_1\left(2F_{66}+F_{12}-2c_1{H}_{66}-c_1{H}_{12}\right)\frac{{\partial }^3{w}_{02}}{\partial x_2\partial y_2^3}\\ =\left(I_1-c_1{I}_3\right){\ddot{u}}_{02}+\left(I_2-2c_1{I}_4+c_1^2{I}_6\right){\ddot{\phi }}_{x2}-c_1\left(I_4-c_1{I}_6\right)\frac{{\ddot{\partial w}}_{02}}{\partial x_2},\end{array}$$

(9d)

$$\begin{array}{c}\left(D_{22}-2c_1{F}_{22}+c_1^2{H}_{22}\right)\frac{{\partial }^2{\phi }_{x2}}{\partial y_2^2}-c_1\left(F_{22}-c_1{H}_{22}\right)\frac{{\partial }^3{w}_{02}}{\partial y_2^3}\\ +\left(D_{21}+D_{66}+c_1^2{H}_{66}+c_1^2{H}_{21}-2c_1{F}_{66}-2c_1{F}_{21}\right)\frac{{\partial }^2{\phi }_{x2}}{\partial x_2\partial y_2}\\ +\left(D_{66}-2c_1{F}_{66}+c_1^2{H}_{66}\right)\frac{{\partial }^2{\phi }_{y2}}{\partial x_2^2}+\left(2c_2{D}_{44}-c_2^2{F}_{44}-A_{44}\right){\phi }_{y2}\\ -\left(c_2^2{F}_{44}-2c_2{D}_{44}+A_{44}\right)\frac{\partial w_{02}}{\partial y_2}-c_1\left(2F_{66}+F_{12}-2c_1{H}_{66}-c_1{H}_{21}\right)\frac{{\partial }^3{w}_{02}}{\partial x_2^2\partial y_2}\\ =I_1-c_1{I}_3{\ddot{v}}_{02}+\left(I_2-2c_1{I}_4+c_1^2{I}_6\right){\ddot{\phi }}_{y2}-c_1\left(I_4-c_1{I}_6\right)\frac{\partial {\ddot{w}}_{02}}{\partial y_2}\end{array}$$

(9e)

For the rectangular cantilever plate fixed at $x=0$ and clamped at $L\left(0\right)$ with the other edges $L$ free, the boundary conditions can be expressed as follows:

$$x_1=0,L\left(0\right),u=v=w={\phi }_x={\phi }_y=0,$$

(10a)

$$\begin{array}{c}{x}_2=L,N_{xx}=N_{yy}=M_{xx}=M_{xy}=0,\\ P_{xx}=P_{xy}=Q_x=R_x=0\end{array}$$

(10b)

$$\begin{array}{c}y=0,b, N_{yy}=N_{xy}=M_{yy}=M_{xy}=0,\\ P_{yy}=P_{xy}=Q_y=R_y=0.\end{array}$$

(10c)

The connection conditions are represented as follows;

$$x_1=L\left(0\right),\frac{w_{01}\left(L\left(0\right)\right)}{\partial x_1}\frac{{\partial }^2{w}_{01}\left(L\left(0\right)\right)}{\partial t\partial x_1}=0,$$

(10d)

$$x_2=L\left(0\right),\frac{w_{02}\left(L\left(0\right)\right)}{\partial x_2}\frac{{\partial }^2{w}_{02}\left(L\left(0\right)\right)}{\partial t\partial x_2}=0.$$

(10e)

3. Two-Mode Nonlinear System

The variables and parameters can be expressed as follows:

$$\begin{array}{c}{\overline{u}}_0=\frac{u_0}{a},{\overline{v}}_0=\frac{v_0}{b},{\overline{w}}_0=\frac{w_0}{h},\overline{x}=\frac{x}{a},\overline{y}=\frac{y}{b},{\overline{\mathsf{\phi }}}_x={\mathsf{\phi }}_x,{\overline{\mathsf{\phi }}}_y={\mathsf{\phi }}_y,\\ {\overline{I}}_i=\frac{1}{{\left(ab\right)}^{\left(i+1\right)/2}\mathsf{\rho }}{I}_i,\overline{t}={\pi }^2{\left(\frac{E}{ab\mathsf{\rho }}\right)}^{1/2}t,\overline{F}=\frac{{\left(ab\right)}^{7/2}}{E{h}^7}F,\overline{P}=\frac{b^2}{E{h}^3}P,\\ \overline{\gamma }=\frac{1}{\sqrt{\mathsf{\rho }\mathrm{E}}}\frac{a^2{b}^2}{h^4}\gamma ,{\overline{ A}}_{ij}=\frac{{\left(ab\right)}^{1/2}}{E{h}^2}{A}_{ij},{\overline{ B}}_{ij}=\frac{{\left(ab\right)}^{1/2}}{E{h}^3}{B}_{ij},{\overline{D}}_{ij}=\frac{{\left(ab\right)}^{1/2}}{E{h}^4}{D}_{ij},\\ {\overline{E}}_{ij}=\frac{{\left(ab\right)}^{1/2}}{E{h}^5}{E}_{ij},{\overline{F}}_{ij}=\frac{{\left(ab\right)}^{1/2}}{E{h}^6}{F}_{ij},{\overline{H}}_{ij}=\frac{{\left(ab\right)}^{1/2}}{E{h}^8}{H}_{ij}.\end{array}$$

(11)

In the following analysis, for convenience, the symbol “-” will be removed, and the first two modes of the nonlinear dynamics of this model are mainly considered. Considering the boundary condition of the model, the modal functions can be expressed as follows:

$$u_i=u_1\left(t\right)\sin \frac{\pi x}{2L_i}\cos \frac{\pi y}{b}+u_2\left(t\right)\sin \frac{3\pi x}{2L_i}\cos \frac{2\pi y}{b},$$

(12a)

$$v_i=v_1\left(t\right)\sin \frac{\pi x}{2L_i}\sin \frac{\pi y}{b}+v_2\left(t\right)\sin \frac{3\pi x}{2L_i}\sin \frac{2\pi y}{b},$$

(12b)

$$w_i=w_1\left(t\right)X_{i1}\left(x\right)Y_1\left(y\right)+w_2\left(t\right)X_{i2}\left(x\right)Y_2\left(y\right),$$

(12c)

$${\phi }_{xi}={\phi }_{xi1}\left(t\right)\sin \frac{\pi x}{2L_i}\cos \frac{\pi y}{b}+{\phi }_{xi2}\left(t\right)\sin \frac{\pi x}{L_i}\cos \frac{2\pi y}{b},$$

(12d)

$${\phi }_{yi}={\phi }_{yi1}\left(t\right)\left(1-\cos \frac{\pi x}{2L_i}\right)\sin \frac{\pi y}{b}+{\phi }_{yi2}\left(t\right)\left(1-\cos \frac{\pi x}{L_i}\right)\sin \frac{2\pi y}{b},$$

(12e)

where $X_{ij}\left(x\right)$ represents the fixed-free beam function in the direction of $x$, and $Y_{ij}\left(y\right)$ denotes the free-free beam function in the direction of $y$:

$$X_{ij}\left(x\right)=sin\frac{{\lambda }_{ij}x}{L_i}-sinh\frac{{\lambda }_{ij}x}{L_i}+{\alpha }_i\left(cos\frac{{\lambda }_{ij}x}{L_i}-cos\frac{{\lambda }_{ij}x}{L_i}\right)$$

(13a)

$$Y_{ij}\left(y\right)=sin\frac{{\mu }_{ij}y}{b}+sinh\frac{{\mu }_{ij}y}{b}+{\beta }_{ij}\left(cosh\frac{{\mu }_{ij}y}{b}+cos\frac{{\mu }_{ij}y}{b}\right)$$

(13b)

${\lambda }_{ij}$ and ${\mu }_{ij}$ are the eigenvalues given by the roots of the transcendental equations

$$\mathrm{c}os{\lambda }_{ij}a·cosh{\lambda }_{ij}a+1=0,cos{\mu }_{ij}b·cosh{\mu }_{ij}b-1=0,$$

(14a)

and

$${\alpha }_{ij}=\frac{sin{\lambda }_{ij}a+sin{\lambda }_{ij}a}{cosh{\lambda }_{ij}a+cos{\lambda }_{ij}a},{\beta }_{ij}=\frac{sinh{\mu }_{ij}{L}_i-sin{\mu }_{ij}{L}_i}{cosh{\mu }_{ij}{L}_i-cos{\mu }_{ij}{L}_i}$$

(14b)

Equations (11), (12a)–(12e), (13a), (13b), (14a) and (14b) are substituted into Equations (8a)–(8e) and (9a)–(9e) with the aid of the boundary conditions and the application of Galerkin’s method, mainly considering the transverse nonlinear oscillations. Therefore, a two degrees-of-freedom governing differential equation of the composite laminated piezoelectric stepped rectangular cantilever plate is derived as follows.

For the inner plate $O_1$:

$$\begin{array}{c}{\ddot{w}}_{11}\left(t\right)+{\omega }_1{}^2{w}_{11}+a_{11}{\dot{w}}_{11}\left(t\right)+a_{12}cos\left({\Omega }_{1}t\right)w_{11}\left(t\right)\\ +a_{13}\cos \left({\Omega }_{2}t\right)w_{11}\left(t\right)+a_{14}cos\left({\Omega }_{3}t\right)w_{11}\left(t\right)\\ +a_{15}{w}_{11}{}^2{w}_{12}+a_{16}{w}_{11}{w}_{12}{}^2+a_{17}{w}_{11}{}^3+a_{18}{w}_{12}{}^3=0,\end{array}$$

(15a)

$$\begin{array}{c}{\ddot{w}}_{12}\left(t\right)+{\omega }_2{}^2{w}_{12}+b_{11}{\dot{w}}_{12}\left(t\right)+b_{12}cos\left({\Omega }_{1}t\right)w_{12}\left(t\right)\\ +a_{13}\cos \left({\Omega }_{2}t\right)w_{11}\left(t\right)+a_{14}cos\left({\Omega }_{3}t\right)w_{11}\left(t\right)\\ +b_{15}{w}_{12}{}^2{w}_{11}+b_{16}{w}_{11}{}^2{w}_{12}+b_{17}{w}_{12}{}^3+b_{18}{w}_{11}{}^3=0\end{array}$$

(15b)

For the outer plate $O_2$:

$$\begin{array}{c}{\ddot{w}}_{21}\left(t\right)+{\omega }_1{}^2{w}_{21}+a_{21}{\dot{w}}_{21}\left(t\right)+a_{22}cos\left({\Omega }_{1}t\right)w_{21}\left(t\right)\\ +a_{23}\cos \left({\Omega }_{2}t\right)w_{21}\left(t\right)+a_{24}cos\left({\Omega }_{3}t\right)w_{21}\left(t\right)\\ +a_{25}{w}_{21}{}^2{w}_{22}+a_{26}{w}_{21}{w}_{22}{}^2+a_{27}{w}_{21}{}^3+a_{28}{w}_{22}{}^3=0,\end{array}$$

(16a)

$$\begin{array}{c}{\ddot{w}}_{22}\left(t\right)+{\omega }_2{}^2{w}_{22}+b_{21}{\dot{w}}_{22}\left(t\right)+b_{22}cos\left({\Omega }_{1}t\right)w_{22}\left(t\right)\\ +a_{23}\cos \left({\Omega }_{2}t\right)w_{22}\left(t\right)+b_{24}cos\left({\Omega }_{3}t\right)w_{22}\left(t\right)\\ +b_{25}{w}_{22}{}^2{w}_{21}+b_{26}{w}_{21}{}^2{w}_{22}+b_{27}{w}_{22}{}^3+b_{28}{w}_{21}{}^3=0\end{array}$$

(16b)

where $a_{ij}$ and $b_{ij}\left(i=1,2;j=1,\hspace{1em},8\right)$ are non- dimensional coefficients; all coefficients are given in Appendix A.

Equations (15a), (15b), (16a) and (16b), including the quadratic, cubic terms, and parametric excitations, describe the nonlinear vibration of the model in the first two modes.

4. Averaged Equations in Polar Form and Cartesian Form

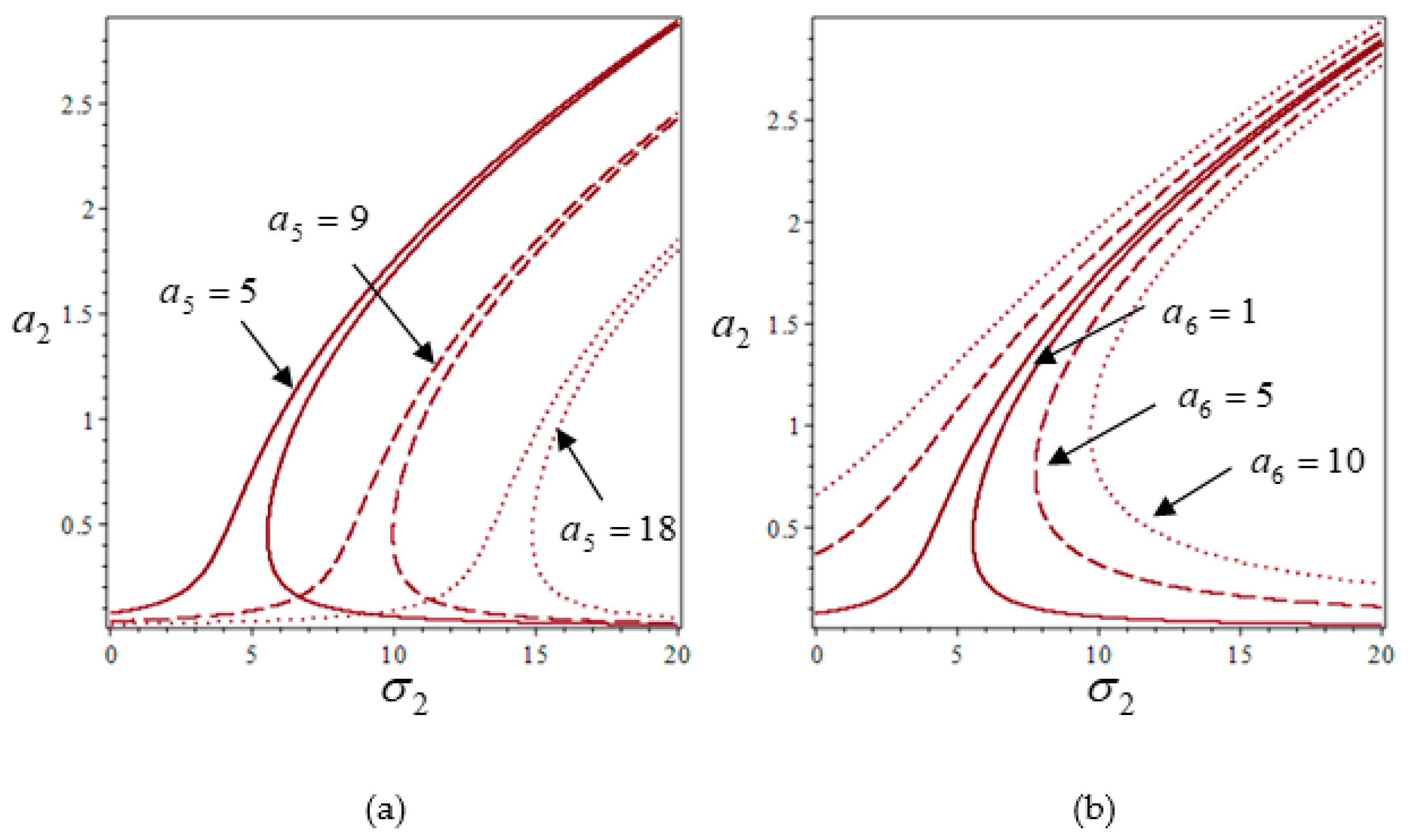
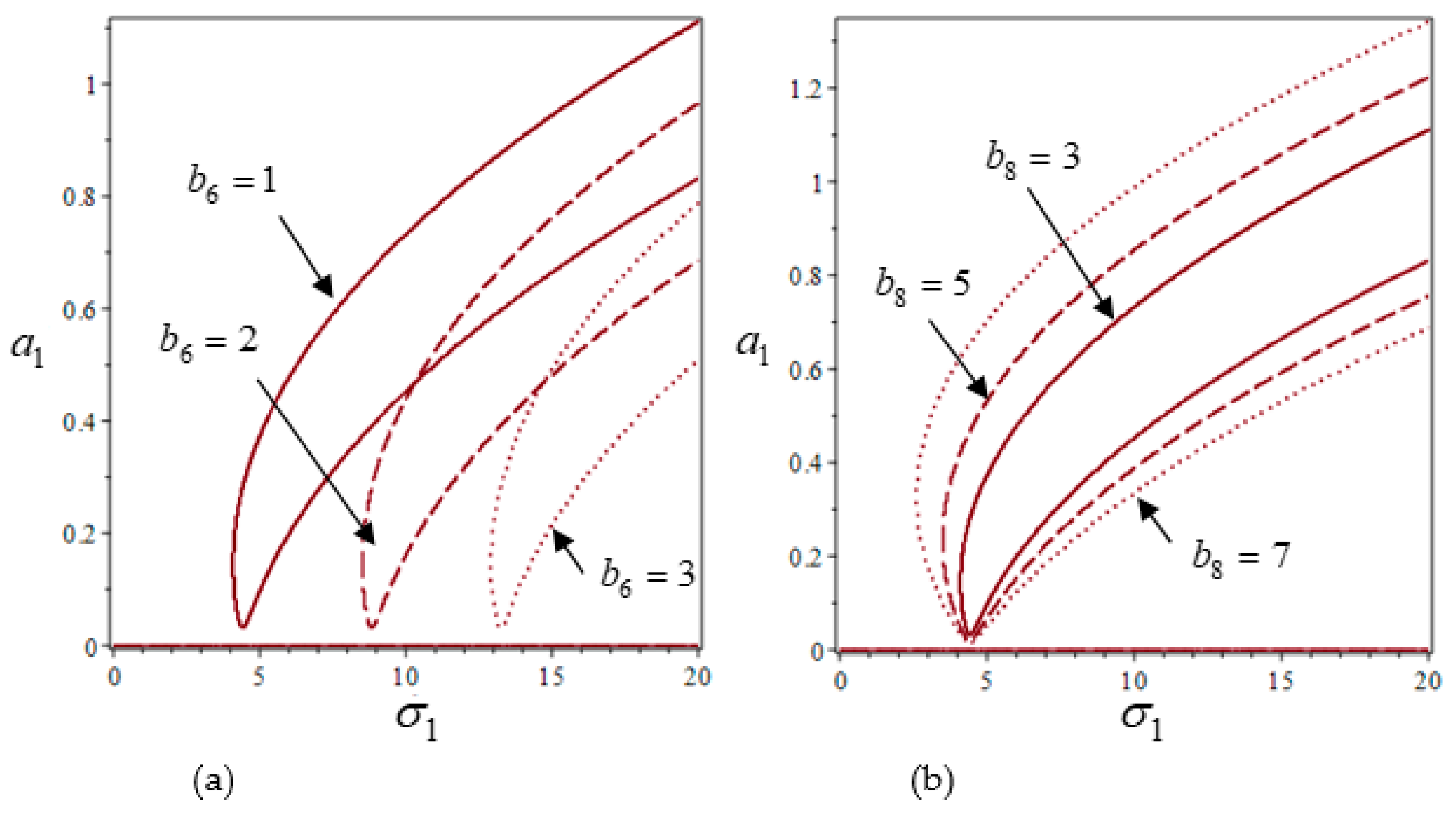
4.1. The Polar Form Four-Dimensional Averaged Equations and Frequency Response Analysis

In order to perform perturbation analysis of Equations (15) and (16), the following multi-scale transformation $a_{ij}\to \epsilon a_{ij}$, $b_{ij}\to \epsilon b_{ij}$ is introduced; Equations (13) and (14) are substituted into equations of motion with small parameters. Then, the multi-scale method is used to find an approximate solution of the original non-autonomous system as follows:

$$x_n\left(t,\mathsf{\epsilon }\right)=x_{n0}\left(T_0,T_1\right)+\mathsf{\epsilon }{x}_{n1}\left(T_0,T_1\right)+\cdots ,n=1,2,$$

(17)

where $T_0=t$,$T_1=\epsilon t$..

Then, the differential operators are as follows:

$$\frac{d}{dt}=\frac{\partial }{\partial T_0}\frac{\partial T_0}{\partial t}+\frac{\partial }{\partial T_1}\frac{\partial T_1}{\partial t}+\cdots =D_0+\mathsf{\epsilon }{D}_1+\cdots ,$$

(18a)

$$\frac{d^2}{d{t}^2}={\left(D_0+\mathsf{\epsilon }{D}_1+\cdots \right)}^2=D_0^2+2\mathsf{\epsilon }{D}_0{D}_1+\cdots$$

(18b)

where $D_0=\frac{\partial }{\partial T_0}$, $D_1=\frac{\partial }{\partial T_1}$.

The case of primary parametric resonance and 1:3 internal resonance are considered, the relationships are as follows:

$${\mathsf{\omega }}_1^2=\frac{1}{9}{\mathsf{\Omega }}^2+{\mathsf{\epsilon }\mathsf{\sigma }}_1,{\omega }_2^2={\mathsf{\Omega }}^2+{\mathsf{\epsilon }\mathsf{\sigma }}_2,{\mathsf{\Omega }}_1={\mathsf{\Omega }}_2={\mathsf{\Omega }}_3=\frac{2}{3}\mathsf{\Omega }$$

(19)

By inserting Equations (17), (18a) and (18b) into Equations (15a), (15b), (16a) and (16b) and balancing the coefficient of ε on the left side and right side of the corresponding equations, the acquired differential equations are given by

Order ${\mathsf{\epsilon }}^0$

$$D_0^2{x}_{10}+\frac{1}{9}{\mathsf{\omega }}_1^2{x}_{10}=0,$$

(20a)

$$D_0^2{x}_{20}+{\mathsf{\omega }}_2^2{x}_{20}=0$$

(20b)

Order ${\mathsf{\epsilon }}^1$

$$\begin{array}{c}{D}_0^2{x}_{11}+\frac{1}{9}{\omega }_1^2{x}_{11}=-a_1{D}_0{x}_{10}-{\sigma }_1{x}_{10}-f_1\mathit{cos}({\Omega }_{1}t)x_{10}-a_3\mathit{cos}({\Omega }_{2}t)x_{10}\\ -a_4\mathit{cos}({\Omega }_{3}t)x_{10}-a_5{x}_{10}^2{x}_{20}-a_6{x}_{10}{x}_{20}^2-a_7{x}_{10}^3-a_8{x}_{20}^3-2D_1{D}_0{x}_{10},\end{array}$$

(21a)

$$\begin{array}{c}{D}_0^2{x}_{21}+{\omega }_2^2{x}_{21}=b_1{D}_0{x}_{20}-{\sigma }_2{x}_{20}-f_2\mathit{cos}({\Omega }_{1}t)x_{20}-b_3\mathit{cos}({\Omega }_{2}t)x_{20}\\ -b_4\mathit{cos}({\Omega }_{3}t)x_{20}-b_5{x}_{10}{x}_{20}^2-b_6{x}_{10}^2{x}_{20}-b_7{x}_{20}^3-b_8{x}_{10}^3-2D_1{D}_0{x}_{20},\end{array}$$

(21b)

The solution of Equation (20) in the complex form is given by

$$x_{10}=A_1\left(T_1\right)e^{-\frac{1}{3}\omega T_0}+{\overline{A}}_1\left(T_1\right)e^{-\frac{1}{3}\omega T_0}$$

(22a)

$$x_{20}=A_2\left(T_1\right)e^{\omega T_0}+{\overline{A}}_2\left(T_1\right)e^{-\omega T_0}$$

(22b)

where the conjugates of $A$ and $B$ are ${\overline{A}}_1$ and ${\overline{A}}_2$, respectively.

The following two expressions can be obtained by substituting Equations (22a) and (22b) into Equation (21a) and (21b),

$$\begin{array}{c}{D}_0^2{x}_{10}+\frac{1}{9}{\omega }_1^2{x}_{10}=(-\frac{1}{3}{\rm I}{a}_1{\omega }_1{A}_1-{\sigma }_1{A}_1-\frac{1}{2}\left(f_1+a_3+a_4\right){\overline{A}}_1-a_5{\overline{A}}_1^2{A}_2-\\ 2a_6{A}_1{\left|A_2\right|}^2-3a_7{A}_1{\left|A_1\right|}^2-{\sigma }_1{A}_1-\frac{2}{3}{\rm I}d{A}_1)e^{i\frac{1}{3}\omega T_0}+cc+NST,\end{array}$$

(23a)

$$\begin{array}{c}{D}_0^2{x}_{20}+{\omega }_2^2{x}_{20}=(-{\rm I}{b}_1{A}_2-{\sigma }_2{A}_2-2b_6{\left|A_1\right|}^2{A}_2-3b_7{A}_2{\left|A_2\right|}^2-b_8{A}_1^3-\\ 2{\rm I}d{A}_2)e^{i\omega T_0}+cc+NST,\end{array}$$

(23b)

where $cc$ represents the parts of the complex conjugates of the right side function of Equation (23), and $NST$ represents the terms that do not produce secular terms.

The polar form of the functions $A_1$, ${\overline{A}}_1$, $A_2$, and ${\overline{A}}_2$ expressed as follows

$$\begin{array}{c}{A}_1=\frac{1}{2}{\beta }_1{e}^{i{\phi }_1},{\overline{A}}_1=\frac{1}{2}{\beta }_1{e}^{-i{\phi }_1},\\ A_2=\frac{1}{2}{\beta }_2{e}^{i{\phi }_2},{\overline{A}}_2=\frac{1}{2}{\beta }_2{e}^{-i{\phi }_2},\end{array}$$

(24)

The real and imaginary parts are separated by substituting Equation (24) into Equation (23a), the polar coordinates form four-dimensional average equations, which are given by

$${\dot{a}}_{11}=-\frac{1}{2}{a}_1{a}_{11}-\frac{3}{8}{a}_5{a}_{11}^2{a}_{22}\mathit{sin}\left({\phi }_2-3{\phi }_1\right),$$

(25a)

$$a_{11}{\dot{\phi }}_1=-\frac{1}{3}{\sigma }_1{a}_{11}+\frac{3}{8}{a}_5{a}_{11}^2{a}_{22}\mathit{cos}\left({\phi }_2-3{\phi }_1\right)+\frac{3}{4}{a}_6{a}_{22}^2{a}_{11}+\frac{9}{8}{a}_7{a}_{11}^3,$$

(25b)

$${\dot{a}}_{22}=-\frac{1}{2}{b}_1{a}_{22}-\frac{1}{8}{b}_8{a}_{11}^3\mathit{sin}\left(3{\phi }_1-{\phi }_2\right),$$

(25c)

$$a_{22}{\dot{\phi }}_2=-{\sigma }_2{a}_{22}+\frac{1}{4}{b}_6{a}_{11}^2{a}_{22}+\frac{3}{8}{a}_7{a}_{22}^3+\frac{1}{8}{b}_8{a}_{11}^3\mathit{sin}\left(3{\phi }_1-{\phi }_2\right),$$

(25d)

when ${\dot{a}}_{11}$, ${\dot{a}}_{22}$ and ${\dot{\phi }}_1$, ${\dot{\phi }}_2$ are zero, and the parameters $a_{11}$, $a_{22}$ and ${\phi }_1$, ${\phi }_2$ are constant and denote the steady vibration of this model. By eliminating the trigonometric function including formula ${\phi }_2,-3{\phi }_1$, in Equation (25), the frequency response function of the structure under the conditions of primary parameter resonance and 1:3 internal res-onance can be obtained.

$${\left(\frac{a_1{a}_{11}}{2}\right)}^2+{\left(\frac{1}{3}{\sigma }_1{a}_{11}-\frac{9}{8}{a}_7{a}_{11}^3-\frac{3}{4}{a}_6{a}_{22}^2{a}_{21}\right)}^2={\left(\frac{3}{8}{a}_5{a}_{11}^2{a}_{22}\right)}^2$$

(26a)

$${\left(\frac{b_1{a}_{22}}{2}\right)}^2+{\left({\sigma }_2{a}_{22}-\frac{1}{4}{b}_6{a}_{11}^2{a}_{22}-\frac{3}{8}{b}_7{a}_{22}^3\right)}^2={\left(\frac{1}{8}{b}_8{a}_{11}^3\right)}^2$$

(26b)

We only consider the steady vibration of the first two modes under two coupling effects. The criteria for a weak coupling effect and a strong coupling effect are the following:

(1)

When the amplitude of the first-order mode is constant and the other first-order mode changes, there exists a weak coupling effect between the two modes when the excitation frequency changes.

(2)

When the amplitude of the two modes varies with the excitation frequency, there exists a strong coupling effect between the two modes.

For the convenience of operation, let $a_{22}=1$ in Equation (26a) and let $a_{11}=1$ in Equation (26b); the amplitude–frequency response of the two modes can be observed. The weak coupling effect between the two modes is considered by the frequency response function as follows:

$${\left(\frac{a_1{a}_{11}}{2}\right)}^2+{\left(\frac{1}{3}{\sigma }_1{a}_{11}-\frac{9}{8}{a}_7{a}_{11}^3-\frac{3}{4}{a}_6{a}_{22}^2{a}_{21}\right)}^2={\left(\frac{3}{8}{a}_5{a}_{11}^2\right)}^2$$

(27a)

$${\left(\frac{b_1{a}_{22}}{2}\right)}^2+{\left({\sigma }_2{a}_{22}-\frac{1}{4}{b}_6{a}_{11}^2{a}_{22}-\frac{3}{8}{b}_7{a}_{22}^3\right)}^2={\left(\frac{1}{8}{b}_8\right)}^2$$

(27b)

The frequency response curves of the two modes can be obtained under different parameters according to the frequency response function Equations (27a) and (27b). Through the analysis of numerous parameters, the shape and size of the amplitude–frequency response curve of the system can be changed by the different values of $a_5$, $a_{6 }$, $b_6$, $b_8$, and the rigidity of the system can be changed by the different symbols $a_7$ and $b_7$. The frequency response curves of the two modes, when $a_1=0.1$, $b_1=0.1$, $a_5=18$, $a_6=5$, $b_6=1$, $b_8=3$, with $a_7$ and $b_7$ taking different values, are shown in Figure 2. The frequency response curves of the first-order mode, with $b_7=5$ and $b_7=-5$, are shown in Figure 2a. The frequency response curves of the second-order mode, with $a_7=5$ and $a_7=-5$, are shown in Figure 2b. It can be seen from the Figure 2 that the system can exhibit different nonlinear stiffness characteristics with different parameters $a_7$, $b_7$, and symbols.

The frequency response curves of the second-order mode when $a_1=0.1$, $b_1=0.1$, $a_7=5$, $b_7=5$, $b_6=1$, $b_8=3$ with $a_5$ and $a_6$ taking different values are shown in Figure 3. The frequency response curves of the second-order mode with $a_7=5$, $a_5=9$, and $a_5=18$ are shown in Figure 3a. The frequency response curves of the second-order mode, with $a_6=1$, $a_6=5$, and $a_6=10$, are shown in Figure 3b. It can be seen from the figure that the amplitude–frequency response curves of the second-order mode shifts to the right with the increase in the parameter values $a_5$, $a_6$.

The frequency response curves of the first-order mode, when $a_1=0.1$, $b_1=0.1$, $a_5=18$, $a_6=5$, $a_7=5$, $b_7=5$, with $b_6$ and $b_8$ taking different values, are shown in Figure 3. The frequency response curves of the second-order mode, with $b_6=1$, $b_6=2$ and $b_6=3$, are shown in Figure 4a. The frequency response curves of the second-order mode, with $b_8=3$, $b_6=5$ and $b_6=7$, are shown in Figure 4b. It can be seen from Figure 4 that the parameters $b_6$, $b_8$ have little influence on the amplitude–frequency response curves of the second-order modes. With the increase in the parameter values, all of the amplitude–frequency response curves of the second-order modes shift to the right, and the amplitude–frequency response curves of the second-order mode are greatly affected.

4.2. Four-Dimensional Averaged Equations in Cartesian Form

The elimination of the secular terms of Equations (23a) and (23b) yields the average equations in complex form as follows,

$$\begin{array}{c}{D}_1{A}_1=-\frac{1}{2}{a}_1{A}_1+\frac{9}{2}I{a}_7{A}_1{\left|A_1\right|}^2+\frac{3}{2}I{\sigma }_1{A}_1+\frac{3}{2}I{a}_5{\overline{A}}_1^2{A}_2\\ +\frac{3}{4}I{f}_1{\overline{A}}_1+3I{a}_6{A}_1{\left|A_2\right|}^2+\frac{3}{4}I{a}_3{\overline{A}}_1+\frac{3}{4}I{a}_4{\overline{A}}_1,\end{array}$$

(28a)

$$D_1{A}_1=\frac{3}{2}I{b}_7{A}_2{\left|A_2\right|}^2+\frac{1}{2}{\sigma }_2{A}_2+\frac{1}{2}I{b}_8{A}_1^3+I{b}_6{\left|A_1\right|}^2{A}_2-\frac{1}{2}{b}_1{A}_2..$$

(28b)

The Cartesian form functions $A$ and $B$ are represented as follows,

$$A_1\left(T_1\right)=x_1\left(T_1\right)+i{x}_2\left(T_1\right)$$

(29a)

$$A_2\left(T_1\right)=x_3\left(T_1\right)+i{x}_4\left(T_1\right)$$

(29b)

Substituting Equations (29a) and (29b) into Equation (28a) and (28b), the Cartesian form averaged equations are given by

$$\begin{array}{c}\dot{x_1}=-\frac{1}{2}{a}_1{x}_1-\frac{9}{2}{a}_7{x}_2\left(x_1^2+x_2^2\right)-\frac{3}{2}{\sigma }_1{x}_2+3a_5{x}_1{x}_2{x}_3\\ -\frac{3}{2}{a}_5\left(x_1^2-x_2^2\right)x_4+\frac{3}{4}{x}_2{f}_1-3a_6{x}_2\left(x_3^2+x_4^2\right)+\frac{3}{4}{a}_3{x}_2+\frac{3}{4}{a}_4{x}_2,\end{array}$$

(30a)

$$\begin{array}{c}\dot{x_1}=-\frac{1}{2}{a}_1{x}_1+\frac{9}{2}{a}_7{x}_1\left(x_1^2+x_2^2\right)+\frac{3}{2}{\sigma }_1{x}_1+\frac{3}{2}{a}_5{x}_1{x}_2{x}_3+\frac{3}{2}{a}_5\left(x_1^2-x_2^2\right)x_3\\ +3a_5{x}_1{x}_2{x}_4+\frac{3}{4}{f}_1{x}_1+3a_6{x}_1\left(x_3^2+x_4^2\right)+\frac{3}{4}{a}_3{x}_1+\frac{3}{4}{a}_4{x}_1,\end{array}$$

(30b)

$$\begin{array}{c}\dot{x_3}=-\frac{3}{2}{a}_7{x}_1\left(x_3^2+x_4^2\right)-\frac{1}{2}{\sigma }_2{x}_4-\frac{1}{2}{b}_8\left(3x_1^2{x}_2-x_2^3\right)\\ -b_6\left(x_1^2+x_2^2\right)x_4-\frac{1}{2}{b}_1{x}_3,\end{array}$$

(30c)

$$\begin{array}{c}\dot{x_4}=\frac{3}{2}{b}_7{x}_3\left(x_3^2+x_4^2\right)+\frac{1}{2}{\sigma }_2{x}_3+\frac{1}{2}{b}_8\left(x_2^3-3x_1{x}_2^2\right)\\ +b_6\left(x_1^2+x_2^2\right)x_3-\frac{1}{2}{b}_1{x}_4\end{array}$$

(30d)

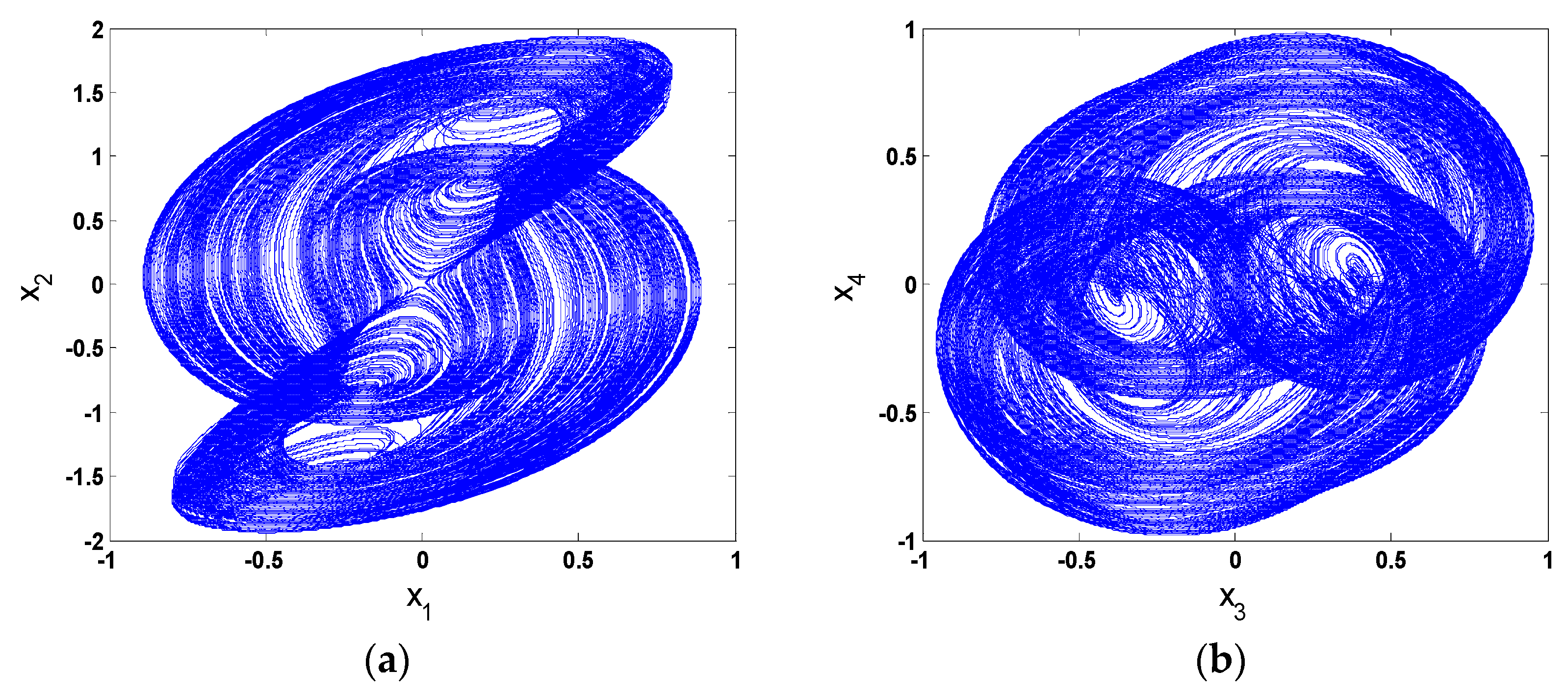
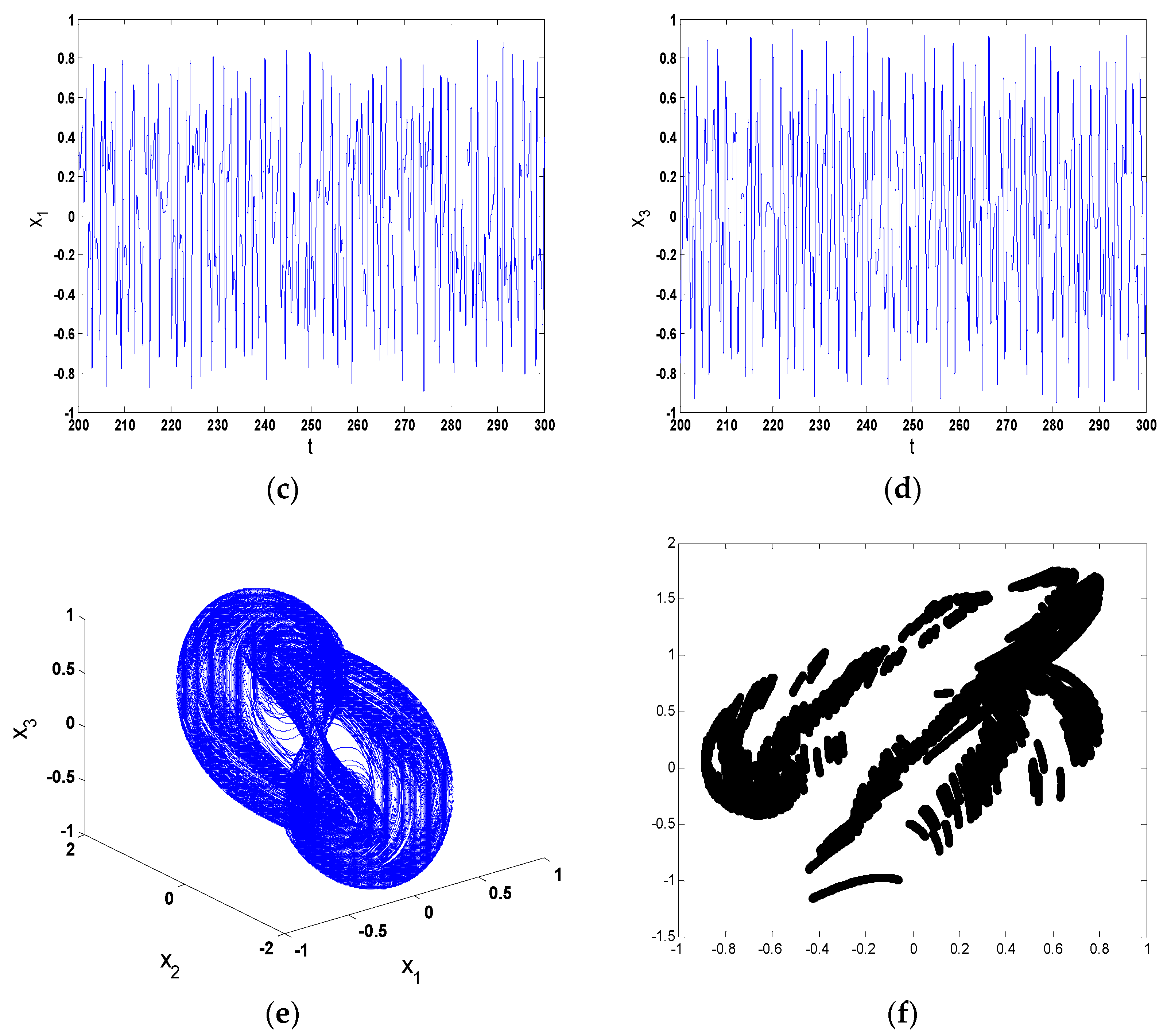
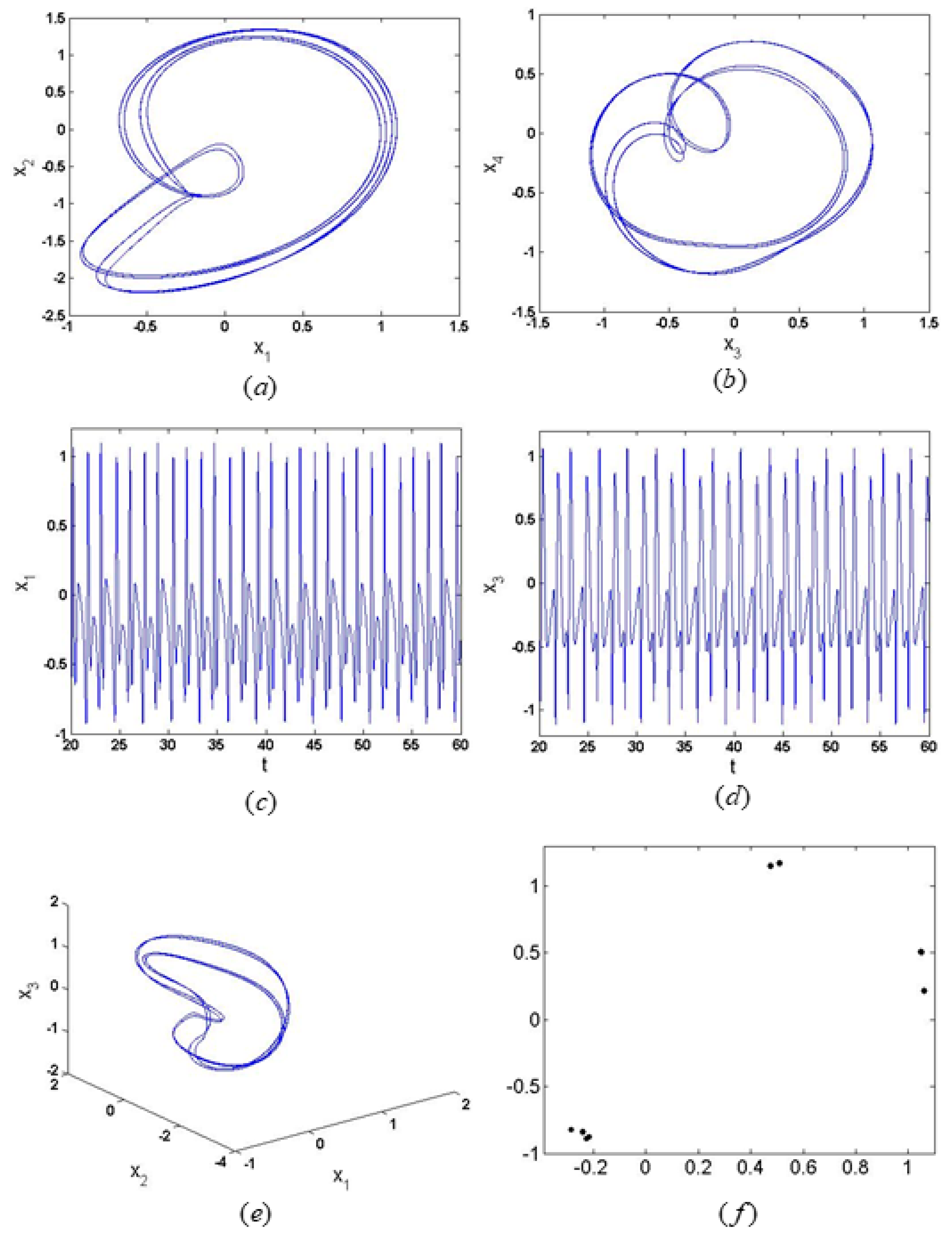
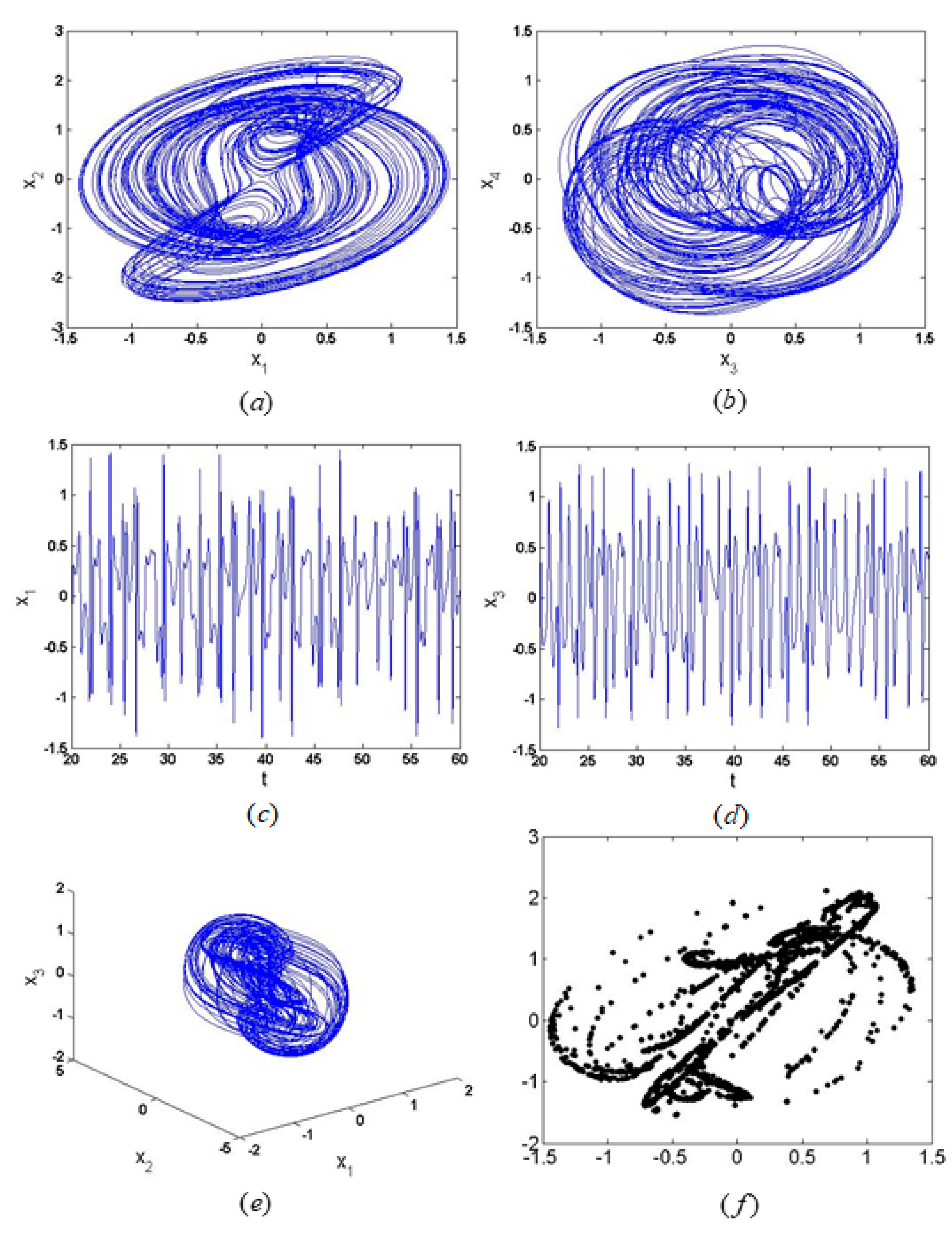
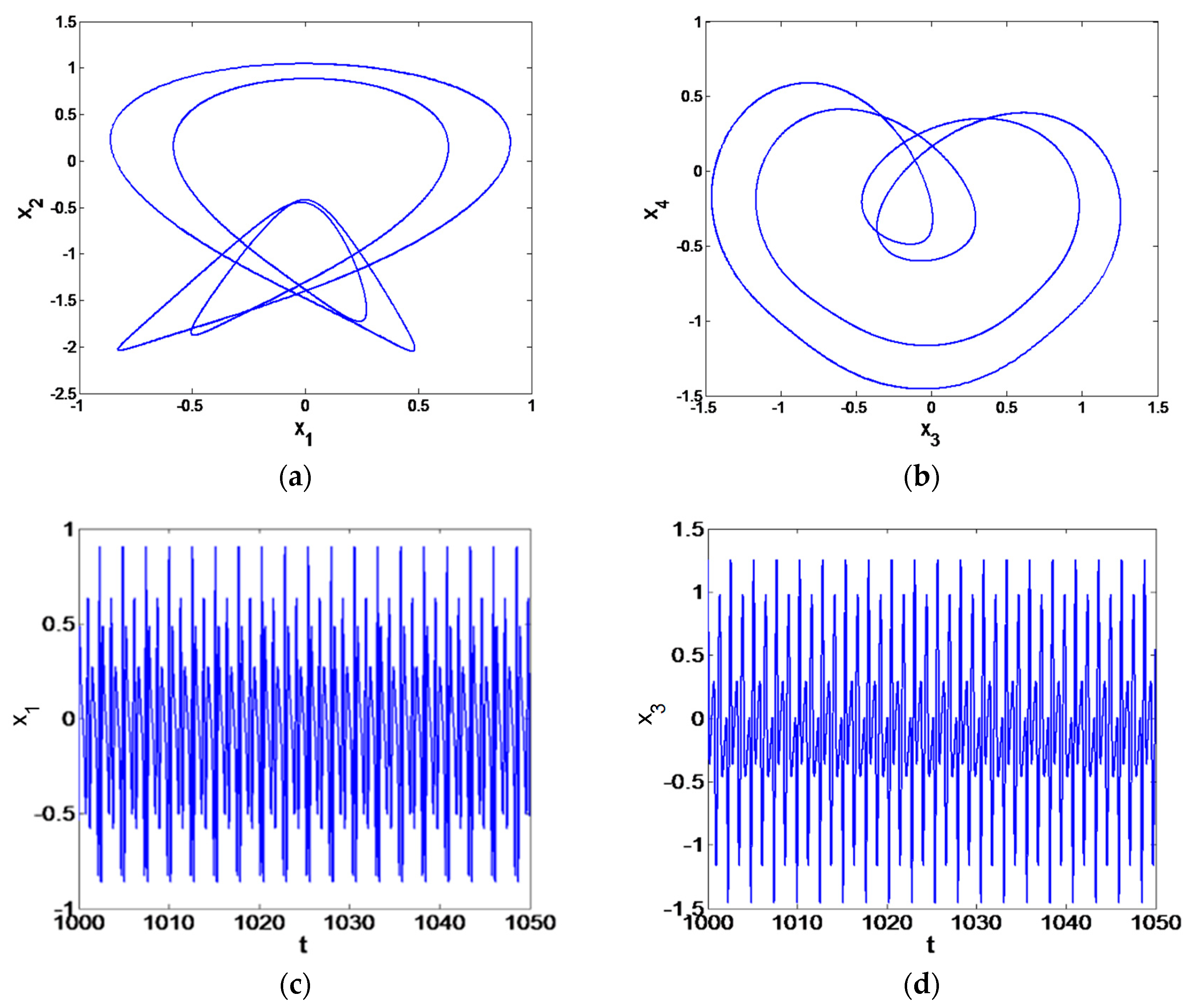
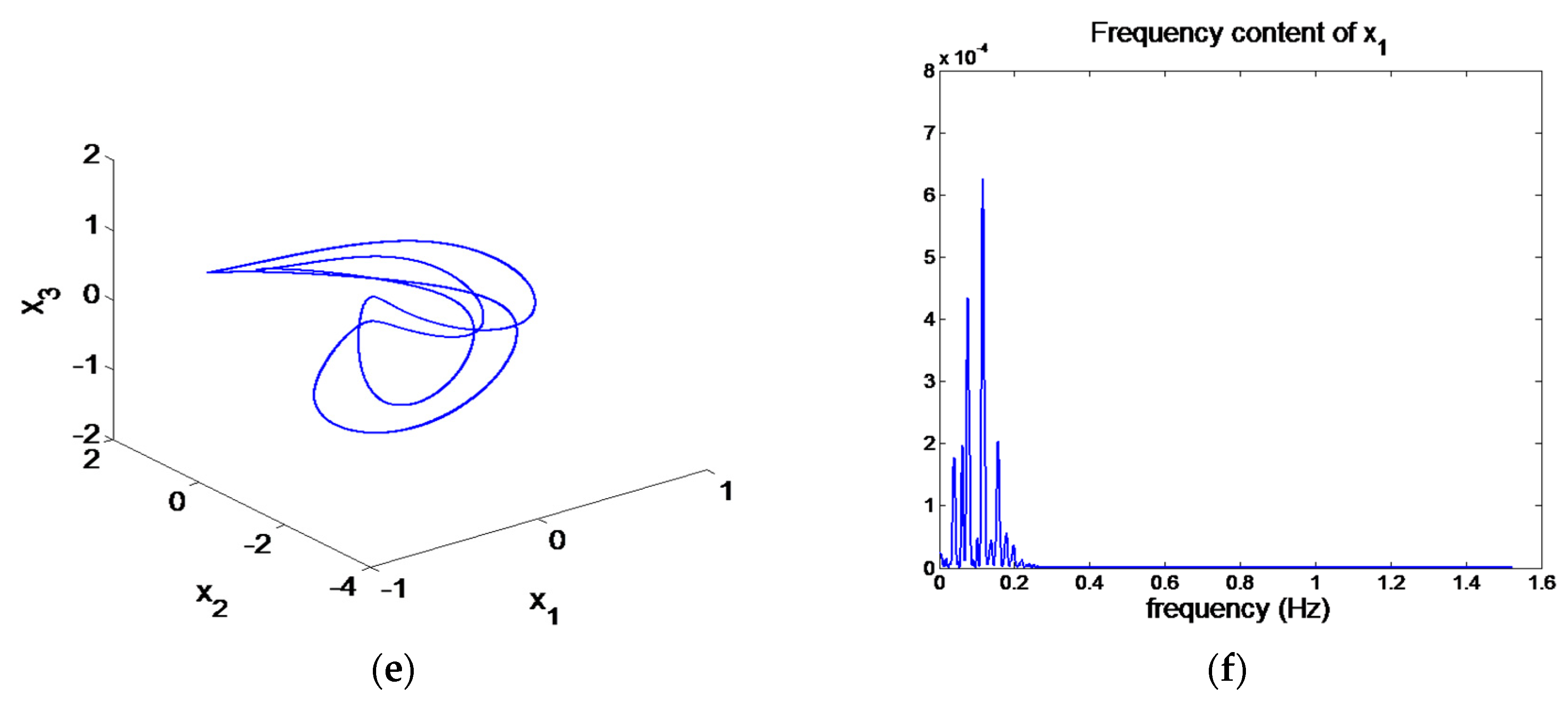
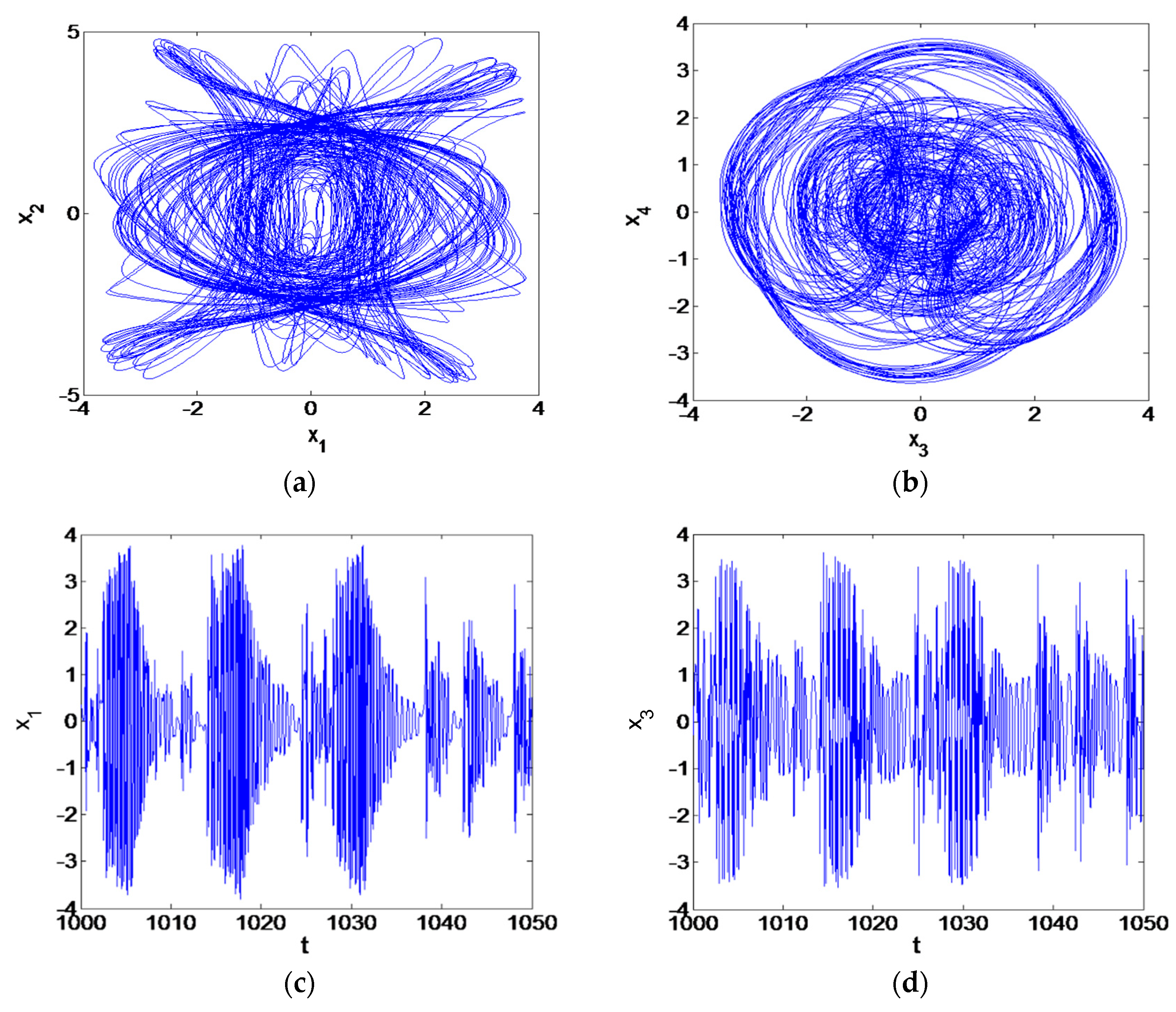
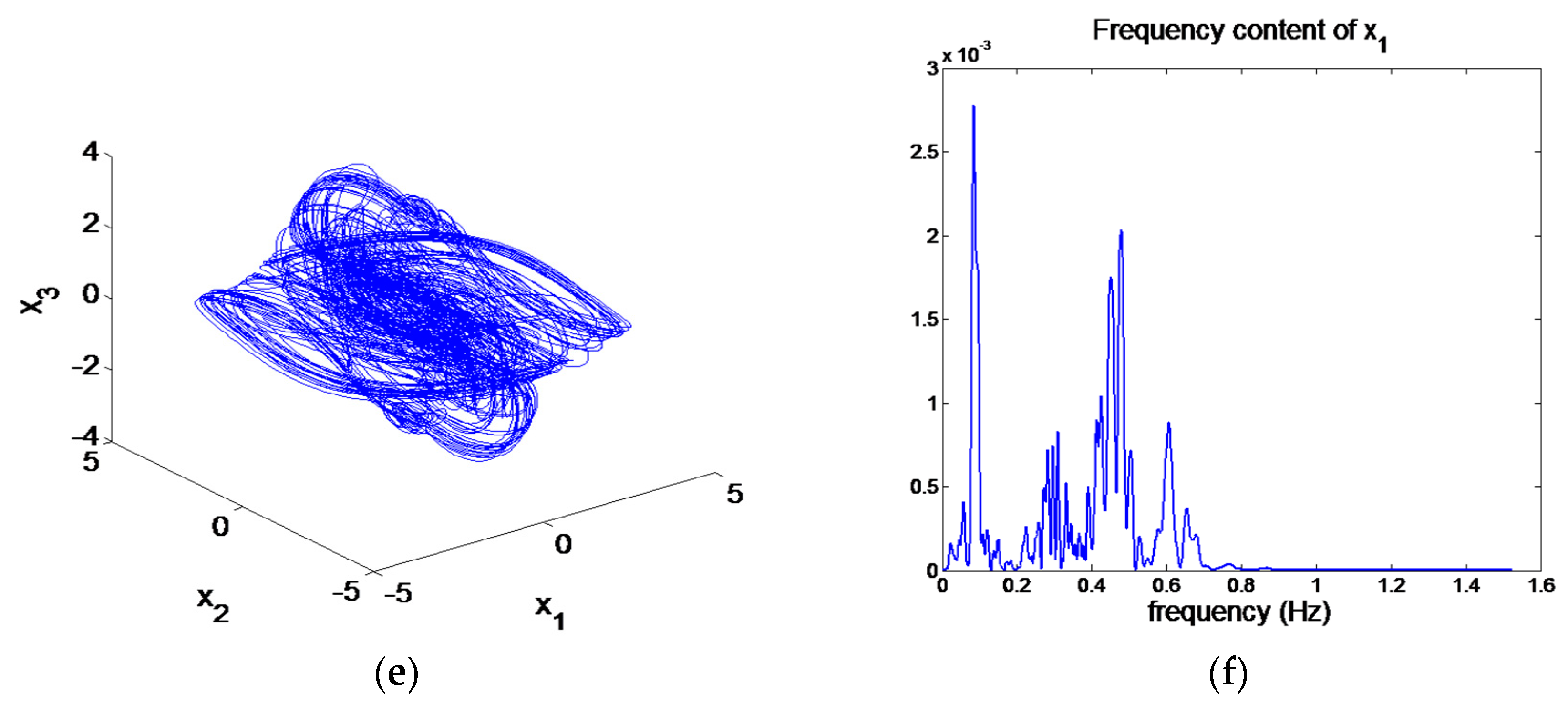
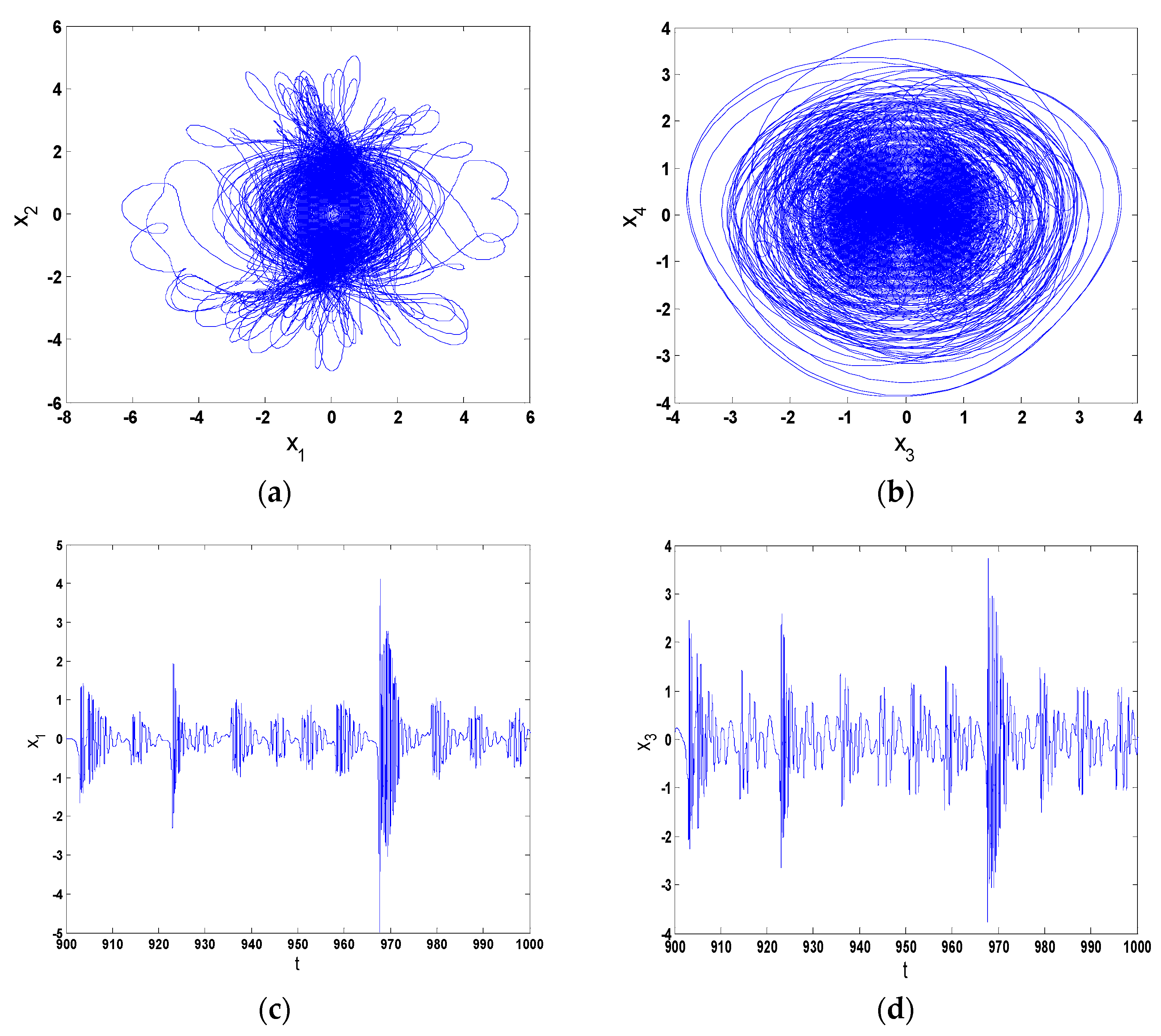
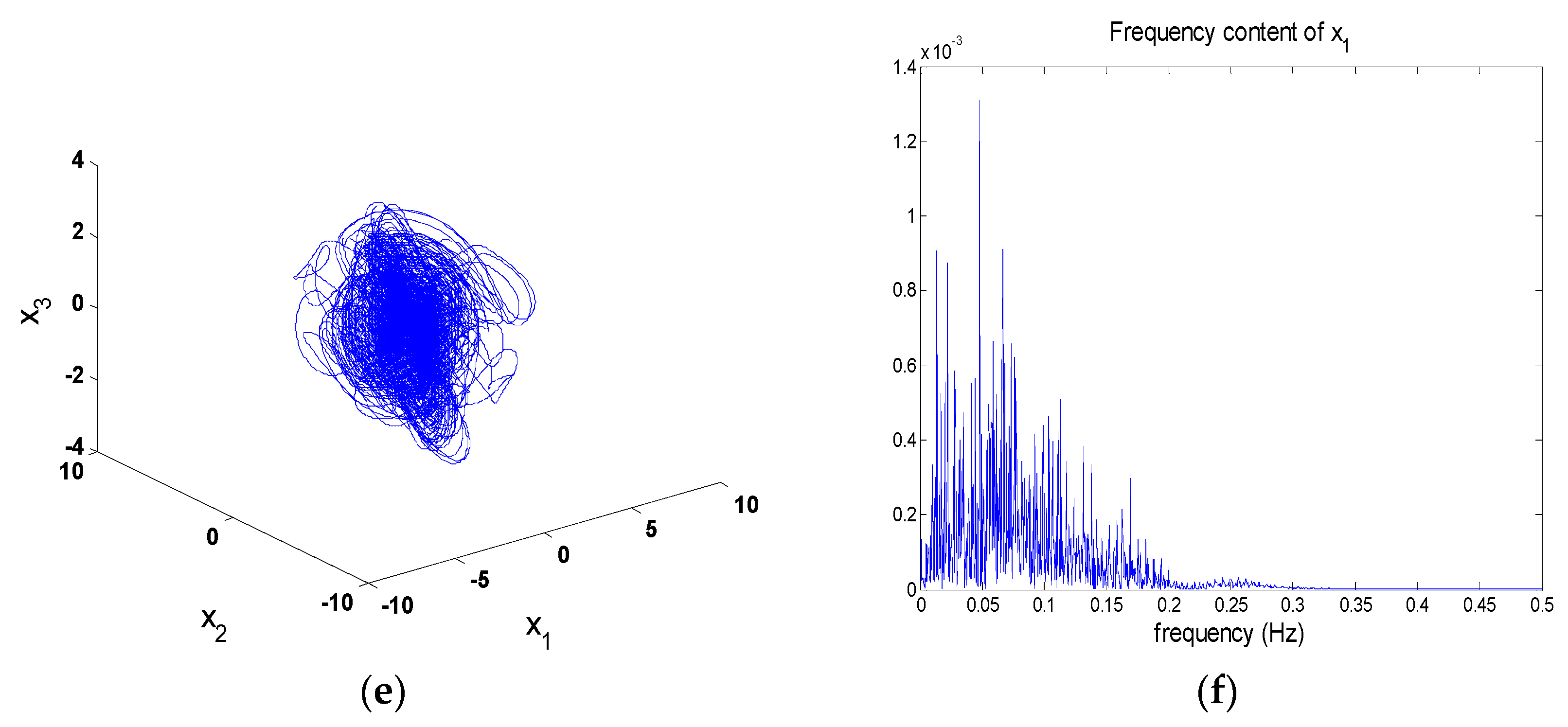
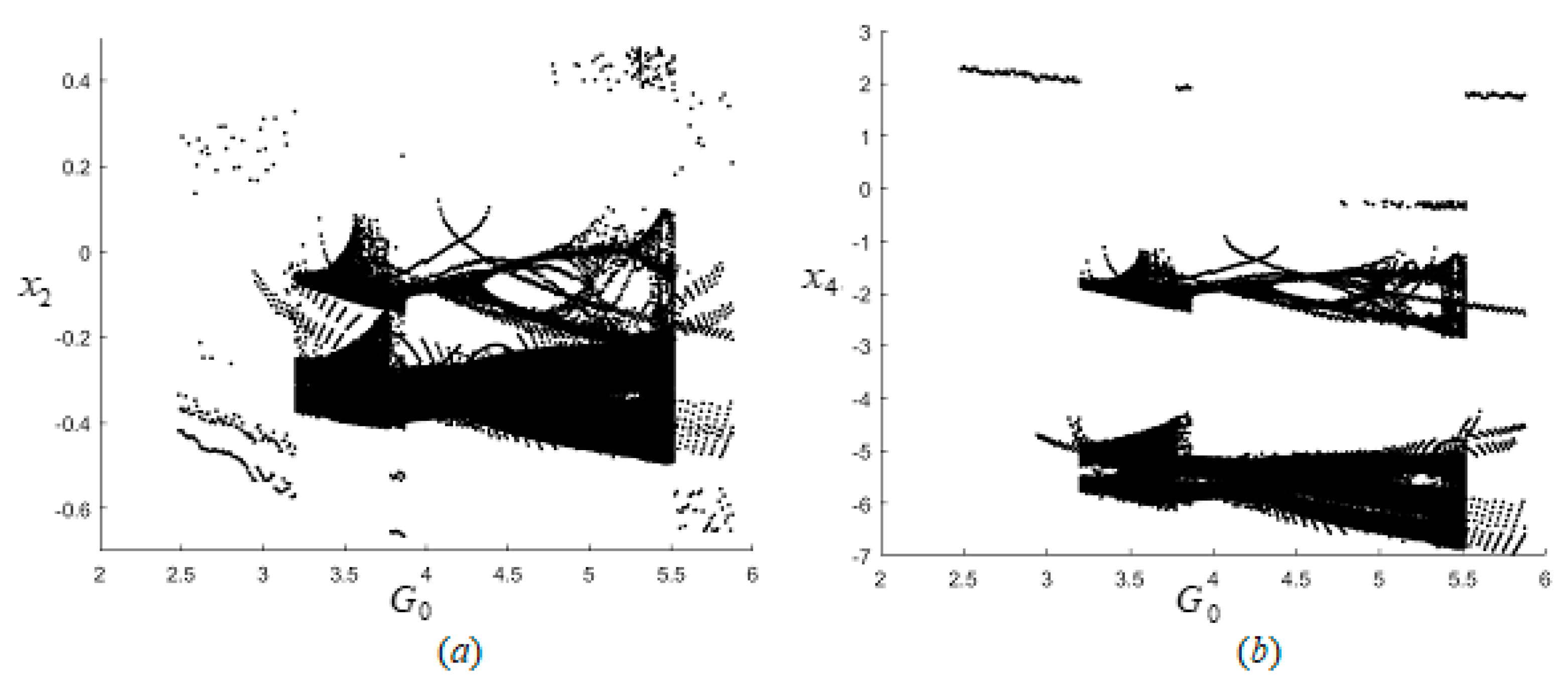
5. Numerical Simulation

In this section, according to the averaged equation in Equations (30a)–(30d), the fourth-order Runge–Kutta method is used to numerically analyze the nonlinear dynamic behaviors of this model. The complex nonlinear dynamics and the influence of different parameters on the motions of the stepped rectangular cantilever plate are discussed.

From the numerical calculations, with different parameters and initial conditions, the bifurcation diagram is drawn using different forcing amplitudes as follows:

$$\begin{array}{c}{a}_1=3.7848,a_3=0.92939,a_4=2.9463,a_5=1.1326,\\ a_6=3.8055,a_7=0.12337,b_1=3.3044,b_6=2.8609,b_7=1.8832,\\ b_8=2.0802,{\sigma }_1=1.4345,{\sigma }_2=2.8415,x_1=0.52058,x_2=0.10872,\\ x_3=-0.098578,x_4=-0.53287.\end{array}$$

The bifurcation diagram, which depicts the relationship between the forcing amplitude $f_1$ versus $x_1$, is shown in Figure 5. When the forcing excitation $f_1$ changes from 3 to 9, three chaotic regions are observed in the system, and chaotic motion and periodic motion alternate. The bifurcation diagram in Figure 5 reveals that the periodic responses of the model are highly sensitive to the external excitation $f_1$. Next, we verify the reliability of the bifurcation diagram by taking different amplitudes of forced excitation $f_1$.

Figure 6, Figure 7, Figure 8 and Figure 9 present the two-dimensional phase portraits, time histories, three-dimensional phase portraits, and Poincare maps for the composite stepped piezoelectric cantilever plate system. In Figure 6, Figure 7, Figure 8 and Figure 9, where Figure (a) shows the two-dimensional phase portraits on the plane ($x_1$, $x_2$); Figure (b) shows the two-dimensional phase portraits on the plane ($x_3$, $x_4$); Figure (c) shows the time history diagrams on the plane ($\mathrm{t}$,$x_1$); Figure (d) shows the time history diagrams on the plane ($t$, $x_1$); Figure (e) shows the three-dimensional phase portraits in space ($x_1$, $x_2$, $x_3$); Figure (f) shows the Poincare maps in space ($x_1$, $x_2$). As shown in Figure 6, when the external excitation $f_1$ is equal to 4.0, the composite stepped piezoelectric cantilever plate system is in chaotic motion. As the external excitation $f_1$ changes to 5.25, a period-8 response of this model occurs, which is shown in Figure 7. The amplitude of the forced excitation continues to increase, and when $f_1=6.5$ and $f_1=8.1$, the system still undergoes chaotic motion, as shown in Figure 8 and Figure 9.

In Figure 6, it is found that the composite stepped piezoelectric cantilever plate system has chaotic motion. The first- and second-mode phase diagrams, Figure 6a,b, as well as the three-dimensional phase diagram, Figure 6e, indicate that the system has undergone chaotic motion. The first- and second-mode time history diagrams, Figure 6c,d, and Poincare map, Figure 6f, also indicate that chaotic motion occurs for the composite stepped piezoelectric cantilever plate system.

When $f_2=5.25$, the composite stepped piezoelectric cantilever plate system exhibits period-8 motion, as shown in Figure 7. Figure 8 and Figure 9 show that the system exhibits chaotic motion, and the chaotic motion is similar. Comparing the time history diagrams of Figure 8 and Figure 9, it is not difficult to find that as the excitation amplitude increases, the amplitudes of both the first and second modes increase. However, compared to Figure 6, the vibration of the system did not increase due to the increase in the amplitude of the forced excitation.

Next, we study the impact of different parameters on the system’s motion characteristics. By select another set of parameters and initial conditions as follows:

$$\begin{array}{c}{a}_1=0.38711,a_3=0.69793,a_4=3.5231,\\ a_5=3.2024,a_6=2.1273,a_7=0.0495,\\ b_1=0.8196,b_6=2.1574 ,b_7=1.8832,\\ b_8=1.2293,{\sigma }_1=30692,{\sigma }_2=3.3388,\\ x_1=0.11306,x_2=-0.41041,\\ x_3=0.31385,x_4=-0.22487\end{array}$$

The chaotic motion of the composite stepped piezoelectric cantilever plate system was assessed according to the criterion of the power spectrum in the descriptive method of chaotic motion. Figure 10 shows the periodic motion of the composite stepped piezoelectric cantilever plate system when the excitation amplitude $f_1$ is 7.1388. Because both the phase portraits and the time history diagrams indicate that the system has undergone periodic motion and there are peaks in the spectrum diagram, it can be determined that the system has undergone periodic motion. Figure 11 shows that the composite stepped piezoelectric cantilever plate system exhibits chaotic motion different from the previous one under this set of parameters. Therefore, it can be concluded that different types of period doubling and chaotic motion can be obtained by changing the system parameters.

Next, the influence of different initial condition on the resonance behavior of the system is studied, and only initial values are changed. Other parameters are the same as those in Figure 10. The initial values are chosen as follows:

$$\begin{array}{c}{x}_1=0.11306,x_2=-0.41041,\\ x_3=0.31385,x_4=-0.22487.\end{array}$$

It can be seen from Figure 12 that different initial values have a great impact on the resonance behavior of the system, and the system presents a completely different chaotic motion.

Finally, we investigate the influence of the piezoelectric excitation parameter on the composite stepped piezoelectric cantilever plate system. The bifurcation diagrams of the first-order and the second-order modes of the system with piezoelectric excitation are shown in Figure 13a,b, respectively. The horizontal axis represents the piezoelectric excitation parameter, and the vertical axis represents the displacement of the first and second modes. The initial conditions and parameter values are as follows:

$$\begin{array}{c}{a}_1=2.6343,a_4=1.1528, a_5=2.2338,a_6=0.19283,\\ a_7=3.8706,a_8=3.1855,a_9=0.1394,b_1=0.40072,\\ b_6=1.445,b_7=3.312,b_8=1.5662,{\sigma }_1=0.31063,\\ {\sigma }_2=3.0766,x_1=1.5662,x_2=0.31063,\\ x_3=1.6166,x_4=0.44727,f_1=0.87402.\end{array}$$

The research results in Figure 13 indicate that as the piezoelectric excitation parameters increase, both the first and second modes of the system exhibit periodic motion, chaotic motion, and then periodic motion. Therefore, the chaotic motion of the system can be restrained by period-doubling bifurcation by adjusting the piezoelectric excitation, and the amplitude of the system vibration can be effectively reduced, so as to maintain the stability and controllability of the system motion.

6. Results

This paper simplified the fully unfolded axially moving wing into a composite stepped piezoelectric cantilever plate model, and then the nonlinear dynamics of the cantilever stepped plate were studied. Based on Hamilton’s principle, the governing equations of the system were obtained. The nonlinear governing equations were further reduced to a two-degree-of-freedom nonlinear system by Galerkin’s method. In addition, the case of primary parametric resonance and 1:3 internal resonance were introduced in this study. Using the multiple scales method, the equations of the original non-autonomous system can be obtained, and a set of four-dimensional averaged equations were acquired. Some conclusions are summarized.

(1)

The present work deals with the dynamic problem of the smart piezoelectric composite structure, dynamic analysis of the PVDF piezoelectric stepped plate, nonlinear transverse vibrations of the symmetric cross-ply composite laminated piezoelectric stepped cantilever plate with fiber-reinforced composite materials subjected to in-plane and out-of-plane excitation, vibration response analysis of the PVDF piezoelectric plate subjected to aerodynamic forces, piezoelectric excitation, and in-plane excitation.

(2)

From the analysis of the frequency response results, it is found that the system exhibits different nonlinear stiffness characteristics, and the amplitude–frequency response curves of the first-order mode and second-order modes are greatly affected by different parameters.

(3)

According to the numerical results of the chaos and bifurcations, it is found that the system exhibits chaotic motion, and the chaotic motion is similar. The different initial values have a great impact on the resonance behavior of the system, and the system presents completely different chaotic motions.

(4)

The influence of the piezoelectric excitation parameter on the composite stepped piezoelectric cantilever plate system is investigated. It is found that the system exhibits complex nonlinear motion, the chaotic motion of the system can be restrained by period-doubling bifurcation by adjusting the piezoelectric excitation, and the amplitude of the system vibration can be effectively reduced, so as to maintain the stability and controllability of the system motion.