Numerical Simulation of Long-Span Bridge Response under Downburst: Parameter Optimization Using a Surrogate Model
Abstract
:1. Introduction
2. Downburst Based on CFD Scheme
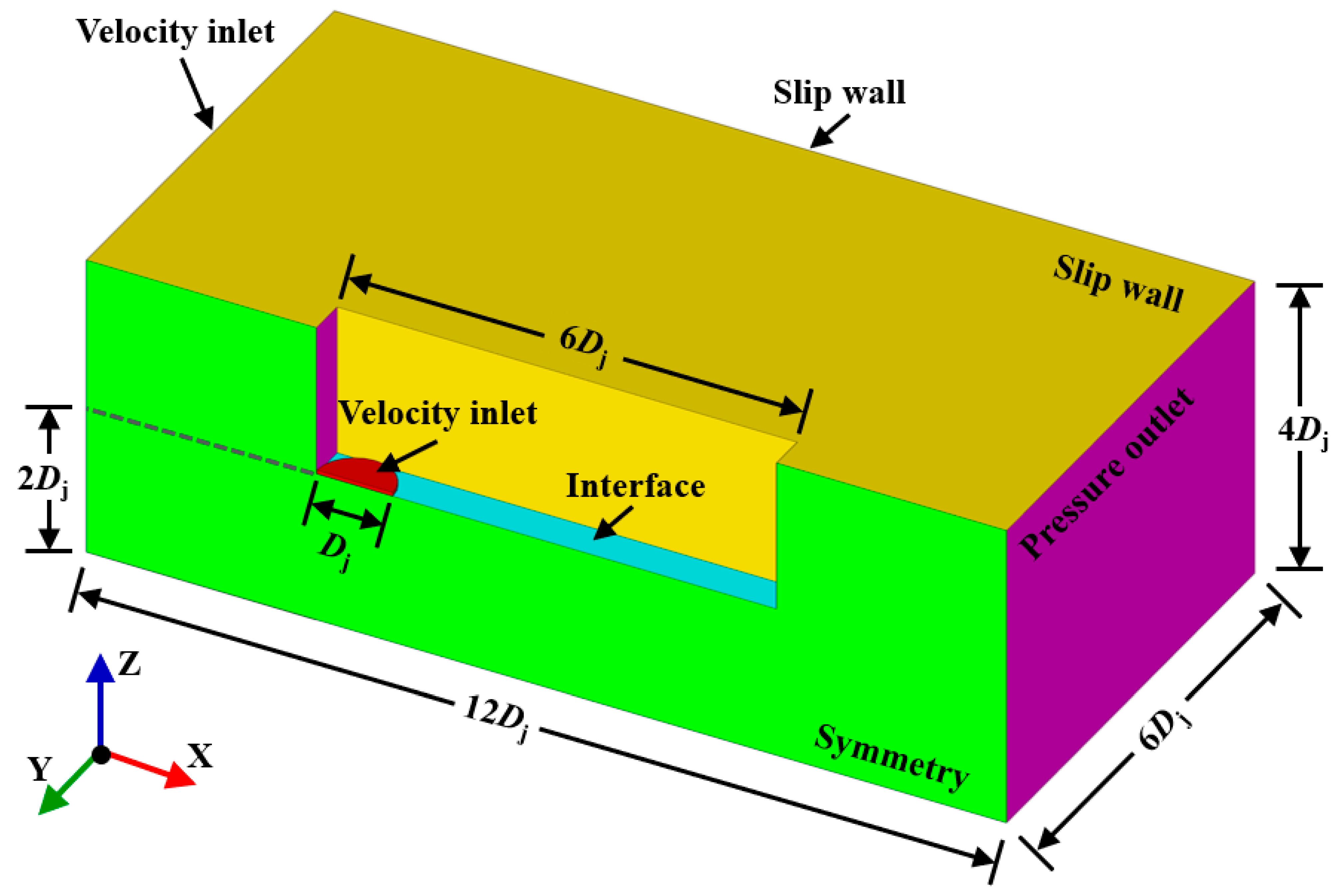
2.1. Stationary Downburst Simulation
- (1)
- Computational domain and mesh
- (2)
- Solution scheme
- (3)
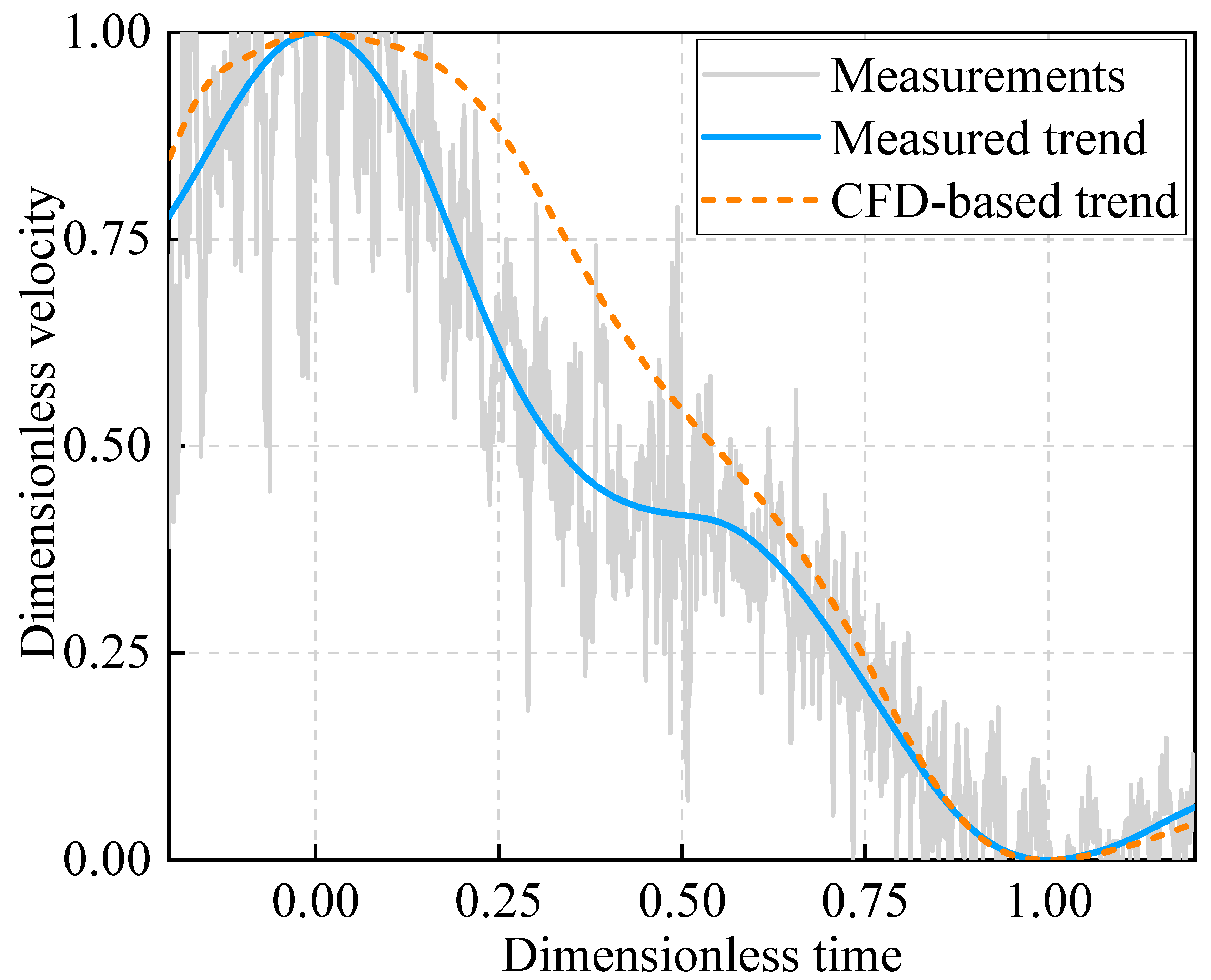
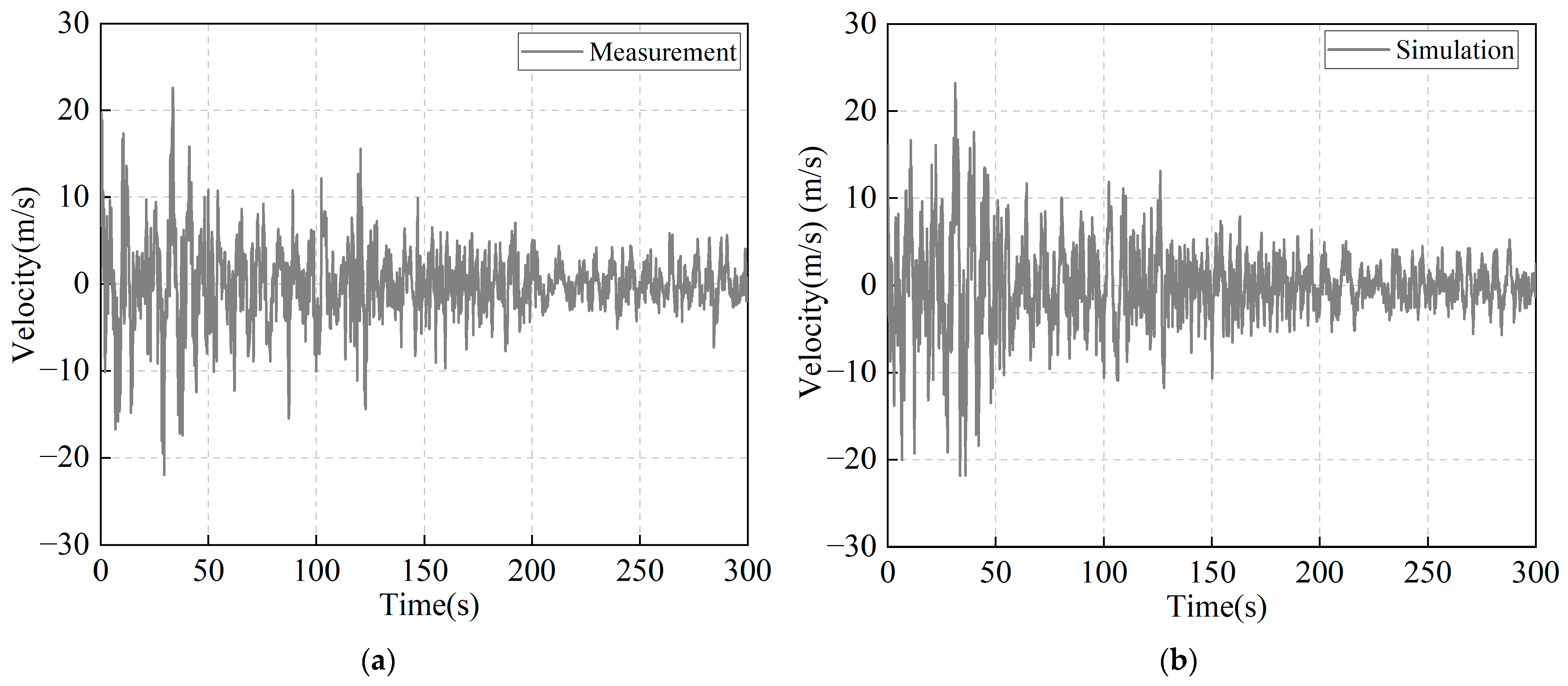
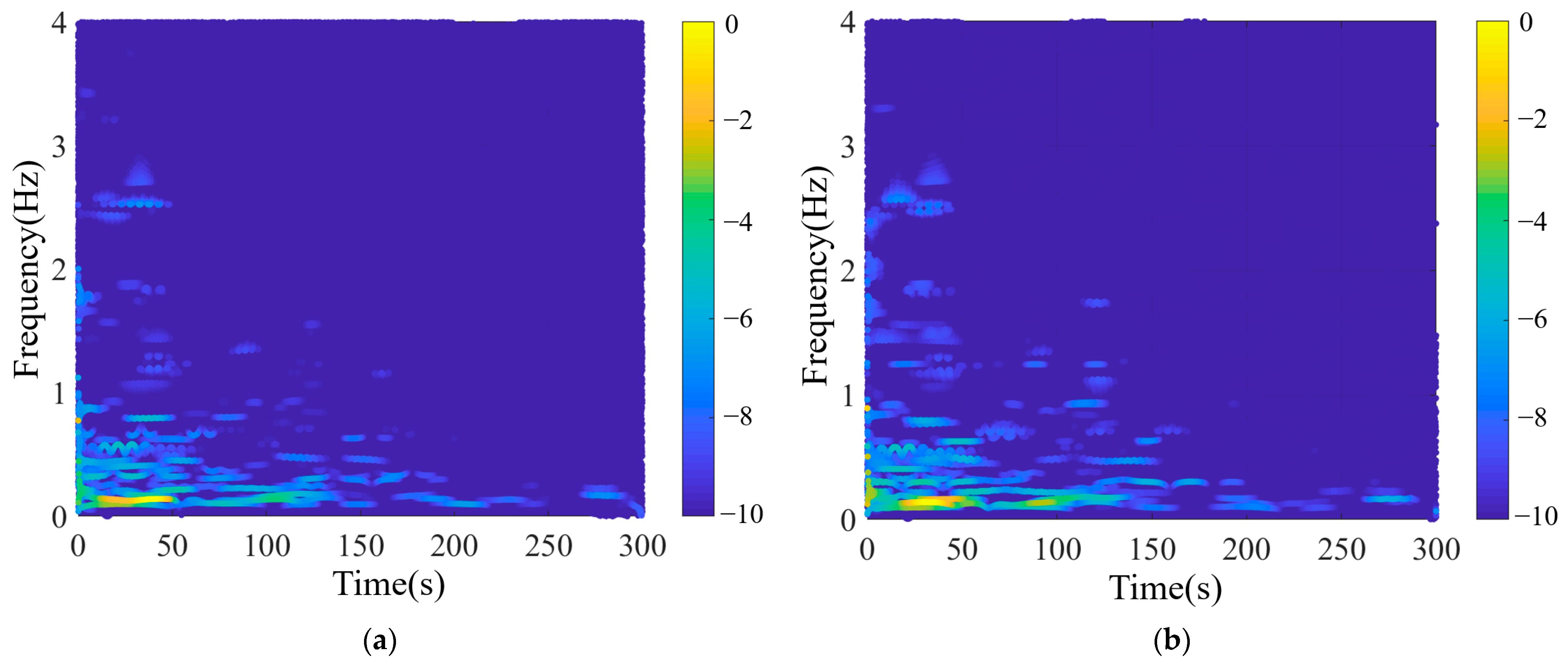
- Validation
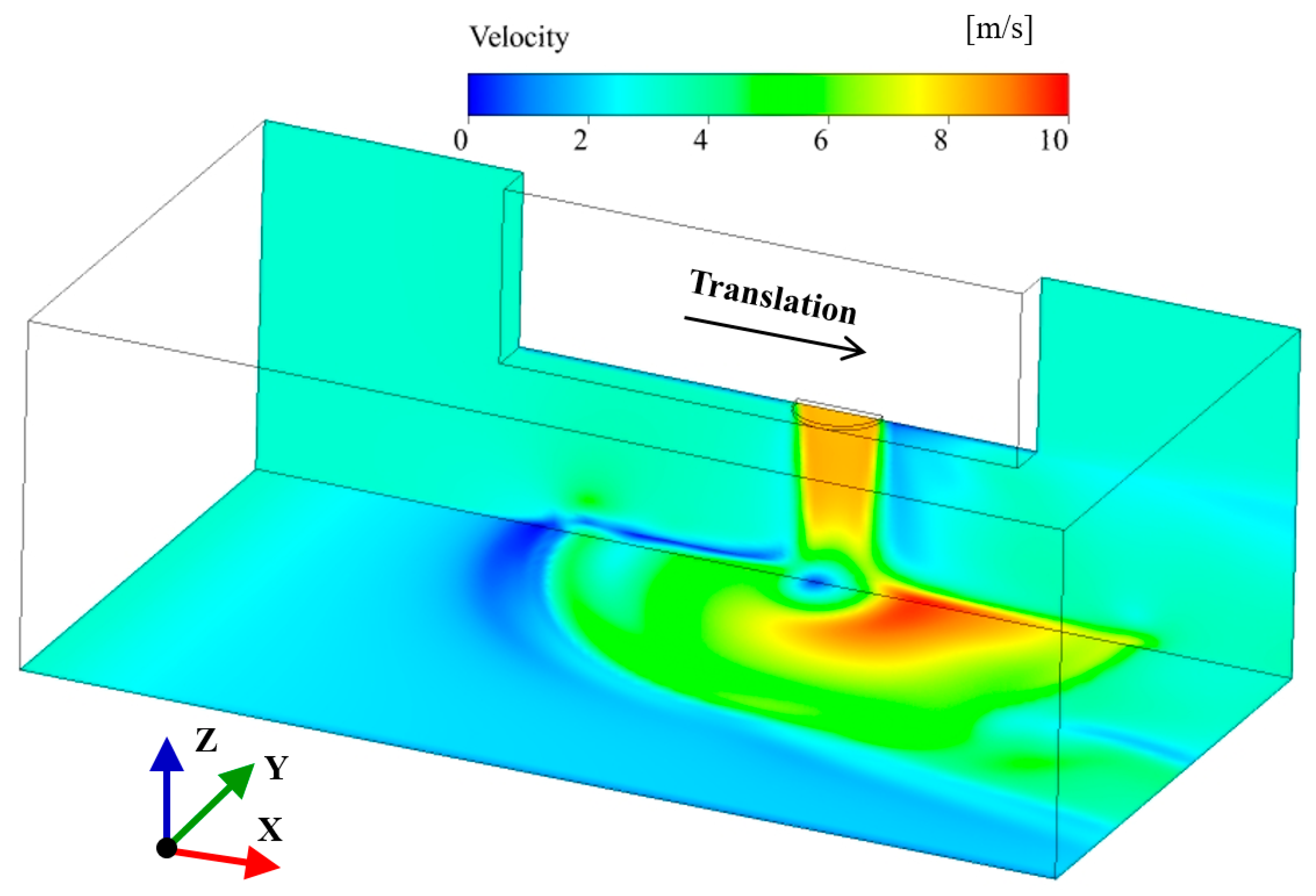
2.2. Moving Downburst Simulation
- (1)
- Numerical set-up
- (2)
- Numerical results
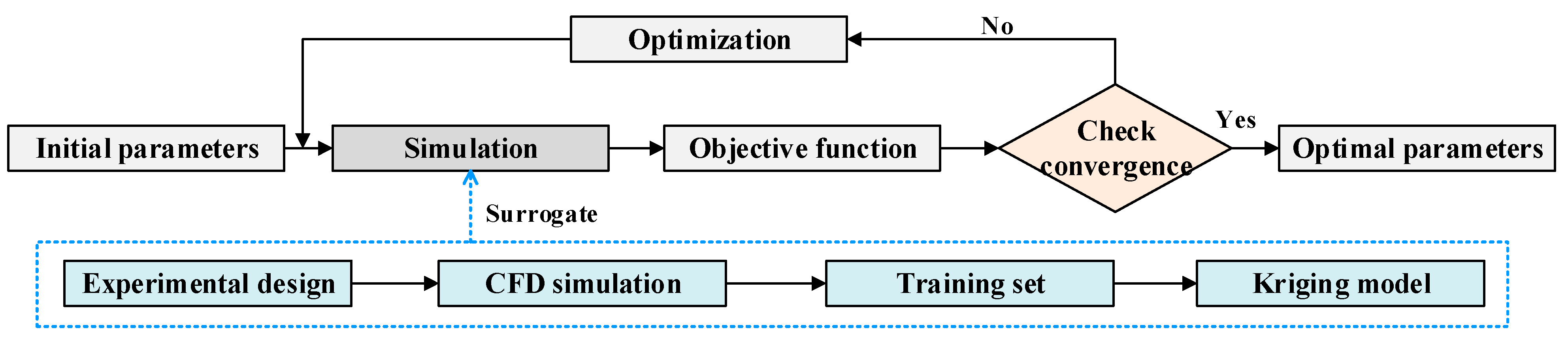
3. Kriging-Based Optimization of Downburst
3.1. Kriging Surrogate Modeling
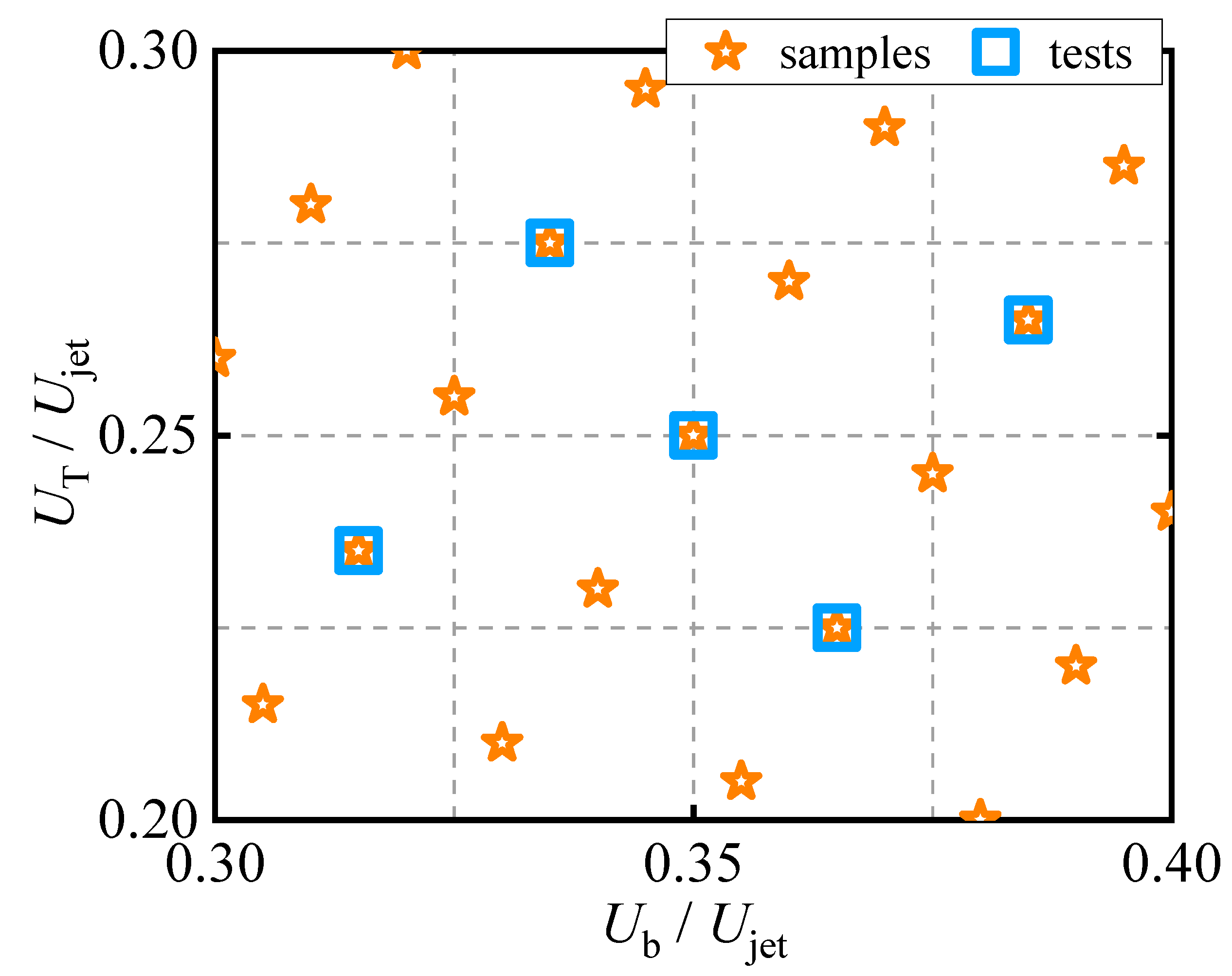
3.2. Experimental Design
3.3. Optimization Strategy
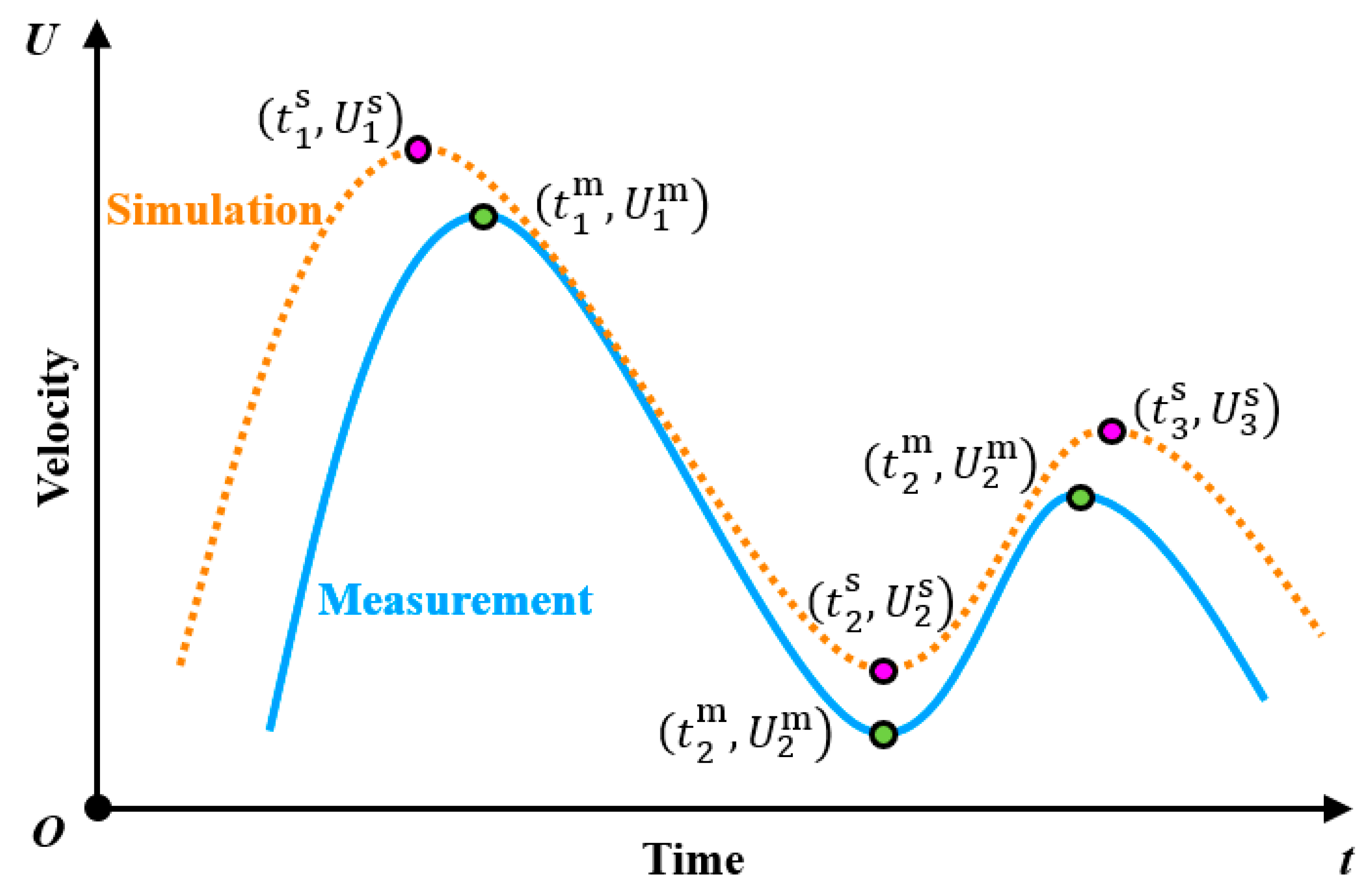
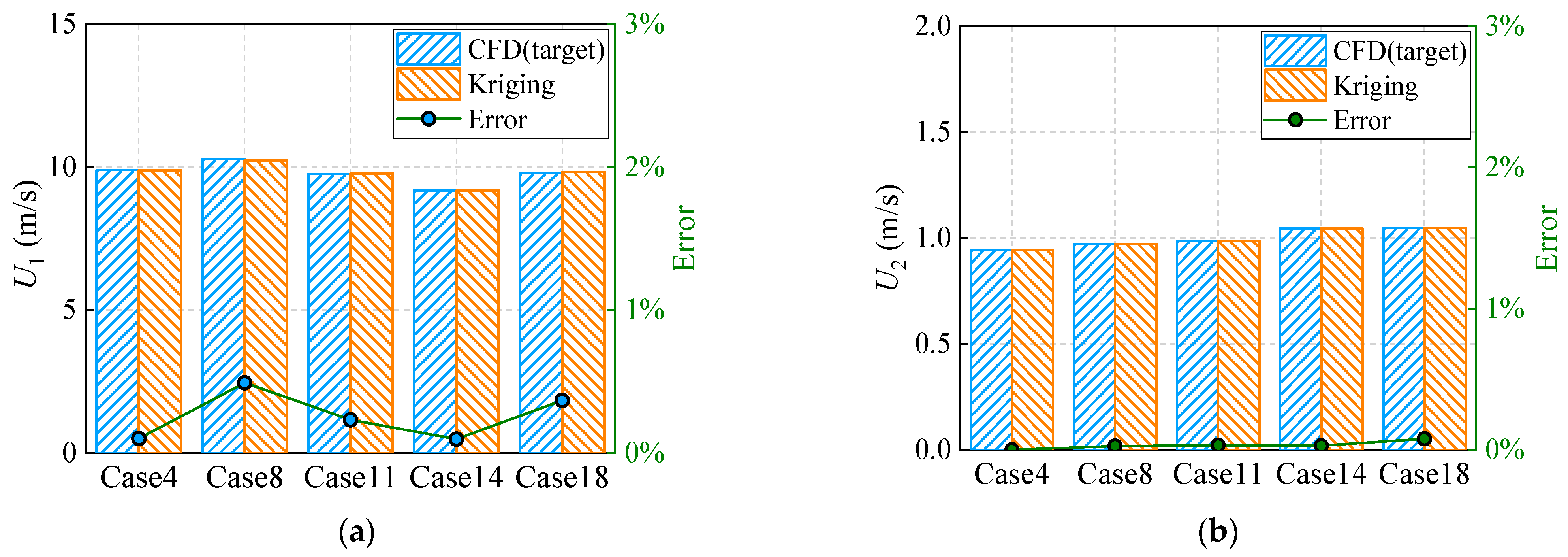
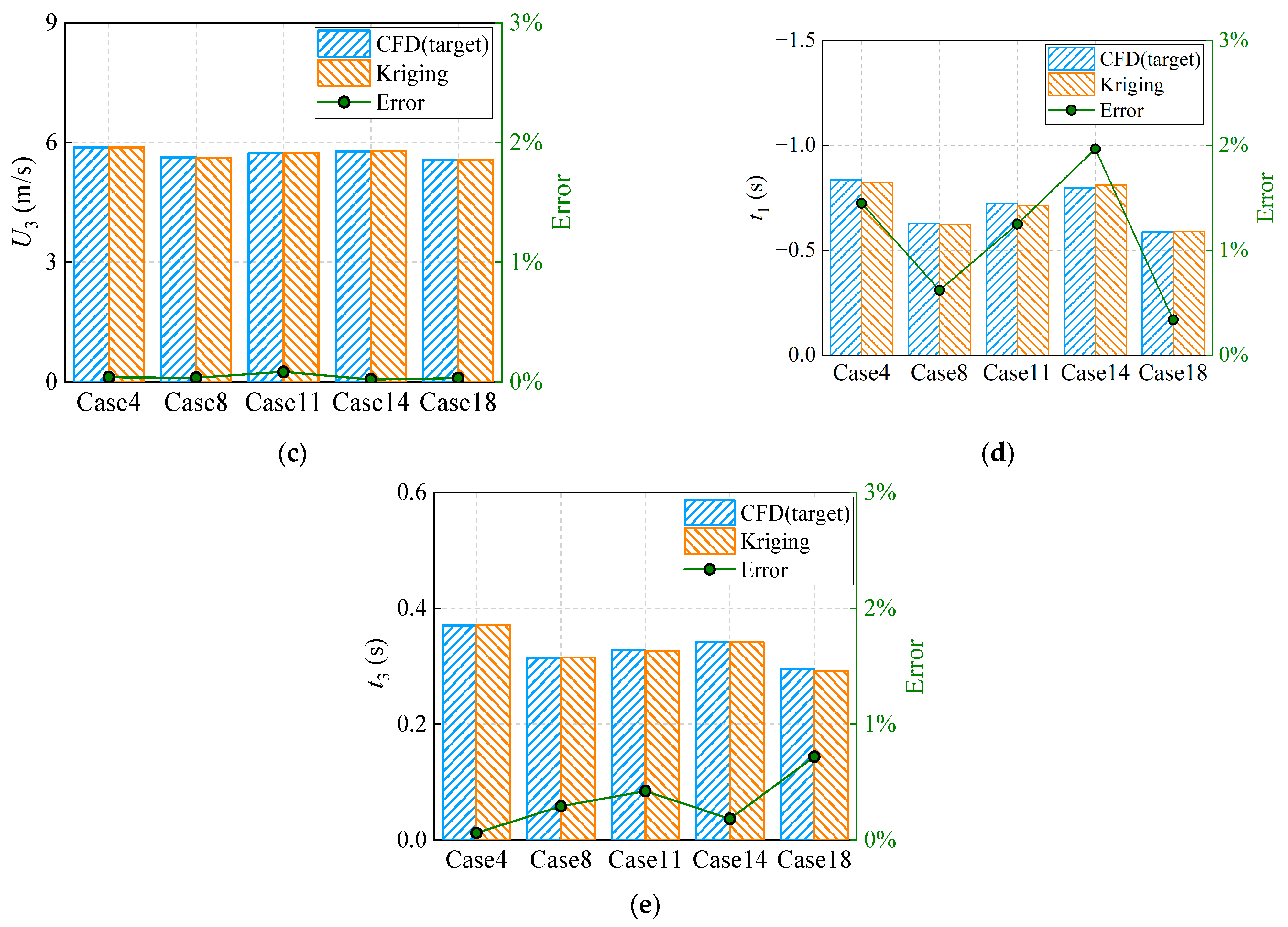
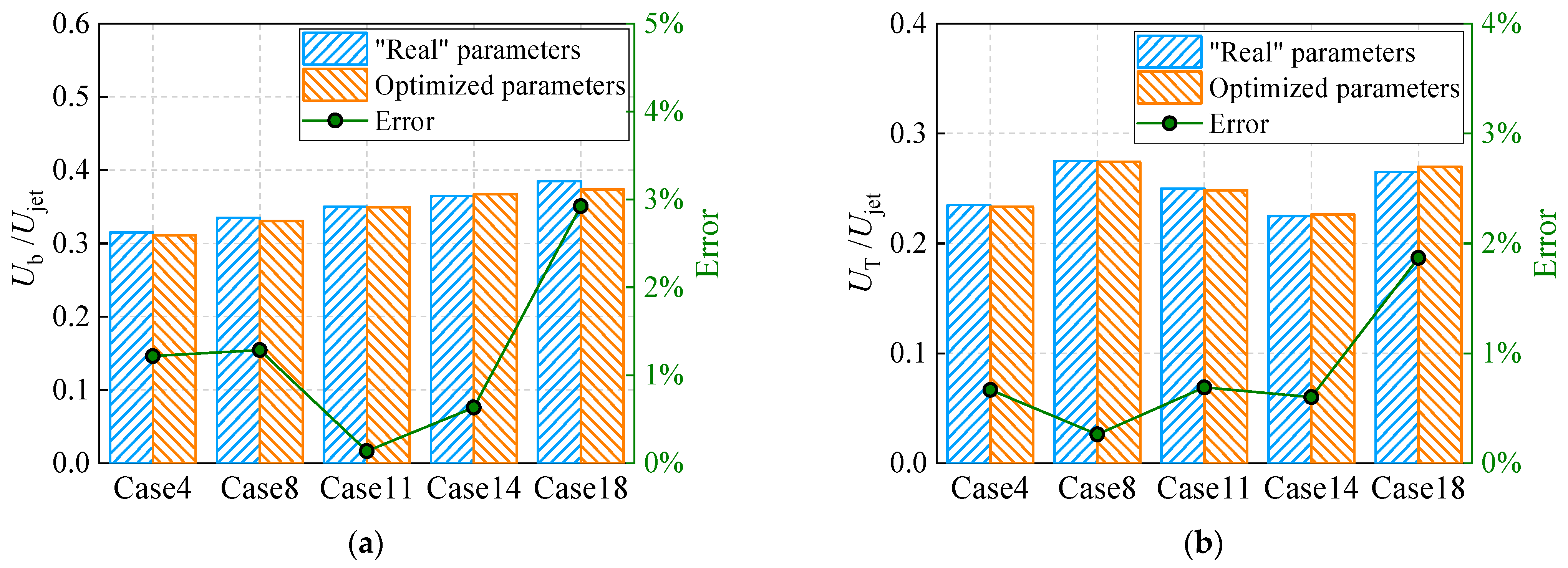
3.4. Validation
4. Downburst-Induced Long-Span Bridge Response
4.1. Long-Span Bridge Model
4.2. Modeling of the Downburst Wind Field
- (1)
- Time-varying mean wind
- (2)
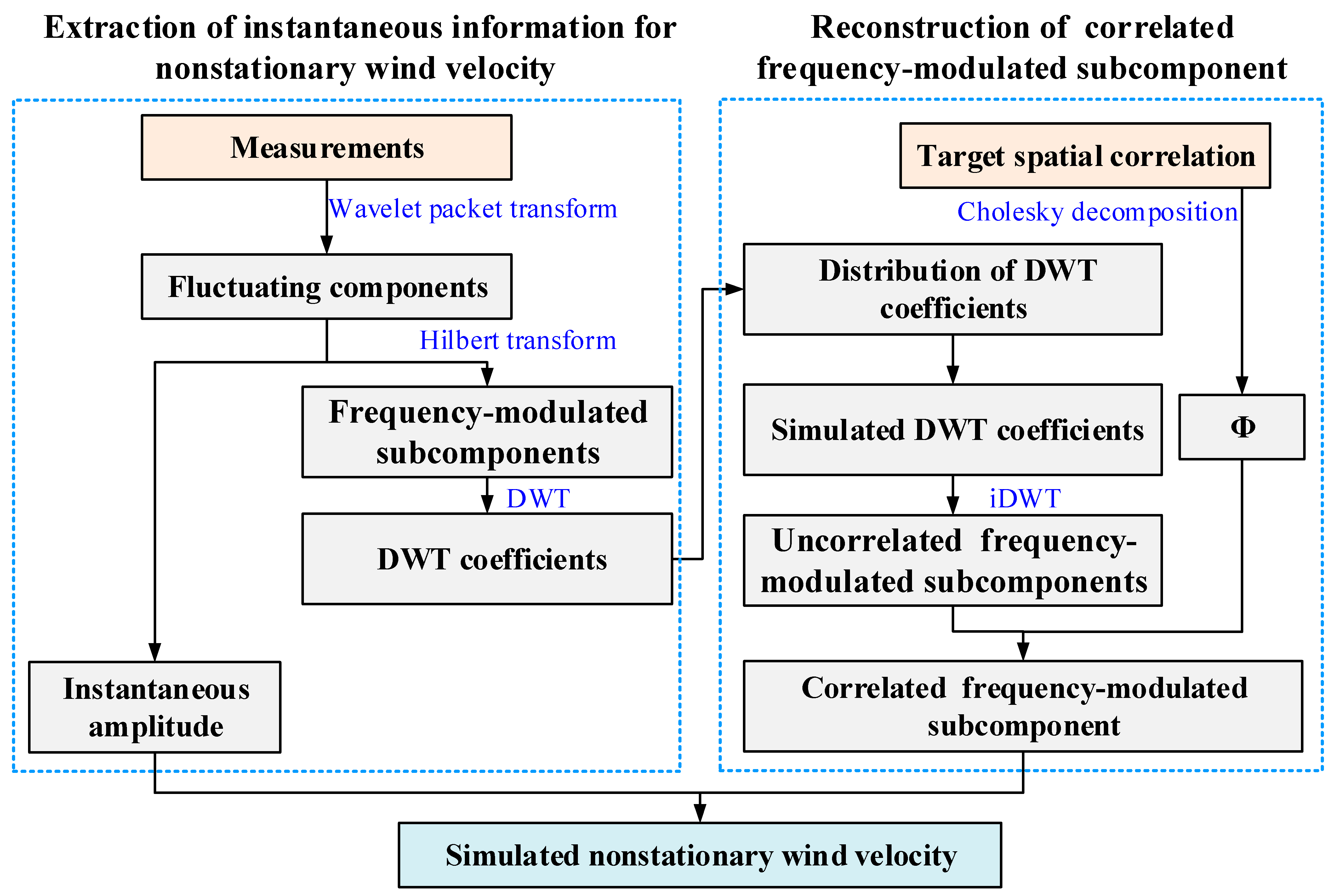
- Nonstationary fluctuating wind
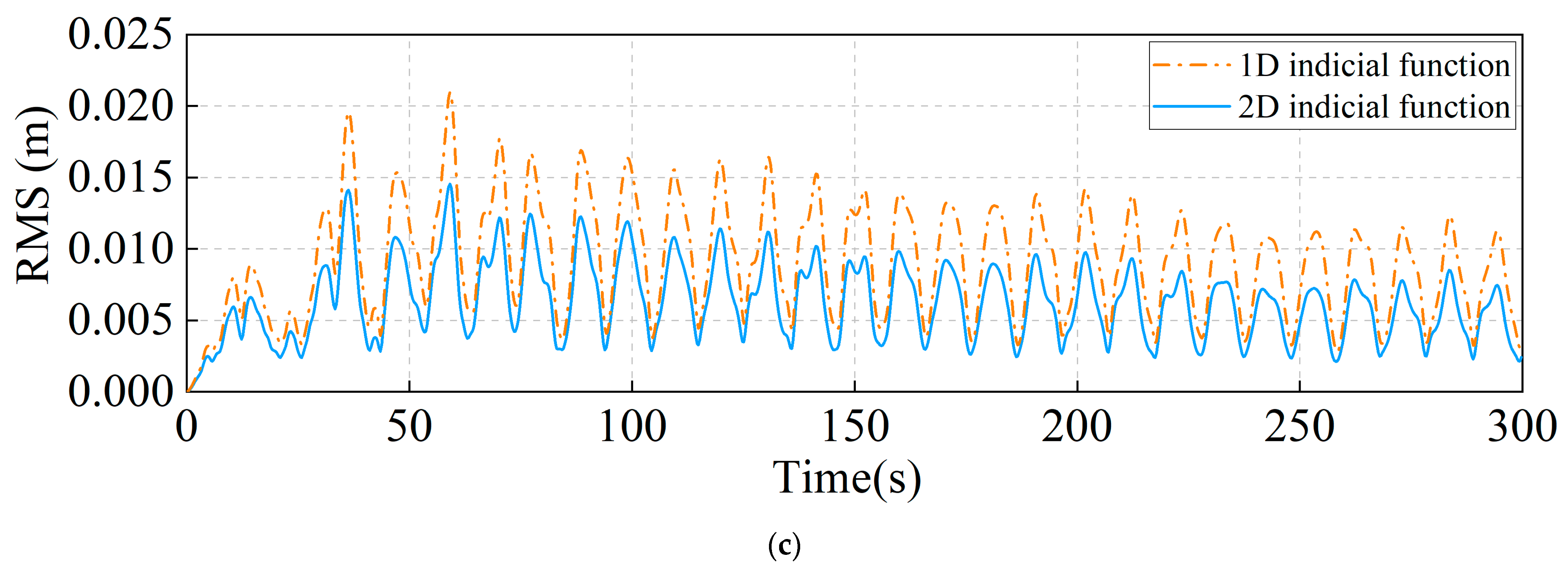
4.3. Transient Aerodynamics
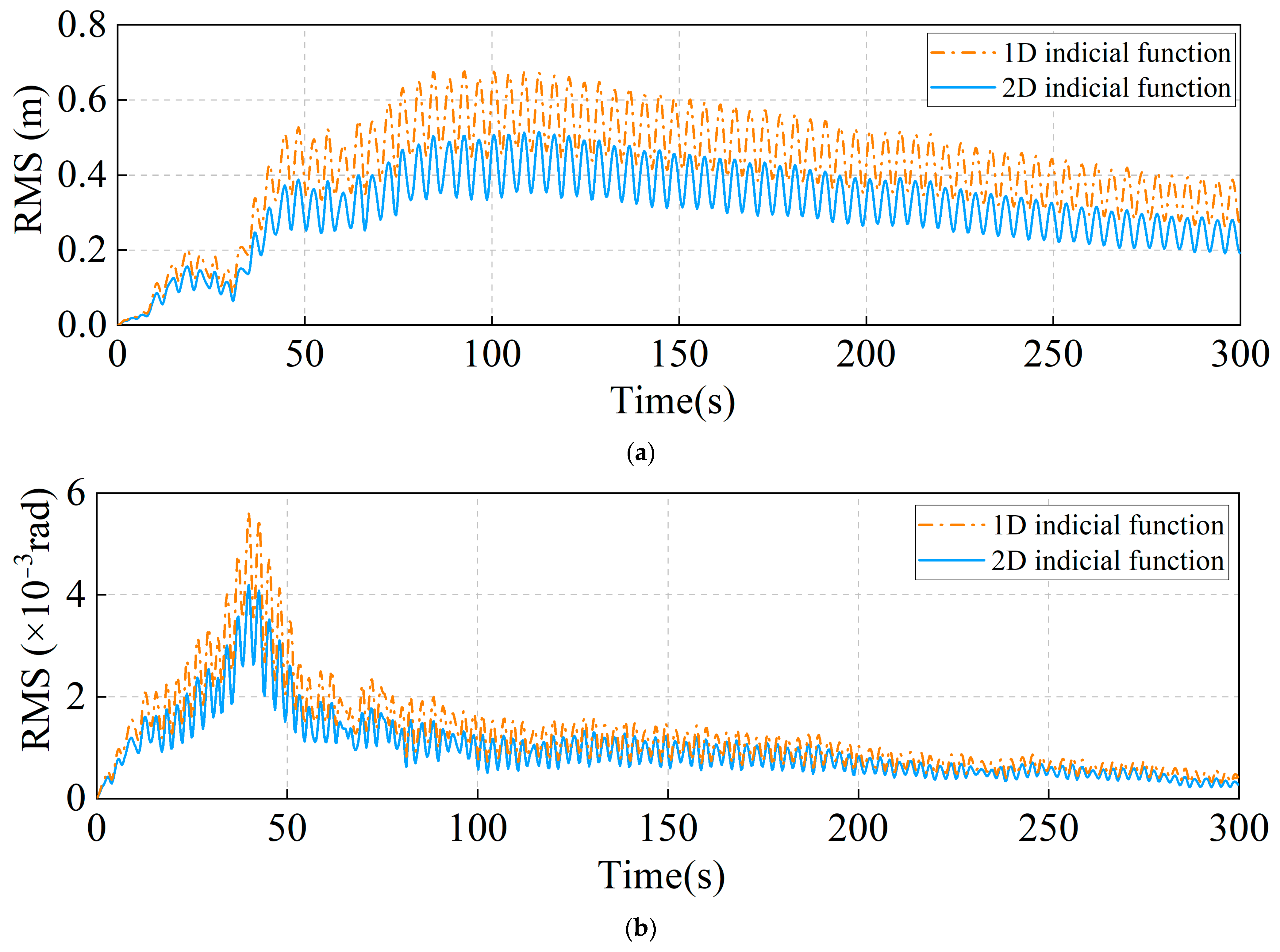
4.4. Transient Wind-Induced Response
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hao, J.; Wu, T. Downburst-induced transient response of a long-span bridge: A CFD-CSD-based hybrid approach. J. Wind Eng. Ind. Aerodyn. 2018, 179, 273–286. [Google Scholar] [CrossRef]
- Twisdale, L.A.; Vickery, P.J. Research on thunderstorm wind design parameters. J. Wind Eng. Ind. Aerodyn. 1992, 41, 545–556. [Google Scholar] [CrossRef]
- Solari, G.; Burlando, M.; De Gaetano, P.; Repetto, M.P. Characteristics of thunderstorms relevant to the wind loading of structures. Wind Struct. 2015, 20, 763–791. [Google Scholar] [CrossRef]
- Fujita, T.T. Tornadoes and downbursts in the context of generalized planetary scales. J. Atmos. Sci. 1981, 38, 1511–1534. [Google Scholar] [CrossRef]
- Hjelmfelt, M.R. Structure and life cycle of microburst outflows observed in Colorado. J. Appl. Meteorol. Climatol. 1988, 27, 900–927. [Google Scholar] [CrossRef]
- Solari, G.; Repetto, M.P.; Burlando, M.; De Gaetano, P.; Pizzo, M.; Tizzi, M.; Parodi, M. The wind forecast for safety management of port areas. J. Wind Eng. Ind. Aerodyn. 2012, 104, 266–277. [Google Scholar] [CrossRef]
- Solari, G. Thunderstorm response spectrum technique: Theory and applications. Eng. Struct. 2016, 108, 28–46. [Google Scholar] [CrossRef]
- Bakke, P. An experimental investigation of a wall jet. J. Fluid Mech. 1957, 2, 467–472. [Google Scholar] [CrossRef]
- Glauert, M. The wall jet. J. Fluid Mech. 1956, 1, 625–643. [Google Scholar] [CrossRef]
- Poreh, M.; Tsuei, Y.; Cermak, J.E. Investigation of a turbulent radial wall jet. J. Appl. Mech. 1967, 34, 457–463. [Google Scholar] [CrossRef]
- Letchford, C.; Chay, M. Pressure distributions on a cube in a simulated thunderstorm downburst. Part B: Moving downburst observations. J. Wind Eng. Ind. Aerodyn. 2002, 90, 733–753. [Google Scholar] [CrossRef]
- Mason, M.; Letchford, C.; James, D. Pulsed wall jet simulation of a stationary thunderstorm downburst, Part A: Physical structure and flow field characterization. J. Wind Eng. Ind. Aerodyn. 2005, 93, 557–580. [Google Scholar] [CrossRef]
- Richter, A.; Ruck, B.; Mohr, S.; Kunz, M. Interaction of severe convective gusts with a street canyon. Urban Clim. 2018, 23, 71–90. [Google Scholar] [CrossRef]
- Selvam, R.P.; Holmes, J. Numerical simulation of thunderstorm downdrafts. J. Wind Eng. Ind. Aerodyn. 1992, 44, 2817–2825. [Google Scholar] [CrossRef]
- Kim, J.; Hangan, H. Numerical simulations of impinging jets with application to downbursts. J. Wind Eng. Ind. Aerodyn. 2007, 95, 279–298. [Google Scholar] [CrossRef]
- Sengupta, A.; Sarkar, P.P. Experimental measurement and numerical simulation of an impinging jet with application to thunderstorm microburst winds. J. Wind Eng. Ind. Aerodyn. 2008, 96, 345–365. [Google Scholar] [CrossRef]
- Aboshosha, H.; Bitsuamlak, G.; El Damatty, A. Turbulence characterization of downbursts using LES. J. Wind Eng. Ind. Aerodyn. 2015, 136, 44–61. [Google Scholar] [CrossRef]
- Abd-Elaal, E.-S.; Mills, J.E.; Ma, X. Numerical simulation of downburst wind flow over real topography. J. Wind Eng. Ind. Aerodyn. 2018, 172, 85–95. [Google Scholar] [CrossRef]
- Tang, J.; Hu, Y.; Song, B.; Yang, H. Unsteady aerodynamic optimization of airfoil for cycloidal propellers based on surrogate model. J. Aircr. 2017, 54, 1241–1256. [Google Scholar] [CrossRef]
- Raul, V.; Leifsson, L. Surrogate-based aerodynamic shape optimization for delaying airfoil dynamic stall using Kriging regression and infill criteria. Aerosp. Sci. Technol. 2021, 111, 106555. [Google Scholar] [CrossRef]
- Bernardini, E.; Spence, S.M.; Wei, D.; Kareem, A. Aerodynamic shape optimization of civil structures: A CFD-enabled Kriging-based approach. J. Wind Eng. Ind. Aerodyn. J. Int. Assoc. Wind Eng. 2015, 144, 154–164. [Google Scholar] [CrossRef] [Green Version]
- Ding, F.; Kareem, A. A multi-fidelity shape optimization via surrogate modeling for civil structures. J. Wind Eng. Ind. Aerodyn. 2018, 178, 49–56. [Google Scholar] [CrossRef]
- Montoya, M.C.; Nieto, F.; Hernández, S.; Kusano, I.; Álvarez, A.; Jurado, J. CFD-based aeroelastic characterization of streamlined bridge deck cross-sections subject to shape modifications using surrogate models. J. Wind Eng. Ind. Aerodyn. 2018, 177, 405–428. [Google Scholar] [CrossRef]
- Jaouadi, Z.; Abbas, T.; Morgenthal, G.; Lahmer, T. Single and multi-objective shape optimization of streamlined bridge decks. Struct. Multidiscip. Optim. 2020, 61, 1495–1514. [Google Scholar] [CrossRef]
- Holmes, J.D.; Hangan, H.M.; Schroeder, J.L.; Letchford, C.W.; Orwig, K.D. A forensic study of the Lubbock-Reese downdraft of 2002. Wind Struct. 2008, 11, 137–152. [Google Scholar] [CrossRef]
- Feng, Y.; Hao, J.; Han, W.; Su, Q.; Wu, T. An optimized numerical tornado simulator and its application to transient wind-induced response of a long-span bridge. J. Wind Eng. Ind. Aerodyn. 2022, 227, 105072. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Mason, M.; Wood, G.; Fletcher, D. Impinging jet simulation of stationary downburst flow over topography. Wind Struct. 2007, 10, 437–462. [Google Scholar] [CrossRef]
- Chay, M.; Letchford, C. Pressure distributions on a cube in a simulated thunderstorm downburst-Part A: Stationary downburst observations. J. Wind Eng. Ind. Aerodyn. 2002, 90, 711–732. [Google Scholar] [CrossRef]
- Howell, R.; Qin, N.; Edwards, J.; Durrani, N. Wind tunnel and numerical study of a small vertical axis wind turbine. Renew. Energy 2010, 35, 412–422. [Google Scholar] [CrossRef] [Green Version]
- Khayrullina, A.; Blocken, B.; Janssen, W.; Straathof, J. CFD simulation of train aerodynamics: Train-induced wind conditions at an underground railroad passenger platform. J. Wind Eng. Ind. Aerodyn. 2015, 139, 100–110. [Google Scholar] [CrossRef]
- Li, C.; Li, Q.; Xiao, Y.; Ou, J. Simulations of moving downbursts using CFD. In Proceedings of the Seventh Asia-Pacific Conference on Wind Engineering, Taipei, Taiwan, 8–12 November 2009. [Google Scholar]
- Fujita, T.T. Andrews AFB Microburst, SMRP Research Paper 205; University of Chicago: Chicago, IL, USA, 1985. [Google Scholar]
- Fujita, T.T.; Byers, H.R. Spearhead echo and downburst in the crash of an airliner. Mon. Weather Rev. 1977, 105, 129–146. [Google Scholar] [CrossRef]
- Butler, K.; Cao, S.; Kareem, A.; Tamura, Y.; Ozono, S. Surface pressure and wind load characteristics on prisms immersed in a simulated transient gust front flow field. J. Wind Eng. Ind. Aerodyn. 2010, 98, 299–316. [Google Scholar] [CrossRef]
- Shirato, H.; Maeta, K.; Kato, Y.; Takasugi, Y. Transient drag force on 2-D bluff bodies under gusty wind condition. In Proceedings of the 7th Asia-Pacific Conference on Wind Engineering, Taipei, Taiwan, 8–12 November 2009. [Google Scholar]
- Hao, J.; Wu, T. Numerical analysis of a long-span bridge response to tornado-like winds. Wind Struct. 2020, 31, 459–472. [Google Scholar]
- Aboutabikh, M.; Ghazal, T.; Chen, J.; Elgamal, S.; Aboshosha, H. Designing a blade-system to generate downburst outflows at boundary layer wind tunnel. J. Wind Eng. Ind. Aerodyn. 2019, 186, 169–191. [Google Scholar] [CrossRef]
- Wang, H.; Wu, T. Hilbert-wavelet-based nonstationary wind field simulation: A multiscale spatial correlation scheme. J. Eng. Mech. 2018, 144, 04018063. [Google Scholar] [CrossRef]
- Feng, Y.; Su, Q.; Hao, J.; Han, W.; Wang, H. A comparative study on the transient wind-induced response of long-span bridges subject to downbursts and typhoons. Eng. Struct. 2023, 280, 115649. [Google Scholar] [CrossRef]
- Gabor, D. Theory of communication. Part 1: The analysis of information. J. Inst. Electr. Eng.-Part III Radio Commun. Eng. 1946, 93, 429–441. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Letchford, C. Numerical simulation of extreme winds from thunderstorm downbursts. J. Wind Eng. Ind. Aerodyn. 2007, 95, 977–990. [Google Scholar] [CrossRef]
- Scanlan, R.H.; Béliveau, J.; Budlong, K.S. Indicial aerodynamic functions for bridge decks. J. Eng. Mech. Div. 1974, 100, 657–672. [Google Scholar] [CrossRef]
- Wu, T.; Kareem, A. Revisiting convolution scheme in bridge aerodynamics: Comparison of step and impulse response functions. J. Eng. Mech. 2014, 140, 04014008. [Google Scholar] [CrossRef]
- Chen, X. Analysis of multimode coupled buffeting response of long-span bridges to nonstationary winds with force parameters from stationary wind. J. Struct. Eng. 2015, 141, 04014131. [Google Scholar] [CrossRef]
- Chen, A. Study of Aerodynamic Performance of Runyang Bridge; Technical Report WT200218; Tongji University: Shanghai, China, 2002. [Google Scholar]
- Jones, R.T. The Unsteady Lift of a Wing of Finite Aspect Ratio; National Advisory Committee for Aeronautics: Boston, MA, USA, 1940. [Google Scholar]
- Chen, X.; Matsumoto, M.; Kareem, A. Aerodynamic coupling effects on flutter and buffeting of bridges. J. Eng. Mech. 2000, 126, 17–26. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Liu, Y.; Li, M.; Zeng, W.; Gu, S.; Gao, Y. The effect of turbulence intensity on the unsteady gust loading on a 5: 1 rectangular cylinder. J. Wind Eng. Ind. Aerodyn. 2022, 225, 104994. [Google Scholar] [CrossRef]
- Li, S.; Li, M.; Wu, B.; Li, K.; Yang, Y. Three-dimensional aerodynamic lift on a rectangular cylinder in turbulent flow at an angle of attack. J. Fluids Struct. 2023, 118, 103859. [Google Scholar] [CrossRef]

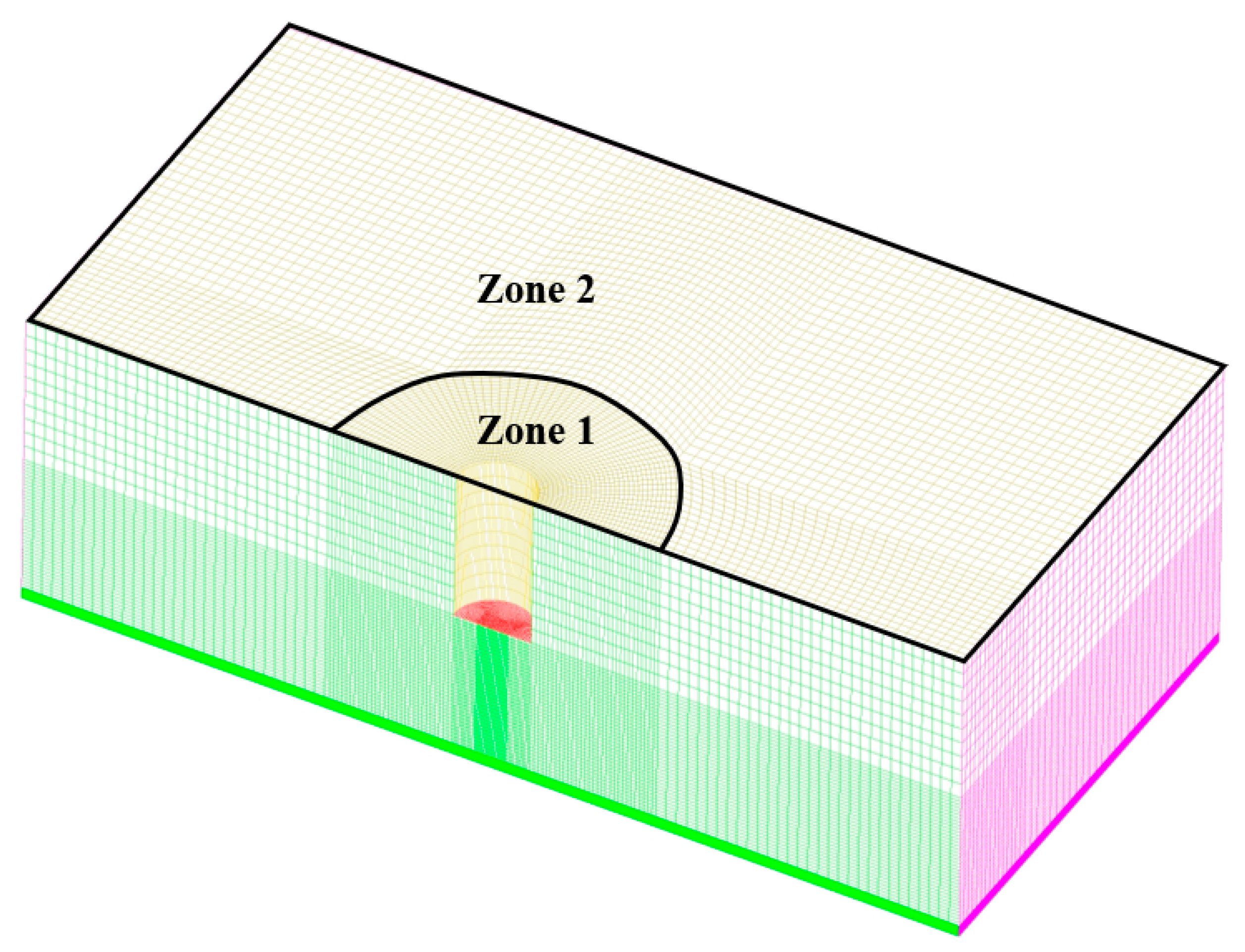
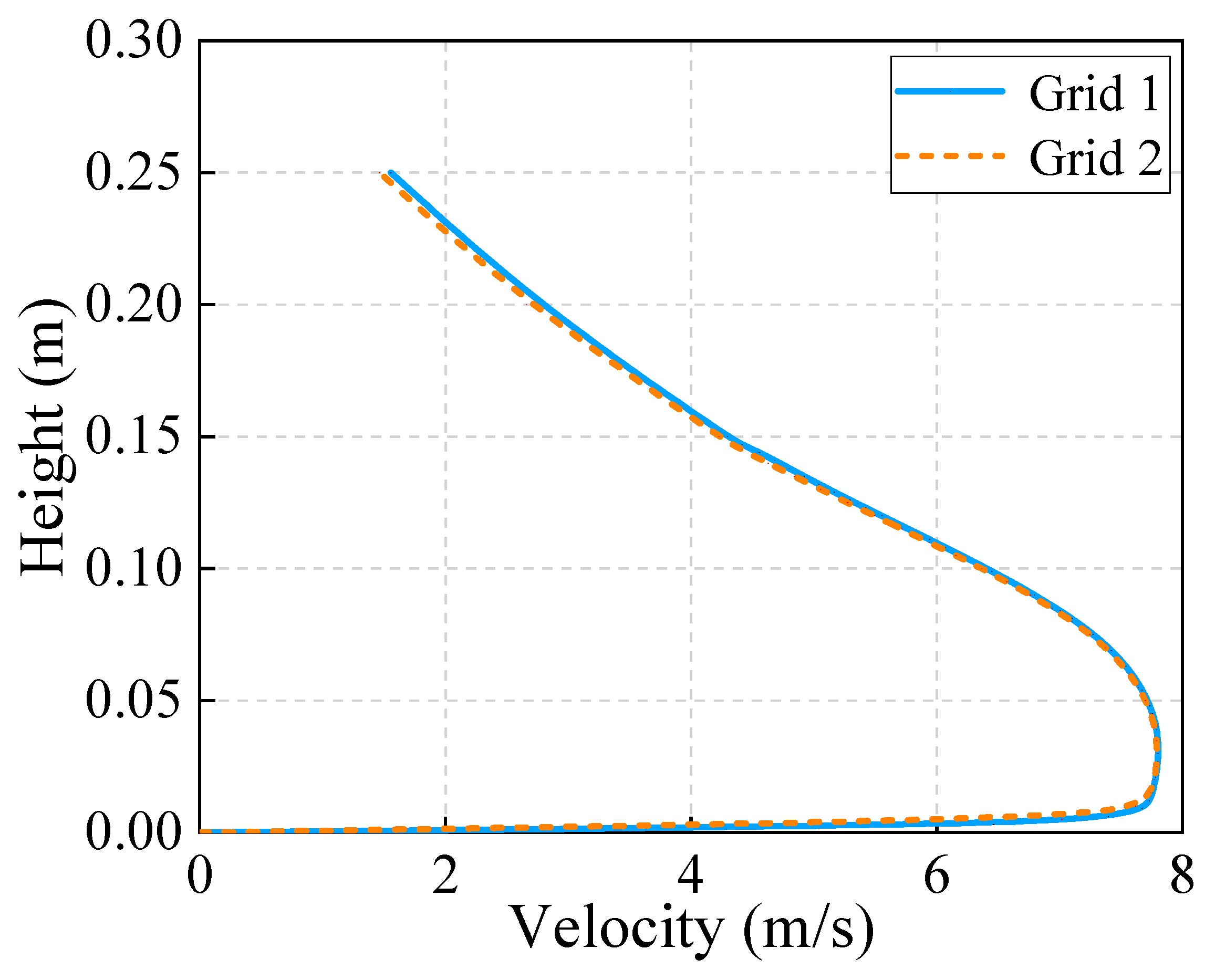
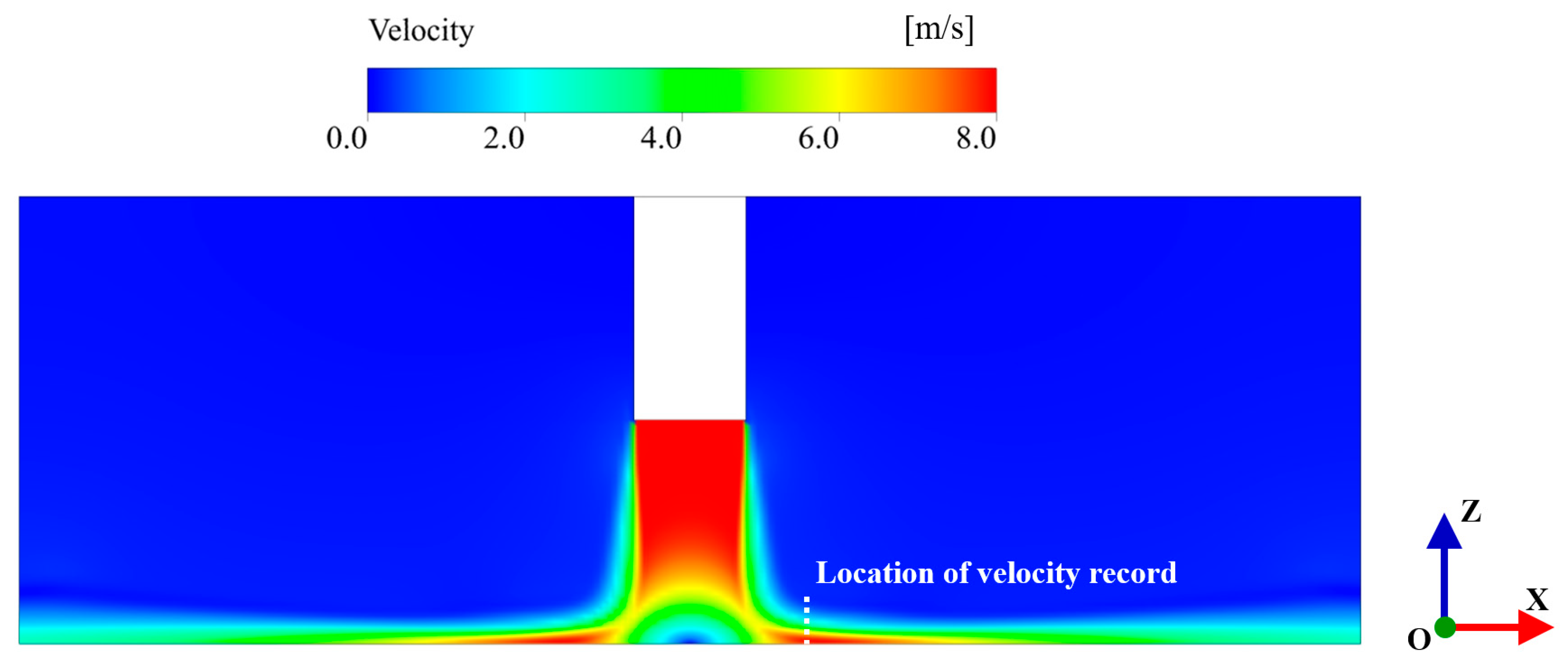
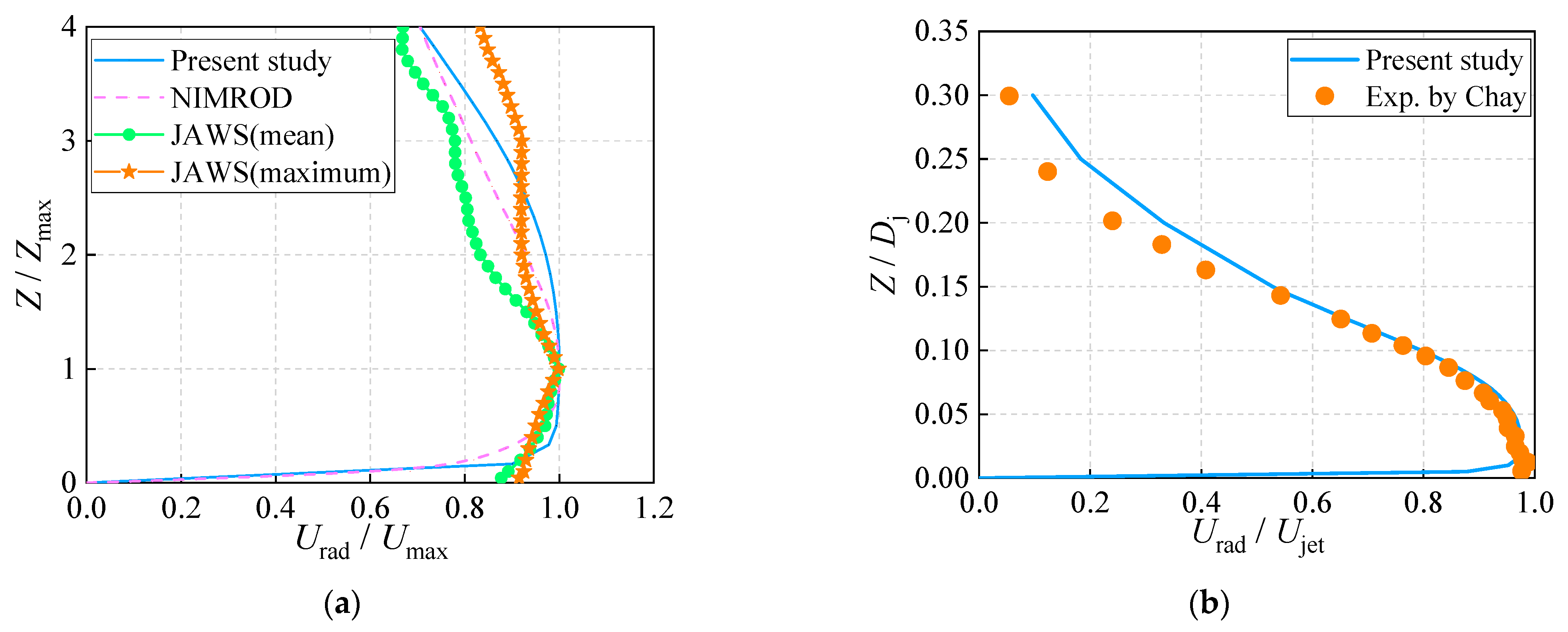


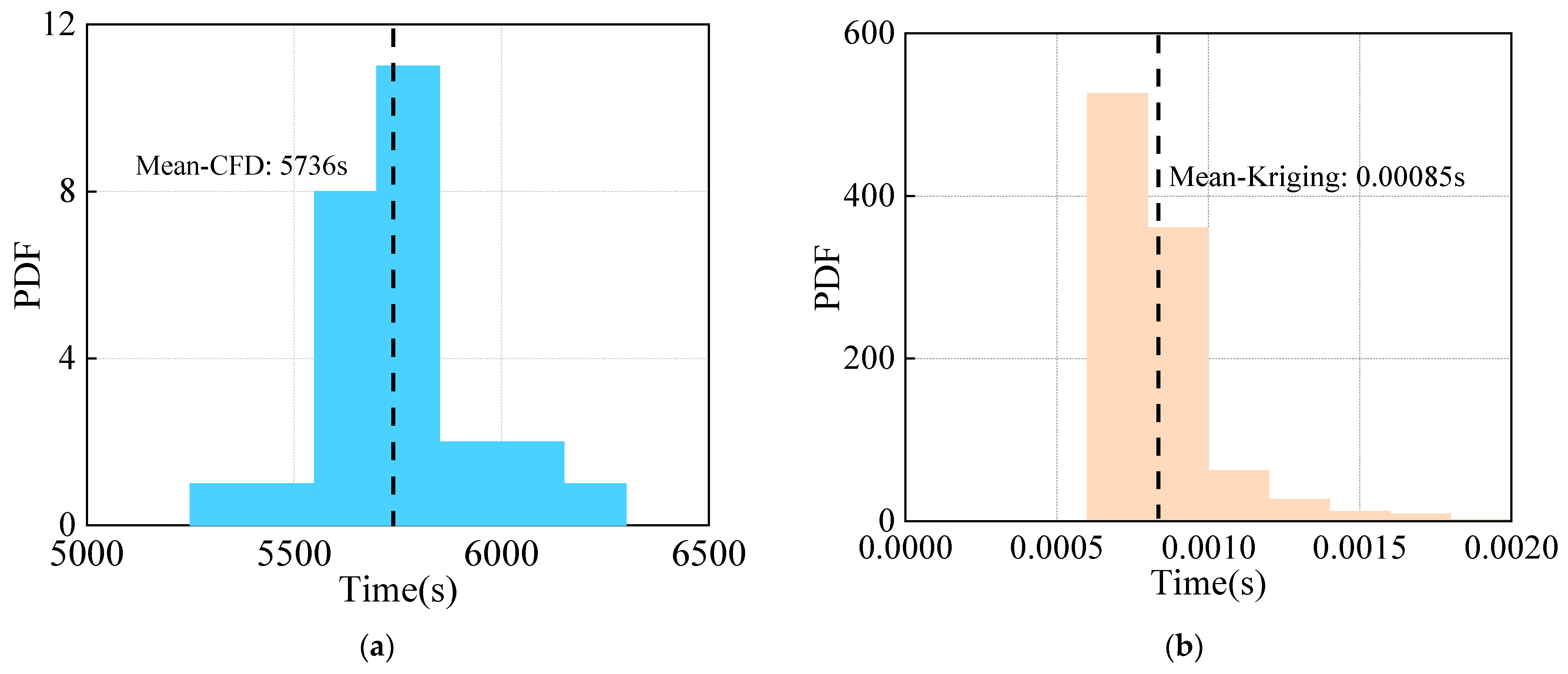



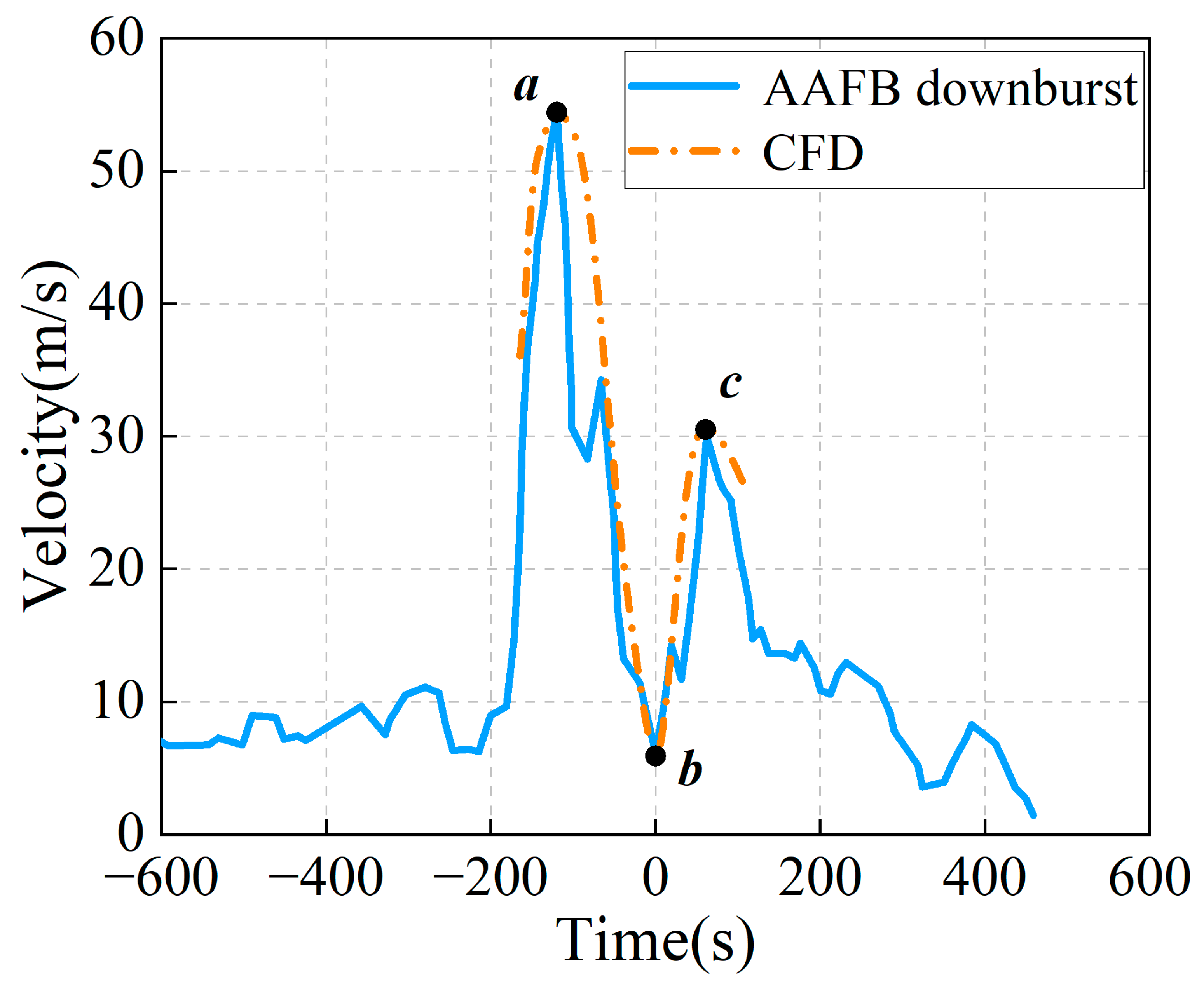
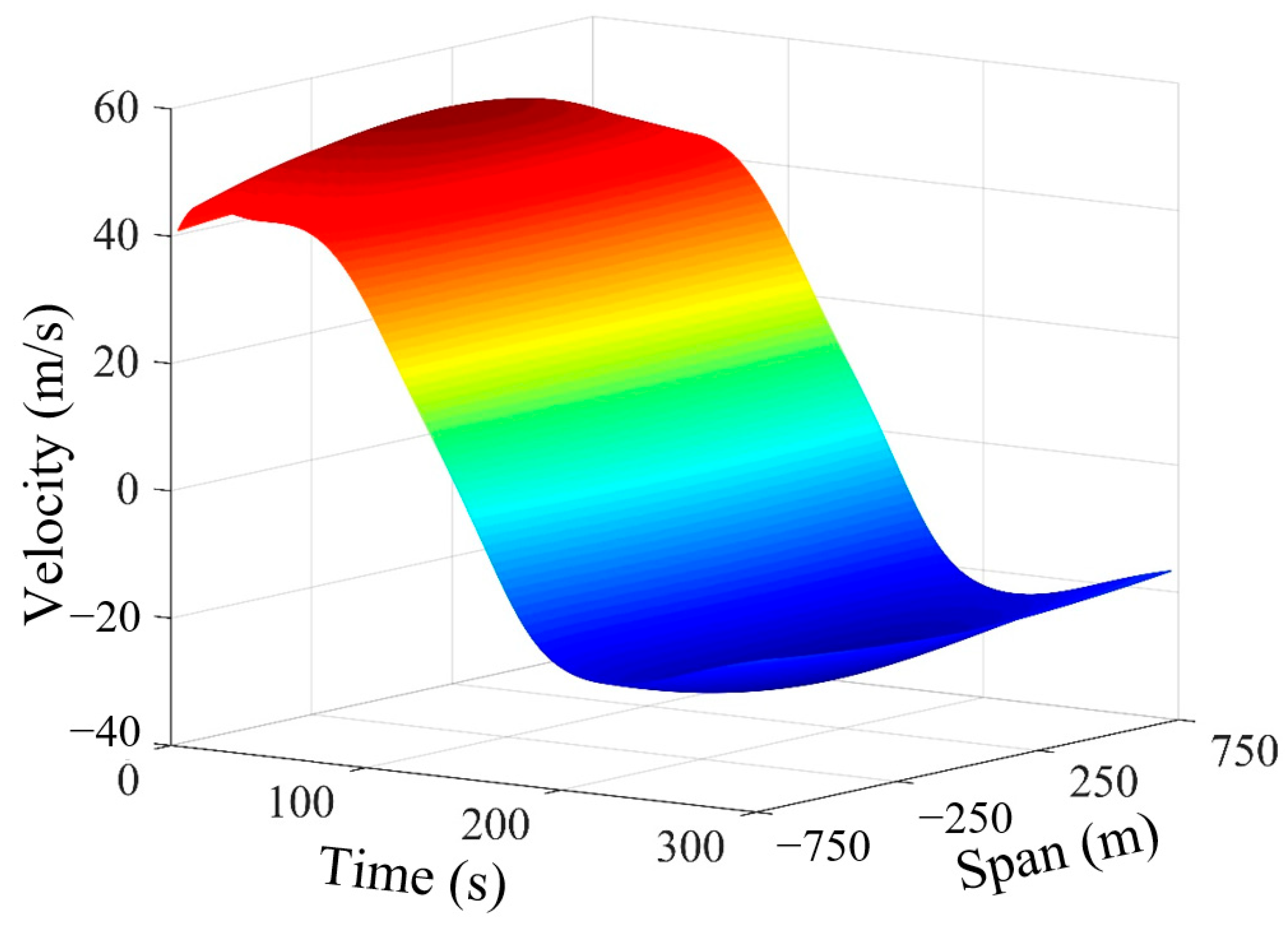
| Zones | Grid 1 | Grid 2 | |
|---|---|---|---|
| Vertical discretization | |||
| Horizontal discretization | Zone1 Zone1 | ||
| Zone2 | |||
| Cell number | / | 4.8 × 105 | 6.2 × 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Xin, L.; Hao, J.; Ding, N.; Wang, F. Numerical Simulation of Long-Span Bridge Response under Downburst: Parameter Optimization Using a Surrogate Model. Mathematics 2023, 11, 3150. https://doi.org/10.3390/math11143150
Feng Y, Xin L, Hao J, Ding N, Wang F. Numerical Simulation of Long-Span Bridge Response under Downburst: Parameter Optimization Using a Surrogate Model. Mathematics. 2023; 11(14):3150. https://doi.org/10.3390/math11143150
Chicago/Turabian StyleFeng, Yu, Lingfeng Xin, Jianming Hao, Nan Ding, and Feng Wang. 2023. "Numerical Simulation of Long-Span Bridge Response under Downburst: Parameter Optimization Using a Surrogate Model" Mathematics 11, no. 14: 3150. https://doi.org/10.3390/math11143150





