Designing a Bayesian Regularization Approach to Solve the Fractional Layla and Majnun System
Abstract
:1. Introduction
- The stochastic BRNNA is applied successfully for the numerical performances of the differential MFLMM.
- The fractional derivatives are implemented to accomplish the accurate performances of differential MFLMM.
- Three different variations based on the MFLMM are numerically simulated through the process of the BRNNA.
- The exactness of the BRNNA is perceived via comparison of performances-based achieved and source solutions.
- The reduceable absolute error (AE) performances authenticate the precision of the BRNNA for solving the MFLMM.
- The correlation/regression, error histograms (EHs), and transition of state (TS) values to solve the MFLMM demonstrate the reliability of the BRNNA.
2. Fractional LMM
3. Designed Methodology
Bayesian Regularization (BR) Scheme
4. Numerical Performances
5. Concluding Remarks
- A soft computing Bayesian regularization-based neural network approach has been suggested successfully for the numerical representations of the MFLMM.
- For the accuracy of the results, the fractional derivatives have been provided to solve the mathematical model.
- The exactness of the proposed BRNNA has been validated through the overlapping of the results.
- The reducible absolute error performances improve the accuracy of the designed BRNNA.
- Twenty neurons have been selected, together with the statics of training 74% and 13%, for both certification and testing.
- The reliability and consistency of the designed BRNNA is demonstrated based on the correlation, transition of state, and performances of error histograms to solve the MFLMM.
Author Contributions
Funding
Conflicts of Interest
References
- Jafari, S.; Ansari, Z.; Golpayegani, S.M.R.H.; Gharibzadeh, S. Is attention a “period window” in the chaotic brain? J. Neuropsychiatry Clin. Neurosci. 2013, 25, E05. [Google Scholar] [CrossRef]
- Sprott, J.C. Dynamical models of happiness. Nonlinear Dyn. Psychol. Life Sci. 2005, 9, 23–36. [Google Scholar]
- Baghdadi, G.; Jafari, S.; Sprott, J.C.; Towhidkhah, F.; Golpayegani, M.H. A chaotic model of sustaining attention problem in attention deficit disorder. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 174–185. [Google Scholar] [CrossRef]
- Tabatabaei, S.S.; Yazdanpanah, M.J.; Jafari, S.; Sprott, J.C. Extensions in dynamic models of happiness: Effect of memory. Int. J. Happiness Dev. 2014, 1, 344–356. [Google Scholar] [CrossRef]
- Farman, M.; Akgül, A.; Aldosary, S.F.; Nisar, K.S.; Ahmad, A. Fractional order model for complex Layla and Majnun love story with chaotic behaviour. Alex. Eng. J. 2022, 61, 6725–6738. [Google Scholar] [CrossRef]
- Dercole, F.; Rinaldi, S. Love stories can be unpredictable: Jules et Jim in the vortex of life. Chaos Interdiscip. J. Nonlinear Sci. 2014, 24, 023134. [Google Scholar] [CrossRef] [PubMed]
- Liao, X.; Ran, J. Hopf bifurcation in love dynamical models with nonlinear couples and time delays. Chaos Solitons Fractals 2007, 31, 853–865. [Google Scholar] [CrossRef]
- Alves-Pires, R. Nonlinear Dynamics in Particle Accelerators; World Scientific: Singapore, 1996; Volume 23. [Google Scholar]
- Newell, A.; Moloney, J. Nonlinear Optics; Addison-Wesley: Reading, MA, USA, 1992. [Google Scholar]
- Cveticanin, L. Resonant vibrations of nonlinear rotors. Mech. Mach. Theory 1995, 30, 581–588. [Google Scholar] [CrossRef]
- Rozhansky, V.A.; Tsendin, L.D. Transport Phenomena in Partially Ionized Plasma; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Wu, X.; Xu, Y.; Zhang, H. Random impacts of a complex damped system. Int. J. Non-Linear Mech. 2011, 46, 800–806. [Google Scholar] [CrossRef]
- Cveticanin, L. Approximate analytical solutions to a class of non-linear equations with complex functions. J. Sound Vib. 1992, 157, 289–302. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, W.; Mahmoud, G.M. On a complex beam–beam interaction model with random forcing. Phys. A Stat. Mech. Appl. 2004, 336, 347–360. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Aly, S.A. On periodic solutions of parametrically excited complex non-linear dynamical systems. Phys. A Stat. Mech. Its Appl. 2000, 278, 390–404. [Google Scholar] [CrossRef]
- Ghanbari, B.; Djilali, S. Mathematical and numerical analysis of a three-species predator-prey model with herd behavior and time fractional-order derivative. Math. Methods Appl. Sci. 2020, 43, 1736–1752. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Umar, M.; Shoaib, M.; Baleanu, D. FMNSICS: Fractional Meyer neuro-swarm intelligent computing solver for nonlinear fractional Lane–Emden systems. Neural Comput. Appl. 2022, 34, 4193–4206. [Google Scholar] [CrossRef]
- Sabir, Z.; Nisar, K.; Raja, M.A.Z.; Ibrahim, A.A.B.A.; Rodrigues, J.J.; Al-Basyouni, K.S.; Mahmoud, S.R.; Rawat, D.B. Design of Morlet wavelet neural network for solving the higher order singular nonlinear differential equations. Alex. Eng. J. 2021, 60, 5935–5947. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Alnahdi, A.S.; Jeelani, M.B.; Abdelkawy, M.A. Numerical investigations of the nonlinear smoke model using the Gudermannian neural networks. Math. Biosci. Eng. 2022, 19, 351–370. [Google Scholar] [CrossRef] [PubMed]
- Sabir, Z.; Wahab, H.A.; Javeed, S.; Baskonus, H.M. An Efficient Stochastic Numerical Computing Framework for the Nonlinear Higher Order Singular Models. Fractal Fract. 2021, 5, 176. [Google Scholar] [CrossRef]
- Sabir, Z. Stochastic numerical investigations for nonlinear three-species food chain system. Int. J. Biomath. 2022, 15, 2250005. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z.; Amin, F.; Saeed, T.; Guerrero-Sanchez, Y. Integrated neuro-swarm heuristic with interior-point for nonlinear SITR model for dynamics of novel COVID-19. Alex. Eng. J. 2021, 60, 2811–2824. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z.; Shoaib, M.; Gupta, M.; Sánchez, Y.G. A stochastic intelligent computing with neuro-evolution heuristics for nonlinear SITR system of novel COVID-19 dynamics. Symmetry 2020, 12, 1628. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z.; Aguilar, J.G.; Amin, F.; Shoaib, M. Neuro-swarm intelligent computing paradigm for nonlinear HIV infection model with CD4+ T-cells. Math. Comput. Simul. 2021, 188, 241–253. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z.; Baskonus, H.M.; Yao, S.W.; Ilhan, E. A novel study of Morlet neural networks to solve the nonlinear HIV infection system of latently infected cells. Results Phys. 2021, 25, 104235. [Google Scholar] [CrossRef]
- Saeed, T.; Sabir, Z.; Alhodaly, M.S.; Alsulami, H.H.; Sánchez, Y.G. An advanced heuristic approach for a nonlinear mathematical based medical smoking model. Results Phys. 2022, 32, 105137. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Guirao, J.L.; Shoaib, M. Integrated intelligent computing with neuro-swarming solver for multi-singular fourth-order nonlinear Emden–Fowler equation. Comput. Appl. Math. 2020, 39, 307. [Google Scholar] [CrossRef]
- Guirao, J.L.; Sabir, Z.; Saeed, T. Design and numerical solutions of a novel third-order nonlinear Emden–Fowler delay differential model. Math. Probl. Eng. 2020, 2020, 7359242. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Golpayegani, S.M.R.H. Layla and Majnun: A complex love story. Nonlinear Dyn. 2016, 83, 615–622. [Google Scholar] [CrossRef]
- Kumar, P.; Erturk, V.S.; Murillo-Arcila, M. A complex fractional mathematical modeling for the love story of Layla and Majnun. Chaos Solitons Fractals 2021, 150, 111091. [Google Scholar] [CrossRef]
- Sabir, Z.; Said, S.B. A fractional order nonlinear model of the love story of Layla and Majnun. Sci. Rep. 2023, 13, 5402. [Google Scholar] [CrossRef]
- Sabir, Z.; Baleanu, D.; Raja, M.A.Z.; Alshomrani, A.S.; Hincal, E. Computational performances of morlet wavelet neural network for solving a nonlinear dynamic based on the mathematical model of the affection of layla and majnun. Fractals 2023, 31, 2340016. [Google Scholar] [CrossRef]
- Sabir, Z.; Guirao, J.L. A Soft Computing Scaled Conjugate Gradient Procedure for the Fractional Order Majnun and Layla Romantic Story. Mathematics 2023, 11, 835. [Google Scholar] [CrossRef]
- Yokuş, A.; Gülbahar, S. Numerical solutions with linearization techniques of the fractional Harry Dym equation. Appl. Math. Nonlinear Sci. 2019, 4, 35–42. [Google Scholar] [CrossRef]
- İlhan, E.; Kıymaz, İ.O. A generalization of truncated M-fractional derivative and applications to fractional differential equations. Appl. Math. Nonlinear Sci. 2020, 5, 171–188. [Google Scholar] [CrossRef]
- Elsonbaty, A.M.R.; Sabir, Z.; Ramaswamy, R.; Adel, W. Dynamical analysis of a novel discrete fractional SITRS model for COVID-19. Fractals 2021, 29, 2140035. [Google Scholar] [CrossRef]
- Mukdasai, K.; Sabir, Z.; Raja, M.A.Z.; Sadat, R.; Ali, M.R.; Singkibud, P. A numerical simulation of the fractional order Leptospirosis model using the supervise neural network. Alex. Eng. J. 2022, 61, 12431–12441. [Google Scholar] [CrossRef]
- Yu, F. Integrable coupling system of fractional soliton equation hierarchy. Phys. Lett. A 2009, 373, 3730–3733. [Google Scholar] [CrossRef]
- Bonilla, B.; Rivero, M.; Trujillo, J.J. On systems of linear fractional differential equations with constant coefficients. Appl. Math. Comput. 2007, 187, 68–78. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Momani, S. On the existence and uniqueness of solutions of a class of fractional differential equations. J. Math. Anal. Appl. 2007, 334, 1–10. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Momani, S.; Ibrahim, R.W. On a fractional integral equation of periodic functions involving Weyl–Riesz operator in Banach algebras. J. Math. Anal. Appl. 2008, 339, 1210–1219. [Google Scholar] [CrossRef]
- De Rochefort, L.; Liu, T.; Kressler, B.; Liu, J.; Spincemaille, P.; Lebon, V.; Wu, J.; Wang, Y. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: Validation and application to brain imaging. Magn. Reson. Med. Off. J. Int. Soc. Magn. Reson. Med. 2010, 63, 194–206. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Huang, H.; Qiu, S.; Liu, Y.; Wu, Y.; Ren, Y.; Mou, J. Application of Bayesian regularization back propagation neural network in sensorless measurement of pump operational state. Energy Rep. 2022, 8, 3041–3050. [Google Scholar] [CrossRef]
- Pereira, A.; Antoni, J.; Leclere, Q. Empirical Bayesian regularization of the inverse acoustic problem. Appl. Acoust. 2015, 97, 11–29. [Google Scholar] [CrossRef]
- Pan, Z.; Lu, W.; Fan, Y.; Li, J. Identification of groundwater contamination sources and hydraulic parameters based on bayesian regularization deep neural network. Environ. Sci. Pollut. Res. 2021, 28, 16867–16879. [Google Scholar] [CrossRef]
- Kiani, A.K.; Khan, W.U.; Raja, M.A.Z.; He, Y.; Sabir, Z.; Shoaib, M. Intelligent backpropagation networks with bayesian regularization for mathematical models of environmental economic systems. Sustainability 2021, 13, 9537. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, X.; Jiang, C.; Liu, S.; Han, Z.; Wang, G. Permeability prediction of multi-stage tight gas sandstones based on Bayesian regularization neural network. Mar. Pet. Geol. 2021, 133, 105320. [Google Scholar] [CrossRef]
- Huang, L.; Bae, Y. Chaotic dynamics of the fractional-love model with an external environment. Entropy 2018, 20, 53. [Google Scholar] [CrossRef]
- Huang, L.; Bae, Y. Nonlinear behavior in fractional-order Romeo and Juliet’s love model influenced by external force with fuzzy function. Int. J. Fuzzy Syst. 2019, 21, 630–638. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H.; Sulaiman, T.A. New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method. Appl. Math. Nonlinear Sci. 2019, 4, 141–150. [Google Scholar] [CrossRef]
- Vajravelu, K.; Sreenadh, S.; Saravana, R. Influence of velocity slip and temperature jump conditions on the peristaltic flow of a Jeffrey fluid in contact with a Newtonian fluid. Appl. Math. Nonlinear Sci. 2017, 2, 429–442. [Google Scholar] [CrossRef]
- Selvi, M.S.M.; Rajendran, L. Application of modified wavelet and homotopy perturbation methods to nonlinear oscillation problems. Appl. Math. Nonlinear Sci. 2019, 4, 351–364. [Google Scholar] [CrossRef]
- Gençoğlu, M.T.; Agarwal, P. Use of quantum differential equations in sonic processes. Appl. Math. Nonlinear Sci. 2021, 6, 21–28. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Senel, M.; Kumar, A.; Yel, G.; Senel, B.; Gao, W. On the Wave Properties of the Conformable Generalized Bogoyavlensky–-Konopelchenko Equation. In Handbook of Fractional Calculus for Engineering and Science; Chapman and Hall/CRC: Boca Raton, FL, USA, 2022; pp. 103–119. [Google Scholar]





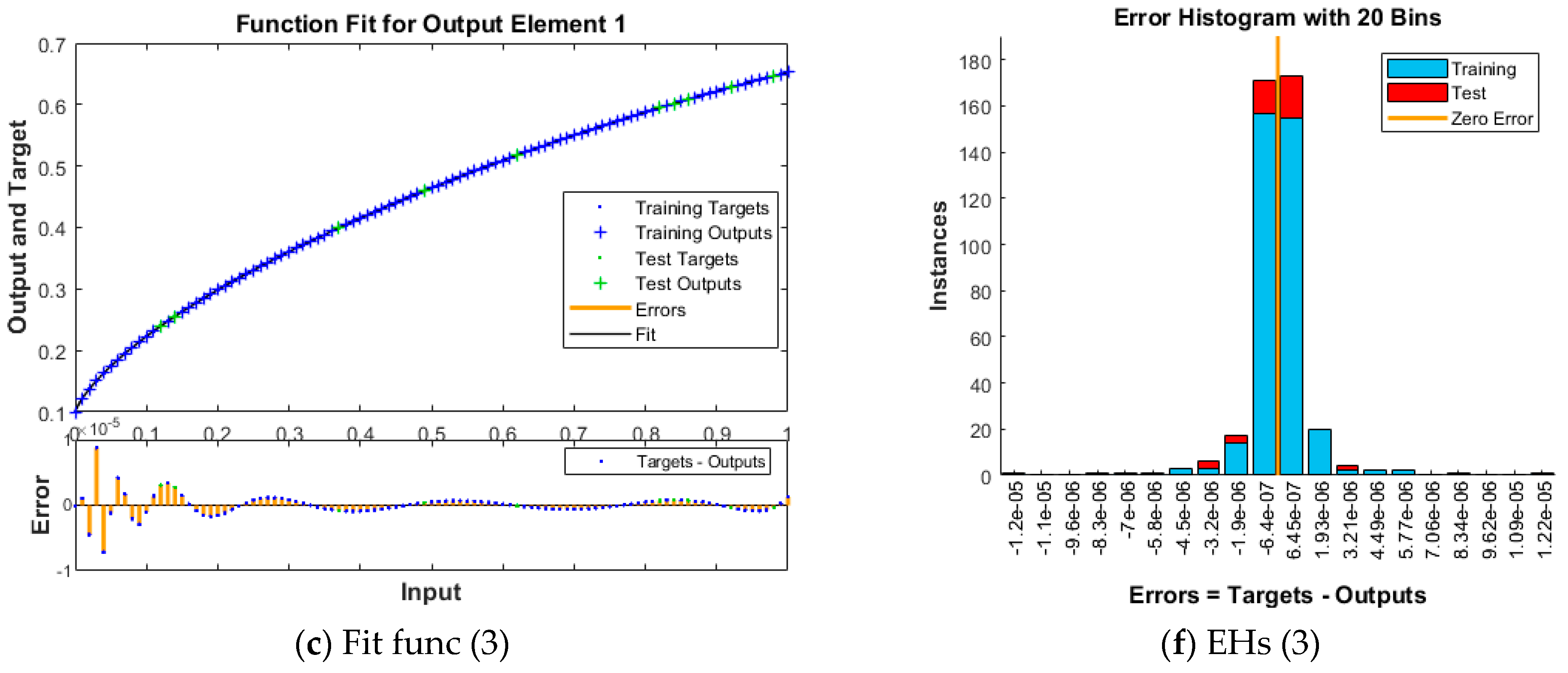


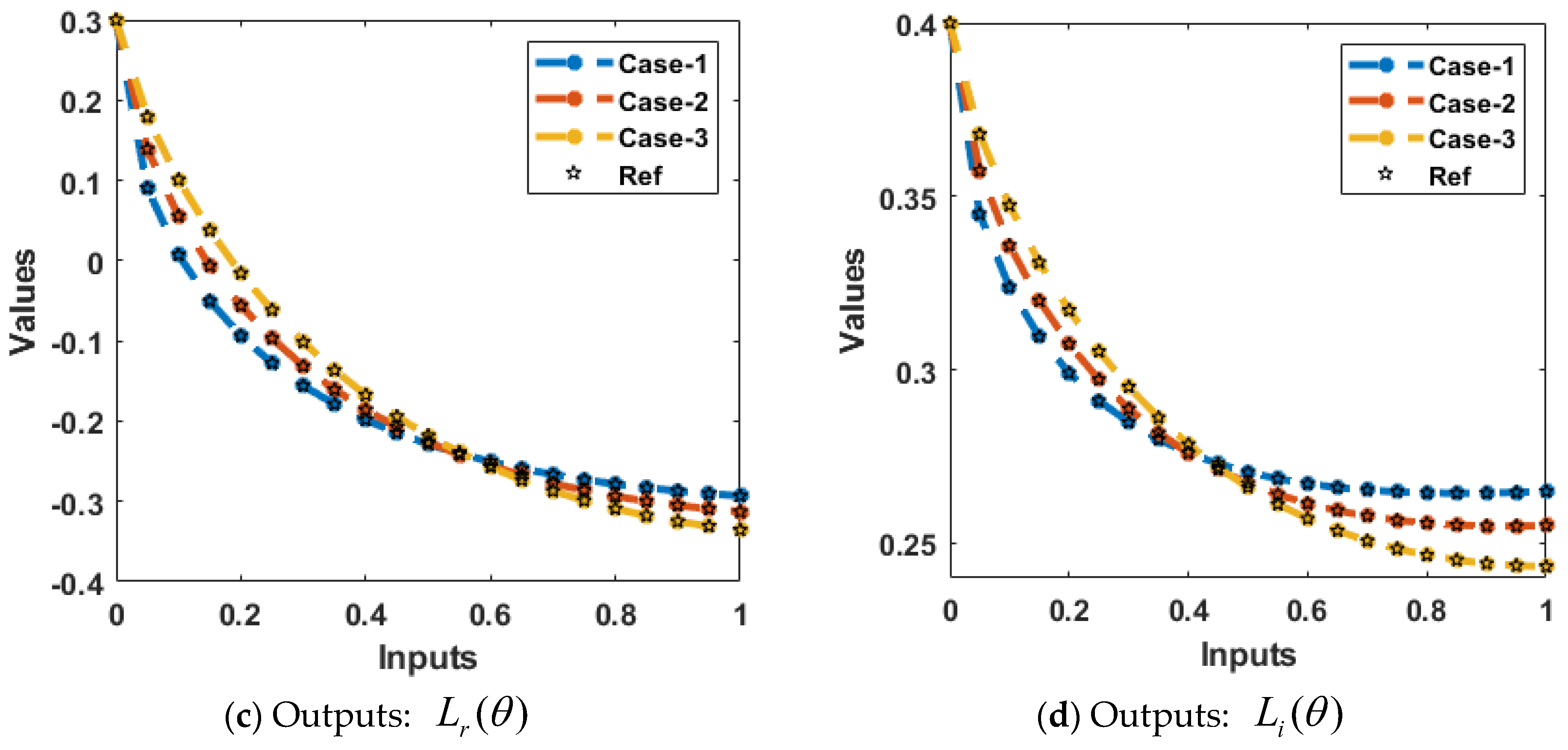
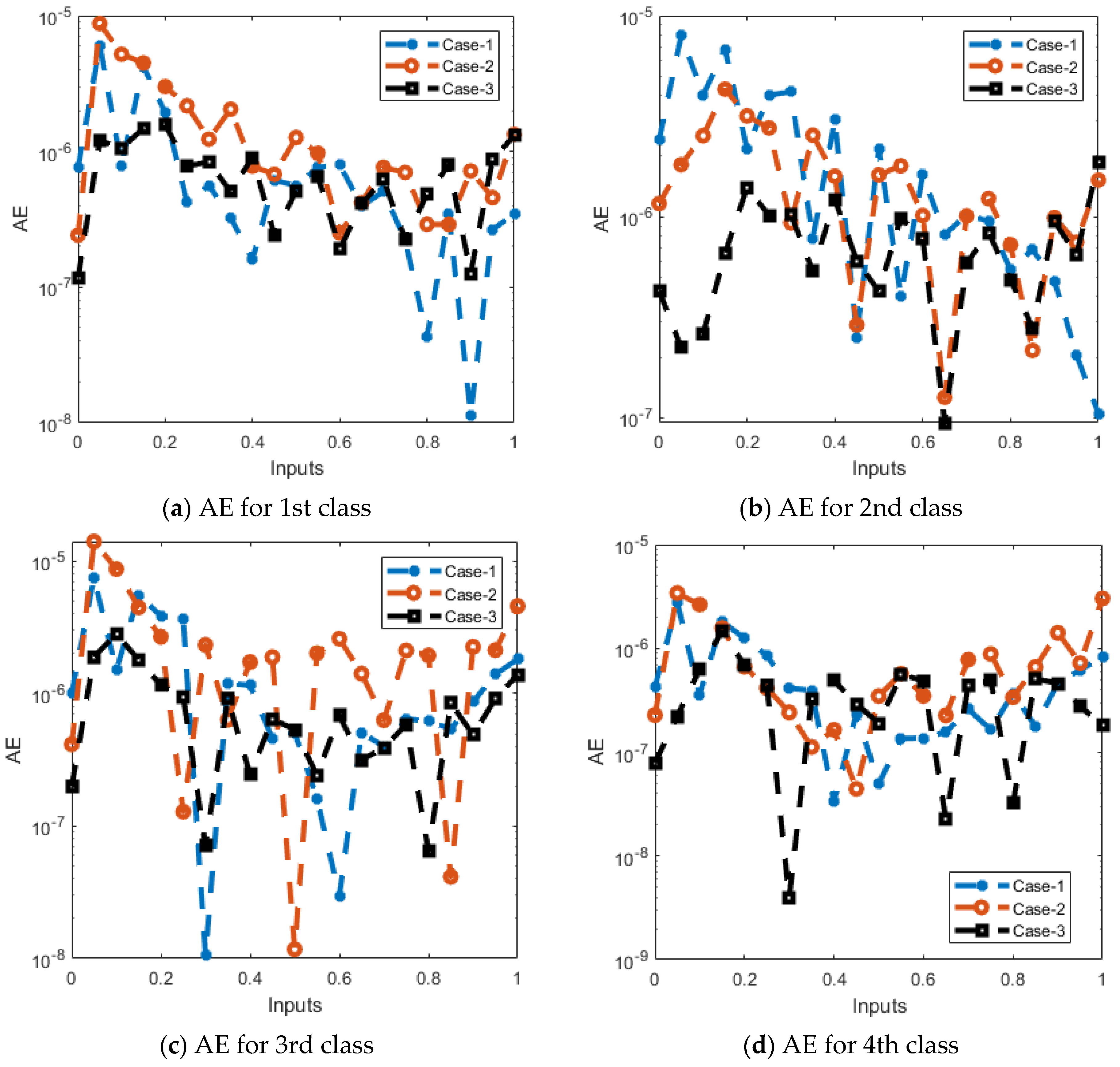
| Case | MSE | Execution | Gradient | Epoch | Time | |
|---|---|---|---|---|---|---|
| Test | Train | |||||
| 1 | 1.65 × 10−11 | 4.67 × 10−11 | 4.67 × 10−11 | 5.12 × 10−8 | 260 | 1 s |
| 2 | 9.35 × 10−12 | 1.65 × 10−11 | 1.77 × 10−11 | 1.48 × 10−8 | 359 | 1 s |
| 3 | 1.55 × 10−12 | 2.65 × 10−12 | 2.66 × 10−12 | 9.10 × 10−9 | 871 | 4 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabir, Z.; Hashem, A.F.; Arbi, A.; Abdelkawy, M.A. Designing a Bayesian Regularization Approach to Solve the Fractional Layla and Majnun System. Mathematics 2023, 11, 3792. https://doi.org/10.3390/math11173792
Sabir Z, Hashem AF, Arbi A, Abdelkawy MA. Designing a Bayesian Regularization Approach to Solve the Fractional Layla and Majnun System. Mathematics. 2023; 11(17):3792. https://doi.org/10.3390/math11173792
Chicago/Turabian StyleSabir, Zulqurnain, Atef F. Hashem, Adnène Arbi, and Mohamed A. Abdelkawy. 2023. "Designing a Bayesian Regularization Approach to Solve the Fractional Layla and Majnun System" Mathematics 11, no. 17: 3792. https://doi.org/10.3390/math11173792





