Impulsive Control of Some Types of Nonlinear Systems Using a Set of Uncertain Control Matrices

Abstract

So many real life problems ranging from medicine, agriculture, biology and finance are modelled by nonlinear systems. In this case, a chaotic nonlinear system is considered and, as opposed to solving Linear Matrix Inequality (LMI), which is the usual approach but cumbersome, a completely different approach was used. In some other cases, the computation of singular value of matrix was used but the method in this study needs not such. In addition, most models, if not all, concentrate on finding a control matrix J under some sufficient conditions. The problem is that only one such matrix J is provided. In reality, the actual control quantity may have a little deviation from the theoretical J. Hence, the study in this paper provides a set of infinite uncertain matrices ${\mathbb{J}}_{\alpha }$ which are able to adapt to control the system under uncertain conditions. It turns out that this new method controls the system in shorter time with less computational complexities.

1. Introduction, Motivation and Model Formulation

Impulses occur and their controls have been studied in many systems such as mechanical, electrical, nanoelectrical and biological systems, just to mention a few. This area of research has kindled the interest of many researchers because of its wide applications in the field of communication, system management, artificial intelligence and robotics which are the seeming future of research in modern day science and technology. Some of the existing chaotic systems which researchers have tried to control are Lorenz’s system [1], Chua’s system [2], Chen’s system [3] and Rössler’s system among others. These were done via different methods.

The methods that have been used in controlling chaotic systems differ from one researcher to the other. Feng et al. in [4] used a combination of memristive neural network and some delay method to develop a quantized intermittent control method which is an extension of the existing intermittent control methods. This was considered more effective in that it would save resources, control cost and information being transmitted among others. A very similar work is in [5].

In 1965, the authors of [6] introduced mathematics of uncertainties which has also influenced the ideas of many researchers in control theory. Nowadays, there are many research works in the area fuzzy control theory. While more attention will be given to impulsive control with time windows, for more diverse thoughts on impulsive control or fuzzy impulsive control, or control with uncertainties, readers can refer to In 1965 [6] introduced mathematics of uncertainties which has also influenced the ideas of many researchers [7] in control theory. Nowadays, there are many researches in the area fuzzy control theory. While more attention will be given to impulsive control with time windows, for more diverse thoughts on impulsive control or fuzzy impulsive control, or control with uncertainties, readers can refer to [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Usually, a nonlinear impulsive control system whose impulses occur within time windows $[n{T}_c,(n+1)T_c)$ as in [25] is

$$\left\{\begin{array}{cc}x(\mathit{t})=\mathbb{B}x(t)+h(x(t)),& n{T}_c\le t<{\pi }_n\\ x(t)=x(t^{-})+Jx(t^{-}),& t=n{T}_c+{\pi }_n\\ x(\mathit{t})=\mathbb{B}x(t)+h(x(t)),& n{T}_c+{\pi }_n<t<(n+1)T_c\end{array}\right.$$

(1)

in which case, $x(t)\in I{R}^n$, is a vector representing the state of the system, $T_c$ is the period within which control takes place, $\mathbb{B}\in I{R}^{n\times n}$ is a matrix which has the system information, $h:I{R}^n⟶I{R}^n$ satisfies that the value of h at zero is zero, $t^{-}$ represents the left limit of time and the control matrix is $J\in I{R}^{n\times n}$ is added anytime within $[n{T}_c,(n+1)T_c)$.

But Feng [26], in 2016, considered impulsive systems which has multiple jumps within time windows. The magnitude of these jumps are unknown. Then, impulses are periodically introduced to control the system. Via Linear Matrix Inequalities (LMIs) [27], the stability criterion for these sort of systems were obtained. The results obtained were used to control the Chua’s oscillator.

In 2017, Feng et al. [28] used a simpler method, some inequality and matrix analysis, rather avoiding LMI, and obtained another sufficient conditions for the stability of nonlinear systems with impulsive time windows. In 2019, [25] also established that the control matrix J in [26,28] needs not be certain in the real sense but can be such that $J\le \mu I$, for a real constant $\mu$.

The limitation of this method is that it can produce only one matrix J which cannot precisely be in real life. There is need to see how far can deviation from J be under which the system can still be controlled. Hence, (1) is adjusted as

$$\left\{\begin{array}{cc}x(\mathit{t})=\mathbb{B}x(t)+h(x(t)),& n{T}_c\le t\le n{T}_c+{\pi }_n\\ x(t)=x(t^{-})+{\mathbb{J}}_{\alpha }x(t^{-}),& t=n{T}_c+{\pi }_n,\alpha \in [0,1)\\ x(\mathit{t})=\mathbb{B}x(t)+h(x(t)),& n{T}_c+{\pi }_n<t(n+1)T_c,\end{array}\right.$$

(2)

where ${\mathbb{J}}_{\alpha }=(1-\alpha )Jfor\alpha \in [0,1)andJ=\mu I$, which gives infinitely many ${\mathbb{J}}_{\alpha }$’s, that are deviations from J by some degrees and still keep the system controlled. When $\alpha =0$, the system becomes (1) and when $\alpha \in (0,1)$, there are many options of useful control matrices which can be adopted depending on the need of the situation. Onasanya et al. [29] in 2021 attempted to obtain the set of deviation matrices but using the method of solving LMI which is more cumbersome.

The model in (1) is such that, within the time window $[n{T}_c,(n+1)T_c)$, a certain impulse J can be introduced to control the chaos. Unfortunately, in real life, it is not always possible to get such certain quantity J; it can rather be a little less or more. However, the model in (2) has accommodated this possible uncertainties in the input of J as ${\mathbb{J}}_{\alpha }$ and has given the degree of freedom within which deviation can be allowed from J.

However, in this paper, using some inequalities without necessarily doing much matrix analysis as in [28] or solving LMI as in [26,28,29], another sufficient conditions were obtained and the stability criterion for (2) were obtained.

In order to do this, let $L=\mathrm{diag}(l_1,l_2,\cdots ,l_n)$ be a diagonal matrix which is positive definite such that ${\left|\right|h(x)\left|\right|}^2\le x^{T}Lx$. Let ${\pi }_n\in [n{T}_c,(n+1)T_c]$, where $n=0,1,2,\cdots$. The goal is to find a set of matrices $\left\{{\mathbb{J}}_{\alpha }\right\}$ which controls the system (2). In addition, in this paper, the set of changeable matrices $\left\{{\mathbb{J}}_{\alpha }\right\}$ have been obtained to control the system (2) and this control method is more flexible and can easily adapt to uncertainties in the system. It has developed a model that can respond more suitably to the uncertain nature of the control impulse.

The structure of the paper is as follows: Section 2 is the main result; Section 3 contains the simulations of numerical examples; Section 4 contains the comparison of the results with those in [28]; Section 5 is the conclusion. Please note that ≈ and ⪅ are respectively approximate and less or equal to in the fuzzy sense and ${\lambda }_i$ and ${\lambda }_u$ are minimum and maximum eigenvalues respectively throughout this paper.

Meanwhile, the following lemma is of importance.

2. Preliminaries

Lemma 1 

([25]). Let $u,v\in I{R}^n$ and $\epsilon >0$. Then

$$2u^{T}v\le \epsilon u^{T}u+\frac{1}{\epsilon }{v}^{T}v.$$

3. Main Results

Theorem 1. 

Let there be $w>0$, $\epsilon >0$, $\delta >0$ and a matrix $Q\in I{R}^{n\times n}$ (symmetric, positive definite) and the set $\left\{{\lambda }_{\alpha }\right\}$, in which case every ${\lambda }_{\alpha }$ has a corresponding control matrix ${\mathbb{J}}_{\alpha }$, such that

(i) 

$\frac{w^2}{4}I-2({\mathbb{B}}^T\mathbb{B}+L)>0$;

(ii) 

$w{T}_c+ln{\lambda }_{\alpha }<0,$ for every $\alpha \in [0,1)$,

where

$${\lambda }_{\alpha }=\frac{{\lambda }_u\left[{(I+{\mathbb{J}}_{\alpha })}^{T}Q(I+{\mathbb{J}}_{\alpha })\right]}{{\lambda }_i(Q)}$$

with

$$Q=\frac{1}{\sqrt{\epsilon }}{[(\frac{w^2}{4\epsilon }-\delta )I-\frac{2}{\epsilon }(Q^{T}Q+L)]}^{\frac{1}{2}}+\frac{w}{2\epsilon }I,$$

then (2) is exponentially stable for every$\alpha \in [0,1)$.

Proof. 

Let

$$\frac{w^2}{4}I-2({\mathbb{B}}^T\mathbb{B}+L)>0,$$

then,

$$\frac{w^2}{4\epsilon }I-\frac{2}{\epsilon }({\mathbb{B}}^T\mathbb{B}+L)>0.$$

Thus, there is a $\delta >0$ that guarantees

$$(\frac{w^2}{4\epsilon }-\delta )I-\frac{2}{\epsilon }({\mathbb{B}}^T\mathbb{B}+L)\ge 0.$$

Letting

$$\mathbb{X}={[(\frac{w^2}{4\epsilon }-\delta )I-\frac{2}{\epsilon }({\mathbb{B}}^T\mathbb{B}+L)]}^{\frac{1}{2}}\ge 0$$

and

$$Q=\frac{1}{\sqrt{\epsilon }}\mathbb{X}+\frac{w}{2\epsilon }I>0,\mathbb{X}=\sqrt{\epsilon }Q-\frac{w}{2\sqrt{\epsilon }}I$$

then

$${\mathbb{X}}^2=(\frac{w^2}{4\epsilon }-\delta )I-\frac{2}{\epsilon }({\mathbb{B}}^T\mathbb{B}+L)\ge 0$$

and

$${\mathbb{X}}^2\le \frac{w^2}{4\epsilon }I-\frac{2}{\epsilon }({\mathbb{B}}^T\mathbb{B}+L).$$

Hence,

$${(\sqrt{\epsilon }Q-\frac{w}{2\sqrt{\epsilon }}I)}^2\le \frac{w^2}{4ϵ}I-\frac{2}{\epsilon }({\mathbb{B}}^T\mathbb{B}+L),$$

from whence

$$\epsilon Q^2+\frac{2}{\epsilon }({\mathbb{B}}^T\mathbb{B}+L)-wQ\le 0.$$

Furthermore, consider the Lyapunov function

$$V_p(x(t))=x^{T}Qx.$$

(3)

By Lemma 1 and Equation (3) it can be shown that, for $[n{T}_c,n{T}_c+{\pi }_n]$,

$$\begin{array}{cc}\hfill {\dot{V}}_p(x(t))& =2x^{T}Q(\mathbb{B}x+h(x))\hfill \\ \hfill & \le \epsilon x^T{Q}^{2}x+\frac{1}{\epsilon }{(\mathbb{B}x+h(x))}^T(\mathbb{B}x+h(x))\hfill \\ \hfill & =x^T(\epsilon Q^2+\frac{2}{\epsilon }({\mathbb{B}}^T\mathbb{B}+L))x\hfill \\ \hfill & =x^T(\epsilon Q^2+\frac{2}{\epsilon }({\mathbb{B}}^T\mathbb{B}+L))x-w{x}^{T}Qx+w{x}^{T}Qx\hfill \\ \hfill & \le x^T(\epsilon Q^2+\frac{2}{\epsilon }({\mathbb{B}}^T\mathbb{B}+L)-wQ)x\hfill \\ \hfill & +w{V}_p(x(t))\hfill \\ \hfill & \le w{V}_p(x(t)).\hfill \end{array}$$

(4)

Hence,

$$V_p(x(t))\le V_p(x(n{T}_c))e^{w(t-n{T}_c)}.$$

(5)

In addition, if $n{T}_c+{\pi }_n<t\le (n+1)T_c$,

$${\dot{V}}_p(x(t))\le w{V}_p(x(t)).$$

(6)

Then,

$$V_p(x(t))\le V_p(x(n{T}_c+{\pi }_n))e^{w(t-n{T}_c-{\pi }_n)}.$$

(7)

If $t=n{T}_c+{\pi }_n$, then the uncertain matrix ${\mathbb{J}}_{\alpha }=(1-\alpha )\mu I={\mu }_{\alpha }I$ is used for control. From the Lyapunov function in (3),

$$\begin{array}{cc}\hfill V_p(x(t))& ⪅\frac{{\lambda }_u\left[{(I+{\mathbb{J}}_{\alpha })}^{T}Q(I+{\mathbb{J}}_{\alpha })\right]}{{\lambda }_i(Q)}{V}_p(x(t^{-}))\hfill \\ \hfill & ={\lambda }_{\alpha }{V}_p(x(t^{-})).\hfill \end{array}$$

(8)

From (8), with $n{T}_c+{\pi }_n\le t<(n+1)T_c$, it can be obtained that

$$V_p(x(n{T}_c+{\pi }_n))\le {\lambda }_{\alpha }{V}_p(x{(n{T}_c+{\pi }_n)}^{-})$$

(9)

and substituting (9) into (7) the following is obtained:

$$V_p(x(t))⪅{\lambda }_{\alpha }{V}_p(x({(n{T}_c+{\pi }_n)}^{-}))e^{w(t-n{T}_c-{\pi }_n)}.$$

(10)

The principle of mathematical induction will be used on n, for $n{T}_c+{\pi }_n\le t<(n+1)T_c$. The following can be obtained for $n=0$:

(i)

In (5) for $0\le t<{\pi }_0$, then

$$V_p(x(t))\le V_p(x(0))e^{wt}.$$

(11)

(ii)

From ${\pi }_0\le t<T_c$, (10) and (11),

$$\begin{array}{cc}\hfill V_p(x(t))& ⪅{\lambda }_{\alpha }{V}_p(x({\pi }_0^{-}))e^{w(t-{\pi }_0)}\hfill \\ \hfill & ⪅{\lambda }_{\alpha }{V}_p(x(0))e^{wt}.\hfill \end{array}$$

(12)

The following can be obtained for $n=1$:

(i)

In (5) and (12), $[T_c,T_c+{\pi }_1)$ and

$$\begin{array}{cc}\hfill V_p(x(t))& \le V_p(x(T_c))e^{w(t-T_c)}\hfill \\ \hfill & ⪅{\lambda }_{\alpha }{V}_p(x(0))e^{wt}.\hfill \end{array}$$

(13)

(ii)

From $[T_c+{\pi }_1,2T_c)$, (10) and (13),

$$\begin{array}{cc}\hfill V_p(x(t))& ⪅{\lambda }_{\alpha }{V}_p(x({(T_c+{\pi }_1)}^{-}))e^{w(t-T_c-{\pi }_1)}\hfill \\ \hfill & ⪅{\lambda }_{\alpha }^2{V}_p(x(0))e^{wt}.\hfill \end{array}$$

(14)

The following can be obtained for $n=2$:

(i)

In (5) and (14), $[2T_c,2T_c+{\pi }_2)$ and

$$\begin{array}{cc}\hfill V_p(x(t))& \le V_p(x(2T_c))e^{w(t-2T_c)}\hfill \\ \hfill & ⪅{\lambda }_{\alpha }^2{V}_p(x(0))e^{wt}.\hfill \end{array}$$

(15)

(ii)

From $[2T_c+{\pi }_2,3T_c)$, (10) and (15),

$$\begin{array}{cc}\hfill V_p(x(t))& ⪅{\lambda }_{\alpha }{V}_p(x({(2T_c+{\pi }_2)}^{-}))e^{w(t-2T_c-{\pi }_2)}\hfill \\ \hfill & ⪅{\lambda }_{\alpha }^3{V}_p(x(0))e^{wt}.\hfill \end{array}$$

(16)

The following can be obtained for $n=s$:

(i)

For $[s{T}_c,s{T}_c+{\pi }_s)$ it can be obtained that

$$\begin{array}{cc}\hfill V_p(x(t))& ⪅{\lambda }_{\alpha }^s{V}_p(x(0))e^{wt}.\hfill \end{array}$$

(17)

(ii)

For $[s{T}_c+{\pi }_s,(s+1)T_c)$,

$$\begin{array}{cc}\hfill V_p(x(t))& ⪅{\lambda }_{\alpha }{V}_p(x({(2T_c+{\pi }_2)}^{-}))e^{w(t-2T_c-{\pi }_2)}\hfill \\ \hfill & ⪅{\lambda }_{\alpha }^{(s+1)}{V}_p(x(0))e^{wt}.\hfill \end{array}$$

(18)

Then, from (17) for $[s{T}_c,s{T}_c+{\pi }_s)$,

$$V_p(x(t))⪅V_p(x(0))e^{s(w{T}_c+ln{\lambda }_{\alpha })}.$$

(19)

In addition, from (18) for $s{T}_c+{\pi }_s<t\le (s+1)T_c$,

$$V_p(x(t))⪅V_p(x(0))e^{(s+1)(w{T}_c+ln{\lambda }_{\alpha })}.$$

(20)

Obviously, since for every $\alpha$ in (19) and (20) $w{T}_c+ln{\lambda }_{\alpha }<0$, then as $t\to \infty$,

$$\underset{t\to \infty }{lim}{V}_p(x(t))=0.$$

□

Corollary 1. 

Given positive constant w and the set $\left\{{\mu }_{\alpha }\right\}$ such that

(i) 

$\frac{w^2}{4}I-2({\mathbb{B}}^T\mathbb{B}+L)>0$;

(ii) 

$w{T}_c+2ln(1+{\mu }_{\alpha })<0,$ for every α,

then system (2) has exponential stability.

Proof. 

Set ${\mathbb{J}}_{\alpha }={\mu }_{\alpha }I$, where ${\mu }_{\alpha }=(1-\alpha )\mu$ and $J=\mu I$. It is known that

$$\begin{array}{ccc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\lambda }_{\alpha }& =& \frac{{\lambda }_u\left[{(I+{\mathbb{J}}_{\alpha })}^{T}Q(I+{\mathbb{J}}_{\alpha })\right]}{{\lambda }_i(Q)}\hfill \end{array}$$

(21)

$$\begin{array}{ccc}& \hspace{1em}\hspace{1em} =& \frac{{(1+{\mu }_{\alpha })}^2{\lambda }_u(Q)}{{\lambda }_i(Q)}\hfill \end{array}$$

(22)

$$\begin{array}{ccc}& \ge & {(1+{\mu }_{\alpha })}^2\hfill \end{array}$$

(23)

Without loss of generality, choose

$${\lambda }_{\alpha }={(1+{\mu }_{\alpha })}^2.$$

Since

$$w{T}_c+2ln(1+{\mu }_{\alpha })<0,$$

then

$$w{T}_c+ln{\lambda }_{\alpha }<0.$$

Hence, the proof is complete. □

Remark 1. 

Consider the control matrix $J=\mu I$ and the uncertain matrix ${\mathbb{J}}_{\alpha }=(1-\alpha )J=(1-\alpha )\mu I={\mu }_{\alpha }I$, the matrix J with the set of matrix ${\mathbb{J}}_{\alpha }$ satisfy $J\le {\mathbb{J}}_{\alpha }$ for all α. Hence, it can be said that the result in this paper generalises the work of [9,10].

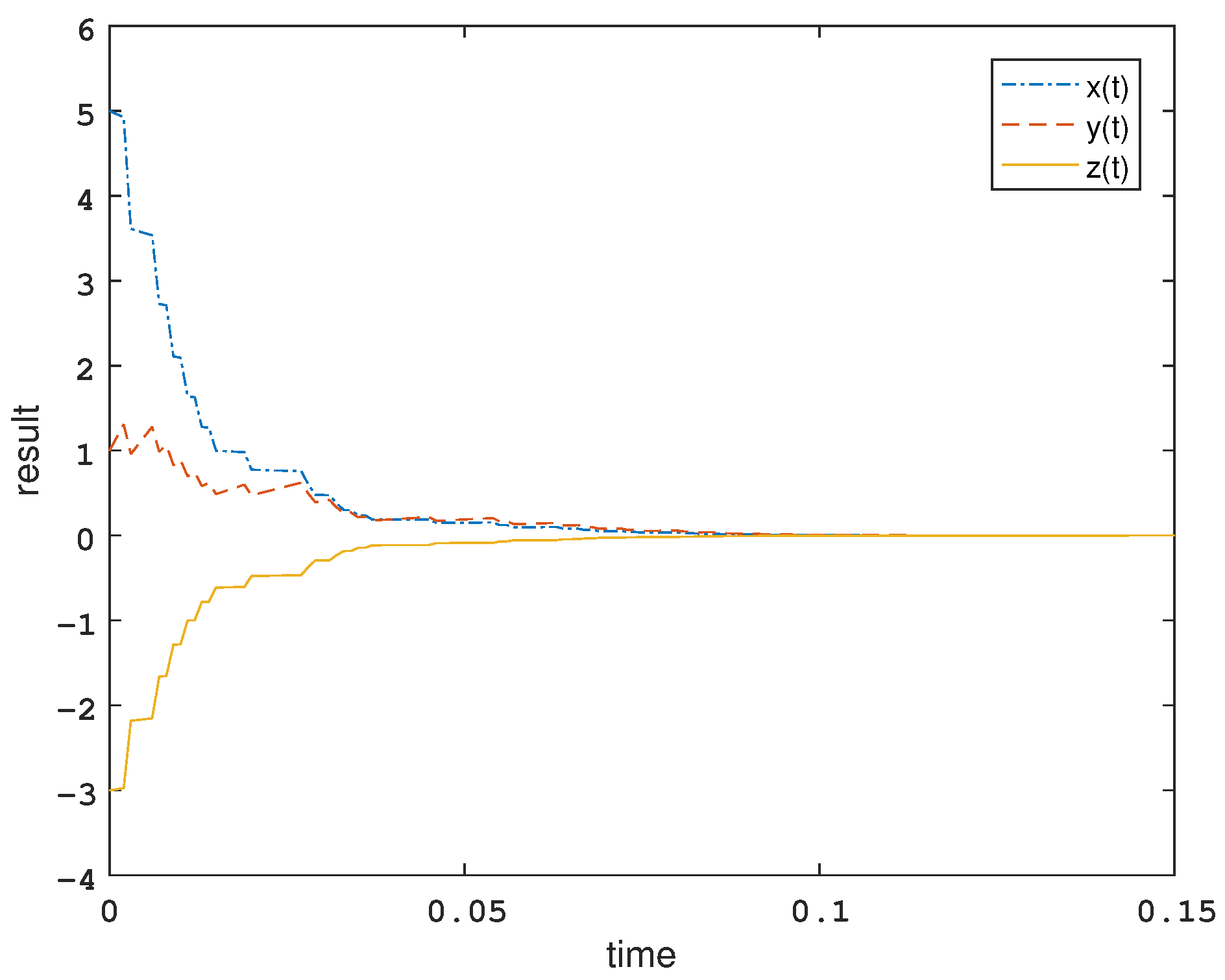
4. Numerical Examples and Simulations

Example 1. 

Lorenz’s system [1] is

$$\left\{\begin{array}{c}{\dot{x}}_1=-\mu x_1+\mu x_2\hfill \\ {\dot{x}}_2=\nu x_1-x_2-x_1{x}_3\hfill \\ {\dot{x}}_3=x_1{x}_2-\omega x_3\hfill \end{array}\right.$$

(24)

Then, (24) is now

$$x=\mathbb{B}x+h(x),$$

where $x={[x_1,x_2,x_3]}^T$ and

$$\mathbb{B}=\left[\begin{array}{ccc}-10& 10& 0\\ 28& -1& 0\\ 0& 0& -\frac{8}{3}\end{array}\right],$$

and $\mu =10$$\nu =28$, $\omega =\frac{8}{3}$ and $d=20$.

This system is chaotic at $x_0$ = [5, 1, −3]^T as shown in Figure 1 and Figure 2.

Set $L=\mathrm{diag}(0,400,400),\epsilon =1,T_c=0.0026$ and $w=90$. It can be shown that

$${\mathbb{B}}^T\mathbb{B}+L=\left[\begin{array}{ccc}884& -128& 0\\ -128& 501& 0\\ 0& 0& 407.1111\end{array}\right]$$

In addition, set

$$J=(\frac{t+1}{t})\ast \mathrm{diag}(-0.2,-0.2,-0.2)$$

and

$${\mathbb{J}}_{\alpha }=(1-\alpha )\ast (\frac{t+1}{t})\ast \mathrm{diag}(-0.2,-0.2,-0.2).$$

To be precise, at $\alpha =0$, $J_0=J$, in which case ${\lambda }_0=0.6400$ and control is guaranteed at $\alpha \in [0,0.444)$.

So, at $\alpha =0.4$, $J_{0.4}=0.6\ast (\frac{t+1}{t})\ast \mathrm{diag}(-0.2,-0.2,-0.2)$, in which case ${\lambda }_{0.4}=0.7744$, and the response curve is in Figure 3.

Example 2. 

Chua’s system [30] is

$$\left\{\begin{array}{cc}{\dot{x}}_1\hfill & =\mu (x_2-x_1-u(x_1))\hfill \\ {\dot{x}}_2\hfill & =x_1-x_2-x_3\hfill \\ {\dot{x}}_3\hfill & =-\varrho x_2\hfill \end{array}\right.$$

(25)

where

$$u(x_1)=\varkappa x_1+0.5(ϵ-\varkappa )(|x_1+1|-|x_1-1|),ϵ<\varkappa <0.$$

Then, (25) is

$$x=\mathbb{B}x+h(x),$$

where $x={[x_1,x_2,x_3]}^T$ and

$$\mathbb{B}=\left[\begin{array}{ccc}-\mu -\mu \varkappa & \mu & 0\\ 1& -1& 1\\ 0& -\varrho & 0\end{array}\right]=\left[\begin{array}{ccc}-2.2362& 9.2156& 0\\ 1& -1& 1\\ 0& -15.9946& 0\end{array}\right],$$

$\mu =9.2156,\varrho =15.9946,ϵ=$−$1.24905,\varkappa =$−$0.75735,\epsilon =1,w=80$ and $T_c=0.0018$.

$${\left|\right|h(x)\left|\right|}^2\le {\mu }^2{(ϵ-\varkappa )}^2,$$

set $L=\mathrm{diag}({\mu }^2{(ϵ-\varkappa )}^2,0,0)=(20.5328,0,0)$.

This system is chaotic at $x_0$ = [5, 1, −3]^T as shown in Figure 4 and Figure 5.

It can be shown that

$${\mathbb{B}}^T\mathbb{B}+L=\left[\begin{array}{ccc}26.5332& -21.6076& 1\\ -21.6076& 341.7545& -1\\ 1& -1& 1\end{array}\right]$$

In addition, set

$$J=(\frac{t+1}{t})\ast \mathrm{diag}(-0.28,-0.28,-0.28)$$

and

$${\mathbb{J}}_{\alpha }=(1-\alpha )\ast (\frac{t+1}{t})\ast \mathrm{diag}(-0.28,-0.28,-0.28).$$

To be precise, at $\alpha =0$, $J_0=J$, in which case ${\lambda }_0=0.5184$ and control of this is guaranteed at $\alpha \in [0,0.75)$.

So, at $\alpha =0.75$, $J_{0.75}=0.25\ast (\frac{t+1}{t})\ast \mathrm{diag}(-0.28,-0.28,-0.28)$, in which case ${\lambda }_{0.75}=0.8649$, and the response curve is in Figure 6.

Example 3. 

Rössler’s system [28] is

$$\left\{\begin{array}{c}{\dot{x}}_1=-x_2-x_3\hfill \\ {\dot{x}}_2=x_1+a{x}_2\hfill \\ {\dot{x}}_3=b{x}_1-c{x}_3+x_1{x}_3\hfill \end{array}\right.$$

(26)

Then, (26) can also be expressed as

$$x=\mathbb{B}x+h(x),$$

where $x={[x_1,x_2,x_3]}^T$ and

$$\mathbb{B}=\left[\begin{array}{ccc}0& -1& -1\\ 1& 0.34& 0\\ 0.4& 0& -4.5\end{array}\right],$$

and $d=20$, $a=0.34$, $c=4.5$ and $b=0.4$.

This system is chaotic at $x_0$ = [−1, 3, −2]^T as shown in Figure 7 and Figure 8.

Set $L=\mathrm{diag}(0,0,400),\epsilon =1,T_c=0.002$ and $w=60$. It can be shown that

$${\mathbb{B}}^T\mathbb{B}+L=\left[\begin{array}{ccc}1.16& 0.34& -1.8\\ 0.34& 1.1156& 1\\ -1.8& 1& 421.25\end{array}\right]$$

In addition, set

$$J=(\frac{t+1}{t})\ast \mathrm{diag}(-0.16,-0.16,-0.16)$$

and

$${\mathbb{J}}_{\alpha }=(1-\alpha )\ast (\frac{t+1}{t})\ast \mathrm{diag}(-0.16,-0.16,-0.16).$$

To be precise, at $\alpha =0$, $J_0=J$, in which case ${\lambda }_0=0.7056$ and control is guaranteed at $\alpha \in [0,0.63)$.

Also, at $\alpha =0.2$, $J_{0.2}=0.8\ast (\frac{t+1}{t})\ast \mathrm{diag}(-0.16,-0.16,-0.16)$, in which case ${\lambda }_{0.2}=0.7604$, and the response curve is in Figure 9.

5. Comparison of Results

Comparing the results of the method in [28] and this paper, one can carefully observe that the control method in this paper saves time in that all of them were achieved in far less than 0.2 unit of time as opposed to what obtains in [28]. As a matter of fact, the control time for the Lorenz’s, Chua’s and Rössler’s systems dropped by about 25%, and can even be less depending on the choice of $\alpha$, compared to the control time in [28]. In addition, there are infinitely many $J\in {\left\{{\mathbb{J}}_{\alpha }\right\}}_{\alpha \in [0,1)}$. One limitation of this method may be the choice of appropriate $\alpha$. The good thing, however, is that the system does not introduce conservatism as ${\mathbb{J}}_{\alpha }$ is time-varying.

6. Conclusions

The set of changeable matrices $\left\{{\mathbb{J}}_{\alpha }\right\}$ have been obtained to control the system (2) rather than one control matrix J. The possibility of infinite choices of control matrices makes this control method more flexible and realistic. Besides that this method is more flexible, it can easily adapt to errors due to uncertainties in the system. Instead of using the LMI and computation of maximum singular value of matrix $(I+J)$, the results were obtained by employing simple inequalities. The result of the simulation shows that this method is less cumbersome and less time consuming. In other words, this new approach is less rigorous, requires less time, basic computational skills and minimal MATLAB programming code. This paper has developed a model that can respond more suitably to the uncertain nature of the control impulse. As a matter of fact, for every $\alpha$, there is a control.