Comparative Sensitivity Analysis of Some Fuzzy AHP Methods
Abstract
:1. Introduction
- (1)
- Identification of the computational stability of the FAHP methods being tested, depending on the selected scale.
- (2)
- Identification of the correlation of the aggregation methods of AHP matrices with the computational stability of the FAHP methods being tested.
- (3)
- Identification of the correlation of the aggregation methods of FAHP matrices with the computational stability of the FAHP methods being tested.
2. Literature Review
3. Materials and Methods
3.1. Fundamentals of the Analytic Hierarchy Process and the Theory of Fuzzy Numbers
3.2. Description of Fuzzy Analytic Hierarchy Process and Defuzzification Methods
3.2.1. Fuzzy Arithmetic Mean Method
3.2.2. Fuzzy Geometric Mean Method
3.2.3. Extent Analysis Method
- Summing up the values of the i-th criterion, we get a sub-total :
- To calculate the DEV divisor, we sum up the obtained values of the sums and perform the division operation :
- To get the DEV value, the above is multiplied by the values of the -th criteria .
3.2.4. Lambda-Max Method
3.2.5. Defuzzification
3.3. Method for the Study of the Stability of the Methods
3.3.1. Algorithm for Checking the Influence of the Scale Employed in FAHP Methods
3.3.2. Algorithm for Checking Methods of AHP Matrices’ Aggregation into FAHP Matrix
3.3.3. Algorithm for Checking the Methods of Aggregating the Fuzzy Matrices
3.3.4. Metrics for Evaluating the Quality of the Model
| Algorithm 1 RRM-BR |
| procedure RRM-BR(W) , , iϵ[1,n] , do while do if end procedure |
| Algorithm 2 RRM-AR |
| procedure RRM-AR(W) , , iϵ[1,n] , , i iϵ[1,n] do while do if end procedure |
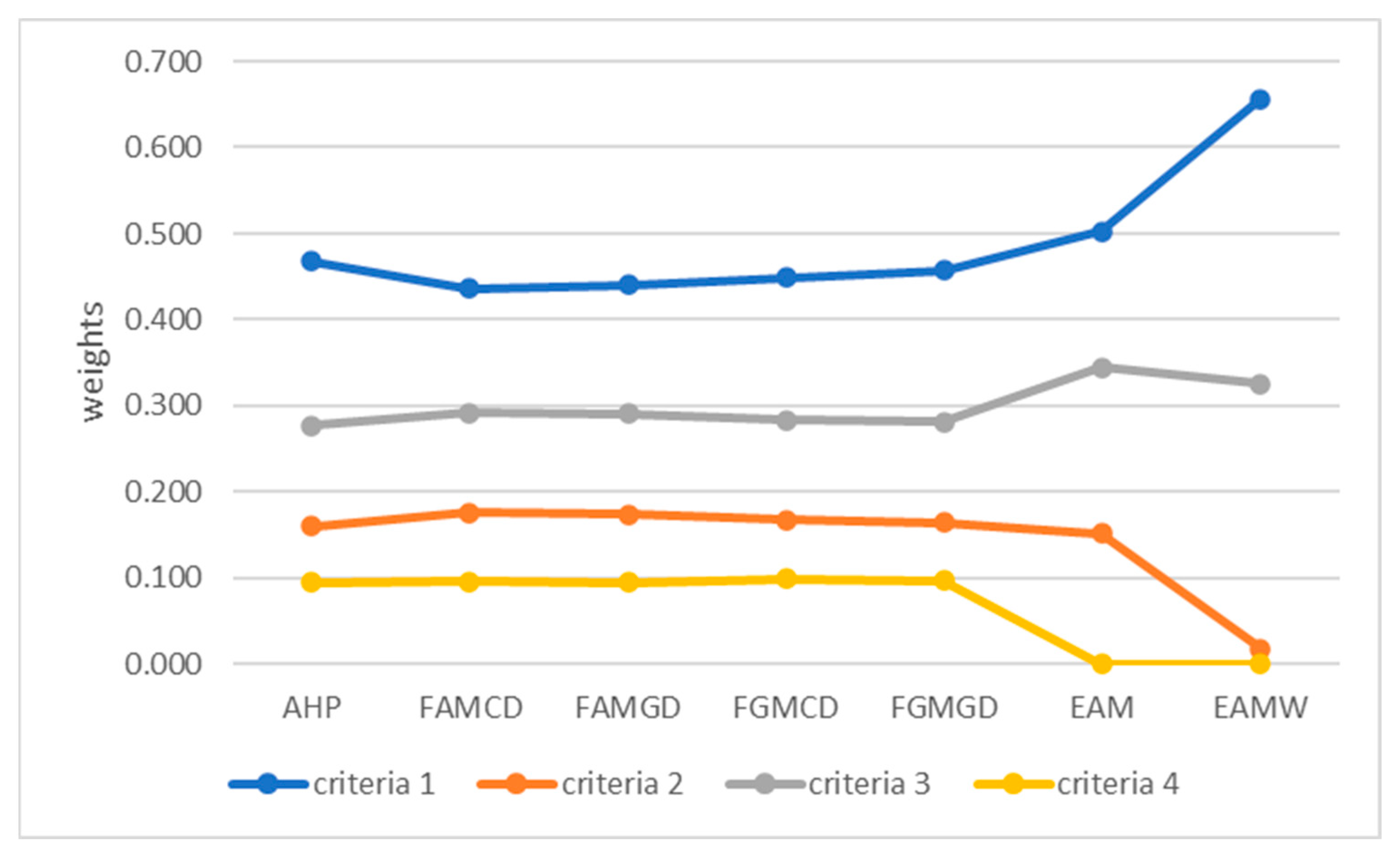
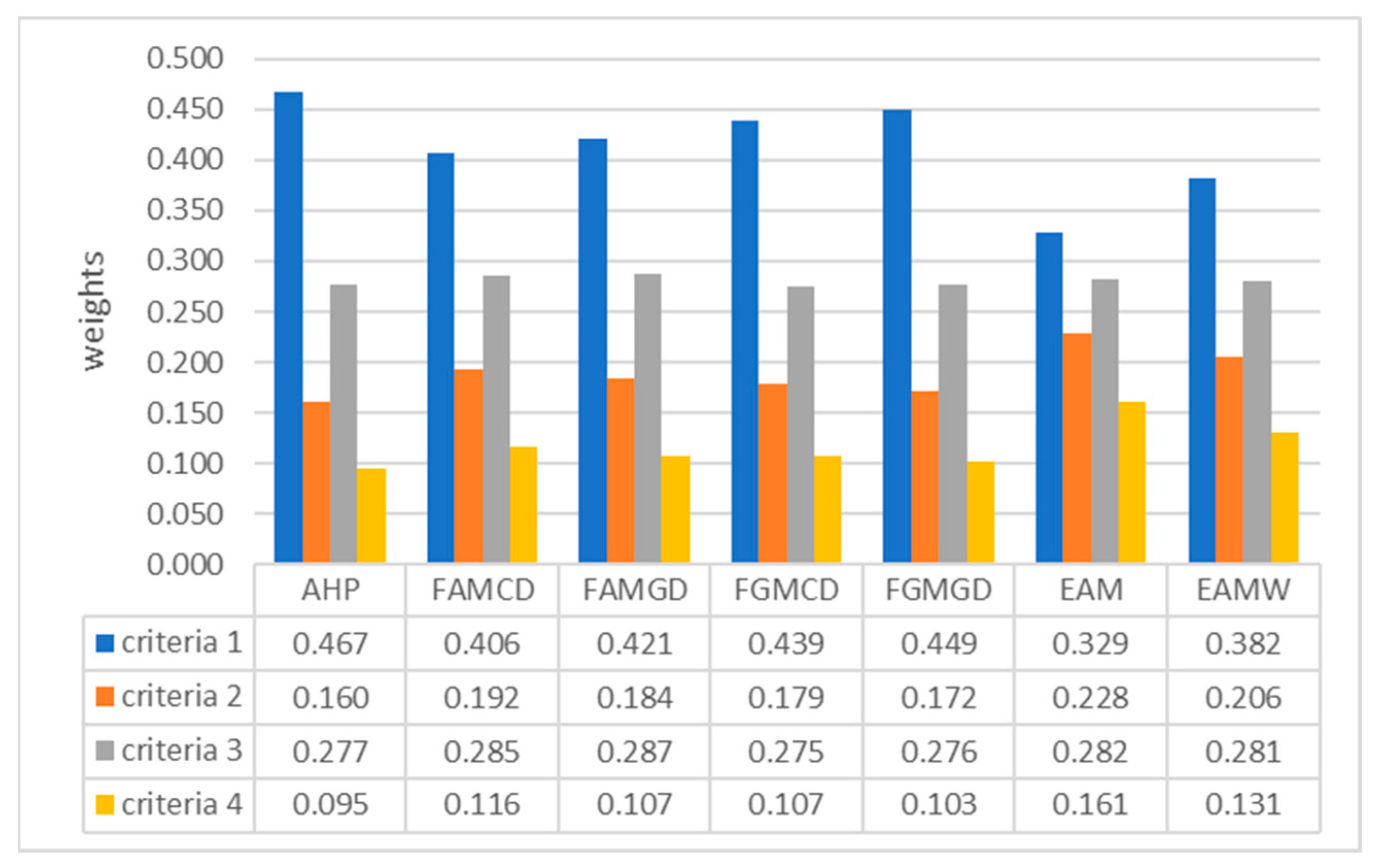
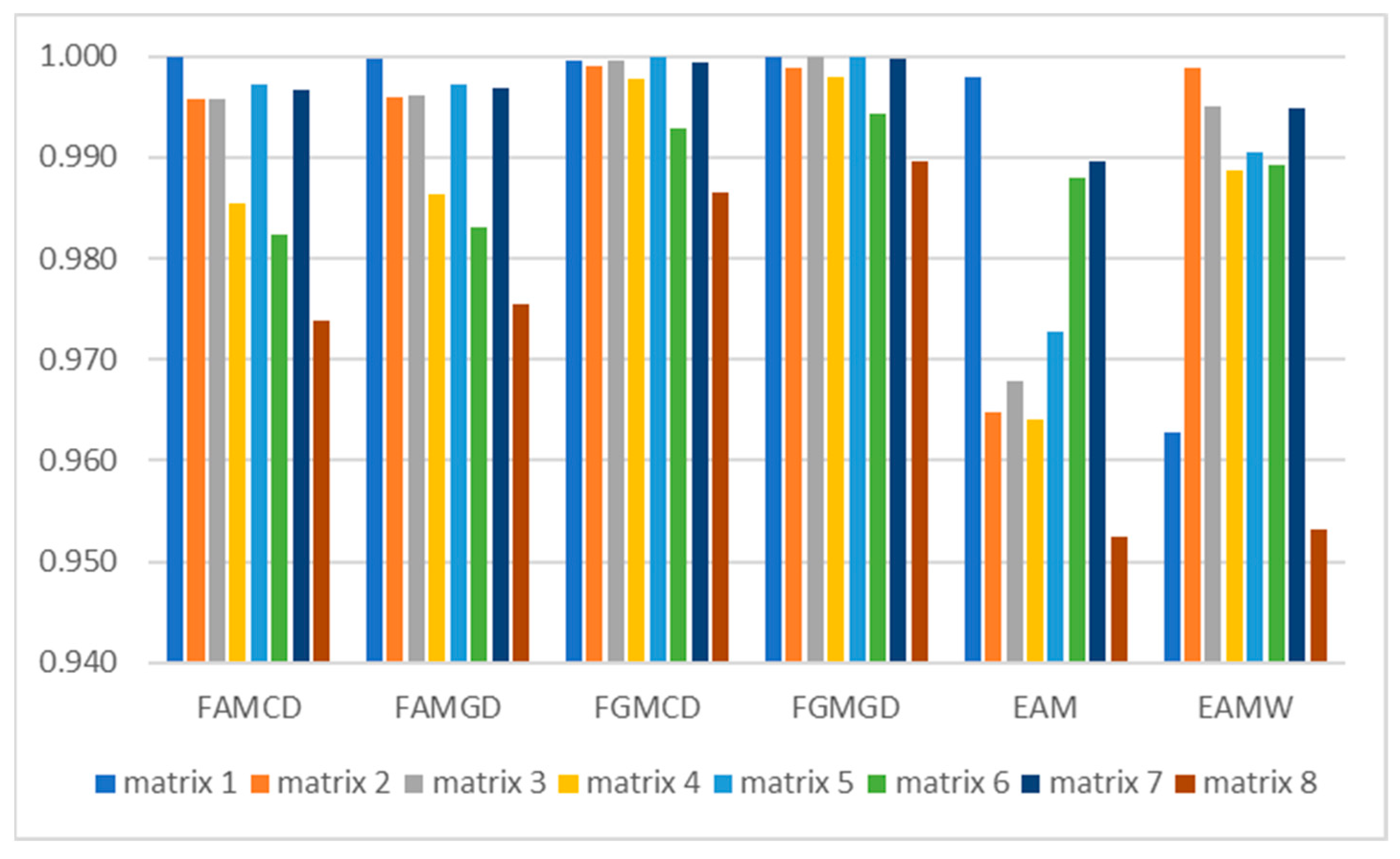
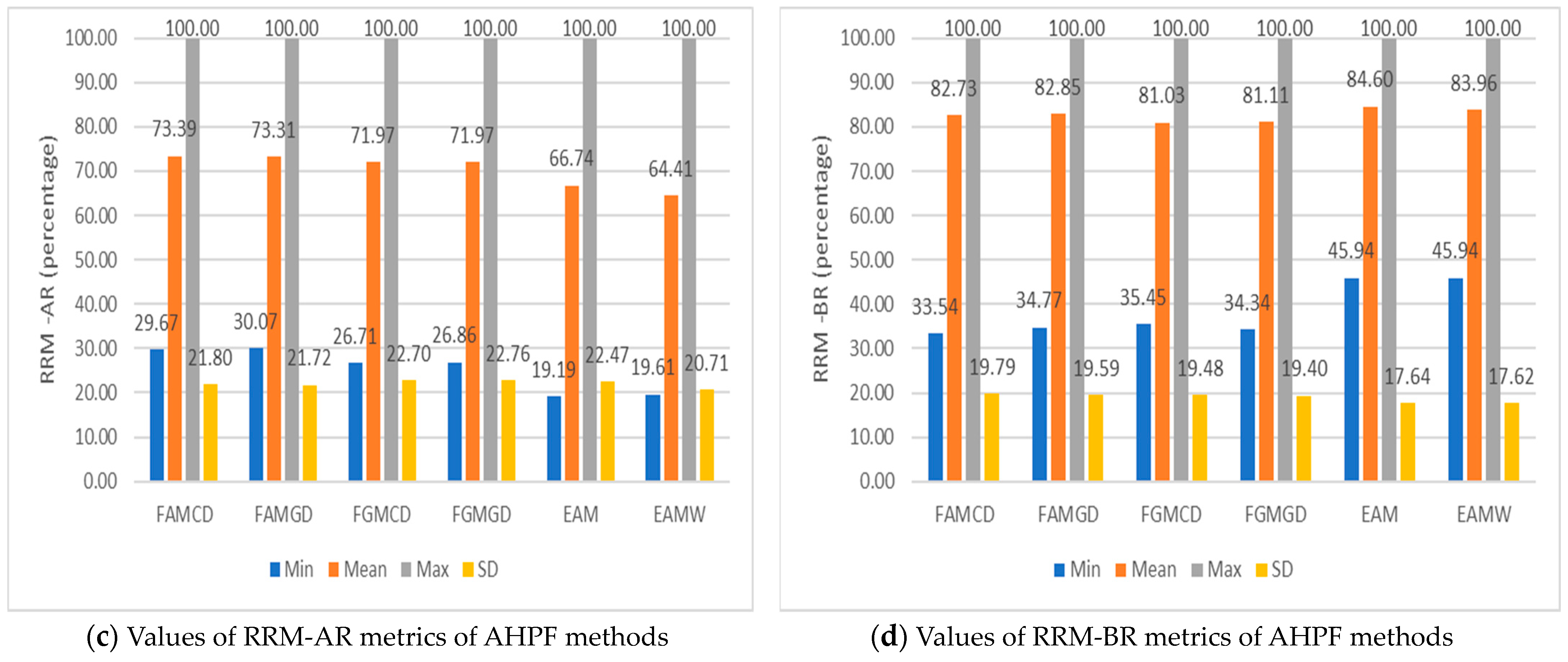
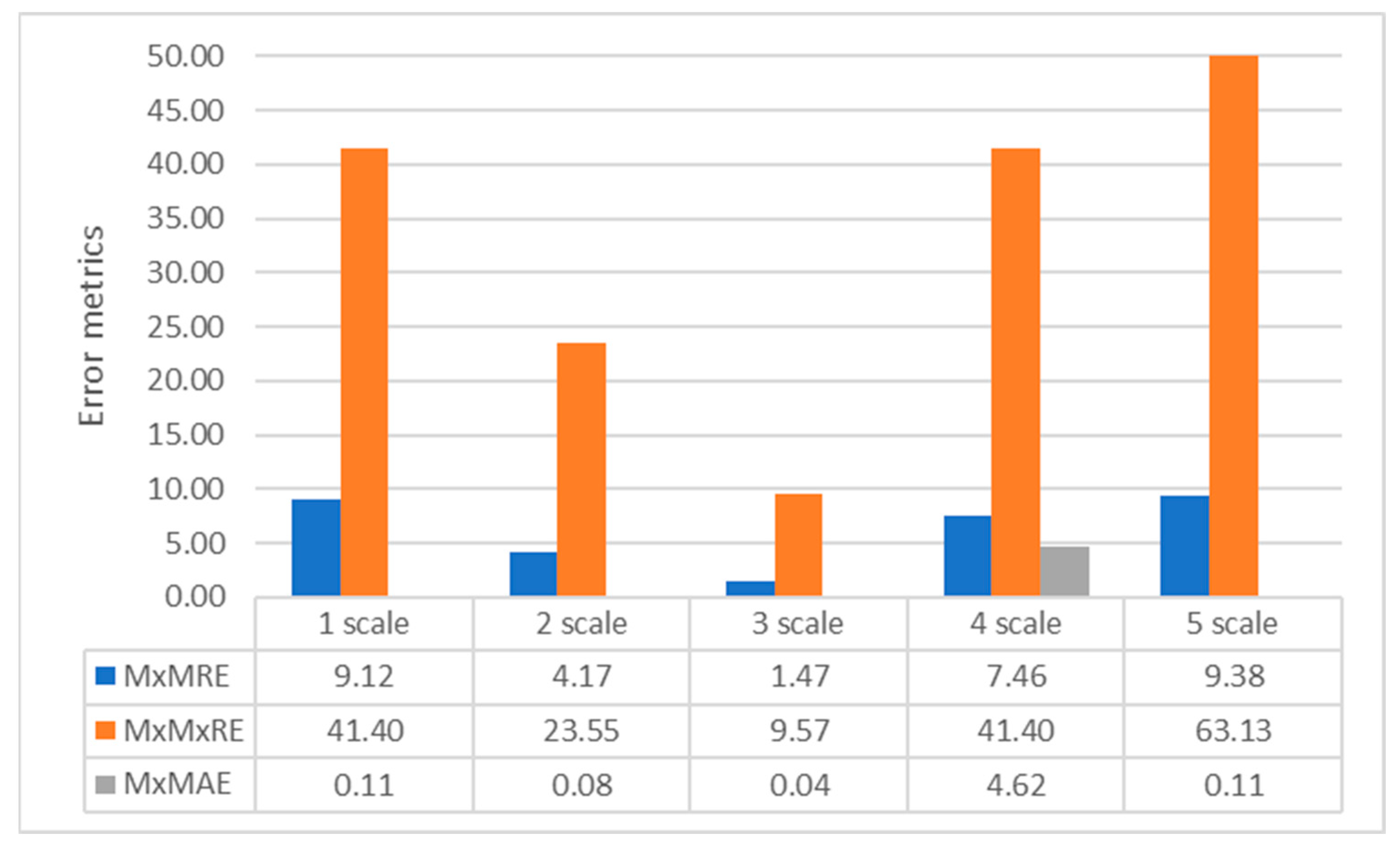
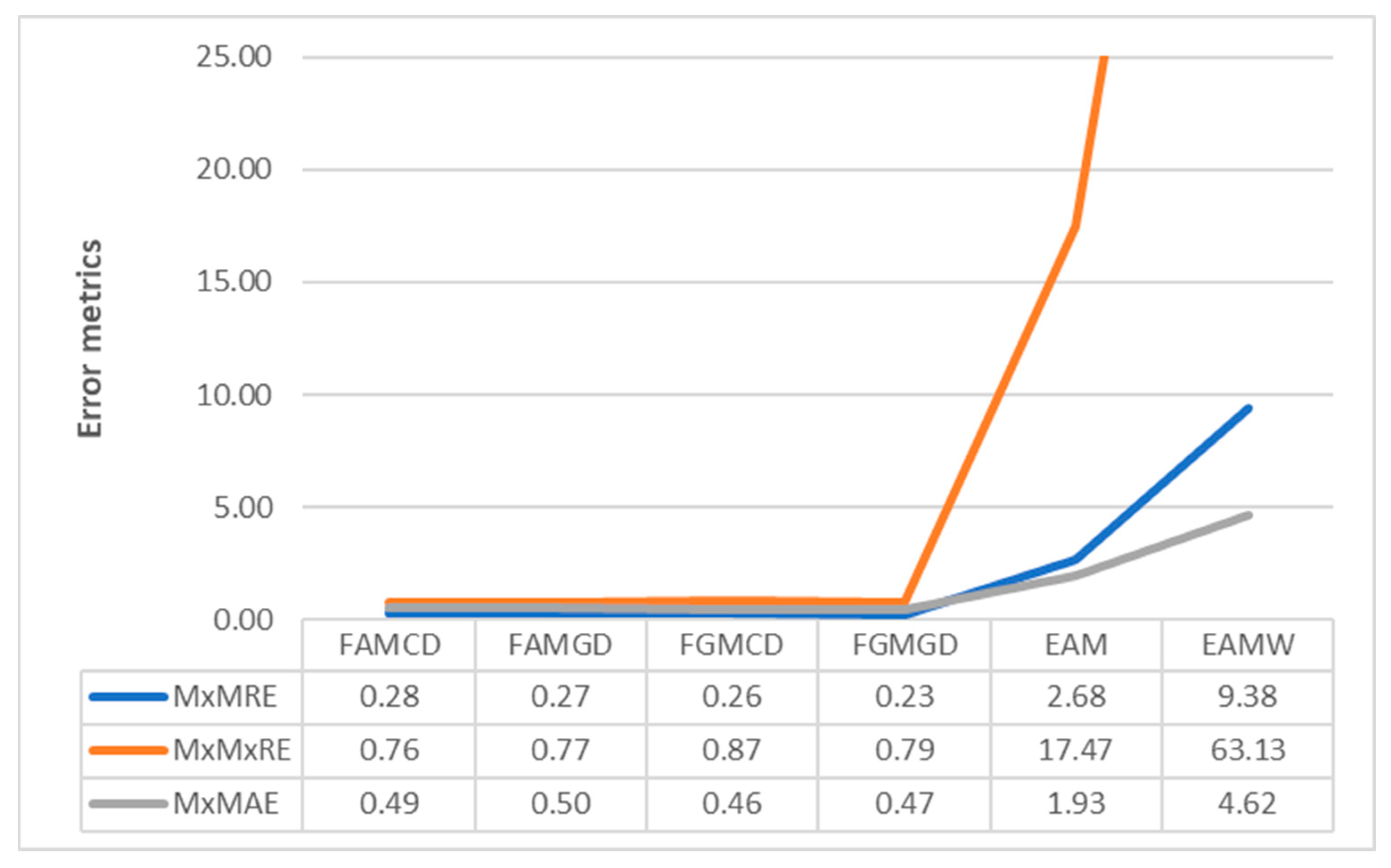
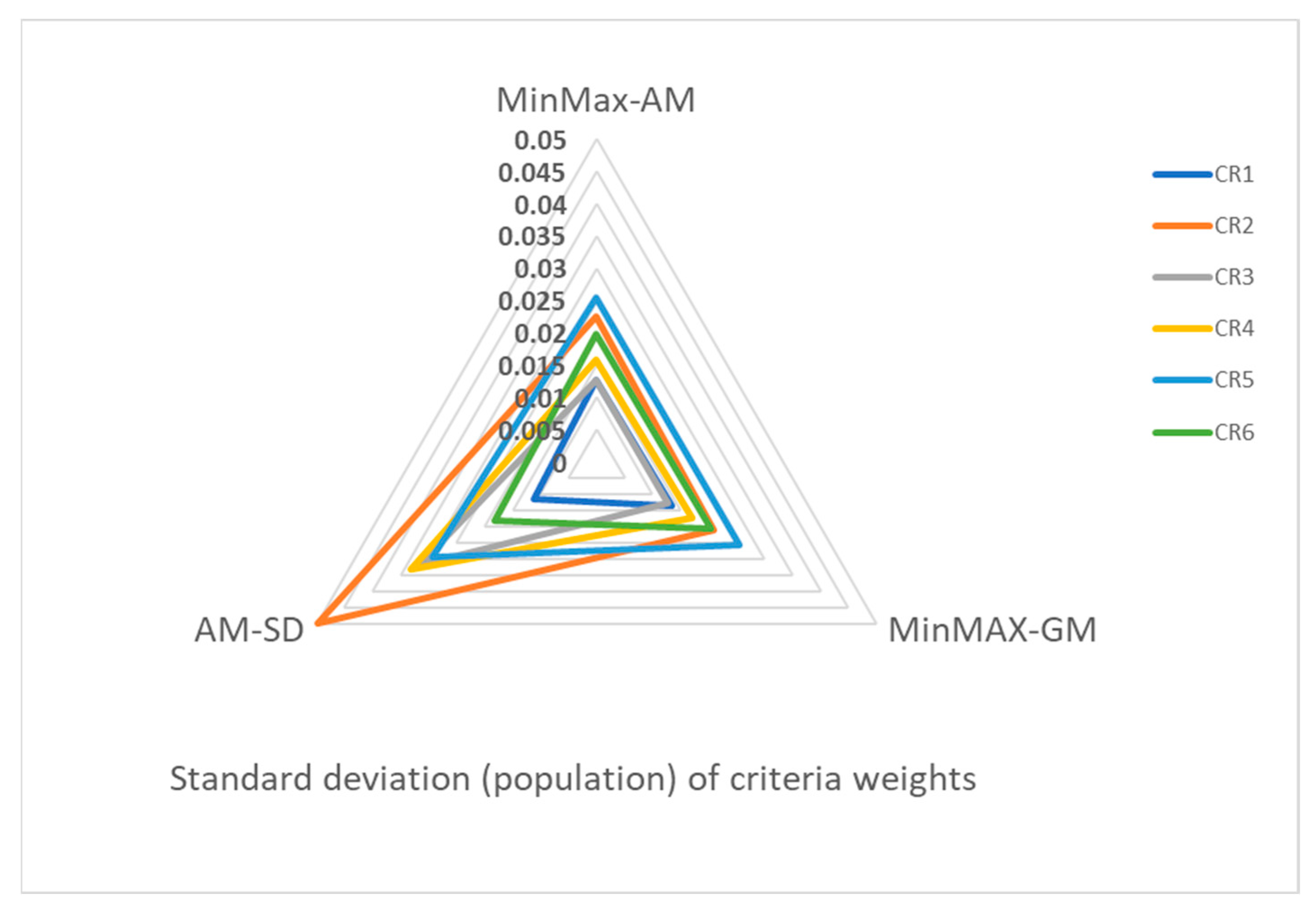
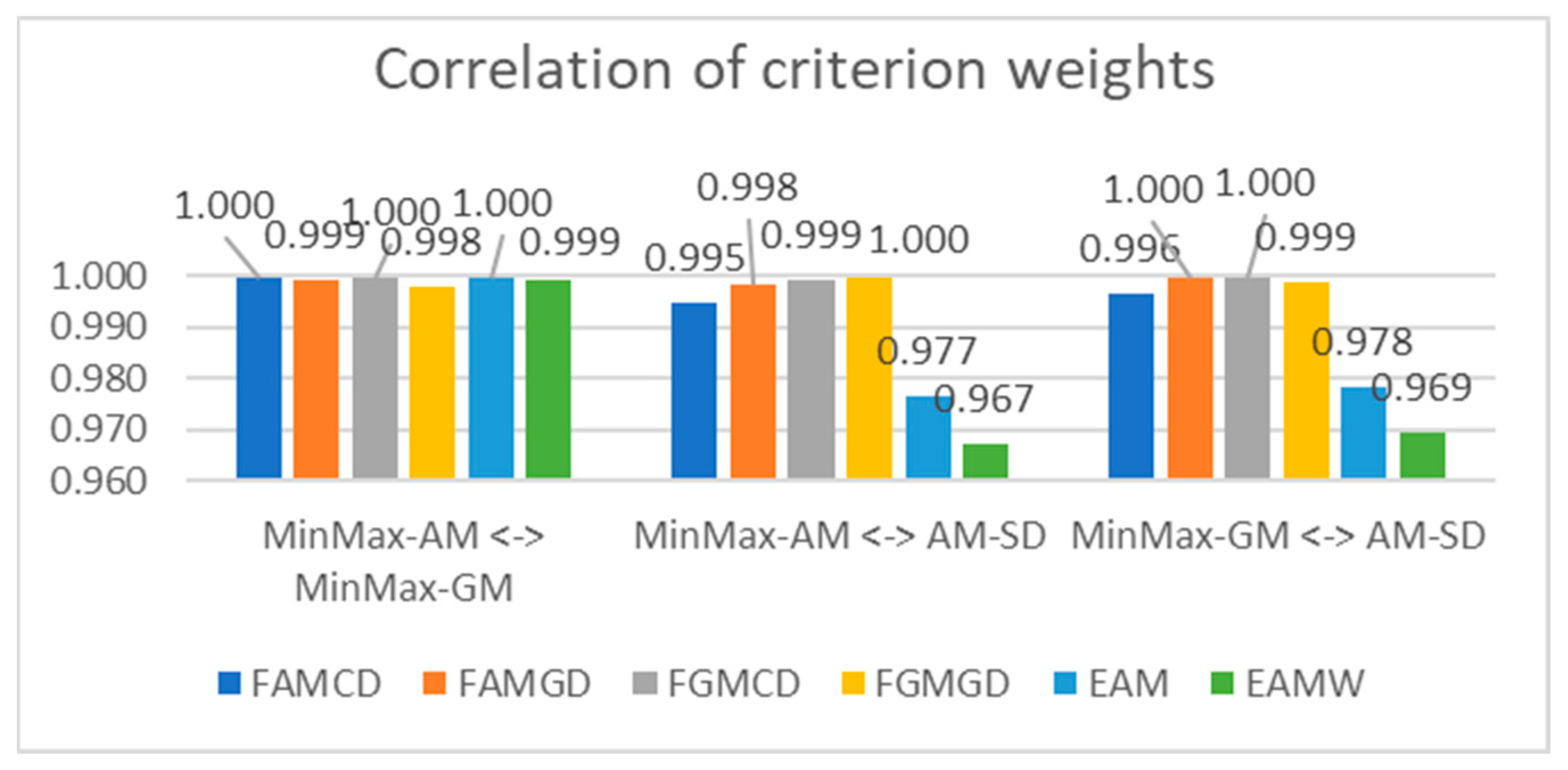
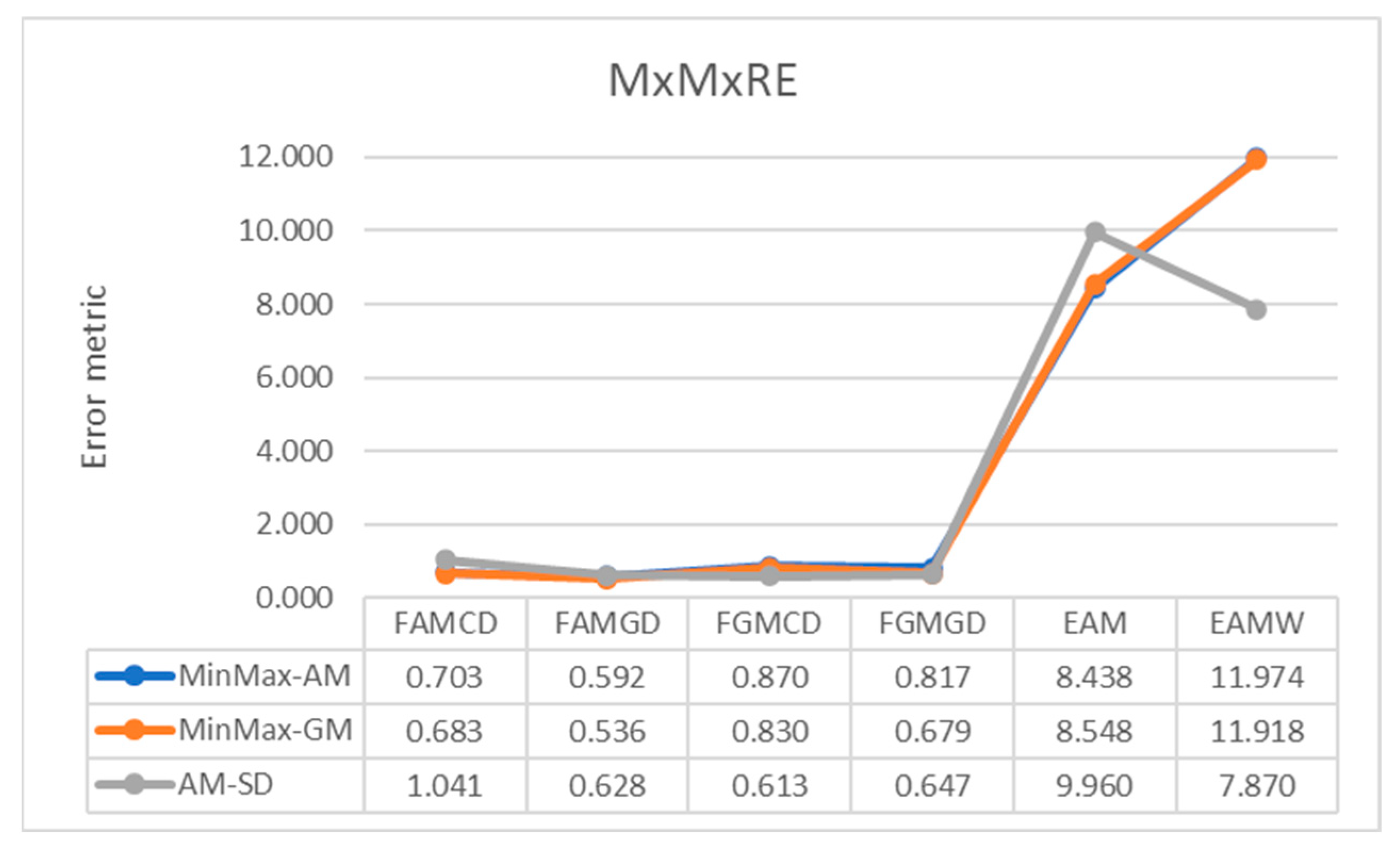
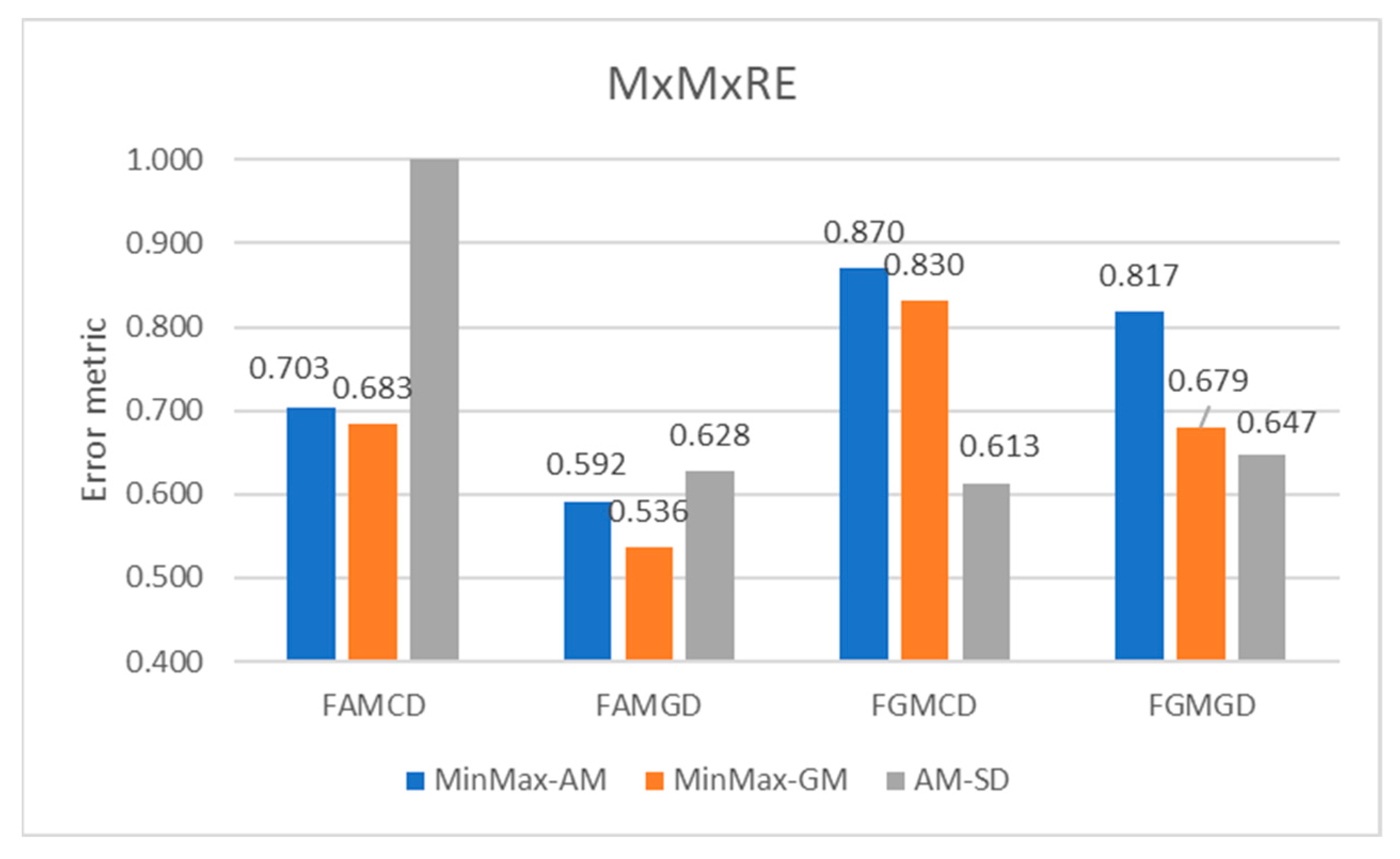
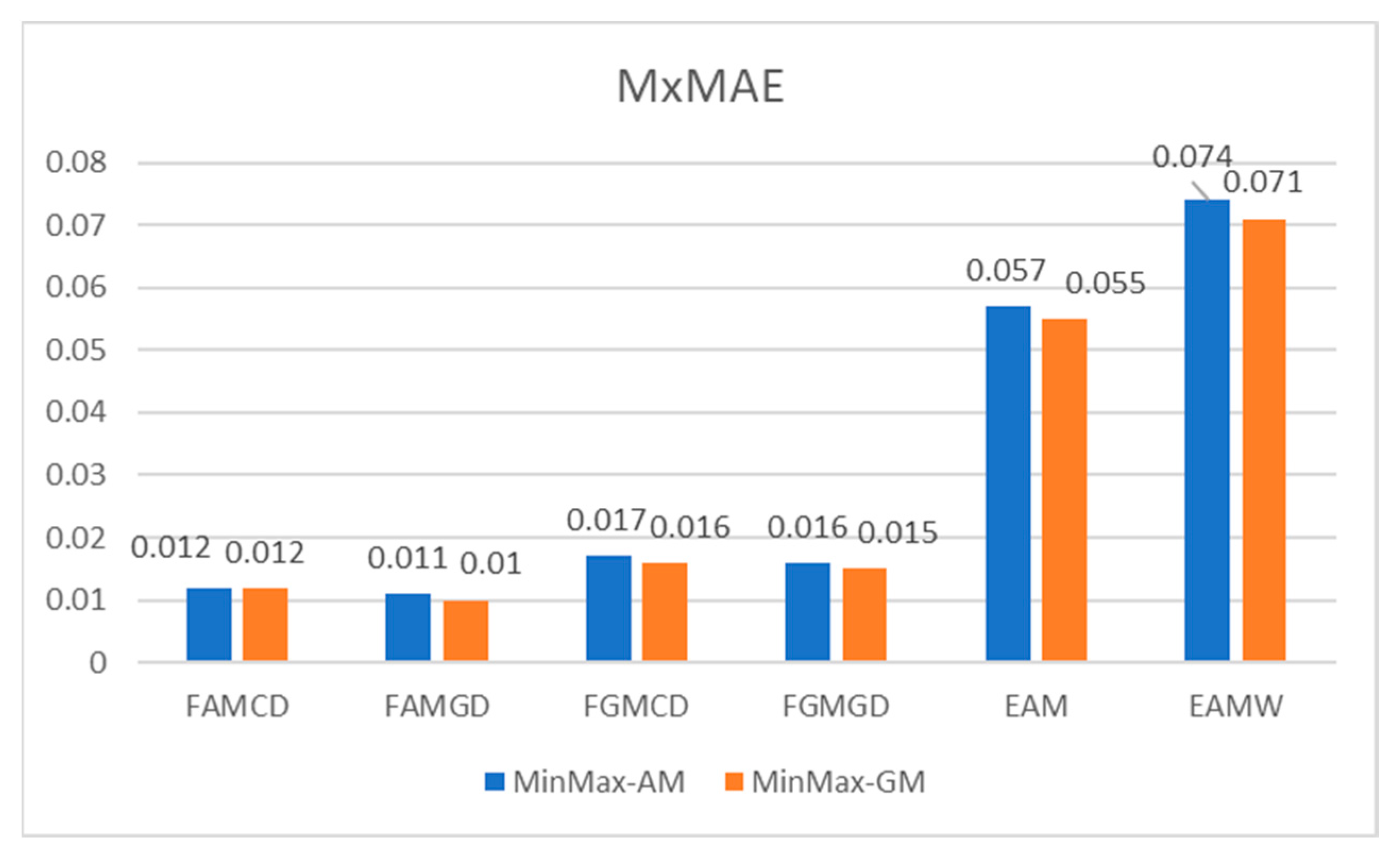
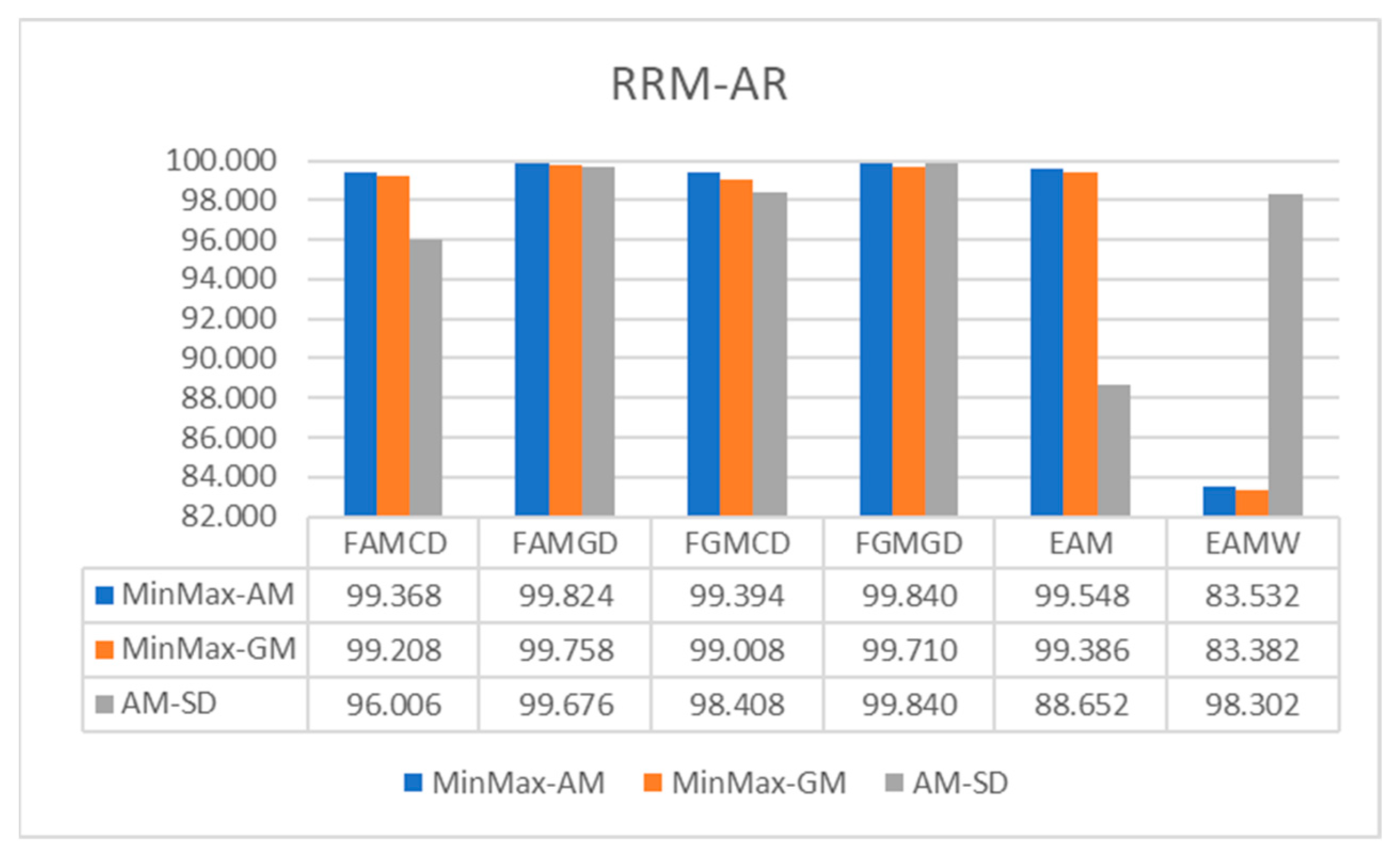
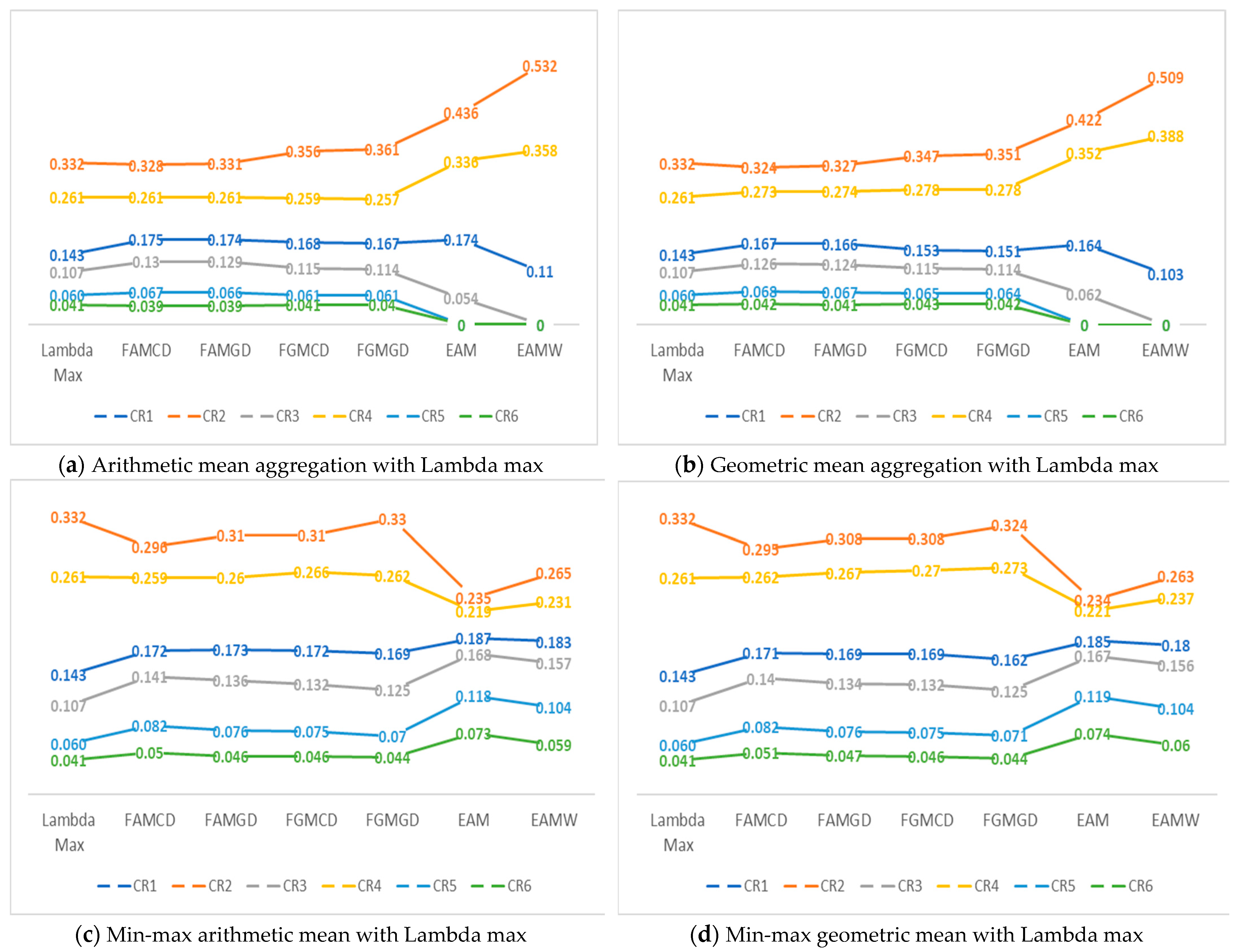
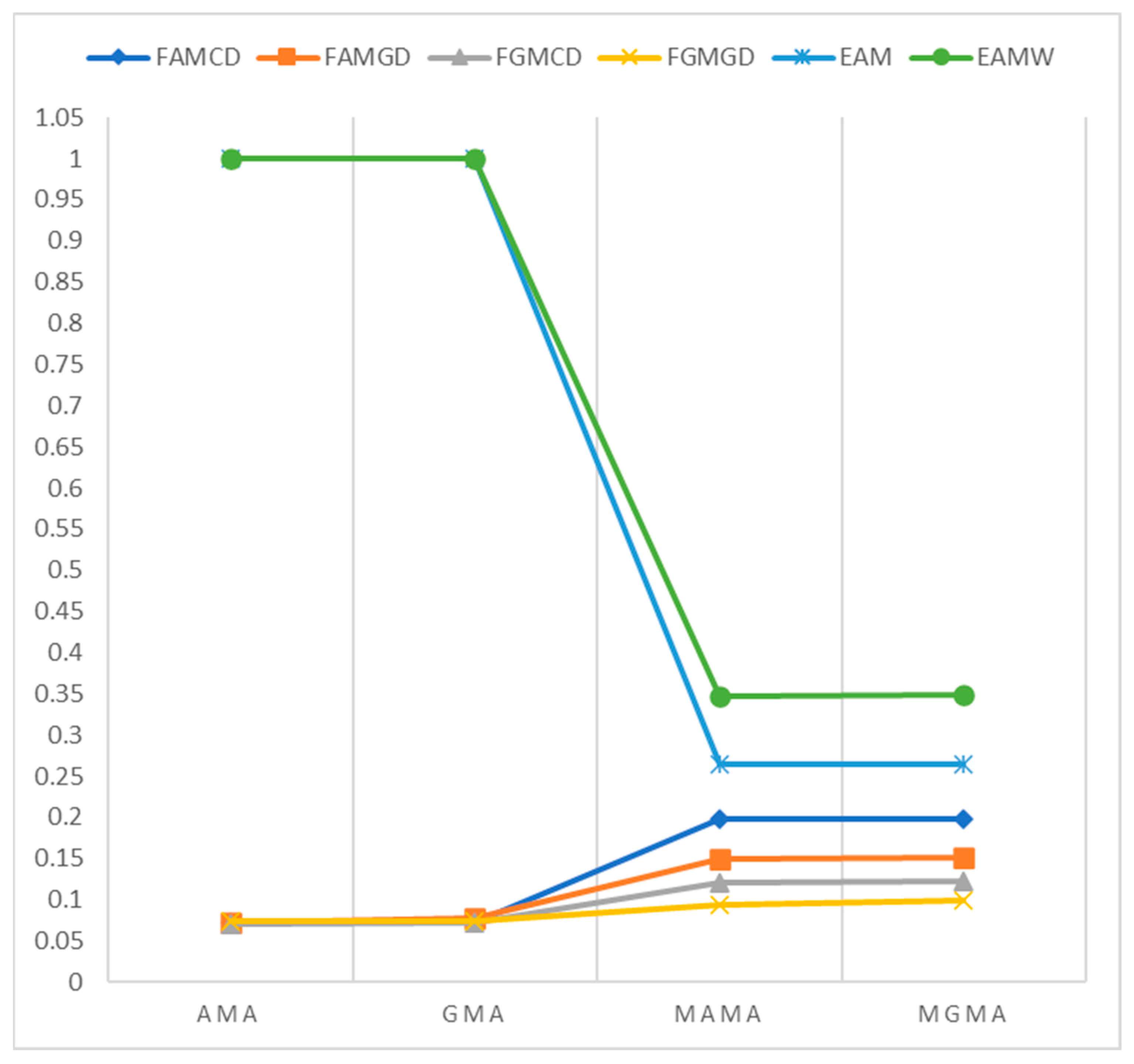
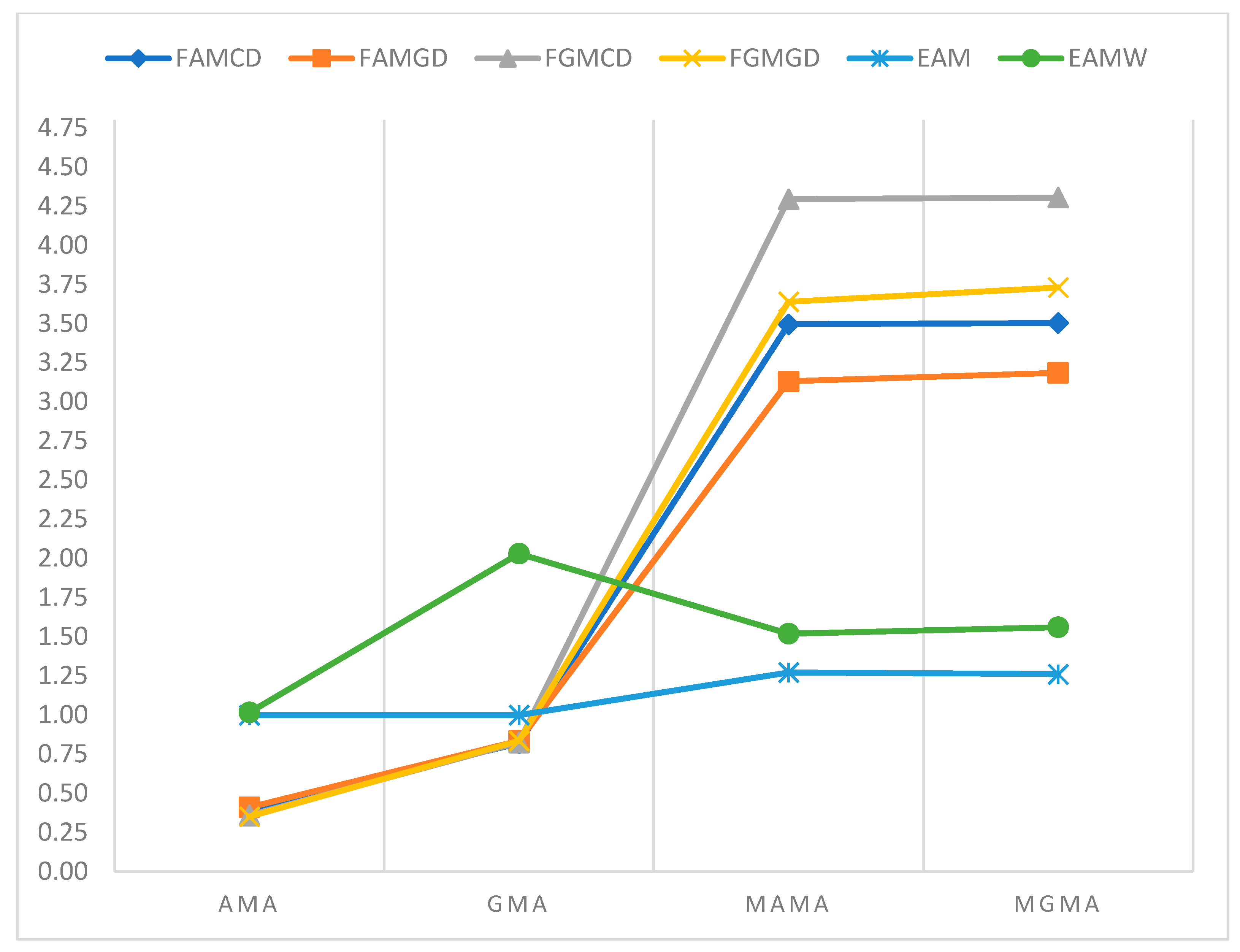
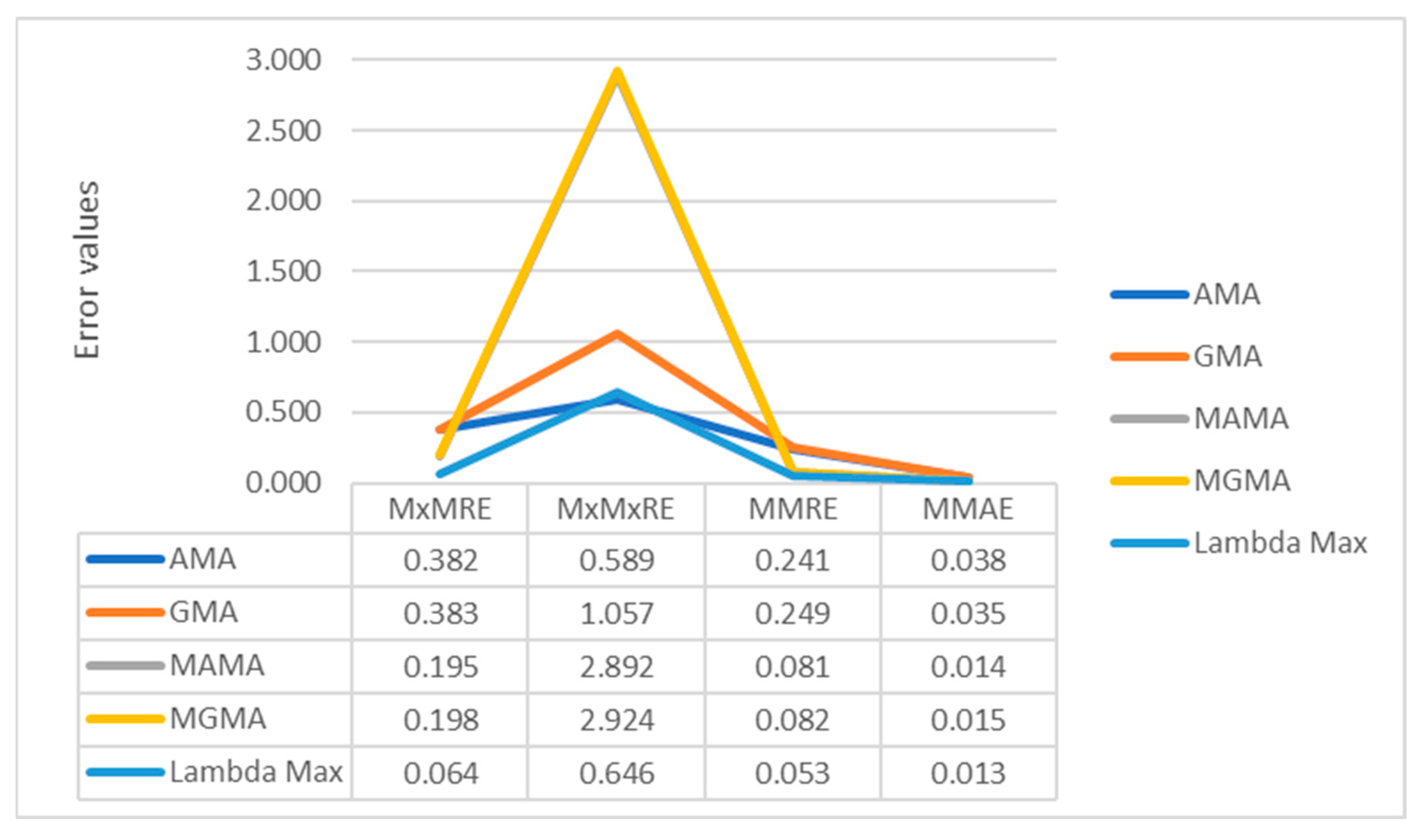
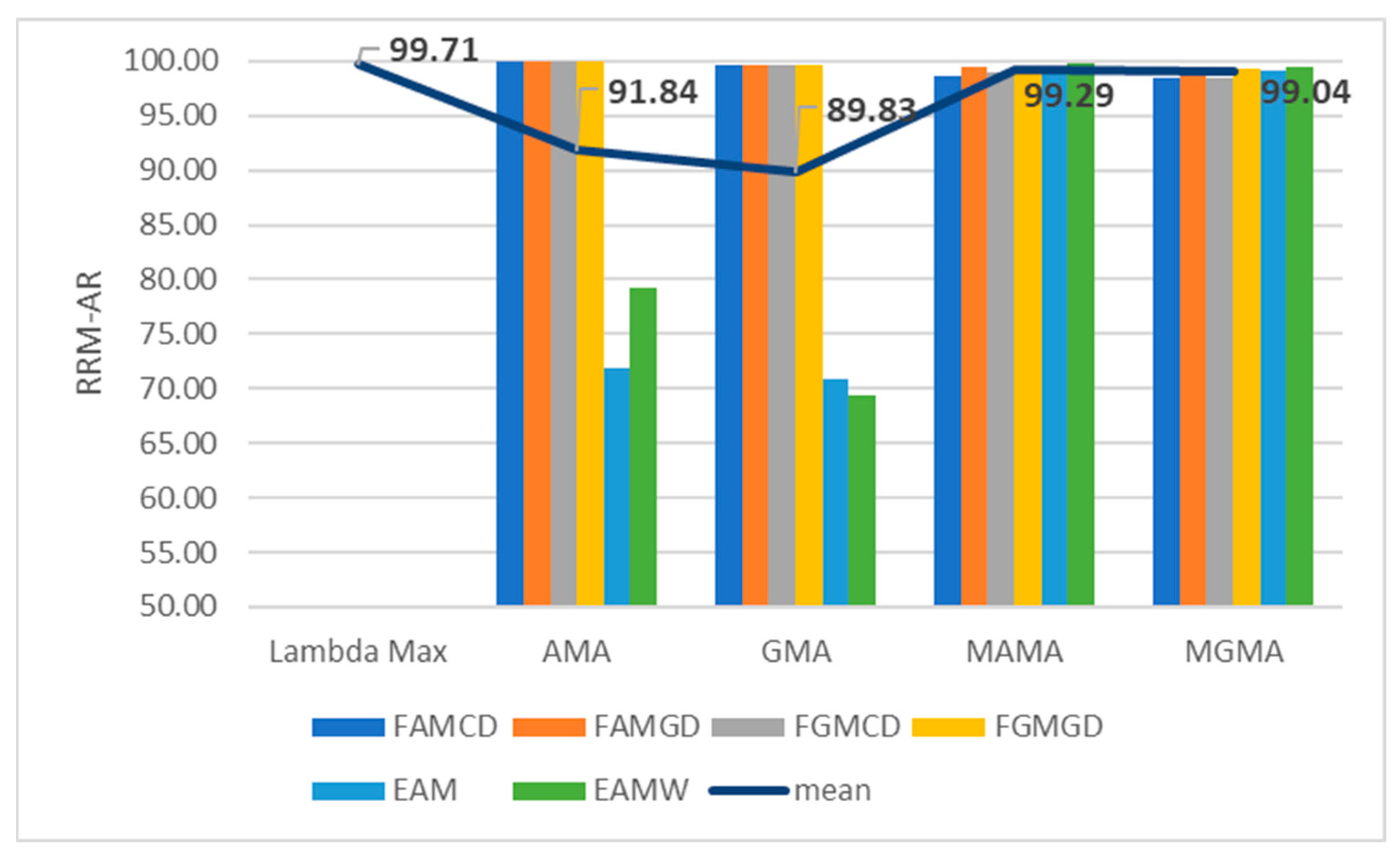
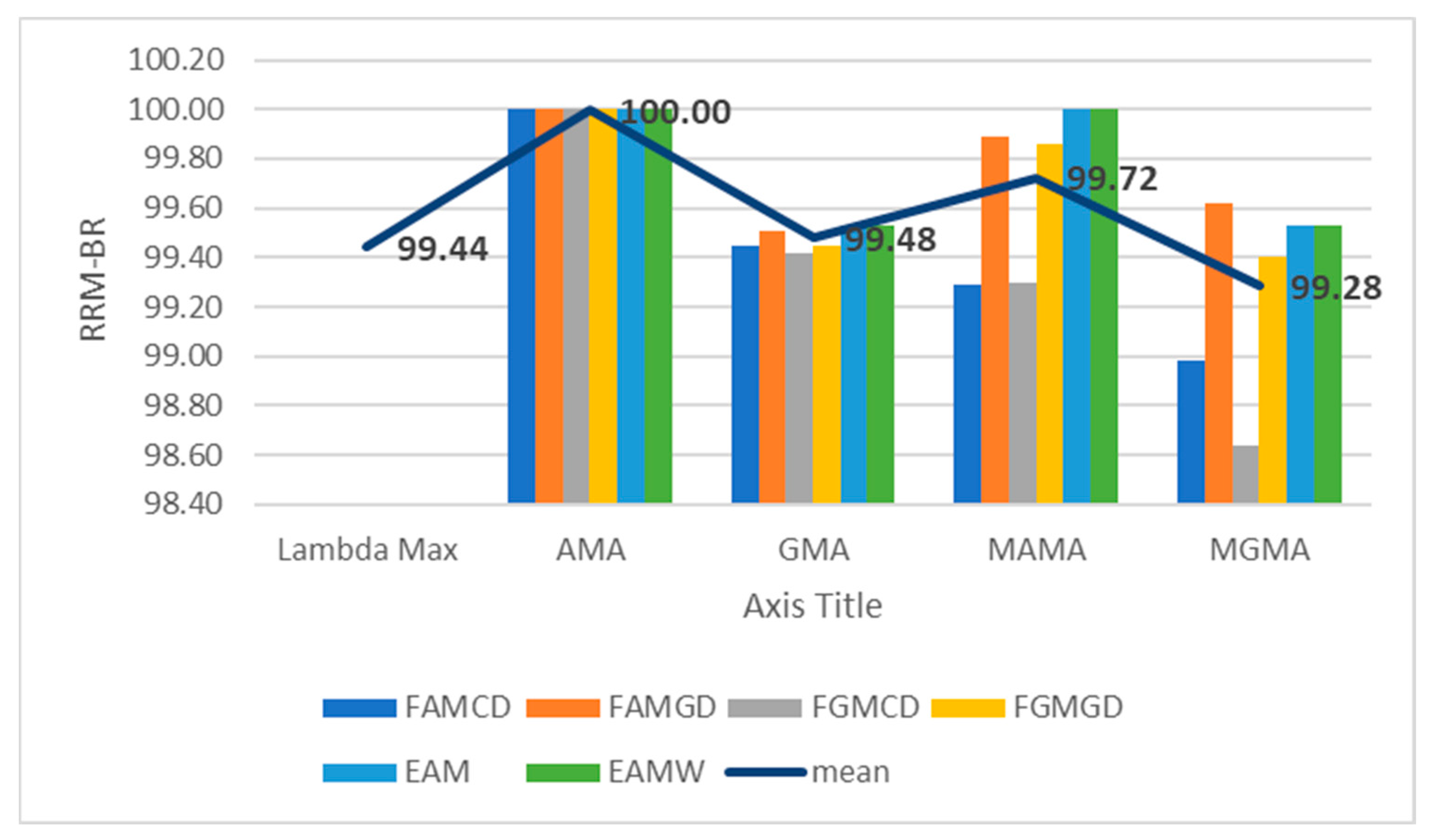
4. Results
5. Discussion
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Vinogradova-Zinkevič, I.; Podvezko, V.; Zavadskas, E.K. Comparative assessment of the stability of AHP and FAHP methods. Symmetry 2021, 13, 479. [Google Scholar] [CrossRef]
- Yager, R.R. A procedure for ordering fuzzy subsets of the unit interval. Inf. Sci. 1981, 24, 143–161. [Google Scholar] [CrossRef]
- Ross, T.J. Properties of membership functions, fuzzification, and defuzzification. In Fuzzy Logic with Engineering Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 2004; pp. 90–119. [Google Scholar] [CrossRef]
- Chang, P.T.; Lee, E.S. The Estimation of Normalized Fuzzy Weights. Computers Math. Applic. 1995, 29, 21–42. [Google Scholar] [CrossRef]
- Bozóki, S. A method for solving LSM problems of small size in the AHP. Cent. Eur. J. Oper. Res. 2003, 11, 17–33. [Google Scholar]
- Cheng, C.H. Evaluating naval tactical missile systems by fuzzy AHP based on the grade value of membership function. Eur. J. Oper. Res. 1997, 96, 343–350. [Google Scholar] [CrossRef]
- van Laarhoven, P.J.M.; Pedrycz, W. A fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Boender, C.G.E.; de Graan, J.G.; Lootsma, F.A. Multi-criteria decision analysis with fuzzy pairwise comparisons. Fuzzy Sets Syst. 1989, 29, 133–143. [Google Scholar] [CrossRef]
- Wang, Y.M.; Elhag, T.M.S.; Hua, Z. A modified fuzzy logarithmic least squares method for fuzzy analytic hierarchy process. Fuzzy Sets Syst. 2006, 157, 3055–3071. [Google Scholar] [CrossRef]
- Pehlivan, N.Y.; Paksoy, T.; Çalik, A. Comparison of methods in FAHP with application in supplier selection. In Fuzzy Analytic Hierarchy Process, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017; pp. 45–76. [Google Scholar] [CrossRef]
- Kazibudzki, P.T. On the Statistical Discrepancy and Affinity of Priority Vector Heuristics in Pairwise-Comparison-Based Methods. Entropy 2021, 23, 1150. [Google Scholar] [CrossRef]
- Buckley, J.J. Ranking alternatives using fuzzy numbers. Fuzzy Sets Syst. 1985, 15, 21–31. [Google Scholar] [CrossRef]
- Lootsma, F.A. Performance evaluation of nonlinear optimization methods via pairwise comparison and fuzzy numbers. Math. Program. 1985, 33, 93–114. [Google Scholar] [CrossRef]
- Chang, D.Y. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Wang, Y.M.; Luo, Y.; Hua, Z. On the extent analysis method for fuzzy AHP and its applications. Eur. J. Oper. Res. 2008, 186, 735–747. [Google Scholar] [CrossRef]
- Mikhailov, L. A fuzzy programming method for deriving priorities in the analytic hierarchy process. J. Oper. Res. Soc. 2000, 51, 341–349. [Google Scholar] [CrossRef]
- Csutora, R.; Buckley, J.J. Fuzzy hierarchic analysis: The Lambda-Max method. Fuzzy Sets Syst. 2001, 120, 181–195. [Google Scholar] [CrossRef]
- Vinogradova, I. Multi-attribute decision-making methods as a part of mathematical optimization. Mathematics 2019, 7, 915. [Google Scholar] [CrossRef]
- Triantaphyllou, E.; Lin, C.T. Development and evaluation of five multiattribute decision-making methods. Int. J. Approx. Reason. 1996, 14, 281–310. [Google Scholar] [CrossRef]
- Yadav, R.; Lee, H.-H. Fabrication, characterization, and selection using FAHP-TOPSIS technique of zirconia, titanium oxide, and marble dust powder filled dental restorative composite materials. Polym. Adv. Technol. 2022, 33, 3286–3295. [Google Scholar] [CrossRef]
- Ristanović, V.; Primorac, D.; Mikić, M. Application of Multi-Criteria Assessment in Banking Risk Management. Zagreb Int. Rev. Econ. Busines 2023, 26, 97–117. [Google Scholar] [CrossRef]
- Ilić, D.; Milošević, I.; Ilić-Kosanović, T. Application of Unmanned Aircraft Systems for smart city transformation: Case study Belgrade. Technol. Forecast. Soc. Chang. 2022, 176, 121487. [Google Scholar] [CrossRef]
- Mei, W.B.; Li, K.; Huang, Y.Z. Research on the Weighting Values of Community Aging-Friendly Construction Indexes with Different Expert Groups. J. Health Care Organ. Provis. Financ. 2023, 60, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Guru, S.; Sinha, A.; Kautish, P. Determinants of medical tourism: Application of Fuzzy Analytical Hierarchical Process. Int. J. Emerg. Mark. 2023, 18, 4819–4842. [Google Scholar] [CrossRef]
- Chai, N.; Zhou, W. Evaluating operational risk for train control system using a revised risk matrix and FD-FAHP-Cloud model: A case in China. Eng. Fail. Anal. 2022, 137, 106268. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, W.; Chen, X.; Langari, R.; Yan, Q. Comprehensive Evaluation of Hydrodynamic Retarders with Fuzzy Analytic Hierarchy Process and Improved Radar Chart. Machines 2023, 11, 849. [Google Scholar] [CrossRef]
- Mehdic, A.; Gunton, T.; Rutherford, M. Assessing the role of subjective judgment and science in environmental impact assessment: Implications and options for reform. J. Environ. Plan. Manag. 2020, 63, 1771–1790. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Marra, M. The state of the art development of AHP (1979–2017): A literature review with a social network analysis. Int. J. Prod. Res. 2017, 55, 6653–6675. [Google Scholar] [CrossRef]
- Koczkodaj, W.W. A new definition of consistency of pairwise comparisons. Math. Comput. Model. 1993, 18, 79–84. [Google Scholar] [CrossRef]
- Koczkodaj, W.W.; Szybowski, J. Pairwise comparisons simplified. Appl. Math. Comput. 2015, 253, 387–394. [Google Scholar] [CrossRef]
- Koczkodaj, W.W.; Urban, R. Axiomatization of inconsistency indicators for pairwise comparisons. Int. J. Approx. Reason. 2018, 94, 18–29. [Google Scholar] [CrossRef]
- Grzybowski, A.Z. Note on a new optimization based approach for estimating priority weights and related consistency index. Expert Syst. Appl. 2012, 39, 11699–11708. [Google Scholar] [CrossRef]
- Grzybowski, A.Z. New results on inconsistency indices and their relationship with the quality of priority vector estimation. Expert Syst. Appl. 2016, 43, 197–212. [Google Scholar] [CrossRef]
- Pant, S.; Kumar, A.; Ram, M.; Klochkov, Y.; Sharma, H.K. Consistency Indices in Analytic Hierarchy Process: A Review. Mathematics 2022, 10, 1206. [Google Scholar] [CrossRef]
- Awan, U.; Hannola, L.; Tandon, A.; Goyal, R.K.; Dhir, A. Quantum computing challenges in the software industry. A fuzzy AHP-based approach. Inf. Softw. Technol. 2022, 147, 106896. [Google Scholar] [CrossRef]
- Zhao, Y.; Deng, C. Analysis of project benefit of solar energy collection and irrigation system based on AHP. Energy Rep. 2022, 8, 122–130. [Google Scholar] [CrossRef]
- Abdulkareem, H.G.; Erzaij, K.R. A spherical fuzzy AHP model for contractor assessment during project life cycle. J. Mech. Behav. Mater. 2022, 31, 369–380. [Google Scholar] [CrossRef]
- Badeel, R.; Subramaniam, S.K.; Muhammed, A.; Hanapi, Z.M. A Multicriteria Decision-Making Framework for Access Point Selection in Hybrid LiFi/WiFi Networks Using Integrated AHP–VIKOR Technique. Sensors 2023, 23, 1312. [Google Scholar] [CrossRef]
- Park, S.; Kim, H.K.; Lee, M. An analytic hierarchy process analysis for reinforcing doctor–patient communication. BMC Prim. Care 2023, 24, 24. [Google Scholar] [CrossRef]
- Wątróbski, J.; Bączkiewicz, A.; Rudawska, I. A Strong Sustainability Paradigm based Analytical Hierarchy Process (SSP-AHP) method to evaluate sustainable healthcare systems. Ecol. Indic. 2023, 154, 110493. [Google Scholar] [CrossRef]
- He, S.; Xu, H.; Zhang, J.; Xue, P. Risk assessment of oil and gas pipelines hot work based on AHP-FCE. Petroleum 2023, 9, 94–100. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Z.; Deng, J.; Feng, Y.; Li, Q. Study on the Evaluation of Emergency Management Capacity of Resilient Communities by the AHP-TOPSIS Method. Int. J. Environ. Res. Public Health 2022, 19, 16201. [Google Scholar] [CrossRef] [PubMed]
- Hsino, M.; Jasiczak, J. Decision-making model using the Analytical Hierarchy Process for the selection of the type of concrete and the method of its maintenance in dry, hot climate conditions. Arch. Civ. Eng. 2023, LXIX, 385–403. [Google Scholar] [CrossRef]
- Laks, I.; Walczak, Z.; Walczak, N. Fuzzy analytical hierarchy process methods in changing the damming level of a small hydropower plant: Case study of Rosko SHP in Poland. Water Resour. Ind. 2023, 29, 100204. [Google Scholar] [CrossRef]
- Singh, T.; Goswami, C.; Patnaik, A.; Lendvai, L. Optimal Design of Ceramic Based Hip Implant Composites Using Hybrid AHP-MOORA Approach. Materials 2022, 15, 3800. [Google Scholar] [CrossRef] [PubMed]
- Basílio, M.P.; Pereira, V.; Costa, H.G.; Santos, M.; Ghosh, A. A Systematic Review of the Applications of Multi-Criteria Decision Aid Methods (1977–2022). Electronics 2022, 11, 1720. [Google Scholar] [CrossRef]
- Liu, Y.; Eckert, C.M.; Earl, C. A review of fuzzy AHP methods for decision-making with subjective judgements. Expert Syst. Appl. 2020, 161, 113738. [Google Scholar] [CrossRef]
- Ahmed, F.; Kilic, K. Comparison of fuzzy extent analysis technique and its extensions with original eigen vector approach. In Proceedings of the 18th International Conference on Enterprise Information Systems, Rome Italy, 25–28 April 2016; SCITEPRESS: Setubal, Portugal; Volume 2, pp. 174–179. [Google Scholar]
- Demirel, T.; Demirel, N.Ç.; Kahraman, C. Fuzzy analytic hierarchy process and its application. In Fuzzy Multi-Criteria Decision Making; Kahraman, C., Ed.; Springer Optimization and Its Applications; Springer: Berlin/Heidelberg, Germany, 2008; Volume 16, pp. 53–83. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Kahraman, C.; Ruan, D. A fuzzy multi-criteria decision approach for software development strategy selection. Int. J. Gen. Syst. 2004, 33, 259–280. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Comparison of eigenvalue, logarithmic least squares and least squares methods in estimating ratios. Math. Model. 1984, 5, 309–324. [Google Scholar] [CrossRef]
- Balusa, B.C.; Gorai, A.K. Sensitivity analysis of fuzzy-analytic hierarchical process (FAHP) decision-making model in selection of underground metal mining method. J. Sustain. Min. 2019, 18, 8–17. [Google Scholar] [CrossRef]
- Wu, C.R.; Chang, C.W.; Lin, H.L. FAHP Sensitivity analysis for measurement nonprofit organizational performance. Qual. Quant. 2008, 42, 283–302. [Google Scholar] [CrossRef]
- Vinogradova, I.; Kliukas, R. Methodology for evaluating the quality of distance learning courses in consecutive stages. Procedia-Soc. Behav. Sci. 2015, 191, 1583–1589. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning. In Learning Systems and Intelligent Robots; Fu, K.S., Tou, J.T., Eds.; Springer: Berlin/Heidelberg, Germany, 1974; pp. 1–10. [Google Scholar] [CrossRef]
- Wang, F. Preference degree of triangular fuzzy numbers and its application to multi-attribute group decision making. Expert Syst. Appl. 2021, 178, 114982. [Google Scholar] [CrossRef]
- Triantaphyllou, E.; Lootsma, F.A.; Pardalos, P.M.; Mann, S.H. On the evaluation and application of different scales for quantifying pairwise comparisons in fuzzy sets. J. Multi-Criteria Decis. Anal. 1994, 3, 133–155. [Google Scholar] [CrossRef]
- Ishizaka, A.; Nguyen, N. Calibrated fuzzy AHP for current bank account selection. Expert Syst. Appl. 2013, 40, 3775–3783. [Google Scholar] [CrossRef]
- Kannan, D.; Khodaverdi, R.; Olfat, L.; Jafarian, A.; Diabat, A. Integrated fuzzy multi criteria decision making method and multiobjective programming approach for supplier selection and order allocation in green supply chain. J. Clean. Prod. 2013, 47, 355–365. [Google Scholar] [CrossRef]
- Gumus, A.T. Evaluation of hazardous waste transportation firms by using a two step fuzzy-AHP and TOPSIS methodology. Expert Syst. Appl. 2009, 36, 4067–4074. [Google Scholar] [CrossRef]
- Sun, C.C. A performance evaluation model by integrating fuzzy AHP and fuzzy TOPSIS methods. Expert Syst. Appl. 2010, 37, 7745–7754. [Google Scholar] [CrossRef]
- Hsu, Y.L.; Lee, C.H.; Kreng, V.B. The application of Fuzzy Delphi Method and Fuzzy AHP in lubricant regenerative technology selection. Expert Syst. Appl. 2010, 37, 419–425. [Google Scholar] [CrossRef]
- Javanbarg, M.; Scawthorn, C.; Kiyono, J.; Shahbodaghkhan, B. Fuzzy AHP-based multicriteria decision making systems using particle swarm optimization. Expert Syst. Appl. 2012, 39, 960–966. [Google Scholar] [CrossRef]
- Lu, W.M.; Wang, T.C. A fuzzy multi-criteria model for the industrial cooperation program transaction strategies: A case in Taiwan. Expert Syst. Appl. 2011, 38, 1490–1500. [Google Scholar] [CrossRef]
- Cebeci, U. Fuzzy AHP-based decision support system for selecting ERP systems in textile industry by using balanced scorecard. Expert Syst. Appl. 2009, 36, 8900–8909. [Google Scholar] [CrossRef]
- Viswanadham, N.; Samvedi, A. Supplier selection based on supply chain ecosystem, performance and risk criteria. Int. J. Prod. Res. 2013, 51, 6484–6498. [Google Scholar] [CrossRef]
- Kurilov, J.; Vinogradova, I.; Kubilinskienė, S. New MCEQLS fuzzy AHP methodology for evaluating learning repositories: A tool for technological development of economy. Technol. Econ. Dev. Econ. 2016, 22, 142–155. [Google Scholar] [CrossRef]
- Trinkūnienė, E.; Podvezko, V.; Zavadskas, E.K.; Jokšienė, I.; Vinogradova, I.; Trinkūnas, V. Evaluation of quality assurance in contractor contracts by multi-attribute decision-making methods. Econ. Res. Ekon. Istraživanja 2017, 30, 1152–1180. [Google Scholar] [CrossRef]
- Baležentis, A.; Baležentis, T.; Misiūnas, A. An integrated assessment of Lithuanian economic sectors based on financial ratios and fuzzy MCDM methods. Technol. Econ. Dev. Econ. 2012, 18, 34–53. [Google Scholar] [CrossRef]
- Vinogradova, I. Uncertainty influence on AHP method ratings. Lith. Math. Collect. LMD Works 2012, 53, 243–248. [Google Scholar] [CrossRef]
- Saaty, R.W. The Analytic Hierarchy Process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Saaty, T.L. The seven pillars of the Analytic Hierarchy Process. In Multiple Criteria Decision Making in the New Millennium. Lecture Notes in Economics and Mathematical Systems; Köksalan, M., Zionts, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 507, pp. 15–37. [Google Scholar] [CrossRef]
- Tzeng, G.H.; Huang, J.J. Multiple Attribute Decision Making: Methods and Applications; CRC: Boca Raton, FL, USA, 2011. [Google Scholar]
- Vinogradova-Zinkevič, I. Application of Bayesian approach to reduce the uncertainty in expert judgments by using a posteriori mean function. Mathematics 2021, 9, 2455. [Google Scholar] [CrossRef]
- Forman, E.; Peniwati, K. Aggregating individual judgements and priorities with the Analytic Hierarchy Process. Eur. Jour. Oper. Res. 1998, 108, 165–169. [Google Scholar] [CrossRef]
- Kubler, S.; Robert, J.; Derigent, W.; Voisin, A.; Le Traon, Y. A state-of the-art survey & testbed of fuzzy AHP (FAHP) applications. Expert Syst. Appl. 2016, 65, 398–422. [Google Scholar] [CrossRef]
- Wang, J.W.; Cheng, C.H.; Huang, K.C. Fuzzy hierarchical TOPSIS for supplier selection. Appl. Soft Comput. 2009, 9, 377–386. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; You, X.Y.; Shan, M.M. A novel approach for failure mode and effects analysis using combination weighting and fuzzy VIKOR method. Appl. Soft Comput. 2015, 28, 579–588. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Methods; Griffin: London, UK, 1970. [Google Scholar]
- Kurilov, J.; Vinogradova, I. Improved fuzzy AHP methodology for evaluating quality of distance learning courses. Int. J. Eng. Educ. 2016, 32, 1618–1624. [Google Scholar]
- Ziemba, P.; Becker, A.; Becker, J. A consensus measure of expert judgment in the fuzzy TOPSIS method. Symmetry 2020, 12, 204. [Google Scholar] [CrossRef]
- Coffey, L.; Claudio, D. In defense of group fuzzy AHP: A comparison of group fuzzy AHP and group AHP with confidence intervals. Expert Syst. Appl. 2021, 178, 114970. [Google Scholar] [CrossRef]
- Meixner, O. Fuzzy AHP group decision analysis and its application for the evaluation of energy sources. In Proceedings of the 10th International Symposium on the Analytic Hierarchy/Network Process, Pittsburgh, PA, USA, 29 July–1 August 2009; Volume 29, pp. 2–16. [Google Scholar]
- Awasthi, A.; Govindan, K.; Gold, S. Multi-tier sustainable global supplier selection using a fuzzy AHP-VIKOR based approach. Int. J. Prod. Econ. 2018, 195, 106–117. [Google Scholar] [CrossRef]
- Chen, S.H.; Wang, P.W.; Chen, C.M.; Lee, H.T. An analytic hierarchy process approach with linguistic variables for selection of an R&D strategic alliance partner. Comput. Ind. Eng. 2010, 58, 278–287. [Google Scholar] [CrossRef]
- Chang, C.W.; Wu, C.R.; Lin, H.L. Applying fuzzy hierarchy multiple attributes to construct an expert decision making process. Expert Syst. Appl. 2009, 36, 7363–7368. [Google Scholar] [CrossRef]







| Intensity of Fuzzy Scale | Definition of Linguistic Variables | User-Defined |
|---|---|---|
| Similar importance (SI) | (_, 1, _) | |
| Moderate importance (MI) | (_, 3, _) | |
| Strong importance (STI) | (_, 5, _) | |
| Very strong importance (VSI) | (_, 7, _) | |
| Extreme importance (EI) | (_, 9, _) | |
| Intermediate values | (_, 2, _) | |
| (_, 4, _) | ||
| (_, 6, _) | ||
| (_, 8, _) |
| Source | SI | MI | STI | VSI | EI | Intermediate Values | |||
|---|---|---|---|---|---|---|---|---|---|
| [61] | (1,1,1) | (2,3,4) | (4,5,6) | (6,7,8) | (9,9,9) | (1,2,3) | (3,4,5) | (5,6,7) | (7,8,9) |
| [62,63] | (1,1,1) | (2,3,4) | (4,5,6) | (6,7,8) | (8,9,10) | (1,2,3) | (3,4,5) | (5,6,7) | (7,8,9) |
| [64] | (1,1,1) | (2,3,4) | (4,5,6) | (6,7,8) | (8,9,9) | (1,2,3) | (3,4,5) | (5,6,7) | (7,8,9) |
| [65] | (0.5,1,2) | (2,3,4) | (4,5,6) | (6,7,8) | (8,9,10) | (1,2,3) | (3,4,5) | (5,6,7) | (7,8,9) |
| [66] | (1,1,3) | (1,3,5) | (3,5,7) | (5,7,9) | (7,9,9) | (1,2,4) | (2,4,6) | (4,6,8) | (6,8,9) |
| [67] | (1,1,1) | (1,3,5) | (3,5,7) | (5,7,9) | (7,9,9) | ||||
| [68] | (1,1,3) | (1,3,5) | (3,5,7) | (5,7,9) | (7,9,11) | ||||
| Aggregation Methods | Formulas | Source |
|---|---|---|
| Min-max with arithmetic mean | [49,69,82] | |
| Min-max with geometric mean | [49,55] | |
| Arithmetic mean with standard deviation | [72] |
| Aggregations Methods | Mean Methods | Source |
|---|---|---|
| Arithmetic mean (AM) | [49,83] | |
| Geometric mean (GM) | [49,84,85] | |
| Min–Max Methods | ||
| Min-max arithmetic mean (MAM) | [49,86] | |
| Min-max geometric mean (MGM) | [49,85,87,88] | |
| Scales | SI | MI | STI | VSI | EI | Intermediate Values | |||
|---|---|---|---|---|---|---|---|---|---|
| 1-scale | (1,1,1) | (2,3,4) | (4,5,6) | (6,7,8) | (8,9,9) | (1,2,3) | (3,4,5) | (5,6,7) | (7,8,9) |
| 2-scale | (0.5,1,2) | (2,3,4) | (4,5,6) | (6,7,8) | (8,9,10) | (1,2,3) | (3,4,5) | (5,6,7) | (7,8,9) |
| 3-scale | (1,1,3) | (1,3,5) | (3,5,7) | (5,7,9) | (7,9,9) | (1,2,4) | (2,4,6) | (4,6,8) | (6,8,9) |
| 4-scale | (1,1,1) | (2,3,4) | (4,5,6) | (6,7,8) | (9,9,9) | (1,2,3) | (3,4,5) | (5,6,7) | (7,8,9) |
| 5-scale | (1,1,1) | (2,3,4) | (1,2,3) | (3,4,5) | |||||
| Matrix 1 | Matrix 2 | Matrix 3 | Matrix 4 | Matrix 5 | Matrix 6 | Matrix 7 | Matrix 8 | Matrix 9 | Matrix 10 | Matrix 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CI | 0.010 | 0.064 | 0.018 | 0.051 | 0.095 | 0.016 | 0.098 | 0.007 | 0.005 | 0.091 | 0.081 |
| CR | 0.011 | 0.072 | 0.016 | 0.046 | 0.086 | 0.013 | 0.078 | 0.005 | 0.004 | 0.067 | 0.060 |
| rank | 4 | 4 | 5 | 5 | 5 | 6 | 6 | 7 | 7 | 7 | 7 |
| Repeating weights | no | no | yes | no | no | no | no | yes | no | no | no |
| Matrix 1 | Matrix 2 | Matrix 3 | Matrix 4 | Matrix 5 | Matrix 6 | Matrix 7 | Matrix 8 | |
|---|---|---|---|---|---|---|---|---|
| CI | 0.007 | 0.057 | 0.008 | 0.092 | 0.007 | 0.092 | 0.012 | 0.098 |
| CR | 0.008 | 0.064 | 0.007 | 0.083 | 0.006 | 0.074 | 0.009 | 0.073 |
| rank | 4 | 4 | 5 | 5 | 6 | 6 | 7 | 7 |
| no | no | yes | no | yes | no | yes | yes |
| Matrix 1 | Matrix 2 | Matrix 3 | Matrix 4 | Matrix 5 | Matrix 6 | Matrix 7 | Matrix 8 | Matrix 9 | Matrix 10 | Matrix 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| min | 85.34 | 68.71 | 98.51 | 80.00 | 58.91 | 99.61 | 45.29 | 100.00 | 99.40 | 53.97 | 83.94 |
| max | 87.18 | 69.04 | 98.76 | 80.69 | 59.41 | 99.73 | 45.96 | 100.00 | 99.47 | 54.51 | 84.88 |
| Matrix 1 | Matrix 2 | Matrix 3 | Matrix 4 | Matrix 5 | Matrix 6 | Matrix 7 | Matrix 8 | ||||
| min | 81.52 | 49.17 | 93.11 | 26.99 | 98.31 | 36.84 | 99.04 | 39.26 | |||
| max | 81.81 | 50.21 | 93.51 | 27.62 | 98.54 | 37.9 | 99.17 | 40.27 |
| 1-Scale | 2-Scale | 3-Scale | 4-Scale | |||||
|---|---|---|---|---|---|---|---|---|
| EAM | EAMW | EAM | EAMW | EAM | EAMW | EAM | EAM | |
| Matrix 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| Matrix 2 | 2 | 2 | 2 | 2 | 0 | 1 | 2 | 2 |
| Matrix 3 | 2 | 2 | 1 | 1 | 0 | 0 | 3 | 3 |
| Matrix 4 | 2 | 2 | 1 | 2 | 0 | 0 | 2 | 2 |
| Matrix 5 | 3 | 3 | 2 | 3 | 1 | 2 | 3 | 3 |
| Matrix 6 | 3 | 3 | 1 | 1 | 0 | 0 | 3 | 3 |
| Matrix 7 | 3 | 3 | 0 | 0 | 0 | 0 | 3 | 3 |
| Matrix 8 | 2 | 3 | 1 | 2 | 0 | 0 | 2 | 5 |
| Matrix 9 | 3 | 4 | 3 | 3 | 2 | 2 | 3 | 4 |
| Matrix 10 | 4 | 4 | 2 | 3 | 0 | 0 | 4 | 4 |
| Matrix 11 | 4 | 4 | 3 | 3 | 1 | 2 | 4 | 4 |
| Matrix 1 | Matrix 2 | Matrix 3 | Matrix 4 | Matrix 5 | Matrix 6 | Matrix 7 | Matrix 8 | |
|---|---|---|---|---|---|---|---|---|
| EAM | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| EAMW | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 3 |
| Criteria/Experts | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 4 | 4 | 3 | 3 | 3 | 2 | 3 | |
| 1 | 1 | 2 | 1 | 2 | 1 | 1 | |
| 3 | 3 | 4 | 4 | 5 | 4 | 4 | |
| 2 | 2 | 1 | 2 | 1 | 3 | 2 | |
| 5 | 5 | 5 | 6 | 4 | 5 | 5 | |
| 6 | 6 | 6 | 5 | 6 | 6 | 6 |
| Decision | Complexity of the Task | Number of Decision-Makers | Nature of the Decision Criteria | Type of PCM | Recommended Methods |
|---|---|---|---|---|---|
| Personal | Low | 1–6 | Precise | General PCM | AHP |
| Personal | Low | 1–6 | Ambiguous | General FPCM | FAMCD or FGMGD |
| Collective | Low | 7–12 | Precise | General FPCM | FAMCD or FGMGD |
| Collective | Low-Medium-High | 7 and more | Precise | Individual PCM | MinMax-AM or MinMax-GM aggregation method with FAMCD or FGMGD |
| Collective | Low | 7–12 | Ambiguous | General FPCM | FAMCD or FGMGD |
| Collective | Low-High | 7 and more | Ambiguous | Individual FPCM | Lambda-Max; AMA aggregation with FAMCD or FGMGD. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vinogradova-Zinkevič, I. Comparative Sensitivity Analysis of Some Fuzzy AHP Methods. Mathematics 2023, 11, 4984. https://doi.org/10.3390/math11244984
Vinogradova-Zinkevič I. Comparative Sensitivity Analysis of Some Fuzzy AHP Methods. Mathematics. 2023; 11(24):4984. https://doi.org/10.3390/math11244984
Chicago/Turabian StyleVinogradova-Zinkevič, Irina. 2023. "Comparative Sensitivity Analysis of Some Fuzzy AHP Methods" Mathematics 11, no. 24: 4984. https://doi.org/10.3390/math11244984







