Revocable-Attribute-Based Encryption with En-DKER from Lattices

Abstract

Cloud computing offers abundant computing resources and scalable storage, but data leakage in the cloud storage environment is a common and critical concern due to inadequate protection measures. Revocable-attribute-based encryption (RABE) is introduced as an advanced form of identity-based encryption (IBE), which encrypts sensitive data while providing fine-grained access control and an effective user revocation mechanism. However, most existing RABE schemes are not resistant to quantum attacks and are limited in their application scenarios due to the revocation model. In this paper, we propose a RABE scheme constructed from lattices. Our scheme has several advantages, including a near-zero periodic workload for the key generation center (KGC), ensuring scalability as the number of users increases. Additionally, the encryptor is relieved from managing a revocation list. Moreover, our scheme guarantees the confidentiality and privacy of other ciphertexts even if the decryption key for a specific period is compromised. We validated the correctness of our scheme and demonstrated its security under the assumption of learning with errors (LWE), which is widely believed to be resistant to quantum attacks. Finally, we provide an application example of our RABE scheme in the electronic healthcare scenario.

1. Introduction

Attribute-based encryption (ABE), introduced by Sahai and Waters [1], is regarded as an advanced variant of identity-based encryption (IBE). Its decryption process only becomes viable when the attributes meet the specified policy, thereby providing a cryptographic primitive for encryption with fine-grained access control. ABE manifests in two distinct forms: ciphertext-policy and key-policy. In ciphertext-policy ABE (CP-ABE) [2,3], ciphertexts are associated with access policies and keys are associated with attributes. Conversely, in key-policy ABE (KP-ABE) [4,5], ciphertexts are associated with attributes and keys are associated with access policies. In this paper, we focus our discussion on KP-ABE.

Over the years, ABE has evolved into a foundational cryptographic primitive, displaying vast potential applications. Researchers have proposed numerous enhanced and extended ABE schemes [4,5,6,7,8] to address essential facets such as expressiveness, efficiency, and security. Notably, ABE schemes resistant to quantum computers, especially those based on lattice cryptography, have received significant attention. The development of these quantum-resistant schemes addresses vital aspects while also presenting new challenges.

In many practical applications of ABE, an efficient revocation mechanism is crucial when users become malicious or their secret keys are compromised. Boneh and Franklin [9] proposed a solution where the key generation center (KGC) periodically generates keys for all non-revoked users. However, this approach results in a periodic workload of $O(N-r)$ for the KGC, potentially becoming a bottleneck as the number of users grows, where N and r represent the maximum number of users and revoked users, respectively. Boldyreva et al. [10] introduced an indirect revocation model employing a binary tree structure and subset-cover framework, effectively reducing the periodic workload of the KGC to $O(rlog(N/r\left)\right)$, a more scalable approach.

Following the work of Boldyreva et al. [10], Chen et al. [11] presented the first lattice-based indirect revocation IBE (RIBE) scheme. However, when extending this scheme to ABE, conflicts arise between fine-grained access control and the coarse-grained binary tree employed for user revocation, presenting challenges for security proofs. So is there a revocable-attribute-based encryption (RABE) from lattices that the encryptor does not need to manage the revocation list?

There have been a few exciting attempts towards addressing this problem [12,13,14]. However, these schemes adopt a direct revocation model proposed by Attrapadung and Imai [15] that eliminates the need for periodic key updates by both the KGC and users. Nevertheless, the encryptor must manage the revocation list and generate ciphertext that can only be decrypted by non-revoked users in specific scenarios.

In practical scenarios, the leakage of decryption keys from external attacks or user errors is frequently observed. Addressing this concern, Seo and Emura [16] introduced a significant security concept known as decryption key exposure resistance (DKER). DKER mandates that the exposure of decryption keys for any time period should not compromise the confidentiality of ciphertexts encrypted for distinct time periods within the context of RIBE schemes. By re-randomizing decryption keys, it is conceivable that the scheme can fulfill the DKER property. Several RABE schemes, relying on number theoretical assumptions, have been proposed to achieve DKER [17,18,19].

Nevertheless, the algebraic structure of lattices makes the re-randomization of a specific key challenging. This difficulty arises because, if a user generates a new decryption key that ensures correctness without possessing knowledge of the trapdoor, they would also have the capability to solve the Small Integer Solution (SIS) problem. So is there a RABE with DKER from lattices?

Katsumata et al. [20] proposed an approach to achieve the partial key re-randomization property from lattices and constructed the first lattice-based RIBE scheme with DKER. Their scheme adopts a two-level structure, where the first level incorporates [11] for revocation, while the second level relies on any lattice-based HIBE scheme [21,22] to fulfill the DKER property. However, this two-level structure cannot be extended to ABE. In ABE, multiple users may correspond to the same policy. Consequently, a revoked user can combine the decryption keys leaked by non-revoked users with the same policy to generate new decryption keys for other time periods.

1.1. Related Work

Qin et al. [23] proposed a server-aided revocation model, utilizing an untrusted server for periodic key updates instead of relying on the user. This innovative approach enables users to achieve arbitrary period decryption while maintaining only a constant-level secret key, thus significantly reducing the user’s workload. Recently, Wang et al. [24] proposed a novel revocation model with a nearly negligible periodic workload for the KGC. Unlike direct revocation, this model eliminates the need for the encryptor to manage a revocation list. Additionally, they introduced a lattice basis delegation approach, enabling the delegation of sampling operations to an untrusted server. This approach significantly reduces the periodic workload associated with user decryption key generation.

Takayasu and Watanabe [25,26] integrated anonymity and DKER for the first time, constructing a RIBE scheme with bounded DKER (B-DKER) and anonymity. Anonymity, as defined by Boyen [27], guarantees that encrypted ciphertext must not reveal the recipient’s identity. Simultaneously, B-DKER ensures the security of RIBE schemes under a priori bounded exposure of decryption keys, representing a weak version of DKER. In a subsequent development, Wang et al. [24] introduced an enhanced form of DKER, named enhanced DKER (En-DKER). En-DKER extends the requirement by ensuring that the exposure of decryption keys in any time period cannot compromise the confidentiality and anonymity of ciphertexts in other time periods.

Wang et al. [28] and Yang et al. [29] proposed two revocable CP-ABE schemes under the learning with errors (LWE) assumption. Furthermore, Yang et al. [30] presented a revocable and multi-authority CP-ABE from the ring learning with errors (RLWE) assumption. Dong et al. [31] proposed a lattice-based RABE scheme with DKER. Huang et al. [32] proposed a multiple authorities CP-ABE scheme with DKER from lattices.

1.2. Technical Overview

Here, we provide a detailed analysis of the difficulties associated with the two open problems mentioned earlier in the introduction. Subsequently, we present the construction approach for our lattice-based RABE with the En-DKER scheme.

First, we define the symbols that may be used in the following discussions. $\mathbf{A}$, $\mathbf{B}$, and $\mathbf{W}$ are matrices in ${\mathbb{Z}}_q^{n\times m}$, ${\mathbf{T}}_{\mathbf{A}}$ is the trapdoor of the matrix $\mathbf{A}$, and $\mathbf{u}$ and $\mathbf{s}$ are random vectors in ${\mathbb{Z}}_q^n$. ${\mathbf{B}}_{ID}$ and ${\mathbf{W}}_t$ are random matrices of identity $ID$ and time period t in ${\mathbb{Z}}_q^{n\times m}$ based on $\mathbf{B}$ and $\mathbf{W}$, respectively. In addition, the KGC manages a binary tree $BT$ and randomly selects a particular leaf node ${\eta }_{ID}$ for each identity $ID$. $\mathsf{Path}\left({\eta }_{ID}\right)$ and $\mathrm{KUNodes}\left({\mathsf{RL}}_{\mathsf{t}}\right)$ are two node sets, where the former represents all nodes on the path from the leaf node ${\eta }_{ID}$ to the root, and the latter represents the smallest nodes subset of non-revoked users in time period t. The detailed introduction of algorithm $\mathrm{KUNodes}$ is in Lemma 8. Assuming that an identity $ID$ has not been revoked at time period t, there must be a node ${\theta }^{*}=\mathsf{Path}\left({\eta }_{ID}\right)\cap \mathrm{KUNodes}\left({\mathsf{RL}}_{\mathsf{t}}\right)$. For each node $\theta \in \mathsf{BT}$, select a uniformly random vector ${\mathbf{u}}_{\theta }$ in ${\mathbb{Z}}_q^n$.

We recall Chen et al.’s [11] RIBE scheme from lattices. As shown in Figure 1, the scheme consists of six algorithms: $\mathsf{Setup}$, $\mathsf{GenSK}$, $\mathsf{KeyUp}$, $\mathsf{GenDK}$, $\mathsf{Enc}$, and $\mathsf{Dec}$. The algorithm $\mathsf{GenSK}$ is run by the KGC to generate the secret key ${\left\{{\mathbf{sk}}_{ID,\theta }\right\}}_{\theta \in \mathsf{Path}\left({\eta }_{ID}\right)}$ for the identity $ID$. The KGC periodically runs the algorithm $\mathsf{KeyUp}$, inputs the revocation list ${\mathsf{RL}}_t$, and outputs and broadcasts the key update ${\left\{{\mathbf{ku}}_{t,\theta }\right\}}_{\theta \in \mathrm{KUNodes}\left({\mathsf{RL}}_t\right)}$. If the user $ID$ has not been revoked at time period t, he can generate the decryption key ${\mathbf{dk}}_{ID,t}$ by adding ${\mathbf{sk}}_{ID,{\theta }^{*}}$ and ${\mathbf{ku}}_{t,{\theta }^{*}}$ in a component-wise fashion. Conversely, if the user $ID$ is revoked, there is no intersection node between the two node sets, ${\mathbf{u}}_{\theta }$ cannot be eliminated, and thus the decryption key ${\mathbf{dk}}_{ID,t}$ cannot be calculated.

However, when extending Chen et al.’s [11] RIBE to RABE, conflicts arise between fine-grained access control and the coarse-grained binary tree employed for user revocation, presenting challenges for security proofs.

Specifically, in the security proof of [11], if the challenge identity $I{D}^{*}$ is revoked, the adversary can still make secret key queries for $I{D}^{*}$. It should be noted that, in this case, the challenger cannot utilize $\mathsf{SampleRight}$ for generation. Instead, for each $\theta \in \mathsf{Path}\left({\eta }_{I{D}^{*}}\right)$, a random vector is chosen as the secret key ${\mathbf{sk}}_{I{D}^{*},\theta }$, and ${\mathbf{u}}_{\theta }$ is assigned the value ${\mathbf{sk}}_{I{D}^{*},\theta }$ multiplied by $\left[\mathbf{A}\right|{\mathbf{B}}_{I{D}^{*}}]$. However, in ABE schemes, there may be multiple policies that satisfy the challenge attribute set ${\mathbf{x}}^{*}$, and a policy may correspond to multiple users as well. This means that there could be multiple revoked users who satisfy ${\mathbf{x}}^{*}$. When responding to the adversary’s secret key queries using the same method, there will be overlapping node sets in $\mathsf{Path}\left({\eta }_{ID}\right)$, leading to conflicts in ${\mathbf{u}}_{\theta }$. Furthermore, if we set ${\mathbf{u}}_{ID,\theta }$ for each $ID$, the update key will be directly related to the $ID$, which will bring us back to the original scheme [9], where the KGC’s period workload is $O(N-r)$.

Chen et al.’s RIBE scheme from lattices [11] does not satisfy DKER. Specifically, if the decryption key $d{k}_{ID,t}$ in time period t is exposed, the adversary can use the key update ${\mathbf{ku}}_{t,{\theta }^{*}}$ to recover the secret key ${\mathbf{sk}}_{ID,{\theta }^{*}}$. As a result, the adversary can do whatever the user with the identity $ID$ can do. Katsumata et al. [20] constructed the first RIBE scheme with DKER from lattices. As shown in Figure 2, $\overline{\mathbf{A}}$ is a matrix in ${\mathbb{Z}}_q^{n\times m}$, and ${\mathbf{T}}_{\overline{\mathbf{A}}}$ is the trapdoor of the matrix $\overline{\mathbf{A}}$. $\overline{\mathbf{s}}$ is a random vector in ${\mathbb{Z}}_q^n$. They divided the ciphertext and decryption key into two levels, where the first level incorporates [11] for revocation, while the second level relies on any lattice-based HIBE scheme [21,22] to fulfill the DKER property.

However, this two-level structure cannot be extended to ABE. In ABE, multiple users may correspond to the same policy. Consequently, a revoked user can use his own partial secret key ${\mathbf{T}}_{\left[\overline{\mathbf{A}}\right|{\mathbf{B}}_{ID}]}$ and combine the decryption keys leaked by non-revoked users with the same policy to generate new decryption keys for other time periods. Interestingly, this issue also leads to the inability of [20] to guarantee anonymity in the event of decryption key leakage.

As shown in Figure 3, Wang et al. [24] constructed the first RIBE scheme with En-DKER from lattices. Luckily, their scheme provided a good solution approach. First, it associates the ciphertext with $\mathrm{KUNodes}\left({\mathsf{RL}}_t\right)$ so that, when the challenger replies to the secret key query, it can be separated according to the access structure as well as whether the node belongs to the challenge nodes set $\mathrm{KUNodes}{\left({\mathsf{RL}}_t\right)}^{*}$. This effectively solves the problem encountered when [11] is extended to ABE. Furthermore, unlike partial secret key re-randomization using a two-level structure in [20], Wang et al.’s scheme [24] achieved full secret key re-randomization. In this way, we can cleverly avoid the collusion problem encountered when extending [20] to ABE. By combining Wang et al.’s revocation model [24] with the BGG+14 [33], we propose the first RABE with En-DKER from lattices.

1.3. Our Contributions

This paper makes the following contributions:

We extend the En-DKER property proposed by Wang et al. [24] in RIBE to RABE. Specifically, the leakage of any time period decryption keys should not compromise the confidentiality of ciphertexts from other time periods. At the same time, adversaries are unable to determine whether the attribute set of the ciphertext for the challenge time period satisfies a specific policy using keys from any other time periods or policies.

By combining Wang et al.’s revocation model [24] with the BGG+14 [33], we propose the first RABE with En-DKER from lattices. Our scheme cleverly avoids the security proof challenges faced when extending Chen et al.’s RIBE scheme [11] to RABE and the collusion issues encountered when extending Katsumata et al.’s RIBE with the DKER scheme [20] to ABE. It is noteworthy that our scheme retains the advantages of near-zero periodic workload for the KGC, and the encryptor does not need to manage a revocation list.

Finally, we validate the correctness and prove the security of our scheme under the LWE assumption.

2. Preliminaries

2.1. Notations

In this paper, we denote the underlying security parameter as $\lambda$. We use $\mathsf{PPT}$ to represent probabilistic polynomial time. We represent vectors with bold lowercase letters, e.g., $\mathbf{v}$, and matrices with uppercase letters, e.g., $\mathbf{A}$. By default, all vectors are considered column vectors. If n is a positive integer, $\left[n\right]=\{1,\dots ,n\}$. For a column vector $\mathbf{x}\in {\mathbb{Z}}_n$, $\left|\right|\mathbf{x}\left|\right|$ denotes the standard Euclidean norm. For a matrix $\mathbf{A}\in {\mathbb{R}}^{n\times m}$, $\tilde{\mathbf{A}}$ is the Gram–Schmidt orthogonalization of $\mathbf{A}$, and $\left|\right|\mathbf{A}\left|\right|$ is the Euclidean norm of the longest column in $\mathbf{A}$.

The statistical distance between two distributions $\mathcal{D}$ and ${\mathcal{D}}^{\prime }$ is denoted as $\mathsf{SD}(\mathcal{D},{\mathcal{D}}^{\prime })$. Two families of distributions $\mathcal{D}={\left\{{\mathcal{D}}_{\lambda }\right\}}_{\lambda \in \mathbb{N}}$ and ${\mathcal{D}}^{\prime }={\left\{{\mathcal{D}}_{\lambda }^{\prime }\right\}}_{\lambda \in \mathbb{N}}$ are considered statistically indistinguishable if there exists a negligible function $\mathsf{negl}(·)$ such that $\mathsf{SD}({\mathcal{D}}_{\lambda },{\mathcal{D}}_{\lambda }^{\prime })\le \mathsf{negl}\left(\lambda \right)$ for all $\lambda \in \mathbb{N}$. Here, $\mathsf{negl}(·)$ is a function satisfying $\mathsf{negl}\left(\lambda \right)\le {\lambda }^{-c}$ for every constant $c>0$ and an integer $N_c$, where $\lambda >N_c$.

2.2. Useful Facts

• Smudging. The given lemma, originally established in [34], asserts that adding large noise often “smudges out” any small values.

Lemma 1 (Smudging Lemma).

Let $B_1$ and $B_2$ be two polynomials over the integers, and let $\mathcal{D}={\left\{{\mathcal{D}}_{\lambda }\right\}}_{\lambda }$ be any $B_1$-bounded distribution family. Define $\mathcal{U}={\left\{{\mathcal{U}}_{\lambda }\right\}}_{\lambda }$ as the uniform distribution over $[-B_2\left(\lambda \right),B_2\left(\lambda \right)]$. The families of distributions $\mathcal{D}+\mathcal{U}$ and $\mathcal{U}$ are statistically indistinguishable if there exists a negligible function $\mathsf{negl}(·)$ such that for all $\lambda \in \mathbb{N}$, $B_1\left(\lambda \right)/B_2\left(\lambda \right)\le \mathsf{negl}\left(\lambda \right)$.

The definition of $\mathcal{B}$-Bounded is as follows.

Definition 1 ($\mathcal{B}$-Bounded).

For a family of distributions $\mathcal{D}={\left\{{\mathcal{D}}_{\lambda }\right\}}_{\lambda \in \mathbb{N}}$ over the integers and a bound $\mathcal{B}=\mathcal{B}\left(\lambda \right)>0$, if for every $\lambda \in \mathbb{N}$ it holds that $P{r}_{x\leftarrow {\mathcal{D}}_{\lambda }}\left[\right|x|\le \mathcal{B}\left(\lambda \right)]=1$, we say that $\mathcal{D}$ is $\mathcal{B}$-bounded.

• Leftover Hash Lemma. Here, we recall the leftover hash lemma from [21].

Lemma 2.

Suppose $m>(n+1)logq+\omega (logn)$. Then, the distribution $(\mathbf{A},\mathbf{AR})$ is statistically indistinguishable from the distribution $(\mathbf{A},\mathbf{B})$, where $\mathbf{A}$ and $\mathbf{B}$ are uniformly chosen matrices in ${\mathbb{Z}}_q^{n\times m}$, and $\mathbf{R}$ is a uniformly chosen matrix in ${\{-1,1\}}^{m\times m}$. Simultaneously, $\mathsf{Pr}\left[\right|\left|\mathbf{R}\right||>20\sqrt{m}]\le \mathsf{negl}\left(m\right)$.

• Full-Rank Different Map. We need this tool to encode identities and time periods as matrices in ${\mathbb{Z}}_q^{n\times n}$.

Definition 2.

A function $\mathsf{H}:{\mathbb{Z}}_q^n\to {\mathbb{Z}}_q^{n\times n}$ is a full-rank different map if the matrix $\mathsf{H}\left(\mathbf{u}\right)-\mathsf{H}\left(\mathbf{v}\right)\in {\mathbb{Z}}_q^{n\times n}$ is full rank, for all distinct $\mathbf{u},\mathbf{v}\in {\mathbb{Z}}_q^n$, and $\mathsf{H}$ is computable in $\mathcal{O}(nlogq)$.

2.3. Background on Lattices

• Lattice. Let n, m, and q be positive integers. An m-dimensional lattice, denoted as $\mathcal{L}$, is a discrete subgroup within ${\mathbb{R}}^m$. Consider ${\mathcal{L}}_q^{\perp }\left(\mathbf{A}\right)$, the q-ary lattice defined as {$\mathbf{x}\in {\mathbb{Z}}^m$: $\mathbf{A}\mathbf{x}=\mathbf{0}$ in ${\mathbb{Z}}_q\}$, where $\mathbf{A}$ is a matrix in ${\mathbb{Z}}_q^{n\times m}$. For any $\mathbf{u}$ in ${\mathbb{Z}}_q^n$, let ${\mathcal{L}}_q^{\mathbf{u}}\left(\mathbf{A}\right)$ denote the coset {$\mathbf{x}\in {\mathbb{Z}}^m$: $\mathbf{A}\mathbf{x}=\mathbf{u}$ in ${\mathbb{Z}}_q\}$.
• Discrete Gaussians. For any parameter $\sigma >0$, the discrete Gaussian distribution is defined ${\rho }_{\mathcal{L},\sigma }\left(\mathbf{x}\right)={\rho }_{\sigma }\left(\mathbf{x}\right)/{\rho }_{\sigma }\left(\mathcal{L}\right)$, where ${\rho }_{\sigma }\left(\mathbf{x}\right)=exp\left(-\pi {\parallel \mathbf{x}\parallel }^2/{\sigma }^2\right)$ and ${\rho }_{\sigma }\left(\mathcal{L}\right)={\sum }_{\mathbf{x}\in \mathcal{L}}{\rho }_{\sigma }\left(\mathbf{x}\right)$.
• The following lemmas represent crucial properties of the discrete Gaussian distribution [35].

Lemma 3.

For positive integers n, m, q with $m>n$, $q>2$, and a matrix $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$, there exists a negligible function $\mathsf{negl}(·)$ such that $\mathsf{Pr}[||\mathbf{x}||>\sigma \sqrt{m}:\mathbf{x}\leftarrow {\mathcal{D}}_{{\mathcal{L}}_q^{\perp }\left(\mathbf{A}\right),\sigma }]\le \mathsf{negl}\left(n\right)$ when $\sigma =\tilde{\Omega }\left(n\right)$.

Lemma 4.

For positive integers n, m, q with $m>2nlogq$, and given $\mathbf{A}\leftarrow {\mathbb{Z}}_q^{n\times m}$ and $\mathbf{e}\leftarrow {\mathcal{D}}_{{\mathbb{Z}}^m,\sigma }$, the distribution of $\mathbf{u}=\mathbf{Ae}$ mod q is statistically close to the uniform distribution over ${\mathbb{Z}}_q^n$.

• Trapdoor Generators. The ensuing lemma outlines properties of algorithms designed for generating short bases of lattices.

Lemma 5.

[36,37,38] For integers n, m, $q>0$. There exist $\mathsf{PPT}$ algorithms with the following properties:

• $\mathsf{TrapGen}(1^n,1^m,q)\to (\mathbf{A},{\mathbf{T}}_{\mathbf{A}})$: On inputting n, m, q, output a matrix $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$ and its trapdoor ${\mathbf{T}}_{\mathbf{A}}\in {\mathbb{Z}}^{m\times m}$, satisfying $\left|\right|{\mathbf{T}}_{\mathbf{A}}\left|\right|\le O(nlogq)$.
• There exists a gadget matrix $\mathbf{G}$, which is a full-rank matrix in ${\mathbb{Z}}_q^{n\times m}$ and has a publicly known trapdoor ${\mathbf{T}}_{\mathbf{G}}$ with $\left|\right|\widetilde{{\mathbf{T}}_{\mathbf{G}}}\left|\right|\le \sqrt{5}$.

• Sampling Algorithms. We review some sampling algorithms from [36,37,38].

Lemma 6.

Let n, m, and q be positive integers. We have the following $\mathsf{PPT}$ algorithms:

• $\mathsf{SamplePre}(\mathbf{A},{\mathbf{T}}_{\mathbf{A}},\sigma ,\mathbf{u})\to \mathbf{s}$: Given a matrix $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$ with trapdoor ${\mathbf{T}}_{\mathbf{A}}$, a vector $\mathbf{u}\in {\mathbb{Z}}_q^n$, and a parameter $\sigma \ge \left|\right|\widetilde{{\mathbf{T}}_{\mathbf{A}}}\left|\right|·\omega \left(\sqrt{logm}\right)$, output a vector $\mathbf{s}\in {\mathbb{Z}}_q^m$ satisfying $\mathbf{A}·{\mathbf{s}}^{\top }={\mathbf{u}}^{\top }$ and $\left|\right|\mathbf{s}\left|\right|\le \sqrt{m}\sigma$.
• $\mathsf{SampleLeft}(\mathbf{A},\mathbf{M},{\mathbf{T}}_{\mathbf{A}},\sigma ,\mathbf{u})\to \mathbf{s}$: Given a matrix $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$ with trapdoor ${\mathbf{T}}_{\mathbf{A}}$, a matrix $\mathbf{M}\in {\mathbb{Z}}_q^{n\times m_0}$, a vector $\mathbf{u}\in {\mathbb{Z}}_q^n$, and a parameter $\sigma \ge \left|\right|\widetilde{{\mathbf{T}}_{\mathbf{A}}}\left|\right|·\omega \left(\sqrt{log(m+m_0)}\right)$, output a vector $\mathbf{s}\in {\mathbb{Z}}_q^{m+m_0}$ distributed statistically close to ${\mathcal{D}}_{{\mathcal{L}}_q^{\mathbf{u}}\left(\left[\mathbf{A}\right|\mathbf{M}]\right),\sigma }$.
• $\mathsf{SampleRight}(\mathbf{A},\mathbf{G},\mathbf{R},{\mathbf{T}}_{\mathbf{G}},\sigma ,\mathbf{u})\to \mathbf{s}$: Given a matrix $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$, the gadget matrix $\mathbf{G}$ with trapdoor ${\mathbf{T}}_{\mathbf{G}}$, a uniform random matrix $\mathbf{R}\leftarrow {\{-1,1\}}^{m\times m}$, a vector $\mathbf{u}\in {\mathbb{Z}}_q^n$, and a parameter $\sigma \ge \left|\right|\widetilde{{\mathbf{T}}_{\mathbf{G}}}\left|\right|·\sqrt{m}·\omega \left(\sqrt{logm}\right)$, output a vector $\mathbf{s}\in {\mathbb{Z}}_q^{2m}$ distributed statistically close to ${\mathcal{D}}_{{\mathcal{L}}_q^{\mathbf{u}}\left(\left[\mathbf{A}\right|\mathbf{AR}+\mathbf{G}]\right),\sigma }$.

• Hardness Assumption. The security of our revocable ABE scheme is reduced to the learning with errors (LWE) assumption.

Assumption 1

(Learning with Errors [39]). Let n, m, q be positive integers, and a parameter $\sigma \in \mathbb{R}$; for any PPT adversary $\mathcal{A}$, there exists a negligible function $\mathsf{negl}(·)$ that satisfies

$$|\mathsf{Pr}[\mathcal{A}(\mathbf{A},{\mathbf{s}}^{\top }\mathbf{A}+\mathbf{e})=1]-\mathsf{Pr}[\mathcal{A}(\mathbf{A},\mathbf{b})=1]|\le \mathsf{negl}\left(\lambda \right),$$

where $\mathbf{A}\leftarrow {\mathbb{Z}}_q^{n\times m}$, $\mathbf{s}\leftarrow {\mathbb{Z}}_q^n$, $\mathbf{b}\leftarrow {\mathbb{Z}}_q^n$, and $\mathbf{e}\leftarrow {\chi }_{\mathsf{LWE}}^m$.

Here, we set ${\chi }_{\mathsf{LWE}}$ is a $B_{\mathsf{LWE}}$-bounded distribution. Moreover, Peikert [40] proved that, if $B_{\mathsf{LWE}}\ge \omega (logn)·\sqrt{n}$, the hardness of the LWE assumption is equivalent to the worst-case ${\mathsf{GapSVP}}_{\gamma }$ with parameter $\gamma =2^{\Omega \left(n^{\epsilon }\right)}$.

• Lattice Evaluation. Here, we review some algorithms that implement the key-homomorphic features from [33,41].

Lemma 7.

Let n, m, and q be positive integers. For any matrices ${\mathbf{B}}_1,\dots ,{\mathbf{B}}_{\ell }\in {\mathbb{Z}}_q^{n\times m}$, any attribute sets $\mathbf{x}\in {\{0,1\}}^{\ell }$, and any Boolean circuit $f:\mathbf{x}\to \{0,1\}$ of depth $\le d$, set ${\mathbf{c}}_i={\mathbf{s}}^{\top }({\mathbf{B}}_i+x_i\mathbf{G})+{\mathbf{e}}_i$, where $i\in [\ell ]$, $\mathbf{s}\in {\mathbb{Z}}_q^n$, and ${\mathbf{e}}_i\leftarrow {\chi }_{\mathsf{LWE}}^m$, there exist algorithms $({\mathsf{Eval}}_{\mathrm{pk}},{\mathsf{Eval}}_{\mathrm{ct}},{\mathsf{Eval}}_{\mathrm{sim}})$ with the following properties:

• ${\mathsf{Eval}}_{\mathrm{pk}}(f,({\mathbf{B}}_1,\dots ,{\mathbf{B}}_{\ell }))\to {\mathbf{B}}_f$: Given a Boolean circuit f and ℓ matrices $({\mathbf{B}}_1,\dots ,{\mathbf{B}}_{\ell })$, output the matrix ${\mathbf{B}}_f$.
• ${\mathsf{Eval}}_{\mathrm{ct}}(f,{\left\{({\mathbf{B}}_i,x_i,{\mathbf{c}}_i)\right\}}_{i\in [\ell ]})\to {\mathbf{c}}_f$: For a Boolean circuit f, ℓ matrices $({\mathbf{B}}_1,\dots ,{\mathbf{B}}_{\ell })$, an attribute set $\mathbf{x}$, and ℓ vectors $({\mathbf{c}}_1,\dots ,{\mathbf{c}}_{\ell })$, output ${\mathbf{c}}_f$. Here, ${\mathbf{c}}_f={\mathbf{s}}^{\top }({\mathbf{B}}_f+f\left(\mathbf{x}\right)\mathbf{G})+{\mathbf{e}}_f$, where ${\mathbf{B}}_f={\mathrm{Eval}}_{\mathrm{pk}}(f,({\mathbf{B}}_1,\dots ,{\mathbf{B}}_{\ell }))$, and $\parallel {\mathbf{e}}_f\parallel \le \mathcal{B}\sqrt{m}·{(m+1)}^d$ with almost negligible probability.
• ${\mathsf{Eval}}_{\mathrm{sim}}(f,{\left\{({\mathbf{S}}_i,x_i^{*})\right\}}_{i\in [\ell ]},\mathbf{A})\to {\mathbf{S}}_f$: Given a Boolean circuit f, ℓ matrices ${\mathbf{S}}_1,\dots ,{\mathbf{S}}_{\ell }\in {\mathbb{Z}}_q^{m\times m}$, a matrix $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$, and an attribute set ${\mathbf{x}}^{*}$, output ${\mathbf{S}}_f$. Ensure $\mathbf{A}{\mathbf{S}}_f-f\left({\mathbf{x}}^{*}\right)\mathbf{G}={\mathbf{B}}_f$, where ${\mathbf{B}}_f={\mathsf{Eval}}_{\mathrm{pk}}(f,(\mathbf{A}{\mathbf{S}}_1-x_1^{*}\mathbf{G},\dots ,\mathbf{A}{\mathbf{S}}_{\ell }-x_{\ell }^{*}\mathbf{G}))$. If ${\mathbf{S}}_1,\dots ,{\mathbf{S}}_{\ell }\in {\{-1,1\}}^{m\times m}$, then $\parallel {\mathbf{S}}_f\parallel \le 20\sqrt{m}·{(m+1)}^d$ with almost negligible probability.

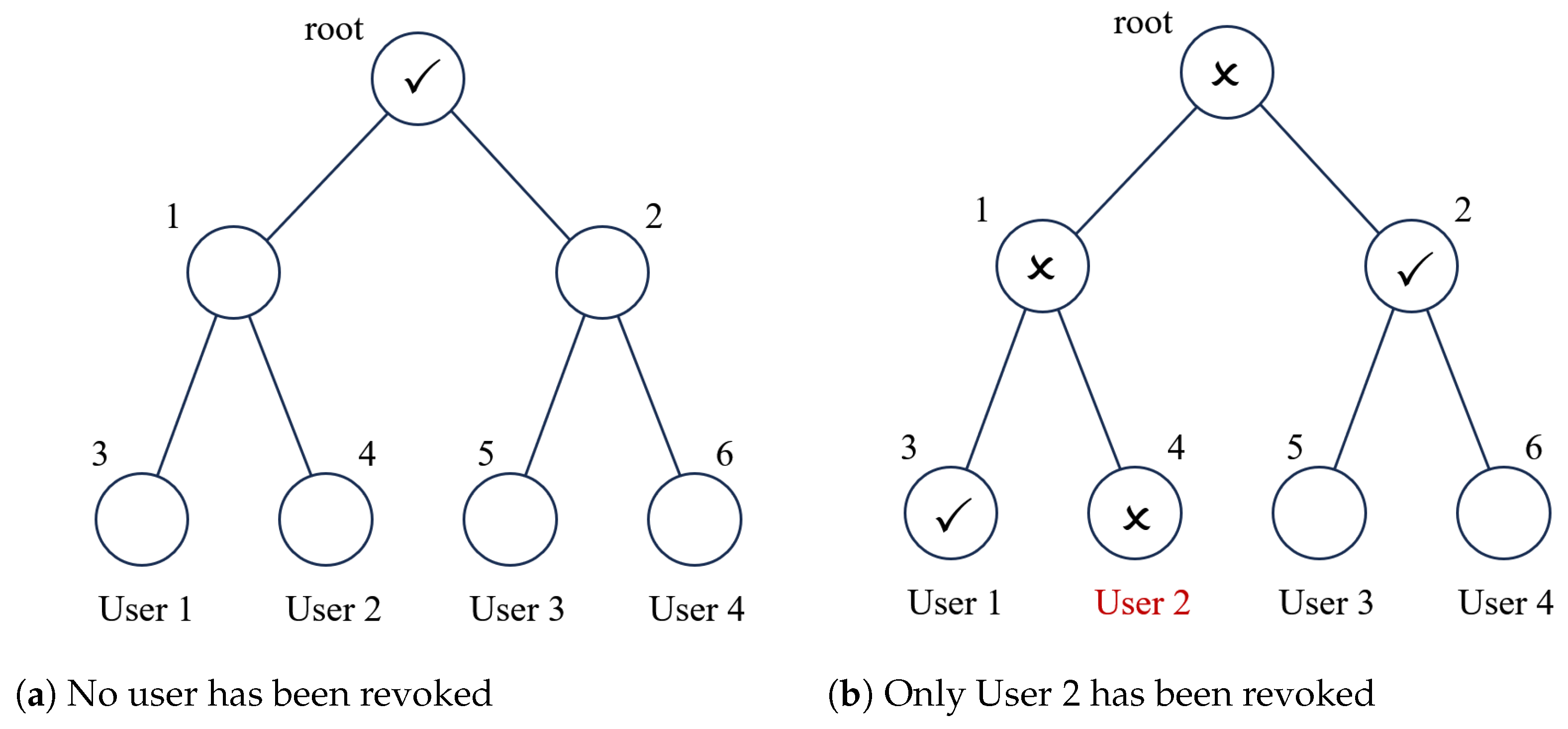
2.4. The Complete Subtree Method

The Complete Subtree (CS) method, introduced by Naor et al. [42], is utilized in indirect revocation schemes to alleviate the periodic workload of the KGC. In this approach, the system constructs a complete binary tree $\mathsf{BT}$. For a non-leaf node $\theta \in \mathsf{BT}$, ${\theta }_l$ and ${\theta }_r$ denote the left and right child nodes of $\theta$, and $\eta$ denotes the leaf node in $\mathsf{BT}$. $\mathsf{Path}\left(\eta \right)$ represents the set of nodes on the path from $\eta$ to the $\mathsf{root}$.

Lemma 8

($\mathrm{KUNodes}$). On inputting the revocation list ${\mathsf{RL}}_t$ for time period t, the $\mathrm{KUNodes}$ algorithm follows these steps: initializes two empty sets X and Y; adds $\mathsf{Path}\left(\eta \right)$ to X for each $\eta \in {\mathsf{RL}}_t$; for each $\theta \in X$, adds ${\theta }_l$ to Y if ${\theta }_l\notin X$, and adds ${\theta }_r$ to Y if ${\theta }_r\notin X$; if Y remains empty, adds $\mathsf{root}$ to Y; finally, outputs Y, which is the smallest subset of nodes representing non-revoked users during time period t.

In Figure 4a, there are no revoked users and $\mathrm{KUNodes}=\left\{\mathrm{root}\right\}$. However, in Figure 4b, User 2 has been revoked and $\mathrm{KUNodes}=\{2,3\}$. For a non-revoked user, the node set $\mathsf{Path}\left(\mathrm{User}\right)$ must have an intersection with the node set $\mathrm{KUNodes}$. For example, in Figure 4b, we have $\mathsf{Path}\left(\mathrm{User}1\right)=\{\mathrm{root},1,3\}$ and $\mathrm{KUNodes}\cap \mathsf{Path}\left(\mathrm{User}1\right)=3$.

3. The Notion of Revocable ABE with En-DKER

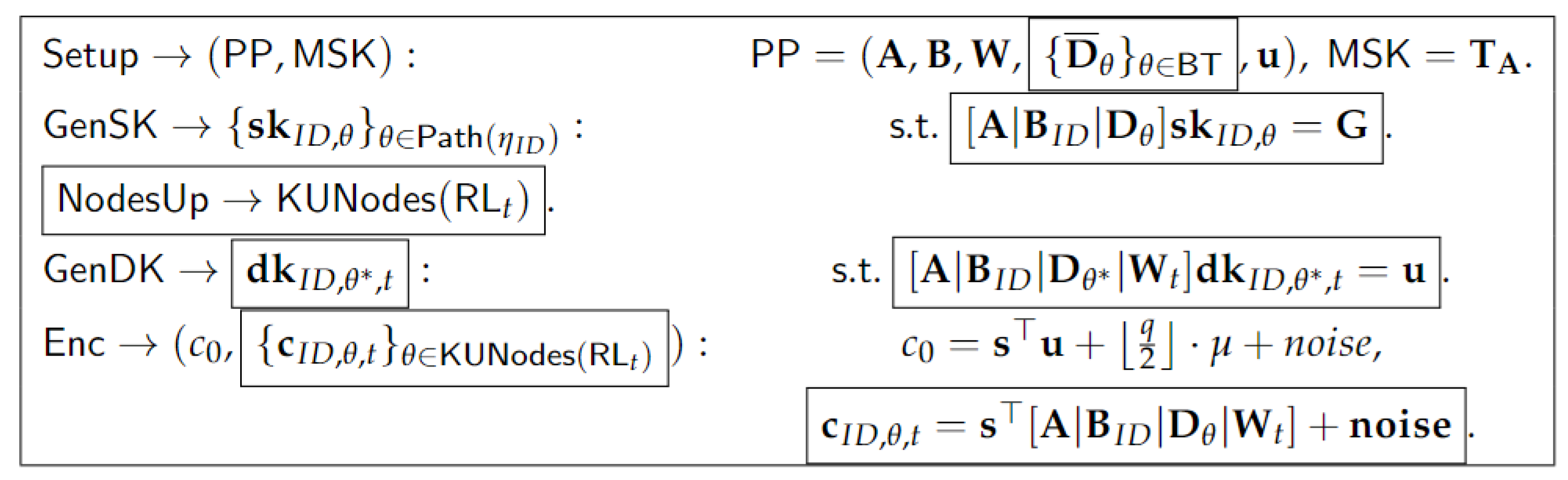
3.1. Syntax and Correctness

Let $\mathcal{ID}$ be an identity space, $\mathcal{M}$ be a message space, $\mathcal{X}$ be an attribute space, $\mathcal{T}$ be a time period space, and $\mathcal{F}$ be a sequence of sets of functions, namely $\mathcal{F}=\{f:{\mathcal{X}}^{\ell }\to \{0,1\}\}$. Our revocable ABE scheme consists of six algorithms $(\mathbf{Setup},\mathbf{GenSK},\mathbf{NodesUp}$, $\mathbf{GenDK},\mathbf{Enc},\mathbf{Dec})$, defined as follows:

• $\mathbf{Setup}\left(1^{\lambda }\right)\to (\mathsf{PP},\mathsf{MSK})$: Executed by the KGC, this algorithm takes as input a security parameter $\lambda$. It produces public parameters $\mathsf{PP}$ and a master secret key $\mathsf{MSK}$.
• $\mathbf{GenSK}(\mathsf{PP},\mathsf{MSK},ID,f)\to {\mathsf{SK}}_{ID,f}$: Executed by the KGC, this algorithm takes as input the public parameters $\mathsf{PP}$, the master secret key $\mathsf{MSK}$, an identity $ID\in \mathcal{ID}$, and a policy function $f\in \mathcal{F}$. It produces a secret key ${\mathsf{SK}}_{ID,f}$.
• $\mathbf{NodesUp}(\mathsf{BT},t,{\mathsf{RL}}_t)\to \mathrm{KUNodes}\left({\mathsf{RL}}_t\right)$: Executed by the KGC, this algorithm takes as input the binary tree $\mathsf{BT}$, a time period $t\in \mathcal{T}$, and the revocation list ${\mathsf{RL}}_t$ for the time period t. It produces and broadcasts a node set $\mathrm{KUNodes}\left({\mathsf{RL}}_t\right)$.
• $\mathbf{GenDK}(\mathsf{PP},{\mathsf{SK}}_{ID,f},\mathrm{KUNodes}\left({\mathsf{RL}}_t\right))\to {\mathsf{DK}}_{ID,f,t}$: Executed by the receiver, this algorithm takes as input the public parameters $\mathsf{PP}$, the secret key ${\mathsf{SK}}_{ID,f}$, and the node set $\mathrm{KUNodes}\left({\mathsf{RL}}_t\right)$. It produces a decryption key ${\mathsf{DK}}_{ID,f,t}$.
• $\mathbf{Enc}(\mathsf{PP},\mathbf{x},\mathrm{KUNodes}\left({\mathsf{RL}}_t\right),\mu )\to {\mathsf{CT}}_{\mathbf{x},t}$: Executed by the sender, this algorithm takes as input the public parameters $\mathsf{PP}$, an attribute set $\mathbf{x}\in {\mathcal{X}}^l$, the node set $\mathrm{KUNodes}\left({\mathsf{RL}}_t\right)$, and a message $\mu \in \mathcal{M}$. It produces a ciphertext ${\mathsf{CT}}_{\mathbf{x},t}$.
• $\mathbf{Dec}({\mathsf{CT}}_{\mathbf{x},t},{\mathsf{DK}}_{ID,f,t})\to {\mu }^{\prime }$: Executed by the receiver, this algorithm takes as input the ciphertext ${\mathsf{CT}}_{\mathbf{x},t}$ and the decryption key ${\mathsf{DK}}_{ID,f,t}$. It produces a message ${\mu }^{\prime }\in \mathcal{M}$.

• Correctness. A revocable ABE scheme is correct if, for all $\lambda \in \mathbb{N}$, $ID\in \mathcal{ID}$, $t\in \mathcal{T}$, $\mu \in \mathcal{M}$, $\mathbf{x}\in {\mathcal{X}}^{\ell }$, and $f\in \mathcal{F}$ that satisfy $f\left(\mathbf{x}\right)=0$, it holds that

$$Pr\left[{\mu }^{\prime }=\mu |\begin{array}{c}(\mathsf{PP},\mathsf{MSK})\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)\\ {\mathsf{SK}}_{ID,f}\leftarrow \mathsf{GenSK}(\mathsf{PP},\mathsf{MSK},ID,f)\\ \mathrm{KUNodes}\left({\mathsf{RL}}_t\right)\leftarrow \mathsf{NodesUp}(\mathsf{BT},t,{\mathsf{RL}}_t)\\ {\mathsf{DK}}_{ID,f,t}\leftarrow \mathsf{GenDK}(\mathsf{PP},{\mathsf{SK}}_{ID,f},\mathrm{KUNodes}\left({\mathsf{RL}}_t\right))\\ {\mathsf{CT}}_{\mathbf{x},t}\leftarrow \mathsf{Enc}(\mathsf{PP},\mathbf{x},t,\mathrm{KUNodes}\left({\mathsf{RL}}_t\right),\mu )\\ {\mu }^{\prime }\leftarrow \mathsf{Dec}({\mathsf{CT}}_{\mathbf{x},t},{\mathsf{DK}}_{ID,f,t})\end{array}\right]=1-\mathsf{negl}\left(\lambda \right).$$

3.2. Security Model of Revocable ABE with En-DKER

We first extend the En-DKER property proposed by Wang et al. [24] in RIBE to RABE. Specifically, the En-DKER property of the RABE scheme, in addition to possessing the features of DKER, also satisfies that adversaries are unable to determine whether the attribute set of the ciphertext for the challenge time period satisfies a specific policy using keys from any other time periods or policies, which is analogous to the anonymity property of the IBE scheme.

Then, we provide the formal definition of selective security via a game between an adversary $\mathcal{A}$ and the challenger $\mathcal{C}$. Set a global variable $t_{cu}\in \mathcal{T}$ with an initial value of 1 to facilitate the generation of the decryption key ${\mathsf{DK}}_{ID,f,t}$ of any time period queried by $\mathcal{A}$. This is particularly useful as the revocation list $\mathsf{RL}$ is dynamically updated following the time period t.

• Initialize: $\mathcal{C}$ establishes a binary tree $\mathsf{BT}$. $\mathcal{A}$ sets the challenge attribute sets ${\mathbf{x}}^{\left(0\right)}$ and ${\mathbf{x}}^{\left(1\right)}$, the challenge time period $t^{*}$, and the challenge node set $\mathrm{KUNodes}{\left({\mathsf{RL}}_{t^{*}}\right)}^{*}$.
• Setup Phase: $\mathcal{C}$ executes the $\mathsf{Setup}$ algorithm, providing the public parameters $\mathsf{PP}$ to $\mathcal{A}$.
• Query Phase: $\mathcal{A}$ adaptively makes the following queries to $\mathcal{C}$:
  • $\mathcal{A}$ sets ${\mathcal{Q}}_0=\left\{ID\right\}$ for user registration queries. $\mathcal{C}$ randomly selects an unassigned leaf node ${\eta }_{ID}$ for $ID$. (At the conclusion of the query, $\mathcal{C}$ acquires ${\mathsf{RL}}_{t^{*}}^{*}$ based on $\mathrm{KUNodes}{\left({\mathsf{RL}}_{t^{*}}\right)}^{*}$ and $\mathsf{BT}$).
  • $\mathcal{A}$ sets ${\mathcal{Q}}_1=\{ID,f\}$ for the secret key queries; $\mathcal{C}$ replies with the corresponding secret key ${\mathsf{SK}}_{ID,f}\leftarrow \mathsf{GenSK}(\mathsf{PP},\mathsf{MSK},ID,f)$. This is subject to the constraint $ID\in {\mathcal{Q}}_0$; if $f\left({\mathbf{x}}^{\left(0\right)}\right)=0$ or $f\left({\mathbf{x}}^{\left(1\right)}\right)=0$, $ID\in {\mathsf{RL}}_{t^{*}}^{*}$.
  • Let $t_{cu}=1$, and loop through the following steps:

    (a)

    $\mathcal{A}$ sets ${\mathcal{Q}}_2=\left\{(ID,f,t_{cu})\right\}$ for the decryption key queries; $\mathcal{C}$ replies with the decryption key ${\mathsf{DK}}_{ID,f,t_{cu}}\leftarrow \mathsf{GenDK}(\mathsf{PP},{\mathsf{SK}}_{ID,f},\mathrm{KUNodes}\left({\mathsf{RL}}_{t_{cu}}\right))$. This is subject to the constraint $ID\in {\mathcal{Q}}_0$; $ID\notin {\mathsf{RL}}_{t_{cu}}$; if $t_{cu}=t^{*}$, $f\left({\mathbf{x}}^{\left(0\right)}\right)\ne 0$ and $f\left({\mathbf{x}}^{\left(1\right)}\right)\ne 0$.

    (b)

    $\mathcal{A}$ sets ${\mathcal{Q}}_3=\left\{(ID,t_{cu})\right\}$ for revocation queries, $\mathcal{C}$ adds $ID$ to the revocation list $\mathsf{RL}$ and updates ${\mathsf{RL}}_{t_{cu}+1}=\mathsf{RL}$. Then, $\mathcal{C}$ sent $\mathrm{KUNodes}\left({\mathsf{RL}}_{t_{cu}+1}\right)$ to $\mathcal{A}$. This is subject to the constraint $ID\in {\mathcal{Q}}_0$; ${\mathsf{RL}}_{t^{*}}={\mathsf{RL}}_{t^{*}}^{*}$.

    (c)

    $t_{cu}=t_{cu}+1$.

• Challenge Phase: $\mathcal{A}$ sets challenge plaintexts ${\mu }^{\left(0\right)}$ and ${\mu }^{\left(1\right)}$. $\mathcal{C}$ randomly chooses a bit $b\leftarrow \{0,1\}$ and replies with the ciphertext ${\mathsf{CT}}_{{\mathbf{x}}^{\left(b\right)},t^{*}}\leftarrow \mathsf{Enc}(\mathsf{PP},{\mathbf{x}}^{\left(b\right)},t^{*},\mathrm{KUNodes}{\left({\mathsf{RL}}_{t^{*}}\right)}^{*},{\mu }^{\left(b\right)})$.
• Guess: $\mathcal{A}$ outputs a guess $b^{\prime }$ of b and succeeds if $b^{\prime }=b$. The advantage of $\mathcal{A}$ is defined as

  $${\mathsf{Adv}}_{\mathsf{RABE},\mathcal{A}}^{\mathsf{SEL}-\mathsf{En}-\mathsf{CPA}}\left(\lambda \right)=|\mathsf{Pr}[b=b^{\prime }]-1/2|.$$

Definition 3.

A revocable ABE with En-DKER scheme is selectively secure if, for any PPT adversaries $\mathcal{A}$, ${\mathsf{Adv}}_{\mathsf{RABE},\mathcal{A}}^{\mathsf{SEL}-\mathsf{En}-\mathsf{CPA}}\left(\lambda \right)$ is at most negligible.

4. Revocable ABE with En-DKER from Lattices

4.1. Our Construction

In our scheme, we set the message space $\mathcal{M}=\{0,1\}$, the identity space $\mathcal{ID}\subset {\mathbb{Z}}_q^n\setminus \left\{{\mathbf{0}}_n\right\}$, the attribute space $\mathcal{X}=\{0,1\}$, a sequence of sets of functions $\mathcal{F}=f:{\{0,1\}}^l\to \{0,1\}$, and the time period space $\mathcal{T}\subset {\mathbb{Z}}_q^n$. For any $B\in \mathbb{N}$, let ${\mathcal{U}}_B$ denote the uniform distribution on $\mathbb{Z}\cap [-B,B]$. $\mathsf{H}(·)$ is a full-rank different map defined in Definition 2 and $\mathbf{G}$ is a gadget matrix defined in Lemma 5.

To ensure the decryption algorithm outputs ⊥ with almost negligible probability when $f\left(\mathbf{x}\right)=1$, we follow the approach of [12,13] and set an encoding function $\mathsf{encode}:\{0,1\}\to {\{0,1\}}^k$ with $k=\omega (log\lambda )$. For each $\mu \in \{0,1\}$, we define $\mathsf{encode}\left(\mu \right)=(\mu ,0,\dots ,0)\in {\{0,1\}}^k$. In addition, our system parameters satisfy the following constraints:

• For sampling: $m>2nlogq$ and $\sigma >\sqrt{m}·\omega \left(\sqrt{m}\right)$.
• For correctness: $k=\omega (log\lambda )$, $O\left({(m+1)}^d(m^{5/2}\sigma +m^{3/2}{\mathsf{B}}_{\mathsf{big}})\right)<q/4B_{\mathsf{LWE}}$.
• For security: $n=O\left(\lambda \right)$, ${\chi }_{\mathsf{LWE}}={\mathcal{U}}_{B_{\mathsf{LWE}}}$, where $B_{\mathsf{LWE}}\ge \omega (logn)·\sqrt{n}$.
• For smudging: ${\chi }_{\mathsf{big}}={\mathcal{U}}_{B_{\mathsf{big}}}$, where $B_{\mathsf{big}}>(m{\sigma }^2+1)2^{\lambda +1}$.

Now, we describe our revocable ABE with En-DKER from lattices construction.

• $\mathbf{Setup}\left(1^{\lambda }\right)\to (\mathsf{PP},\mathsf{MSK})$: On inputting a security parameter $\lambda$, the detailed process is as follows:
  • Run the algorithm $\mathsf{TrapGen}(1^n,1^m,q)$ to generate $(\mathbf{A},{\mathbf{T}}_{\mathbf{A}})$, where $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$.
  • Choose random matrices ${\left\{{\mathbf{B}}_i\right\}}_{i\in [\ell ]},\mathbf{W}$ in ${\mathbb{Z}}_q^{n\times m}$, and a random matrix $\mathbf{U}$ in ${\mathbb{Z}}_q^{n\times k}$.
  • Build a binary tree $\mathsf{BT}$ with at least N leaf nodes. For each node $\theta \in \mathsf{BT}$, select a random matrix ${\mathbf{D}}_{\theta }$ in ${\mathbb{Z}}_q^{n\times m}$.
  • Output $\mathsf{PP}=\{\mathbf{A},{\left\{{\mathbf{B}}_i\right\}}_{i\in [\ell ]},\mathbf{W},\mathbf{U},{\left\{{\mathbf{D}}_{\theta }\right\}}_{\theta \in \mathsf{BT}}\}$, $\mathsf{MSK}=\{{\mathbf{T}}_{\mathbf{A}},\mathsf{BT}\}$.
• $\mathbf{GenSK}(\mathsf{PP},\mathsf{MSK},ID,f)\to {\mathsf{SK}}_{ID,f}$: On inputting the public parameters $\mathsf{PP}$, the master secret key $\mathsf{MSK}$, an identity $ID\in \mathcal{ID}$, and a policy function $f\in \mathcal{F}$, the detailed process is as follows:
  • If $ID$ belongs to a newly registered user in the system, then randomly pick an unassigned leaf node ${\eta }_{ID}$ from $\mathsf{BT}$ and store $ID$ in it.
  • Compute ${\mathbf{B}}_f={\mathsf{Eval}}_{\mathrm{pk}}(f,({\mathbf{B}}_1,\dots ,{\mathbf{B}}_{\ell }))$.
  • For each $\theta \in \mathsf{Path}\left({\eta }_{ID}\right)$, generate ${\mathbf{K}}_{ID,f,\theta }\in {\mathbb{Z}}_q^{3m\times m}$, satisfying $\left[\mathbf{A}\right|{\mathbf{B}}_f\left|{\mathbf{D}}_{\theta }\right]{\mathbf{K}}_{ID,f,\theta }=\mathbf{G}$.

    (a)

    Choose a random matrix ${\mathbf{K}}_{ID,f}^{\prime }$ in ${\mathcal{D}}_{\mathbb{Z},\sigma }^{2m\times m}$ and set ${\mathbf{Z}}_{ID,f}=\left[\mathbf{A}\right|{\mathbf{B}}_f]{\mathbf{K}}_{ID,f}^{\prime }\in {\mathbb{Z}}_q^{m\times m}$.

    (b)

    Sample ${\mathbf{K}}_{ID,f,\theta }^{″}\leftarrow \mathsf{SampleLeft}(\mathbf{A},{\mathbf{D}}_{\theta },{\mathbf{T}}_{\mathbf{A}},\sigma ,\mathbf{G}-{\mathbf{Z}}_{ID,f})$.

    (c)

    Divide ${\mathbf{K}}_{ID,f}^{\prime }$ and ${\mathbf{K}}_{ID,f,\theta }^{″}$ into two parts, ${\mathbf{K}}_{1,ID,f}^{\prime }$, ${\mathbf{K}}_{2,ID,f}^{\prime }$ and ${\mathbf{K}}_{1,ID,f,\theta }^{″}$, ${\mathbf{K}}_{2,ID,f,\theta }^{″}$ with m rows per part. Then, generate

    $${\mathbf{K}}_{ID,f,\theta }={\left[\begin{array}{ccc}{\left({\mathbf{K}}_{1,ID,f}^{\prime }+{\mathbf{K}}_{1,ID,f,\theta }^{″}\right)}^{\top }|& {\left({\mathbf{K}}_{2,ID,f}^{\prime }\right)}^{\top }|& {\left({\mathbf{K}}_{2,ID,f,\theta }^{\prime \prime }\right)}^{\top }\end{array}\right]}^{\top }.$$

  • Output ${\mathsf{SK}}_{ID,f}={\left\{{\mathbf{K}}_{ID,f,\theta }\right\}}_{\theta \in \mathsf{Path}\left({\eta }_{ID}\right)}$.
• $\mathbf{NodesUp}(\mathsf{BT},t,{\mathsf{RL}}_t)\to \mathrm{KUNodes}\left({\mathsf{RL}}_t\right)$: On inputting the binary tree $\mathsf{BT}$, a time period $t\in \mathcal{T}$, and the revocation list ${\mathsf{RL}}_t$ for the time period t, the KGC generates and broadcasts a set $\mathrm{KUNodes}\left({\mathsf{RL}}_t\right)$ for the time period t.
• $\mathbf{GenDK}(\mathsf{PP},{\mathsf{SK}}_{ID,f},\mathrm{KUNodes}\left({\mathsf{RL}}_t\right))\to {\mathsf{DK}}_{ID,f,t}$: On inputting the public parameters $\mathsf{PP}$, the secret key ${\mathsf{SK}}_{ID,f}$, and the node set $\mathrm{KUNodes}\left({\mathsf{RL}}_t\right)$, the detailed process is as follows:
  • Set ${\theta }^{*}=\mathsf{Path}\left({\eta }_{ID}\right)\cap \mathrm{KUNodes}\left({\mathsf{RL}}_t\right)$. If ${\theta }^{*}=Ø$, outputs ⊥. Otherwise, continue the following steps.
  • Compute ${\mathbf{W}}_t=\mathbf{W}+\mathsf{H}\left(t\right)\mathbf{G}$.
  • Generate ${\mathbf{DK}}_{ID,f,t}\in {\mathbb{Z}}_q^{4m\times k}$, satisfying $\left[\mathbf{A}\right|{\mathbf{B}}_f|{\mathbf{D}}_{{\theta }^{*}}\left|{\mathbf{W}}_t\right]{\mathbf{DK}}_{ID,f,t}=\mathbf{U}$.

    (a)

    Choose a random matrix ${\tilde{\mathbf{K}}}_{ID,f,t}\in {\chi }_{\mathsf{big}}^{4m\times k}$. Set ${\mathbf{H}}_{ID,f,t}=\left[\mathbf{A}\right|{\mathbf{B}}_f|{\mathbf{D}}_{{\theta }^{*}}\left|{\mathbf{W}}_t\right]{\tilde{\mathbf{K}}}_{ID,f,t}$ and send to the server.

    (b)

    The server samples ${\widetilde{{\mathbf{K}}^{\prime }}}_{ID,f,t}\leftarrow \mathsf{SamplePre}(\mathbf{G},{\mathbf{T}}_{\mathbf{G}},\sigma ,\mathbf{U}-{\mathbf{H}}_{ID,f,t})$ and sends to the user.

    (c)

    Compute ${\widetilde{{\mathbf{K}}^{″}}}_{ID,f,t}={\mathbf{K}}_{f,{\theta }^{*}}{\widetilde{{\mathbf{K}}^{\prime }}}_{ID,f,t}$, satisfying $\left[\mathbf{A}\right|{\mathbf{B}}_f\left|{\mathbf{D}}_{{\theta }^{*}}\right]{\widetilde{{\mathbf{K}}^{″}}}_{ID,f,t}=\mathbf{U}-{\mathbf{H}}_{ID,f,t}$, where ${\widetilde{{\mathbf{K}}^{″}}}_{ID,f,t}\in {\mathbb{Z}}_q^{3m\times k}$.

    (d)

    Divide ${\tilde{\mathbf{K}}}_{ID,f,t}$ into four parts: ${\tilde{\mathbf{K}}}_{1,ID,f,t}$, ${\tilde{\mathbf{K}}}_{2,ID,f,t}$, ${\tilde{\mathbf{K}}}_{3,ID,f,t}$, ${\tilde{\mathbf{K}}}_{4,ID,f,t}$, and ${\widetilde{{\mathbf{K}}^{″}}}_{ID,f,t}$ into three parts: ${\widetilde{{\mathbf{K}}^{″}}}_{1,ID,f,t}$, ${\widetilde{{\mathbf{K}}^{″}}}_{2,ID,f,t}$, ${\widetilde{{\mathbf{K}}^{″}}}_{3,ID,f,t}$, with m rows per part. Then, generate

    $${\mathbf{DK}}_{ID,f,t}={\left[\begin{array}{cc}{\left(\begin{array}{c}{\tilde{\mathbf{K}}}_{1,ID,f,t}+{\widetilde{{\mathbf{K}}^{″}}}_{1,ID,f,t}\\ {\tilde{\mathbf{K}}}_{2,ID,f,t}+{\widetilde{{\mathbf{K}}^{″}}}_{2,ID,f,t}\end{array}\right)}^{\top }|& {\left(\begin{array}{c}{\tilde{\mathbf{K}}}_{3,ID,f,t}+{\widetilde{{\mathbf{K}}^{″}}}_{3,ID,f,t}\\ {\tilde{\mathbf{K}}}_{4,ID,f,t}\end{array}\right)}^{\top }\end{array}\right]}^{\top }.$$

  • Output ${\mathsf{DK}}_{ID,f,t}={\mathbf{DK}}_{ID,f,t}$.
• $\mathbf{Enc}(\mathsf{PP},\mathbf{x},\mathrm{KUNodes}\left({\mathsf{RL}}_t\right),\mu )\to {\mathsf{CT}}_{\mathbf{x},t}$: On inputting the public parameters $\mathsf{PP}$, an attribute set $\mathbf{x}=\{x_1,\dots ,x_{\ell }\}\in {\mathcal{X}}^{\ell }$, the node set $\mathrm{KUNodes}\left({\mathsf{RL}}_t\right)$, and a message $\mu \in \mathcal{M}$, the detailed process is as follows:
  • Choose a random vector $\mathbf{s}$ in ${\mathbb{Z}}_q^n$.
  • Choose random matrices ${\mathbf{R}}_i$, ${\mathbf{S}}_{\theta }$, and $\mathbf{V}$ in ${\{-1,1\}}^{m\times m}$, where $i\in [\ell ]$, $\theta \in \mathrm{KUNodes}\left({\mathsf{RL}}_t\right)$.
  • Choose noise $\mathbf{e}\leftarrow {\chi }_{\mathsf{LWE}}^k$ and a noise vector ${\mathbf{e}}^{\prime }\leftarrow {\chi }_{\mathsf{LWE}}^m$.
  • Generate ${\mathsf{CT}}_{\mathbf{x},t}=\{{\mathbf{c}}_{in},{\left\{{\mathbf{c}}_i\right\}}_{i\in [\ell ]},{\left\{{\mathbf{c}}_{\theta }\right\}}_{\theta \in \mathrm{KUNodes}\left({\mathsf{RL}}_t\right)},{\mathbf{c}}_t,{\mathbf{c}}_{out}\}$, where

    $$\begin{array}{cc}& {\mathbf{c}}_{out}={\mathbf{s}}^{\top }\mathbf{U}+⌊\frac{q}{2}⌋·\mathsf{encode}\left(\mu \right)+\mathbf{e}\in {\mathbb{Z}}_q^k,\hfill \\ & {\mathbf{c}}_{in}={\mathbf{s}}^{\top }\mathbf{A}+{\mathbf{e}}^{\prime }\in {\mathbb{Z}}_q^m,\hfill \\ & {\mathbf{c}}_t={\mathbf{s}}^{\top }{\mathbf{W}}_t+{\mathbf{e}}^{\prime }\mathbf{V}\in {\mathbb{Z}}_q^m,\hfill \\ \hfill i\in [\ell ]:& {\mathbf{c}}_i={\mathbf{s}}^{\top }({\mathbf{B}}_i+x_i\mathbf{G})+{\mathbf{e}}^{\prime }{\mathbf{R}}_i\in {\mathbb{Z}}_q^m,\hfill \\ \hfill \theta \in \mathrm{KUNodes}\left({\mathsf{RL}}_t\right):& {\mathbf{c}}_{\theta }={\mathbf{s}}^{\top }{\mathbf{D}}_{\theta }+{\mathbf{e}}^{\prime }{\mathbf{S}}_{\theta }\in {\mathbb{Z}}_q^m.\hfill \end{array}$$
  • Output ${\mathsf{CT}}_{\mathbf{x},t}$.
• $\mathbf{Dec}({\mathsf{CT}}_{\mathbf{x},t},{\mathsf{DK}}_{ID,f,t})\to {\mu }^{\prime }$: On inputting the ciphertext ${\mathsf{CT}}_{\mathbf{x},t}$ and the decryption key ${\mathsf{DK}}_{ID,f,t}$, the detailed process is as follows:
  • If $f\left(\mathbf{x}\right)=1$, outputs ⊥. Otherwise, continue the following steps.
  • Compute ${\mathbf{c}}_f={\mathsf{Eval}}_{\mathrm{ct}}(f,{\left\{(x_i,{\mathbf{B}}_i,{\mathbf{c}}_i)\right\}}_{i=1}^{\ell })\in {\mathbb{Z}}_q^m$.
  • Compute ${\mathbf{c}}^{\prime }={\mathbf{c}}_{out}-[{\mathbf{c}}_{in}|{\mathbf{c}}_f|{\mathbf{c}}_{{\theta }^{*}}\left|{\mathbf{c}}_t\right]{\mathbf{DK}}_{ID,f,t}\in {\mathbb{Z}}_q^k$.
  • Output ${\mu }^{\prime }$ by computing $\mathsf{encode}\left({\mu }^{\prime }\right)=\lfloor \frac{q}{2}·{\mathbf{c}}^{\prime }\rceil$.
• Correctness. We analyze the correctness of the scheme.
  • When $f\left(\mathbf{x}\right)=1$, the probability of the last $k-1$ coordinates being 0 is $2^{-(k-1)}=2^{-\omega (log\lambda )}$, which is negligible in $\lambda$. Consequently, the decryption algorithm outputs ⊥ with all but negligible probability.
  • When $f\left(\mathbf{x}\right)=0$, according to the correctness of the ${\mathsf{Eval}}_{\mathsf{ct}}$ algorithm, we have ${\mathbf{c}}_f={\mathbf{s}}^{\top }{\mathbf{B}}_f+{\mathbf{e}}^{\prime }{\mathbf{R}}_f$. Therefore,

$$\begin{array}{cc}\hfill {\mathbf{c}}^{\prime }& ={\mathbf{c}}_{out}-[{\mathbf{c}}_{in}|{\mathbf{c}}_f|{\mathbf{c}}_{{\theta }^{*}}\left|{\mathbf{c}}_t\right]{\mathbf{DK}}_{ID,f,t}\hfill \\ \hfill & ={\mathbf{s}}^{\top }\mathbf{U}+⌊\frac{q}{2}⌋·\mathsf{encode}\left(\mu \right)-{\mathbf{s}}^{\top }[\mathbf{A}|{\mathbf{B}}_f|{\mathbf{D}}_{{\theta }^{*}}|{\mathbf{W}}_t]{\mathbf{DK}}_{ID,f,t}+\mathbf{noise}\hfill \\ \hfill & =⌊\frac{q}{2}⌋·\mathsf{encode}\left(\mu \right)+\mathbf{noise},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill \mathbf{noise}& =\mathbf{e}-{\mathbf{e}}^{\prime \top }[{\mathbf{I}}_m|{\mathbf{R}}_f|{\mathbf{S}}_{{\theta }^{*}}|\mathbf{V}]{\mathbf{DK}}_{ID,f,t}\hfill \\ \hfill & =\mathbf{e}-{\mathbf{e}}^{\prime \top }[{\mathbf{I}}_m|{\mathbf{R}}_f|{\mathbf{S}}_{{\theta }^{*}}|\mathbf{V}]\left[\begin{array}{c}{\tilde{\mathbf{K}}}_{1,ID,f,t}+{\mathbf{K}}_{1,ID,f}^{\prime }{\widetilde{{\mathbf{K}}^{\prime }}}_{ID,f,t}+{\mathbf{K}}_{1,ID,f,{\theta }^{*}}^{″}{\widetilde{{\mathbf{K}}^{\prime }}}_{ID,f,t}\\ {\tilde{\mathbf{K}}}_{2,ID,f,t}+{\mathbf{K}}_{2,ID,f}^{\prime }{\widetilde{{\mathbf{K}}^{\prime }}}_{ID,f,t}\\ {\tilde{\mathbf{K}}}_{3,ID,f,t}+{\mathbf{K}}_{2,ID,f,{\theta }^{*}}^{″}{\widetilde{{\mathbf{K}}^{\prime }}}_{ID,f,t}\\ {\tilde{\mathbf{K}}}_{4,ID,f,t}\end{array}\right].\hfill \end{array}$$

Correctness now follows since $\mathbf{noise}$ is small and should not affect $⌊\frac{q}{2}⌋·\mathsf{encode}\left(\mu \right)$. Moreover, the following inequalities hold except with negligible probability:

• From Lemma 2, we have $||\mathbf{S}||$ and $||{\mathbf{V}}_{{\theta }^{*}}||\le 20\sqrt{m}$.
• From Lemma 7, we have $||{\mathbf{R}}_f||\le 20\sqrt{m}·{(m+1)}^d$.
• Because $\mathbf{e}\leftarrow {\chi }_{\mathsf{LWE}}^k$ and ${\mathbf{e}}^{\prime }\leftarrow {\chi }_{\mathsf{LWE}}^m$, we have $||\mathbf{e}||\le B_{\mathsf{LWE}}\sqrt{k}$ and $||{\mathbf{e}}^{\prime }||\le B_{\mathsf{LWE}}\sqrt{m}$.

$$\begin{array}{cc}\hfill ||\mathbf{noise}||& =||\mathbf{e}-{\mathbf{e}}^{\prime \top }[{\mathbf{I}}_m|\mathbf{R}|{\mathbf{S}}_{{\theta }^{*}}|\mathbf{V}]{\mathbf{DK}}_{ID,f,t}||\hfill \\ \hfill & \le ||\mathbf{e}||+||{\mathbf{e}}^{\prime \top }||·||[{\mathbf{I}}_m|\mathbf{R}|{\mathbf{S}}_{{\theta }^{*}}|\mathbf{V}]{\mathbf{DK}}_{ID,f,t}||\hfill \\ \hfill & \le O\left(B_{\mathsf{LWE}}{(m+1)}^d(m^{5/2}\sigma +m^{3/2}{\mathsf{B}}_{\mathsf{big}})\right)<q/4,\hfill \end{array}$$

and we can obtain $\mu$ by computing $\mathsf{encode}\left(\mu \right)=\lfloor \frac{q}{2}·{\mathbf{c}}^{\prime }\rceil$.

4.2. Security Proof

We show that our RABE construction is secure in the following theorem:

Theorem 1.

Our proposed RABE scheme with En-DKER is $\mathsf{IND}$-$\mathsf{CPA}$ secure under the assumption that the $\mathsf{LWE}$ problem is hard.

Proof. 

We consider a sequence of games, and the change between each successive game is only by a negligible amount ${\mathsf{negl}}_x\left(\lambda \right)$. Let ${\mathcal{P}}_{\mathcal{A},x}\left(\lambda \right)$ be the function that represents the probability of the adversary $\mathcal{A}$ correctly guessing the challenge bit b in ${\mathsf{Game}}_x^{\left(b\right)}$. The first game is the original $\mathsf{IND}$-$\mathsf{CPA}$ secure game for our RABE scheme, so the advantage of $\mathcal{A}$ is ${\mathsf{Adv}}_{\mathsf{RABE},\mathcal{A}}^{\mathsf{SEL}-\mathsf{En}-\mathsf{CPA}}\left(\lambda \right)=|{\mathcal{P}}_{\mathcal{A},0}\left(\lambda \right)-1/2|$. The final hybrid is one where the ciphertext is independent with the bit b, and the advantage of the adversary $\mathcal{A}$ is zero, so the advantage of $\mathcal{A}$ is ${\mathcal{P}}_{\mathcal{A},4}\left(\lambda \right)=1/2$. So, for all $\lambda \in \mathbb{N}$, we have ${\mathsf{Adv}}_{\mathsf{RABE},\mathcal{A}}^{\mathsf{SEL}-\mathsf{En}-\mathsf{CPA}}\left(\lambda \right)\le {\sum }_{x\in \left[4\right]}|{\mathcal{P}}_{\mathcal{A},x-1}\left(\lambda \right)-{\mathcal{P}}_{\mathcal{A},x}\left(\lambda \right)|\le {\sum }_{x\in \left[4\right]}{\mathsf{negl}}_x\left(\lambda \right).$ □

• The Series of Games. Let $\mathcal{A}$ be the adversary in the security definition of the RABE with En-DKER and adhere to the security model defined in Section 3.2. We consider the following series of games.
• ${\mathbf{Game}}_0^{\left(b\right)}$: This is the original $\mathsf{IND}$-$\mathsf{CPA}$ secure game for our RABE scheme, and $\mathcal{B}$ chooses a random bit $b\leftarrow \{0,1\}$.
• ${\mathbf{Game}}_1^{\left(b\right)}$: In this game, we change the generation way of matrices ${\left\{{\mathbf{B}}_i\right\}}_{i\in [\ell ]}$, ${\left\{{\mathbf{D}}_{\theta }\right\}}_{\theta \in \mathsf{BT}}$, and $\mathbf{W}$.
  • Choose random matrices ${\mathbf{R}}_i^{*}$, ${\mathbf{S}}_{\theta }^{*}$, and ${\mathbf{V}}^{*}$ in ${\{-1,1\}}^{m\times m}$, where $i\in [\ell ]$ and $\theta \in \mathsf{BT}$.
  • For each $i\in [\ell ]$, $\theta \in \mathsf{BT}$, we set ${\mathbf{B}}_i={\mathbf{AR}}_i^{*}-x_i^{\left(b\right)}\mathbf{G}$, $\mathbf{W}={\mathbf{AV}}^{*}-\mathsf{H}\left(t^{*}\right)\mathbf{G}$,

    $${\mathbf{D}}_{\theta }=\left\{\begin{array}{c}\mathbf{A}{\mathbf{S}}_{\theta }^{*},if\theta \in \mathrm{KUNodes}{\left({\mathsf{RL}}_{t^{*}}\right)}^{*}\hfill \\ \mathbf{A}{\mathbf{S}}_{\theta }^{*}+\mathbf{G},otherwise\hfill \end{array}\right..$$

We show that ${\mathsf{Game}}_0^{\left(b\right)}$ is statistically indistinguishable from ${\mathsf{Game}}_1^{\left(b\right)}$. By Lemma 2, $(\mathbf{A},{\mathbf{AR}}_i^{*},{\mathbf{AS}}_{\theta }^{*},{\mathbf{AV}}^{*})$ is statistically close to $(\mathbf{A},{\mathbf{B}}_i,{\mathbf{D}}_{\theta },\mathbf{W})$, where ${\mathbf{B}}_i,{\mathbf{D}}_{\theta },\mathbf{W}$ are the independently random matrices in ${\mathbb{Z}}_q^{n\times m}$, $i\in [\ell ]$ and $\theta \in \mathsf{BT}$. Moreover, the difference between $({\mathbf{AR}}_i^{*},{\mathbf{AS}}_{\theta }^{*},{\mathbf{AV}}^{*})$ and $({\mathbf{AR}}_i^{*}-x_i^{\left(b\right)}\mathbf{G},{\mathbf{AS}}_{\theta }^{*}+\mathbf{G},{\mathbf{AV}}^{*}-\mathsf{H}\left(t^{*}\right)\mathbf{G})$ is merely syntactic. So, there exists a negligible function ${\mathsf{negl}}_1(·)$ satisfying $|{\mathcal{P}}_{\mathcal{A},0}\left(\lambda \right)-{\mathcal{P}}_{\mathcal{A},1}\left(\lambda \right)|\le {\mathsf{negl}}_1\left(\lambda \right)$ for any adversary $\mathcal{A}$.

• ${\mathbf{Game}}_2^{\left(b\right)}$: In this game, we change the generation way of the secret key ${\mathsf{SK}}_{ID,f}$ for secret key query of $(ID,f)$, mainly divided into the following three cases:
  • Case 1: $f\left({\mathbf{x}}^{\left(b\right)}\right)=0$. In this case, the user $ID$ must have been revoked before the challenge time period $t^{*}$, i.e., $\mathsf{Path}\left({\eta }_{ID}\right)\cap \mathrm{KUNodes}{\left({\mathsf{RL}}_{t^{*}}\right)}^{*}=\varnothing$, as per the secret key query restriction in the security model. So, for each $\theta \in \mathsf{Path}\left({\eta }_{ID}\right)$, ${\mathbf{D}}_{\theta }=\mathbf{A}{\mathbf{S}}_{\theta }^{*}+\mathbf{G}$.
    • Perform operation 3.(a) in algorithm $\mathsf{GenSK}$.
    • Sample ${\mathbf{K}}_{ID,f,\theta }^{″}\leftarrow \mathsf{SampleRight}(\mathbf{A},{\mathbf{S}}_{\theta }^{*},\mathbf{G},{\mathbf{T}}_{\mathbf{G}},\sigma ,\mathbf{G}-{\mathbf{Z}}_{ID,f})$.
  • Case 2: $f\left({\mathbf{x}}^{\left(b\right)}\right)\ne 0$ and $ID\notin {\mathsf{RL}}_{t^{*}}$. In this case, ${\mathbf{D}}_{{\theta }^{*}}=\mathbf{A}{\mathbf{S}}_{{\theta }^{*}}^{*}$, where ${\theta }^{*}=\mathsf{Path}\left({\eta }_{ID}\right)\cap \mathrm{KUNodes}\left({\mathsf{RL}}_{t^{*}}\right)$. So, the challenger cannot use $\mathbf{G}$ and algorithm $\mathsf{SampleRight}$ to sample ${\mathbf{K}}_{ID,f,{\theta }^{*}}^{″}$. Furthermore, ${\mathbf{Z}}_{ID,f}$ can only be randomly selected once, so we need to use the $\mathsf{SampleRight}$ algorithm to sample ${\mathbf{K}}_{ID,f}^{\prime }$.
    • Sample ${\mathbf{K}}_{ID,f,{\theta }^{*}}^{″}\leftarrow {\mathcal{D}}_{\mathbb{Z},\sigma }^{2m\times m}$ and set ${\mathbf{Z}}_{ID,f}=[\mathbf{A}|{\mathbf{D}}_{{\theta }^{*}}]{\mathbf{K}}_{ID,f,{\theta }^{*}}^{″}$.
    • For other nodes $\theta \in \mathsf{Path}\left({\eta }_{ID}\right)$ and $\theta \ne {\theta }^{*}$, the challenger computes ${\mathbf{K}}_{ID,f,\theta }^{″}\leftarrow \mathsf{SampleRight}(\mathbf{A},{\mathbf{S}}_{\theta }^{*},\mathbf{G},{\mathbf{T}}_{\mathbf{G}},\sigma ,{\mathbf{Z}}_{ID,f})$.
    • Compute ${\mathbf{R}}_f^{*}={\mathsf{Eval}}_{\mathrm{sim}}\left(f,{\left\{(x_i^{\left(b\right)},{\mathbf{R}}_i^{*})\right\}}_{i=1}^{\ell },\mathbf{A}\right)$ and obtain a low-norm matrix ${\mathbf{R}}_f^{*}\in {\mathbb{Z}}_q^{m\times m}$ such that $\mathbf{A}{\mathbf{R}}_f^{*}-f\left({\mathbf{x}}^{\left(b\right)}\right)\mathbf{G}={\mathbf{B}}_f$. By the definition, we have ${\mathbf{R}}_f^{*}\le 20\sqrt{m}·{(m+1)}^d$. Moreover, $\sigma =\sqrt{5}·(1+||{\mathbf{R}}_f^{*}||)·\varpi \left(\sqrt{\log m}\right)$ as needed for algorithm $\mathsf{SampleRight}$.
    • Sample ${\mathbf{K}}_{ID,f}^{\prime }\leftarrow \mathsf{SampleRight}(\mathbf{A},{\mathbf{R}}_f^{*},-f\left({\mathbf{x}}^{\left(b\right)}\right)\mathbf{G},{\mathbf{T}}_{\mathbf{G}},\sigma ,\mathbf{G}-{\mathbf{Z}}_{ID,f})$.
  • Case 3: $f\left({\mathbf{x}}^{\left(b\right)}\right)\ne 0$ and $ID\in {\mathsf{RL}}_{t^{*}}$. In this case, $\mathsf{Path}\left({\eta }_{ID}\right)\cap \mathrm{KUNodes}\left({\mathsf{RL}}_{t^{*}}\right)=\varnothing$, and ${\mathbf{D}}_{\theta }=\mathbf{A}{\mathbf{S}}_{\theta }^{*}+\mathbf{G}$, for each $\theta \in \mathsf{Path}\left({\eta }_{ID}\right)$.
    • Perform the operation 3.(a) in algorithm $\mathbf{GenSK}$.
    • Sample ${\mathbf{K}}_{ID,f,\theta }^{″}\leftarrow \mathsf{SampleRight}(\mathbf{A},{\mathbf{S}}_{\theta }^{*},\mathbf{G},{\mathbf{T}}_{\mathbf{G}},\sigma ,\mathbf{G}-{\mathbf{Z}}_{ID,f})$.

We show that ${\mathsf{Game}}_1^{\left(b\right)}$ is statistically indistinguishable from ${\mathsf{Game}}_2^{\left(b\right)}$. By Lemma 6, ${\mathbf{K}}_{ID,f}^{\prime }$ and ${\mathbf{K}}_{ID,f,\theta }^{″}$ sampled via algorithm $\mathsf{SampleLeft}$ and algorithm $\mathsf{SampleRight}$ are statistically close to randomly chosen in ${\mathcal{D}}_{\mathbb{Z},\sigma }^{2m\times m}$. Moreover, ${\mathbf{Z}}_{ID,f}=[\mathbf{A}|{\mathbf{B}}_f]{\mathbf{K}}_{ID,f}^{\prime }$ and ${\mathbf{Z}}_{ID,f}=[\mathbf{A}|{\mathbf{D}}_{{\theta }^{*}}]{\mathbf{K}}_{ID,f,{\theta }^{*}}^{″}$ are statistically indistinguishable from a random matrix selected in ${\mathbb{Z}}_q^{n\times 2m}$. So, there exists a negligible function ${\mathsf{negl}}_2(·)$ satisfying $|{\mathcal{P}}_{\mathcal{A},1}\left(\lambda \right)-{\mathcal{P}}_{\mathcal{A},2}\left(\lambda \right)|\le {\mathsf{negl}}_2\left(\lambda \right)$ for any adversary $\mathcal{A}$.

• ${\mathbf{Game}}_3^{\left(b\right)}$: In this game, we change the generation way of the decryption key ${\mathsf{DK}}_{ID,f,t}$ for decryption key query of $(ID,f,t)$, when $f\left({\mathbf{x}}^{\left(b\right)}\right)=0$, $ID\notin {\mathsf{RL}}_{t^{*}}$ and $t\ne t^{*}$.
  • Sample ${\widehat{\mathbf{K}}}_t\leftarrow \mathsf{SampleRight}(\mathbf{A},{\mathbf{V}}^{*},(\mathsf{H}\left(t\right)-\mathsf{H}\left(t^{*}\right))\mathbf{G},{\mathbf{T}}_{\mathbf{G}},\sigma ,\mathbf{G})$.
  • Perform the operation 2.(a) and 2.(b) in algorithm $\mathsf{GenDK}$ to generate ${\tilde{\mathbf{K}}}_{ID,f,t}$ and ${\widetilde{{\mathbf{K}}^{\prime }}}_{ID,f,t}$.
  • Compute ${\widehat{\mathbf{K}}}_{ID,f,t}^{″}={\widehat{\mathbf{K}}}_t{\widetilde{{\mathbf{K}}^{\prime }}}_{ID,f,t}$, satisfying $[\mathbf{A}|{\mathbf{W}}_t]{\widehat{\mathbf{K}}}_{ID,f,t}^{″}=\mathbf{U}-{\mathbf{H}}_{ID,f,t}$.
  • Divide ${\widehat{\mathbf{K}}}_{ID,f,t}^{″}$ into two parts: ${\widehat{\mathbf{K}}}_{1,ID,f,t}^{″}$ and ${\widehat{\mathbf{K}}}_{2,ID,f,t}^{″}$, with m rows per part. Set

    $${\widehat{\mathbf{DK}}}_{ID,f,t}={\left[\begin{array}{cc}{\left(\begin{array}{c}{\tilde{\mathbf{K}}}_{1,ID,f,t}+{\widehat{\mathbf{K}}}_{1,ID,f,t}^{″}\\ {\tilde{\mathbf{K}}}_{2,ID,f,t}\end{array}\right)}^{\top }|& {\left(\begin{array}{c}{\tilde{\mathbf{K}}}_{3,ID,f,t}\\ {\tilde{\mathbf{K}}}_{4,ID,f,t}+{\widehat{\mathbf{K}}}_{2,ID,f,t}^{″}\end{array}\right)}^{\top }\end{array}\right]}^{\top }\in {\mathbb{Z}}_q^{4m\times k}.$$

We show that ${\mathsf{Game}}_2^{\left(b\right)}$ is statistically indistinguishable from ${\mathsf{Game}}_3^{\left(b\right)}$. Recall in ${\mathsf{Game}}_2^{\left(b\right)}$

$${\mathbf{DK}}_{ID,f,t}={\left[\begin{array}{cc}{\left(\begin{array}{c}{\tilde{\mathbf{K}}}_{1,ID,f,t}+{\widetilde{{\mathbf{K}}^{″}}}_{1,ID,f,t}\\ {\tilde{\mathbf{K}}}_{2,ID,f,t}+{\widetilde{{\mathbf{K}}^{″}}}_{2,ID,f,t}\end{array}\right)}^{\top }|& {\left(\begin{array}{c}{\tilde{\mathbf{K}}}_{3,ID,f,t}+{\widetilde{{\mathbf{K}}^{″}}}_{3,ID,f,t}\\ {\tilde{\mathbf{K}}}_{4,ID,f,t}\end{array}\right)}^{\top }\end{array}\right]}^{\top }.$$

By the triangle inequality for statistical distance and Lemma 1, when $B_{\mathsf{big}}>(m{\sigma }^2+1)2^{\lambda +1}$, there exists a negligible function ${\mathsf{negl}}_{smudge}(·)$ for all $\lambda \in \mathbb{N}$,

$$\begin{array}{cc}\hfill & \mathsf{SD}({\tilde{\mathbf{K}}}_{1,ID,f,t}+{\widetilde{{\mathbf{K}}^{″}}}_{1,ID,f,t},{\tilde{\mathbf{K}}}_{1,ID,f,t}+{\widehat{\mathbf{K}}}_{1,ID,f,t}^{″})\hfill \\ \hfill & \le \mathsf{SD}({\tilde{\mathbf{K}}}_{1,ID,f,t}+{\widetilde{{\mathbf{K}}^{″}}}_{1,ID,f,t},{\tilde{\mathbf{K}}}_{1,ID,f,t})+\mathsf{SD}({\tilde{\mathbf{K}}}_{1,ID,f,t},{\tilde{\mathbf{K}}}_{1,ID,f,t}+{\widehat{\mathbf{K}}}_{1,ID,f,t}^{″})\hfill \\ \hfill & \le mk·{\mathsf{negl}}_{smudge}(·)+mk·{\mathsf{negl}}_{smudge}(·)\hfill \\ \hfill & =2mk·{\mathsf{negl}}_{smudge}(·).\hfill \end{array}$$

In the remaining 3m rows, each m row’s statistical distance is equal to $mk·{\mathsf{negl}}_{smudge}(·)$. So, in the adversary’s view,

$$|{\mathcal{P}}_{\mathcal{A},2}\left(\lambda \right)-{\mathcal{P}}_{\mathcal{A},3}\left(\lambda \right)|\le 5mk·{\mathsf{negl}}_{smudge}(·).$$

• ${\mathbf{Game}}_4^{\left(b\right)}$: In this game, we change the generation way of the matrix $\mathbf{A}$ and the ciphertexts.
  • Choose a random matrix $\mathbf{A}$ in ${\mathbb{Z}}_q^{n\times m}$.
  • Choose ${\mathbf{c}}_{out}^{*}\leftarrow {\mathbb{Z}}_q^k$ and ${\mathbf{c}}_{in}^{*},{\mathbf{c}}_i^{*},{\mathbf{c}}_{\theta }^{*},{\mathbf{c}}_{t^{*}}^{*}\leftarrow {\mathbb{Z}}_q^m$, where $\theta \in \mathrm{KUNodes}{\left({\mathsf{RL}}_{t^{*}}\right)}^{*}$ and $i\in [\ell ]$.

It remains to be shown that ${\mathsf{Game}}_3^{\left(b\right)}$ and ${\mathsf{Game}}_4^{\left(b\right)}$ are computationally indistinguishable under the hardness of the LWE problem. If there exists a non-negligible function $\delta (·)$ such that $|{\mathcal{P}}_{\mathcal{A},3}\left(\lambda \right)-{\mathcal{P}}_{\mathcal{A},4}\left(\lambda \right)|\ge \delta (·)$, we can also construct an $\mathsf{LWE}$ algorithm $\mathcal{B}$ under $\mathcal{A}$ such that ${\mathsf{Adv}}_{\mathcal{B}}^{\mathsf{LWE}}\left(\lambda \right)\ge \delta \left(\lambda \right)$ for all $\lambda \in \mathbb{N}$.

• LWE Instance: $\mathcal{B}$ begins by obtaining an ${\mathsf{LWE}}_{n,q,\sigma }$ challenger of two random matrices $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$, $\mathbf{U}\in {\mathbb{Z}}_q^{n\times k}$ and two vectors $\mathbf{c}\in {\mathbb{Z}}_q^k$, ${\mathbf{c}}^{\prime }\in {\mathbb{Z}}_q^m$, where $\mathbf{c}\in {\mathbb{Z}}_q^k$ and ${\mathbf{c}}^{\prime }\in {\mathbb{Z}}_q^m$ are either random or ${\mathbf{c}}^{\prime }={\mathbf{s}}^{\top }\mathbf{A}+{\mathbf{e}}^{\prime }$ and $\mathbf{c}={\mathbf{s}}^{\top }\mathbf{U}+\mathbf{e}$ for some random vector $\mathbf{s}\in {\mathbb{Z}}_q^n$ and $\mathbf{e}\leftarrow {\chi }_{\mathsf{LWE}}^k$, ${\mathbf{e}}^{\prime }\leftarrow {\chi }_{\mathsf{LWE}}^m$.
• Public Parameters: $\mathcal{A}$ sets the challenge attributes ${\mathbf{x}}^{\left(0\right)}$ and ${\mathbf{x}}^{\left(1\right)}$, time period $t^{*}$, and node set $\mathrm{KUNodes}{\left({\mathsf{RL}}_{t^{*}}\right)}^{*}$. Then, $\mathcal{B}$ sets the public parameters $\mathsf{PP}$ as in ${\mathsf{Game}}_3^{\left(b\right)}$: Uniformly random matrices ${\mathbf{R}}_i^{*}$, ${\mathbf{S}}_{\theta }^{*}$, and ${\mathbf{V}}^{*}$ in ${\{-1,1\}}^{m\times m}$, ${\mathbf{B}}_i={\mathbf{AR}}_i^{*}+x_i^{\left(b\right)}\mathbf{G}$, $\mathbf{W}={\mathbf{AV}}^{*}-\mathsf{H}\left(t^{*}\right)\mathbf{G}$,

  $${\mathbf{D}}_{\theta }=\left\{\begin{array}{c}\mathbf{A}{\mathbf{S}}_{\theta }^{*},if\theta \in \mathrm{KUNodes}{\left({\mathsf{RL}}_{t^{*}}\right)}^{*}\hfill \\ \mathbf{A}{\mathbf{S}}_{\theta }^{*}+\mathbf{G},otherwise\hfill \end{array}\right.,$$

  where $i\in [\ell ]$ and $\theta \in \mathsf{BT}$.
• Query Phase: $\mathcal{B}$ answers $\mathcal{A}$’s user registration, secret key, decryption key, and revocation queries as in ${\mathsf{Game}}_3^{\left(b\right)}$.
• Challenge Phase: $\mathcal{A}$ sets two messages ${\mu }^{\left(0\right)}$, ${\mu }^{\left(1\right)}\in \{0,1\}$. $\mathcal{B}$ computes ${\mathbf{c}}_{in}^{*}={\mathbf{c}}^{\prime }$, ${\mathbf{c}}_i^{*}={\mathbf{c}}^{\prime }{\mathbf{R}}_i^{*}$, ${\mathbf{c}}_{\theta }^{*}={\mathbf{c}}^{\prime }{\mathbf{S}}_{\theta }^{*}$, and ${\mathbf{c}}_{t^{*}}^{*}={\mathbf{c}}^{\prime }{\mathbf{V}}^{*}$, ${\mathbf{c}}_{out}^{*}=\mathbf{c}+\mathsf{encode}\left({\mu }^{\left(b\right)}\right)·⌊\frac{q}{2}⌋$, where $i\in [\ell ]$ and $\theta \in \mathrm{KUNodes}{\left({\mathsf{RL}}_{t^{*}}\right)}^{*}$.

When the LWE challenge is pseudorandom,

$$\begin{array}{cc}& {\mathbf{c}}_{out}^{*}=\mathbf{c}+\mathsf{encode}\left({\mu }^{\left(b\right)}\right)·⌊\frac{q}{2}⌋={\mathbf{s}}^{\top }\mathbf{U}+\mathsf{encode}\left({\mu }^{\left(b\right)}\right)·⌊\frac{q}{2}⌋+\mathbf{e},\hfill \\ & {\mathbf{c}}_{in}^{*}=\mathbf{c}={\mathbf{s}}^{\top }\mathbf{A}+{\mathbf{e}}^{\prime },\hfill \\ & {\mathbf{c}}_{t^{*}}^{*}={\mathbf{s}}^{\top }(\mathbf{A}{\mathbf{V}}^{*}-\mathsf{H}\left(t^{*}\right)\mathbf{G}+\mathsf{H}\left(t^{*}\right)\mathbf{G})+{\mathbf{e}}^{\prime }{\mathbf{V}}^{*}={\mathbf{s}}^{\top }{\mathbf{W}}_t+{\mathbf{e}}^{\prime }{\mathbf{V}}^{*},\hfill \\ \hfill i\in [\ell ]:& {\mathbf{c}}_i^{*}={\mathbf{s}}^{\top }(\mathbf{A}{\mathbf{R}}_i^{*}-x_i^{\left(b\right)}\mathbf{G}+x_i^{\left(b\right)}\mathbf{G})+{\mathbf{e}}^{\prime }{\mathbf{R}}_i^{*}={\mathbf{s}}^{\top }({\mathbf{B}}_i+x_i^{\left(b\right)}\mathbf{G})+{\mathbf{e}}^{\prime }{\mathbf{R}}_i^{*},\hfill \\ \hfill \theta \in \mathrm{KUNodes}{\left({\mathsf{RL}}_{t^{*}}\right)}^{*}:& {\mathbf{c}}_{\theta }^{*}=({\mathbf{s}}^{\top }\mathbf{A}+{\mathbf{e}}^{\prime }){\mathbf{S}}_{\theta }^{*}={\mathbf{s}}^{\top }{\mathbf{D}}_{\theta }+{\mathbf{e}}^{\prime }{\mathbf{S}}_{\theta }^{*},\hfill \end{array}$$

the ciphertexts are distributed exactly as in ${\mathsf{Game}}_3^{\left(b\right)}$. When the LWE challenge is random, the ciphertexts are distributed exactly as in ${\mathsf{Game}}_4^{\left(b\right)}$.

• Guess: $\mathcal{A}$ outputs a guess $b^{\prime }$ of b. Then, $\mathcal{B}$ outputs $\mathcal{A}$’s guess as the answer to the ${\mathsf{LWE}}_{n,q,\sigma }$ challenge it is trying to solve.

Note that, when the LWE challenge is pseudorandom, $\mathcal{A}$’s view is as in ${\mathsf{Game}}_3^{\left(b\right)}$; when the LWE challenge is random, $\mathcal{A}$’s view is as in ${\mathsf{Game}}_4^{\left(b\right)}$. So, if the $\mathsf{LWE}$ assumption holds, there exists a negligible function ${\mathsf{negl}}_4(·)$, satisfying $|{\mathcal{P}}_{\mathcal{A},3}\left(\lambda \right)-{\mathcal{P}}_{\mathcal{A},4}\left(\lambda \right)|\le {\mathsf{negl}}_4\left(\lambda \right)$.

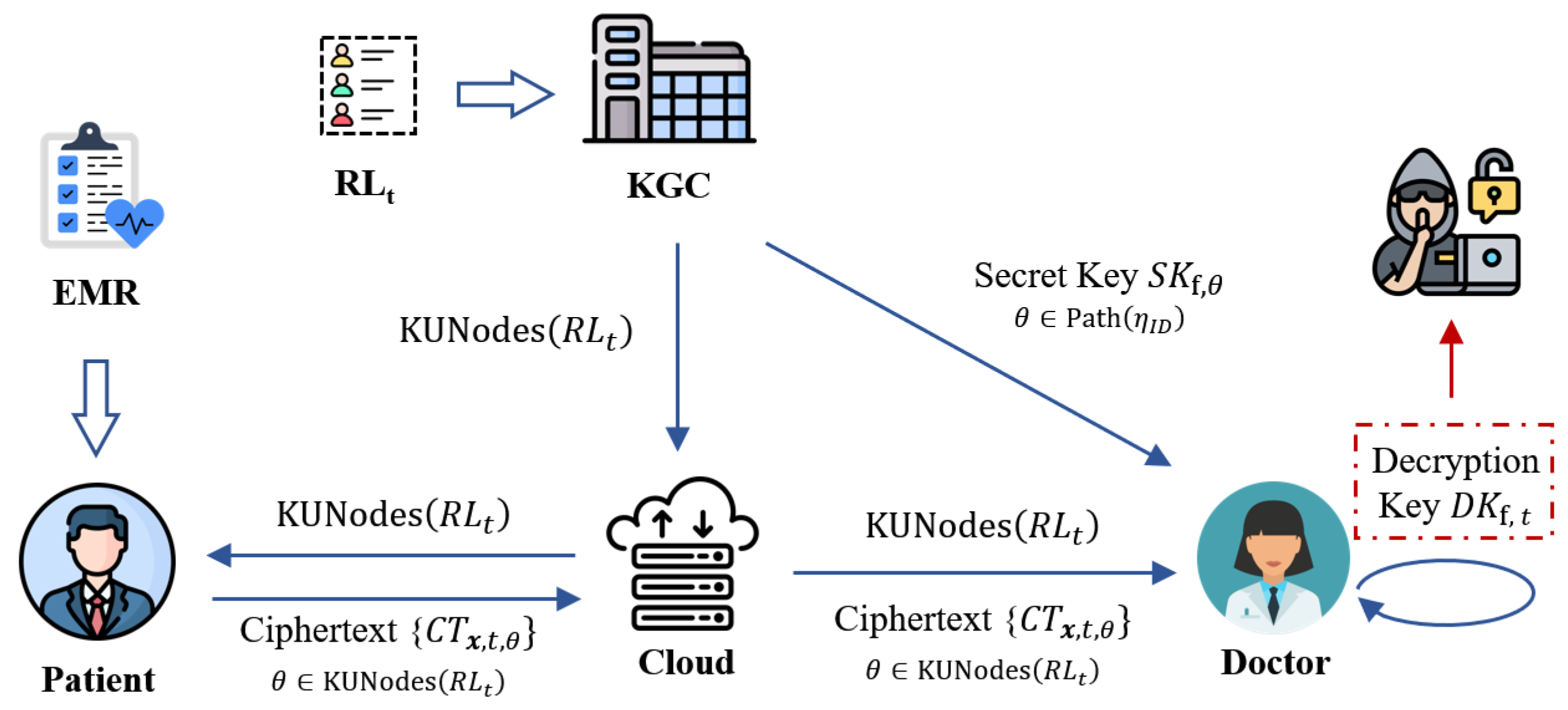
5. Application in Practice

In this section, we provide an application example of our RABE scheme with En-DKER in the electronic healthcare scenario.

As shown in Figure 5, the system primarily consists of three entities: KGC, patient, and doctor. The KGC is responsible for generating secret keys for system users and periodically publishing a set of nodes representing the non-revoked users. As the data owner, the patient encrypts their electronic medical record (EMR) and shares with attending physicians. Additionally, doctors can periodically generate their decryption keys, and only doctors who satisfy the access policy and have not been revoked can decrypt and access the EMR information of the patient.

Our scheme also satisfies the En-DKER property, ensuring that the leakage of decryption keys from any time period should not compromise the confidentiality of ciphertexts from other time periods. Additionally, adversaries cannot determine whether the attribute set of ciphertext for the challenge time period satisfies a specific policy using keys from any other time periods or policies.

6. Conclusions

To enhance the practicality of the lattice-based RABE scheme, we extend the En-DKER property from RIBE to RABE. This extension ensures that the leakage of any time period decryption keys should not compromise the confidentiality of ciphertexts from other time periods. Additionally, adversaries are unable to determine whether the attribute set of the ciphertext for the challenge time period satisfies a specific policy using keys from any other time periods or policies. Building upon the BGG+14 scheme, we then construct the first RABE with En-DKER from lattices. Our scheme retains advantages such as near-zero periodic workload for the KGC, and the encryptor is relieved from managing a revocation list. Finally, we validate the correctness and prove the security of our scheme under the LWE assumption.

However, this scheme is based on the LWE assumption, which requires complex inverse algorithms and matrix multiplication for trapdoor generation, making it unsuitable for practical applications. In the future, we plan to extend the approach to the ring LWE assumption, aiming to develop a more advantageous scheme that addresses the computational complexity and storage requirements.