Identifying a Space-Dependent Source Term and the Initial Value in a Time Fractional Diffusion-Wave Equation

Abstract

This paper is focused on the inverse problem of identifying the space-dependent source function and initial value of the time fractional nonhomogeneous diffusion-wave equation from noisy final time measured data in a multi-dimensional case. A mollification regularization method based on a bilateral exponential kernel is presented to solve the ill-posedness of the problem for the first time. Error estimates are obtained with an a priori strategy and an a posteriori choice rule to find the regularization parameter. Numerical experiments of interest show that our proposed method is effective and robust with respect to the perturbation noise in the data.

1. Introduction

Recently, time or space fractional differential equations have attracted intensive attentions. All kinds of models applying fractional partial differential equations have been successfully used to describe anomalous diffusion phenomena due to nonlocal property of fractional order derivatives. In the past decades, fractional order partial differential equations have been widely used in nuclear magnetic resonance, semiconductors, viscoelastic materials, heterogeneous aquifer, quantum optics, molecular spectroscopy, polymer, porous media, solid surface diffusion, financial research, and underground fluid flow.

There has been a lot of papers on the theories and applications of fractional order differential equations; one can refer to Refs. [1,2]. The direct problems for fractional equations and the inverse problems for space and time fractional equations have been researched in recent years; refer to Refs. [3,4,5,6,7,8,9,10]. By finding additional data, one can identify the unknown data for time and space fractional equations; refer to Refs. [11,12,13,14,15,16,17,18,19,20]. However, there are only a few studies on the time fractional diffusion-wave equation. Furthermore, the work for the inverse problem of this part is still in the preliminary stage. In Ref. [21] the authors identified time source terms for time fractional inhomogeneous, and nonlinear wave equations were considered, but only the existence, uniqueness, and a priori estimation formula of the solution are given, as the posterior case is not given. It is known that the prior rule depends on prior information, and the accuracy of prior information will affect the accuracy of the prior regular solution. Whereas the posterior regulation is only related to the measurement data and has nothing to do with the prior information, which makes the regular solution obtained by the posterior rule closer to the exact solution than that obtained by the prior rule. In this paper, we will discuss not only prior rule analysis but also posterior rule analysis. We give the error estimation and convergence proof, respectively. Numerical examples are given to verify the results. We introduce several results on the deterministic case. In addition, there are also some very recent papers on the stochastic case; if the interested reader wants to see a variety of this topic, one can refer to Refs. [22,23] and for more related and similar studies one can refer to Refs. [24,25,26,27,28,29].

In this article, an inverse space-dependent source problem and the initial value for a time fractional diffusion-wave equation are studied in a bounded domain. Let $\mathsf{\Omega }$ be a bounded domain in $R^d$ with a sufficiently smooth boundary $\partial \mathsf{\Omega }$. We will consider the following time fractional diffusion-wave problem.

$$\left\{\begin{array}{c}{\partial }_{0+}^{\alpha }u(x,t)+Lu(x,t)=f\left(x\right)g\left(t\right),x\in \mathsf{\Omega },0\le t\le T,\hfill \\ u(x,0)=a\left(x\right),x\in \overline{\mathsf{\Omega }},\hfill \\ {\partial }_{t}u(x,0)=b\left(x\right),x\in \overline{\mathsf{\Omega }},\hfill \\ u(x,t)=0,x\in \partial \mathsf{\Omega },0<t\le T,\hfill \\ u(x,T)=h\left(x\right),x\in \mathsf{\Omega }.\hfill \end{array}\right.$$

(1)

where $1<\alpha <2$ and ${\partial }_{0+}^{\alpha }u(x,t)$ is the left Caputo fractional derivative and $L$ [3,4] is a symmetric uniformly elliptic operator defined on $D\left(L\right)=H^2\left(\mathsf{\Omega }\right)\cap H_0^1\left(\mathsf{\Omega }\right)$ and given by

$$\begin{array}{c}\hfill Lu(x,t)=-\sum _{i,j=1}^d\frac{\partial }{\partial x_j}\left(a_{ij}\left(x\right)\frac{\partial }{\partial x_i}u(x,t)\right)+c\left(x\right)u(x,t),x\in \mathsf{\Omega }.\end{array}$$

(2)

in which the coefficients satisfy

$$\begin{array}{c}\hfill a_{ij}=a_{ji},1\le i,j\le d,a_{i,j}\in C^1\left(\overline{\mathsf{\Omega }}\right),\end{array}$$

(3)

$$\begin{array}{c}\hfill \sigma \sum _{i=1}^d{\xi }_i^2\le \sum _{i,j=1}^d{a}_{ij}\left(x\right){\xi }_i{\xi }_j,({\xi }_1,\dots ,{\xi }_d)\in R^d,\sigma >0,\end{array}$$

(4)

$$\begin{array}{c}\hfill c\left(x\right)\ge 0,x\in \overline{\mathsf{\Omega }},c\left(x\right)\in C\left(\overline{\mathsf{\Omega }}\right).\end{array}$$

(5)

Here, our purpose is to identify the spatial source $f\left(x\right)$ and the initial value $a\left(x\right),b\left(x\right)$ in problem (1) from the data as follows:

$$\begin{array}{c}\hfill u(x,T)=h\left(x\right),x\in \mathsf{\Omega }.\end{array}$$

(6)

Since the data $h\left(x\right)$ is based on the observation of the physical instruments, there must be errors, and $h^{\delta }\left(x\right)$ is the corresponding measurement data. Let the exact data $h\left(x\right)$ be approximated by measurement data $h^{\delta }\left(x\right)$ such that

$$\begin{array}{c}\hfill |h\left(x\right)-h^{\delta }\left(x\right)|<\delta .\end{array}$$

(7)

The process of identifying source problems for fractional diffusion equations $(0<\alpha <1)$ has been extensively studied. Ref. [9] determined the space-dependent source term from the final time data in a multi-dimensional case by using the reproducible kernel Hilbert space method. Zheng and Wei [20] solved the Cauchy problem of the time fractional diffusion equations on a strip domain by using the Fourier truncation method. Gong and Wei [30] proposed an integral equation method to identify an inverse time-dependent source term in a one-dimensional time-fractional diffusion-wave equation. Yang and Qu [31] use the Fourier truncation method to identify the initial value on non-homogeneous time fractional diffusion wave equations. However, to the best of our knowledge, there are few studies on the inverse problems for time fractional diffusion-wave equations. In this chapter, we identify an inverse space-dependent source function and the initial value from noisy final time measured data in a special bounded domain. By comparing several methods in the literature [32], it can be seen that the regular solution obtained by the mollification regularization method is better than other methods. So, in this article, the mollification regularization method is used to solve the inverse source problem and initial value problem of a fractional diffusion-wave equation $1<\alpha <2$.

The paper is organized as following: In Section 2, we present some auxiliary mathematical conclusions. In Section 3, we illustrate a conditional stability and the ill-posedness of the inverse source problem and initial value problem. A priori and a posteriori parameter choice rules are given and error estimates are obtained in Section 4. In Section 5, some numerical examples are carried out to demonstrate the efficiency of the proposed method. Finally, we give a conclusion in Section 6.

2. Preliminaries

In this section, we introduce the definitions and some lemmas.

Definition 1.

The left Caputo fractional derivative is defined by (see [1,3]):

$$\begin{array}{c}\hfill {\partial }_{0+}^{\alpha }u(x,t)=\frac{1}{\mathsf{\Gamma }(n-\alpha )}{\int }_0^t\frac{{\partial }^{n}u}{\partial s^n}(x,s)\frac{1}{{(t-s)}^{\alpha -n+1}}ds,(n=[\Re \left(\alpha \right)]+1,t>0),\end{array}$$

Definition 2.

The Mittag–Leffler function is (see [1]):

$$\begin{array}{c}\hfill E_{\alpha ,\beta }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\mathsf{\Gamma }(\alpha k+\beta )},z\in \mathbb{C}.\end{array}$$

(8)

where $\alpha >0,\beta \in \mathbb{C}$ are arbitrary constants.

Lemma 1.

If $0<\alpha <2$ and $\beta \in \mathbb{R}$ is arbitrary (see [33]), we will suppose that $\mu$ is such that $\frac{\pi \alpha }{2}<\mu <min\{\pi ,\pi \alpha \}.$ Then there exists a constant $C_{11}=C_{11}(\alpha ,\beta ,\mu )>0$ such that

$$\begin{array}{c}\hfill |E_{\alpha ,\beta }\left(z\right)|\le \frac{C_1}{1+\left|z\right|},\mu \le \left|argz\right|\le \pi .\end{array}$$

(9)

Lemma 2.

If $\alpha >0,\lambda >0$ and $m\in N,$ we have (see [33])

$$\begin{array}{c}\hfill \frac{d^m}{d{t}^m}{E}_{\alpha ,1}(-\lambda t^{\alpha })=-\lambda t^{\alpha -m}{E}_{\alpha ,\alpha -m+1}(-\lambda t^{\alpha }),t>0,\lambda \simeq n^2.\end{array}$$

(10)

Lemma 3.

When $1<\alpha <2$ and $T>0$ are constants, there is a finite point such that $E_{\alpha ,\alpha }(-n^2{T}^{\alpha })=0$ (see [33]). Let the set of points of $E_{\alpha ,\alpha }(-n^2{T}^{\alpha })=0$ be $K=\{n_1,n_2,\dots ,n_N\}.$

Lemma 4.

When $1<\alpha <2,$ there are positive constants $C_{21}$ and $C_{22}$, which only relies on $\alpha ,T,$ and $n^2,$ such that (see [33])

$$\begin{array}{c}\hfill \frac{C_{21}}{n^2}\le \left|E_{\alpha ,1(-n^2{T}^{\alpha })}\right|\le \frac{C_{22}}{n^2},n\notin K.\end{array}$$

(11)

The even bilateral exponential function is defined as:

$$\begin{array}{c}\hfill V_{\mu }\left(x\right):=\frac{\mu }{2}{e}^{-\mu \left|x\right|},0<\mu <1,x\in R^d.\end{array}$$

(12)

and there is

$$\begin{array}{c}\hfill {\int }_{R^d}{V}_{\mu }\left(x\right)dx:={\int }_{R^d}\frac{\mu }{2}{e}^{-\mu \left|x\right|}dx=1,0<\mu <1.\end{array}$$

Here, we define operator ${\omega }_{\mu }$ as follows:

$$\begin{array}{c}\hfill {\omega }_{\mu }f\left(x\right):=V_{\mu }\ast f\left(x\right)={\int }_{R^d}{V}_{\mu }\left(t\right)f(x-t)dt={\int }_{R^d}{V}_{\mu }(x-t)f\left(t\right)dt.\end{array}$$

(13)

3. A Conditional Stability and Ill-Posedness

In this part, we use the mollification regularization method to determine the space-dependent source term $f\left(x\right)$ and initial value $a\left(x\right),b\left(x\right)$ for problem (1) by the measurement data $u(x,T)=h\left(x\right),x\in \mathsf{\Omega }.$ Consulting Ref. [15], the solution of (1) is

$$\begin{array}{cc}\hfill u(x,t)& =\sum _{n=1}^{\infty }{E}_{\alpha ,1}(-n^2{t}^{\alpha })(a,{\phi }_n){\phi }_n+\sum _{n=1}^{\infty }t{E}_{\alpha ,2}(-n^2{t}^{\alpha })(b,{\phi }_n){\phi }_n\hfill \\ \hfill & +\sum _{n=1}^{\infty }(f,{\phi }_n){\int }_0^{t}g(t-\tau ){\tau }^{\alpha -1}{E}_{\alpha ,\alpha }(-n^2{\tau }^{\alpha })d\tau {\phi }_n\left(x\right).\hfill \end{array}$$

(14)

here $(a,{\phi }_n)$ and $(b,{\phi }_n)$ are Fourier coefficients. ${\phi }_n$ is an orthonormal basis of $L^2\left(\mathsf{\Omega }\right),n=1,2,\dots .$

Remember $(.,.)$ as the inner product of $L^2\left(\mathsf{\Omega }\right),$ define the following function space.

$$H^p\left(\mathsf{\Omega }\right)=\{\psi \in L^2\left(\mathsf{\Omega }\right)\mid \sum _{n=1}^{\infty }{(1+n^2)}^p|(\psi ,{\phi }_n){|}^2<\infty \},$$

(15)

with the norm

$${\parallel \psi \parallel }_{H^p\left(\mathsf{\Omega }\right)}=\{\sum _{n=1}^{\infty }{(1+n^2)}^p|(\psi ,{\phi }_n){{|}^2\}}^{\frac{1}{2}}.$$

(16)

Take $t=T$ in Equation (14), we can get the first Fredholm integral formula, which $f,a,b$ satisfies

$${\mathcal{A}}_{1}f\left(x\right)={\int }_{\mathsf{\Omega }}f\left(\xi \right){\kappa }_1(x,\xi )d\xi =w_1\left(x\right).$$

(17)

$${\mathcal{A}}_{2}a\left(x\right)={\int }_{\mathsf{\Omega }}a\left(\xi \right){\kappa }_2(x,\xi )d\xi =w_2\left(x\right).$$

(18)

$${\mathcal{A}}_{3}b\left(x\right)={\int }_{\mathsf{\Omega }}b\left(\xi \right){\kappa }_3(x,\xi )d\xi =w_3\left(x\right).$$

(19)

where

$${\kappa }_1(x,\xi )=\sum _{n=1}^{\infty }{\nu }_n\left(T\right){\phi }_n\left(\xi \right){\phi }_n\left(x\right),$$

(20)

$${\kappa }_2(x,\xi )=\sum _{n=1}^{\infty }{E}_1^{\alpha }(-n^2{T}^{\alpha }){\phi }_n\left(\xi \right){\phi }_n\left(x\right),$$

(21)

$${\kappa }_3(x,\xi )=\sum _{n=1}^{\infty }T{E}_2^{\alpha }(-n^2{T}^{\alpha }){\phi }_n\left(\xi \right){\phi }_n\left(x\right).$$

(22)

$${\nu }_n\left(T\right)={\int }_0^{T}g(T-\tau ){\tau }^{\alpha -1}{E}_{\alpha ,\alpha }(-n^2{\tau }^{\alpha })d\tau ,$$

$$w_1\left(x\right)=h\left(x\right)-u_1(x,T)-u_2(x,T,),$$

$$w_2\left(x\right)=h\left(x\right)-u_2(x,T)-\sum _{n=1}^{\infty }(f,{\phi }_n){\nu }_n\left(T\right)=u_1(x,T),$$

$$w_3\left(x\right)=h\left(x\right)-u_1(x,T)-\sum _{n=1}^{\infty }(f,{\phi }_n){\nu }_n\left(T\right)=u_2(x,T).$$

Because ${\kappa }_1(x,\xi )={\kappa }_1(\xi ,x),$ ${\kappa }_2(x,\xi )={\kappa }_2(\xi ,x),$ ${\kappa }_3(x,\xi )={\kappa }_3(\xi ,x),$ we know ${\kappa }_1,{\kappa }_2,{\kappa }_3$ are self-adjoint operators. Let ${\mathcal{A}}_1^{*}$ be the adjoint operator of ${\mathcal{A}}_1$, ${\mathcal{A}}_2^{*}$ be the adjoint operator of ${\mathcal{A}}_2$, and ${\mathcal{A}}_3^{*}$ be the adjoint operator of ${\mathcal{A}}_3$, respectively, and use the orthogonality of ${\left\{{\phi }_n\right\}}_{n=1}^{\infty }$ in space $l^2\left(\mathsf{\Omega }\right).$ We obtain

$${\mathcal{A}}_1^{*}{w}_1\left(x\right)={\int }_{\mathsf{\Omega }}{w}_1\left(\xi \right){\kappa }_1(x,\xi )d\xi ,\xi \in \mathsf{\Omega }.$$

(23)

and we have

$${\mathcal{A}}_1^{*}{\mathcal{A}}_1{\phi }_n\left(\xi \right)={\nu }_n^2\left(T\right){\phi }_n\left(\xi \right).$$

(24)

thus, ${\sigma }_n^1=\left|{\nu }_n\left(T\right)\right|$ is the singular value of operator ${\mathcal{A}}_1.$ Define:

$${\psi }_n^1\left(x\right)=\left\{\begin{array}{c}{\phi }_n\left(x\right),{\nu }_n\left(T\right)\ge 0,\hfill \\ -{\phi }_n\left(x\right),{\nu }_n\left(T\right)<0.\hfill \end{array}\right.$$

(25)

we know that ${\left\{{\psi }_n^1\right\}}_{n=1}^{\infty }$ is orthonormal on $L^2\left(\mathsf{\Omega }\right),$ and satisfies

$${\mathcal{A}}_1{\phi }_n\left(\xi \right)={\sigma }_n^1{\psi }_n^1\left(x\right)={\nu }_n\left(T\right){\phi }_n\left(x\right),$$

$${\mathcal{A}}_1^{*}{\psi }_n^1\left(x\right)={\sigma }_n^1{\phi }_n\left(\xi \right)={\nu }_n\left(T\right){\psi }_n^1\left(\xi \right).$$

So, the singular system for the operator ${\mathcal{A}}_1$ is $({\sigma }_n^1;{\phi }_n;{\psi }_n^1).$

By the same token, the singular system for the operators ${\mathcal{A}}_2$ and ${\mathcal{A}}_3$ are $({\sigma }_n^2;{\phi }_n;{\psi }_n^2)$ and $({\sigma }_n^3;{\phi }_n;{\psi }_n^3),$ here

$${\sigma }_n^2=\left|E_{\alpha ,1}(-{\lambda }_n^2{T}^{\alpha })\right|,$$

$${\psi }_n^2\left(x\right)=\left\{\begin{array}{c}{\phi }_n\left(x\right),E_{\alpha ,1}(-n^2{T}^{\alpha })\ge 0,\hfill \\ -{\phi }_n\left(x\right),E_{\alpha ,1}(-n^2{T}^{\alpha })<0.\hfill \end{array}\right.$$

(26)

and

$${\sigma }_n^3=\left|T{E}_{\alpha ,2}(-n^2{T}^{\alpha })\right|,$$

$${\psi }_n^3\left(x\right)=\left\{\begin{array}{c}{\phi }_n\left(x\right),E_{\alpha ,2}(-n^2{T}^{\alpha })\ge 0,\hfill \\ -{\phi }_n\left(x\right),E_{\alpha ,2}(-n^2{T}^{\alpha })<0.\hfill \end{array}\right.$$

(27)

Remark 1.

When ${\kappa }_1=\varnothing ,{\kappa }_2=\varnothing ,{\kappa }_3=\varnothing ,$ the kernel function for operators ${\mathcal{A}}_1$ as in Equation (17), ${\mathcal{A}}_2$ as in Equation (18), and ${\mathcal{A}}_3$ as in Equation (19). Here, this situation is regarded as a special case.

Next, the general case will be discussed, which are ${\kappa }_1\ne \varnothing ,{\kappa }_2\ne \varnothing ,{\kappa }_3\ne \varnothing .$

When ${\kappa }_1\ne \varnothing ,{\kappa }_2\ne \varnothing ,{\kappa }_3\ne \varnothing ,$ the kernel functions for operators ${\mathcal{A}}_1,{\mathcal{A}}_2,{\mathcal{A}}_3$ are expressed as:

$${\kappa }_1(x,\xi )=\sum _{n=1,n\notin {\kappa }_1}^{\infty }{\nu }_n\left(T\right){\phi }_n\left(x\right){\phi }_n\left(\xi \right),$$

$${\kappa }_2(x,\xi )=\sum _{n=1,n\notin {\kappa }_2}^{\infty }{E}_{\alpha ,1}(-n^2{T}^{\alpha }){\phi }_n\left(x\right){\phi }_n\left(\xi \right),$$

$${\kappa }_3(x,\xi )=\sum _{n=1,n\notin {\kappa }_3}^{\infty }T{E}_{\alpha ,2}(-n^2{T}^{\alpha }){\phi }_n\left(x\right){\phi }_n\left(\xi \right),$$

The kernel spaces for the operators ${\mathcal{A}}_1,{\mathcal{A}}_2,{\mathcal{A}}_3$ are as follows:

(1) When ${\kappa }_1\ne \varnothing ,$

$$N\left({\mathcal{A}}_1\right)=span\{{\phi }_n:n\in {\kappa }_1\}.$$

When ${\kappa }_1=\varnothing ,$

$$N\left({\mathcal{A}}_1\right)=\left\{0\right\}.$$

(2) When ${\kappa }_2\ne \varnothing ,$

$$N\left({\mathcal{A}}_2\right)=span\{{\phi }_n:n\in {\kappa }_2\}.$$

When ${\kappa }_2=\varnothing ,$

$$N\left({\mathcal{A}}_2\right)=\left\{0\right\}.$$

(3) When ${\kappa }_3\ne \varnothing ,$

$$N\left({\mathcal{A}}_3\right)=span\{{\phi }_n:n\in {\kappa }_3\}.$$

When ${\kappa }_3=\varnothing ,$

$$N\left({\mathcal{A}}_3\right)=\left\{0\right\}.$$

The ranges for operators ${\mathcal{A}}_1,{\mathcal{A}}_2,{\mathcal{A}}_3$ are written as:

$$R\left({\mathcal{A}}_1\right)=\{w_1\in L^2\left(\mathsf{\Omega }\right)\mid (w_1,{\phi }_n)=0,n\in {\kappa }_1;\sum _{n=1,n\notin {\kappa }_1}^{\infty }{\left(\frac{(w_1,{\phi }_n)}{{\nu }_n\left(T\right)}\right)}^2<+\infty \}.$$

$$R\left({\mathcal{A}}_2\right)=\{w_2\in L^2\left(\mathsf{\Omega }\right)\mid (w_2,{\phi }_n)=0,n\in {\kappa }_2;\sum _{n=1,n\notin {\kappa }_2}^{\infty }{\left(\frac{(w_2,{\phi }_n)}{E_{\alpha ,1}(-n^2{T}^{\alpha })}\right)}^2<+\infty \}.$$

$$R\left({\mathcal{A}}_3\right)=\{w_3\in L^2\left(\mathsf{\Omega }\right)\mid (w_3,{\phi }_n)=0,n\in {\kappa }_3;\sum _{n=1,n\notin {\kappa }_3}^{\infty }{\left(\frac{(w_3,{\phi }_n)}{T{E}_{\alpha ,2}(-n^2{T}^{\alpha })}\right)}^2<+\infty \}.$$

From Equation (17), for all n, the inverse space source term problem is unique when ${\nu }_n\left(T\right)\ne 0$. However, if n exists such that ${\nu }_n\left(T\right)=0,$ then the inverse source problem is not unique. In this case, there are infinitely many solutions to the integral equation and the solutions are expressed as:

$$f\left(x\right)=\sum _{n=1,n\notin {\kappa }_1}^{\infty }(w_1,{\phi }_n)/{\nu }_n\left(T\right){\phi }_n\left(x\right)+\sum _{{\nu }_n=0}{C}_n{\phi }_n\left(x\right),\forall C_n.$$

However, it only has one optimal approximate solution in $L^2\left(\mathsf{\Omega }\right)$, as follows:

$$f\left(x\right)=\sum _{n=1,n\notin {\kappa }_1}^{\infty }(w_1,{\phi }_n)/{\nu }_n\left(T\right){\phi }_n\left(x\right).$$

(28)

Proof. 

Suppose $f\left(\xi \right)={\sum }_{n=1}^{\infty }{f}_n{\phi }_n\left(\xi \right),$ putting into Equation (17) with $w_1={\sum }_{n=1,n\notin {\kappa }_1}^{\infty }$$(w_1,{\phi }_n){\phi }_n,$ according to the orthonormality of $\left\{{\phi }_n\right\},$ it is not hard to obtain the result.

Similarly, the optimal approximate solutions of $a\left(x\right),b\left(x\right)$ in $L^2\left(\mathsf{\Omega }\right)$ are as follows:

$$a\left(x\right)=\sum _{n=1,n\notin {\kappa }_2}^{\infty }(w_2,{\phi }_n)/E_{\alpha ,1}(-n^2{T}^{\alpha }){\phi }_n\left(x\right).$$

(29)

$$b\left(x\right)=\sum _{n=1,n\notin {\kappa }_3}^{\infty }(w_3,{\phi }_n)/T{E}_{\alpha ,2}(-n^2{T}^{\alpha }){\phi }_n\left(x\right).$$

(30)

Using Equations (17), (18), and (19) we can get the above conclusion.

From Ref. [33], we know that ${\mathcal{A}}_1,{\mathcal{A}}_2,{\mathcal{A}}_3$ are linear compact operators in $L^2\left(\mathsf{\Omega }\right).$ According to the inverse unbounded compact operator, when $\delta \to 0$, it is still not guaranteed that the solution of the equation converges to the exact solution in a certain metric space, so we can only seek a good regularization method to get the approximate solution. So, the inverse source term problem and the initial values we discussed are ill-posed.

We define the a priori boundary for $f\in H^p\left(\mathsf{\Omega }\right)\cap N{\left({\mathcal{A}}_1\right)}^{\perp },a\in H^p\left(\mathsf{\Omega }\right)\cap N{\left({\mathcal{A}}_2\right)}^{\perp },b\in H^p\left(\mathsf{\Omega }\right)\cap N{\left({\mathcal{A}}_3\right)}^{\perp }$ as follows:

$${\parallel f\parallel }_{H^p}\left(\mathsf{\Omega }\right)\le E_1,p>0,E_1>0.$$

(31)

$${\parallel a\parallel }_{H^p}\left(\mathsf{\Omega }\right)\le E_2,p>0,E_2>0.$$

(32)

$${\parallel b\parallel }_{H^p}\left(\mathsf{\Omega }\right)\le E_3,p>0,E_3>0.$$

(33)

□

Lemma 5.

If $g\in C[0,T],m<g\left(x\right),$ m is the smallest value of g in the interval $[0<x<T].$ Using Lemmas 2 and 4, we get

$$|V_n\left(T\right)\ge \frac{C_{21}m}{n^4}.$$

Proof. 

$$\begin{array}{cc}\hfill |V_n\left(T\right)|& =|{\int }_0^{T}g(T-\tau ){\tau }^{\alpha -1}{E}_{\alpha ,\alpha }(-n^2{T}^{\alpha })d\tau |\hfill \\ \hfill & \ge |m{\int }_0^T{\tau }^{\alpha -1}{E}_{\alpha ,\alpha }(-n^2{T}^{\alpha })d\tau |\hfill \\ \hfill & =|-\frac{m}{n^2}{E}_{\alpha ,1}(-n^2{T}^{\alpha })|\hfill \\ \hfill & \ge \frac{C_{21}m}{n^4}.\hfill \end{array}$$

□

Theorem 1.

If for any $f\left(x\right)\in H^p\left(\mathsf{\Omega }\right)\cap N{\left({\mathcal{A}}_1\right)}^{\perp }$ which satisfies Equation (31), we have

$$\parallel f\parallel \le C_{12}{E}_1^{\frac{2}{p+2}}{\parallel {\mathcal{A}}_{1}f\parallel }^{\frac{p}{p+2}},$$

(34)

Here $C_{12}={\left(\frac{1}{m{C}_{21}}\right)}^{-\frac{p}{p+2}}.$

Proof. 

If $f\left(x\right)\in H^p\left(\mathsf{\Omega }\right)\cap N{\left({\mathcal{A}}_1\right)}^{\perp },$ there is

$$f=\sum _{n=1,n\notin {\kappa }_1}^{\infty }(f,{\phi }_n){\phi }_n.$$

we use $\parallel {\mathcal{A}}_1{f\parallel }^2={\sum }_{n=1,n\notin {\kappa }_1}^{\infty }{\nu }_n^2{(f,{\phi }_n)}^2,$ Lemma 4, and $H\ddot{o}lder$ inequality, we get

$$\begin{array}{cc}\hfill {\parallel f\parallel }^2& =\sum _{n=1,n\notin {\kappa }_1}^{\infty }{(f,{\phi }_n)}^2\le \sum _{n=1,n\notin {\kappa }_1}^{\infty }\frac{\left(\right|{\nu }_n\left(T\right){\left|(f,{\phi }_n)\right)}^{\frac{4}{p+2}}}{{\nu }_n^2\left(T\right)}\left(\right|{\nu }_n\left(T\right){\left|(f,{\phi }_n)\right)}^{\frac{2p}{p+2}}\hfill \\ \hfill & \le {\left(\sum _{n=1,n\notin {\kappa }_1}^{\infty }\frac{{(f,{\phi }_n)}^2}{|{\nu }_n^p\left(T\right)|}\right)}^{\frac{2}{p+2}}(\sum _{n=1,n\notin {\kappa }_1}^{\infty }|{\nu }_n\left(T\right){{|}^2{(f,{\phi }_n)}^2)}^{\frac{p}{p+2}}\hfill \\ \hfill & \le {\left(\sum _{n=1,n\notin {\kappa }_1}^{\infty }\left({\left(\frac{n^2}{C_{21}}\right)}^p{(f,{\phi }_n)}^2\right)\right)}^{\frac{2}{p+2}}{\parallel {\mathcal{A}}_{1}f\parallel }^{\frac{2p}{p+2}}\hfill \\ \hfill & \le {\left(\frac{1}{m{C}_{21}}\right)}^{-\frac{2p}{p+2}}{E}_1^{\frac{4}{p+2}}{\parallel {\mathcal{A}}_{1}f\parallel }^{\frac{2p}{p+2}}.\hfill \end{array}$$

So,

$$\parallel f\parallel \le C_{12}{E}_1^{\frac{2}{p+2}}{\parallel {\mathcal{A}}_{1}f\parallel }^{\frac{p}{p+2}},$$

□

Theorem 2.

If for any $a\left(x\right)\in H^p\left(\mathsf{\Omega }\right)\cap N{\left({\mathcal{A}}_2\right)}^{\perp }$, which satisfies Equation (32), we have

$$\parallel a\parallel \le C_{21}^{-\frac{p}{p+2}}{\parallel {\mathcal{A}}_{2}a\parallel }^{\frac{p}{p+2}}{E}_2^{\frac{2}{p+2}}.$$

(35)

Proof. 

The proof is similar to the proof of Theorem 1, which is omitted here. □

Theorem 3.

If for any $b\left(x\right)\in H^p\left(\mathsf{\Omega }\right)\cap N{\left({\mathcal{A}}_3\right)}^{\perp }$ which satisfies Equation (33), we have

$$\parallel b\parallel \le {\left(T{C}_{21}\right)}^{-\frac{p}{p+2}}{\parallel {\mathcal{A}}_{3}b\parallel }^{\frac{p}{p+2}}{E}_3^{\frac{2}{p+2}}.$$

(36)

Proof. 

The proof is similar to the previous theorem as in the proof of Theorem 1. □

4. Mollification Regularization and Error Estimates

4.1. An a Priori Approach for Problem (1)

In this section, we utilize mollification method to solve problem (1). The terminal measurement data in problem (1) is softened by a bilateral exponential function and is converted into the following question:

$$\left\{\begin{array}{c}{\partial }_{0+}^{\alpha }{u}^{\mu ,\delta }(x,t)+L{u}^{\mu ,\delta }(x,t)=f^{\mu ,\delta }\left(x\right)g^{\mu ,\delta }\left(t\right),x\in \mathsf{\Omega },0\le t\le T,\hfill \\ u^{\mu ,\delta }(x,0)=a^{\mu ,\delta }\left(x\right),x\in \overline{\mathsf{\Omega }},\hfill \\ {\partial }_t{u}^{\mu ,\delta }(x,0)=b^{\mu ,\delta }\left(x\right),x\in \overline{\mathsf{\Omega }},\hfill \\ u^{\mu ,\delta }(x,t)=0,x\in \partial \mathsf{\Omega },0\le t\le T,\hfill \\ u^{\mu ,\delta }(x,T)=(V_{\mu }\left(x\right)\ast h\left(x\right)),x\in \mathsf{\Omega }.\hfill \end{array}\right.$$

(37)

Thus, we get $w_1^{\mu ,\delta }$ after using the mollification method expressed as

$$w_1^{\mu ,\delta }=(V_{\mu }\ast h)\left(x\right)-u_1(x,T)-u_2(x,T),$$

and the first Fredholm integral formula becomes

$${\mathcal{A}}_{1}f\left(x\right)={\int }_{\mathsf{\Omega }}f\left(\xi \right){\kappa }_1(x,\xi )d\xi =w_1^{\mu ,\delta }\left(x\right).$$

According to the above, we can get the regular solution of $f\left(x\right)$ as

$$f^{\mu ,\delta }\left(x\right)=\sum _{{\nu }_n\ne 0}^{\infty }(w_1^{\mu ,\delta },{\phi }_n)/{\nu }_n\left(T\right){\phi }_n\left(x\right).$$

(38)

Theorem 4.

If the functions $f$ and $f^{\mu ,\delta }$ are uniformly Lipschitz on $L^2\left(\mathsf{\Omega }\right)$, we will assume that (7) holds. Then we have

$$\begin{array}{c}\hfill \parallel f-f^{\mu ,\delta }\parallel \le \frac{n^4}{C_{21}m}(\frac{1}{2}{\epsilon }^2+1)\delta .\end{array}$$

(39)

When

$$\begin{array}{c}\hfill n=\frac{\delta }{E_1},\end{array}$$

(40)

we have

$$\parallel f-f^{\mu ,\delta }\parallel \le \frac{1}{C_{21}m{E}_1^4}(\frac{1}{2}{\epsilon }^2+1){\delta }^5\to 0as\delta \to 0.$$

(41)

Proof. 

Using the triangle inequality, from the Parseval equality and the properties of the double integral, we have

$$\begin{array}{c}\hfill \parallel f-f^{\mu ,\delta }\parallel \le \parallel f-f^{\mu }\parallel +\parallel f^{\mu }-f^{\mu ,\delta }\parallel .\end{array}$$

(42)

Using Lemma 5, the first part of Equation (42) is as follows:

$$\begin{array}{cc}\hfill \parallel f-f^{\mu }\parallel & =\parallel \sum _{{\nu }_n\ne 0}^{\infty }(w_1,{\phi }_n)/{\nu }_n\left(T\right){\phi }_n\left(x\right)-\sum _{{\nu }_n\ne 0}^{\infty }(w_1^{\mu },{\phi }_n)/{\nu }_n\left(T\right){\phi }_n\left(x\right)\parallel \hfill \\ \hfill & =\parallel \sum _{{\nu }_n\ne 0}^{\infty }((w_1-w_1^{\mu }),{\phi }_n)/{\nu }_n\left(T\right){\phi }_n\left(x\right)\parallel \le \frac{n^4}{C_{21}m}\parallel w_1-w_1^{\mu }\parallel ,\hfill \end{array}$$

here

$$\begin{array}{cc}\hfill \parallel w_1-w_1^{\mu }\parallel & =\parallel h\left(x\right)-h^{\mu }\left(x\right)\parallel ={\int }_{R^d}{|h\left(x\right)-h^{\mu }\left(x\right)|}^{2}dx\hfill \\ \hfill & ={\int }_{R^d}{|{\int }_{R^d}\{h\left(x\right)V_{\mu }(x-t)-h\left(t\right)V_{\mu }(x-t)\}dt|}^{2}dx,\hfill \end{array}$$

Let $y=x-t,dy=-dt,$ then we have

$$\begin{array}{cc}\hfill |{\int }_{R^d}\{h\left(x\right)V_{\mu }(x-t)-f\left(t\right)V_{\mu }(x-t)\}{dt|}^2& =|{\int }_{R^d}[h\left(x\right)-h\left(t\right)]V_{\mu }{\left(y\right)dy|}^2\hfill \\ \hfill & =|{\int }_{R^d}[h\left(x\right)-h(x-y)]V_{\mu }{\left(y\right)dy|}^2\hfill \\ \hfill & ={\int }_{R^d}{|h\left(x\right)-h(x-y)|}^{2}dy{\int }_{R^d}{\left|V_{\mu }\left(y\right)\right|}^{2}dy\hfill \\ \hfill & \le \frac{1}{2}{\int }_{R^d}{|h\left(x\right)-h(x-y)|}^{2}dy,\hfill \end{array}$$

when $y\le \delta ,$ we can get ${|h\left(x\right)-h(x-y)|}^2\le {\epsilon }^2.$

So,

$$\begin{array}{c}\hfill |{\int }_{R^d}\{h\left(x\right)V_{\mu }(x-t)-h\left(t\right)V_{\mu }(x-t)\}{dt|}^2\le \frac{1}{2}{\epsilon }^2,\end{array}$$

and

$$\begin{array}{c}\hfill \parallel w_1-w_1^{\mu }\parallel \le {\int }_{R^d}{|h\left(x\right)-h^{\mu }\left(x\right)|}^{2}dy\le \frac{1}{2}{\epsilon }^2\delta .\end{array}$$

Thus, we obtain

$$\begin{array}{c}\hfill \parallel f-f^{\mu }\parallel \le \frac{n^2}{C_{21}m}\parallel w_1-w_1^{\mu }\parallel \le \frac{n^4}{2C_{21}m}{\epsilon }^2\delta .\end{array}$$

(43)

The second part of Equation (42) is:

$$\begin{array}{cc}\hfill \parallel f^{\mu }-f^{\mu ,\delta }\parallel & \le \frac{n^2}{C_{21}m}\parallel w_1^{\mu }-w_1^{\mu ,\delta }\parallel =\frac{n^2}{C_{21}m}\parallel h^{\mu }-h^{\mu ,\delta }\parallel \hfill \\ \hfill & \le \frac{n^2}{C_{21}m}{\int }_{R^d}[h(x-t)V_{\mu }\left(t\right)-h^{\delta }(x-t)V_{\mu }\left(t\right)]dt\hfill \\ \hfill & =\frac{n^4}{C_{21}m}\delta {\int }_{R^d}{V}_{\mu }\left(t\right)dt=\frac{n^4}{C_{21}m}\delta .\hfill \end{array}$$

(44)

By combining the estimates of Equations (43) and (44), we obtain Equation (39) □

Theorem 5.

If the functions $a\left(x\right)$ and $a^{\mu ,\delta }$ are uniformly Lipschitz on $L^2\left(\mathsf{\Omega }\right)$, we will assume that (7) holds. Then we have

$$\begin{array}{c}\hfill \parallel a\left(x\right)-a^{\mu ,\delta }\parallel \le \frac{n^2}{C_{21}}(\frac{1}{2}{\epsilon }^2+1)\delta .\end{array}$$

(45)

When

$$\begin{array}{c}\hfill n=\frac{\delta }{E_2},\end{array}$$

(46)

we have

$$\parallel a\left(x\right)-a^{\mu ,\delta }\parallel \le \frac{1}{C_{21}{E}_2^2}(\frac{1}{2}{\epsilon }^2+1){\delta }^3\to 0as\delta \to 0.$$

(47)

Proof. 

Using the triangle inequality, from the Parseval equality and the properties of the double integral, there is

$$\begin{array}{c}\hfill \parallel a-a^{\mu ,\delta }\parallel \le \parallel a-a^{\mu }\parallel +\parallel a^{\mu }-a^{\mu ,\delta }\parallel .\end{array}$$

(48)

Using Lemma 4, the first part of Equation (48) is as follows:

$$\begin{array}{cc}\hfill \parallel a-a^{\mu }\parallel & =\parallel \sum _{n=1,n\notin {\kappa }_2}^{\infty }(w_2,{\phi }_n)/E_{\alpha ,1}(-n^2{T}^{\alpha }){\phi }_n\left(x\right)-\sum _{n=1,n\notin {\kappa }_2}^{\infty }(w_2^{\mu },{\phi }_n)/E_{\alpha ,1}(-n^2{T}^{\alpha }){\phi }_n\left(x\right)\parallel \hfill \\ \hfill & =\parallel \sum _{n=1,n\notin {\kappa }_2}^{\infty }((w_2-w_2^{\mu }),{\phi }_n)/E_{\alpha ,1}(-n^2{T}^{\alpha }){\phi }_n\left(x\right)\parallel \le \frac{n^2}{C_{21}}\parallel w_2-w_2^{\mu }\parallel \hfill \end{array}$$

here

$$\begin{array}{cc}\hfill \parallel w_2-w_2^{\mu }\parallel & =\parallel h\left(x\right)-h^{\mu }\left(x\right)\parallel =\parallel w_1-w_1^{\mu }\parallel \le \frac{1}{2}{\epsilon }^2\delta .\hfill \end{array}$$

So,

$$\begin{array}{c}\hfill \parallel a-a^{\mu }\parallel \le \frac{n^2}{C_{21}}\frac{1}{2}{\epsilon }^2\delta .\end{array}$$

(49)

The second part of Equation (48) is:

$$\begin{array}{cc}\hfill \parallel a^{\mu }-a^{\mu ,\delta }\parallel & \le \frac{n^2}{C_{21}}\parallel w_2^{\mu }-w_2^{\mu ,\delta }\parallel =\frac{n^2}{C_{21}}\parallel h^{\mu }-h^{\mu ,\delta }\parallel \hfill \\ \hfill & \le \frac{n^2}{C_{21}}{\int }_{R^d}[h(x-t)V_{\mu }\left(t\right)-h^{\delta }(x-t)V_{\mu }\left(t\right)]dt\hfill \\ \hfill & =\frac{n^2}{C_{21}}\delta {\int }_{R^d}{V}_{\mu }\left(t\right)dt=\frac{n^2}{C_{21}}\delta .\hfill \end{array}$$

(50)

By combining the estimates of Equations (49) and (50), we obtain Equation (45) □

Theorem 6.

If the functions $b\left(x\right)$ and $b^{\mu ,\delta }$ are uniformly Lipschitz on $L^2\left(\mathsf{\Omega }\right)$, we will assume that (7) holds and use Lemma 2. We then have

$$\begin{array}{c}\hfill \parallel b\left(x\right)-b^{\mu ,\delta }\parallel \le \frac{n^2}{C_{21}T}(\frac{1}{2}{\epsilon }^2+1)\delta .\end{array}$$

(51)

When

$$\begin{array}{c}\hfill n=\frac{\delta }{E_3},\end{array}$$

(52)

we have

$$\parallel b\left(x\right)-b^{\mu ,\delta }\parallel \le \frac{1}{C_{21}T{E}^3}(\frac{1}{2}{\epsilon }^2+1){\delta }^3\to 0as\delta \to 0.$$

(53)

The proof is similar to the proof of Theorem 5, which is omitted here.

4.2. An a Posteriori Approach for Problem (1) 

According to the Morozov inconsistency principle [34], the posterior regularization parameter selection rule is given, that is, the solution $n$ of the following equation is selected as the posterior regularization parameter, where we define:

$$\begin{array}{c}\hfill \parallel V_{\mu }\ast h^{\delta }-h^{\delta }\parallel =\tau \delta .\end{array}$$

(54)

Here, $V_{\mu }\ast h^{\delta }=h^{\mu ,\delta }.$

Lemma 6.

Below are the following inequalities:

$$\begin{array}{c}\hfill \parallel V_u\ast h^{\delta }-h\parallel \le (\tau +1)\delta ,\\ \hfill \end{array}$$

(55)

Proof. 

$$\begin{array}{cc}\hfill \parallel V_u\ast h^{\delta }-h\parallel & =\parallel V_u\ast h^{\delta }-h^{\delta }+h^{\delta }-h\parallel \hfill \\ \hfill & \le \parallel V_u\ast h^{\delta }-h^{\delta }\parallel +\parallel h^{\delta }-h\parallel \hfill \\ \hfill & \le \tau \delta +\delta \le (\tau +1)\delta .\hfill \end{array}$$

(56)

Therefore, Lemma 6 is proved. □

Lemma 7.

If $\delta >0,$ then the functions

$$q\left(\mu \right)=\parallel V_u\ast h^{\delta }-h^{\delta }\parallel .$$

have the following properties:

$$\begin{array}{cc}\hfill & \left(1\right)q\left(\mu \right)iscontinuousfunction;\hfill \\ \hfill & \left(2\right)\underset{\mu \to \infty }{lim}q\left(\mu \right)=\parallel h^{\delta }\parallel ;\hfill \\ \hfill & \left(3\right)\underset{\mu \to 0}{lim}q\left(\mu \right)=0;\hfill \\ \hfill & \left(4\right)qisastrictlyincreasingfunction.\hfill \end{array}$$

The proof of this lemma is similar to Ref. [35]. We omit the proof here.

Theorem 7.

Let $f\left(x\right)$ be the exact solution of problem (1), and $f^{\mu ,\delta }\left(x\right)$ be the regular approximation solution of problem (1). The Inequalities (7) and (11) hold. Then, we have

$$\begin{array}{cc}\hfill \parallel f-f^{\mu ,\delta }\parallel & \le \frac{n^4}{C_{21}m}(\tau +1)\delta .\hfill \end{array}$$

(57)

When the regularization parameter $n$ is chosen as (40), we have

$$\begin{array}{cc}\hfill \parallel f-f^{\mu ,\delta }\parallel & \le \frac{1}{C_{21}m{E}_1^4}(\tau +1){\delta }^5\to 0as\delta \to 0.\hfill \end{array}$$

(58)

Proof. 

$$\begin{array}{cc}\hfill \parallel f-f^{\mu ,\delta }\parallel & =\parallel \sum _{n=1,n\notin {\kappa }_1}^{\infty }\frac{(w_1,{\phi }_n)}{V_n\left(T\right)}{\phi }_n-\sum _{n=1,n\notin {\kappa }_1}^{\infty }\frac{(w_1^{\mu ,\delta },{\phi }_n)}{V_n\left(T\right)}{\phi }_n\parallel \hfill \\ \hfill & \le \parallel \sum _{n=1,n\notin {\kappa }_1}^{\infty }\frac{(w_1-w_1^{\mu ,\delta },{\phi }_n)}{V_n\left(T\right)}{\phi }_n\parallel \hfill \\ \hfill & \le \frac{n^4}{C_{21}m}\parallel w_1-w_1^{\mu ,\delta }\parallel =\frac{n^4}{C_{21}m}\parallel h-h^{\mu ,\delta }\parallel \hfill \\ \hfill & \le \frac{n^4}{C_{21}m}(\tau +1)\delta .\hfill \end{array}$$

□

Theorem 8.

Let $a\left(x\right)$ be the exact solution of problem (1), and $a^{\mu ,\delta }\left(x\right)$ be the regular approximation solution of problem (1). The Inequalities (7) and (11) hold. Then, we have

$$\begin{array}{cc}\hfill \parallel a-a^{\mu ,\delta }\parallel & \le \frac{n^2}{C_{21}}(\tau +1)\delta .\hfill \end{array}$$

(59)

When the regularization parameter $n$ is chosen as (46), we have

$$\begin{array}{cc}\hfill \parallel a-a^{\mu ,\delta }\parallel & \le \frac{1}{C_{21}{E}_2^2}(\tau +1){\delta }^3\to 0as\delta \to 0.\hfill \end{array}$$

(60)

The proof is similar to Theorem 4.

Theorem 9.

Let $b\left(x\right)$ be the exact solution of problem (1), and $b^{\mu ,\delta }\left(x\right)$ be the regular approximation solution of problem (1). The Inequalities (7) and (11) hold. Then, we have

$$\begin{array}{cc}\hfill \parallel b-b^{\mu ,\delta }\parallel & \le \frac{n^2}{C_{21}T}(\tau +1)\delta .\hfill \end{array}$$

(61)

When the regularization parameter $n$ is chosen as (52), we have

$$\begin{array}{cc}\hfill \parallel b-b^{\mu ,\delta }\parallel & \le \frac{1}{C_{21}T{E}_3^2}(\tau +1){\delta }^3\to 0as\delta \to 0.\hfill \end{array}$$

(62)

The Proof is similar with Theorem 4.

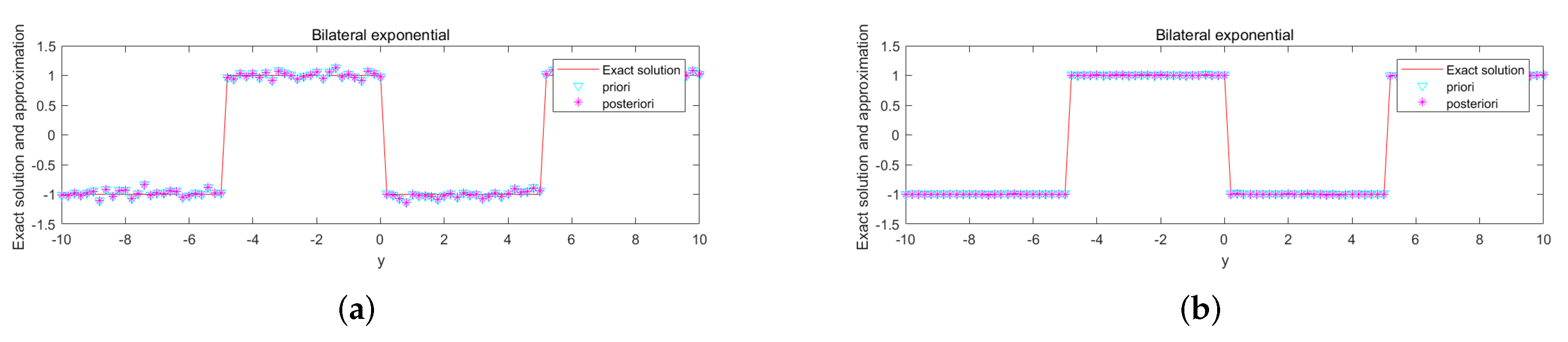
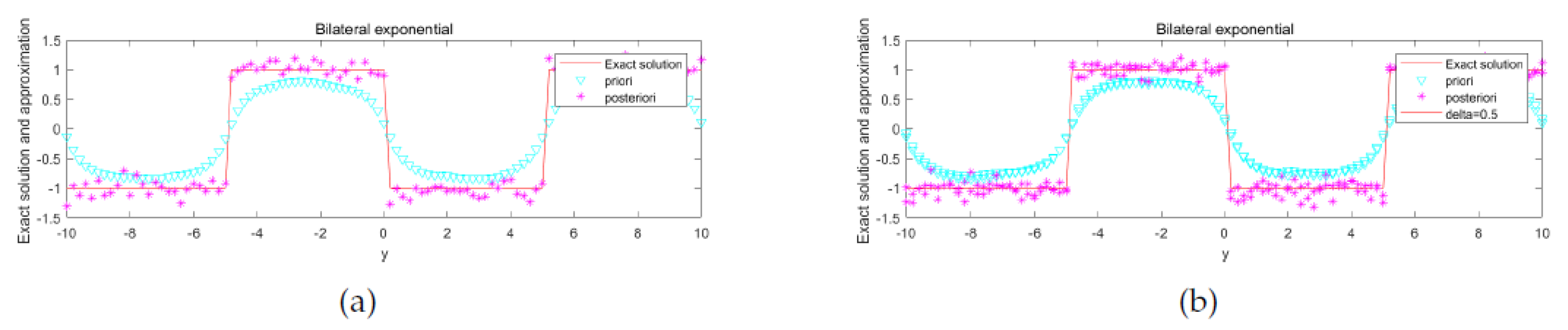
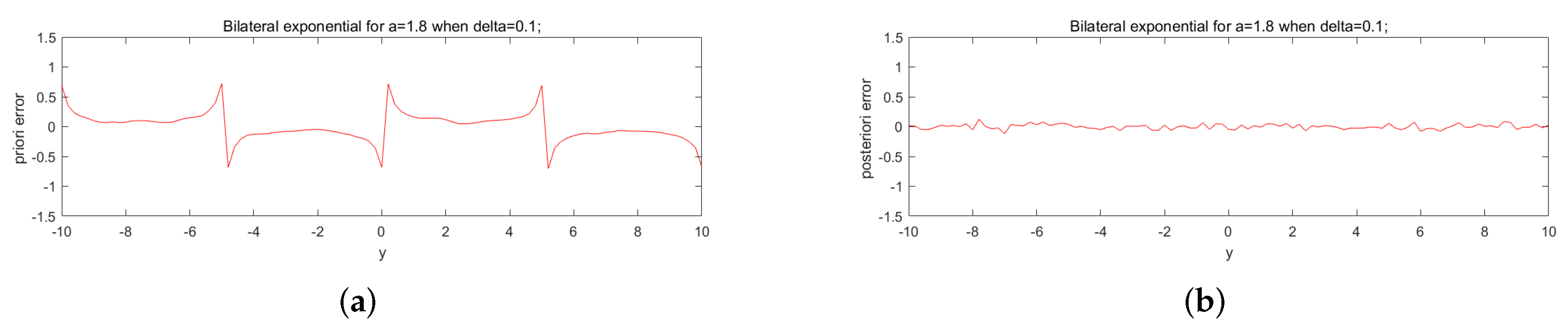
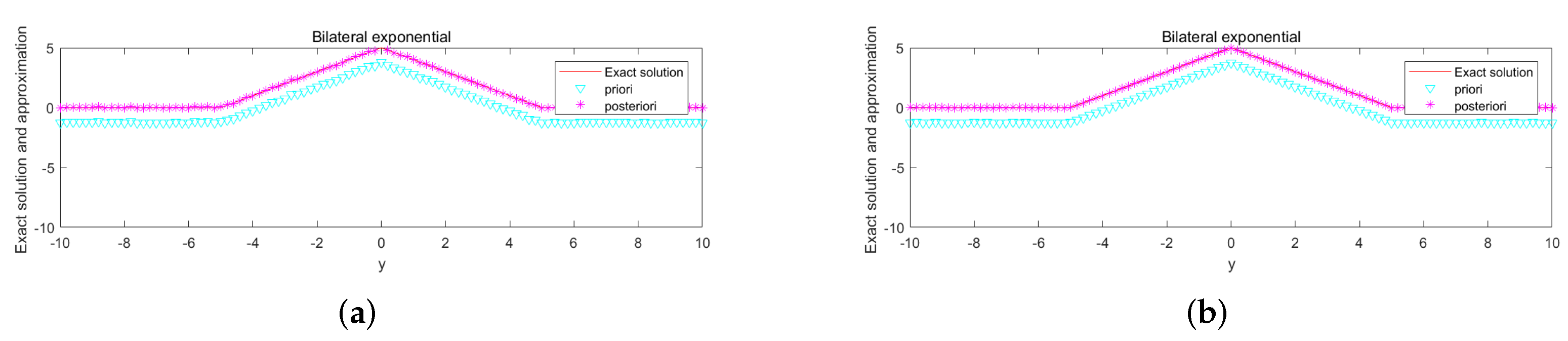
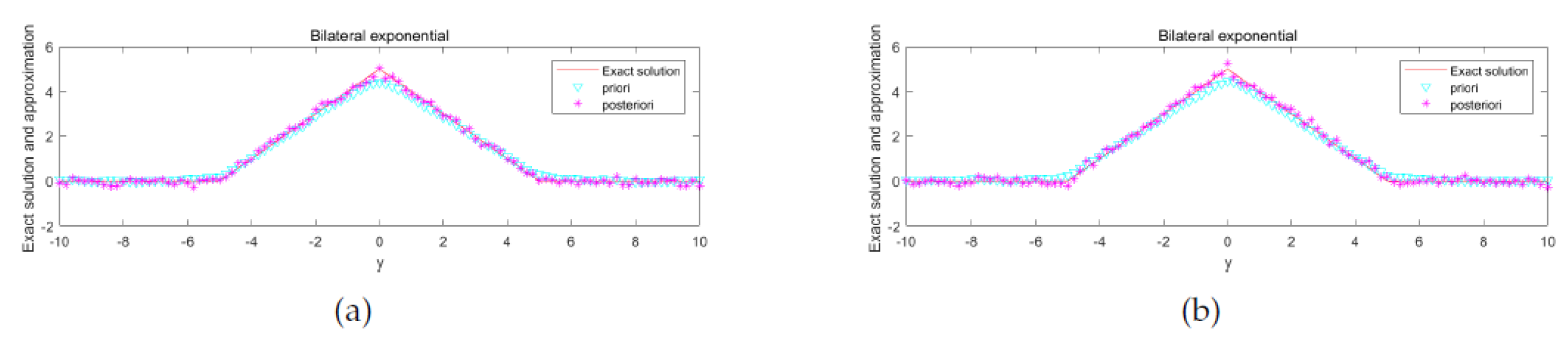
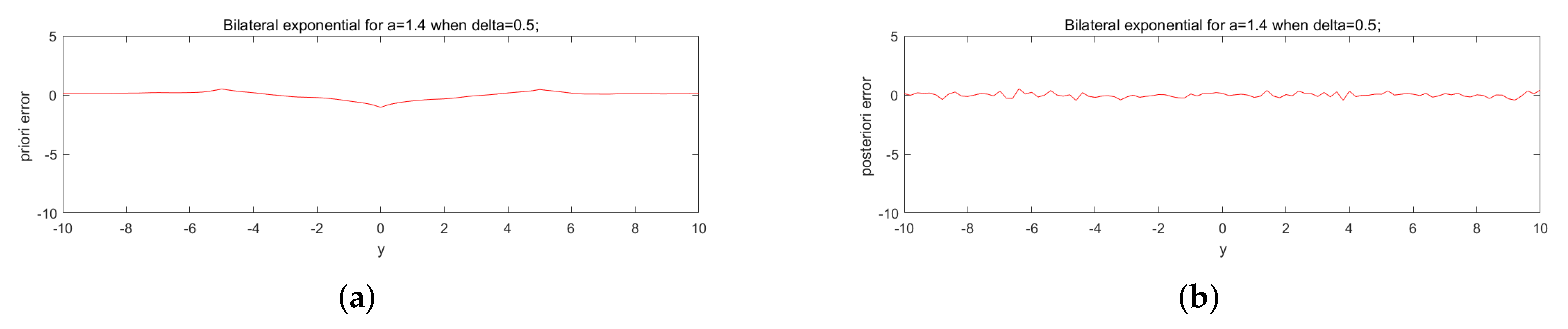
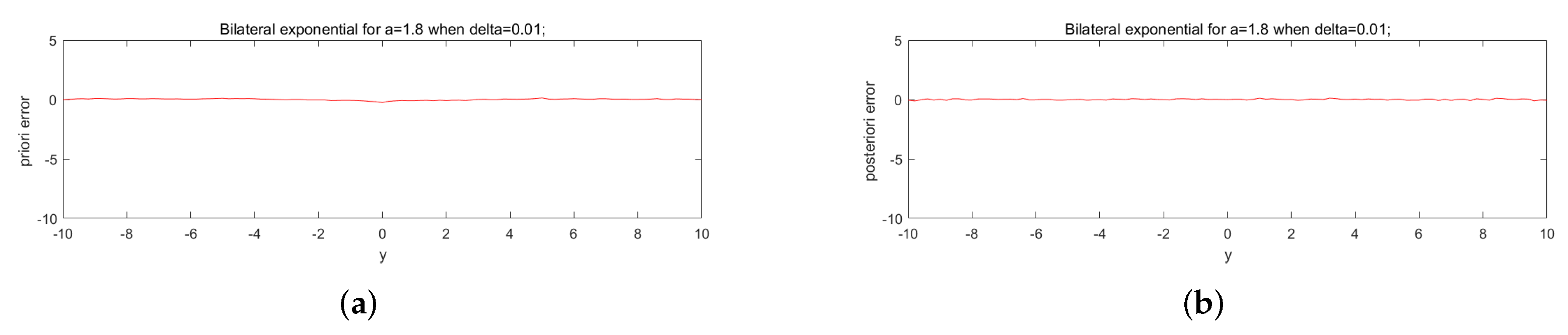
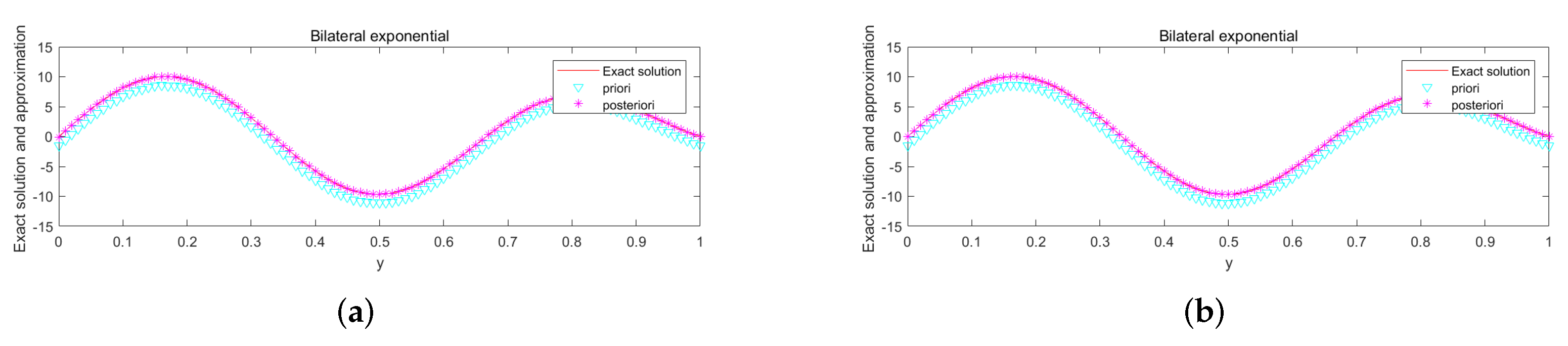
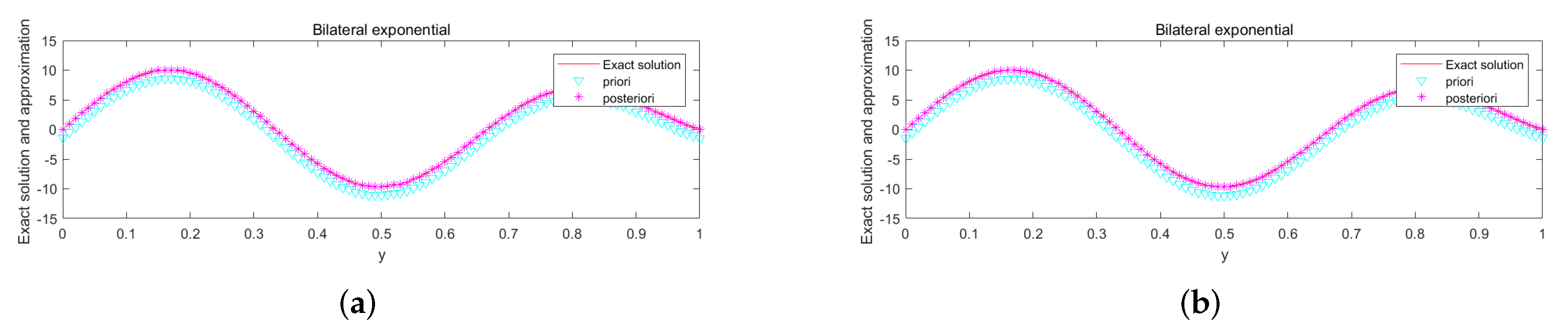
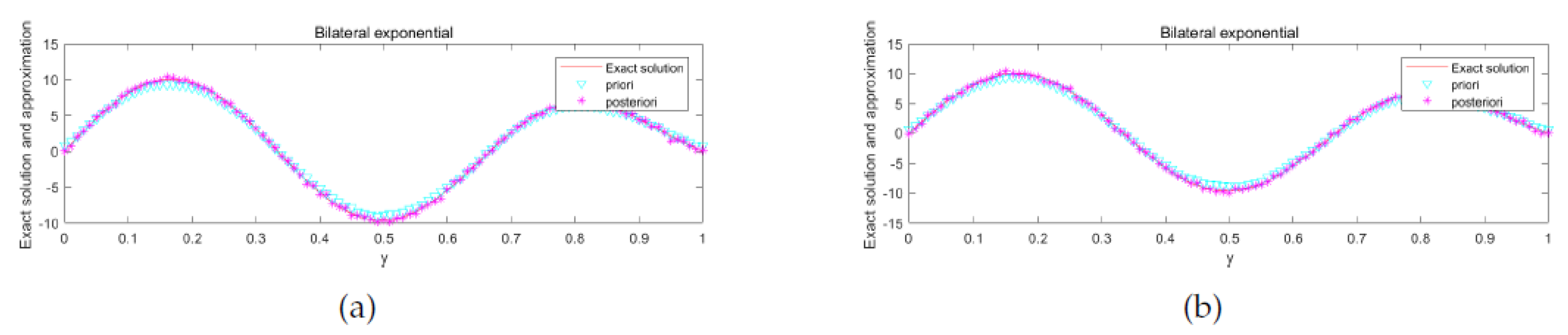
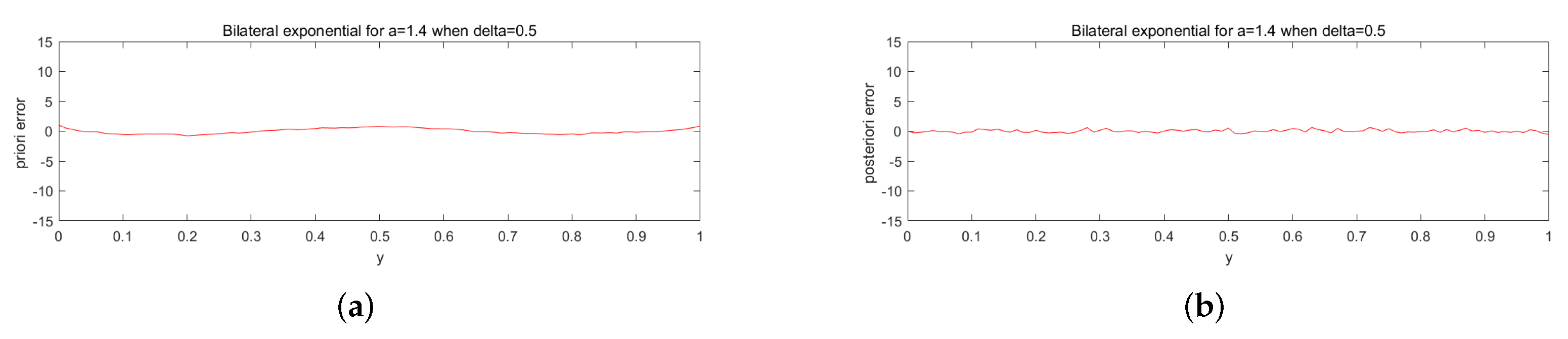
5. Numerical Aspect

Numerical Implementation

In this section, numerical examples are used to verify the validity of the mollification regularization method with a bilateral exponential kernel under an a priori and an a posteriori regularization parameter choice rule, respectively. All the computations related to the problem were performed via MALAB2017b.

In the following experiments, the discrete interval is $[-10,10],$ sample point $N=100$. The numerical test results of the prior and posterior regularization methods are compared.

Assume that the sequence ${h\left(x_i\right)}_{i=1}^N$ denotes samples from the function $h\left(x\right)$ on an equidistant grid. Subsequently, a perturbation with a randomly uniform distribution is added to each data. Meanwhile, perturbation data can be obtained:

$$\begin{array}{c}\hfill h^{\delta }=h+ϵrand\left(size\left(h\right)\right),\end{array}$$

(63)

where

$$h={(h\left(x_1\right),\dots ,h\left(x_N\right))}^T,x_i=(i-1)\mathsf{\Delta }x,$$

$$\mathsf{\Delta }x=\frac{1}{N-1},i=1,2,\dots ,N.$$

Then, the total noise $\delta$ can be measured in the sense of the Root Mean Square Error based on

$$\begin{array}{c}\hfill \delta :=\parallel h^{\delta }{-h\parallel }_{l^2}=\sqrt{\frac{1}{N}\sum _{i=1}^N{(h_i^{\delta }-h_i)}^2}.\end{array}$$

(64)

Here, the random number sequences are created by “rand(.)”, with elements being pseudo-random numbers that show a homogeneous distribution. A random entries array is returned by rand (size(h)), whose size is equal to that of $h.$ Here, $rel\left(pr\right)$ is the relative error between the exact solution and the regular solution under the prior rules. $rel\left(po\right)$ is the relative error between the exact solution and the regular solution under the posterior rules.

Example 1.

We consider the following Cauchy problem of a space-dependent source function $f\left(x\right).$

$$\begin{array}{c}\hfill f\left(x\right)=10sin\left(3\pi x\right)e^{-x^5}+x^{\alpha }{(1-x)}^4\end{array}$$

(65)

Example 2.

We consider the following Cauchy problem of initial value $a\left(x\right)$ of the time-fractional non homogeneous diffusion equation.

$$a\left(x\right)=\left\{\begin{array}{c}0,-10\le x\le -5,\hfill \\ x+5,-5\le x\le 0,\hfill \\ 5-x,0\le x\le 5,\hfill \\ 0,5\le x\le 10.\hfill \end{array}\right.$$

(66)

Example 3.

Consider a discontinuous function of the initial value $b\left(x\right)$.

$$b\left(x\right)=\left\{\begin{array}{c}-1,-10\le x\le -5,\hfill \\ 1,-5\le x\le 0,\hfill \\ -1,0\le x\le 5,\hfill \\ 1,5\le x\le 10.\hfill \end{array}\right.$$

(67)

The comparison of the numerical effectiveness using a priori and a posteriori parameter choice rules for $\alpha =1.4$ and $\alpha =1.8$ are shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13. As can be seen from the above figures, the regularization inversion method provided in this chapter can accurately reconstruct the spacial source term $f\left(x\right)$ and the initial value $a\left(x\right),b\left(x\right)$. In

Table 1. The relative error of Example 1.

Error Level $\mathit{\delta }$	$\mathit{rel}\left(\mathit{pr}\right)$ ($\mathit{\alpha }$ = 1.4)	$\mathit{rel}\left(\mathit{po}\right)$ ($\mathit{\alpha }$ = 1.4)	$\mathit{rel}\left(\mathit{pr}\right)$ ($\mathit{\alpha }$ = 1.8)	$\mathit{rel}\left(\mathit{po}\right)$ ($\mathit{\alpha }$ = 1.8)
1 × ${10}^{-1}$	0.2362	0.069	0.2352	0.0070
1 × ${10}^{-2}$	0.2361	7.6050 × ${10}^{-4}$	0.2351	6.7405 × ${10}^{-4}$

,

Table 2. The relative error of Example 2.

Error Level $\mathit{\delta }$	$\mathit{rel}\left(\mathit{pr}\right)$ ($\mathit{\alpha }$ = 1.4)	$\mathit{rel}\left(\mathit{po}\right)$ ($\mathit{\alpha }$ = 1.4)	$\mathit{rel}\left(\mathit{pr}\right)$ ($\mathit{\alpha }$ = 1.8)	$\mathit{rel}\left(\mathit{po}\right)$ ($\mathit{\alpha }$ = 1.8)
1 × ${10}^{-1}$	0.0507	0.0504	0.0462	0.0417
1 × ${10}^{-2}$	0.0106	0.0047	0.0108	0.0048

and

Table 3. The relative error of Example 3.

Error Level $\mathit{\delta }$	$\mathit{rel}\left(\mathit{pr}\right)$ ($\mathit{\alpha }$=1.4)	$\mathit{rel}\left(\mathit{po}\right)$ ($\mathit{\alpha }$ = 1.4)	$\mathit{rel}\left(\mathit{pr}\right)$ ($\mathit{\alpha }$ = 1.8)	$\mathit{rel}\left(\mathit{po}\right)$ ($\mathit{\alpha }$ = 1.8)
1 × ${10}^{-1}$	0.6094	0.0224	0.6095	0.0212
1 × ${10}^{-2}$	0.6091	0.0025	0.6091	0.0024

we can see that both of the rules achieve satisfactory effects for three examples. We also find that the error between the exact solution and the regularized solution decreases as the noise level decreases. It can also be seen from the tables that the a posteriori result in our method is better than the a priori result.

Table 4. Running times of Example 1, Example 2, and Example 3.

Example	$\mathit{\alpha }=1.8$	$\mathit{\delta }$	Running Time (s)
eg. 1	1.8	0.5	0.186
eg. 2	1.8	0.5	0.163
eg. 3	1.8	0.5	0.177

shows the elapsed time for Examples 1–3 programs under the same conditions $(\alpha =1.8,\delta =0.5).$ Here the parameter in Morozov’s inconsistency principle is set as $\tau =1.1$.

We use different noisy levels with $\delta =0.5,1\times {10}^{-1},1\times {10}^{-2},$ respectively, to study the numerical stability of our algorithm. Three tables show the results from different error levels of the problem. We notice that the results of the Error Norm depend not only on the error level $\delta$ but also on the fractional order $\alpha$.

Figure 1, Figure 2 and Figure 3 present the exact initial value and the reconstructed initial value $a\left(x\right)$ when $\alpha =1.4$ and $\alpha =1.8$, respectively, and we can see that the numerical results match the exact ones quite well under $\delta =0.5,1\times {10}^{-1}$ and $\delta =1\times {10}^{-2}.$ It can be seen from Figure 4 and Figure 5 that our regularization method is stable and efficient. Figure 6, Figure 7 and Figure 8 illustrate the exact solution and approximate solution of the initial value $b\left(x\right)$ at $\delta =0.5,1\times {10}^{-1}$ and $\delta =1\times {10}^{-2}.$ Figure 9Figure 10 show the error results, from which it can be seen that the method proposed in this paper is stable and effective for the identification of the initial value $b\left(x\right)$. Figure 11, Figure 12 and Figure 13 present the exact source function and the numerical solutions of $f\left(x\right)$ when $\alpha =1.4$ and $\alpha =1.8.$ It can be seen from Figure 14, Figure 15 and Figure 16 that the proposed method is suitable for source item identification, and our findings are stable and effective under both prior and posterior rules.

6. Conclusions

In this article, we propose a novel regularization method based on the bilateral kernel, to solve a Cauchy problem of a multi-dimensional time fractional diffusion-wave equation in a special bounded domain. We studied an inverse space-dependent source term and the initial value from the noisy final time measured data. The error estimates are given under prior and posterior rules. The numerical examples above show the numerical stability of the proposed method. Furthermore, our approach of the posterior rule is superior to the prior rule and the accuracy of the procedure is quite acceptable.