Advancing COVID-19 Understanding: Simulating Omicron Variant Spread Using Fractional-Order Models and Haar Wavelet Collocation
Abstract
:1. Introduction
2. Preliminaries
Haar Wavelets
3. Mathematical Model
3.1. Formulation of Fractional Model
3.2. Basic Reproductive Number
4. Existence and Uniqueness
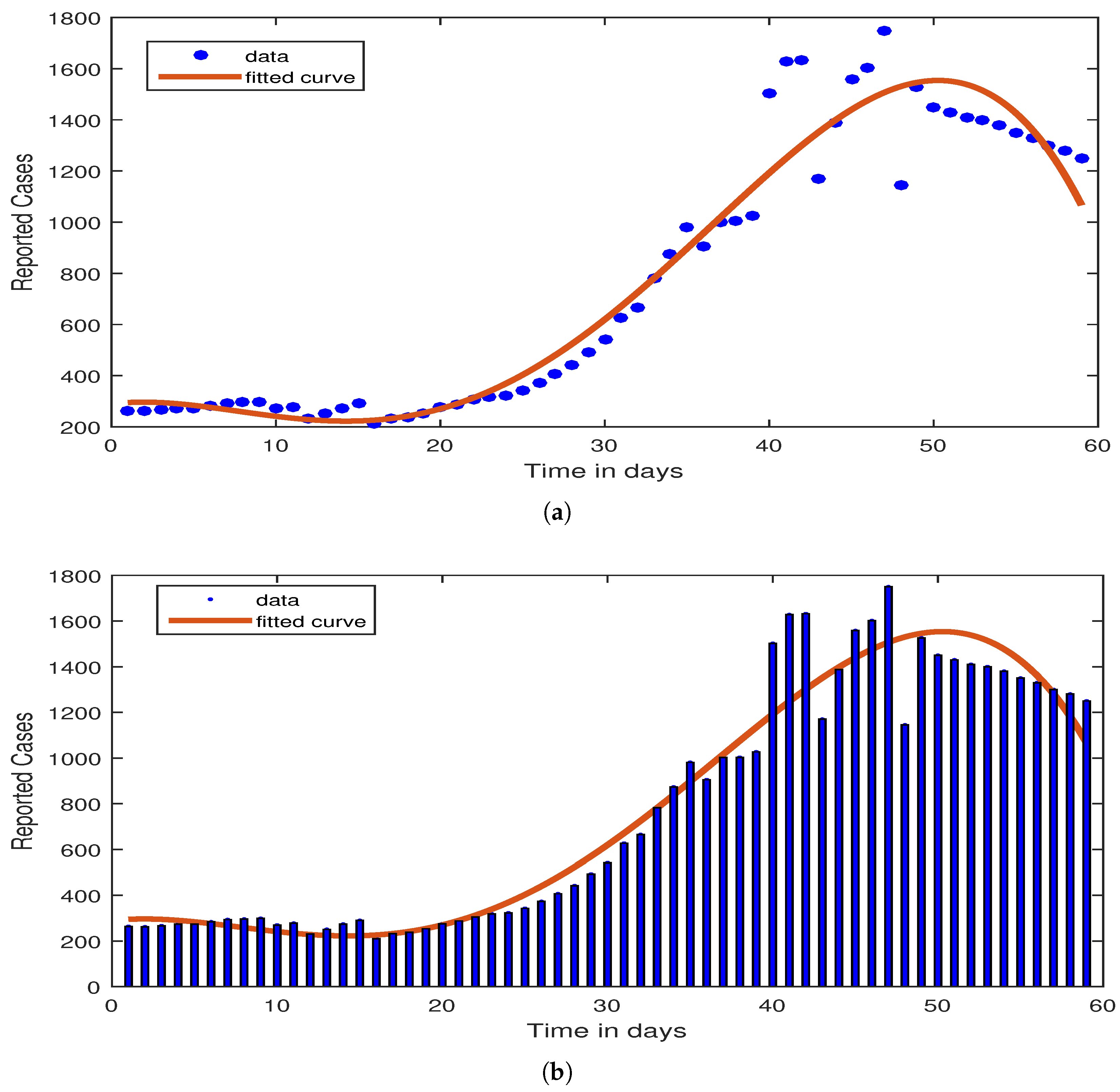
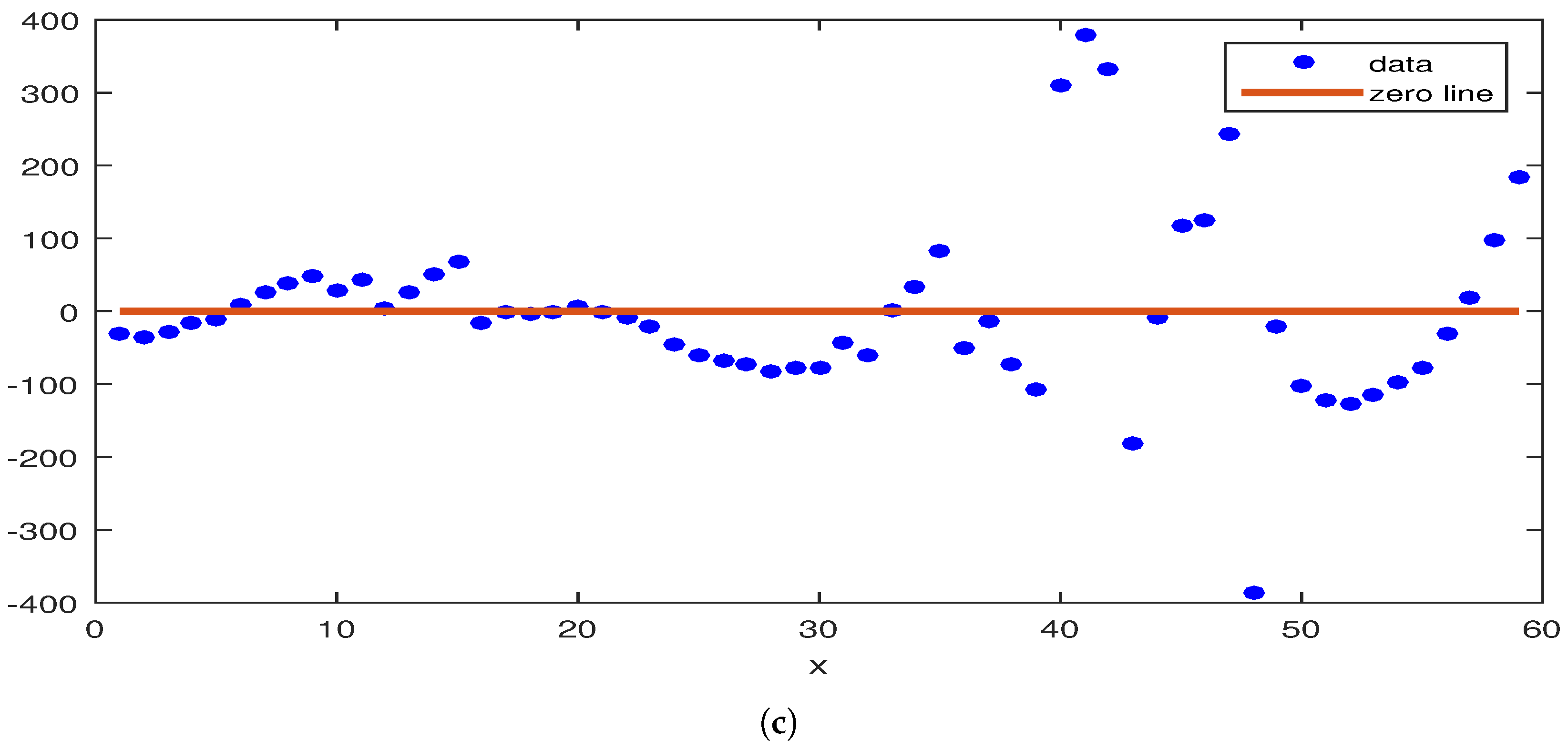
5. Parameter Estimation
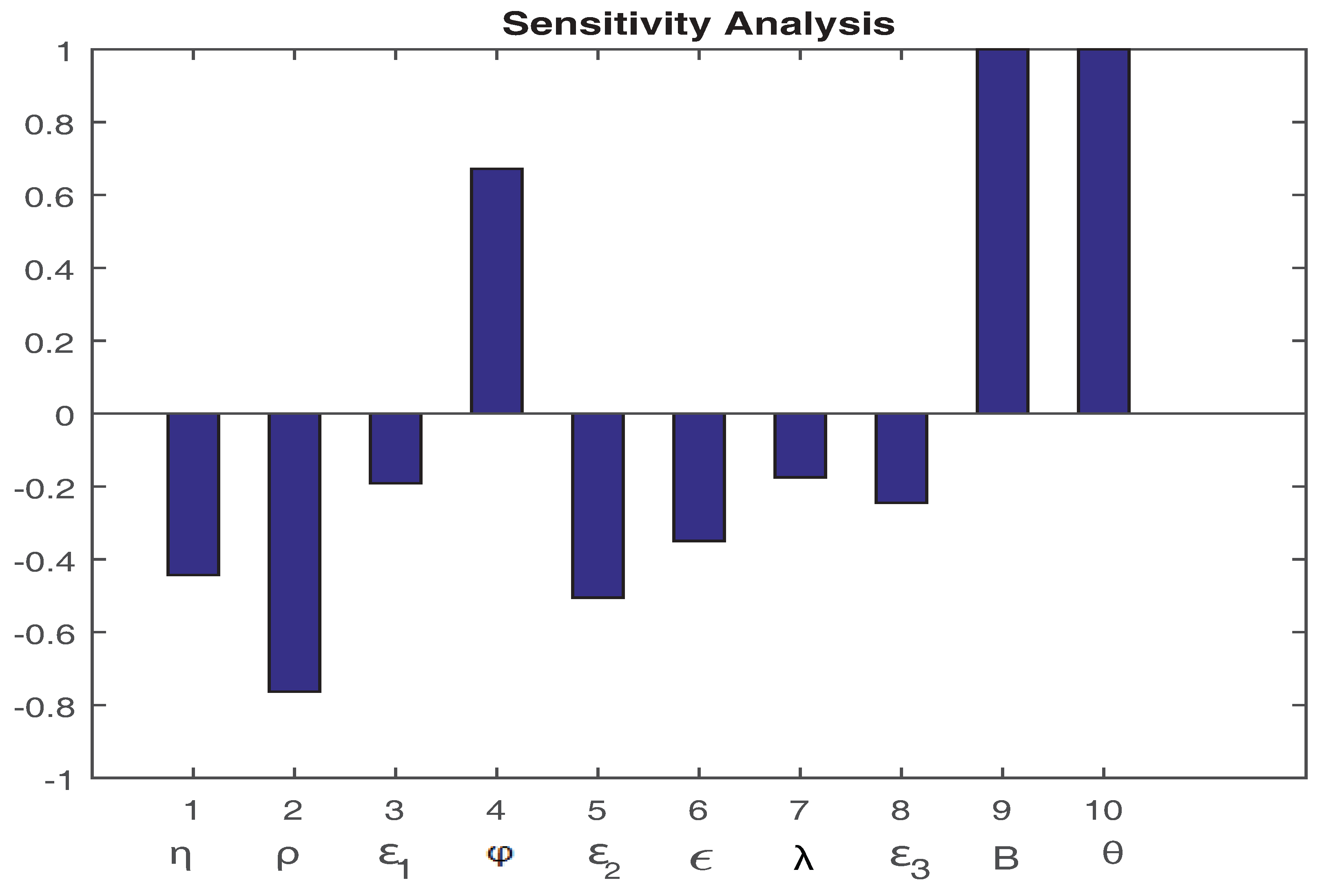
6. Sensitivity Analysis
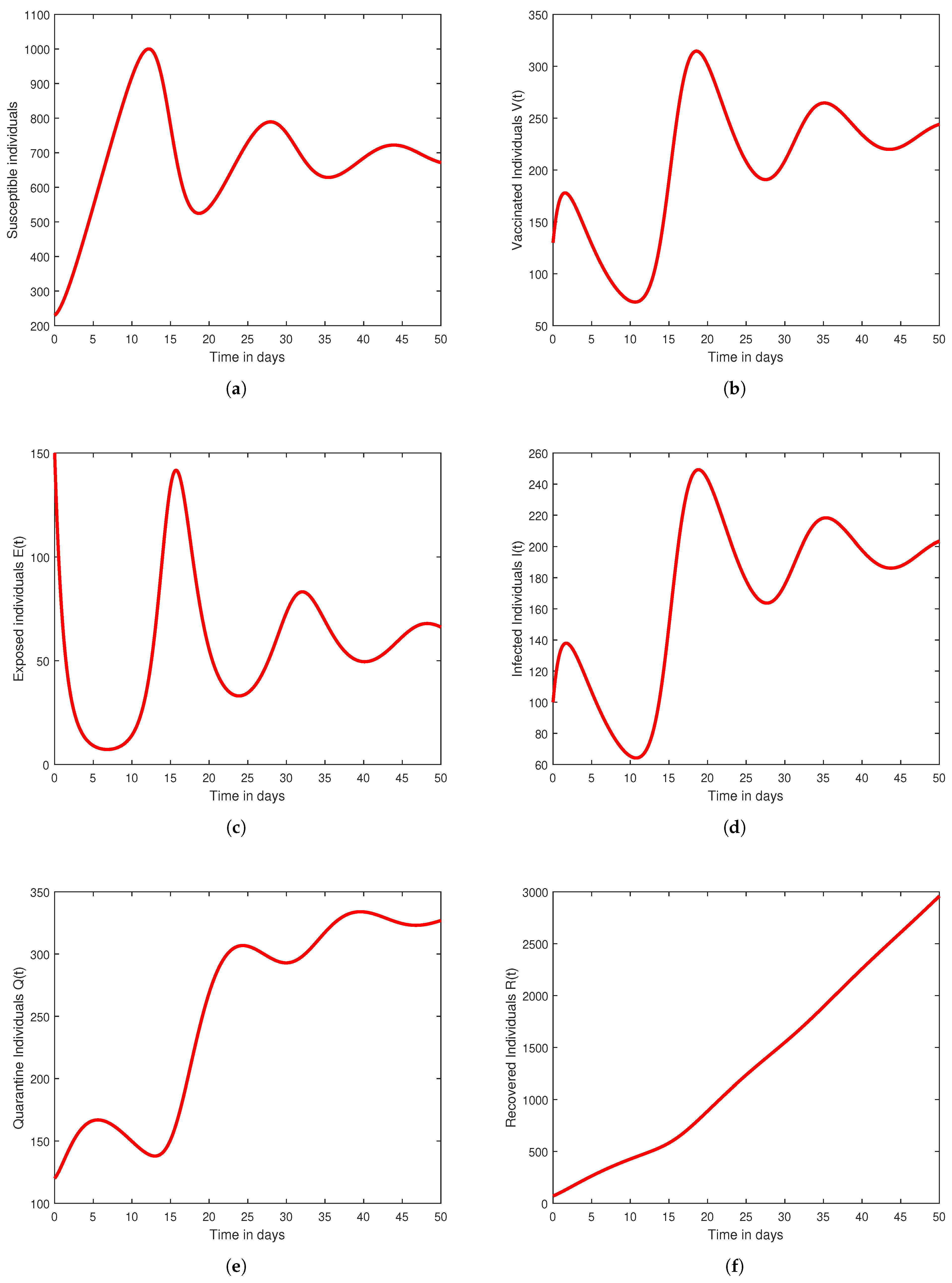
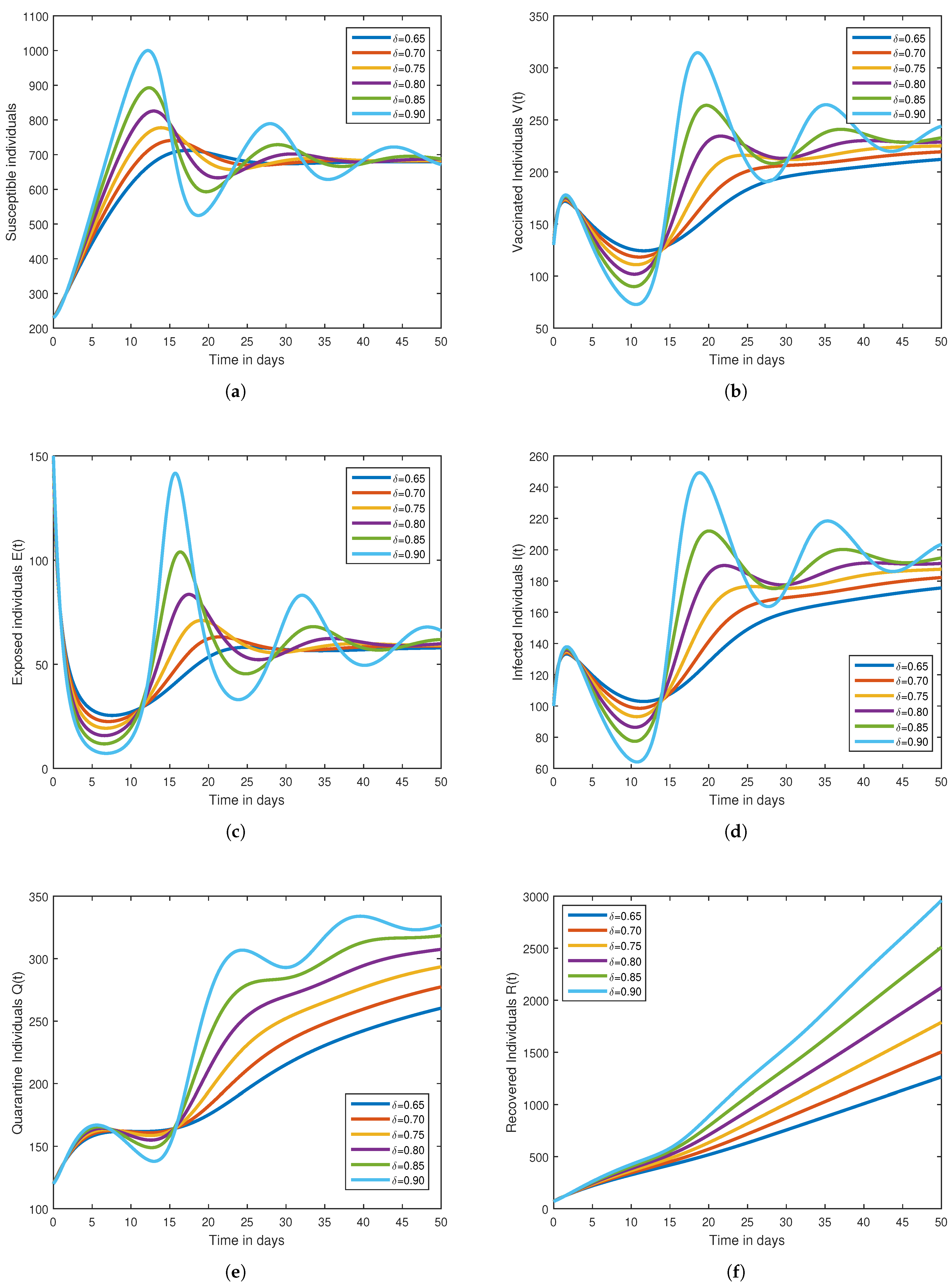
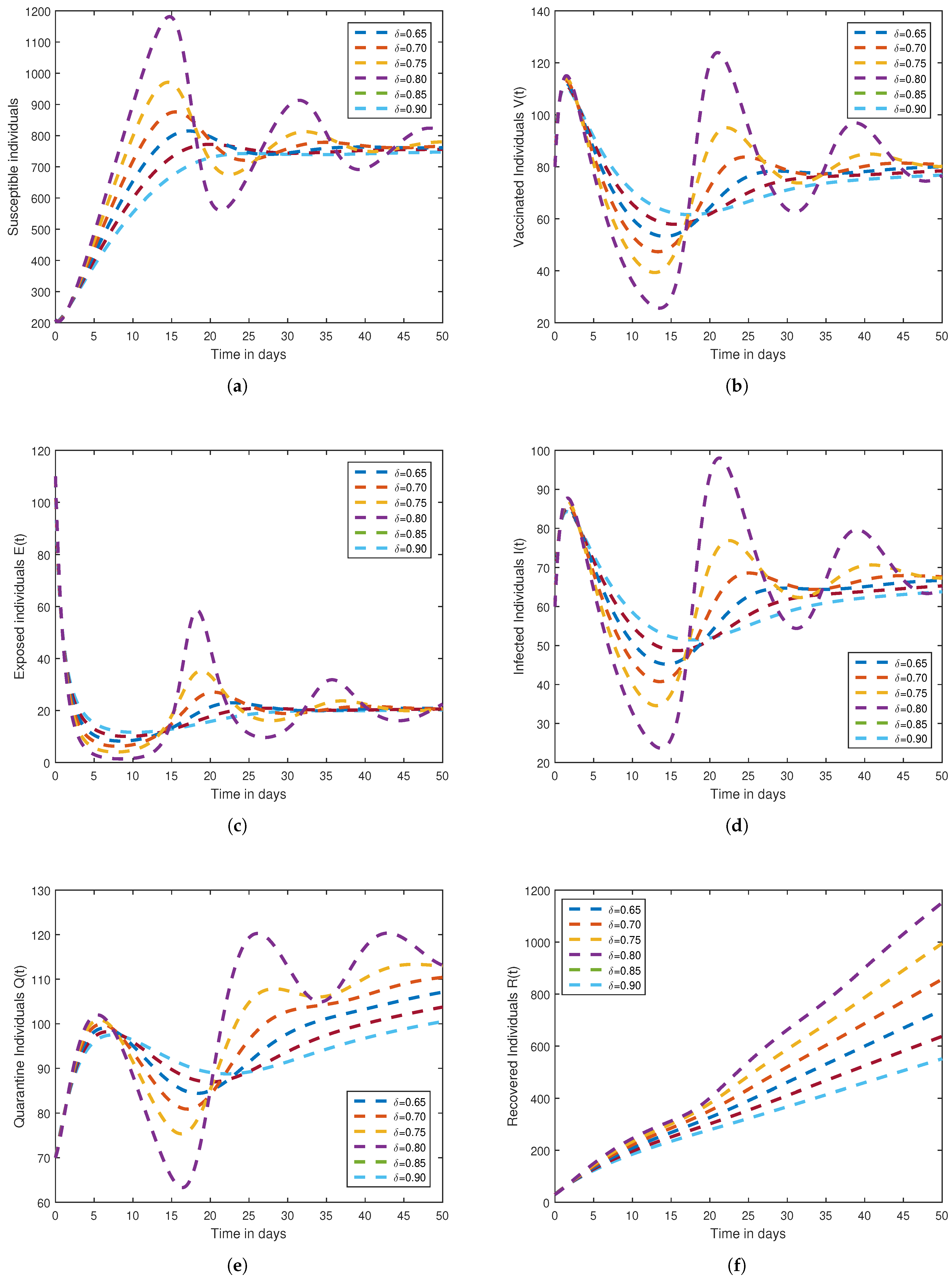
7. Numerical Scheme and Graphical Results
Graphical Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Omrani, A.S.; Al-Tawfiq, J.A.; Memish, Z.A. Middle East respiratory syndrome coronavirus (MERS-CoV): Animal to human interaction. Pathog. Glob. Health 2015, 109, 354–362. [Google Scholar] [CrossRef]
- World Health Organization. Weekly Epidemiological Update on COVID-19—11 January 2023. Available online: https://www.who.int/publications/m/item/weekly-epidemiological-update-on-covid-19---11-january-2023 (accessed on 11 January 2023).
- Tay, M.Z.; Poh, C.M.; Rénia, L.; MacAry, P.A.; Ng, L.F. The trinity of COVID-19: Immunity, inflammation and intervention. Nat. Rev. Immunol. 2020, 20, 363–374. [Google Scholar] [CrossRef] [PubMed]
- Backer, J.A.; Klinkenberg, D.; Wallinga, J. Incubation period of 2019 novel coronavirus (2019-nCoV) infections among travellers from Wuhan, China, 20–28 January 2020. Eurosurveillance 2020, 25, 2000062. [Google Scholar] [CrossRef] [PubMed]
- Kronbichler, A.; Kresse, D.; Yoon, S.; Lee, K.H.; Effenberger, M.; Shin, J.I. Asymptomatic patients as a source of COVID-19 infections: A systematic review and meta-analysis. Int. J. Infect. Dis. 2020, 98, 180–186. [Google Scholar] [CrossRef]
- Khan, A.; Zarin, R.; Hussain, G.; Ahmad, N.A.; Mohd, M.H.; Yusuf, A. Stability analysis and optimal control of covid-19 with convex incidence rate in Khyber Pakhtunkhawa (Pakistan). Results Phys. 2021, 20, 103703. [Google Scholar] [CrossRef]
- Khan, A.; Zarin, R.; Akgul, A.; Saeed, A.; Gul, T. Fractional optimal control of COVID-19 pandemic model with generalized Mittag-Leffler function. Adv. Differ. Equ. 2021, 2021, 387. [Google Scholar] [CrossRef]
- Alqarni, M.S.; Alghamdi, M.; Muhammad, T.; Alshomrani, A.S.; Khan, M.A. Mathematical modeling for novel coronavirus (COVID-19) and control. Numer. Methods Partial. Differ. Equ. 2022, 38, 760–776. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Zarin, R.; Khan, S.; Saeed, A.; Gul, T.; Humphries, U.W. Fractional dynamics and stability analysis of COVID-19 pandemic model under the harmonic mean type incidence rate. Comput. Methods Biomech. Biomed. Eng. 2022, 25, 619–640. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunuba, Z.; Cuomo-Dannenburg, G.; et al. Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand. Imperial College COVID-19 Response Team. 2020. Available online: https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-NPI-modelling-16-03-2020.pdf (accessed on 16 March 2020).
- Marathe, A.; Lewis, B.; Chen, J. COVID-19: Understanding the spread of infectious diseases. Nat. Rev. Phys. 2020, 2, 447–456. [Google Scholar]
- Hethcote, H.W.; Shuai, Z.; Van den Driessche, P. COVID-19 transmission dynamics in the United States: A mathematical model with a realistic age structure. Math. Biosci. Eng. 2021, 18, 2672–2690. [Google Scholar] [CrossRef]
- Yopadhyay, A.; Nabar, N.R.; Salathé, M. A review of data-driven epidemiological models of infectious diseases. In Global Dynamics of Infectious Diseases: Impact of Social Heterogeneity; Springer: Berlin, Germany, 2021; pp. 19–41. [Google Scholar]
- Liu, P.; Huang, X.; Zarin, R.; Cui, T.; Din, A. Modeling and numerical analysis of a fractional order model for dual variants of SARS-CoV-2. Alex. Eng. J. 2023, 65, 427–442. [Google Scholar] [CrossRef]
- Daniloski, Z.; Guo, X.; Sanjana, N.E. The D614G mutation in SARS-CoV-2 spike increases transduction of multiple human cell types. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef]
- Saberi, M.; Moshksayan, K.; Barati, M.; Soleymani, F.; Eftekhari, P. Modeling and analysis of COVID-19 infection dynamics with fractional-order derivatives. Chaos Solitons Fractals 2021, 146, 110844. [Google Scholar]
- Goyal, M.; Baskonus, H.M.; Prakash, A. An efficient technique for a time fractional model of lassa hemorrhagic fever spreading in pregnant women. Eur. Phys. J. Plus 2019, 134, 482. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Prakasha, D.G.; Baskonus, H.M.; Yel, G. New approach for the model describing the deathly disease in pregnant women using Mittag-Leffler function. Chaos Solitons Fractals 2020, 134, 109696. [Google Scholar] [CrossRef]
- Alqahtani, R.T.; Ahmad, S.; Akgül, A. Dynamical analysis of bio-ethanol production model under generalized nonlocal operator in Caputo sense. Mathematics 2021, 9, 2370. [Google Scholar] [CrossRef]
- Agarwal, P.; Singh, R. Modelling of transmission dynamics of Nipah virus (Niv): A fractional order approach. Phys. A Stat. Mech. Its Appl. 2020, 547, 124243. [Google Scholar] [CrossRef]
- Zarin, R.; Khan, A.; Yusuf, A.; Abdel-Khalek, S.; Mustafa Inc. Analysis of fractional COVID-19 epidemic model under Caputo operator. Math. Methods Appl. Sci. 2021, 6, 115–122. [Google Scholar] [CrossRef]
- Zarin, R.; Khan, A.; Kumar, P. Fractional-order dynamics of Chagas-HIV epidemic model with different fractional operators. AIMS Math. 2022, 7, 18897–18924. [Google Scholar] [CrossRef]
- Baleanu, D.; Fernez, A.; Akgül, A. On a fractional operator combining proportional and classical differintegrals. Mathematics 2020, 8, 360. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar] [CrossRef]
- Andrew, O.; Abbas, M.; Abdel-Aty, A.-H. Assessing the impact of SARS-CoV-2 infection on the dynamics of dengue and HIV via fractional derivatives. Chaos Solitons Fractals 2022, 162, 112427. [Google Scholar]
- Omame, A.; Abbas, M.; Onyenegecha, C.P. Backward bifurcation and optimal control in a co-infection model for SARS-CoV-2 and ZIKV. Results Phys. 2022, 37, 105481. [Google Scholar] [CrossRef]
- Agarwal, P.; Choi, J.; Paris, R.B. Extended Riemann-Liouville fractional derivative operator and its applications. J. Nonlinear Sci. Appl. (JNSA) 2015, 8, 451–466. [Google Scholar] [CrossRef]
- Zarin, R.; Khan, A.; Inc, M.; Humphries, U.W.; Karite, T. Dynamics of five grade leishmania epidemic model using fractional operator with Mittag–Leffler kernel. Chaos Solitons Fractals 2021, 147, 110985. [Google Scholar] [CrossRef]
- Agarwal, P.; Choi, J. Fractional calculus operators and their image formulas. J. Korean Math. Soc. 2016, 53, 1183–1210. [Google Scholar] [CrossRef]
- Atangana, A. Non validity of index law in fractional calculus: A fractional differential operator with Markovian and non-Markovian properties. Phys. A Stat. Mech. Its Appl. 2018, 505, 688–706. [Google Scholar] [CrossRef]
- Zarin, R. Modeling and numerical analysis of fractional order hepatitis B virus model with harmonic mean type incidence rate. Comput. Methods Biomech. Biomed. Eng. 2022, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Zarin, R.; Ahmed, I.; Kumam, P.; Zeb, A.; Din, A. Fractional modeling and optimal control analysis of rabies virus under the convex incidence rate. Results Phys. 2021, 28, 104665. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Akgül, A.; Baleanu, D. Analysis of the fractional tumour-immune-vitamins model with Mittag–Leffler kernel. Results Phys. 2020, 19, 103559. [Google Scholar] [CrossRef]
- Atangana, A. A novel Covid-19 model with fractional differential operators with singular and non-singular kernels: Analysis and numerical scheme based on Newton polynomial. Alexandria Eng. J. 2021, 60, 3781–3806. [Google Scholar] [CrossRef]
- Bansal, K.; Arora, S.; Pritam, K.S.; Mathur, T.; Agarwal, S. Dynamics of Crime Transmission Using Fractional-Order Differential Equations. Fractals 2022, 30, 2250012. [Google Scholar] [CrossRef]
- Pritam, K.S.; Mathur, T.; Agarwal, S. Underlying dynamics of crime transmission with memory. Chaos Solitons Fractals 2021, 146, 110838. [Google Scholar] [CrossRef]
- Rahman, M.U.; Ahmad, S.; Arfan, M.; Akgül, A.; Jarad, F. Fractional Order Mathematical Model of Serial Killing with Different Choices of Control Strategy. Fractal Fract. 2022, 6, 162. [Google Scholar] [CrossRef]
- Zhi, S.; Deng, L.-Y.; Qing, J.C. Numerical Solution of Differential Equations by Using Haar Wavelets. In Proceedings of the International Conference on Wavelet Analysis and Pattern Recognition, Beijing, China, 2–4 November 2007; pp. 1039–1044. [Google Scholar]
- Shah, K.; Khan, Z.A.; Ali, A.; Amin, R.; Khan, H.; Khan, A. Haar wavelet collocation approach for the solution of fractional order COVID-19 model using Caputo derivative. Alex. Eng. J. 2020, 59, 3221–3231. [Google Scholar] [CrossRef]
- Prakash, B.; Setia, A.; Alapatt, D. Numerical solution of nonlinear fractional SEIR epidemic model by using Haar wavelets. J. Comput. Sci. 2017, 22, 109–118. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. A new analysis of the Fornberg-Whitham equation pertaining to a fractional derivative with Mittag-Leffler-type kernel. Eur. Phys. J. Plus 2018, 133, 70. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Purohit, S.D.; Swroop, R. A hybrid analytical algorithm for nonlinear fractional wave-like equations. Math. Model. Nat. Phenom. 2019, 14, 304. [Google Scholar] [CrossRef]
- Caputo, M.; Mainardi, F. A new dissipation model based on memory mechanism. Pure Appl. Geophys. 1971, 91, 134–147. [Google Scholar] [CrossRef]
- Chen, Y.; Yi, M.; Yu, C. Error analysis for numerical solution of fractional differential equation by Haar wavelets method. J. Comput. Sci. 2012, 3, 367–373. [Google Scholar] [CrossRef]
- Lepik, Ü.; Hein, H. Haar wavelets. In Haar Wavelets; Springer: Cham, Switzerland, 2014; pp. 7–20. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Reproduction number and sub-threshold endemic equilbria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–38. [Google Scholar] [CrossRef]
- Taylor, A.E.; Lay, D.C. Introduction to Functional Analysis; Wiley: New York, NY, USA, 1958; Volume 1. [Google Scholar]
- Available online: https://www.who.int/countries/pak/ (accessed on 23 August 2022).
- Mandal, M.; Jana, S.; Nandi, S.K.; Khatua, A.; Adak, S.; Kar, T.K. A model based study on the dynamics of COVID-19: Prediction and control. Chaos Solitons Fractals 2020, 136, 109889. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, W. Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl. Math. Comp. 2010, 216, 2276–2285. [Google Scholar] [CrossRef]
- Majak, J.; Shvartsman, B.; Karjust, K.; Mikola, M.; Haavajõe, A.; Pohlak, M. On the accuracy of the Haar wavelet discretization method. Compos. Part B Eng. 2015, 80, 321–327. [Google Scholar] [CrossRef]
- Zarin, R.; Khaliq, H.; Khan, A.; Ahmed, I.; Humphries, U.W. A Numerical Study Based on Haar Wavelet Collocation Methods of Fractional-Order Antidotal Computer Virus Model. Symmetry 2023, 15, 621. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raizah, Z.; Zarin, R. Advancing COVID-19 Understanding: Simulating Omicron Variant Spread Using Fractional-Order Models and Haar Wavelet Collocation. Mathematics 2023, 11, 1925. https://doi.org/10.3390/math11081925
Raizah Z, Zarin R. Advancing COVID-19 Understanding: Simulating Omicron Variant Spread Using Fractional-Order Models and Haar Wavelet Collocation. Mathematics. 2023; 11(8):1925. https://doi.org/10.3390/math11081925
Chicago/Turabian StyleRaizah, Zehba, and Rahat Zarin. 2023. "Advancing COVID-19 Understanding: Simulating Omicron Variant Spread Using Fractional-Order Models and Haar Wavelet Collocation" Mathematics 11, no. 8: 1925. https://doi.org/10.3390/math11081925
APA StyleRaizah, Z., & Zarin, R. (2023). Advancing COVID-19 Understanding: Simulating Omicron Variant Spread Using Fractional-Order Models and Haar Wavelet Collocation. Mathematics, 11(8), 1925. https://doi.org/10.3390/math11081925






