Statistical Depth in Spatial Point Process
Abstract
:1. Introduction
2. Methodology
2.1. Penalized Metric
2.2. Smoothing Metric
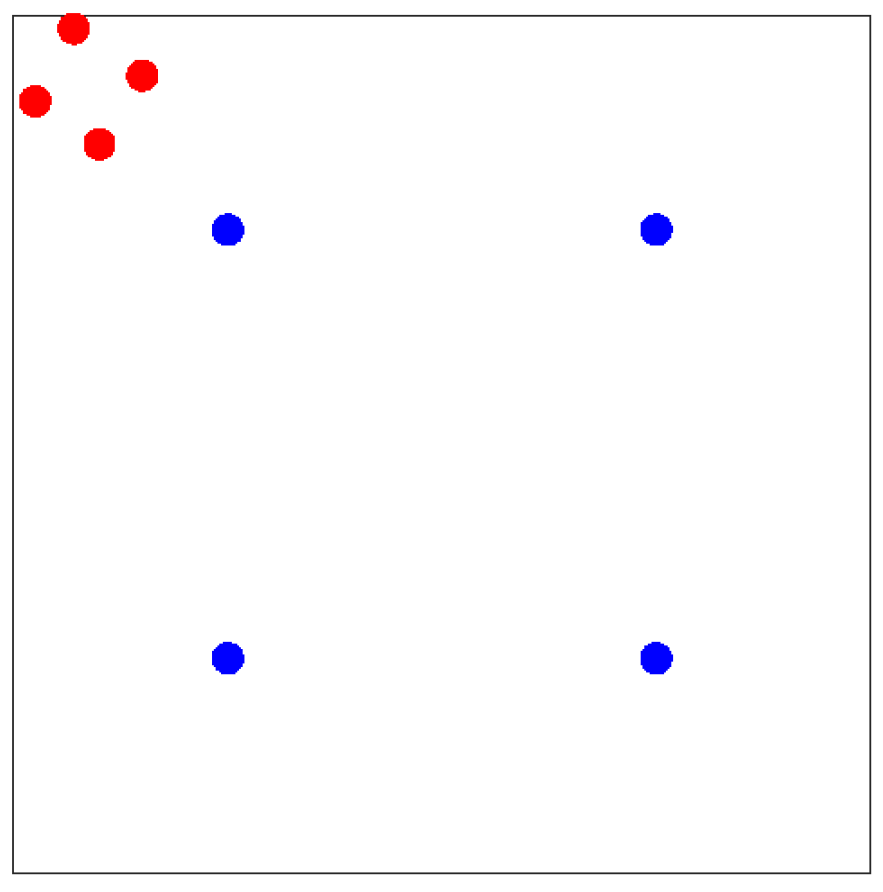
2.2.1. Mapping between Spatial Point Process and Bivariate Function
2.2.2. Definition of Smoothing Metric
2.3. Spatial Metric Depth for Spatial Point Process
- () Linear invariance: For point processes in any general rectangular domain, Definition 4 can still be adopted to define the depth value via the two metrics. We let be an arbitrary point process in without overlapping points. We suppose a and c are any positive numbers, and b and d are any real numbers. We denote , and in domain . Then, .
- () Vanishing at infinity: For any , depth value if the cardinality of rises to infinity.
- () Continuity in : For any , and , there exists such that .
- () Continuity in P: For any , and , there exists such that P—almost surely for all with P—almost surely, where measures the topology of weak convergence on .
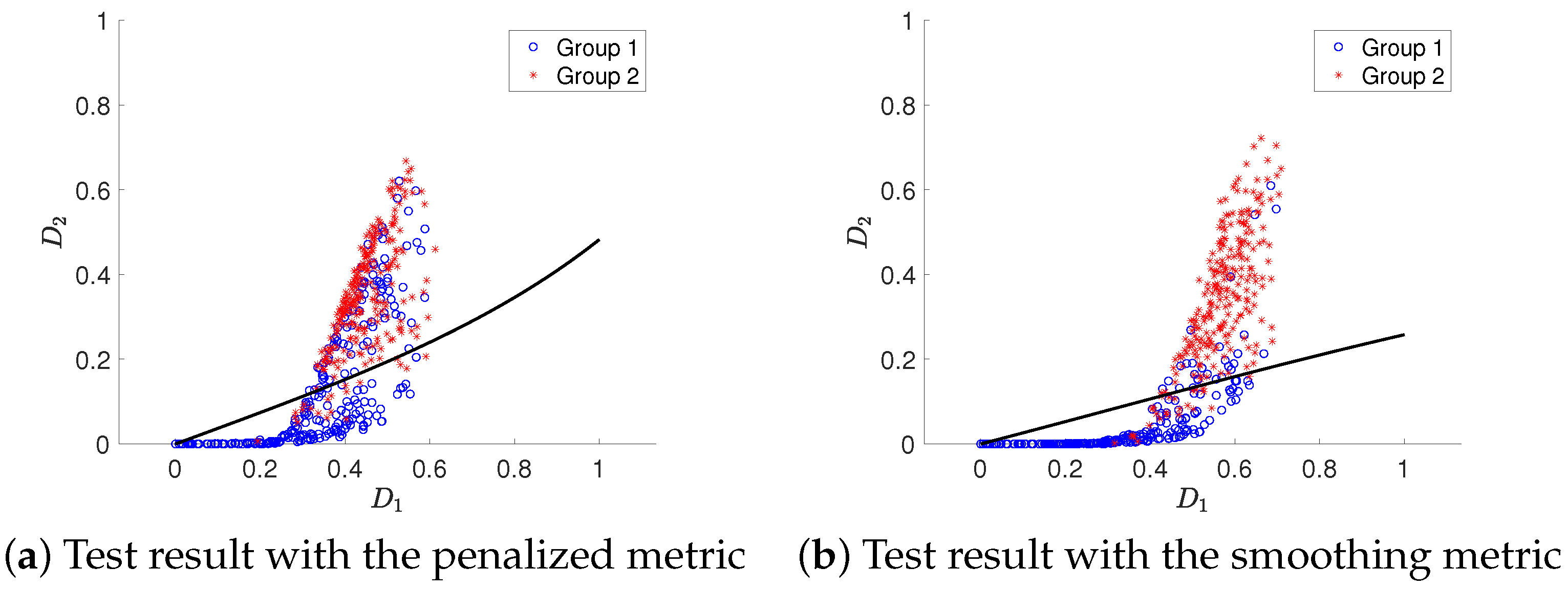
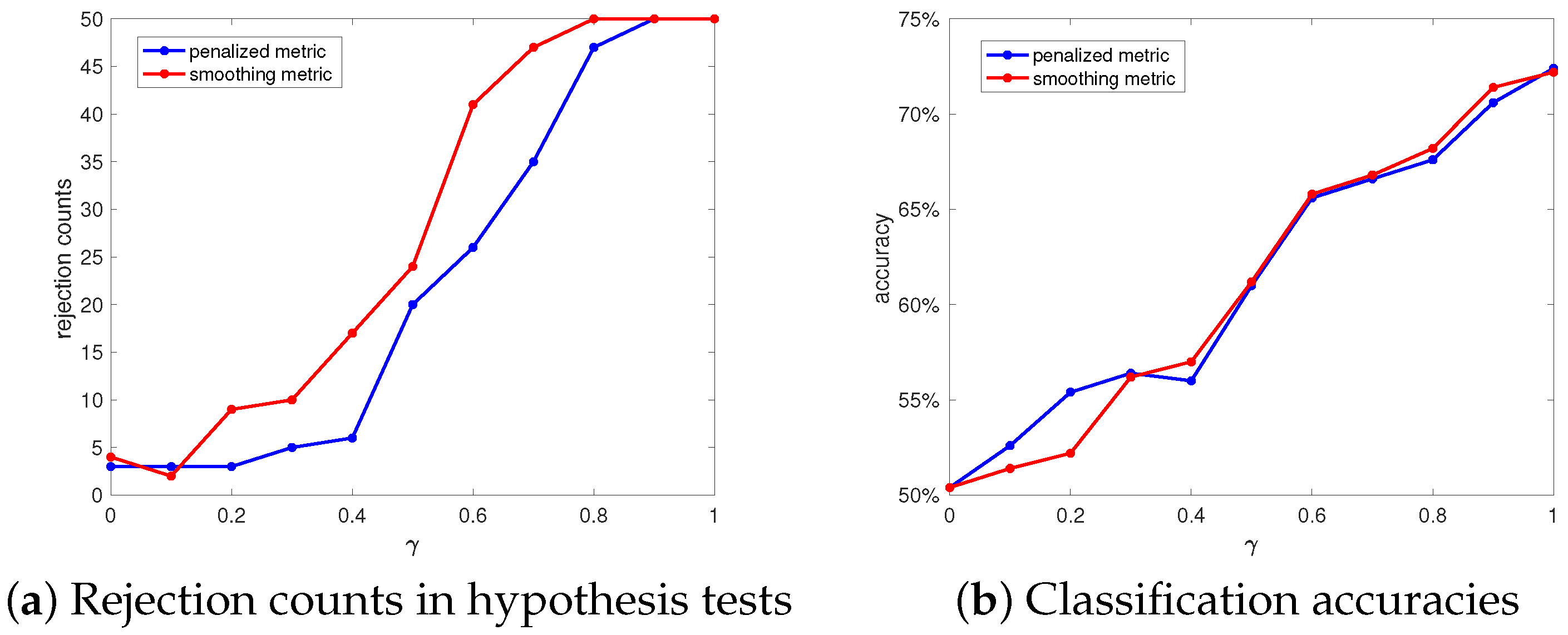
2.4. Depth-Based Hypothesis Testing
- : The two groups of point process realizations follow the same distribution;
- : The two groups of point process realizations do not follow the same distribution.
| Algorithm 1 Hypothesis testing algorithm based on spatial metric depth |
|
3. Simulation Illustrations
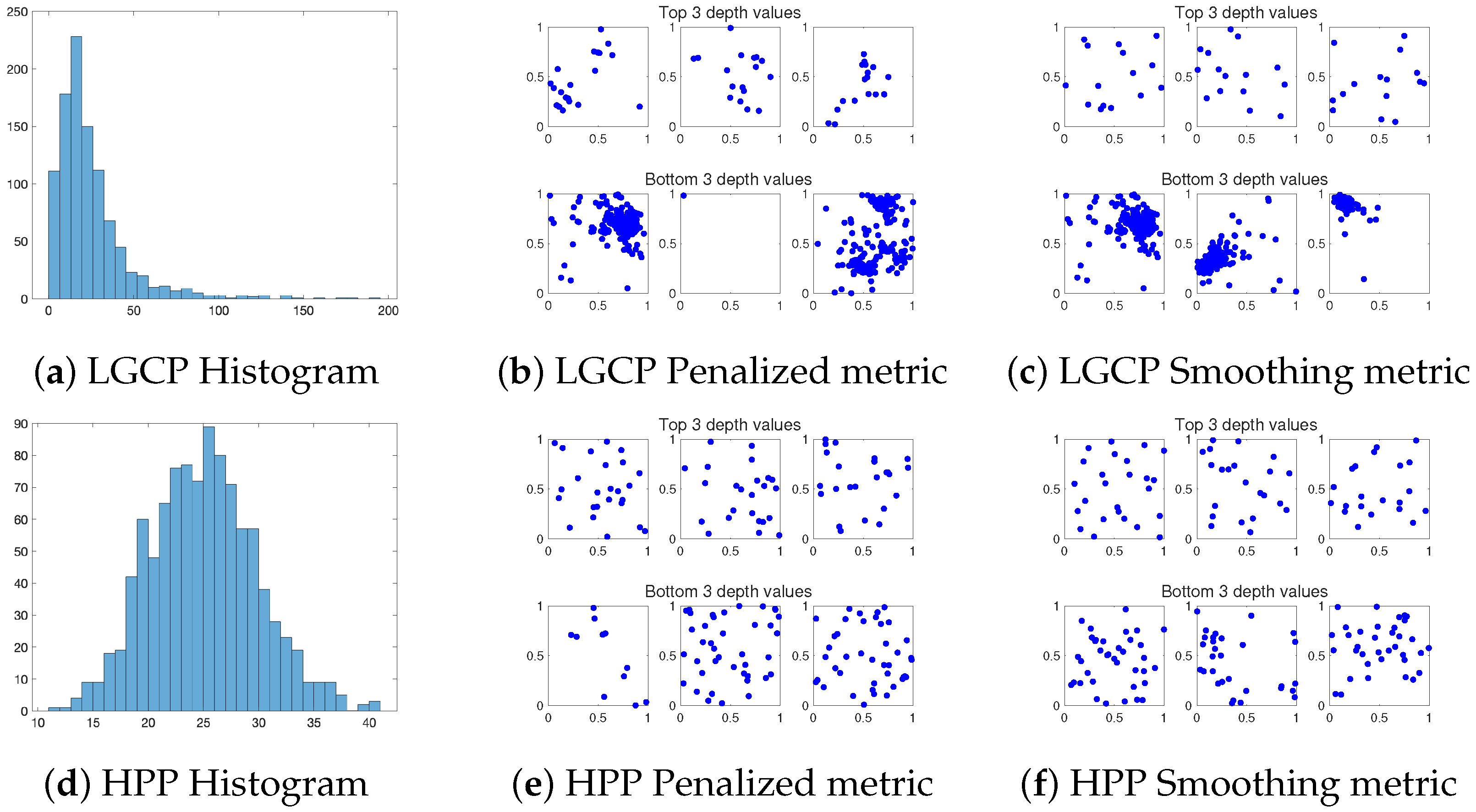
3.1. Example 1: Log Gaussian Cox Process and Homogeneous Poisson Process
- Group 1 (LGCP): 1000 independent LGCP realizations on with the Gaussian random field given above;
- Group 2 (HPP): 1000 independent HPP realizations in with constant intensity function .
- A uniformly random subsample with size 100 from Group 1 vs. another uniformly random subsample with size 100 from Group 1.
- A uniformly random subsample with size 100 from Group 2 vs. another uniformly random subsample with size 100 from Group 2.
- A uniformly random subsample with size 100 from Group 1 vs. a uniformly random subsample with size 100 from Group 2.
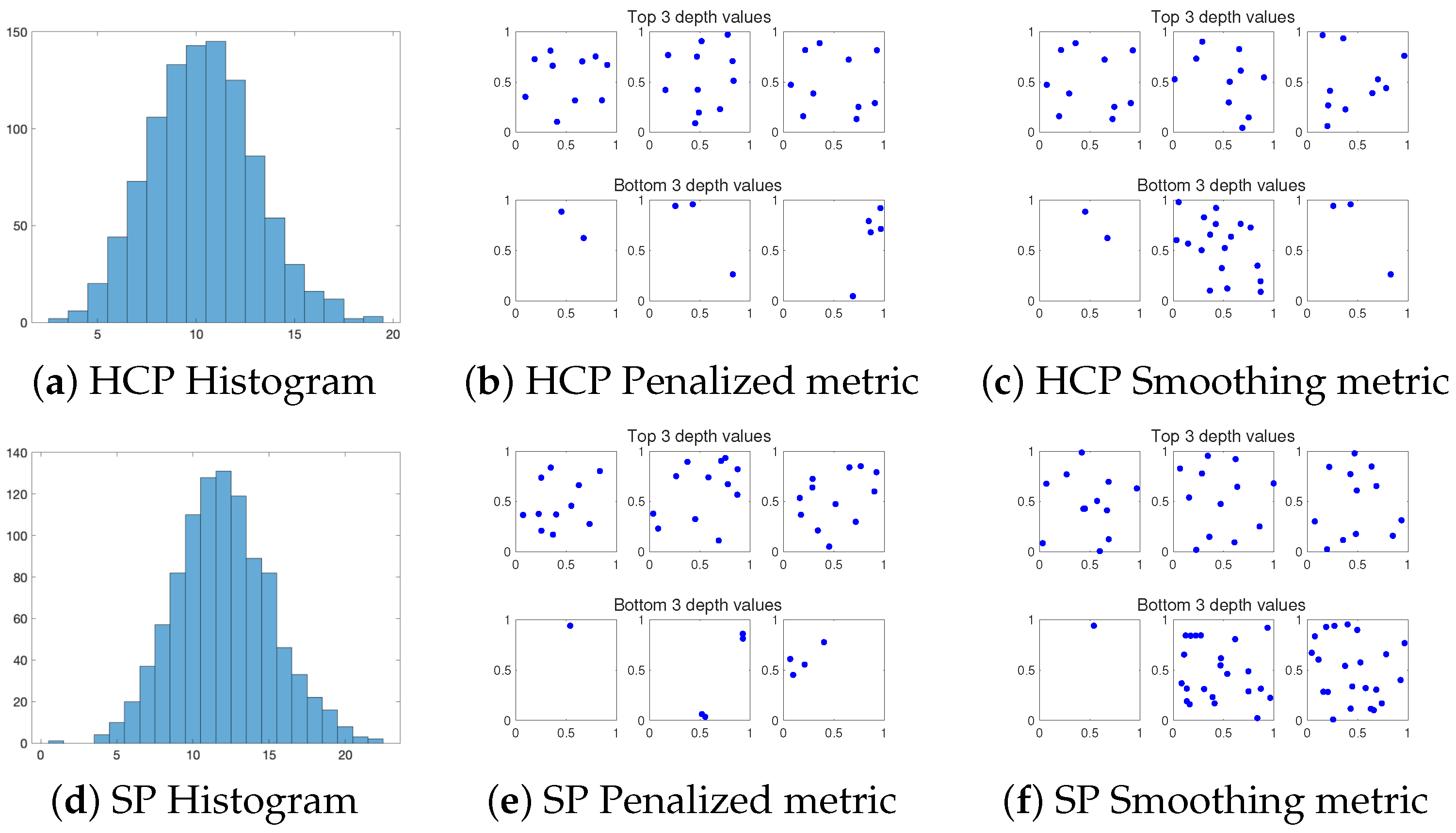
3.2. Example 2: Hard Core Process and Strauss Process
- Group 3 (HCP): 1000 independent Hard core processes in domain with and .
- Group 4 (SP): 1000 independent Strauss processes in domain with , and .
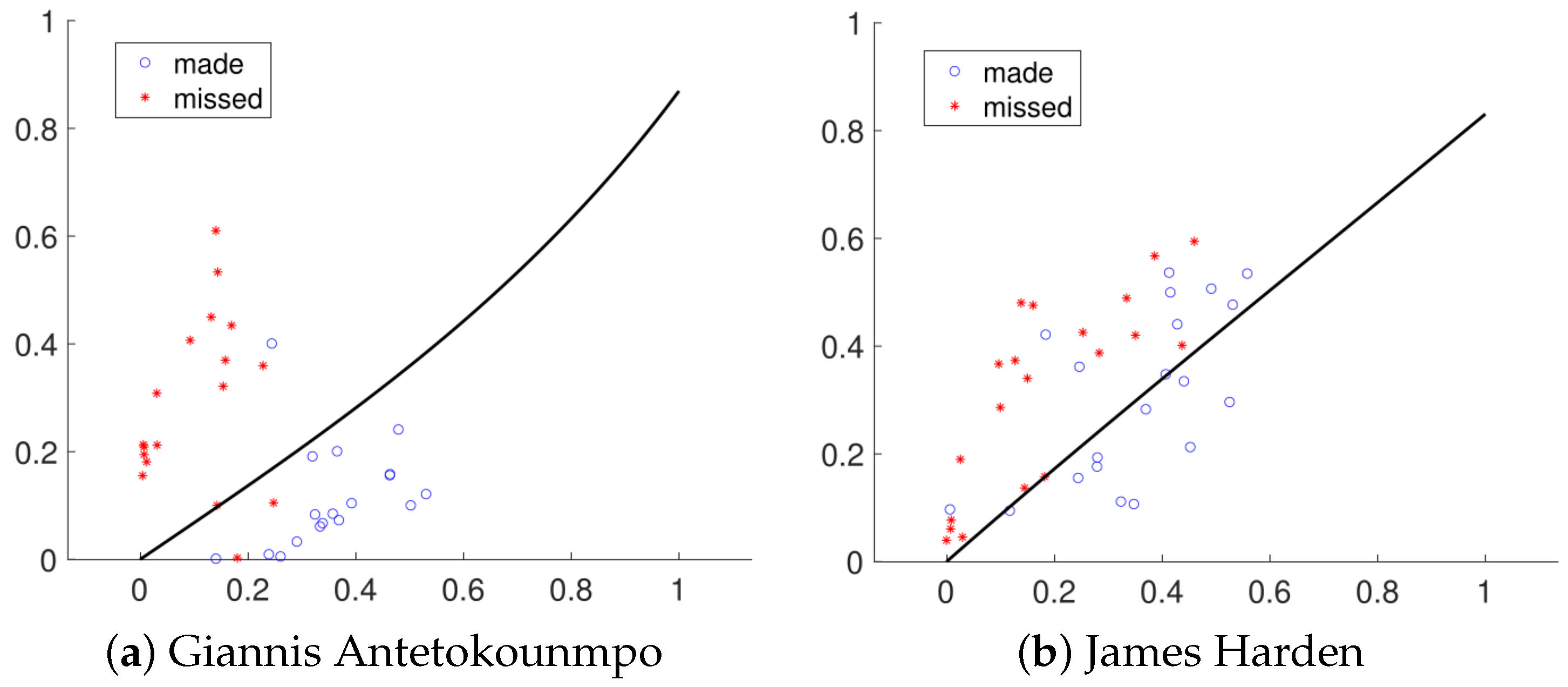
4. Real Data Analysis
5. Summary and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of the Properties of the Penalized Metric
- Nonnegativity: Trivial.
- Zero distance of a point process with itself: Trivial.
- Symmetry: Trivial.
- The Triangle Inequality: We suppose there are three point processes , , with cardinality k, m, n, respectively. Then, based on the fact that the conventional Hausdorff metric is a proper metric, we have
Appendix B. Proof of the Bijection Mapping between Point Process and Its Smoothed Process
- Kernel function in Equation (1) is linearly independent: for any , for .
Appendix C. Proof of Proposition 1
Appendix D. Interpretation of the Properties in Proposition 2
- Fix the cardinality of as a finite integer m; suppose there exists at least one individual point approaching the boundary of the point process domain. If the smoothing metric is applied, then is always finite based on the result in Proposition 1. If the penalized metric is applied, then is finite if the point process domain is bounded. Thus, is always finite for any process in a bounded domain.
- The cardinality of (denoted as m) approaches infinity. In this case, the penalty term of the penalized metric is infinite, which leads to the infinite value of the distance. For the smoothing metric, the value is , which approaches infinity with respect to m.
Appendix E. Proof of Proposition 3
References
- Baddeley, A.; Bárány, I.; Schneider, R. Spatial point processes and their applications. In Stochastic Geometry: Lectures Given at the CIME Summer School Held in Martina Franca, Italy, 13–18 September 2004; Springer: Berlin/Heidelberg, Germany, 2007; pp. 1–75. [Google Scholar]
- Waagepetersen, R.; Guan, Y. Two-step estimation for inhomogeneous spatial point processes. J. R. Stat. Soc. Ser. B Stat. Methodol. 2009, 71, 685–702. [Google Scholar] [CrossRef]
- Talgat, A.; Kishk, M.A.; Alouini, M.S. Nearest neighbor and contact distance distribution for binomial point process on spherical surfaces. IEEE Commun. Lett. 2020, 24, 2659–2663. [Google Scholar] [CrossRef]
- Byers, S.; Raftery, A.E. Nearest-neighbor clutter removal for estimating features in spatial point processes. J. Am. Stat. Assoc. 1998, 93, 577–584. [Google Scholar] [CrossRef]
- Pei, T.; Zhu, A.X.; Zhou, C.; Li, B.; Qin, C. Detecting feature from spatial point processes using Collective Nearest Neighbor. Comput. Environ. Urban Syst. 2009, 33, 435–447. [Google Scholar] [CrossRef]
- Bar-Hen, A.; Emily, M.; Picard, N. Spatial cluster detection using nearest neighbor distance. Spat. Stat. 2015, 14, 400–411. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Evans, R.J.; Kandeepan, S. Nearest neighbor distance distribution in hard-core point processes. IEEE Commun. Lett. 2016, 20, 1872–1875. [Google Scholar] [CrossRef]
- Tukey, J.W. Mathematics and the picturing of data. In Proceedings of the International Congress of Mathematicians, Vancouver, BC, Canada, 21–29 August 1974; Volume 2, pp. 523–531. [Google Scholar]
- Liu, R.Y. On a notion of data depth based on random simplices. Ann. Stat. 1990, 18, 405–414. [Google Scholar] [CrossRef]
- Liu, R.Y.; Singh, K. A quality index based on data depth and multivariate rank tests. J. Am. Stat. Assoc. 1993, 88, 252–260. [Google Scholar]
- Dyckerhoff, R.; Mosler, K.; Koshevoy, G. Zonoid data depth: Theory and computation. In Proceedings of the COMPSTAT; Springer: Berlin/Heidelberg, Germany, 1996; pp. 235–240. [Google Scholar]
- López-Pintado, S.; Romo, J. On the concept of depth for functional data. J. Am. Stat. Assoc. 2009, 104, 718–734. [Google Scholar] [CrossRef]
- Nieto-Reyes, A. On the properties of functional depth. In Recent Advances in Functional Data Analysis and Related Topics; Physica: Heidelberg, Germany, 2011; pp. 239–244. [Google Scholar]
- Dai, X.; Lopez-Pintado, S.; Initiative, A.D.N. Tukey’s depth for object data. J. Am. Stat. Assoc. 2023, 118, 1760–1772. [Google Scholar] [CrossRef]
- Geenens, G.; Nieto-Reyes, A.; Francisci, G. Statistical depth in abstract metric spaces. Stat. Comput. 2023, 33, 46. [Google Scholar] [CrossRef]
- Liu, S.; Wu, W. Generalized mahalanobis depth in point process and its application in neural coding. Ann. Appl. Stat. 2017, 11, 992–1010. [Google Scholar] [CrossRef]
- Qi, K.; Chen, Y.; Wu, W. Dirichlet depths for point process. Electron. J. Stat. 2021, 15, 3574–3610. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, C.; Wu, W. A unified framework on defining depth for point process using function smoothing. Comput. Stat. Data Anal. 2022, 175, 107545. [Google Scholar] [CrossRef]
- Zhou, X.; Ma, Y.; Wu, W. Statistical depth for point process via the isometric log-ratio transformation. Comput. Stat. Data Anal. 2023, 187, 107813. [Google Scholar] [CrossRef]
- Illian, J.; Penttinen, A.; Stoyan, H.; Stoyan, D. Statistical Analysis and Modelling of Spatial Point Patterns; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Li, J.; Cuesta-Albertos, J.A.; Liu, R.Y. DD-classifier: Nonparametric classification procedure based on DD-plot. J. Am. Stat. Assoc. 2012, 107, 737–753. [Google Scholar] [CrossRef]
- Zuo, Y.; Serfling, R. General notions of statistical depth function. Ann. Stat. 2000, 28, 461–482. [Google Scholar]
- Wilcox, R.R. Two-Sample, Bivariate Hypothesis Testing Methods Based on Tukey’s Depth. Multivar. Behav. Res. 2003, 38, 225–246. [Google Scholar] [CrossRef]
- Berman, M. Testing for spatial association between a point process and another stochastic process. J. R. Stat. Soc. Ser. C Appl. Stat. 1986, 35, 54–62. [Google Scholar] [CrossRef]
- Schoenberg, F.P. Testing separability in spatial-temporal marked point processes. Biometrics 2004, 60, 471–481. [Google Scholar] [CrossRef] [PubMed]
- Guan, Y. A KPSS test for stationarity for spatial point processes. Biometrics 2008, 64, 800–806. [Google Scholar] [CrossRef] [PubMed]
- Fuentes-Santos, I.; González-Manteiga, W.; Mateu, J. A nonparametric test for the comparison of first-order structures of spatial point processes. Spat. Stat. 2017, 22, 240–260. [Google Scholar] [CrossRef]
- Liu, R.Y.; Parelius, J.M.; Singh, K. Multivariate analysis by data depth: Descriptive statistics, graphics and inference. Ann. Stat. 1999, 27, 783–858. [Google Scholar] [CrossRef]
- Lange, T.; Mosler, K.; Mozharovskyi, P. Fast nonparametric classification based on data depth. Stat. Pap. 2014, 55, 49–69. [Google Scholar] [CrossRef]
- Zhou, X.; Wu, W. Depth-Based Statistical Inferences in the Spike Train Space. arXiv 2023, arXiv:2311.13676. [Google Scholar]
- Daley, D.J.; Vere-Jones, D. An Introduction to the Theory of Point Processes: Volume I: Elementary Theory and Methods; Springer: New York, NY, USA, 2003. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Wu, W. Statistical Depth in Spatial Point Process. Mathematics 2024, 12, 595. https://doi.org/10.3390/math12040595
Zhou X, Wu W. Statistical Depth in Spatial Point Process. Mathematics. 2024; 12(4):595. https://doi.org/10.3390/math12040595
Chicago/Turabian StyleZhou, Xinyu, and Wei Wu. 2024. "Statistical Depth in Spatial Point Process" Mathematics 12, no. 4: 595. https://doi.org/10.3390/math12040595





