Novel Proportional–Integral–Derivative Control Framework on Continuous-Time Positive Systems Using Linear Programming
Abstract
:1. Introduction
2. Preliminaries
- (i)
- The matrix A is Hurwitz;
- (ii)
- There exists a vector such that .
3. Main Results
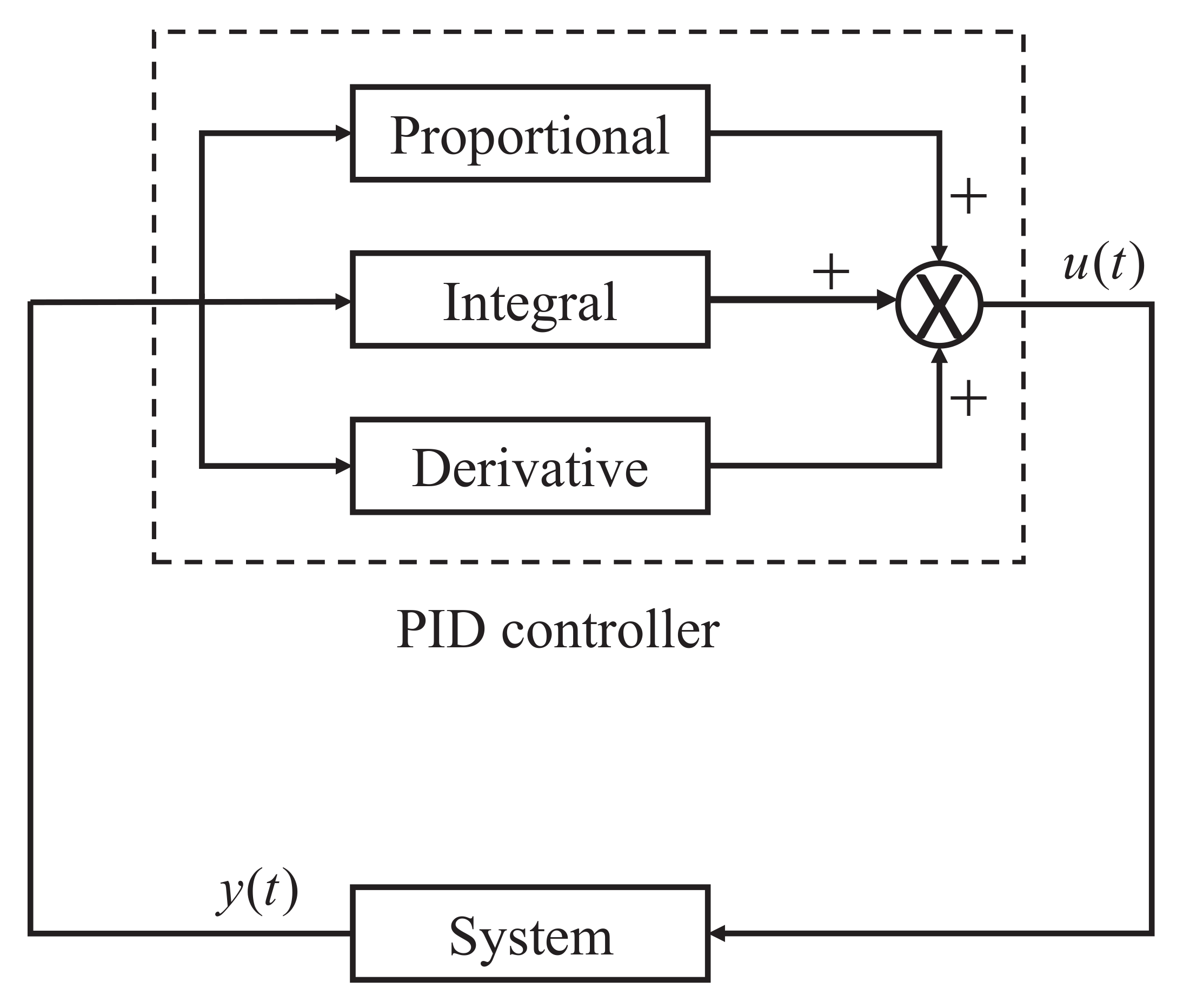
3.1. PID Control
| Algorithm 1 Parameter selection and matrix invertibility. |
| Input: System matrices , and C; Parameters , and ; Output: ;
|
3.2. Observer-Based PID Control
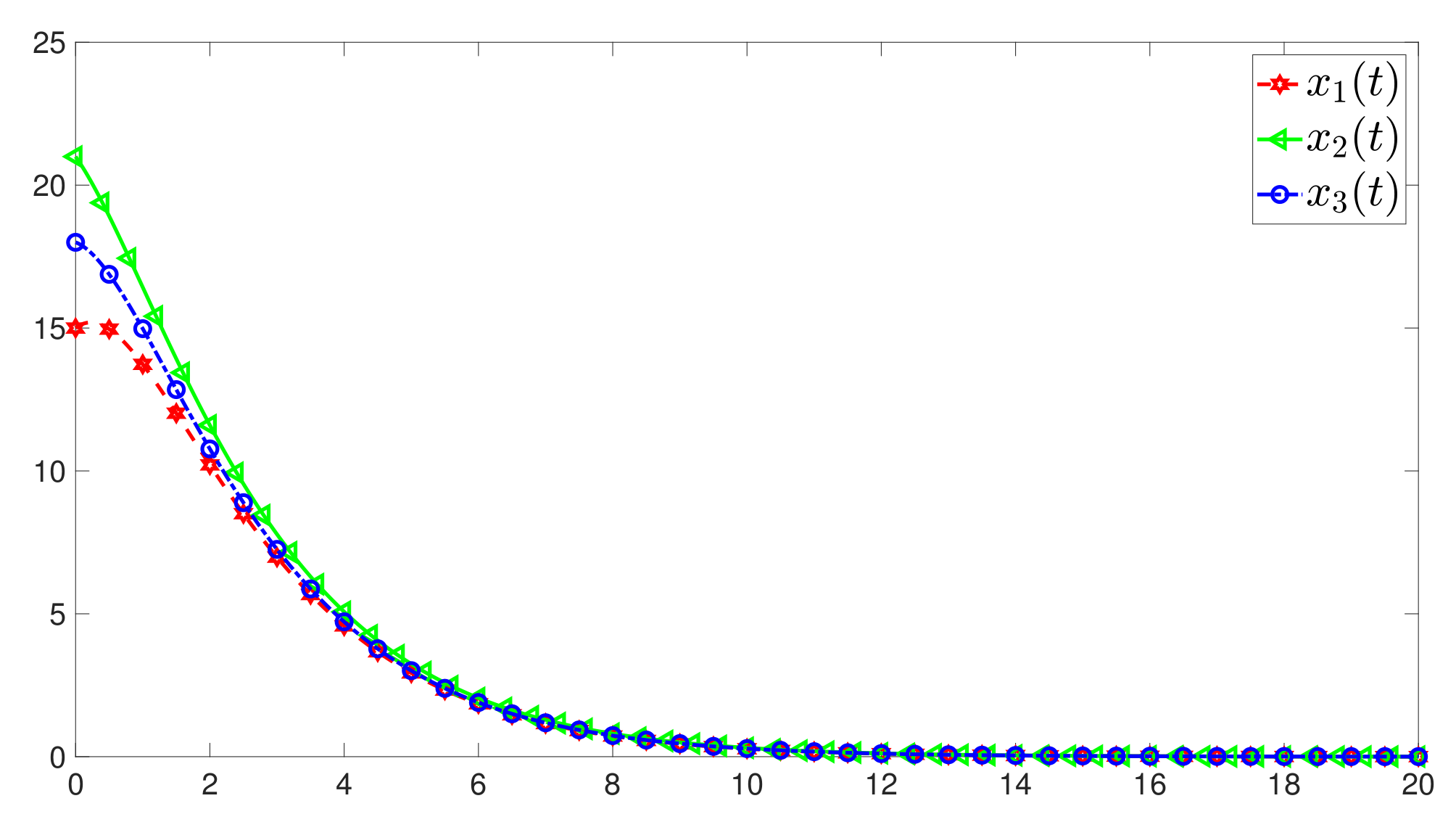
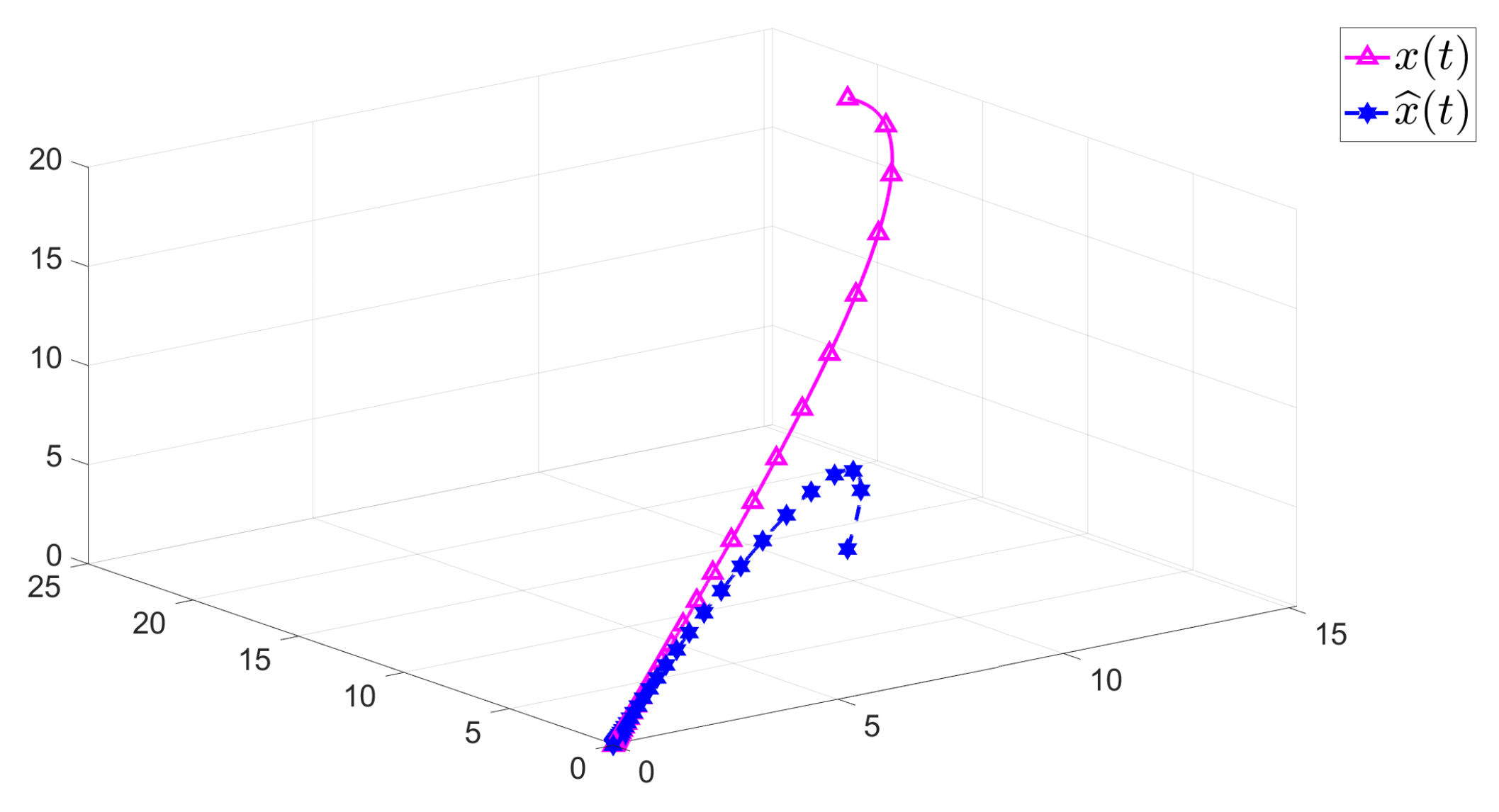
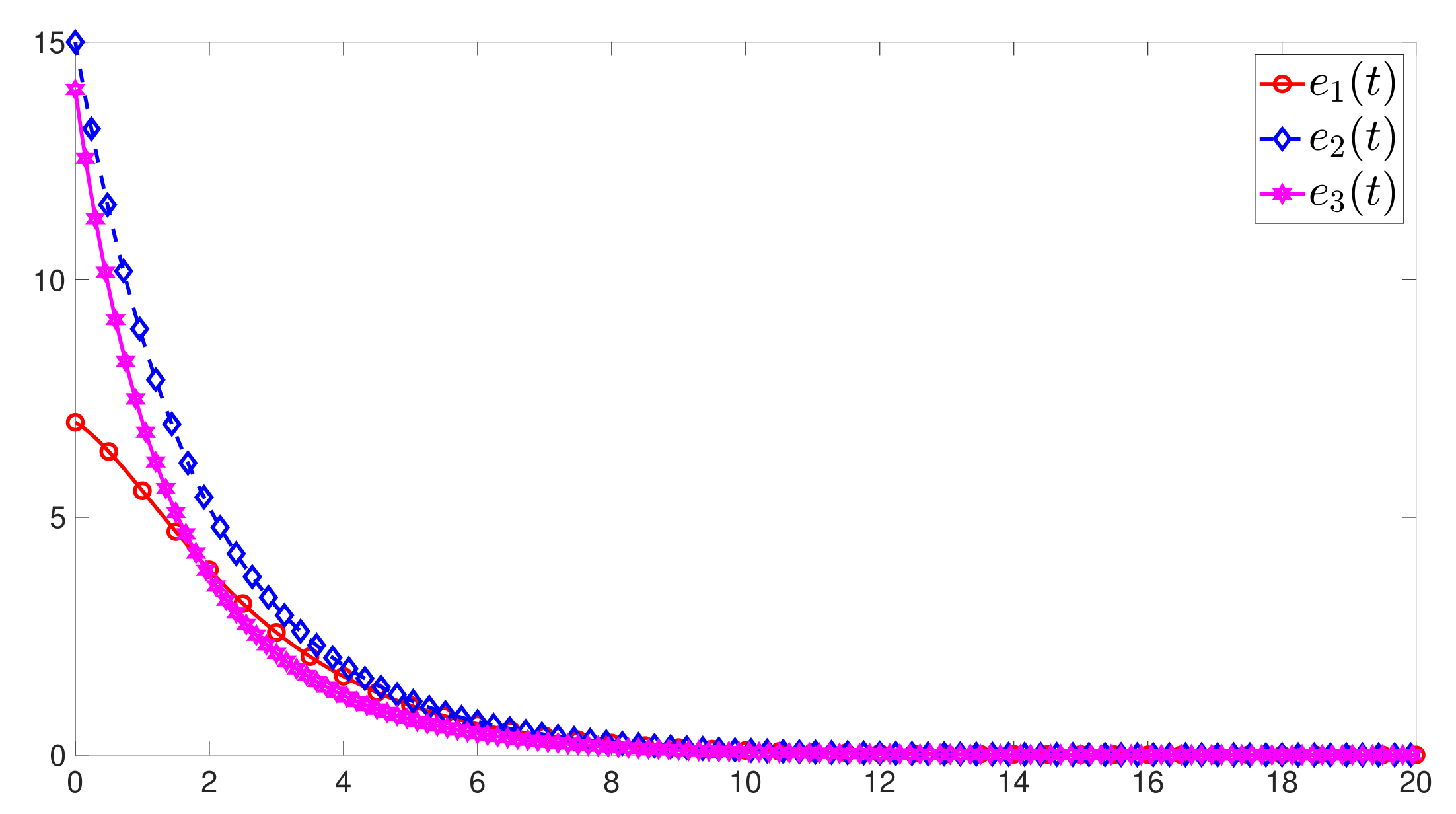
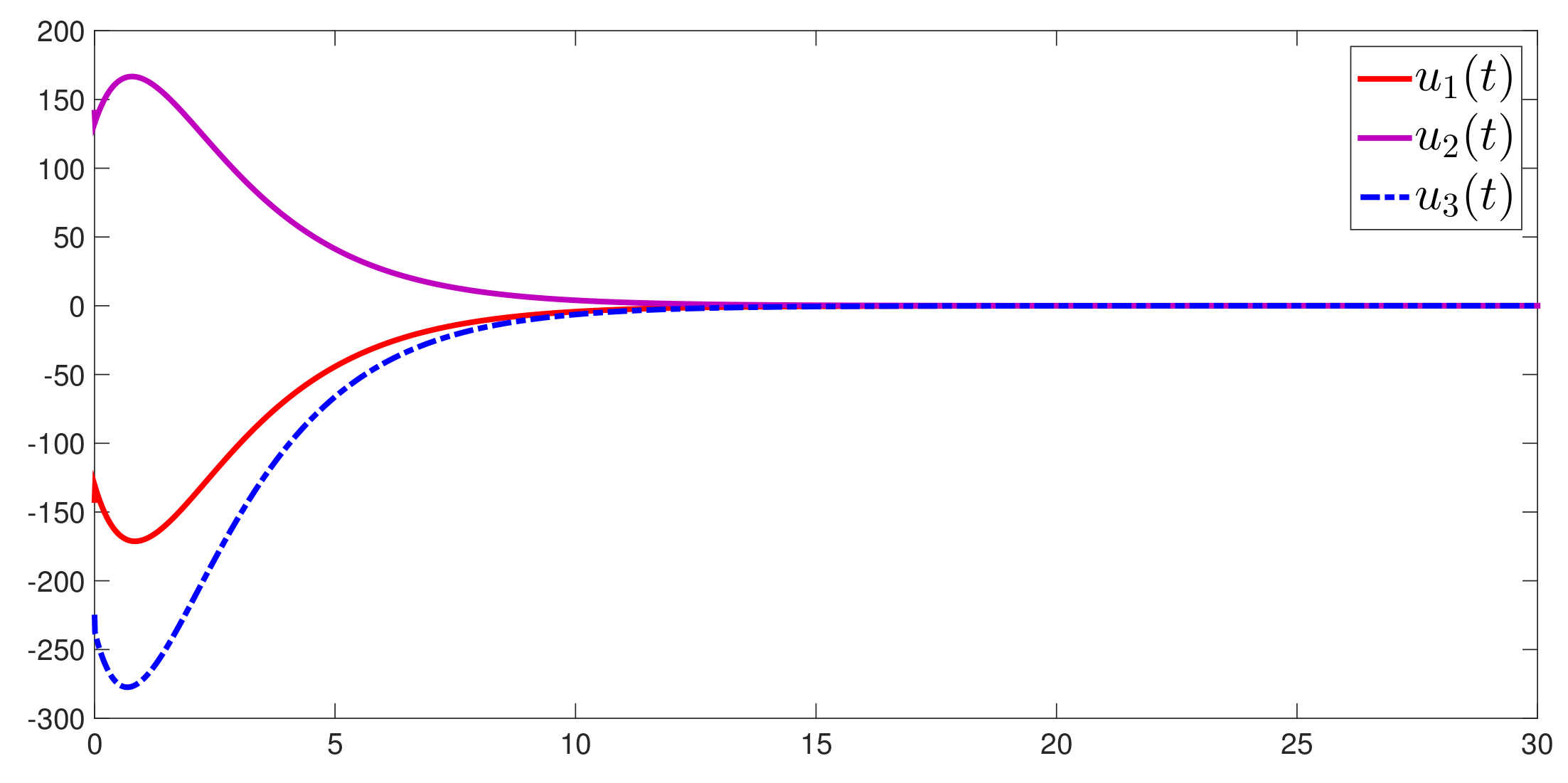
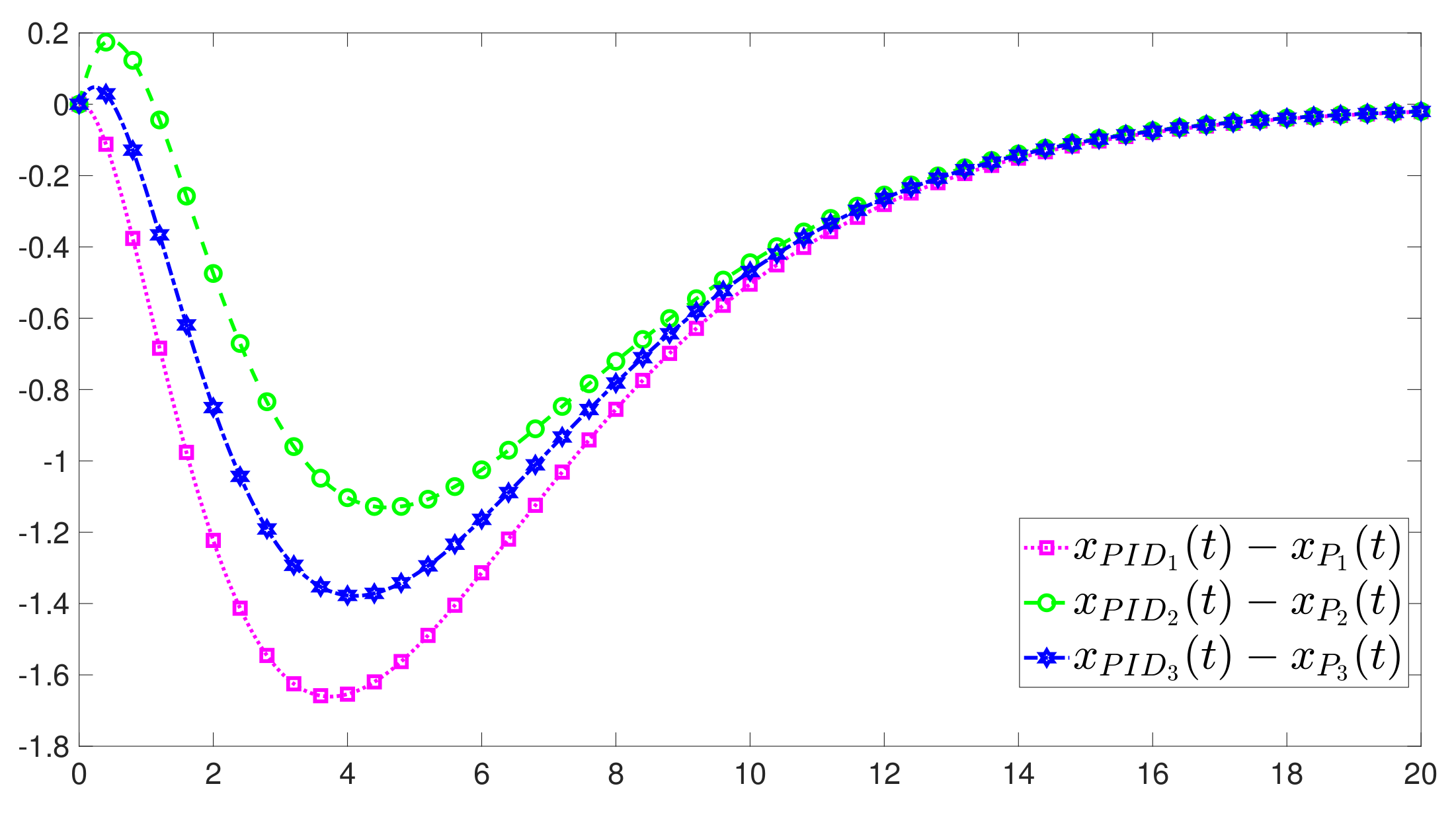
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, F.; Wang, Q.G.; Lee, T.H. On the design of multivariable PID controllers via LMI approach. Automatica 2002, 38, 517–526. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, L.; Zhao, Z.; Bai, X. H∞ fuzzy PID control for discrete time-delayed TS fuzzy systems. Neurocomputing 2019, 332, 91–99. [Google Scholar] [CrossRef]
- Tharanidharan, V.; Sakthivel, R.; Ren, Y.; Anthoni, S.M. Robust finite-time PID control for discrete-time large-scale interconnected uncertain system with discrete-delay. Math. Comput. Simul. 2022, 192, 370–383. [Google Scholar] [CrossRef]
- Li, Y.; Ang, K.H.; Chong, G.C. PID control system analysis and design. IEEE Control Syst. Magaz. 2006, 26, 32–41. [Google Scholar]
- Zhao, D.; Wang, Z.; Wei, G.; Han, Q.L. A dynamic event-triggered approach to observer-based PID security control subject to deception attacks. Automatica 2020, 120, 109128. [Google Scholar] [CrossRef]
- Luenberger, D. An introduction to observers. IEEE Trans. Autom. Control 1971, 16, 596–602. [Google Scholar] [CrossRef]
- Yao, L.; Wen, H.K. Design of observer based adaptive PID controller for nonlinear systems. Int. J. Innov. Comput. Inf. Control. 2013, 9, 667–677. [Google Scholar]
- Wen, P.; Dong, H.; Huo, F.; Li, J.; Lu, X. Observer-based PID control for actuator-saturated systems under binary encoding scheme. Neurocomputing 2022, 499, 54–62. [Google Scholar] [CrossRef]
- Farina, L.; Rinaldi, S. Positive Linear Systems: Theory and Applications; John Wiley Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Fornasini, E.; Valcher, M.E. Linear copositive Lyapunov functions for continuous-time positive switched systems. IEEE Trans. Autom. Control 2010, 55, 1933–1937. [Google Scholar] [CrossRef]
- Briat, C. Robust stability and stabilization of uncertain linear positive systems via integral linear constraints: L1-gain and L∞-gain characterization. Int. J. Robust Nonlinear Control 2013, 23, 1932–1954. [Google Scholar] [CrossRef]
- Rami, M.A.; Tadeo, F.; Helmke, U. Positive observers for linear positive systems, and their implications. Int. J. Control 2011, 84, 716–725. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Co-ordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Sun, Y.; Tian, Y.; Xie, X.J. Stabilization of positive switched linear systems and its application in consensus of multiagent systems. IEEE Trans. Autom. Control 2017, 62, 6608–6613. [Google Scholar] [CrossRef]
- Van Den Hof, J.M. Positive linear observers for linear compartmental systems. SIAM J. Control Optim. 1998, 36, 590–608. [Google Scholar] [CrossRef]
- Efimov, D.; Raïssi, T.; Zolghadri, A. Control of nonlinear and LPV systems: Interval observer-based framework. IEEE Trans. Autom. Control 2013, 58, 773–778. [Google Scholar] [CrossRef]
- Mazenc, F.; Bernard, O. Interval observers for linear time-invariant systems with disturbances. Automatica 2011, 47, 140–147. [Google Scholar] [CrossRef]
- Rami, M.A.; Helmke, U.; Tadeo, F. Positive observation problem for linear time-delay positive systems. In Proceedings of the 2007 Mediterranean Conference on Control & Automation, Athens, Greece, 27–29 June 2007; pp. 1–6. [Google Scholar]
- Rami, M.A.; Tadeo, F. Positive observation problem for linear discrete positive systems. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 4729–4733. [Google Scholar]
- Li, S.; Xiang, Z.; Lin, H.; Karimi, H.R. State estimation on positive Markovian jump systems with time-varying delay and uncertain transition probabilities. Inf. Sci. 2016, 369, 251–266. [Google Scholar] [CrossRef]
- Su, H.; Wu, H.; Lam, J. Positive edge-consensus for nodal networks via output feedback. IEEE Trans. Autom. Control 2018, 64, 1244–1249. [Google Scholar] [CrossRef]
- Zhu, S.; Han, Q.L.; Zhang, C. l1-gain performance analysis and positive filter design for positive discrete-time Markov jump linear systems: A linear programming approach. Automatica 2014, 50, 2098–2107. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, J.; Huang, M.; Tan, X. Disturbance observer-based event-triggered control of switched positive systems. IEEE Trans. Circuits Syst. II Express Briefs 2023. [Google Scholar] [CrossRef]
- Paulusová, J.; Vesely, V.; Paulus, M.; Robust, P.I. controller design for positive systems. In Proceedings of the 2020 Cybernetics & Informatics (K&I), Velke Karlovice, Czech Republic, 29 January–1 February 2020; pp. 1–4. [Google Scholar]
- Liu, J.J.; Zhang, M.; Lam, J.; Du, B.; Kwok, K.W. PD control of positive interval continuous-time systems with time-varying delay. Inf. Sci. 2021, 580, 371–384. [Google Scholar] [CrossRef]
- Liu, J.J.; Yang, N.; Kwok, K.W.; Lam, J. Proportional-derivative controller design of continuous-time positive linear systems. Int. J. Robust Nonlinear Control 2022, 32, 9497–9511. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, J.; Jia, X.; Wu, D. Linear programming-based proportional-integral-derivative control of positive systems. IET Control Theory Appl. 2023, 17, 1342–1353. [Google Scholar] [CrossRef]
- Zaidi, I.; Chaabane, M.; Tadeo, F.; Benzaouia, A. Static state-feedback controller and observer design for interval positive systems with time delay. IEEE Trans. Circuits Syst. II Express Briefs 2014, 62, 506–510. [Google Scholar] [CrossRef]
- Pang, B.; Zhang, Q. Stability analysis and observer-based controllers design for T-S fuzzy positive systems. Neurocomputing 2018, 275, 1468–1477. [Google Scholar] [CrossRef]
- Ren, Y.; Sun, G.; Feng, Z. Observer-based stabilization for switched positive system with mode-dependent average dwell time. ISA Trans. 2017, 70, 37–45. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Zhou, X.; Lin, F.; Yang, Y.; Zhang, J. Novel Proportional–Integral–Derivative Control Framework on Continuous-Time Positive Systems Using Linear Programming. Mathematics 2024, 12, 617. https://doi.org/10.3390/math12040617
Li Q, Zhou X, Lin F, Yang Y, Zhang J. Novel Proportional–Integral–Derivative Control Framework on Continuous-Time Positive Systems Using Linear Programming. Mathematics. 2024; 12(4):617. https://doi.org/10.3390/math12040617
Chicago/Turabian StyleLi, Qingbo, Xiaoyue Zhou, Fengyu Lin, Yahao Yang, and Junfeng Zhang. 2024. "Novel Proportional–Integral–Derivative Control Framework on Continuous-Time Positive Systems Using Linear Programming" Mathematics 12, no. 4: 617. https://doi.org/10.3390/math12040617




