Stochastic Synchronization of Impulsive Reaction–Diffusion BAM Neural Networks at a Fixed and Predetermined Time
Abstract
:1. Introduction
2. Preliminaries
- 1.
- holds for any non-zero initial condition , where is an ST function;
- 2.
- For any and , there exists a such that for all for any case where ;
- 3.
- for any , where is the expected valued of and is a positive constant.
- 1.
- ,
- 2.
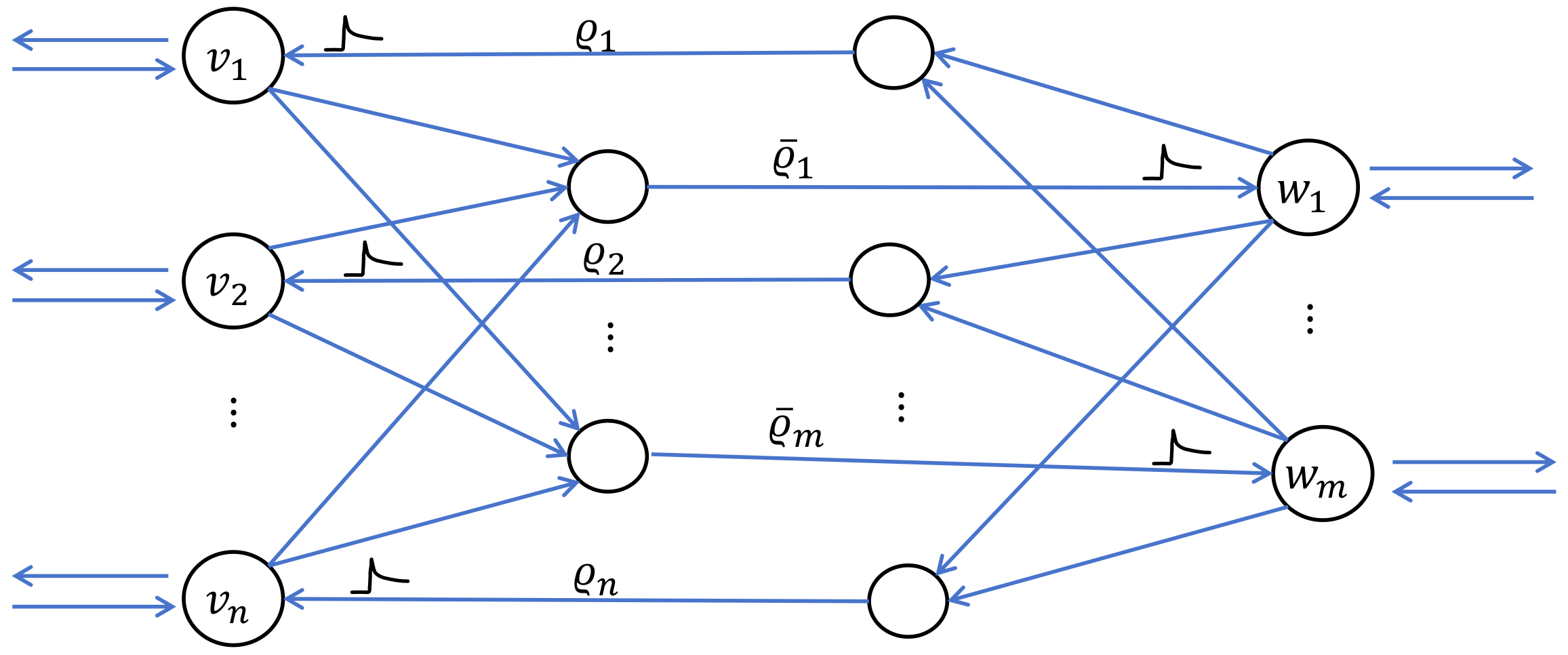
3. Main Results
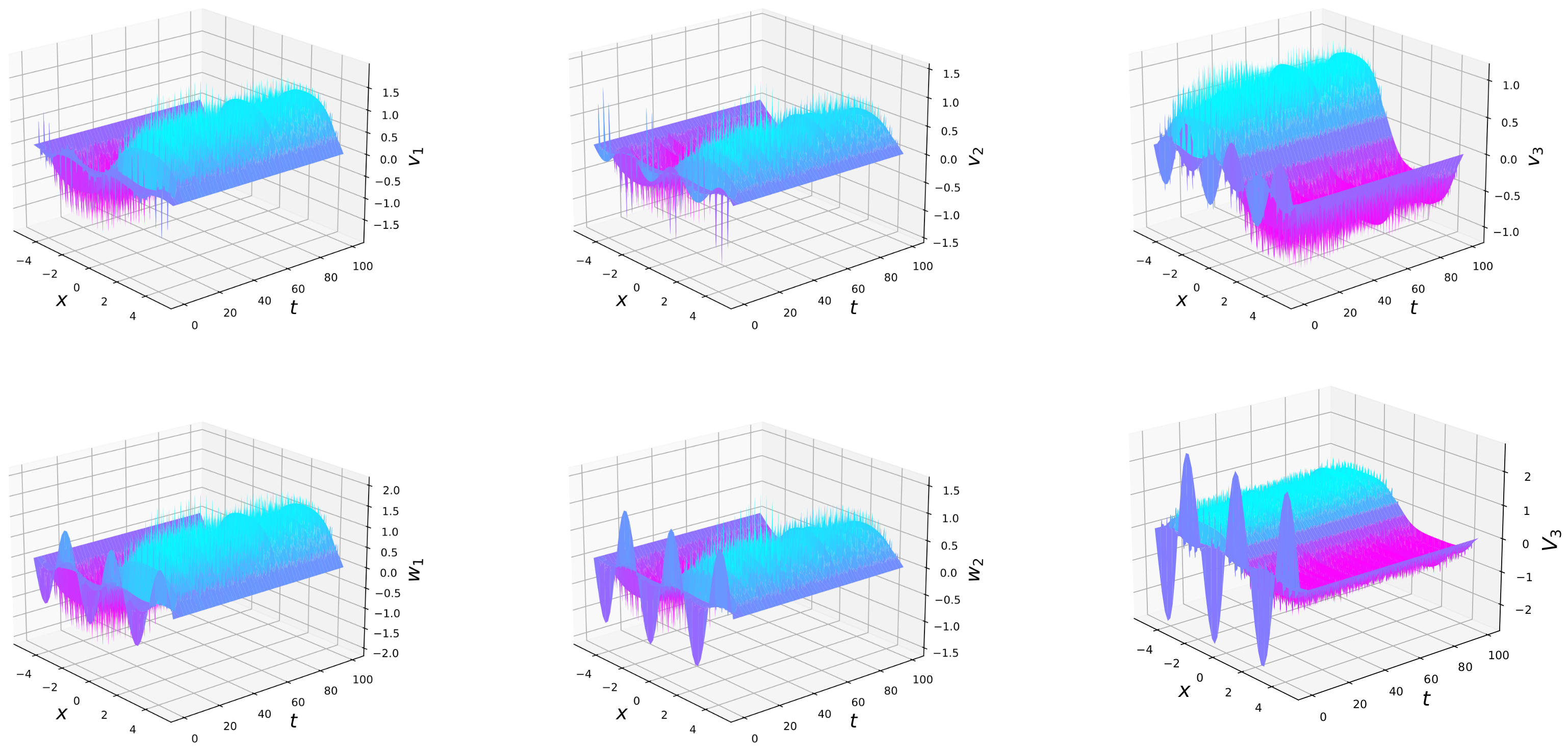
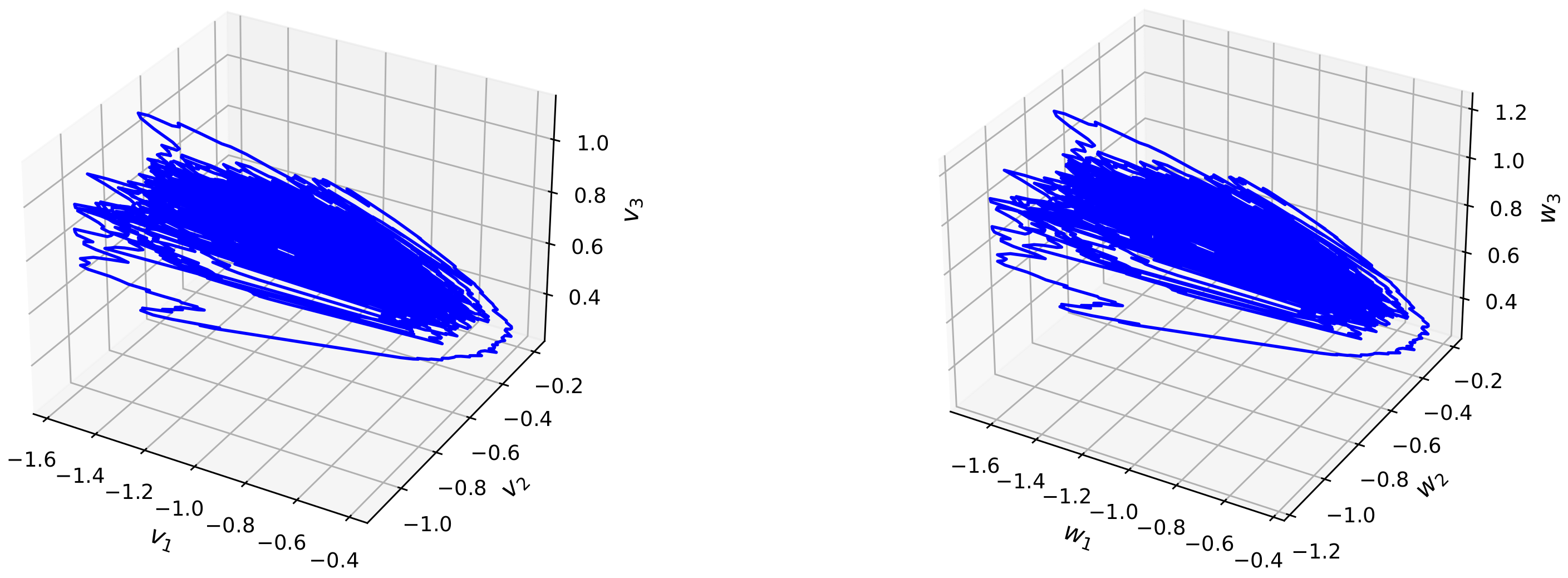
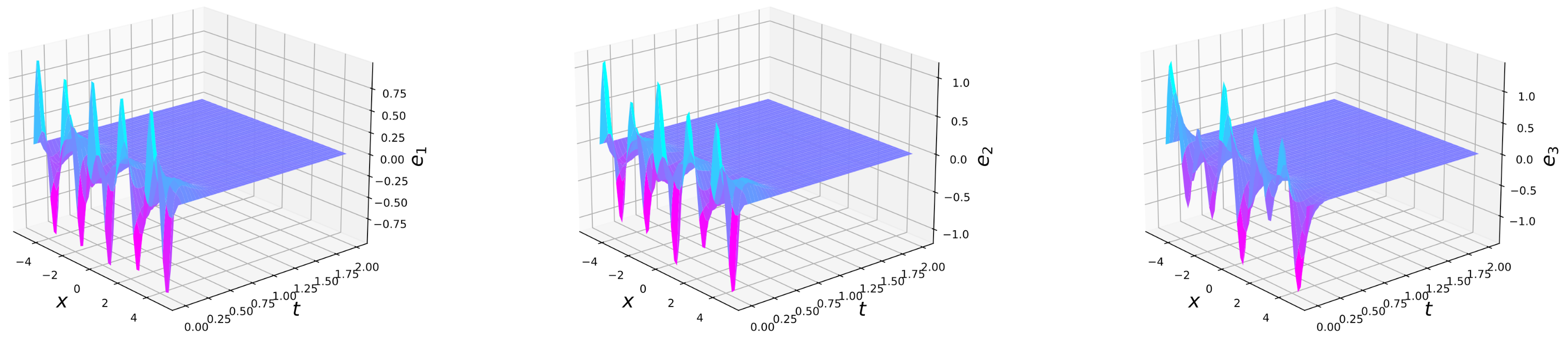
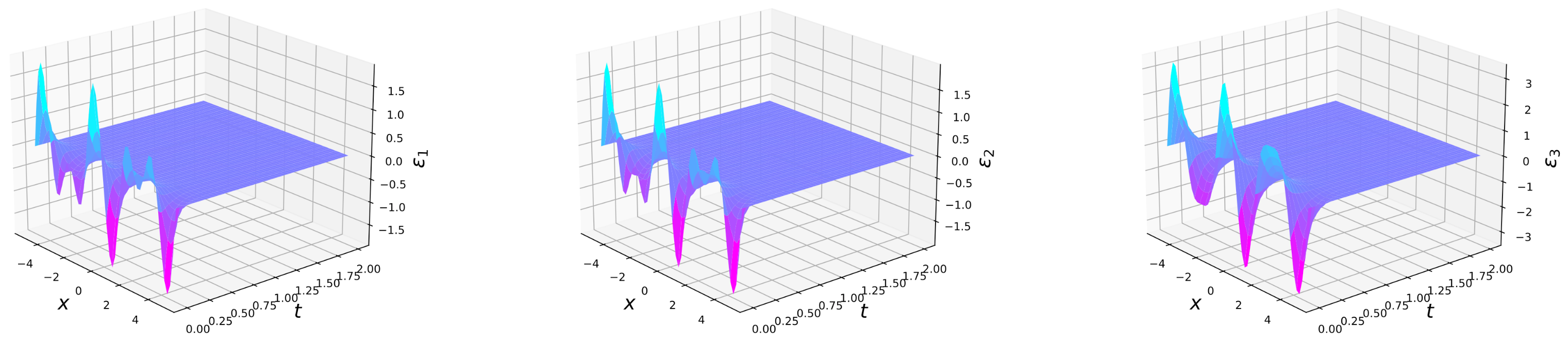
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kosko, B. Adaptive bi-directional associative memories. Appl. Opt. 1987, 26, 4947–4960. [Google Scholar] [CrossRef]
- Kosko, B. Bi-directional associative memories. IEEE Trans. Syst. Man Cybern. 1988, 18, 49–60. [Google Scholar] [CrossRef]
- Hasan, S.M.R.; Siong, N.K. A VLSI BAM neural network chip for pattern recognition applications. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 164–168. [Google Scholar]
- Wang, L.; Jiang, M.; Liu, R.; Tang, X. Comparison BAM and discrete Hopfield networks with CPN for processing of noisy data. In Proceedings of the 2008 9th International Conference on Signal Processing, Beijing, China, 26–29 October 2008; pp. 1708–1711. [Google Scholar]
- Wang, W.; Wang, X.; Luo, X. Finit-time projective synchronization of memristor-based BAM neural networks and applications in image encryption. IEEE Access 2018, 6, 56457–56476. [Google Scholar] [CrossRef]
- Li, S.; Li, H.; Wang, J. A new bi-directional associative memory model based on BAM networks. Neurocomputing 2009, 72, 2408–2414. [Google Scholar]
- Demirkaya, O.; Asyali, M.; Sahoo, P. Image Processing with MATLAB: Applications in Medicine and Biology; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Song, Q.; Cao, J. Global exponential robust stability of cohen-grossberg neural network with time-varying delays and reaction-diffusion terms. J. Frankl. Inst. 2006, 343, 705–719. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J. Global exponential synchronization of delayed BAM neural networks with reaction-diffusion terms and the Neumann boundary conditions. Bound. Value Probl. 2012, 2012, 2. [Google Scholar] [CrossRef]
- Zhang, H.; Pal, N.R. Distributed adaptive tracking synchronization coupled reaction-diffusion neural network. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1462–1475. [Google Scholar] [CrossRef]
- Mahemuti, R.; Halik, A.; Abdurahman, A. General decay synchronization of delayed bam neural networks with reaction-diffusion terms. Adv. Differ. Equ. 2020, 2020, 457. [Google Scholar] [CrossRef]
- Sun, Y.; Hu, C.; Yu, J.; Shi, T. Synchronization of fractional-order reaction-diffusion neural networks via mixed boundary control. Appl. Math. Comput. 2023, 450, 127982. [Google Scholar] [CrossRef]
- Li, X.; Song, S. Research on synchronization of chaotic delayed neural networks with stochastic perturbation using impulsive control method. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 3892–3900. [Google Scholar] [CrossRef]
- Rogers, L.C.G. Arbitrage with fractional Brownian motion. Math. Financ. 1997, 7, 95–105. [Google Scholar] [CrossRef]
- Comte, F.; Renault, E. Long memory continuous time models. J. Econom. 1996, 73, 101–149. [Google Scholar] [CrossRef]
- Torres, J.J.; Muñoz, M.A.; Cortés, J.M.; Mejías, J.F. Special issue on emergent effects in stochastic neural networks with application to learning and information processing. Neurocomputing 2021, 461, 632–634. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Wang, Y.; Lombardi, F.; Han, J. A Survey of Stochastic Computing Neural Networks for Machine Learning Applications. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 2809–2824. [Google Scholar] [CrossRef]
- Wang, X.; Cao, J.; Zhou, X.; Liu, Y.; Yan, Y.; Wang, J. A novel framework of prescribed time/fixed time/finite time stochastic synchronization control of neural networks and its application in image encryption. Neural Netw. 2023, 165, 755–773. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Liu, H.; Zhang, B.; Wu, G. Extraction of if-then rules from trained neural network and its application to earthquake prediction. In Proceedings of the Third IEEE International Conference on Cognitive Informatics, Victoria, BC, Canada, 17 August 2004; pp. 109–115. [Google Scholar]
- Hu, B.; Guan, Z.; Chen, G.; Lewis, F.L. Multistability of delayed hybrid impulsive neural networks with application to associative memories. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1537–1551. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Li, C.; Ouyang, D.; Nguang, S.K. Impulsive synchronization of unbounded delayed inertial neural networks with actuator saturation and sampled-data control and its application to image encryption. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1460–1473. [Google Scholar] [CrossRef] [PubMed]
- Hertz, J.; Krogh, A.; Palmer, R.G. Introduction to the Theory of Neural Computation; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Sader, M.; Abdurahman, A.; Jiang, H. General decay synchronization of delayed BAM neural networks via nonlinear feedback control. Appl. Math. Comput. 2018, 337, 302–314. [Google Scholar] [CrossRef]
- Hu, D.; Tan, J.; Shi, K.; Ding, K. Switching synchronization of reaction-diffusion neural networks with time-varying delays. Chaos Solitons Fractals 2022, 155, 111766. [Google Scholar] [CrossRef]
- Wei, T.; Lin, P.; Zhu, Q.; Wang, L.; Wang, Y. Dynamical behavior of nonautonomous stochastic reaction-diffusion neural-network models. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1575–1580. [Google Scholar] [CrossRef]
- Wei, T.; Xie, X.; Li, X. Input-to-state stability of delayed reaction-diffusion neural networks with multiple impulses. AIMS Math. 2020, 6, 5786–5860. [Google Scholar] [CrossRef]
- Chen, W.; Ren, G.; Yu, Y.; Yuan, X. Quasi-synchronization of heterogeneous stochastic coupled reaction-diffusion neural networks with mixed time-varying delays via boundary control. J. Franklin Inst. 2023, 360, 10080–10099. [Google Scholar] [CrossRef]
- Velmurugan, G.; Rakkiyappan, R.; Cao, J. Finite-time synchronization of fractional-order memristor-based neural networks with time delays. Neural Netw. 2016, 73, 36–46. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, L.; Peng, H.; Xiao, J.; Yang, Y.; Zheng, M.; Zhao, H. Finite-time synchronization for memristor-based BAM neural 343 networks with stochastic perturbations and time-varying delays. Int. J. Robust Nonlinear Control 2018, 28, 5118–5139. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Wu, X.; Huang, T.; Wang, Q. Finite-time passivity and synchronization of coupled reaction–diffusion neural networks with multiple weights. IEEE Trans. Cybern. 2019, 49, 3385–3397. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, W.; Wu, Y.; Li, W. Finite-time synchronization of fractional-order fuzzy time-varying coupled neural networks subject to reaction–diffusion. IEEE Trans. Fuzzy Syst. 2023, 31, 3423–3432. [Google Scholar] [CrossRef]
- Wan, Y.; Cao, J.; Wen, G. Robust fixed-time synchronization of delayed Cohen-Grossberg neural networks. Neural Netw. 2016, 73, 86–94. [Google Scholar] [CrossRef]
- You, J.; Abdurahman, A.; Sadik, H. Fixed/Predefined-Time synchronization of complex-valued stochastic BAM neural networks with stabilizing and destabilizing impulse. Mathematics 2022, 10, 4384. [Google Scholar] [CrossRef]
- Lin, L.; Wang, Q.; He, B.; Chen, Y.; Peng, X.; Mei, R. Adaptive Predefined-Time Synchronization of Two Different Fractional-Order Chaotic Systems With Time-Delay. IEEE Access 2021, 9, 31908–31920. [Google Scholar] [CrossRef]
- Wu, J.; Wang, X.; Liu, W. Smooth control steering global predefined-time synchronization for a class of nonlinear systems. IEEE Control Syst. Lett. 2023, 7, 1255–1260. [Google Scholar] [CrossRef]
- Abdurahman, A.; Abdusaimaiti, M.; Jiang, H. Fixed/predefined-time lag synchronization of complex-valued BAM neural networks with stochastic perturbations. Appl. Math. Comput. 2023, 444, 127811. [Google Scholar] [CrossRef]
- Li, R.; Cao, J.; Alsaedi, A.; Alsaadi, F. Exponential and fixed-time synchronization of Cohen–Grossberg neural networks with time-varying delays and reaction-diffusion terms. Appl. Math. Comput. 2017, 313, 37–51. [Google Scholar] [CrossRef]
- Sadik, H.; Abdurahman, A.; Tohti, R. Fixed-Time synchronization of reaction-diffusion fuzzy neural networks with stochastic perturbations. Mathematics 2023, 11, 1493. [Google Scholar] [CrossRef]
- Lee, L.; Liu, Y.; Liang, J.; Cai, X. Finite time stability of nonlinear impulsive systems and its applications in sampled-data systems. ISA Trans. 2015, 57, 172–178. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Khoo, S.; Man, Z. Finite-time stability and instability of stochastic nonlinear systems. Automatica 2011, 47, 2671–2677. [Google Scholar] [CrossRef]
- Abudusaimaiti, M.; Abdurahman, A.; Jiang, H. Fixed/predefined-time synchronization of fuzzy neural networks with stochastic perturbations. Chaos Solitons Fractals 2022, 154, 111596. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E.; Plya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Li, H.; Li, C.; Huang, T. Fixed-time stability and stabilization of impulsive dynamical systems. J. Frankl. Inst. 2017, 354, 8626–8644. [Google Scholar] [CrossRef]
| Ref. | Synchronization Type | Reaction-Diffusion Term | Impulse Effect | Stochastic Perturbation | Number Field |
|---|---|---|---|---|---|
| [11] | General decay | with | without | without | |
| [24] | Switching | with | without | without | |
| [27] | Quasi | with | without | with | |
| [31] | FNT | with | without | without | |
| [33] | FXT/PDT | without | with | with | |
| [36] | FXT/PDT | without | without | with | |
| [38] | FXT | with | without | with | |
| This paper | FXT/PDT | with | with | with |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahemuti, R.; Kasim, E.; Sadik, H. Stochastic Synchronization of Impulsive Reaction–Diffusion BAM Neural Networks at a Fixed and Predetermined Time. Mathematics 2024, 12, 1204. https://doi.org/10.3390/math12081204
Mahemuti R, Kasim E, Sadik H. Stochastic Synchronization of Impulsive Reaction–Diffusion BAM Neural Networks at a Fixed and Predetermined Time. Mathematics. 2024; 12(8):1204. https://doi.org/10.3390/math12081204
Chicago/Turabian StyleMahemuti, Rouzimaimaiti, Ehmet Kasim, and Hayrengul Sadik. 2024. "Stochastic Synchronization of Impulsive Reaction–Diffusion BAM Neural Networks at a Fixed and Predetermined Time" Mathematics 12, no. 8: 1204. https://doi.org/10.3390/math12081204
APA StyleMahemuti, R., Kasim, E., & Sadik, H. (2024). Stochastic Synchronization of Impulsive Reaction–Diffusion BAM Neural Networks at a Fixed and Predetermined Time. Mathematics, 12(8), 1204. https://doi.org/10.3390/math12081204






