Channel Engineering for Nanotransistors in a Semiempirical Quantum Transport Model
Abstract
:1. Introduction
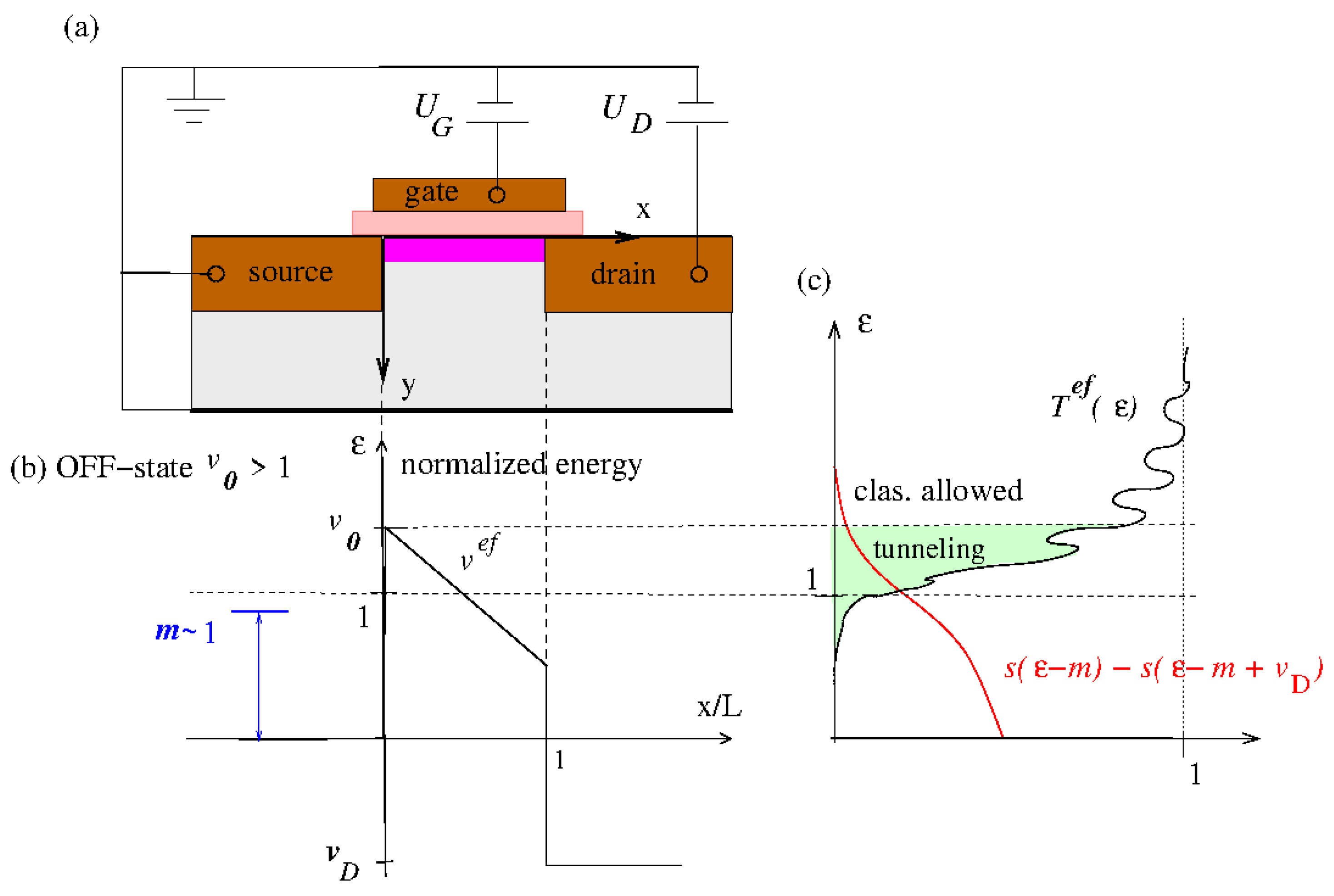
2. Semiempirical Transistor Model
2.1. Scale-Invariant Drain Current
2.2. Calibration of the System Parameters
3. The Calibration Functions
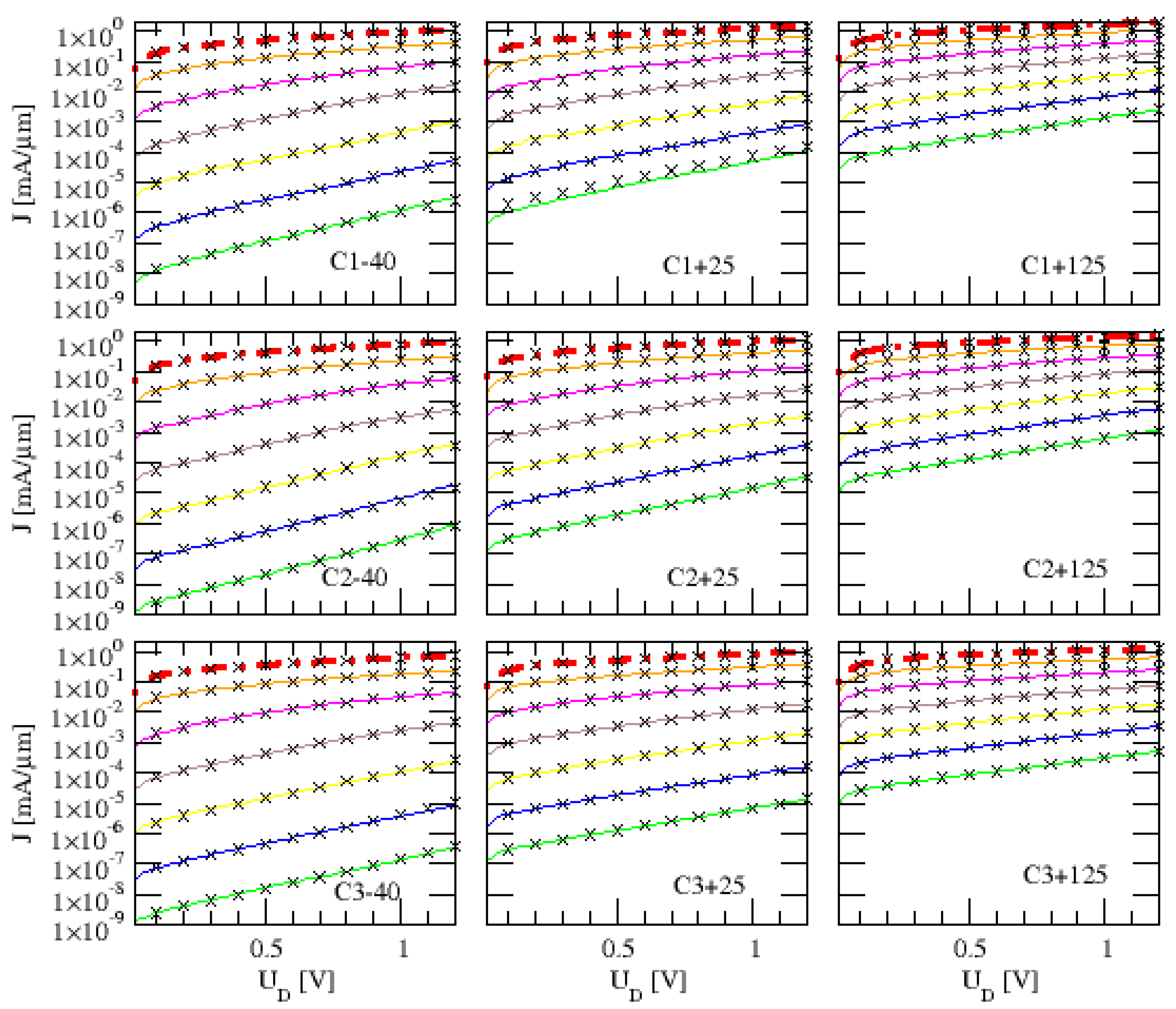
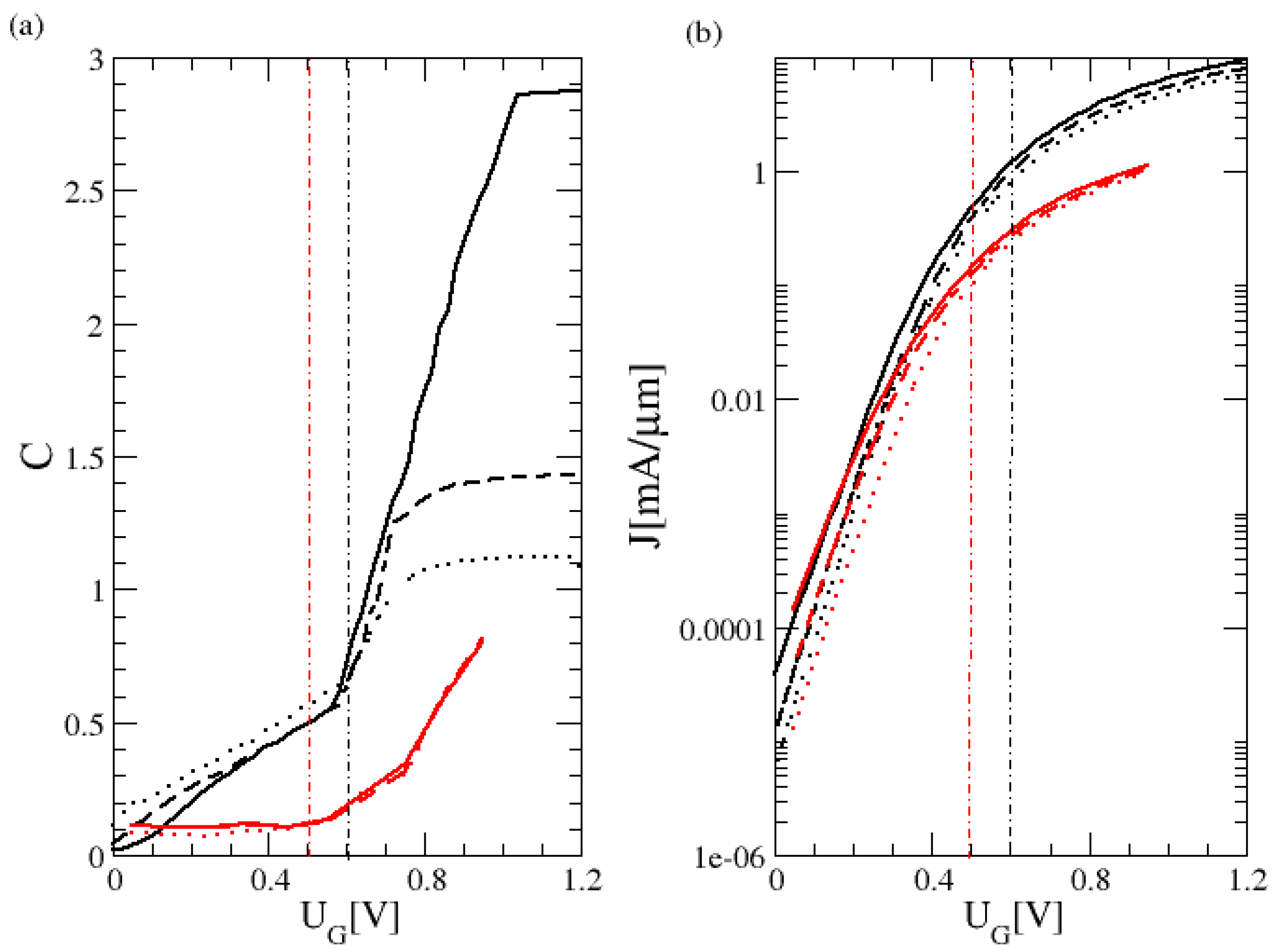
3.1. Experimental and Theoretical Output Characteristic
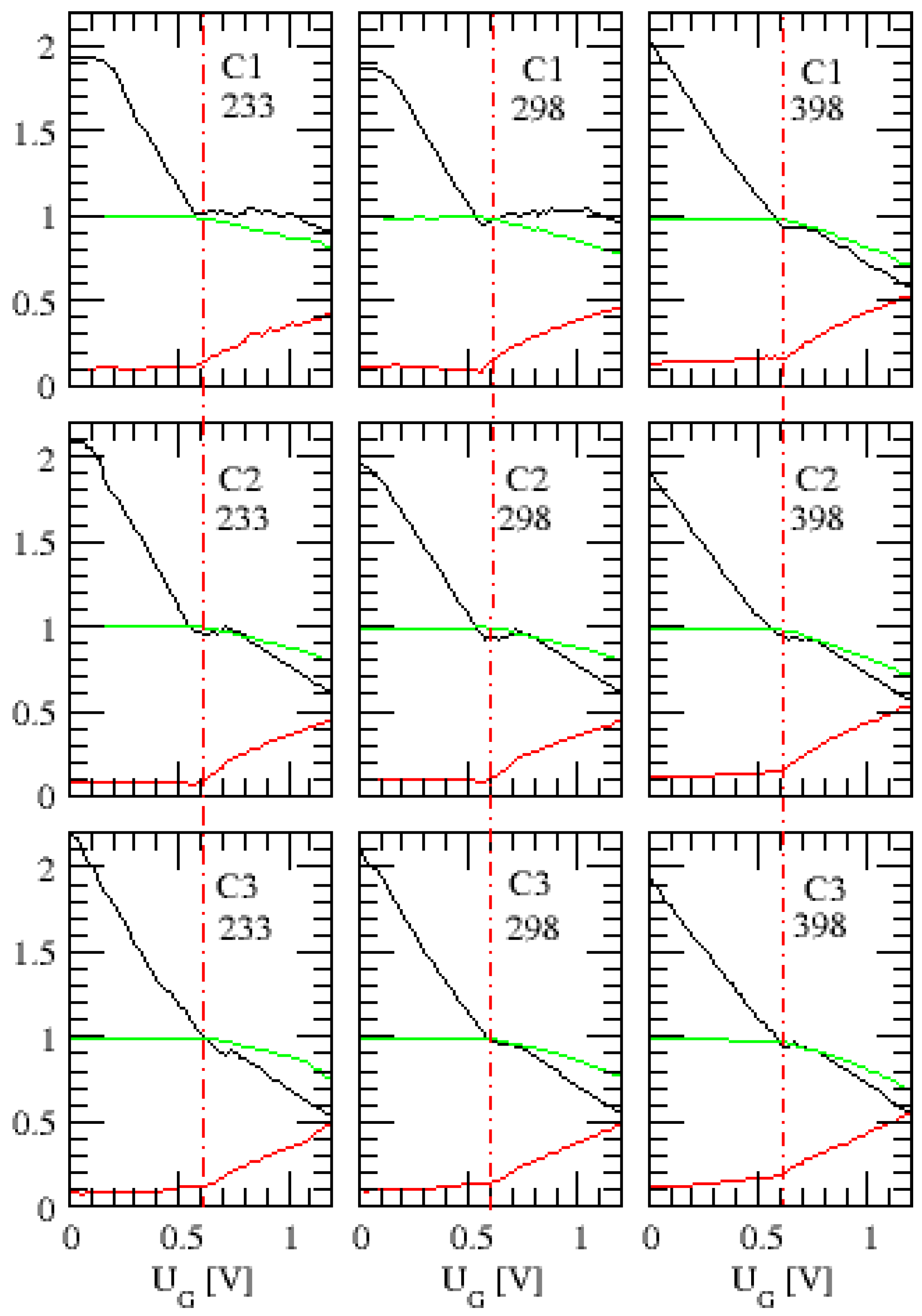
3.2. The Calibration Functions for Barrier Height and Device Temperature
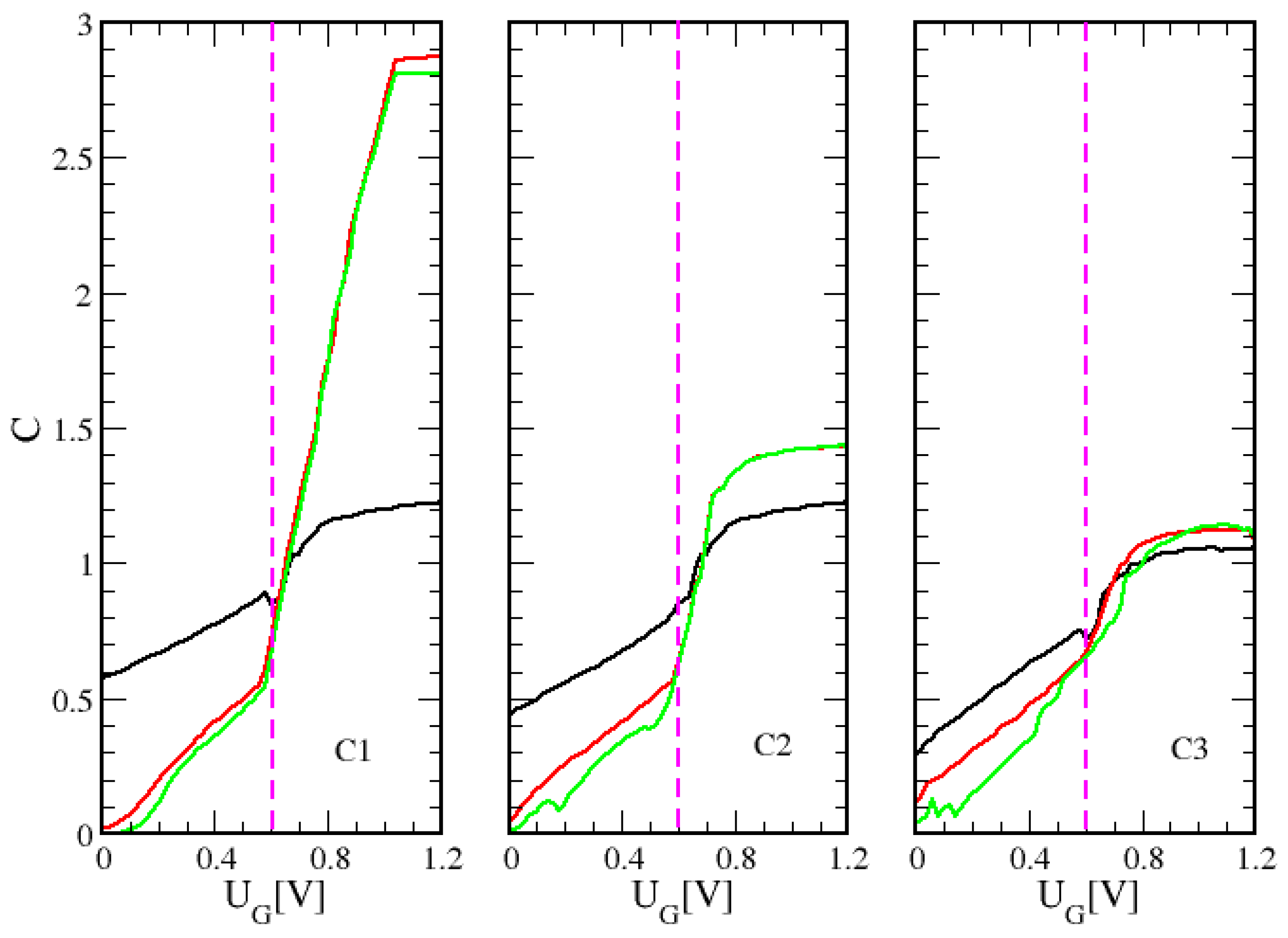
3.3. The Calibration Function for the Overlap Parameter and Transfer Characteristic
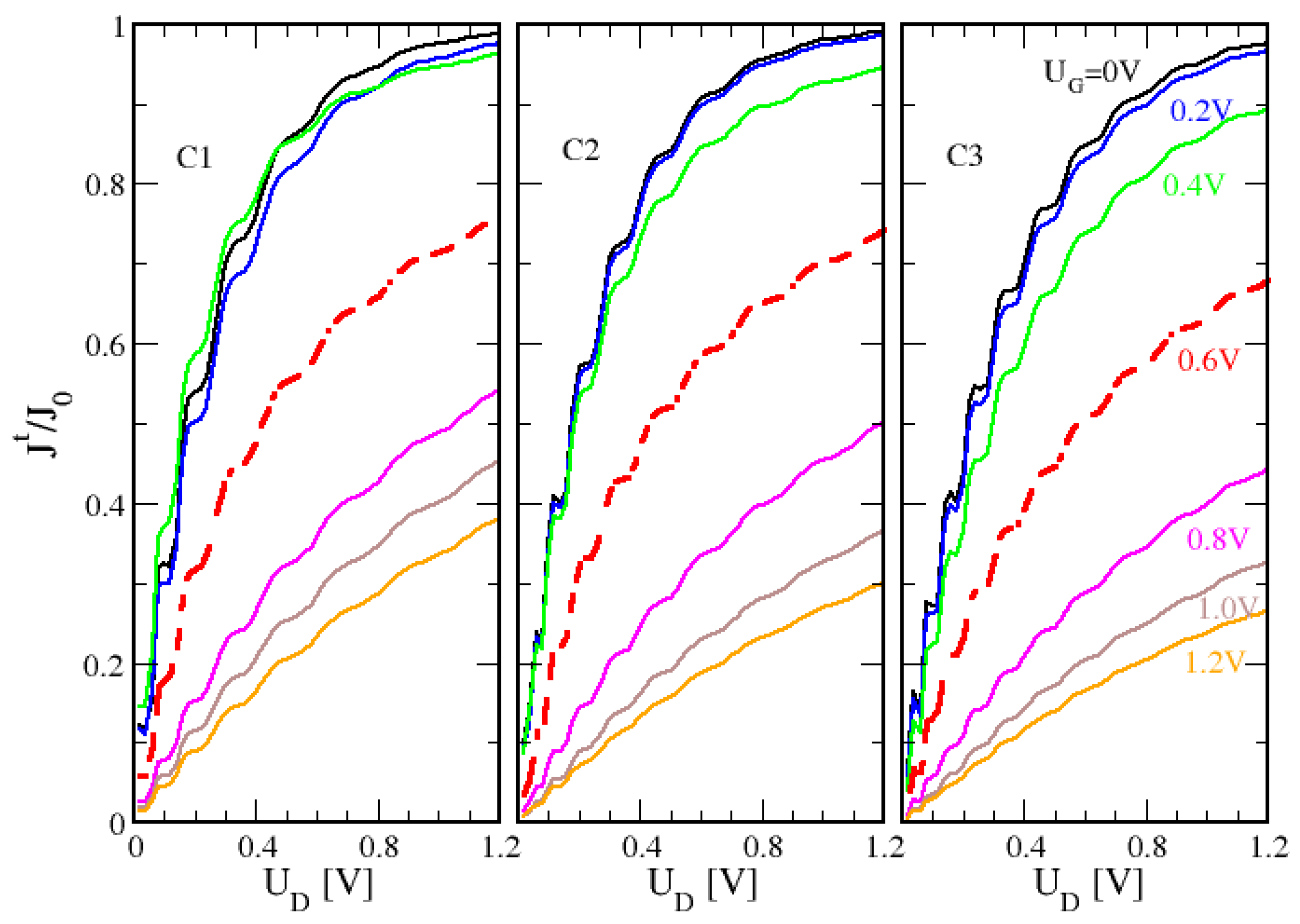
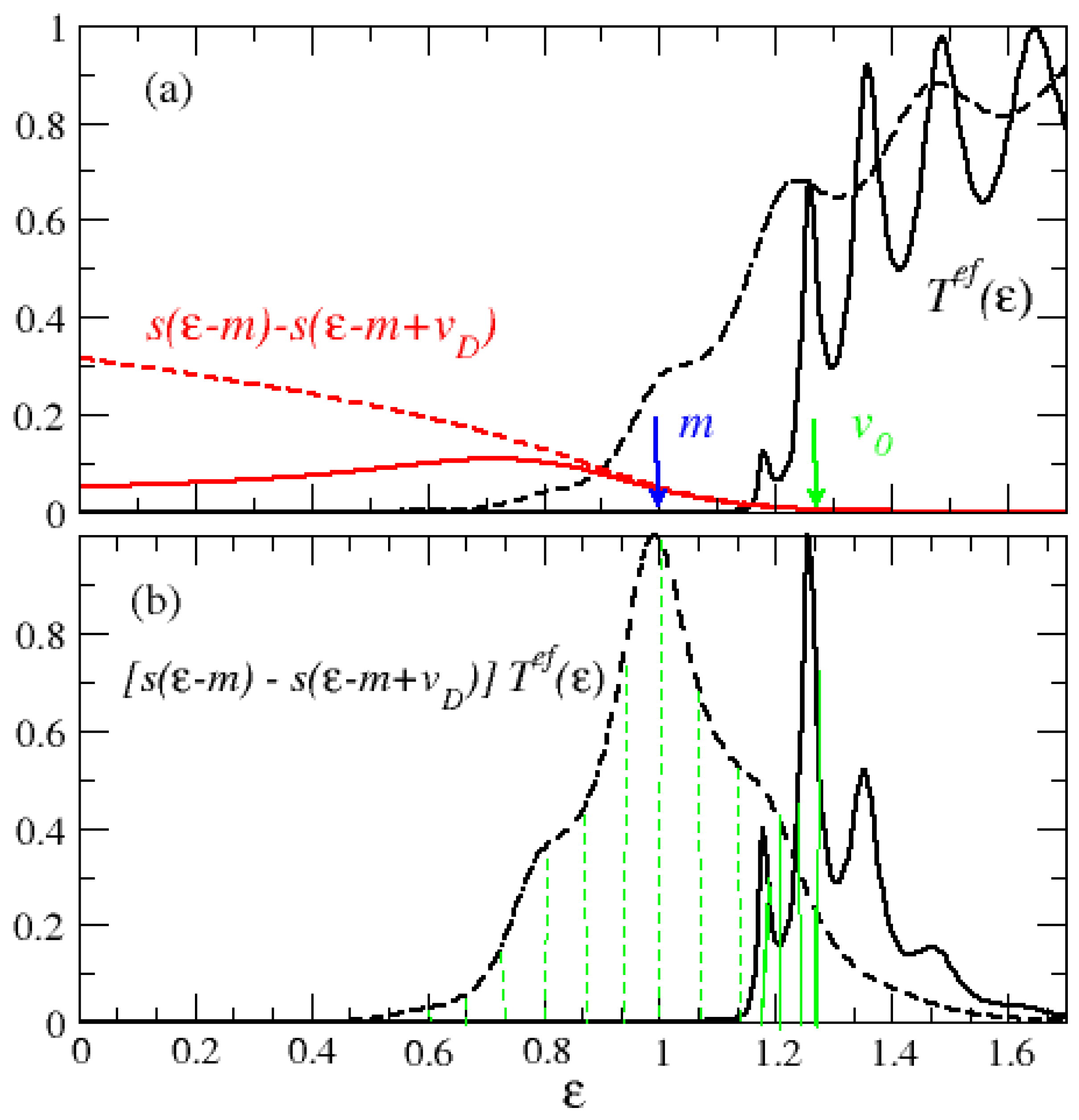
4. Tunneling Current
5. Conclusions for Channel Engineering
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Review of the Semiempirical Model
Appendix A.1. Single-Level Abrupt Transition Approximation (SMAT)
Appendix A.2. Drain Current and Effective Current Transmission
Appendix A.3. Scale-Invariant Form of the Basic Equations
References
- Natori, K. Ballistic metal-oxide-semiconductor field effect transistor. J. Appl. Phys. 1994, 76, 4879–4890. [Google Scholar] [CrossRef] [Green Version]
- Gilbert, M.J.; Ferry, D.K. Efficient quantum three-dimensional modeling of fully depleted ballistic silicon-on-insulator metal-oxide-semiconductor field-effect-transistors. J. Appl. Phys. 2004, 95, 7954–7960. [Google Scholar] [CrossRef]
- Nemnes, G.A.; Wulf, U.; Racec, P.N. Nano-transistors in the Landauer–Büttiker formalism. J. Appl. Phys. 2004, 96, 596–604. [Google Scholar] [CrossRef]
- Kim, K.; Kwon, O.; Seo, J.; Won, T.; Birner, S.; Trellakis, A. Two-Dimensional Quantum Effects and Structural Optimization of FinFETs with Two-Dimensional Poisson-Schödinger Solver. J. Korean Phys. Soc. 2004, 45, 1384–1390. [Google Scholar]
- Nemnes, G.A.; Wulf, U.; Racec, P.N. Nonlinear I-V characteristics of nanotransistors in the Landauer-Büttiker formalism. J. Appl. Phys. 2005, 98, 84308. [Google Scholar] [CrossRef]
- Polizzi, E.; Abdallah, N.B. Subband decomposition approach for the simulation of quantum electron transport in nanostructures. J. Comput. Phys. 2005, 202, 150–180. [Google Scholar] [CrossRef]
- Walls, T.J.; Likharev, K.K. Two-dimensional quantum effects in “ultimate” nanoscale metal-oxide-semiconductor field-effect transistors. J. Appl. Phys. 2008, 104, 124307. [Google Scholar] [CrossRef]
- Pourghaderi, M.A.; Magnus, W.; Sorée, B.; Meuris, M.; De Meyer, K.; Heyns, M. Ballistic current in metal-oxide-semiconductor field-effect transistors: The role of device topology. J. Appl. Phys. 2009, 106, 53702. [Google Scholar] [CrossRef]
- Farzana, E.; Chowdhury, S.; Ahmed, R.; Ziaur, M.; Khan, R. Analysis of temperature and wave function penetration effects in nanoscale double-gate MOSFETs. Appl. Nanosci. 2012, 3, 109–117. [Google Scholar] [CrossRef]
- Vyurkov, V.; Semenikhin, I.; Filippov, S.; Orlikovsky, A. Quantum simulation of an ultrathin body field-effect transistor with channel imperfections. Solid State Electron. 2012, 70, 106–113. [Google Scholar] [CrossRef]
- Svizhenko, A.; Anantram, M.P.; Govindan, T.R.; Biegel, B.; Venugopal, R. Two-dimensional quantum mechanical modeling of nanotransistors. J. Appl. Phys. 2002, 91, 2343–2354. [Google Scholar] [CrossRef]
- Venugopal, R.; Ren, Z.; Datta, S.; Lundstrom, M.S.; Jovanovic, D. Simulating quantum transport in nanoscale transistors: Real versus mode-space approaches. J. Appl. Phys. 2002, 92, 3730–3739. [Google Scholar] [CrossRef]
- Ren, Z.; Venugopal, R.; Goasguen, S.; Datta, S.; Lundstrom, M.S. NanoMOS 2.5: A Two-Dimensional Simulator for Quantum Transport in Double-Gate MOSFETs. IEEE Trans. Electron Devices 2003, 50, 1914–1925. [Google Scholar]
- Mamaluy, D.; Mannargudi, A.; Vasileska, D.; Sabathil, M.; Vogl, P. Contact block reduction method and its application to a 10 nm MOSFET device. Semicond. Sci. Technol. 2004, 19, S118–S121. [Google Scholar] [CrossRef]
- Luisier, M.; Schenk, A.; Fichtner, W. Quantum transport in two- and three-dimensional nanoscale transistors: Coupled mode effects in the nonequilibrium Green’s function formalism. J. Appl. Phys. 2006, 100, 43713. [Google Scholar] [CrossRef]
- Martinez, A.; Bescond, M.; Barker, J.R.; Svizhenkov, A.; Anantram, M.P.; Millar, C.; Asenov, A. A Self-Consistent Full 3-D Real-Space NEGF Simulator for Studying Nonperturbative Effects in Nano-MOSFETs. IEEE Trans. Electron Devices 2007, 54, 2213–2222. [Google Scholar] [CrossRef]
- Khan, H.R.; Mamaluy, D.; Vasileska, D. Quantum Transport Simulation of Experimentally Fabricated Nano-FinFET. IEEE Trans. Electron Devices 2007, 54, 784–796. [Google Scholar] [CrossRef]
- Luisier, M.; Schenk, A. Atomistic Simulation of Nanowire Transistors. J. Comput. Theor. Nanosci. 2008, 5, 1031–1045. [Google Scholar] [CrossRef]
- Autran, J.-L.; Munteanu, D. Simulation of Electron Transport in Nanoscale Independent-Gate Double-Gate Devices Using a Full 2D Green’s Function Approach. J. Comput. Theor. Nanosci. 2008, 5, 1120–1127. [Google Scholar] [CrossRef]
- Kurniawan, O.; Bai, P.; Li, E. Ballistic calculation of nonequilibrium Green’s function in nanoscale devices using finite element method. J. Phys. D 2009, 42, 105109. [Google Scholar] [CrossRef]
- Razavi, P.; Fagas, G.; Ferain, I.; Yu, R.; Das, S.; Colinge, J.-P. Influence of channel material properties on performance of nanowire transistors. J. Appl. Phys. 2012, 111, 124509. [Google Scholar] [CrossRef]
- Mamaluy, D.; Gao, X. The fundamental downscaling limit of field effect transistors. Appl. Phys. Lett. 2015, 106, 193503. [Google Scholar] [CrossRef]
- Sinha, S.; Yeric, G.; Chandra, V.; Cline, B.; Cao, Y. Exploring sub-20 nm FinFET design with predictive technology models. In Proceedings of the 49th Annual Design Automation Conference DAC, San Francisco, CA, USA, 3–7 June 2012; ACM: New York, NY, USA, 2012; pp. 283–288, ISBN 978-1-4503-1199-1. [Google Scholar]
- Paydavosi, N.; Venugopalan, S.; Chauhan, Y.S.; Duarte, J.P.; Jandhyala, S.; Niknejad, A.M.; Hu, C.C. BSIM—SPICE Models Enable FinFET and UTB IC Designs. IEEE Access 2013, 1, 201–215. [Google Scholar] [CrossRef]
- Agarwal, H.; Gupta, C.; Kushwaha, P.; Yadav, C.; Duarte, J.P.; Khandelwal, S.; Hu, C.; Chauhan, Y.S. Analytical Modeling and Experimental Validation of Threshold Voltage in BSIM6 MOSFET Mode. IEEE J. Electron Devices Soc. 2015, 3, 240–243. [Google Scholar] [CrossRef]
- Kushwaha, P.; Paydavosi, N.; Khandelwal, S.; Yadav, C.; Agarwal, H.; Duarte, J.P.; Hu, C.; Chauhan, Y.S. Modeling the impact of substrate depletion in FDSOI MOSFETs. Solid-State Electron. 2015, 104, 6–11. [Google Scholar] [CrossRef]
- Khandelwal, S.; Agarwal, H.; Kushwaha, P.; Duarte, J.P.; Medury, A.; Chauhan, Y.S.; Salahuddin, S.; Hu, C. Unified Compact Model Covering Drift-Diffusion to Ballistic Carrier Transport. IEEE Electron Device Lett. 2016, 37, 134–137. [Google Scholar] [CrossRef]
- Lundstrom, M. Elementary Scattering Theory of the Si MOSFET. IEEE Electron Device Lett. 1997, 18, 361–363. [Google Scholar] [CrossRef]
- Lundstrom, M.; Ren, Z. Essential Physics of Carrier Transport in Nanoscale MOSFETs. IEEE Trans. Electron Devices 2002, 49, 133–141. [Google Scholar] [CrossRef]
- Khakifirooz, A.; Nayfeh, O.M.; Antoniadis, D. A Simple Semiempirical Short-Channel MOSFET Current–Voltage Model Continuous Across All Regions of Operation and Employing Only Physical Parameters. IEEE Trans. Electron Devices 2009, 56, 1674–1689. [Google Scholar] [CrossRef]
- Lundstrom, M.S.; Antoniadis, D.A. Compact Models and the Physics of Nanoscale FETs. IEEE Trans. Electron Devices 2014, 61, 225–233. [Google Scholar] [CrossRef]
- Rakheja, S.; Lundstrom, M.S.; Antoniadis, D.A. An Improved Virtual-Source-Based Transport Model for Quasi-Ballistic Transistors—Part I: Capturing Effects of Carrier Degeneracy, Drain-Bias Dependence of Gate Capacitance, and Nonlinear Channel-Access Resistance. IEEE Trans. Electron Devices 2015, 62, 2786–2793. [Google Scholar] [CrossRef]
- Rakheja, S.; Lundstrom, M.S.; Antoniadis, D.A. An Improved Virtual-Source-Based Transport Model for Quasi-Ballistic Transistors—Part II: Experimental Verification. IEEE Trans. Electron Devices 2015, 62, 2794–2801. [Google Scholar] [CrossRef]
- Jimenez, D.; Saenz, J.J.; Iniquez, B.; Sune, J.; Marsal, L.F.; Pallares, J. Unified compact model for the ballistic quantum wire and quantum well metal-oxide-semiconductor field-effect-transistor. J. Appl. Phys. 2003, 94, 1061–1068. [Google Scholar] [CrossRef]
- Sverdlov, V.A.; Walls, T.J.; Likharev, K.K. Nanoscale silicon MOSFETs: A theoretical study. IEEE Trans. Electron Devices 2003, 50, 1926–1933. [Google Scholar] [CrossRef]
- Walls, T.J.; Sverdlov, V.A.; Likharev, K.K. Nanoscale SOI MOSFETs: A comparison of two options. Solid State Electron. 2004, 48, 857–865. [Google Scholar] [CrossRef]
- Wulf, U.; Richter, H. Scale-Invariant Drain Current in Nano-FETs. J. Nano Res. 2010, 10, 49–62. [Google Scholar] [CrossRef]
- Wulf, U.; Krahlisch, M.; Richter, H. Scaling properties of ballistic nano-transistors. Nanoscale Res. Lett. 2011, 6, 365. [Google Scholar] [CrossRef] [PubMed]
- Wulf, U.; Krahlisch, M.; Kučera, J.; Richter, H.; Höntschel, J. A quantitative model for quantum transport in nano-transistors. Nanosyst. Phys. Chem. Math. 2013, 4, 800–809. [Google Scholar]
- Wulf, U.; Kučera, J.; Richter, H.; Wiatr, M.; Höntschel, J. Characterization of nanotransistors in a semiempirical model. Thin Solid Films 2016, 613, 6–10. [Google Scholar] [CrossRef]
- The transistors B1 and B2 in [40] are p-channel transistors and don’t belong to the series of C-transistors.
- Krahlisch, M.; Wulf, U.; Kučera, J.; Richter, H.; Höntschel, J. Analytical expressions for the drain current of a nanotransistor in the off-state regime. Phys. Status Solidi C 2014, 11, 113–116. [Google Scholar] [CrossRef]
- Careful inspection of Figure 2 shows a decrease of the drain current with increasing temperature in the deep ON-state regime
- Racec, P.N.; Wulf, U.; Kučera, J. Integration of quantum transport models in classical device simulators. Solid State Electron. 2000, 44, 881–886. [Google Scholar] [CrossRef]
- Stern, F. Self-Consistent Results for n-Type Si Inversion Layers. Phys. Rev. B 1972, 5, 4891–4899. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wulf, U.; Kučera, J.; Richter, H.; Horstmann, M.; Wiatr, M.; Höntschel, J. Channel Engineering for Nanotransistors in a Semiempirical Quantum Transport Model. Mathematics 2017, 5, 68. https://doi.org/10.3390/math5040068
Wulf U, Kučera J, Richter H, Horstmann M, Wiatr M, Höntschel J. Channel Engineering for Nanotransistors in a Semiempirical Quantum Transport Model. Mathematics. 2017; 5(4):68. https://doi.org/10.3390/math5040068
Chicago/Turabian StyleWulf, Ulrich, Jan Kučera, Hans Richter, Manfred Horstmann, Maciej Wiatr, and Jan Höntschel. 2017. "Channel Engineering for Nanotransistors in a Semiempirical Quantum Transport Model" Mathematics 5, no. 4: 68. https://doi.org/10.3390/math5040068



