A 2D Non-Linear Second-Order Differential Model for Electrostatic Circular Membrane MEMS Devices: A Result of Existence and Uniqueness
Abstract
1. Introduction to the Problem
2. From the Cassani Model to the Proposed Model
3. An Overview of Circular Membrane MEMS Devices
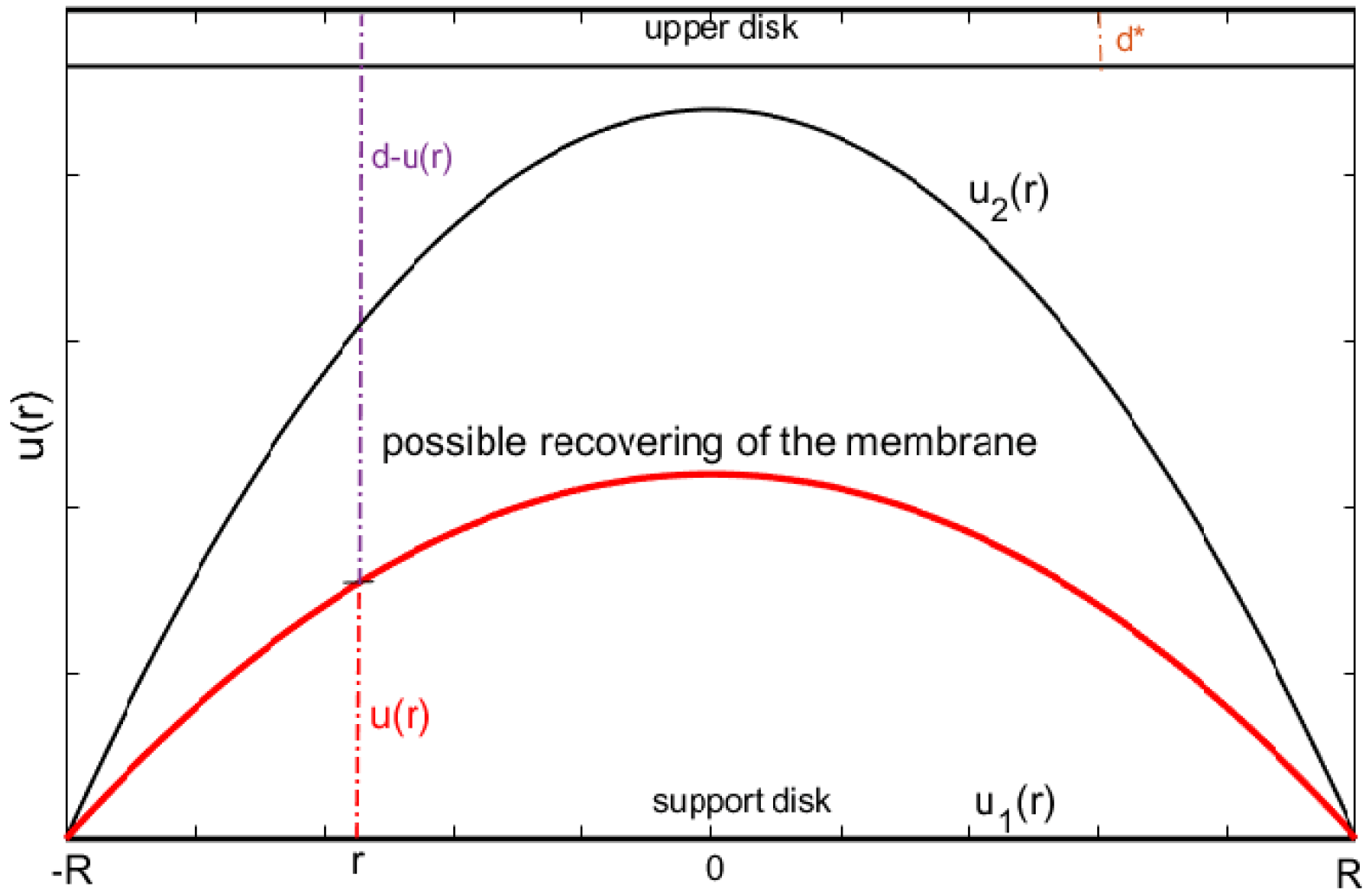
3.1. The Circular Membrane MEMS Actuator
3.2. The Circular Membrane MEMS Transducer
3.2.1. Circular Plate MEMS Transducer: Behavior under the Effect of p
3.2.2. Circular Membrane MEMS Transducer: Behavior under the Effect of p
3.3. Link between p and
4. Formulation of the Problem
The Proposed Model
5. Formulation of the Proposed Model in Terms of Mean Curvature
6. General Formulation of the Problem
7. Preliminary Lemmas
- If and are real, then, in either the interval or the interval , there exists a solution of the form:in which can be obtained by the following recurrence relation:with and .
8. A Result of the Existence of at Least One Solution to the Problem (5)
9. On the Uniqueness of the Solution to the Problem (5)
10. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MEMS | Micro-Electro-Mechanical Systems |
References
- Pelesko, J.A.; Bernstein, D.H. Modeling MEMS and NEMS; Chapman & Hall/CRC: Boca Raton, FL, USA; London, UK; New York, NY, USA; Washington, DC, USA, 2003. [Google Scholar]
- Nathanson, N.H.; Newell, W.E.; Wickstrom, R.A.; Lewis, J.R. The Resonant Gate Transistor. IEEE Trans. Electr. Dev. 1964, 14, 117–119. [Google Scholar] [CrossRef]
- Di Barba, P.; Wiak, S. MEMS: Field Models and Optimal Design; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Feng, J.; Liu, C.; Zhang, W.; Hao, S. Static and Dynamic Mechanical Behaviors of Electrostatic MEMS Resonator with Surface Processing Error. Micromachines 2018, 9, 34. [Google Scholar] [CrossRef] [PubMed]
- Daeichin, M.; Ozdogan, M.; Twfighian, S.; Miles, R. Dynamic Response of a Tunable MEMS Accelerometer Based on Repulsive Force. Sens. Actuators A Phys. 2019, 289, 34–43. [Google Scholar] [CrossRef]
- Javaheri, H.; Ghanati, P. A Case Study on the Numerical Solution and Reduced Order Model of MEMS. Sens. Imaging 2018, 19, 22–31. [Google Scholar] [CrossRef]
- Di Barba, P.; Fattorusso, L.; Versaci, M. Electrostatic Field in Terms of Geometric Curvature in Membrane MEMS Devices. Commun. Appl. Ind. Math. 2017, 8, 165–184. [Google Scholar] [CrossRef]
- Mashinchi Joubari, R.; Asghari, R. Analytical Solution for Nonlinear Vibration of Micro-Electro-Mechanical System (MEMS) by Frequency-Amplitude Formulation Method. J. Math. Comput. Sci. 2012, 4, 371–379. [Google Scholar] [CrossRef]
- Angiulli, G.; Jannelli, A.; Morabito, F.C.; Versaci, M. Reconstructing the Membrane Detection of a 1D Electrostatic-Driven MEMS Device by the Shooting Method: Convergence Analysis and Ghost Solutions Identification. Comput. Appl. Math. 2018, 37, 4484–4498. [Google Scholar] [CrossRef]
- Versaci, M.; Angiulli, G.; Fattorusso, L.; Jannelli, A. On the Uniqueness of the Solution for a Semi-Linear Elliptic Boundary Value Problem of the Membrane MEMS Device for Reconstructing the Membrane Profile in Absence of Ghost Solutions. Int. J. Non-Linear Mech. 2019, 109, 24–31. [Google Scholar] [CrossRef]
- Fattorusso, L.; Versaci, M. A New One-Dimensional Electrostatic Model for Membrane MEMS Devices. In Proceedings of the World Congress on Engineering, London, UK, 4–6 July 2018; Volume 35. [Google Scholar]
- Herrera-May, A.; Aguilera-Cortes, L.; Garcia-Ramirez, P. Resonant Magnetic Field Sensors Based on MEMS Technology. Sensors 2009, 9, 1691–1695. [Google Scholar] [CrossRef] [PubMed]
- Imai, S.; Tsukioka, T. A Magnetic MEMS Actuator Using a Permanent Magnet and Magnet Fluid Enclosed in a Cavity Sandwiched by Polymer Diaphrams. Precis. Eng. 2014, 38, 548–554. [Google Scholar] [CrossRef]
- Mohammadi, A.K.; Ali, N.A. Effect of High Electrostatic Actuation on Thermoelastic Damping in Thin Rectangular Microplate Resonators. J. Theor. Appl. Mech. 2015, 53, 317–329. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, L.; Li, L.; Wiao, Z.; Cao, Q. Design and Analysis of the Elastic-Beam Delaying Mechanism in a Micro-Mechanical Systems Device. Micromachines 2018, 9, 567. [Google Scholar] [CrossRef] [PubMed]
- Takayama, Y. Developing a MEMS Device with Built-In Microfluidics for Biophysical Single Cell Characterization. Micromachines 2018, 9, 275. [Google Scholar] [CrossRef] [PubMed]
- Karumuri, S.R. Micro-Electro-Mechanical-Systems (MEMS) Technology. Arch. Appl. Sci. Res. 2012, 4, 307–314. [Google Scholar]
- Ciuti, G.; Ricotti, L.; Menciassi, A.; Dario, P. MEMS Sensor Technologies for Human Centered Applications in Healthcare, Physical Activities, Safety and Environmental Sensing: A Review on Research Activities in Italy. Sensors 2015, 15, 6441–6468. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y. Silicon-Based Sensors for Biomedical Applications: A Review. Sensors 2019, 19, 2908. [Google Scholar] [CrossRef] [PubMed]
- Di Barba, P.; Lorenzi, A. A Magneto-Thermo-Elastic Identification Problem with a Moving Boundary in a Micro-Device. Milan J. Math. 2013, 81, 347–383. [Google Scholar] [CrossRef]
- Esposito, P.; Ghoussoub, N.; Guo, Y. Mathematical Analysis of Partial Differential Equations Modeling Electrostatic MEMS; American Mathematical Society/Courant Institute of Mathematical Sciences (AMS): Providence, RI, USA, 2010. [Google Scholar]
- Cassani, D.; Fattorusso, L.; Tarsia, A. Non-local Dynamic Problems with Singular Nonlinearities and Application to MEMS. Prog. Nonlinear Differ. Equ. Appl. 2014, 85, 185–206. [Google Scholar]
- Cassani, D.; d’O, J.M.; Ghossoub, N. On a Fourth Order Elliptic Problem with a Singular Nonlinearity. Adv. Nonlinear Stud. 2009, 9, 177–197. [Google Scholar] [CrossRef]
- Versaci, M.; Morabito, F.C. Membrane Micro Electro-Mechanical Systems for Industrial Applications. In Handbook of Research on Advanced Mechatronic Systems and Intelligent Robotics; IGI Global: Hershey, PA, USA, 2019. [Google Scholar]
- Versaci, M.; Angiulli, G.; Calcagno, S.; Di Barba, P.; Jannelli, A. Recovering the Membrane Profile of an Electrostatic MEMS Device: A Comparison of Numerical Approaches. In Proceedings of the Eighteenth Biennial IEEE Conference on Electromagnetic Field Computation (CEFC 2018), Hangzhou, China, 28–31 October 2018; Volume 9. [Google Scholar]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Tu Lorin, W. Differential Geometry—Connections, Curvature, and Characteristic Classes; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Bailey, P.B.; Shampine, L.F.; Waltman, P.E. Nonlinear Two Point Boundary Value Problems; Academic Press: Cambridge, MA, USA, 1968. [Google Scholar]
- Boyce, W.E.; DiPrima, R.C. Elementary Differential Equations and Boundary Value Problems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Bowman, F. Introduction to Bessel Functions; Dover Pubblications: Mineola, NY, USA, 2013. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Barba, P.; Fattorusso, L.; Versaci, M. A 2D Non-Linear Second-Order Differential Model for Electrostatic Circular Membrane MEMS Devices: A Result of Existence and Uniqueness. Mathematics 2019, 7, 1193. https://doi.org/10.3390/math7121193
Di Barba P, Fattorusso L, Versaci M. A 2D Non-Linear Second-Order Differential Model for Electrostatic Circular Membrane MEMS Devices: A Result of Existence and Uniqueness. Mathematics. 2019; 7(12):1193. https://doi.org/10.3390/math7121193
Chicago/Turabian StyleDi Barba, Paolo, Luisa Fattorusso, and Mario Versaci. 2019. "A 2D Non-Linear Second-Order Differential Model for Electrostatic Circular Membrane MEMS Devices: A Result of Existence and Uniqueness" Mathematics 7, no. 12: 1193. https://doi.org/10.3390/math7121193
APA StyleDi Barba, P., Fattorusso, L., & Versaci, M. (2019). A 2D Non-Linear Second-Order Differential Model for Electrostatic Circular Membrane MEMS Devices: A Result of Existence and Uniqueness. Mathematics, 7(12), 1193. https://doi.org/10.3390/math7121193






