Radiative MHD Sutterby Nanofluid Flow Past a Moving Sheet: Scaling Group Analysis
Abstract
:1. Introduction
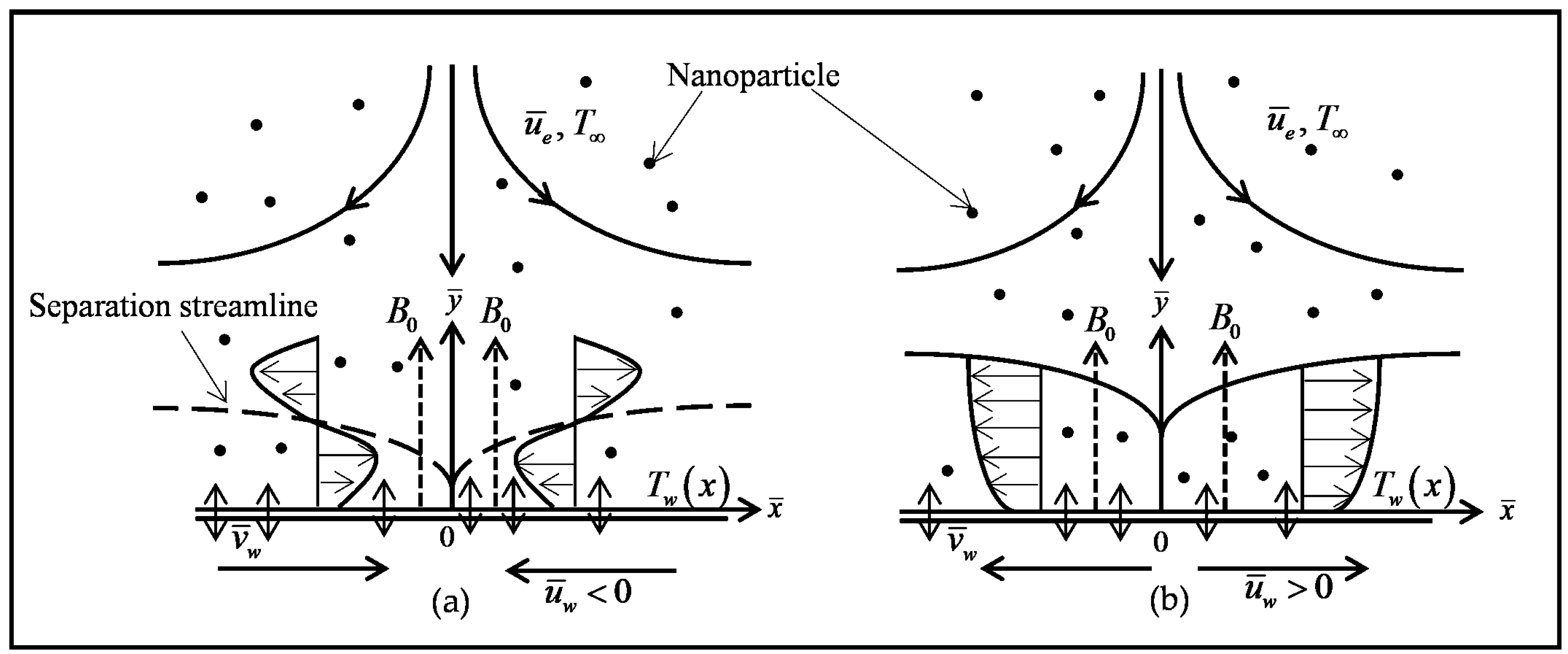
2. Problem Formulation
3. Non-Dimensionalization of the Governing Equations
4. Scaling Group Analysis
5. Stability Analysis
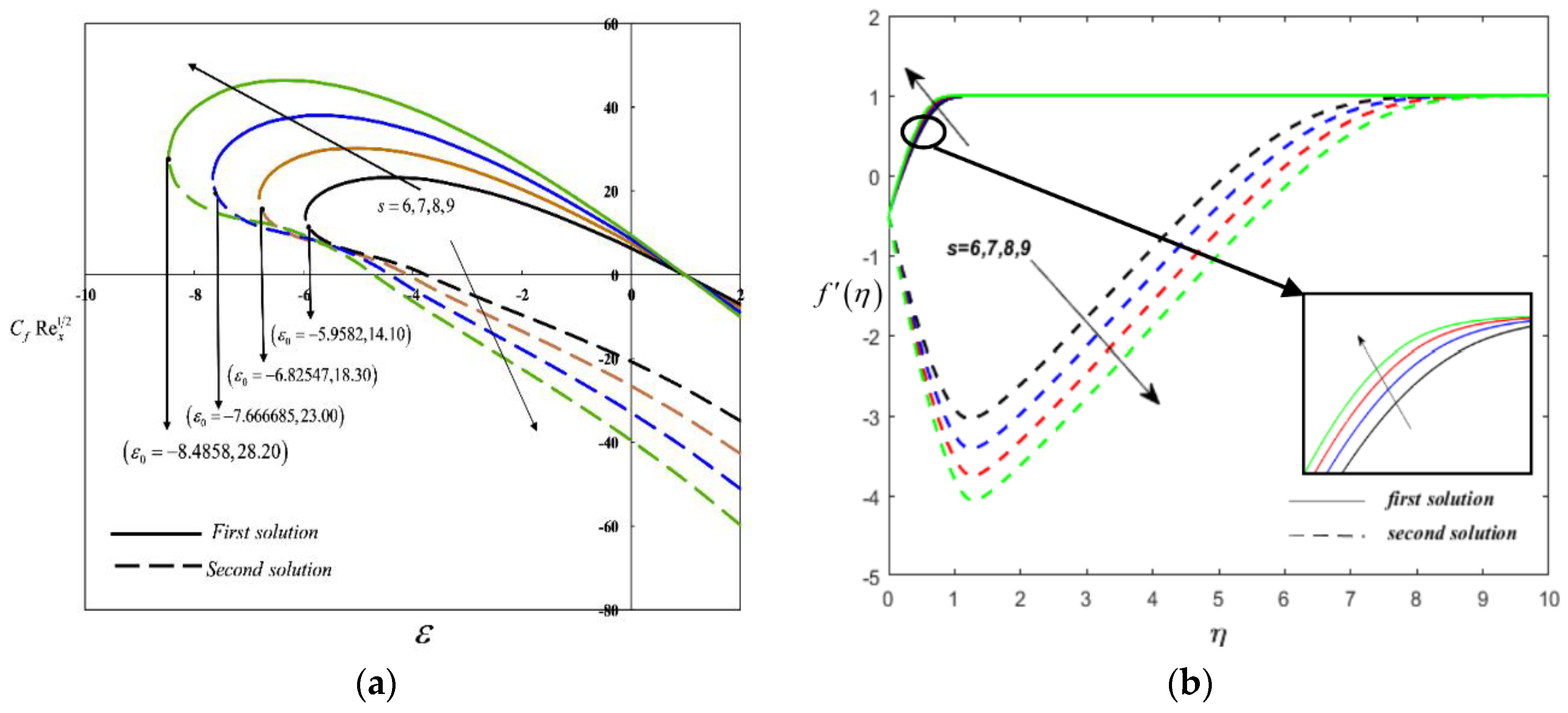
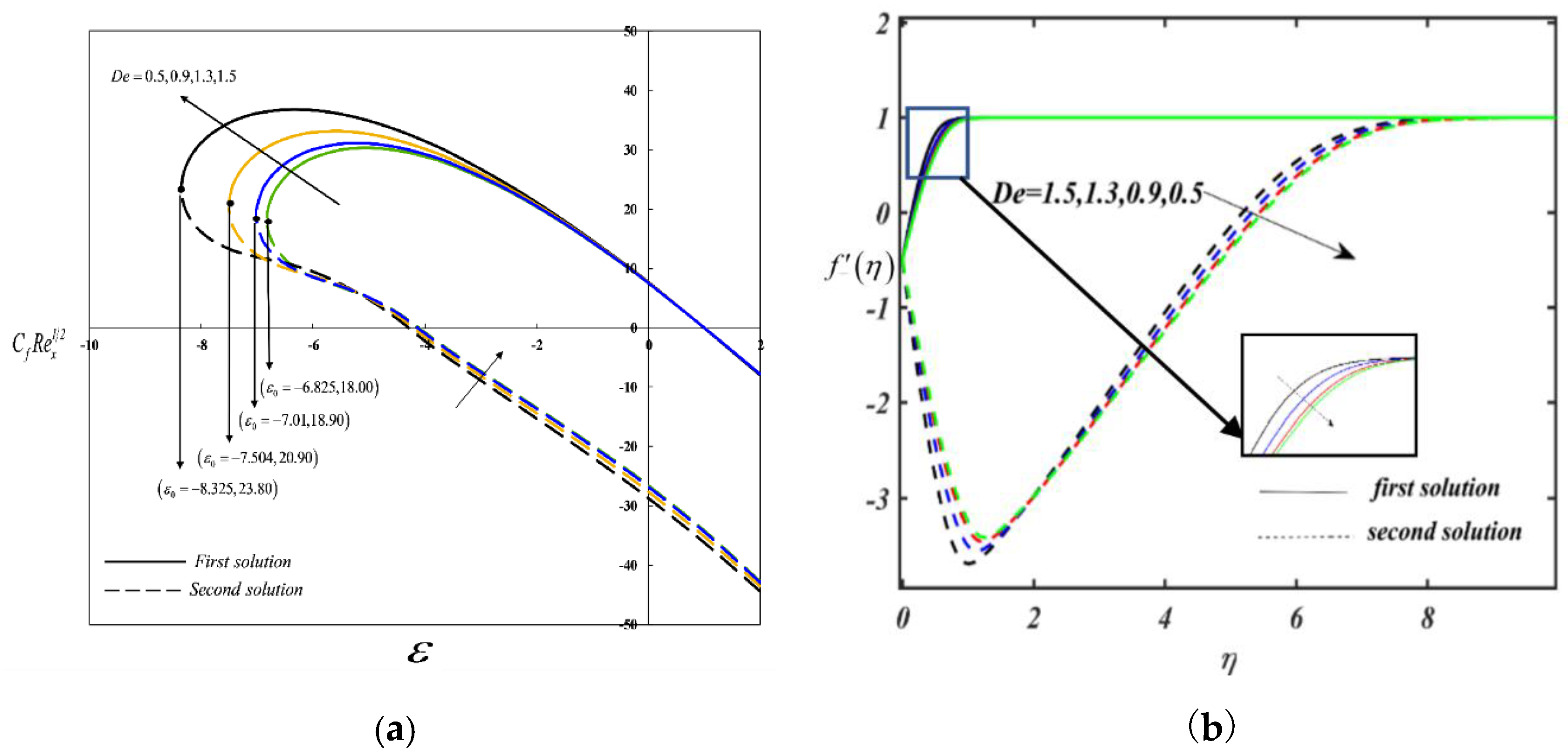
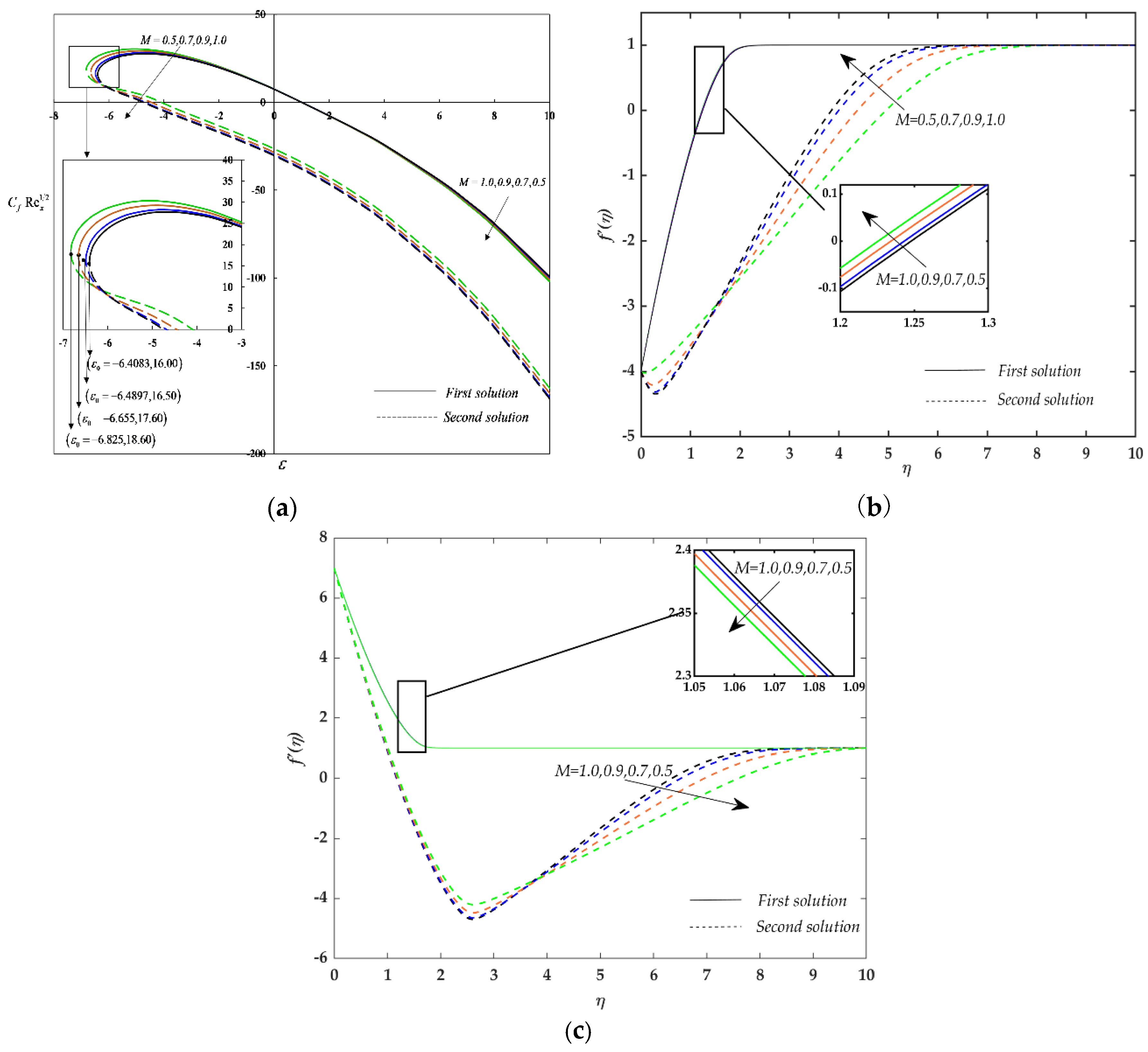
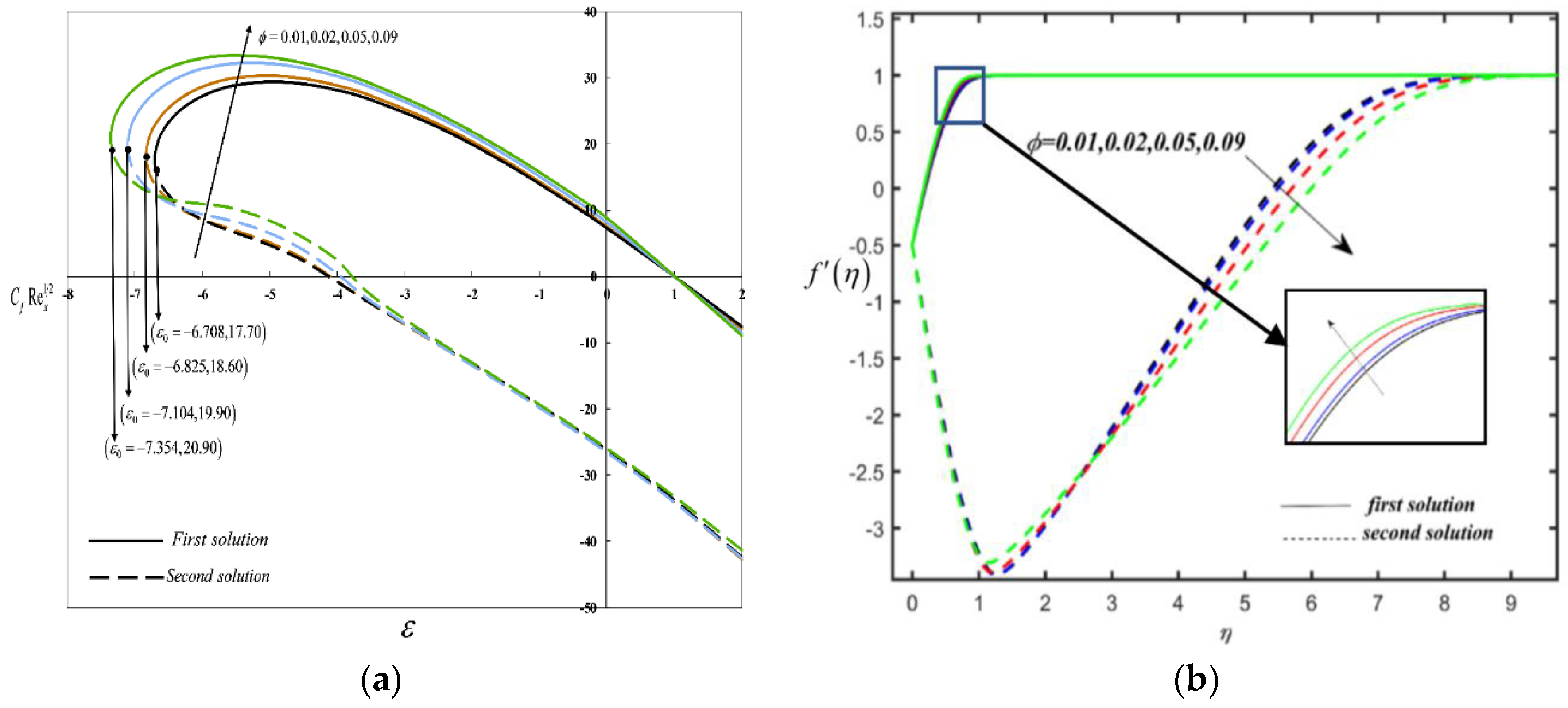
6. Results and Discussion
7. Conclusions
- An increment in the suction parameter, the Deborah number, and the nanoparticle volume fraction delay flow separation.
- The dominance of the magnetic parameter in the fluid flow regime accelerates flow separation.
- Non-unique solutions are observed when governing parameters, such as the suction parameter, the Deborah number, the magnetic number, the radiation parameter, and the nanoparticle volume fraction, vary.
- The increment in the radiation parameter slightly enhances the convective heat transfer rate past a permeable shrinking sheet.
- Stability analysis elucidates the first solution as a stable solution, and the second solution as an unstable solution.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Roman letters | |
| dimensional positive constant | |
| A1 | first order Rivlin–Erickson tensor |
| magnetic field strength | |
| specific heat capacity | |
| CH3(CH2)4CH3 | n-Hexane |
| Deborah number | |
| material time constant | |
| Fe3O4 | magnetite |
| constant mass transfer parameter | |
| I | identity tensor |
| thermal conductivity | |
| Rosseland mean absorption coefficient | |
| magnetic parameter | |
| power-law index | |
| pressure | |
| Prandtl number | |
| radiation parameter | |
| S | extra stress tensor |
| T | Cauchy stress tensor |
| dimensional time variable | |
| wall temperature | |
| free stream temperature | |
| reference temperature | |
| dimensionless velocity | |
| dimensional velocity | |
| reference velocity | |
| V | velocity field |
| normal reference velocity | |
| dimensionless surface mass flux velocity | |
| dimensional surface mass flux velocity | |
| dimensionless Cartesian coordinates | |
| dimensional Cartesian coordinates | |
| Greek letters | |
| thermal diffusivity | |
| second invariant strain tensor | |
| smallest eigenvalue | |
| stretching/shrinking parameter | |
| critical value | |
| similarity variable | |
| dimensionless temperature | |
| viscosity at low shear rates | |
| dynamic viscosity | |
| kinematic viscosity | |
| density | |
| electrical conductivity | |
| Stefan Boltzmann constant | |
| dimensionless time variable | |
| nanoparticle volume fraction | |
| stream function | |
| Subscripts | |
| base fluid | |
| condition at the free stream | |
| nanofluid | |
| solid fractions | |
| condition at the wall | |
| Superscript | |
| differentiation with respect to | |
References
- Sutterby, J.L. Laminar converging flow of dilute polymer solutions in conical sections: Part I. Viscosity data, new viscosity model, tube flow solution. AIChE J. 1966, 12, 63–68. [Google Scholar] [CrossRef]
- Sutterby, J.L. Laminar converging flow of dilute polymer solutions in conical sections. II. Trans. Soc. Rheol. 1965, 9, 227–241. [Google Scholar] [CrossRef]
- Batra, R.L.; Eissa, M. Helical flow of a Sutterby model fluid. Polym. Plast. Technol. Eng. 1994, 33, 489–501. [Google Scholar] [CrossRef]
- Bergeron, V. Designing intelligent fluids for controlling spray applications. C. R. Phys. 2003, 4, 211–219. [Google Scholar] [CrossRef]
- Giudice, D.; Haward, S.J.; Shen, A.Q. Relaxation time of dilute polymer solutions: A microfluidic approach. J. Rheol. 2017, 61, 327–337. [Google Scholar] [CrossRef] [Green Version]
- Rehage, H.; Hoffmann, H. Viscoelastic surfactant solutions: Model systems for rheological research. Mol. Phys. 1991, 74, 933–973. [Google Scholar] [CrossRef]
- Fujii, T.; Miyatake, O.; Fujii, M.; Tanaka, H.; Murakami, K. Natural convective heat transfer from a vertical isothermal surface to a non-Newtonian Sutterby fluid. Int. J. Heat Mass Tranf. 1973, 16, 2177–2187. [Google Scholar]
- Fujii, T.; Miyatake, O.; Fujii, M.; Tanaka, H.; Murakami, K. Natural convective heat-transfer from a vertical surface of uniform heat flux to a non-Newtonian Sutterby fluid. Int. J. Heat Mass Tranf. 1974, 17, 149–154. [Google Scholar]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. Fed. 1995, 231, 99–103. [Google Scholar]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Taylor, R.A.; Abu-Nada, E.; Rashidi, S.; et al. Recent advances in modeling and simulation of nanofluid flows-Part II: Applications. Phys. Rep. 2019, 791, 1–59. [Google Scholar] [CrossRef]
- Naganthran, K.; Basir, M.F.M.; Alharbi, S.O.; Nazar, R.; Alwatban, A.M.; Tlili, I. Stagantion point flow with time-dependent bionanofluid past a sheet: Richardson extrapolation technique. Processes 2019, 7, 722. [Google Scholar] [CrossRef] [Green Version]
- Pop, I.; Naganthran, K.; Nazar, R.; Ishak, A. The effect of vertical throughflow on the boundary layer flow of a nanofluid past a stretching/shrinking sheet. Int. J. Numer. Method Heat 2017, 27, 1910–1927. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady three-dimensional MHD non-axisymmetric Homann stagnation point flow of a hybrid nanofluid with stability analysis. Mathematics 2020, 8, 784. [Google Scholar] [CrossRef]
- Khan, M.I.; Qayyum, S.; Hayat, T.; Alsaedi, A. Stratified flow of Sutterby fluid with homogeneous-heterogeneous reactions and Catteneo-Christov heat flux. Int. J. Numer. Method Heat 2019, 29, 2977–2992. [Google Scholar] [CrossRef]
- Mir, N.A.; Alqarni, M.S.; Farooq, M.; Malik, M.Y. Analysis of heat generation/absorption in thermally stratified Sutterby fluid flow with Cattaneo-Christov theory. Microsyst. Technol. 2019, 25, 3365–3373. [Google Scholar]
- Mouli, G.B.C.; Gangadhar, K.; Raju, B.H.S. On spectral relaxation approach for Soret and Dufour effects on Sutterby fluid past a stretching sheet. Int. J. Ambient Energy 2019. [Google Scholar] [CrossRef]
- Nadeem, S.; Maraj, E.N. Peristaltic flow of Sutterby nanofluid in a curved channel with compliant walls. J. Comput. Theor. Nanos. 2015, 12, 226–233. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S. Nano Sutterby fluid model for the peristaltic flow in small intestines. J. Comput. Theor. Nanos. 2013, 10, 2491–2499. [Google Scholar] [CrossRef]
- Hayat, T.; Ayub, S.; Alsaedi, A.; Tanveer, A.; Ahmad, B. Numerical simulation for peristaltic activity of Sutterby fluid with modified Darcy’s law. Results Phys. 2017, 7, 762–768. [Google Scholar] [CrossRef]
- Ahmad, S.; Farooq, M.; Javed, M.; Anjum, A. Double stratification effects on chemically reactive squeezed Sutterby fluid flow with thermal radiation and mixed convection. Results Phys. 2018, 8, 1250–1259. [Google Scholar] [CrossRef]
- Hayat, T.; Afzal, S.; Khan, M.I.; Alsaedi, A. Irreversibility aspects to flow of Sutterby fluid subject to nonlinear heat flux and Joule heating. Appl. Nanosci. 2019, 9, 1215–1226. [Google Scholar] [CrossRef]
- Hayat, T.; Masood, F.; Qayyum, S.; Alsaedi, A. Sutterby fluid flow subject to homogeneous-heterogeneous reactions and nonlinear radiation. Physica A 2020, 544, 123439. [Google Scholar] [CrossRef]
- Nawaz, M. Role of hybrid nanoparticles in thermal performance of Sutterby fluid, the ethylene glycol. Physica A 2020, 537, 122447. [Google Scholar] [CrossRef]
- Wang, F.; Wang, N.; Yu, F.; Wang, X.; Cui, J. Study on micro-structure, solid solubility and tensile properties of 5A90 Al-Li alloy cast by low-frequency electromagnetic casting processing. J. Alloys Compd. 2020, 820, 153318. [Google Scholar] [CrossRef]
- Beg, O.A.; Ferdows, M.; Karim, M.E.; Hasan, M.M.; Bég, T.A.; Shamshuddin, M.D.; Kadir, A. Computation of non-isothermal thermo-convective micropolar fluid dynamics in a wall MHD generator system with non-linear distending wall. Int. J. Appl. Comput. Math. 2020, 6, 42. [Google Scholar]
- Raptis, A.; Perdikis, C.; Takhar, H.S. Effect of thermal radiation on MHD flow. Appl. Math. Comput. 2004, 153, 645–649. [Google Scholar] [CrossRef]
- Sabir, Z.; Imran, A.; Umar, M.; Zeb, M.; Shoaib, M.; Raja, M.A.Z. A numerical approach for two-dimensional Sutterby fluid flow bounded at a stagnation point with an inclined magnetic field and thermal radiation impacts. Therm. Sci. 2020, 186. [Google Scholar] [CrossRef]
- Bilal, S.; Sohail, M.; Naz, R.; Malik, M.Y.; Alghamdi, M. Upshot of ohmically dissipated Darcy-Forchheimer slip flow of magnetohydrodynamic Sutterby fluid over radiating linearly stretched surface in view of Cash and Crap method. Appl. Math. Mech. Engl. Ed. 2019, 40, 861–876. [Google Scholar] [CrossRef]
- Prandtl, L. Über Flussigkeitsbewegungen bei sehr kleiner Reibung. Verhandl. III Intern. Math. 1904, 484–491. Available online: https://ci.nii.ac.jp/naid/20000989592/ (accessed on 20 July 2020).
- Schwarz, F. Symmetries of differential equations: From Sophus Lie to computer algebra. SIAM Rev. 1988, 30, 450–481. [Google Scholar] [CrossRef]
- Pakdemirli, M.; Yurusoy, M. Similarity transformations for partial differential equations. SIAM Rev. 1998, 40, 96–101. [Google Scholar] [CrossRef]
- Naganthran, K.; Basir, M.F.M.; Thumma, T.; Ige, E.O.; Nazar, R.; Tlili, I. Scaling group analysis of bioconvective micropolar fluid flow and heat transfer in a porous medium. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Hamad, M.A.A.; Pop, I. Scaling transformations for boundary layer flow near the stagnation-point on a heated permeable stretching surface in a porous medium saturated with a nanofluid and heat generation/absorption effects. Transp. Porous Media 2011, 87, 25–39. [Google Scholar] [CrossRef]
- Azhar, E.; Iqbal, Z.; Maraj, E.N. Impact of entropy generation on stagnation-point flow of Sutterby nanofluid: A numerical analysis. Z. Naturforsch. 2016, 71, 837–848. [Google Scholar] [CrossRef]
- Azhar, E.; Iqbal, Z.; Ijaz, S.; Maraj, E.N. Numerical approach for stagnation point flow of Sutterby fluid impinging to Cattaneo-Christov heat flux model. Pramana J. Phys. 2018, 91, 61. [Google Scholar] [CrossRef]
- Naganthran, K.; Basir, M.F.M.; Kasihmuddin, M.S.M.; Ahmed, S.E.; Olumide, F.B.; Nazar, R. Exploration of dilatant nanofluid effects conveying microorganism utilizing scaling group analysis: FDM Blottner. Physica A 2020, 549, 124040. [Google Scholar] [CrossRef]
- Brinkman, H. The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 1952, 20, 571. [Google Scholar] [CrossRef]
- Hewitt, G.F.; Shires, G.L.; Bott, T.R. Process Heat Transfer; CRC Press: Boca Raton, FL, USA, 1994; p. 987. [Google Scholar]
- Merkin, J.H. Mixed convection boundary layer flow on a vertical surface in a saturated porous medium. J. Eng. Math. 1980, 14, 301–313. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1985, 20, 171–179. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Layek, G.C. Effects of suction/blowing on steady boundary layer stagnation-point flow and heat transfer towards a shrinking sheet with thermal radiation. Int. J. Heat Mass Tranf. 2011, 54, 302–307. [Google Scholar] [CrossRef]
- Tie-Gang, F.; Ji, Z.; Shan-Shan, Y. Viscous flow over an unsteady shrinking sheet with mass transfer. Chin. Phys. Lett. 2009, 26, 014703. [Google Scholar] [CrossRef]

| Physical Properties | Fluid Phase (n-Hexane /CH3(CH2)4CH3) | Solid Phase Magnetite (Fe3O4) |
|---|---|---|
| 2.78 | 670 | |
| 551 | 5180 | |
| 82 | 9.7 | |
| Pr | 4.36 |
| Present Result | Bhattacharyya et al. [41] | |||
|---|---|---|---|---|
| First Solution | Second Solution | First Solution | Second Solution | |
| 1.40224078 | ||||
| 1.49566974 | ||||
| 1.50715589 | ||||
| 1.48929822 | ||||
| 1.32881685 | 0 | |||
| 1.08223113 | 0.11670214 | |||
| Radiation Parameter (Rd) | ||||||
|---|---|---|---|---|---|---|
| First Solution | Second Solution | |||||
| −1.5 | 0.5 | −1846.311663 | −1846.31001 | |||
| −3.5 | −1845.804534 | −1845.803095 | ||||
| −5.5 | −1845.296838 | −1845.296378 | ||||
| −6.5 | −1845.042742 | −1845.042486 | ||||
| −1.5 | 1.2 | −1846.051576 | −1846.046864 | |||
| −3.5 | −1845.195172 | −1845.191067 | ||||
| −5.5 | −1844.337149 | −1844.335834 | ||||
| −6.5 | −1843.907426 | −1843.906694 | ||||
| −1.5 | 3.5 | −1845.128211 | −1845.099751 | |||
| −3.5 | −1844.064298 | −1844.051593 | ||||
| −5.5 | −1842.553219 | −1842.549137 | ||||
| −6.5 | −1841.795465 | −1841.793188 | ||||
| ε | γ1 | |
|---|---|---|
| First Solution | Second Solution | |
| −6.8 | 0.5844 | −0.4163 |
| −6.82 | 0.2842 | −0.1794 |
| −6.822 | 0.2339 | −0.1354 |
| −6.8250 | 0.1128 | −0.0237 |
| −6.82520 | 0.0961 | −0.0077 |
| −6.825250 | 0.0911 | −0.0028 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fayyadh, M.M.; Naganthran, K.; Basir, M.F.M.; Hashim, I.; Roslan, R. Radiative MHD Sutterby Nanofluid Flow Past a Moving Sheet: Scaling Group Analysis. Mathematics 2020, 8, 1430. https://doi.org/10.3390/math8091430
Fayyadh MM, Naganthran K, Basir MFM, Hashim I, Roslan R. Radiative MHD Sutterby Nanofluid Flow Past a Moving Sheet: Scaling Group Analysis. Mathematics. 2020; 8(9):1430. https://doi.org/10.3390/math8091430
Chicago/Turabian StyleFayyadh, Mohammed M., Kohilavani Naganthran, Md Faisal Md Basir, Ishak Hashim, and Rozaini Roslan. 2020. "Radiative MHD Sutterby Nanofluid Flow Past a Moving Sheet: Scaling Group Analysis" Mathematics 8, no. 9: 1430. https://doi.org/10.3390/math8091430






