Optimal Control of Dengue Transmission with Vaccination
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Model
2.2. The Equilibrium Points
2.3. The Basic Reproductive Number
2.4. Local Stability of Equilibrium Points
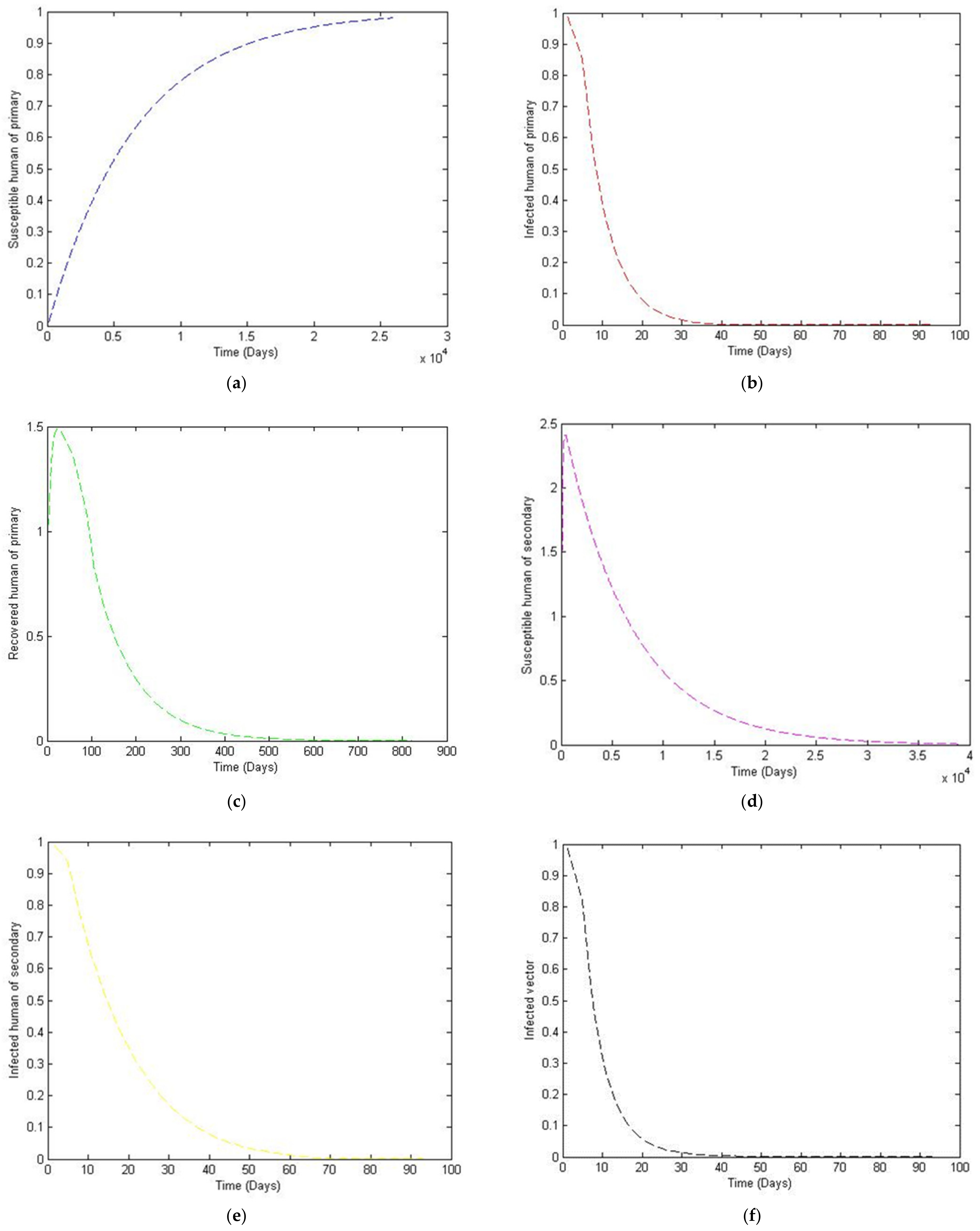
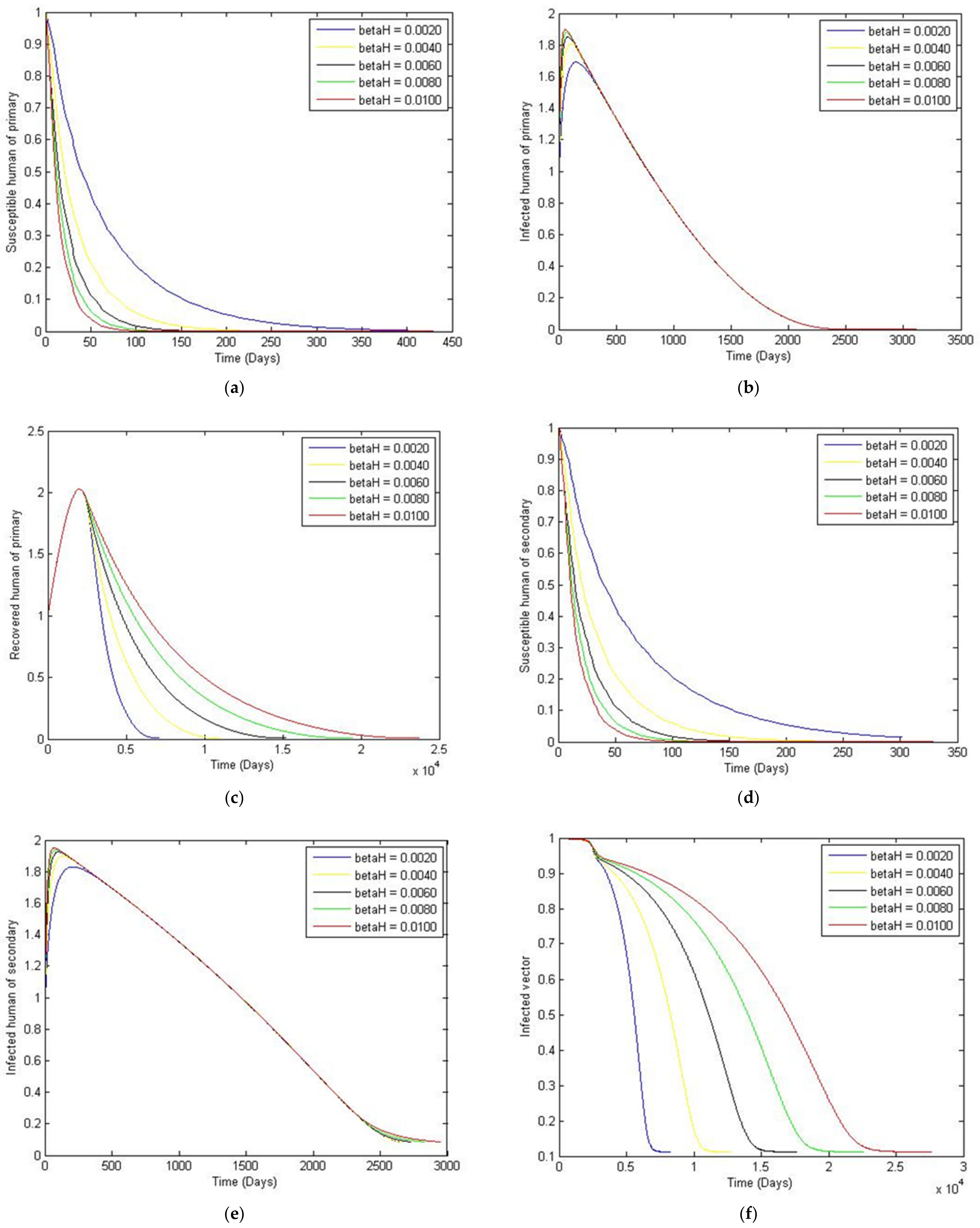
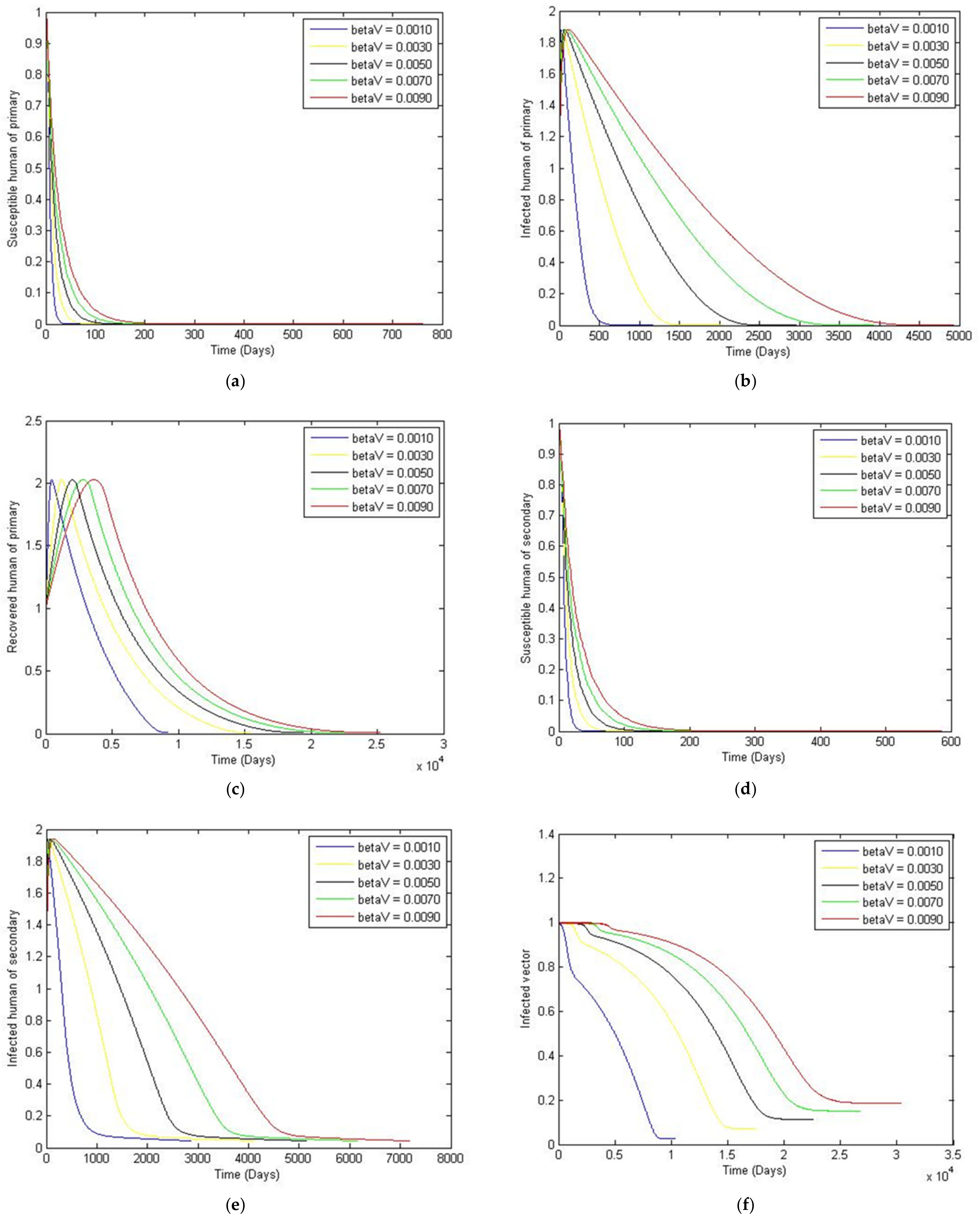
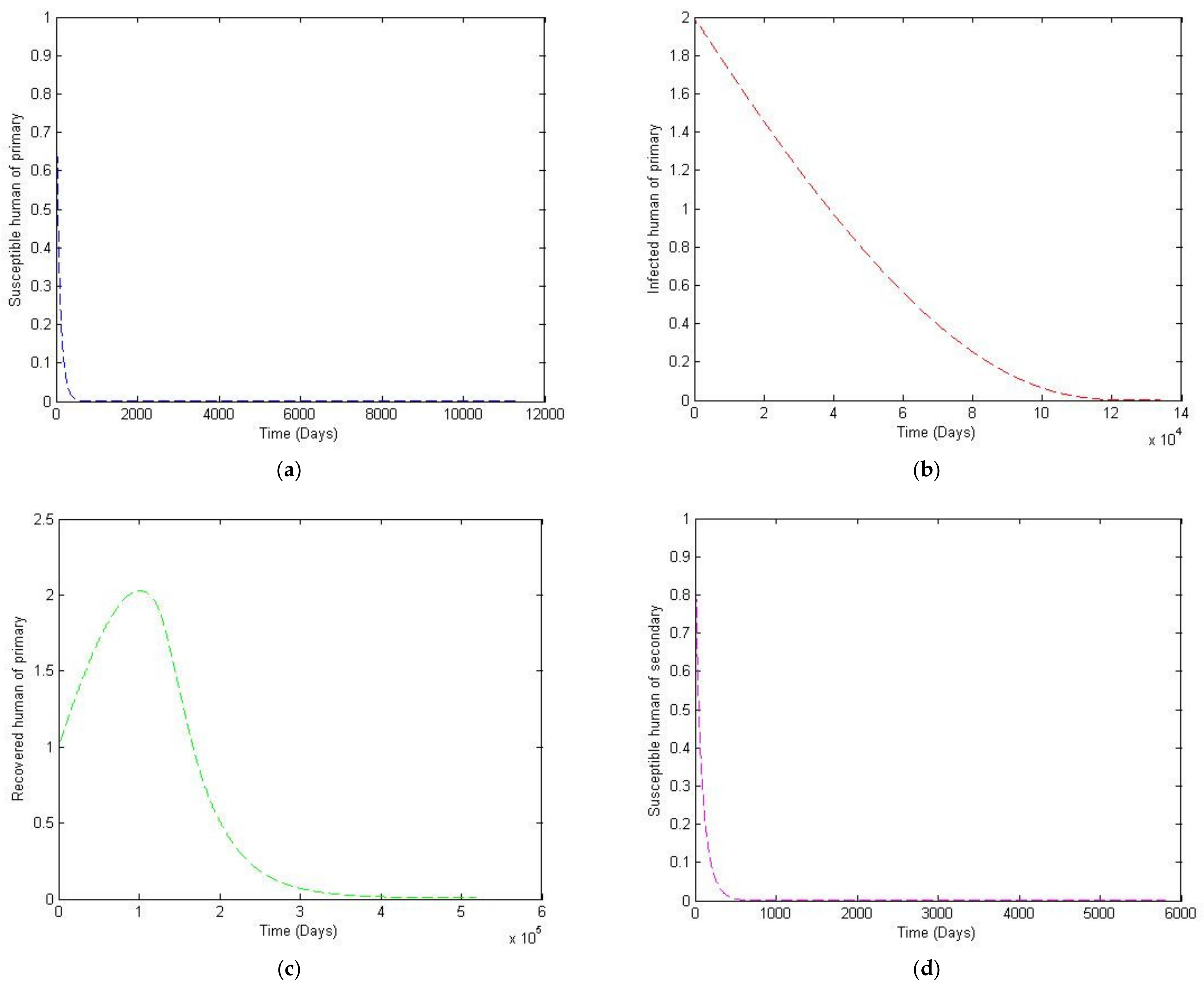
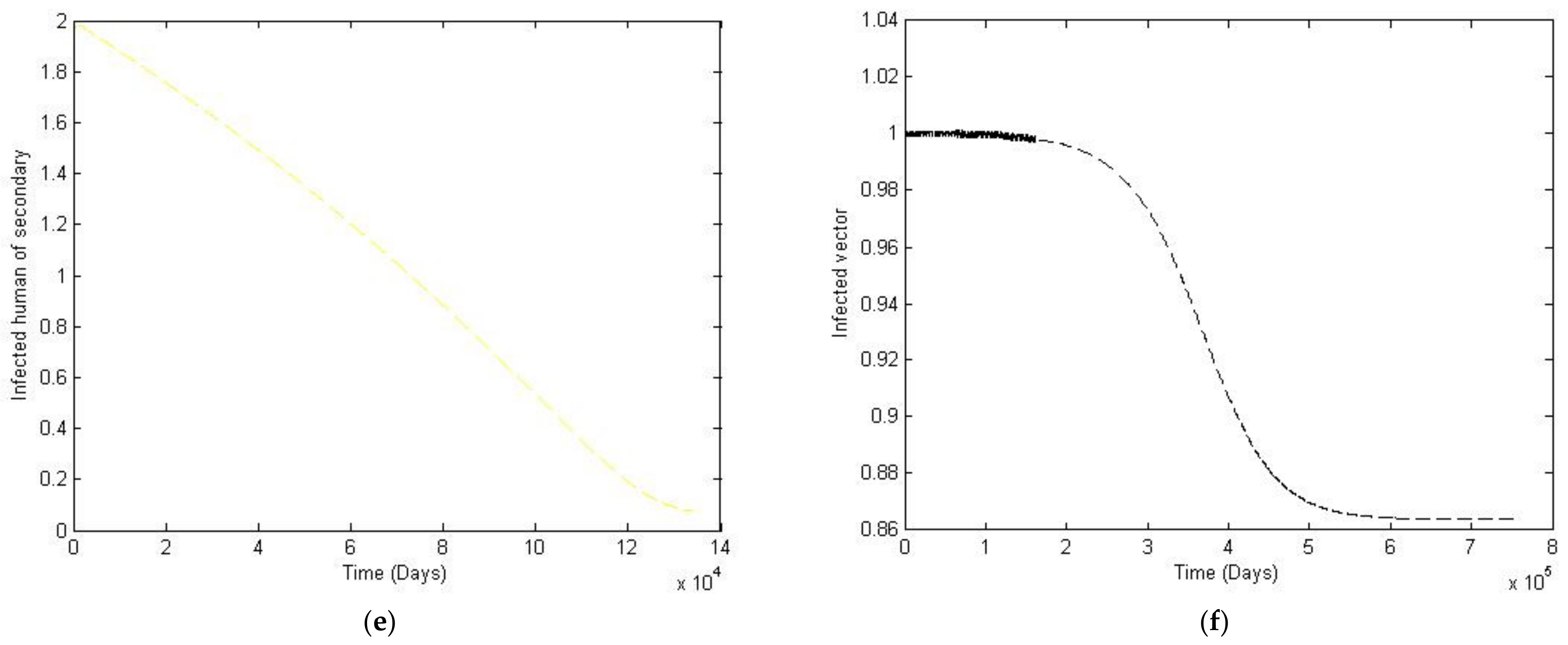
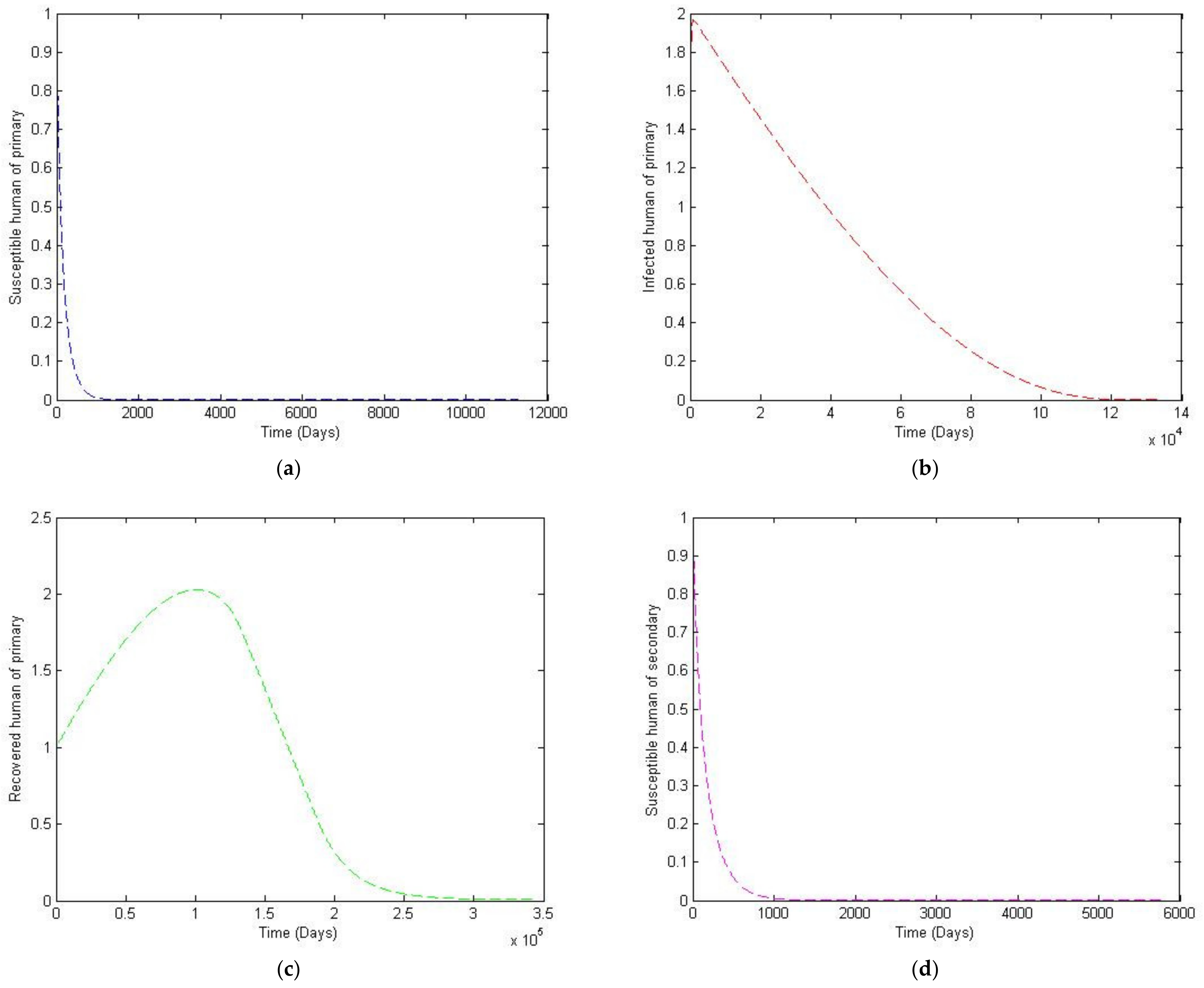
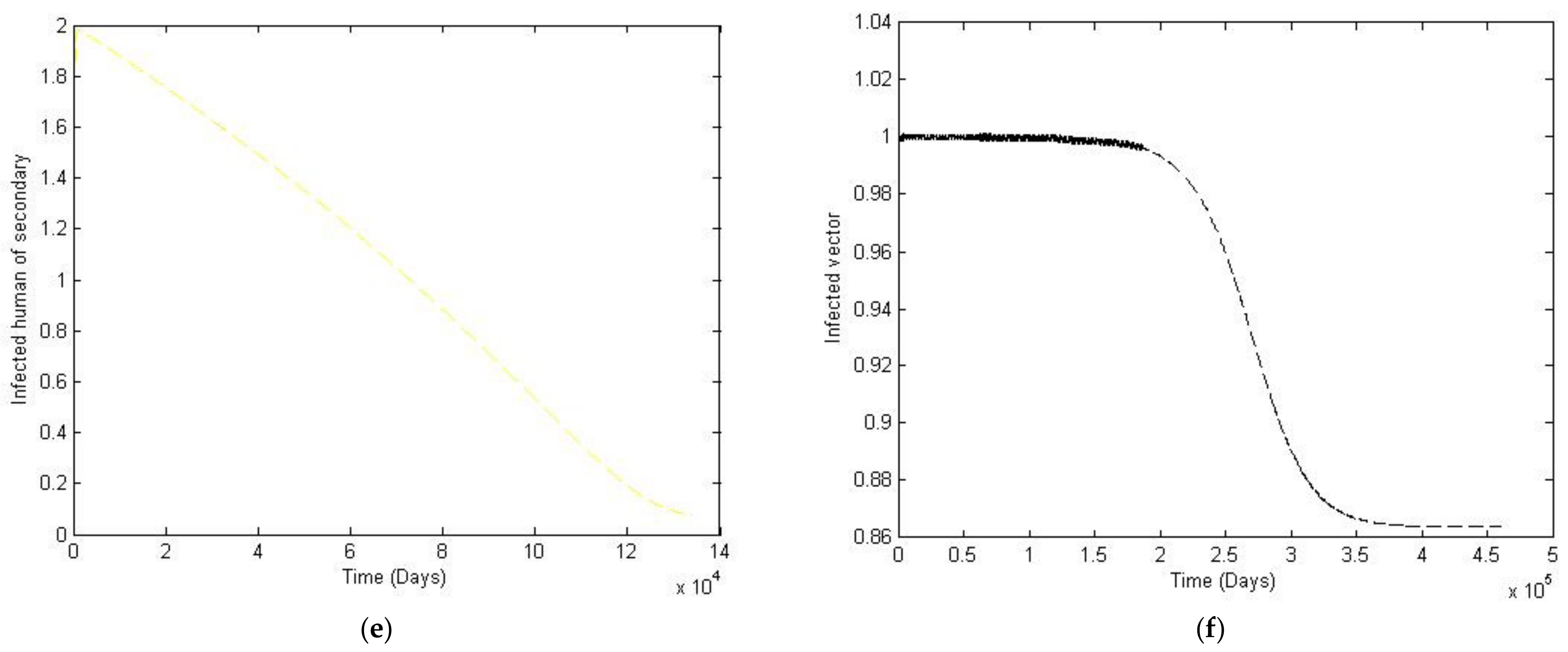
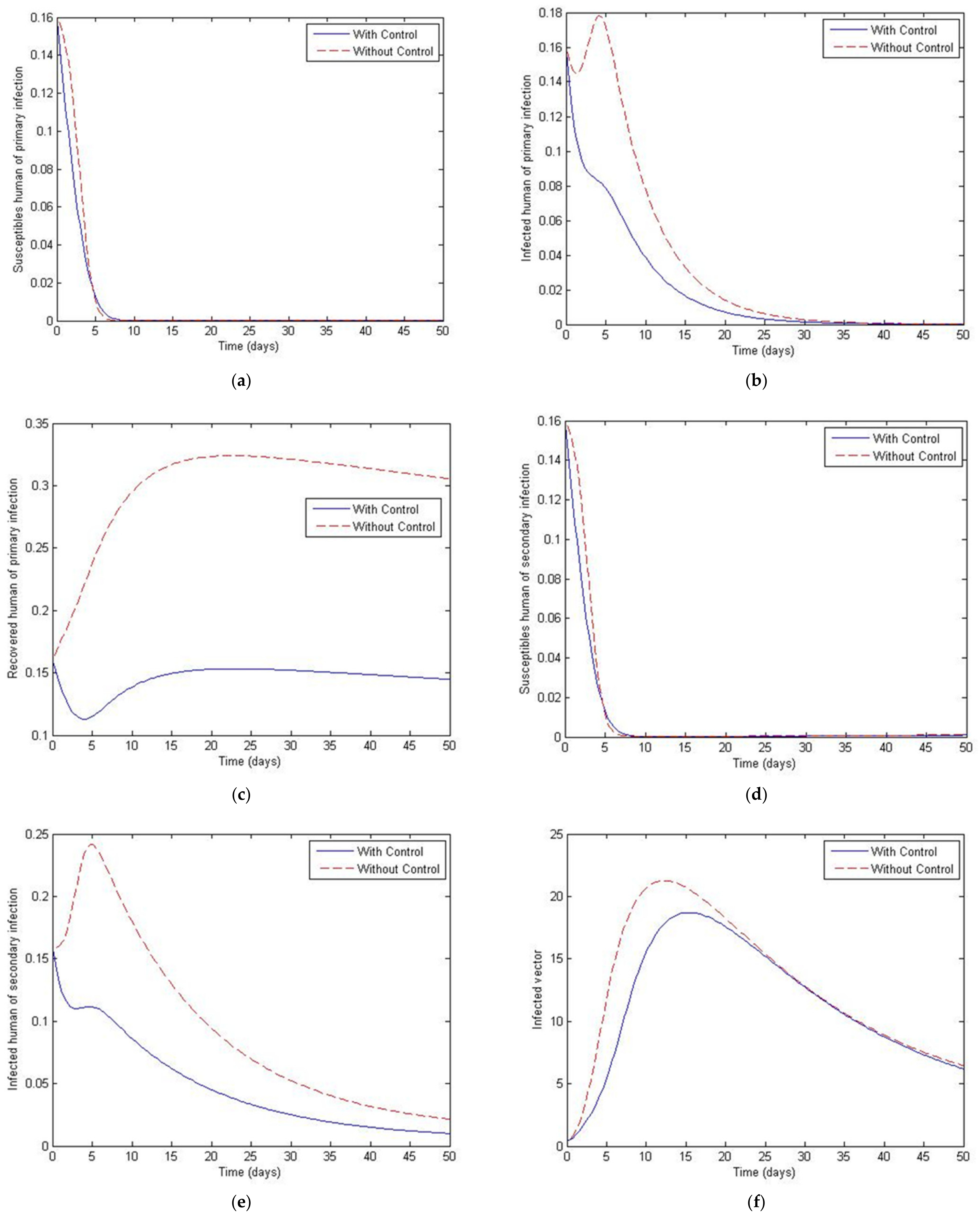
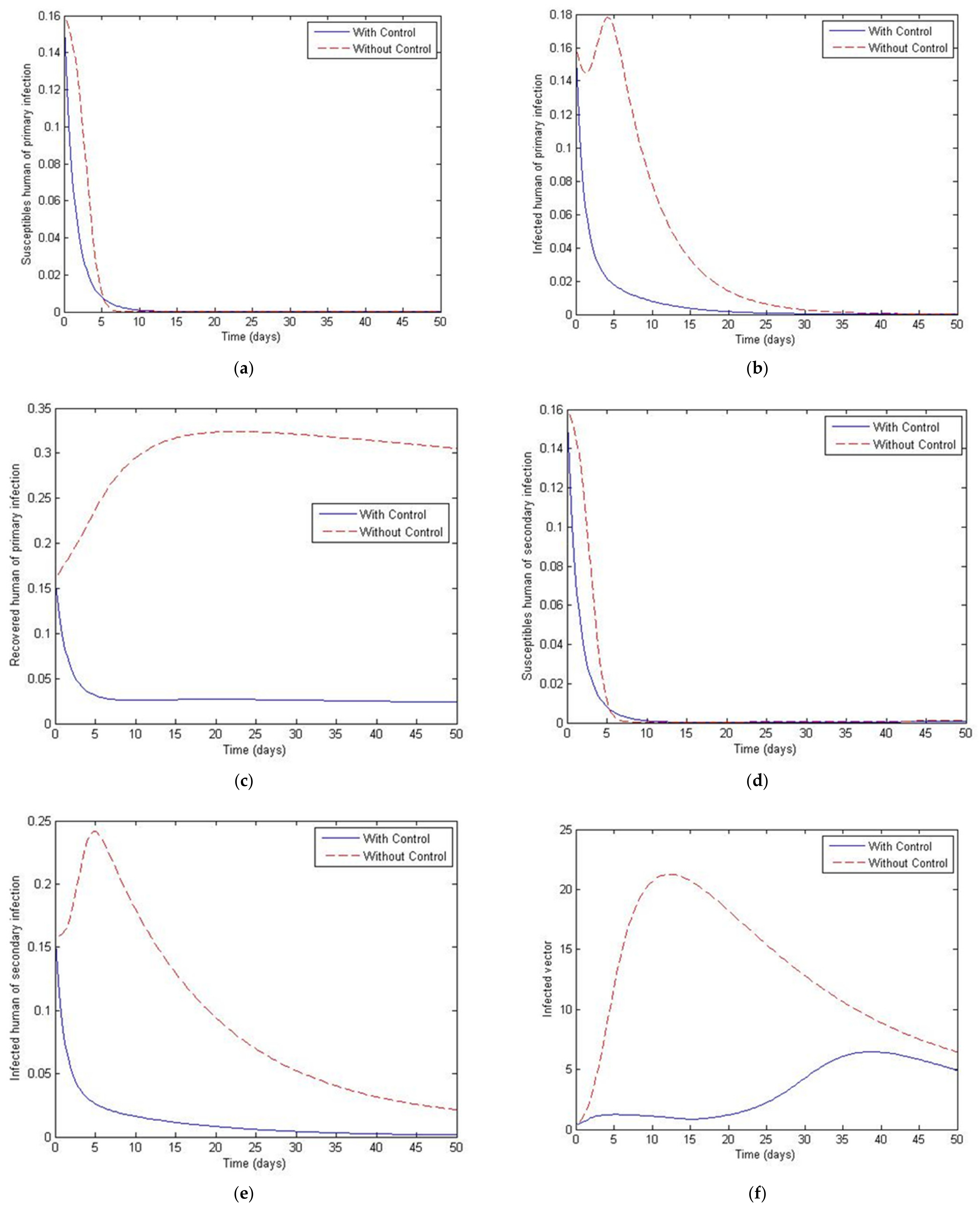
3. Numerical Simulation
- Case 1: the number humans and the number of vectors , while for
- Case 2: the number of humans and the number of vectors to investigate their implications.
Sensitivity Analysis of Parameters
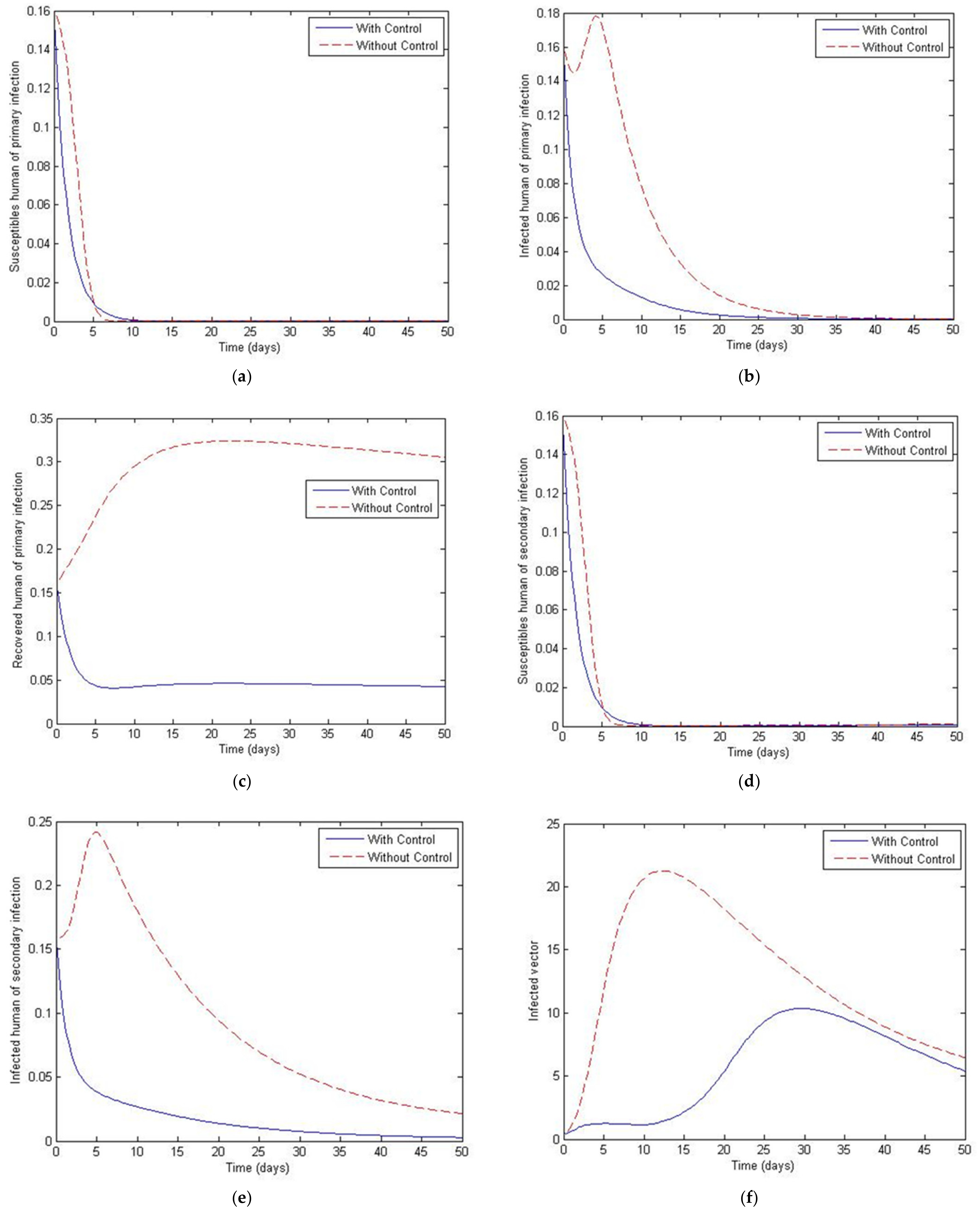
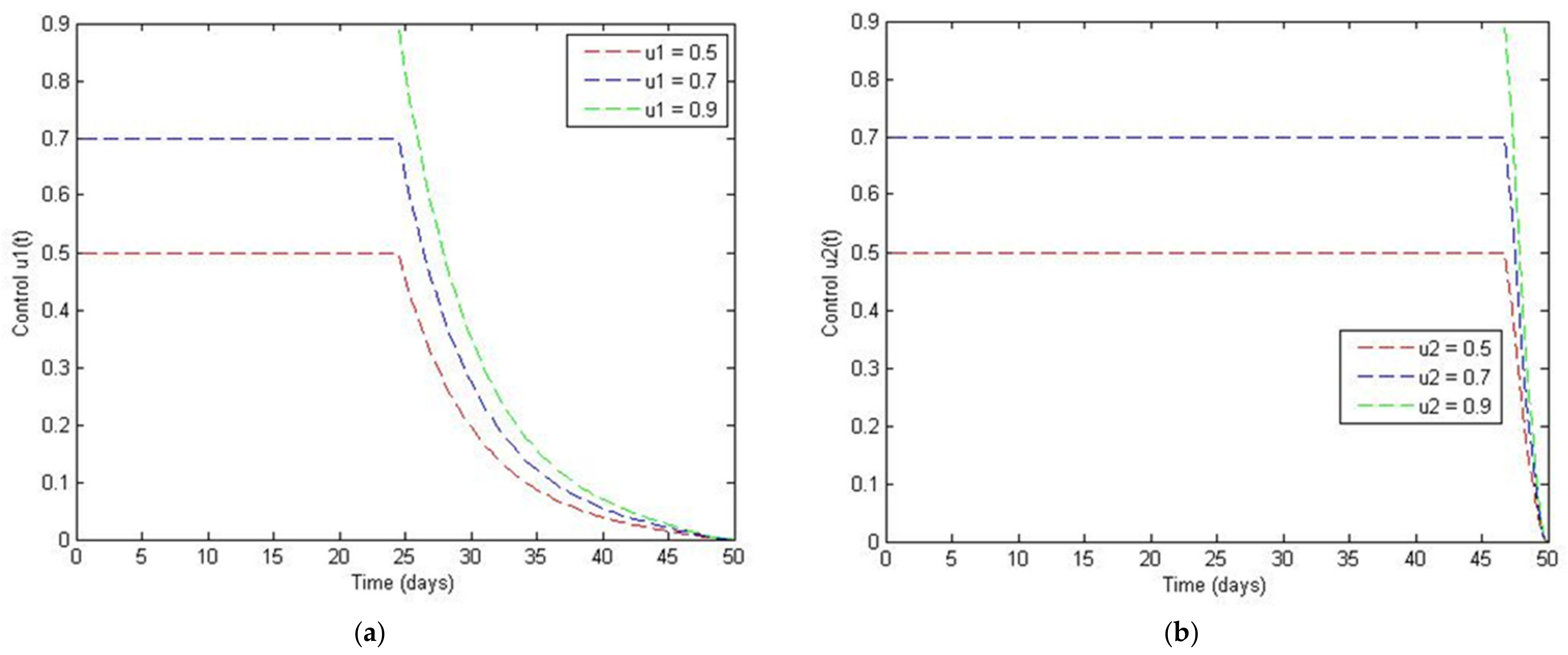
4. The Optimal Control Problem
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- World Health Organization. Dengue and Severe Dengue. Available online: https://www.who.int/news-room/fact-sheets/detail/dengue-and-severe-dengue (accessed on 5 January 2021).
- Aguas, R.; Dorigatti, I.; Coudeville, L.; Luxembrurger, C.; Ferguson, N.M. Cross-serotype interactions and disease outcome prediction of dengue infections in Vietnam. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef]
- Guzman, M.G.; Harris, E. Dengue. Lancet 2015, 385, 453–465. [Google Scholar] [CrossRef]
- Esteva, L.; Vargas, C. Coexistence of different serotypes of dengue virus. J. Math. Biol. 2003, 46, 31–47. [Google Scholar] [CrossRef] [PubMed]
- Gubler, D.J. Dengue and dengue hemorrhagic fever. Clin. Microbiol. Rev. 1998, 11, 480–496. [Google Scholar] [CrossRef] [Green Version]
- Chaturvedi, U.C.; Nagar, R. Dengue and dengue haemorrhagic fever: Indian perspective. J. Biosci. 2008, 33, 429–441. [Google Scholar] [CrossRef]
- Adams, B.; Holmes, E.C.; Zhang, C.; Mammen, M.P., Jr.; Nimmannitya, S.; Kalayanarooj, S.; Boots, M. Cross-protective immunity can account for the alternating epidemic pattern of dengue virus serotypes circulating in Bangkok. Proc. Natl. Acad. Sci. USA 2006, 103, 14234–14239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Capeding, M.R.; Tran, N.H.; Hadinegoro, S.R.S.; Ismail, H.I.H.M.; Chotpitayasunondh, T.; Chua, M.N.; Luong, C.Q.; Rusmil, K.; Wirawan, D.N.; Nallusamy, R.; et al. Clinical efficacy and safety of a novel tetravalent dengue vaccine in healthy children in Asia: A phase 3, randomised, observer-masked, placebo-controlled trial. Lancet 2014, 384, 1358–1365. [Google Scholar] [CrossRef]
- World Health Organization. Fact Sheet: Questions and Answers on Dengue Vaccines: Phase III Study of CYD-TDV. Available online: http://www.who.int/immunization/research/development/WHO_dengue_vaccine_QA_July2014.pdf (accessed on 5 January 2021).
- Villar, L.; Dayan, G.H.; Arredondo-Garcia, J.L.; Rivera, D.M.; Cunha, R.; Deseda, C.; Reynales, H.; Costa, M.S.; Morales-Ramirez, J.O.; Carrasquilla, G.; et al. Efficacy of a tetravalent dengue vaccine in children in Latin America. N. Engl. J. Med. 2015, 372, 113–123. [Google Scholar] [CrossRef]
- Biswal, S.; Reynales, H.; Saez-Llorens, X.; Lopez, P.; Borja-Tabora, C.; Kosalaraksa, P.; Sirivichayakul, C.; Watanaveeradej, V.; Rivera, L.; Espinoza, F.; et al. Efficacy of a tetravalent dengue vaccine in healthy children and adolescents. N. Engl. J. Med. 2019, 381, 2009–2019. [Google Scholar] [CrossRef]
- Sabchareon, A.; Wallace, D.; Sirivichayakul, C.; Limkittikul, K.; Chanthavanich, P.; Suvannadabba, S.; Jiwariyavej, V.; Dulyachai, W.; Pengsaa, K.; Wartel, T.A.; et al. Protective efficacy of the recombinant, live-attenuated, CYD tetravalent dengue vaccine in Thai schoolchildren: A randomised, controlled phase 2b trial. Lancet 2012, 380, 1559–1567. [Google Scholar] [CrossRef]
- World Health Organization. Updated Questions and Answers Related to the Dengue Vaccine Dengvaxia® and Its Use. Available online: https://www.who.int/immunization/diseases/dengue/q_and_a_dengue_vaccine_dengvaxia_use/en/ (accessed on 5 January 2021).
- Esteva, L.; Vargas, C. A model for dengue disease with variable human population. J. Math. Biol. 1999, 38, 220–240. [Google Scholar] [CrossRef]
- Pongsumpun, P.; Kongnuy, R.; Lopez, D.G.; Tang, I.M.; Dubois, M.A. Contact infection spread in an SEIR model: An analytical approach. Sci. Asia 2013, 39, 410–415. [Google Scholar] [CrossRef] [Green Version]
- Pongsumpun, P. The dynamical model of dengue vertical transmission. Curr. Appl. Sci. Technol. 2017, 17, 48–61. [Google Scholar]
- Chanprasopchai, P.; Tang, I.M.; Pongsumpun, P. The SEIR dynamical transmission model of dengue disease with and without the vertical transmission of the virus. Am. J. Appl. Sci. 2017, 14, 1123–1145. [Google Scholar] [CrossRef] [Green Version]
- Syafruddin, S.; Noorani, S.M. A SIR model for spread of dengue fever disease (simulation for south sulawesi Indonesia and selangor Malaysia). World J. Model. Simul. 2013, 9, 96–105. [Google Scholar]
- Yaacob, Y. Analysis of a dengue disease transmission model without immunity. MATEMATIKA Malays. J. Ind. Appl. Math. 2007, 23, 75–81. [Google Scholar]
- Singh, B.; Jain, S.; Khandelwal, R.; Porwal, S.; Ujjainkar, G. Analysis of a dengue disease transmission model with vaccination. Adv. Appl. Sci. Res. 2014, 5, 237–242. [Google Scholar]
- Tasman, H.; Supriatna, A.K.; Nuraini, N.; Soewono, E. A dengue vaccination model for immigrants in a two-age-class population. Int. J. Math. Math. Sci. 2012, 2012, 236352. [Google Scholar] [CrossRef] [Green Version]
- Aguiar, M.; Stollenwerk, N.; Halstead, S.B. The impact of the newly licensed dengue vaccine in endemic countries. PLoS Negl Trop Dis. 2016, 10, e0005179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aguiar, M.; Stollenwerk, N. Mathematical models of dengue fever epidemiology: Multi-strain dynamics, immunological aspects associated to disease severity and vaccines. Commun. Biomath. Sci. 2017, 1, 1–12. [Google Scholar] [CrossRef]
- Viriyapong, R.; Tavaen, S. Global stability and optimal control of melioidosis transmission model with hygiene care and treatment. NU. Int. J. Sci. 2019, 16, 31–48. [Google Scholar]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F.M. Dynamics of dengue epidemics when using optimal control. Math. Comput. Model. 2010, 52, 1667–1673. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F.M. Vaccination models and optimal control strategies to dengue. Math. Biosci. 2014, 247, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agustoa, A.B.; Khan, M.A. Optimal control strategies for dengue transmission in Pakistan. Math. Biosci. 2018, 305, 102–121. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Mage, A.R.; Messakh, J.J.; Djahi, B.S. Optimal vaccination strategy for dengue transmission in Kupang city, Indonesia. Heliyon 2020, 6, e05345. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Public Health Thailand. Dengue Fever. Available online: http://www.boe.moph.go.th/boedb/surdata/disease.php?dcontent=old&ds=66 (accessed on 5 January 2021).
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.Q.; Wong, P.J.Y. Dengue transmission: Mathematical model with discrete time delays and estimation of the reproduction number. J. Biol. Dyn. 2019, 13, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Prathumwan, D.; Trachoo, K.; Chaiya, I. Mathematical modeling for prediction dynamics of the coronavirus disease 2019 (COVID-19) pandemic, quarantine control measures. Symmetry 2020, 12, 1404. [Google Scholar] [CrossRef]
- NewsDesk. Thailand Reports 71,000 Dengue Cases in 2020. Available online: outbreaknewstoday.com/thailand-reports-71000-dengue-cases-in-2020/ (accessed on 16 July 2021).
- Chitnis, N.; Hyman, J.M.; Cushing, J.M. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar] [CrossRef]
- Lukes, D.L. Differential Equations: Classical to Controlled; Academic Press: London, UK; New York, NY, USA, 1982. [Google Scholar]
- Chanprasopchai, P.; Tang, I.M.; Pongsumpun, P. SIR model for dengue disease with effect of dengue vaccination. Comput. Math. Methods Med. 2018, 2018, 9861572. [Google Scholar] [CrossRef]
- Xue, L.; Ren, X.; Magpantay, F.; Sun, W.; Zhu, H. Optimal control of mitigation strategies for dengue virus transmission. Bull. Math. Biol. 2021, 83, 1–28. [Google Scholar] [CrossRef] [PubMed]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman and Hall/CRC: Boca Raton, FL, USA; New York, NY, USA, 2007. [Google Scholar]









| Variables | Definition |
|---|---|
| The number of humans susceptible to primary infection | |
| The number of humans with a primary infection | |
| The number of humans who have recovered from a primary infection | |
| The number of humans susceptible to secondary infection | |
| The number of humans with a secondary infection | |
| The number of humans who have recovered from a secondary infection | |
| The number of susceptible vectors | |
| The number of infected vectors |
| Parameters | Definition |
|---|---|
| The biting rate of the vector population | |
| The vaccine efficiency | |
| The recurrent infection rate | |
| The total number of humans in the study population | |
| The total number of vectors in the study population | |
| The transmission rate of dengue virus from vector to human | |
| The transmission rate of dengue virus from human to vector | |
| The birth and natural mortality rate of the human population | |
| The natural mortality rate of the vector population | |
| The mortality rate from infection of the human population | |
| The mortality rate from infection of the vector population | |
| The recovery rate of those with a primary infection | |
| The recovery rate of those with a secondary infection |
| Parameters | Disease-Free | Endemic | References |
|---|---|---|---|
| 1/7 | 1/7 | [1,9], [15,16,17], [29,33] | |
| 1/2 | 1/2 | [1,9], [15,16,17], [29,33] | |
| 1/(30 × 6) | 1/(30 × 6) | [1,2,3,4] | |
| 10.000 | 10.000 | assumed | |
| 10.000 | 10.000 | assumed | |
| 0.0000080 | 0.0050 | assumed | |
| 0.0000065 | 0.0030 | assumed | |
| 1/(365 × 70) | 1/(365 × 70) | [1,9], [15,16,17], [29,33] | |
| 1/14 | 1/14 | [1,9], [15,16,17], [29,33] | |
| 1/180 | 1/180 | assumed | |
| 1/14 | 1/14 | assumed | |
| 1/10 | 1/10 | [1,9], [15,16,17], [29,33] | |
| 1/14 | 1/14 | [1,9], [15,16,17], [29,33] |
| Parameters | Sensitivity |
|---|---|
| 0.5 | |
| 0.5 | |
| 0.5 | |
| 0.5 | |
| 0.5 | |
| −0.0001141 | |
| −0.1666667 | |
| −0.20825858 | |
| −0.3333333 | |
| −0.2916001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chamnan, A.; Pongsumpun, P.; Tang, I.-M.; Wongvanich, N. Optimal Control of Dengue Transmission with Vaccination. Mathematics 2021, 9, 1833. https://doi.org/10.3390/math9151833
Chamnan A, Pongsumpun P, Tang I-M, Wongvanich N. Optimal Control of Dengue Transmission with Vaccination. Mathematics. 2021; 9(15):1833. https://doi.org/10.3390/math9151833
Chicago/Turabian StyleChamnan, Anusit, Puntani Pongsumpun, I-Ming Tang, and Napasool Wongvanich. 2021. "Optimal Control of Dengue Transmission with Vaccination" Mathematics 9, no. 15: 1833. https://doi.org/10.3390/math9151833






